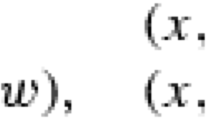On the moduli space of equilateral plane pentagons

Abstract

We give two new proofs of the well-known result that the moduli space $M_5$ of equilateral plane pentagons is a closed surface of genus four. Moreover, we construct a new algebraic description of this space, also in the non-equilateral case, as a real affine algebraic surface F defined by a polynomial p(x, y, z) of degree 12. This allows a visualization using the Surfer software.

1 Introduction

The moduli space of equilateral pentagons has been known to be homeomorphic to a surface of genus four by a series of works. The study probably goes back to a bachelor thesis of Walker (1985) at Princeton. Hausman (1989) article implicitly contains the claim. Then, the articles by Havel (1991), Kamiyama (1996), Kapovich and Millson (1995) and a Ph.D thesis by Jaggi (1992) present its proofs from several viewpoints. These articles are discussing the problem in more general setting, say, for equilateral polygons in general, or for polygons with prescribed edge lengths.

On the other hand, the moduli space of convex equilateral pentagons can be identified with that of equiangular pentagons by the Schwarz–Christoffel mapping. This fact is implicitly explained in Kojima et al. (1999) that geometrizes the moduli space in question by hyperbolic geometry. In addition, Bavard and Ghys (1992) and Morin and Nishi (2000) have developed the study of this moduli space furthermore. Their studies have several similarities with the study for pentagons with prescribed edge lengths. Note also that Kojima and Yamashita (1993) discusses the moduli space with combined case under the restriction that the convex pentagon extends to a star shaped pentagon.

The purpose of this paper is to add more computational aspect to the study of the moduli space of equilateral pentagons and its friends. We provide two hopefully new simple topological proofs for the moduli space in question to be actually a surface of genus four. Then, we find a purely algebraic description of the moduli space explicitly as a real algebraic variety of degree 12 in the Euclidean space of dimension 3 and visualize it with the aid of computer graphics. Furthermore, we extend our visualization to the moduli space of pentagons with not necessary equiangular but prescribed edge lengths.

The pictures of moduli spaces in this paper are produced using the free Surfer software (Website of the Surfer software: http://www.imaginary.org/program/surfer) of Oberwolfach. The first author has given a talk on these and other constructions using the Surfer software at a 2015 conference in honor of Gert-Martin Greuel (Klaus 2017).

2 The moduli space $M_n$ of equilateral plane n-gons

An equilateral plane n-gon (short: n-gon) consists of n points $(p_1, p_2, \ldots , p_n)$ (including the order) in the complex plane, such that the distances of two consecutive points (consecutive in cyclic order) are all non-zero and equal. If the n points are not all pairwise different, the n-gon is called degenerate. Hence the set of n-gons is a subset of $\mathbb {C}^n$ and we can give it the subspace topology. Two such n-gons $(p_k)$ and $(p'_k)$ are similar if there is an affine linear automorphism $z\mapsto az+b$ of $\mathbb {C}$ which maps $p_k$ to $p'_k$ for all k. Let $M_n$ be the set of similarity classes of all n-gons with the quotient topology with respect to the group action of all affine linear automorphism. We call $M_n$ the moduli space of (equilateral plane) n-gons.

By the affine linear automorphism $z\mapsto (p_1-p_n)^{-1}(z-p_n)$, every n-gon is equivalent to exactly one n-gon with $p_1=1$ and $p_n=0$. If we set $z_k:=p_{k+1}-p_{k} \in \mathbb {C}$ for $k<n$, this shows that $M_n$ is given in $\mathbb {C}^{n-1}$ as the set of solutions of

$$\begin{aligned}&|z_k| = 1 \quad \text{ for } \text{ all } \quad k=1,2,\ldots ,n-1 \end{aligned}$$

(1)

$$\begin{aligned}&z_1+z_2+\cdots +z_{n-1}+1 = 0. \end{aligned}$$

(2)

The following result is well-known (see Kapovich and Millson 1995, for example). For the convenience of the reader, we recall the standard proof.

Theorem 2.1

$M_n$ is a compact real affine variety of dimension $n-3$ in $\mathbb {R}^{2n-2}$ which is connected for $n>3$. For n odd, $M_n$ is a closed smooth $(n-3)$-dimensional manifold. Moreover, the tangent bundle of $M_n$ is stably trivial, in particular $M_n$ is orientable. For n even, $M_n$ has singularities and hence is not smooth.

Proof

Obviously, Eqs. (1) and (2) define a real affine variety of dimension $n-3$. Let $S^1 := \{z\in \mathbb {C}|\,|z|=1\} = \{(x,y)\in \mathbb {R}^2|\, x^2+y^2=1\}$ be the unit sphere, then $M_n = (S^1)^{n-1} \cap H$ in $\mathbb {C}^{n-1}=\mathbb {R}^{2n-2}$. Here, H is the affine hyperplane in $\mathbb {C}^{n-1}$ given by

$$\begin{aligned} h(z_1,\ldots ,z_{n-1}) := z_1+z_2+\cdots +z_{n-1}+1 = 0. \end{aligned}$$

As the torus $(S^1)^{n-1}$ is compact, this follows also for $M_n$.

As $M_3$ consists of two points represented by the two triangles

$$\begin{aligned} \left( 0,1,\frac{1}{2}(1\pm i\sqrt{2})\right) , \end{aligned}$$

it is not connected, $|\pi _0(M_3)|=2$. For $n>3$, it is possible to ‘fold’ the last two non-fixed points $p_{n-1}$ and $p_{n-2}$ such that $p_{n-2}=p_n=0$. Then the remaining part of the configuration $(p_1, p_2, \ldots , p_{n-2})$ forms an $(n-2)$-gon. For the set of components, this shows that $|\pi _0(M_n)| \le |\pi _0(M_{n-2}|$. Note that $|\pi _0(M_2)|=|\pi _0(M_5)|=1$. It follows that $|\pi _0(M_n)|=1$ for all $n>3$.

Now we show for n odd that 0 is a regular value of $h:(S^1)^{n-1}\rightarrow \mathbb {C}$ and hence $M_n$ is a smooth manifold (Milnor 1997). The differential of h at a point $(z_1=e^{it_1},\ldots ,z_{n-1}=e^{it_{n-1}})$ is given by

$$\begin{aligned} dh(z_1,\ldots ,z_{n-1}) = iz_1dt_1+\cdots +iz_{n-1}dt_{n-1}. \end{aligned}$$

As the $z_k$ are non-zero, it holds $1\le rk(dh)\le 2$ for the rank of the differential, where $rk(dh)=1$ if and only if the $z_k$ are linear dependent over $\mathbb {R}$. This is the case if and only if $z_k=\lambda _k z_1$ with $\lambda _k=\pm 1$ for all $k>1$. With Eq. (2) this yields $z_1(1+\lambda _2+\cdots +\lambda _{n-1})+1=0$, hence $z_1=\pm 1$ and $1+\lambda _2+\cdots +\lambda _{n-1} = -z_1 = \mp 1$. As $1+\lambda _2+\cdots +\lambda _{n-1} \equiv n-1$ mod 2, the last equation has no solution $\lambda _2,\ldots ,\lambda _{n-1}$ for n odd. Thus for n odd, there are no singular points in $h^{-1}(0)$, i.e. 0 is a regular value of h and $M_n$ is a smooth submanifold of $(S^1)^{n-1}$ of codimension 2. Because of

$$\begin{aligned} TM_n \oplus \nu = T(S^1)^{n-1} = (S^1)^{n-1}\times \mathbb {R}^{n-1} \end{aligned}$$

with trivial normal bundle $\nu =h^*(\{0\}\times \mathbb {R}^2)$, the tangent bundle $TM_n$ is stably trivial.

For n even, the above argument shows that the singular points of h are given by $z_k=\pm 1$ with $z_1+z_2+\cdots +z_{n-1}+1 = 0$, which form in particular a non-empty set. $\square$

Geometrically, it is straightforward to see that $M_4$ is the union of three copies of $S^1$ given by $(1,1+z,z,0)$, $(1,1+z,1,0)$ and (1, 0, z, 0) (where $z\in S^1$), with intersections given by the degenerate 4-gons (1, 0, 1, 0), (1, 2, 1, 0) and $(1,0,-1,0)$. Hence $M_4$ is a CW complex which is homotopy equivalent to the wedge of four 1-spheres. In particular, $M_4$ is not a 1-manifold, but has three singular points.

We will study the closed 2-manifold $M_5$ in the next two section.

3 The moduli space of pentagons

Now we give two hopefully new proofs of the following well-known theorem. Our proofs work with an explicit cellular structure of the configuration space.

Theorem 3.1

$M_5$ is a closed oriented surface of genus 4.

First proof: As we already know that

$$\begin{aligned} M_5 = \{(1=p_1,p_2,p_3,p_4,p_5=0)\} \end{aligned}$$

is a connected closed oriented 2-manifold, it is enough to compute the Euler characteristics and we perform this by constructing a cell decomposition for $M_5$.

Because of the triangle inequality, it holds $p_3\in C$ where C is the intersection of two closed discs of radius 2 with centres $p_1=1$ and $p_5=0$.

Note that C has a canonical cell decomposition into the interior which is one open 2-cell $\breve{C}$, and the boundary, which consists of two 1-cells $\partial ^\pm C$ and two 0-cells $P^\pm :=\frac{1}{2}(1\pm i\sqrt{15})$, which form the intersection of the two spheres of radius 2 with centres $P_1=1$ and $p_5=0$.

If $p_3\ne p_1$ then there are exactly 2 different positions for $p_2$ if $|p_3-p_1|<2$ and exactly one position given by $p_2=\frac{1}{2}(p_1+p_3)$ if $|p_3-p_1|=2$. The analogous statement concerning $p_4$ is true for $p_3\ne p_5$. If $p_3$ is in the degenerate position $p_3 = p_1$, then there are infinitely many positions for $p_2$ given by the circle of radius 1 around $p_3 = p_1 = 1$. The analogous statement concerning $p_4$ is true for $p_3 = p_5$.

This shows that the forgetful map $M_5 \rightarrow C$ given by $(p_2,p_3,p_4)\mapsto p_3$ is on the image points

• $(1\times 1):1$ (i.e., bijective) on $P^\pm$,

• $(2\times 1):1$ respectively $(1\times 2):1$ on $\partial ^\pm C$,

• $(2\times 2):1$ on $\breve{C}-\{0,1\}$,

• $(\infty \times 2):1$ on 1 and $(2\times \infty ):1$ on 0, where $\infty$ stands for a set which is equivalent to $S^1$.

Hence, if we neglect for a moment the degenerate points $p_1=1$ and $p_5=0$ in $\dot{C}$, the inverse image of the forgetful map consists of 4 2-cells, 4 1-cells and 2 0-cells. In total this gives $2-4+4=2$ for the Euler characteristics, hence a 2-sphere $S^2$. Now we consider the 2 degenerate positions for $p_3$. Each point in a small disc neighborhood around these positions has 4 inverse images, defining 8 disjoint small discs (without centers) on $S^2$. In each degenerate position for $p_3$, there are for $p_2$ respectively $p_4$ two continuous sets of loci (in fact, circles $S^1$), and two discrete loci for the other point. This yields a gluing of the 8 small discs in $S^2$ by 4 handles. Thus $M_5$ is a closed surface of genus 4. $\square$

Second proof: We introduce a redundant notation $z_5 = p_1 - p_5 = 1$ with $\arg z_5 = 2\pi$ for our convenience. Then the set of convex pentagons including degenerate case to convex quadrilaterals or triangles can be identified with

$$\begin{aligned} \Delta = \{ 0 \le \arg z_1 \le \arg z_2 \le \arg z_3 \le \arg z_4 \le \arg z_5 = 2\pi \}. \end{aligned}$$

This is a pentagon-like space bounded by five curvelinear edges $\{ \arg z_i = \arg z_{i+1} \} \cap \Delta \; (i = 1, 2, \ldots , 5)$ with vertices consisting of five degenerate triangles $\{ \arg z_i = \arg z_{i+1} \} \cap \{\arg z_{i+1} = \arg z_{i+2} \} \; (i = 1, 2, \ldots , 5)$, where indices run modulo 5.

On the other hand, for any equilateral pentagon represented by

$$\begin{aligned} (z_1, z_2, z_3, z_4, z_5), \end{aligned}$$

there is at least one (and at most four) permutation $\sigma$ in the symmetric group $\mathfrak {S}_4$ of degree 4 such that

$$\begin{aligned} 0 \le \arg z_{\sigma (1)} \le \arg z_{\sigma (2)} \le \arg z_{\sigma (3)} \le \arg z_{\sigma (4)} \le \arg z_5 = 2\pi \end{aligned}$$

holds. Thus if we let $\Delta _{\sigma }$ be the set of equilateral pentagons satisfying the inequalities above, then

$$\begin{aligned} M_5 = \bigcup _{\sigma \in \mathfrak {S}_4} \Delta _{\sigma }. \end{aligned}$$

Obviously, the interior of $\Delta _{\sigma }'s$ dose not intersect each other and this union gives a cellular decomposition of $M_5$ by twenty-four pentagons. Each edge meets exactly two pentagons since the equality in arguments breaks in two ways and each vertex is shared by four pentagons because each one of two equalities in arguments breaks in two ways independently. Thus the Euler characteristic is $30-60+24 = -6$, and $M_5$ has genus four. $\square$

4 Algebraic parametrization of $M_5$

In this section we construct a real algebraic description and visualization of $M_5$ as a surface in $\mathbb {R}^3$ which is given by a polynomial of degree 12.

With Eq. (2) we can eliminate the forth complex variable as

$$\begin{aligned} z_4 = -(z_1 + z_2 + z_3 +1) \end{aligned}$$

and then the four equations for $z_k=x_k+iy_k$ in (1) are given by $|z_1|^2 = |z_2|^2 = |z_3|^2 = 1$ and

$$\begin{aligned} (x_1+x_2+x_3+1)^2+(y_1+y_2+y_3)^2 = 1. \end{aligned}$$

(3)

In particular, $M_5$ is the sub-manifold of $(S^1)^3$ defined by Eq. (3).

Now we use the rational parametrization

$$\begin{aligned}&\phi : \mathbb {R}\rightarrow S^1,\\&\phi (t) := \left( \frac{t^2-1}{t^2+1}, \frac{2t}{t^2+1} \right) \end{aligned}$$

which is a diffeomorphism $\mathbb {R}\cong S^1-{1}$. For $t\mapsto \pm \infty$, it holds that $\phi (t)\mapsto 1$, hence $\phi$ gives a homeomorphism of the one-point compactification of $\mathbb {R}$ to $S^1$ where the point at infinity is mapped to 1.

Because of $M_5\subset (S^1)^3$ we introduce three real parameters $t_1$, $t_2$ and $t_3$ for the parametrization of the three torus variables in (3). This gives

$$\begin{aligned} \left( \frac{t_1^2-1}{t_1^2+1} + \frac{t_2^2-1}{t_2^2+1} + \frac{t_3^2-1}{t_3^2+1} + 1\right) ^2 + \left( \frac{2t_1}{t_1^2+1} + \frac{2t_2}{t_2^2+1} + \frac{2t_3}{t_3^2+1}\right) ^2 = 1. \end{aligned}$$

Nominators can be cleared by multiplication with $((t_1^2+1)(t_2^2+1)(t_3^2+1))^2$ which is non-zero for all $t_1,t_2,t_3$. In order to make the equation more readable, we rename the variables as $(t_1,t_2,t_3)=:(x,y,z)$. Then a short computation shows that Eq. (3) is equivalent to the following polynomial equation of order 12:

$$\begin{aligned}&4(2x^2y^2z^2 + x^2y^2 + x^2z^2 + y^2z^2 - 1)^2 +4(x(y^2+1)(z^2+1) \nonumber \\&\quad +\,\, (x^2+1)y(z^2+1) + (x^2+1)(y^2+1)z)^2 \nonumber \\&\quad -\,\, ((x^2+1)(y^2+1)(z^2+1))^2 = 0. \end{aligned}$$

(4)

The following picture of the set $F\subset \mathbb {R}^3$ of solutions of (4) was produced using the free Surfer software of Oberwolfach:

Note that the smooth surface F is non-compact because the rational parametrization $\phi$ of $S^1$ misses the point $1\in S^1$ which corresponds to the positive and negative end $\pm \infty$ in $\mathbb {R}$. As $\phi$ glues both ends together, it can be considered as the 1-periodic identification in $[-1,1]/(-1\sim 1) \cong S^1$. As we have used $\phi$ three times in the embedding $\mathbb {R}^3\rightarrow (S^1)^3$, $(x,y,z)\mapsto (\phi (x),\phi (y),\phi (z))$, we obtain the moduli space $M_5$ of pentagons by a 3-periodic compactification of F at infinity. As F has 6 tubes running to infinity, we obtain $M_5$ by glueing the antipodal ends of these tubes together which yields 3 compact handles. Together with the handle which is located in the centre of F, we see that $M_5$ is a closed connected surface formed by 4 handles. Thus the picture confirms the result that $M_5$ has genus 4.

5 Moduli spaces of non-equilateral pentagons

It is well-known that the moduli space of such pentagons with fixed edge lengths $d_1$, $d_2,\ldots , d_5$ can be singular. Singularities appear if and only if $\sum _{i=1}^5 \epsilon _i d_l =0$ for some choice of signs $\epsilon _i = \pm$. The proof of this statement can be given with a similar argument as in the case of equilateral n-gons of odd order.

Moreover, the moduli space depends on the choice of the lengths $d_k$ and in the smooth case is diffeomorphic to one of the following six spaces (Shimamoto and Vanderwaart 2005; Curtis and Steiner 2006): the sphere, the torus, the sphere with two, three, or four handles, the disjoint union of two tori.

Now we apply the method of parametrization of the last section which also works for non-equilateral pentagons. The system of Eqs. (1) and (2) reads now

$$\begin{aligned}&|z_k| = d_k \quad \text{ for } \quad k=1,2,3,4 \quad (1')\\&z_1+z_2+z_3+z_4+d_5 = 0\quad (2'). \end{aligned}$$

and eliminating $z_4$ by $(2')$ yields

$$\begin{aligned} (x_1+x_2+x_3+d_5)^2+(y_1+y_2+y_3)^2 = d_4^2\quad (3'). \end{aligned}$$

With the parametrization $x_k=d_k\frac{t^2-1}{t^2+1}$ and $y_k=d_k\frac{2t}{t^2+1}$ we obtain

$$\begin{aligned}&\left( d_1\frac{t_1^2-1}{t_1^2+1} + d_2\frac{t_2^2-1}{t_2^2+1} + d_3\frac{t_3^2-1}{t_3^2+1} + d_5\right) ^2 \\&\quad + \left( d_1\frac{2t_1}{t_1^2+1} + d_2\frac{2t_2}{t_2^2+1} + d_3\frac{2t_3}{t_3^2+1}\right) ^2 = d_4^2. \end{aligned}$$

Clearing nominators gives the following large equation of order 12:

$$\begin{aligned}&[d_1(t_1^2-1)(t_2^2+1)(t_3^2+1) + d_2(t_1^2+1)(t_2^2-1)(t_3^2+1) \\&\quad +\,d_3(t_1^2+1)(t_2^2+1)(t_3^2-1) + d_5(t_1^2+1)(t_2^2+1)(t_3^2+1)]^2 \\&\quad +\,4[d_1t_1(t_2^2+1)(t_3^2+1) + d_2(t_1^2+1)t_2(t_3^2+1) \\&\quad +\,d_3(t_1^2+1)(t_2^2+1)t_3]^2 = [d_4(t_1^2+1)(t_2^2+1)(t_3^2+1)]^2. \end{aligned}$$

As the surfer software allows only four parameters, we replace $d_1,d_2,d_3,d_4,d_5$ by a, b, c, d, 1 and $t_1,t_2,t_3$ by x, y, z. The following series of pictures have been produced with this formula and certain parameter values.

Parameters: $a=0.6$, $b=0.6$, $c=0.6$, $d=1$, type of configuration space: genus 3 surface.

Parameters: $a=0.4$, $b=0.4$, $c=0.4$, $d=0.4$, type of configuration space: sphere.

Parameters: $a=0.1$, $b=0.1$, $c=1$, $d=1$, type of configuration space: two disjoint tori.

Parameters: $a=0.05$, $b=0.05$, $c=0.1$, $d=1$, type of configuration space: genus 2 surface.

Parameters: $a=0.1$, $b=0.1$, $c=0.4$, $d=0.7$, type of configuration space: genus 2 surface.