Pentagonal maps on the torus and the plane

Abstract

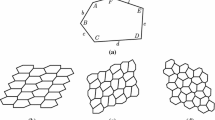
We know pentagonal tilings of the plane where vertex degree sequence (vds) of faces are same. There are three such tilings, namely, Prismatic pentagonal tiling (by type 1 pentagons of vds $3^34^2$), Cairo pentagonal tiling (by type 2 pentagons of vds $3^24^13^14^1$), and Floret pentagonal tiling (by type 3 pentagons of vds $3^46^1$) (https://en.wikipedia.org/wiki/Pentagonal_tiling). In this article, we are interested on the class of pentagonal tilings of the plane whose faces are pentagons of types 1, 2 and 3. There are infinitely many tilings of the plane by pentagons of types 1 and 2. We show that there are exactly six pentagonal tilings on the plane, including above three, by the faces of types 1, 2 and 3, where the face cycles of the degree four vertices are of same type. We also consider maps on the torus which are quotient of above type of tilings on the plane by latices. We have found bounds of the number of orbits of faces under the automorphism group of the maps. We show that our bounds on the number of orbits are sharp.