1 Introduction

In recent years, Operational Modal Analysis (OMA) has gained increasing attention. The development of sensor and computer technology, nowadays, is possible to record the vibration behavior of structures with high resolution. While in some areas, such as mechanical engineering, it has been obvious for some years to permanently monitor machines using suitable monitoring systems, the application of such systems in the construction industry has not yet become a standard. Unlike large volume series production in mechanical engineering, bridge construction has prototype character making each bridge unique. This hinders the standardization due to low volume. However, bridge structures are essential for the infrastructure network and represent a large asset of a country. Therefore, there is a great interest in global, effective, practicable and economic structural health monitoring systems that can help to minimize maintenance costs and extend the lifetime of the bridges. Modal-based monitoring systems are very promising in this context since modal parameters are global parameters of a structure, which depend on the physical properties (stiffness and mass).

Figure 1 shows the numerous parameter influencing the vibrational behavior of a structure, which inevitably affects the modal parameters to different extents [1]. Furthermore, the recording of the vibration behavior is significantly determined by the measurement chain used, which in turn is significantly influenced by numerous influencing factors. The aim is to detect and localize variations due to changes in the supports and structural stiffness changes. The basic prerequisite for a reliable monitoring system is to know the different characteristic effects of the individual influencing parameters on the modal parameters and to be able to distinguish these from the changes caused by damage. This paper focuses on the investigation of the influencing factors, unknown excitation forces and changes in structural stiffness (dark gray in Figure 1) [2].

Fig. 1
figure 1

Influencing parameters on the modal-based structural health monitoring [2]

Full size image

The emphasis is the investigation of the influence of the temporally and spatially variable stiffness and mass distributions of the operational loads on the estimation of the modal parameters. Finally, the quality of the estimated modal parameters is measured based on whether structural changes in stiffness and damage to the supports can still be detected and localized independently of the operating loads.

The mass ratio of the operating loads (vehicles) to the dead weight of the bridge is low, so that an influence of the vehicle mass on the vibration behavior of the bridge is to be expected. In addition, the road roughness in combination with the vehicle travel speed is crucial for the force amplitude leading to the excitation of the bridge. Basically, the literature distinguishes between two investigation approaches of vehicle–bridge interaction. The direct approach is the investigation of the measured response vibrations of the bridge due to moving vehicles. The indirect approach, on the other hand, investigates the response vibrations of the vehicle during the crossing of a bridge. The disadvantage of the indirect approach is that the response vibrations of a vehicle are sensitive to the roughness of the road surface. In addition, localisation of damage is usually only possible at low speeds. Furthermore, the indirect approach only allows periodic monitoring, but not permanent monitoring. Therefore, the direct approach is pursued under simulation of half-vehicle models in this paper. Like the previous studies concerning pedestrian traffic [2], no work could be found that systematically investigates the influence of road traffic on the scatter of modal parameters and analyzes the robustness of OMA methods to this non-stationary source of excitation for estimating the modal parameters of an invariant system. These investigations will be the subject of this paper [2].

2 Modal-based damage identification

The modal-based damage identification is based on the comparison of a reference state (RS) and a later possibly damaged comparative state (CS). If there are changes between RS and CS, a change in the system can be concluded. The modal parameters, natural frequencies, mode shapes and modal damping are global parameters and functions of the stiffness and mass of a structure. In the context of the modal-based damage identification presented in this paper, the term damage describes any structural stiffness changes that occur. The basic idea of the modal-based damage analysis is that damage processes are primarily associated with stiffness changes and stiffness reductions. Thus, the modal parameters change accordingly in dependence of the stiffness changes. According to Rytter [3], four different stages of damage identification are distinguished, whereby only the first two stages (identification and localisation) are dealt with in this paper. In the context of this paper, only damage identification methods based on natural frequencies and mode shapes are considered. The reason for this is that modal damping has no clear connection to progressive damage processes [4]. Furthermore, modal damping is strongly dependent on the calculation method used, so that it cannot be considered as a reliable damage identification parameter. Stewering [5] and Bungard [6] describe numerous modal-based damage identification methods with different advantages and disadvantages. Experts agree that a suitable combination of several methods is promising, but there are different views on which combination provides the most reliable results and is globally applicable to different systems. In particular, the suitability of damage identification procedures considering the influence of operational loads has not been investigated so far. In this paper, the following four methods are examined and compared [2]:

  1. (1)

    Natural frequency

  2. (2)

    Mode shape

  3. (3)

    Curvature of the mode shape

  4. (4)

    Continuous Wavelet Transformation (CWT) of the difference of the mode shape [7]

The curvature of the mode shape is calculated using the Mixed Approach (v2) [8].

3 Numerical investigations

The aim of the numerical investigations is to work out the characteristic behavior of the modal parameters as a function of the respective influencing factor. It is expressly pointed out that the numerical investigations do not claim to be able to reproduce experimental tests as accurately as possible in quantitative terms. Rather, they are intended to identify qualitative relationships between the individual and combined factors influencing the modal parameters. It is not a finite element model updating method. The goal is to develop a modal-based monitoring system that can provide damage identification and localisation without the need for numerical comparisons. Based on these target parameters, a finite element model was created in MATLAB® (R2019b). In the following, the modeling for the bridge superstructure and the vehicle traffic is presented. Subsequently, the results of the simulations performed are presented.

3.1 Modeling approach: bridge superstructure

A bridge superstructure can be considered as a continuum with infinite degrees of freedom (DOF) from a mechanical point of view. Theoretically, this has an infinite number of natural frequencies. For modal-based damage analysis, the spatial discretization of the physical properties mass, stiffness and damping of the bridge superstructure is crucial. In the context of the MATLAB® scripts created in this work, the bridge superstructure is represented as a finite element model based on Bernoulli beam theory. Due to the slenderness of the bridge superstructure (\(L>5 \cdot b\) or \(5 \cdot h\)) and the exclusive consideration of the bending mode shapes, the shear deformation can be neglected. For this reason, the Timoshenko beam theory is not applied [9]. The damping ratio of the structure alone was taken to be 1% and 2% for the first two modes, with Rayleigh damping assumed thereafter. The differential equation of motion of a Bernoulli beam with mass matrix M, damping matrix C and stiffness matrix K due to an arbitrary excitation f(t) can be formulated as follows:

$${\varvec{M}}\cdot \ddot{{\varvec{w}}}+{\varvec{C}}\cdot \dot{{\varvec{w}}}+{\varvec{K}}\cdot {\varvec{w}}={\varvec{f}}(t)$$
(1)

\(\ddot{{\varvec{w}}},\dot{{\varvec{w}}} \: {\rm and } \: {\varvec{w}}\) are the acceleration, velocity and displacement vector of the beam. In practice, the sensors record the response vibrations of the bridge structure, which is excited to vibrate by a wide variety of excitation sources (wind, traffic, etc.). Therefore, the solution of the differential equation of motion w(t) is calculated using the Newmark-β-method for arbitrary initial conditions. This method belongs to the implicit numerical integration methods (one-step method). It is an approximation method, where the accuracy of the solution as well as the stability of the method is chosen depending on the size of the time step ∆t. The integration parameters of the Newmark-β-method are chosen to be β = 0.25 and γ = 0.5. With this choice of parameters, the method is necessarily stable and no artificial damping occurs [10]. Different bearing arrangements can be considered with the help of the corresponding boundary conditions in the finite element model. This modeling approach allows the simulation of vibration measurements considering the multitude of factors influencing the estimated modal parameters (Figure 1) [11].

3.2 Modeling approach: vehicle traffic and road roughness

The vehicle traffic modeling approach presented in this paper is based on the modeling method introduced in Obrien et al. [12]. The diversity of vehicles constitutes a major challenge related to modal-based monitoring. The stiffness and damping characteristics of the vehicles are usually not known. The mass ratios can be approximately estimated depending on the type of vehicle (car, truck and heavy-duty vehicle). Probabilistic approaches, comparable to those used for the simulation of pedestrian characteristics [2], cannot be found in the literature. Damages relevant to bridge structures are the truck and heavy-duty vehicle crossings. In addition, these types of vehicles are expected to have the greatest influence on the vibration behavior of bridges due to their heavy weight. The dynamic behavior of the vehicles is in turn largely determined by the road roughness [13].

A coupled bridge-vehicle interaction model is chosen. The bridge is further modeled as a one-dimensional Bernoulli beam. The vehicles are modeled as half-vehicle models (HVM) considering two axles (front and rear) [12] (Fig. 2). A HVM has four degrees of freedom to represent the vertical displacement ys of the sprung mass ms, its pitching motion θs and the vertical displacement y1 and y2 of the unsprung masses mu,1 and mu,2. The sprung mass ms represents the weight of the body of a vehicle and the unsprung masses mu,1 and mu,2 represent the loads of the front (index 1) and rear axle (index 2). The sprung mass ms is connected to the axle masses via a combination of linear springs (ks,1 and ks,2) and viscous dampers (cs,1 and cs,2). The axle masses are in turn connected to the beam via linear springs ku,1 and ku,2, which represent the tires for the front and rear axles. The mass moment of inertia of the vehicle body (sprung mass ms) is Is. The distances of the axles to the center of gravity os of the sprung mass ms are defined by D1 and D2. Despite the highly simplified representation of a vehicle, this allows the basic dynamic properties of the vehicle–bridge interaction to be studied. [11, 12]

Fig. 2
figure 2

Model of a continuous beam considering constant velocity half-vehicle models [11]

Full size image

The road roughness r is determined according to ISO 8608 (2016–11) [14]. This assumes that the same statistical properties can be adopted along a section of road to be classified. An artificial road roughness profile r(x) can be calculated as follows [14]:

$$r\left(x\right)=\sum_{i=0}^{N}\sqrt{\Delta n}\cdot \sqrt{2}\cdot {2}^{k}\cdot {10}^{-3}\cdot \frac{{n}_{0}}{i\cdot \Delta n}\cdot {\rm cos}\left(2\cdot \pi \cdot i\cdot \Delta n\cdot x+{\varphi }_{i}\right)$$
(2)

x is the abscissa and can take values between 0 and the length of the road profile L. B is the sampling interval and nmax is the maximum theoretical sampling spatial frequency. The following relationships apply: \(\Delta n=1/L\), \({n}_{{\rm max}}=1/B\) and \(N={n}_{{\rm max}}/\Delta n=L/B\). k is a constant value that can take values between 3 and 9 (category A–H) depending on the road profile according to ISO 8608 (2016–2011) [14]. The spatial frequency n0 is to be assumed to be 0.1 rotations per meter and ϕi is the phase angle uniformly distributed between 0 and 2π [15]. Figure 2 shows the overall system with the relevant parameters to represent the HVM systems. xaa,1,j and xaa,2,j are the arrival distances of the jth HVM system separately for the front (index 1) and rear (index 2) axes, respectively. The velocity v of the HVM systems is assumed constant. Overtaking of the HVM systems due to different driving speeds is possible. A coupled system of differential equations of motion of the bridge model and the HVM systems is set up, which can be solved using the Newmark-β-method. The differential equation of motion for an HVM system according to [12] is:

$${{\varvec{M}}}_{HVM}{\ddot{{\varvec{y}}}}_{HVM}+{{\varvec{C}}}_{HVM}{\dot{{\varvec{y}}}}_{HVM}+{{\varvec{K}}}_{HVM}{{\varvec{y}}}_{HVM}={{\varvec{f}}}_{HVM}$$
(3)

\({{\varvec{M}}}_{{\rm HVM}}\), \({{\varvec{C}}}_{{\rm HVM}}\) and \({{\varvec{K}}}_{{\rm HVM}}\) are the mass, damping and stiffness matrices of an HVM system:

$${{\varvec{M}}}_{HVM}=\left[\begin{array}{cc}\begin{array}{cc}{m}_{s}& 0\\ 0& {I}_{s}\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}{m}_{u,1}& 0\\ 0& {m}_{u,2}\end{array}\end{array}\right]$$
(4)
$${{\varvec{C}}}_{HVM}=\left[\begin{array}{cc}\begin{array}{cc}{c}_{s,1}+{c}_{s,2}& {D}_{1}{c}_{s,1}-{D}_{2}{c}_{s,2}\\ {D}_{1}{c}_{s,1}-{D}_{2}{c}_{s,2}& {D}_{1}^{2}{c}_{s,1}+{D}_{2}^{2}{c}_{s,2}\end{array}& \begin{array}{cc}-{c}_{s,1}& -{c}_{s,2}\\ -{D}_{1}{c}_{s,1}& {D}_{2}{c}_{s,2}\end{array}\\ \begin{array}{cc}-{c}_{s,1 }& -{D}_{1}{c}_{s,1}\\ -{c}_{s,2} & { D}_{2}{c}_{s,2}\end{array}& \begin{array}{cc}{c}_{s,1}& 0\\ 0& {c}_{s,2}\end{array}\end{array}\right]$$
(5)
$${{\varvec{K}}}_{HVM}=\left[\begin{array}{cc}\begin{array}{cc}{k}_{s,1}+{k}_{s,2}& {D}_{1}{k}_{s,1}-{D}_{2}{k}_{s,2}\\ {D}_{1}{k}_{s,1}-{D}_{2}{k}_{s,2}& {D}_{1}^{2}{k}_{s,1}+{D}_{2}^{2}{k}_{s,2}\end{array}& \begin{array}{cc}-{k}_{s,1}& -{k}_{s,2}\\ -{D}_{1}{k}_{s,1}& {D}_{2}{k}_{s,2}\end{array}\\ \begin{array}{cc}-{k}_{s,1}& -{D}_{1}{k}_{s,1}\\ -{k}_{s,2}& { D}_{2}{k}_{s,2}\end{array}& \begin{array}{cc}{k}_{s,1}& 0\\ 0& {k}_{s,2}\end{array}\end{array}\right]$$
(6)

The load vector fHVM includes the time-dependent interaction forces applied by the HVM system:

$${{\varvec{f}}}_{HVM}={\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}-{F}_{t,1}& -{F}_{t,2}\end{array}\end{array}\right]}^{T}$$
(7)

The dynamic interaction force on tire nn is given by \({F}_{{\rm t},{\rm nn}}={k}_{{\rm u},{\rm nn}}\left[{y}_{{\rm u},{\rm nn}}-\left({w}_{{\rm nn}}+{r}_{{\rm nn}}\right)\right]\) for \(nn={\rm 1,2}\), where wnn is the vertical deformation of the beam and rnn is the height of the road profile (road roughness r) under tire nn. As an example, the system of differential equations of motion for the beam with N DOFs coupled with \(m=2\) HVM systems, each having \(h=4\) DOFs, is shown below. The load vector fG can be used to describe the coupling of the bridge model, with the respective HVM system. For the coupled overall system with \(N+m\cdot h\) degrees of freedom of the Bernoulli beam (N DOFs) and considering m HVM systems (each h DOFs), which pass the bridge in the observation period tBer, the following relationship results:

$${{\varvec{M}}}_{G}\ddot{{\varvec{u}}}+{{\varvec{C}}}_{G}\dot{{\varvec{u}}}+{{\varvec{K}}}_{G}{\varvec{u}}={{\varvec{f}}}_{G}$$
(8)

The global acceleration- \(\ddot{{\varvec{u}}}\), velocity- \(\dot{{\varvec{u}}}\) and displacement vectors \({\varvec{u}}\) are given by:

$${\mathbf{u}} = \Bigg\{ \begin{array}{ll} {\mathbf{w}}_{(Nx1)} \\ {\mathbf{y}}_{({hx1})}^{HVM,1} \\ {\mathbf{y}}_{(hx1)}^{HVM,2} \\ \end{array}\Bigg\} \quad {\dot{\mathbf{u}}} = \Bigg\{ \begin{array}{ll} \dot{\mathbf{w}}_{(Nx1)} \\ \dot{\mathbf{y}}_{(hx1)}^{HVM,1} \\ \dot{\mathbf{y}}_{(hx1)}^{HVM,2} \\ \end{array} \Bigg\} \quad \mathbf{u} = \Bigg\{ \begin{array}{ll} \mathbf{w}_{(Nx1)} \\ \mathbf{y}_{(hx1)}^{HVM,1}\\ \mathbf{y}_{(hx1)}^{HVM,2} \\ \end{array}\Bigg\}$$
(9)

\({{\varvec{M}}}_{{\rm G}} \left(N+m\cdot h\times N+m\cdot h\right)\) and \({{\varvec{C}}}_{{\rm G}} \left(N+m\cdot h\times N+m\cdot h\right)\) are the combined mass and damping matrices of the overall system. \({{\varvec{K}}}_{{\rm G}} \left(N+m\cdot h\times N+m\cdot h\right)\) is the coupled time-dependent global stiffness matrix and \({{\varvec{f}}}_{{\rm G}} \left(N+m\cdot h\times 2\right)\) is the force vector of the total system. The total system matrices are:

$${{\varvec{M}}}_{G}=\left[\begin{array}{ccc}{{\varvec{M}}}_{B}& 0& 0\\ 0& {{\varvec{M}}}_{HVM,1}& 0\\ 0& 0& {{\varvec{M}}}_{HVM,2}\end{array}\right]$$
(10)
$$\varvec{C}_{G} = \left[ \begin{array}{lll} \varvec{C}_{B} & 0 & 0\\ 0 & \varvec{C}_{HVM,1} & 0 \\ 0 & 0 & \varvec{C}_{HVM,2} \\ \end{array} \right]$$
(11)
$${{\varvec{K}}}_{G}=\left[\begin{array}{ccc}{{\varvec{K}}}_{B}+{{\varvec{K}}}_{B,HVM,1}+{{\varvec{K}}}_{B,HVM,2}& {{\varvec{K}}}_{B-HVM,1}& {{\varvec{K}}}_{B-HVM,2}\\ {{\varvec{K}}}_{HVM-B,1}& {K}_{HVM,1}& 0\\ {{\varvec{K}}}_{HVM-B,2}& 0& {{\varvec{K}}}_{HVM,2}\end{array}\right]$$
(12)

\({{\varvec{M}}}_{{\rm B}}\), \({{\varvec{C}}}_{{\rm B}}\) and \({{\varvec{K}}}_{{\rm B}}\) are the mass, damping and stiffness matrices of the beam. The system matrices of the two HVM systems \({{\varvec{M}}}_{{\rm HVM},{\rm m}}\), \({{\varvec{C}}}_{{\rm HVM},{\rm m}}\) and \({{\varvec{K}}}_{{\rm HVM},{\rm m}}\) for \(m={\rm 1,2}\) are obtained according to Eqs. (2)–(4). The \({{\varvec{K}}}_{{\rm B},{\rm HVM},{\rm m}}\) \(\left(N\times N\right)\), \({{\varvec{K}}}_{{\rm B}-{\rm HVM},{\rm m}}\) \(\left(N\times h\right)\) and \({{\varvec{K}}}_{{\rm HVM}-{\rm B},{\rm m}}\) \(\left(h\times N\right)\) components of the global stiffness matrix \({{\varvec{K}}}_{{\rm G}}\) of the total system couple the m HVM systems to the beam:

$${{\varvec{K}}}_{B,HVM,m}={{\varvec{H}}}_{b}\cdot {\left[{{\varvec{H}}}_{b}\cdot \left[\begin{array}{cc}{k}_{u,1,m}& 0\\ 0& {k}_{u,2,m}\end{array}\right]\right]}^{T}$$
(13)
$${{\varvec{K}}}_{B-HVM,m}=\left[\begin{array}{ccc}0& 0& -{{\varvec{H}}}_{b}\cdot \left[\begin{array}{cc}{k}_{u,1,m}& 0\\ 0& {k}_{u,2,m}\end{array}\right]\end{array}\right]$$
(14)
$${{\varvec{K}}}_{HVM-B,m}={\left({{\varvec{K}}}_{B-HVM,m}\right)}^{T}$$
(15)

The location matrix \({{\varvec{H}}}_{{\rm b}}\) for a two-axis HVM system has the dimension \(\left(N\times 2\right)\) and contains zero entries everywhere except for the nodal degrees of freedom of the elements on which the axes of the respective HVM system are located:

$${{\varvec{H}}}_{b}=\left[\begin{array}{c}\begin{array}{cc}0& 0\\ {{\varvec{h}}}_{1}& 0\end{array}\\ \begin{array}{cc}0& {{\varvec{h}}}_{2}\\ 0& 0\end{array}\end{array}\right]$$
(16)

\({{\varvec{h}}}_{1}\) and \({{\varvec{h}}}_{2}\) are the Hermitian approach functions, for the front (index 1) and rear (index 2) axes of the respective HVM system. The force vector of the total system \({{\varvec{f}}}_{{\rm G}} \left(N+m\cdot h\times 2\right)\) under consideration of static axle loads P1,m and P2,m results to:

$${{\varvec{f}}}_{G}=\left[\begin{array}{c}\begin{array}{c}\sum_{i=1}^{m}{{\varvec{H}}}_{b}\cdot \left[\begin{array}{c}{P}_{1,m}-{k}_{u,1,m}\cdot {r}_{1,m}\\ {P}_{2,m}-{k}_{u,2,m}\cdot {r}_{2,m}\end{array}\right]\\ 0\\ 0\end{array}\\ \begin{array}{c}{k}_{u,{\rm 1,1}}\cdot {r}_{{\rm 1,1}}\\ {k}_{u,{\rm 2,1}}\cdot {r}_{{\rm 2,1}}\\ 0\end{array}\\ \begin{array}{c}0\\ {k}_{u,{\rm 1,2}}\cdot {r}_{{\rm 1,2}}\\ {k}_{u,{\rm 2,2}}\cdot {r}_{{\rm 2,2}}\end{array}\end{array}\right]$$
(17)

For further information on this model approach, it is referred to [12].

3.3 Influence of vehicle traffic and road roughness on modal parameters

In the following, the simulations and related results regarding the influence of vehicle traffic and road roughness on the estimated modal parameters are presented. One of the main challenges is to reasonably estimate the model parameters for the HVM systems. For the own investigations, simplified estimates were made, since only very rough model parameters can be found in the literature due to diversity of vehicle types and the numerous component groups. To investigate the effects of the basic influencing factors, like driving speed, road roughness and the mass ratio between vehicle and bridge, two different HVM simulations were chosen. Koether [16] gives an overview of the permissible dimensions and weights for transport vehicles. Figure 3 shows the two selected vehicle types, which are simulated in a highly simplified way as HVM.

Fig. 3
figure 3

Modeling of the HVM systems [11]

Full size image

The parameters for the first simulation (HVM-1) were chosen in analogy to the literature research in [12]. O'Brien et al. [12] simulated a two-axle truck with a weight of 18 t. This corresponds to the truck type “single vehicle” in Fig. 3. Only the axle distances D1 and D2 are chosen to be 4.5 m instead of 2.375 m in [12] according to the selected truck model (Fig. 3). To investigate the influence of mass input by transport vehicles, an additional articulated vehicle (vehicle combination) with four axles and a weight of 38 t was selected as HVM (HVM-2) (Fig. 3). A parameter study was performed to investigate the influence of the moving vehicles on the estimation of the modal parameters. The calculation period chosen was tcal = 600 s with a sampling rate of 100 Hz and a time discretisation of Δt = 0.01 s. A maximum of 200 HVM systems per calculation period tBer can pass the bridge. Table 1 shows the parameters chosen for the HVM systems. The values of O' Brien et al. [12] were assumed as a basis (Table 2).

Table 1 Parameters of the HVM systems [2]
Full size table
Table 2 Probabilistic approaches to the properties of HVM systems [2]
Full size table

To account for the stochastic nature of road traffic, probabilistic distribution functions were applied for some vehicle characteristics:

20 calculations were performed per scenario. In total, four speed ranges \(v=50{\rm km}/{\rm h}\), \(80{\rm km}/{\rm h}\), \(100{\rm km}/{\rm h}\) and \(130{\rm km}/{\rm h}\) were investigated. Within a speed category, a uniform distribution of \(\pm 10\%\) was applied. For the consideration of the influence of the road condition, three different roughness profiles were considered: AB, BC and CD [15]. Worse road profiles do not generally occur in the German road network. A possible underloading or overloading of the vehicles was considered for the body mass ms of the HVM systems by applying a uniform distribution of − 20% to + 50%. The minimum distance for vehicles is 50 m from a speed of \(50{\rm km}/{\rm h}\). Therefore, a logarithmic normal distribution with a mean value \(\overline{x }=50 {\rm m}\) and standard deviation σ = 5 m was assumed for the calculation of the arrival distance of the HVM systems, related to the beginning of the bridge. Depending on these properties, the times at which the front and rear axles, respectively, reach and leave the bridge can be calculated. In analogy to the road bridge investigated in Sect. 0, a three-span continuous beam with the spans 18 m–24 m–18 m and an element length le of 0.5 m was chosen as beam model. The following parameters describe the beam model: ρ = 2 300 kg/m3, E = 30 000 N/m2, Iy = 0.5274 m4 and A = 8.79 m2.

3.3.1 Validation of the “vehicle traffic” excitation source

The validation of the excitation by the HVM systems is performed by recalculating the analyses performed by O'Brien et al. [12] who calculated the response oscillations of an HVM system during the passage of a 15 m simply supported beam (EI = 1.846·1010 Nm2, m = 28 125 kg/m, ξ = 3%). The selected parameters for the HVM system according to [12] correspond to those of the selected HVM-1-system (Table 1). Only the center distances D1 and D2 to the center of gravity os of the sprung mass ms are 2.375 m for O'Brien et al. [12] instead of 4.5 m for the HVM-1-system. The road roughness profile generated O'Brien et al. [12] according to the ISO standard (ISO 8608 1995 [17]). Figure 4 on the left shows the road roughness profile for category AB according to their own calculation as well as the response accelerations of the HVM system (right). The black dashed lines indicate the maximum and minimum accelerations of the calculations according to O'Brien et al. [12]. A clear agreement can be seen. Due to the random generation of the road profile, the results of O'Brien et al. [12] cannot be recalculated exactly.

Fig. 4
figure 4

Generated roughness profile for the category AB from own considerations (left) [11] and comparison of the response accelerations of the HVM-1-system from own calculations with the extreme values according to [12] (right) [11]

Full size image

Furthermore, the estimated natural frequencies of the beam model as well as the point masses of the HVM-1-system agree very well with the results of O'Brien et al. [12]. These are shown in Fig. 5 (left). The deformation behavior of the beam model, when a HVM-1-system passes over it, was also validated by comparison calculations with the software environment Stab2d [18]. The results are shown in Fig. 5 (right) and show a clear agreement.

Fig. 5
figure 5

Comparison of the estimated natural frequencies from own calculations with the results of [12] (left) [11] and validation of the vertical deformation uBB of the Bernoulli beam when passing an HVM-1-system from own calculations (right) [11]

Full size image

3.3.2 Effects of vehicular traffic on the estimated modal parameters

In the following, the results of the analysis on the influence of vehicle traffic on the scattering of the modal parameters are presented. Investigation parameters are vehicle speed, road roughness, and mass of HVM systems. The natural frequencies of the simulated three-span continuous beam without considering vehicle traffic are f1 = 3.1958 Hz, f2 = 5.2311 Hz and f3 = 6.2755 Hz. These were used as reference values for the automated estimation of the modal parameters using the Frequency Domain Decomposition (FDD) method [19]. The natural frequencies of the individual masses of the HVM systems and the mean value calculated from them for the respective HVM system are shown in Table 3. The natural frequencies of the HVM-2 are lower than those of the HVM-1 due to the increased mass. The averaged natural frequency of the HVM-1 is in the range of the third natural frequency of the beam, that of the HVM-2 between the first and second natural frequency.

Table 3 Natural frequencies of the HVM systems [2]
Full size table

Figure 6 shows the dispersions of the estimated natural frequencies of the beam considering the HVM-1 vehicle traffic. The results are shown separately for the speed and road roughness profiles.

Fig. 6
figure 6

Results of own calculations: scattering of the estimated natural frequencies of the beam considering vehicle traffic (HVM-1) as a function of driving speed v and road roughness category [11]

Full size image

No correlation between the speed or road roughness category and the scattering of the natural frequencies of the beam can be detected. The maximum percentage deviations of the natural frequencies from the mean value show similar magnitudes independent of the HVM system (Table 4). The percentage deviations are comparable to those due to structural stiffness changes. This is critical with respect to modal-based damage identification.

Table 4 Results of own calculations: percentage deviation of the natural frequencies of the beam taking into account the vehicle traffic [11]
Full size table

Considering the scattering of the mode shapes in Fig. 7 at an average driving speed of \(v=130{\rm km}/{\rm h}\) and the road roughness category CD, remarkable scattering is only visible for the third mode shape due to HVM-1 traffic (Fig. 7 left). The mean value of the mode shape amplitudes is shown in red. The scatter range is marked with black hatching. In contrast, the HVM-2 traffic (Fig. 7 right) leads to almost no scattering of the mode shape amplitudes.

Fig. 7
figure 7

Results of own calculations: Scatter area of estimated mode shapes considering vehicle traffic with v = 130 km/h (road roughness category CD): HVM-1 (left) and HVM-2 (right)[11]

Full size image

This can be attributed to the position of the natural frequencies of the HVM systems in relation to the natural frequencies of the beam. The averaged natural frequency from all three point masses of the HVM-1-systems corresponds approximately to the third natural frequency of the beam (Table 3). Therefore, an increased scattering range of this mode shape occurs when this type of vehicle passes. This can be observed regardless of the driving speed or road roughness category. The correlation between the excitation and component frequency has already been established in the study of pedestrian traffic [2].

In conclusion, vehicle traffic leads to negligible amplitude scatter of the mode shapes if the frequency of the vehicle does not coincide with the natural frequency of the beam. In the parametric study performed in this work, only two vehicle types were applied exemplarily and thus two natural frequencies. In relation to practice, this case can be evaluated as very unlikely due to the diversity of road traffic. Therefore, the frequency spectrum of real road traffic is broadband, making resonance excitation of the bridge by road traffic very unlikely. The results of this parametric study should therefore be regarded as conservative. Nevertheless, they show that the mode shapes are not sensitive to the operational loads due to road traffic. Therefore, they are very well suited for modal-based damage analysis.

3.3.3 Influence of vehicle traffic on damage identification

In the following, the influence of the previously presented scattering of modal parameters on modal-based damage identification is explained. The mean value from the 20 simulations per scenario was selected as the input parameter for the damage identification procedures in each case. This means that for the undamaged reference state, the mean value from 20 simulations was used, taking into account the stochastic properties of the simulated vehicle traffic, and for the damaged comparative state, the mean value from 20 simulations of the respective damage scenario was used. Two damage scenarios were investigated. D1 represents a symmetrical maximum stiffness reduction of 20% over the left column of the mid-span. The stiffness reduction was represented in the numerical FE model by reducing the Young's modulus of the corresponding Bernoulli beam element [11]. This extends over a total length of 3 m. The damage scenario D2 additionally considers a symmetrical stiffness reduction of 20% in the center of the mid-span over a total length of 6 m and a pronounced stiffness reduction in the support area of the partial damage D1 (20% stiffness reduction over a total length of 4 m). The corresponding stiffness distributions of the damage scenarios D1 and D2 are shown in Fig. 8.

Fig. 8
figure 8

Results of own calculations: stiffness distribution of the damage scenarios: D1 (left) and D2 (right) [11]

Full size image

The mean value of the modal parameters of the undamaged structural system, of the presented parameter study, is used as the reference condition. This means that the mean value of the modal parameters of the four investigated driving speeds as well as the mean value of the modal parameters of the three road traffic categories was taken. For the damage scenarios, the road roughness category CD and the speed categories v1 = 50 km/h and v4 = 130 km/h were investigated in each case. In this way, the most conservative case was analyzed. Table 5 shows the percentage changes of the natural frequencies depending on the damage scenario, related to the averaged natural frequencies of the undamaged state (Table 4). The indices indicate the simulated road roughness category (here CD), the driving speed (50 = 50 km/h or 130 = 130 km/h) and the damage scenario (D1 or D2).

Table 5 Results of own calculations: Percentage deviation of the natural frequencies of the beam considering vehicle traffic and damage scenario D1 (left) and D2 (right) [11]
Full size table

The damage D1 leads to significantly lower frequency changes (− 1.06% to + 0.16%) compared to the scattering due to road traffic (− 2.92% to + 3.37%) (Table 4). Only the damage scenario D2 leads to percentage changes in the first and third natural frequency (− 2.16% to − 1.57%), which is of a magnitude comparable to that of road traffic. Based on this, it must be stated again that the natural frequencies are not suitable for a reliable damage identification due to their high sensitivity to the operational loads.

On the other hand, the changes of the curvatures of the mode shapes allow the localisation of the stiffness reduction in the center of the field. Figure 9 shows the changes of the curvatures for the damage scenario HVM2-50-CD-D2 (gray) in relation to the undamaged reference state HVM2-CD-UG (black). The local increase of the curvature of the first mode shape in the damaged area allows the localisation of the damage D2.

Fig. 9
figure 9

Results of own calculations: Change of curvatures of the mode shapes for the HVM2-CD-UG ↔ HVM2-CD-50-D2 scenario [11]

Full size image

The CWT allows the localisation of damage in the region of the central columns of continuous beams. Damage is indicated by high CWT coefficients (≈ 1). Since the passage of HVM-1 vehicles led to amplitude scattering of the third mode shape, in Fig. 10 the results of the CWT considering the first three mode shapes are shown on the left and those without considering the third mode shape are shown on the right. The exclusion of the third mode shape allows the clear localisation of the damage D1 (Fig. 10 top right). The results of the CWT for the damage scenario D2 are shown in Fig. 10 below. In both cases (with or without ϕ3), both damage locations can be localized. However, the two damaged areas are clearly more recognizable with the exclusion of the third mode shape.

Fig. 10
figure 10

Results of own calculations: CWT consideration of the first three mode shapes (left) and consideration of the first two mode shapes (right): HVM1-CD-UG ↔ HVM1-CD-50-D1 (top) and HVM1-CD-UG ↔ HVM1-CD-50-D2 (bottom) [11]

Full size image

4 In situ measurements

In addition to the numerical investigations, the vibration behavior of the road bridge at Blohnstreet (BL-bridge) was investigated (Fig. 11 left). This is located between Durmersheimerstreet and Vogesenstreet and crosses the river Alb in Karlsruhe (Germany). It is a three-span (18 m, 24 m, 18 m) pre-stressed concrete bridge built in 1962.

Fig. 11
figure 11

Top view of the bridge at Blohnstreet [11] (left) Longitudinal section of the BL bridge [11] (right)

Full size image

In Fig. 11 (right), the longitudinal section of the bridge is shown. The width of the cross section is 13 m. The two carriageways have a width of 7.50 m [11]. To the left and right of the carriageway is a 2.50 m wide pedestrian and cycle path [11]. The bridge superstructure has hollow bodies over large areas to save dead weight. The bridge is supported at the eastern end (toward Durmersheimerstreet) by roller bearings and at the western end by a linear tilt bearing. The intermediate supports are supported by pot bearings. In addition, the BL bridge has a constant slope of 3.68% from the eastern end toward the west. At the western end (toward Vogesenstreet), the bridge fans out due to the lane guidance. The BL bridge is frequently passed by truck transporters because of the companies located in the area. [11]

5 Measurement concept of the bridge

Eleven Menhir measuring devices from SEMEX-EngCon GmbH [20] with MEMS (micro-electro-mechanical system) acceleration sensors were available for the measurements. A multiple measurement setup with nine reference sensors (RS) and two moving sensors (MS) was selected to achieve the highest possible resolution of the measurement grid (Fig. 12). The position of the nine RS was chosen based on the local extremes of the first three modes, ensuring observability of the relevant first three modes in each measurement setup. The support axes are marked by black dashed lines. A total of twelve configurations were chosen for the multiple measurement setup to achieve a fine measurement grid. An equidistant sensor spacing was not observed. The focus was on recording the areas of the mode shapes with local extreme points and inflection points as precisely as possible since their changes are relevant for localizing possible damage cases. The two outermost RS (#1 and #9) partially led to singularity problems when applying the merging strategies due to the similar information content to RS #2 and #8. Therefore, only the remaining seven RS (#2 to #8) were considered for the estimation of the modal parameters. [11]

Fig. 12
figure 12

Measurement setups for own measurements on the BL bridge [11]

Full size image

The sampling rate was chosen to be constant at 1000 Hz. A measurement period of 40 min was scheduled for each measurement setup. For moving and realigning the sensors, 10 min were calculated. Each Menhir device [20] was equipped with its own GPS antenna for high-precision synchronization of the wirelessly connected measurement units. The data transmission was wireless via WLAN. The selected time windows for the estimation of the modal parameters included 10 min and 20 min. The focus of the measurement campaign was to investigate the influence of road traffic on the scattering of the estimated modal parameters. [11]

5.1 Procedure of the evaluation and estimation of the natural frequencies

The measured acceleration time data were first processed by trend cleaning as well as high and low pass filters (4th-order Butterworth filters with cut-off frequencies of 0.5 Hz and 20 Hz). The natural frequencies of the BL bridge were identified considering the associated modes. Figure 13 shows the acceleration time data as well as the associated frequency spectra of the road traffic BL bridge (Fig. 13). As a result of the road traffic, the noise component in the time signal is high. This leads to the fact that the third natural frequency of the BL bridge disappears in the noise and could not be estimated reliably. In addition, clear peaks can be seen at about 7 Hz and 11 Hz. Since these additional peaks were seen in all frequency spectra regardless of timing and regardless of traffic volume, they are probably torsional modes or lateral or horizontal modes of the BL bridge. The acceleration curve allows the tracing of vehicle crossings.

Fig. 13
figure 13

Acceleration time histories and frequency spectrum of the BL bridge [11]

Full size image

Figure 14 shows the evolution of the estimated first two natural frequencies (black) and the averaged air temperature (black dotted) for the respective time window. The selected time window was 20 min. The air temperature was measured at the north-east and south-west axes of the BL bridge in the center of the second span (Fig. 11). The average first and second natural frequencies of all time windows are also shown (Fig. 14 dashed gray line). The natural frequencies were estimated using the FDD method considering only the reference sensors. Significant scattering during the day is evident. The first natural frequency varies between − 0.86% and + 0.72%. The scatter range of the second natural frequency is between − 3.22% and + 1.42%. A clear correlation between the average air temperature and the average values of the first two natural frequencies is not evident. Therefore, it can be assumed that the operating loads are the main cause for the large scatter range of the natural frequencies.

Fig. 14
figure 14

Evolution of the first (left) and second (right) natural frequency (black) of the BL bridge considering the air temperature (black dotted line) [11]

Full size image

5.2 Influence of the measurement chain and the vehicle traffic on the estimated mode shapes

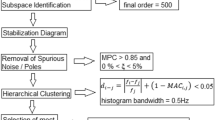
In the following, the influence of the OMA estimation procedure on the consistency of the estimated mode shapes is analyzed. Here, the three OMA estimation methods (1) Frequency Domain Decomposition (FDD) method [21], (2) Covariance-Driven Stochastic Subspace Identification (Cov-SSI) method [22, 23] and (3) Correlation Signal subset-based Stochastic Subspace Identification method [22, 24] are compared. The effects of the merging strategies as well as the selected signal length on the estimated mode shapes are shown. The Post Global Estimation Re-Scaling (PoGER) method [25, 26] and the Pre Global Estimation Re-Scaling (PreGER) method [25, 27] based on the FDD method are considered.

5.2.1 Influence of the OMA estimation procedure

For the comparison of the three OMA estimation methods studied, the mode shapes are estimated using the data of the nine RS. The amplitudes at the support axes are assumed to be zero. The observability of the first and second mode is guaranteed. The estimated first two bending mode shapes for the three investigated OMA estimation methods FDD, CoV-SSI and CoS-SSI are shown in Fig. 15. Based on the FDD method, the first mode shape can be estimated congruently for all time windows. The estimated second mode shape, however, shows non-negligible amplitude scattering (Fig. 15, right). However, these are not synchronization problems due to the uniform occurrence and the non-existing characteristic peaks of individual sensors [11, 28]. It is assumed that an increased sampling rate or sensors with a better signal to noise ratio would be more suitable for this bridge. In contrast, the application of the two SSI methods leads to much worse estimates. Already the first mode shape shows large amplitude scattering for both estimation methods (Fig. 15 mid and bottom left). The second mode shape can be estimated successfully with the CoS-SSI method only for three time signals. The CoV-SSI method can successfully estimate the modes for more time windows, but the estimated mode shapes have amplitude scatter that exceeds those dispersions of the modes estimated by the FDD method. If mode shapes cannot be estimated successfully, the amplitudes are shown as zero points for the corresponding time windows. This shows that the FDD method is to be preferred. An explanation for the large differences between the SSI methods as well as the FDD method could not be found yet. This is the subject of our current investigations.

Fig. 15
figure 15

Estimated first (left) and second (right) mode shapes of the BL-Bridge: FDD (top), CoV-SSI (mid) and CoS-SSI (bottom) methods with a sampling rate of 1000 Hz and a signal length of 20 min [11]

Full size image

5.2.2 Influence of the merging strategy and the signal length

Twelve measurement setups with a total of seven RS and two MS were selected for a finer measurement grid (Fig. 12). The two merging strategies PoGER [26] and PreGER [27] were used. Furthermore, two signal lengths with 10 min and 20 min were investigated. Figure 16 compares the results of the two merging strategies with a signal length of 10 min.

Fig. 16
figure 16

BL bridge: estimated mode shapes with a signal length of 10 min and a sampling rate of 1000 Hz with the PoGER method (left) and the PreGER method (right) [11]

Full size image

The PoGER method shows significant and non-negligible amplitude scatter at both modes. Considering the averaged amplitudes for a modal-based damage analysis would be associated with large uncertainties, since the scatter significantly exceeds possible changes due to damage. In contrast, the PreGER method provides congruent mode shape estimates, especially for the first mode shape. Spline interpolation could eliminate the individual peaks. The estimates of the second mode shape show larger amplitude scatter and peaks. This was also observed in the static measurement setup, so it is not primarily due to the estimation procedure. Doubling the signal length to 20 min yields nearly congruent mode shape estimates for both merging strategies (Fig. 17). However, the PreGER is still preferred over the PoGER method. These results confirm the high relevance of the signal length, which was shown in [2, 11, 29]. With increasing signal length, the quality of the estimated modal parameters increases.

Fig. 17
figure 17

BL bridge: estimated mode shapes with a signal length of 20 min and a sampling rate of 1000 Hz with the PoGER method (left) and the PreGER method (right) [11]

Full size image

6 Summary and conclusion

In this paper, the influence of operational loads from vehicle traffic on the estimation of modal parameters and subsequent modal-based damage analysis was investigated numerically and experimentally. Special attention was paid to the consideration of the temporally and spatially variable stiffness and mass distributions due to different traffic densities. Furthermore, the influence of the signal length, the OMA estimation method, and the multiple measurement setup were evaluated. A numerical model using half-vehicle models for discrete modeling was presented. The diversity of the vehicles was accounted for by probabilistic approaches to the physical parameters of the models. It was found that the signal length is crucial for the quality of the estimated modal parameters. Furthermore, the scatter of these decreases with increasing traffic density due to the increasing broadband excitation. Regardless of this, modes in the range of the excitation frequency are subject to larger scatter than those outside the frequency range of the excitation source. For road bridges, a dominant excitation frequency is very unlikely due to the large variety and the associated different natural frequencies of the vehicles. The consideration of the mean values from a certain number of time windows allows to compensate the scattering due to the temporally and spatially variable mass, stiffness and damping properties resulting from the moving vehicles within the considered time window. Within the in situ measurements, the numerical findings could be validated. Furthermore, it was shown that congruent mode shape estimates could be obtained most reliably using the FDD method. Finally, the influence of the merging strategy was analyzed for multiple measurement setups. It was found that the PreGER method is preferable compared to the PoGER method. In conclusion, the findings suggest that a modal-based condition monitoring of bridges under ambient conditions can be successfully performed, especially, under high demands on the measurement chain and with appropriate choice of the damage identification methods. The importance of mode shapes for a reliable modal-based monitoring system is shown, since these are suitable as damage localisation parameters even under significant influence of operating loads.