Evaluation of the residual carrying capacity of a large-scale model bridge through frequency shifts

Abstract

Structural systems are often subjected to degradation processes due to different kinds of phenomena like unexpected loadings, ageing of the materials, and fatigue cycles. This is true, especially for bridges, in which their safety evaluation is crucial for planning maintenance activities. This paper discusses the experimental evaluation of the residual carrying capacity from frequency changes due to distributed damage scenarios. For this purpose, in the laboratory of the University of Bologna, an experimental reinforced concrete model bridge was built and loaded. The applied forces produced bending moments causing up to three increasing levels of damage severity, namely early and diffused concrete cracking, and finally rebar yielding. By processing the acceleration signals recorded during the dynamic tests on the model bridge, the main natural frequencies of the bridge were obtained and the remaining bearing capacity was estimated based on the damage state. The opening and closure of cracks during a dynamic excitation produced a biased estimation of natural frequencies related to each damaged condition. The frequency decay predicted by the theory of breathing cracks applied to the performed experiments properly estimated the losses in the carrying capacity.

1 Introduction

During the lifespan of critical structures, owing to ensure their safety, repeated inspections are fundamental, especially for the maintenance management delivered by bridge owners. Dealing with concrete structures, several threats can adversely affect their bearing capacity and stability. First, the material ageing is mainly due to the combination of an aggressive environment with a lack of maintenance works, often producing corrosion of steel rebar and concrete cover losses. The increasing traffic demand of recent decades certainly influences the fatigue behaviour of the materials involved in the construction, even if the occurrence of cracks in concrete bridges is due to exceedance of the cracking bending moment often caused by the transit of exceptional transports or heavyweight drops on bridge deck surfaces [1]. Cracks could often not be visible to naked eyes or unskilled inspectors, which means that field testing is usually required for an unbiased damage grading.

Static and dynamic field tests strongly help in assessing the health of an existing structure, but often require the experience of skilled people able to properly design and schedule the activities required for a sound interpretation of the outcoming data. The tests should be carefully planned by taking into account the operability of the structure that is the object of investigation. For instance, concerning bridges and highways, the stoppage of the traffic flowing on them produces large distress to the users and, sometimes, huge profit losses. That is the reason why many researchers choose to carry out ambient vibration tests dealing with this class of structures. Besides, very useful information is gathered by investigating the behaviour of scaled models [2, 3] or existing structures soon to be demolished [4, 5]. These studies are still the only possibility for research validation in the field of structural monitoring of heavily damaged structures. The advantage of scaled bridges or small structural components built in the laboratory is to freely deal with any kind of sensor (or networks) and to easily handle, or simulate, the presence of damage, to confirm damage identification algorithms [6,7,8]. No significant restrictions, or constraints, can limit the possibility of investigating structural behaviour or material mechanics on laboratory structures rather than on existing structures (e.g., feasibility due to the operational conditions or a limited level of damage that can be simulated on existing structures without affecting their safety). The level of detail of a structural replica typically depends upon the purpose of the study. For example, dealing with Reinforced Concrete (RC) structures, Maeck et al. [9]. addressed the problem of cracked RC beams, investigating their static and dynamic behaviour; more recently, regarding the dynamic behaviour of structures influenced by the occurrence of damage, Masciotta et al. [10]. rigorously explored the effects of support settlement-induced cracks on the natural frequencies and modal shapes of masonry arches. Sometimes, once the complexity of the problem arises, the accuracy of the structural replica and the level of detail also need to be improved. For example, this is the case of wind tunnel tests [11].

Even if, from the probabilistic point of view, the problem of estimating the residual bearing capacity of structures is still in progress, many studies are already present in the literature concerning the assessment of the life-cycle performance and the benefits of Structural Health Monitoring (SHM) [12,13,14] However, to the authors’ knowledge, no deterministic relationship exists for assessing the remaining life of an existing structure. In [15], the authors discussed the links between the frequency decay of an RC beam with the damage produced by increasing loads according to the breathing cracks theory from a deterministic point of view. Thus, the focus of this paper is the validation of the proposed theory with data from a realistic bridge deck at different levels of residual capacity associated with progressive damage states.

The proposed theory [15] requires the calculation of the bending capacity and the assessment of the fundamental frequency only. Therefore, it could be used even for existing bridges by recording the vibration induced by traffic flows, thus testing bridges without any hindrance in their operability condition. Several algorithms have been deployed during the last 2 decades concerning the so-called “Operational Modal Analysis”, to be able to extract the dynamic features of a structure (e.g., natural frequencies, mode shapes, and damping ratios) by recording and processing acceleration data either in the time domain [16] or in the frequency domain [17, 18].

Vibration-based methods are widely used in the SHM field concerning the evolution of the modal parameter and, in particular, with regard to the detection of structural damage since the beginning of the twenty-first century [19]. Other methods were used at that time and further techniques have been developed later; most of them are collected in a very detailed review provided by Moughty et al. [20].

However, these techniques may be affected by low signal-to-noise ratios associated with low amplitudes of excitation or closely spaced modes in the power spectra because of the effect of damping. Qu et al. proposed a solution for these problems suggesting the use of higher order spectra and amending the frequency domain algorithm considering the angle criterion among the modal vectors [21,22,23].

Although the use of operational and experimental modal analysis has already become widespread concerning vibration-based structural monitoring and damage detection, different environmental and operational variables may provide biased estimates of the modal parameters [24]. For instance, concerning the natural frequencies, the magnitude of temperature-induced frequency shifts may be larger than those caused by the occurrence of damage, or at least, comparable [25, 26]. The quantification of the environmental influence on the modal features is still one of the challenging problems faced by the scientific community which proposed several approaches to this problem [27,28,29].

It should be mentioned that dense networks of sensors usually give more information about the modal shapes by improving their spatial resolution; however, in real cases, a higher number of sensors mean higher costs and wider datasets that sometimes cannot be paid for or managed by the Public Administration. For instance, dealing with large and strategic buildings, the benefit-to-cost ratio certainly encourages the use of a large sensor network. However, this is not the case for ordinary structures, since their high number and limited relevance constrains the budget. The research of an appropriate sensor layout allows the reduction of the number of devices involved in the investigation [30], giving a potential solution to this problem. Therefore, according to this observation and wishing to be in line with a realistic Public Administration effort for a small and simple bridge, only two accelerometers were used in this paper to investigate the decay of a limited set of natural frequencies.

This paper first introduces the geometry of the bridge deck, presenting the structural details and the mechanical properties provided by technical reports and preliminary investigation. Then, the static load test and the dynamic identification of the undamaged model allow the validation, and the improvement of the accuracy, of the mechanical parameters assigned to the numerical model. Moreover, the effect of the non-symmetric load is investigated through the FE model. Finally, three damage scenarios are generated in the laboratory specimen with increasing severity of the damage. The frequency degradation detected via each dynamic investigation at the end of each damage step is explained through the breathing crack theory proposed by the authors in the previous work [15]. In conclusion, the resulting frequency decay is used to infer the value of the maximum moment applied to the bridge from the experimental frequencies. Thus, the comparison of this value with the yielding moment suggests the value of the residual bending moment until that limit.

2 Materials and methods

2.1 The geometry of the tested bridge model

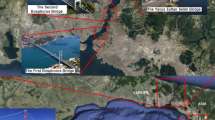
The object of this investigation is a small concrete bridge, designed as a geometrically scaled replica of an existing concrete bridge placed near the city of Bologna, both of which are illustrated in Fig. 1. The material properties were selected according to the material classes commonly used in bridge design practice.

Fig. 1

The existing bridge (on the left) and the investigated scaled model (on the right)

The details about the geometry of the model bridge and the experimental setup are described in the following discussion. The strength classes and mechanical properties of the materials used for the construction are summarized in Table 1.

Table 1 Mechanical properties of the construction materials employed in the erection of the bridge and introduced into the FE model of the bridge

The concrete was obtained with 350 kg/m³ of Portland cement CEM II/A-LL 42.5R, a water–cement ratio varying from 0.53 to 0.59, sand in the range 0.1–1 mm, and gravel in the range 5–15 mm complying with a granulometric curve for thin sections. In agreement with the European Standard EN 206 [31], the poured concrete achieved the strength class C28/35 with a density ρ equal to 2300 kg/m³. The cubic compressive strength R_ck determined by laboratory tests was found to be 38 MPa. The density was derived by weighing cubic samples. Then, ultrasonic tests were performed on the same specimens. The obtained experimental value of the dynamic elastic modulus is 36 GPa. According to the ratio between the static and dynamic moduli, approximately equal to 0.9 [32, 33], this value was reduced to 32 GPa, to be consistent with the Italian Standard [34].

The bridge is composed of two concrete piled raft foundations, two concrete walls which make up the abutments, and a concrete deck. Each foundation raft is constrained by six Tubfix piles with a diameter of 127 mm and a length of 6000 mm. The two piers are 3000 mm wide, 1500 mm high, and 400 mm thick; such dimensions allow neglecting the piers’ contribution to the bridge deck dynamic behaviour.

The cross-section of the deck is composed of a 6000 × 3000 × 100 mm³ concrete slab and four hollow rectangular girders. Two 200 × 400 mm rectangular beams were used as head beams resting over the deck bearings laying on the piers. The longitudinal section of the bridge is shown in Fig. 2. Ten ø16 bars were placed on the lower layer of the beams and four ø12 bars at the top. The slab reinforcement was set out with a bidirectional ø6/100 mm steel mesh. After the bridge completion, the concrete slab was finished with 25 mm of asphalt (Fig. 3). Finally, the bridge deck is sustained by eight 15 mm neoprene pads, positioned below the head beams, and centred on the axis line of the main beams (Fig. 4).

Fig. 2

Longitudinal vertical section of the concrete deck

Fig. 3

Transverse vertical section of the concrete deck

Fig. 4

The “U-Shape” girder cross-section (on the left) and the head beam cross-section (on the right)

2.2 Material mechanical characterization

The bridge model was set out to study the effect of a diffused crack pattern on the fundamental natural frequency, estimating the bridge residual bearing capacity by looking at the frequency decay due to the presence of damage. The laboratory campaign consisted of both static 4 Point Bending Tests (4PBT) and dynamic tests for the material property characterization; a bridge numeric counterpart was then used for the experimental data validation.

2.2.1 Static load test: 4-point bending test (4PBT)

Two pairs of UPN 300 steel profiles were bolted to two IPE 500 steel beams creating the loading system (Figs. 5, 6). Two ø36 mm Dywidag rods were used in transferring the applied load to the anchoring system for which the reactions were provided by two pairs of Tubfix piles with diameter ø127 mm and length L = 10,000 mm. The anchors were designed to balance the maximum forces applied by the two hydraulic jacks. The beam pair was designed by limiting the allowable deflection under the maximum load, such that its influence on the force distribution over the bridge deck could be disregarded. Therefore, the applied load acted directly on each of the four main girders, thanks to the eight loading points illustrated in Fig. 6.

Fig. 5

Static load test setup: on the left is shown the static loading system

Fig. 6

Experimental setup for the loading system: cross-section of the bridge and longitudinal section of the loading beam (a), plan view (b), and lateral view (c)

The model bridge was loaded up to 100 kN, remaining in the linear-elastic stress range of the materials and avoiding any crack occurrence. The forces exerted at each loading point were calculated by solving the equilibrium problem, that remains statically determined until the occurrence of the first crack. However, due to the relative position among the piles and the bridge, the loading setup was not fully symmetric compared to the bridge longitudinal axis, so the forces applied at these points resulted in different fractions of the total load. Forces equal to 14%, 21%, 29%, and 36% of the total load P acted on the four beams instrumented with the Linear Variable Differential Transducers (LVDT’s) 1, 2, 3, and 4, respectively. Those values will be taken to be constant in the following section concerning the numerical interpretation of the test, where the bridge deck was loaded avoiding the occurrence of any crack, validating the elastic properties of the bridge.

A total of six vertical displacements were recorded during the experimental campaign. The positions of the LVDTs are marked in Figs. 7 and 8: while four transducers measured the vertical deflection at the mid-span of the main beams, the remaining two recorded the vertical displacements near the supports due to the shortening of the rubber bearings. The measurement range of the LVDTs transducers (1–4) placed at the beam mid-span was set to 100 mm, while the two LVDTs “s01” and “s02” were placed near the supports, had a range of 20 mm. In summary, the bridge elastic behaviour was described by six load–displacement curves at the six reference points.

Fig. 7

Plan view of the concrete bridge and the position of the LVDTs adopted for the static load test (measurement range: red marks 0–100 mm; green marks 0–20 mm)

Fig. 8

Setup for the static load test

Solving the equilibrium of the concrete cross-section and following the guidelines given by the Standards dealing with bearing devices [35] and the neoprene rubber datasheet [36], the initial bending rigidity of the bridge and the axial stiffness of the rubber pads were analytically computed and then compared with the values inferred from the two experimental curves. The analytical bridge rigidity EJ₀ matched exactly with $2.55 \cdot 10^{5} \;{\text{kNm}}^{{2}}$, the one reckoned from the mid-span load–displacement curve. Otherwise, following the rubber bearings guidelines, the axial stiffness of a neoprene pad is given as a function of the rubber shear modulus G and the shape factor S of the pad. According to the manufacturing company, these values hold 0.9 MPa and 2.5, respectively. By considering the rubber incompressibility, the straight calculation suggested by Eq. (1) [35] led to a first approximation of the pad axial stiffness k_V, equal to $1.5 \cdot 10^{5}$ kN/m, as being proportional to the bearing stress σ_V

$$k_{V} = 20GS + 3\sigma_{V} .$$

(1)

The comparison with the support load–displacement curves proved a biased estimation of the neoprene axial stiffness: the backward stiffness calculation suggested a proper value for the axial stiffness equal to $2.8 \cdot 10^{5}$ kN/m. This means that the lateral confinement exerted by the concrete surfaces on a single pad was higher than the one considered by the Standards, and highlights the prerequisite of executing load tests for assessing the correct support stiffness, to be included in the dynamic calculations.

2.2.2 Dynamic identification of the bridge model

Actually, for SHM purposes, it is a common practice to align several sensors on the symmetry axis of the bridge with other sensors placed on transversal rows for the torsional mode detection. In the present study, eight tri-axial MEMS accelerometers were placed according to the grid-shape arrangement illustrated in Fig. 9 to identify all the modal features. Although the choice of using more sensors, or the one concerning the fusion of data provided by different setups (multi-setup technique [37, 38]), might lead to a more clear representation of the mode shapes due to a better spatial resolution, the selected minimal setup was able to detect and clearly distinguish the first six mode shapes of interest. Each sensor acquired 2000 samples per second for 8 min, a time-lapse greater than 2000 times the fundamental period of the bridge [39]. Thus, once the signal noise was spread over the frequency band of 1000 Hz, each signal was resampled to 400 Hz for reducing the computational cost, even though complying with a sampling frequency higher than 2.4 times the maximum frequency of interest, as suggested by Ventura et al. [39].

Fig. 9

The setup used for the dynamic test

The SENSR CX-1 accelerometer [40] was widely used by the authors dealing with the dynamic investigation of complex structures (e.g., historic masonry arch bridges [41, 42] or steel bridges [3]), and performed very well in all environmental conditions. This sensor measures acceleration in the range ± 1.5 g with 10^–6 g of resolution.

After a preliminary evaluation of the potential sources of excitation to be used for the dynamic identification, a set of random hammer hits was used as an excitation source for the bridge. While the use of impulsive excitation simulates the effect of the vehicles crossing the bridge head joints, the impulse is able to excite the whole frequency band. The weight of the rubber hammer used for exciting the bridge was approximately equal to 300 g with a “flying” length of 10 cm. By hitting the hammer at the bottom of the bridge beams in several positions with a time interval of 10 s, a large number of dynamic modes were excited. The first six frequencies were estimated through the time-series data processing both in time and frequency domains, using the Covariance Stochastic Subspace Identification method (SSI-COV) [43,44,45] and the Frequency Domain Decomposition technique (FDD) [17, 46], respectively. Both SSI and FDD algorithms are available in a MatLab Environment [47, 48] and the needed input parameters were set accordingly to what was suggested by Magalhlaes et al. [44, 49]. Concerning the case under investigation, by setting the model order and the time lag equal to 100 and 1 s, respectively, the results in terms of stable poles validated the frequencies detected by the FDD algorithm. All the recorded time-series were processed processing the entire length of the recorded signal. The use of the Hanning window of 4096 samples and a 50% overlap between two subsequent intervals reduced the leakage effect in the time-series processing.

Figure 10 collects the result of the two procedures: the solid line representing the first singular value computed through the Singular Value Decomposition (SVD) of the spectral matrix decomposition, leading to estimates of the frequencies associated with the bridge vibration modes of interest. Alternatively, the red stars represent the stable poles given by the SSI procedure; their alignment is normally associated with each natural frequency of the system. Finally, the dashed line refers to the coherence computed among the time-series, giving information about the reliability of the frequency detected once its value becomes higher than 0.80. Moreover, the information contained in the singular vectors provided via the FDD algorithm at the position of each local maxima provided the coordinates of the modal shapes related to each frequency (Fig. 11).

Fig. 10

First singular value of the spectral matrix (solid line), coherence (dashed line), and stable poles given by SSI procedure

Fig. 11

First six mode shapes identified through the operational modal analysis

2.2.3 Numeric interpretation of the experimental tests

The numerical representation of the model bridge is then built with the Italian version of the commercial FE software STRAND (Fig. 12) for verifying the mechanical parameters (e.g., rigidity of the supports and the concrete deck) obtained through the tests, even considering the non-symmetric load condition. Three-dimensional solid eight-node brick elements were selected to model the geometry of the concrete deck. Then, the element properties were assigned by combining the test outcomes and the reference properties suggested by the Italian Standards [34], or the delivery documents of the manufacturing company.

Fig. 12

FE numerical model of the concrete deck

Regarding the loads, while the asphalt layer laying above the concrete slab was defined as a distributed surface mass, the force acting on each concrete cube was spread as equivalent pressure in 150 × 150 mm² square area on the bridge slab. Finally, the rubber pads placed below each main beam were modelled using equivalent elastic springs.

Then, linear static and modal analyses were carried out simulating the load test and extracting the dynamic features, respectively.

Concerning the static load test, Figs. 13 and 14 confirm the excellent fit among the load–displacement curves at the supports and the bridge mid-span, respectively, with their numerical counterparts.

Fig. 13

Load–displacement curves measured at the supports “Exp_s” compared with the results of a set of linear static analyses performed on FE model “FEM”

Fig. 14

Load–displacement curves measured at the mid-span of the four main beams “LVDT_(1–4)” compared with the corresponding numerical curves “NLS_(01–04)” provided by a set of linear static analyses performed on FE model

A good match was even observed for the dynamic behaviour. Table 2 summarizes the values of the fundamental frequencies, either estimated through the dynamic investigation or obtained by carrying out the modal analysis on the FE model. The corresponding modal shapes are illustrated in Fig. 15. The differences between the presented data are always lower than 10% for all the modes and fit quite exactly for the first frequency which was used to assess the initial and the residual carrying capacity of the bridge deck.

Table 2 List of identified modal shapes, modal frequencies, and damping ratio

Fig. 15

Lowest six mode shapes of the FE model

The accuracy of the FE model in terms of comparison among the mode shapes resulting from the application of FDD and their numerical counterpart can be validated by the computation of the well-known Modal Assurance Criterion (MAC) [50]. The Modal Assurance Criterion is applied by convolving the identified modal shapes with the numerical ones (Fig. 16). Even the consistency of the FE model was proved, with all the values in the MAC matrix main diagonal being higher than 85%. Therefore, the obtained FE model can describe accurately either the static or the dynamic behaviour of the laboratory bridge by itself.

Fig. 16

Bar-plots of the MAC and its value obtained convolving the experimental modal shapes with those provided by the FE model

2.3 Description of progressive damage states

Due to the complex handling of the test apparatus, only three damage conditions were considered in the study. The load was increased steadily, naming “D0” the undamaged state, the initial limit state of concrete cracking (D1) was achieved through the first load step, then an intermediate step up to a fully stabilised crack pattern (D2), and finally reaching the yielding of the steel rebars (D3) with a deck residual deflection of more than 100 mm. Although the value of the total bending moments acting on the bridge can be easily computed by solving the equilibrium problem, the value associated with each damage step was inferred from the experimental load–displacement curve, leading to estimated values of 430 kNm, 910 kNm, and 1300 kNm, for the states D1, D2, and D3, respectively. During the test, the mid-span displacement and the crack opening increased up to 93 mm and 1.4 mm, respectively, with residual values of 55 mm and 1.0 mm after the removal of the load. The final condition of the concrete bridge showed the residual deformation and the set of cracks illustrated in Fig. 17. The crack developed along with 85% of the span.

Fig. 17

Residual deformation experienced at the end of the load test (a) and the observed crack pattern (b)

Each damaged configuration was then investigated by performing dynamic tests accordingly to the previous identification phase using some random hammer hits as a source of excitation after the removal of the static load. The three levels of damage severity reached during the static load test produced frequency losses equal to 5%, 18.1%, and 21.6% compared with the one associated with the undamaged state.

It is well known that the natural frequencies of a structure are strictly dependent on its stiffness when no changes occur in both the mass distribution and the environment temperature. For the examined case, because all the dynamic tests were performed at the same temperature, roughly equal to 30 °C, the frequency shifts are the direct consequence of a stiffness loss caused by the occurrence of damage. The ongoing continued monitoring of the bridge will quantify the frequency trends over the daily temperature variations, essentially due to the changes in concrete and asphalt stiffnesses.

In this study, only the two accelerometers named 2056 and 2049 (Fig. 9) were used for the frequency identification at the end of each damage step, even though only one sensor can be used for detecting frequency changes. Because the influence of the damage on higher modes is not of concern for this paper, those modes were neglected.

However, dealing with more complex real cases, a higher number of sensors or the roving sensor technique [51] can help in achieving a detailed stiffness change distribution along with the bridge structure.

3 Assessment of the residual bending capacity

The typical crack pattern associated with a distributed load acting on a bridge was replicated experimentally by performing a load test on the deck model in the non-linear range beyond the onset of the concrete cracking.

The stiffness and the frequency changes detected in the experiment allow checking of the theoretical analysis presented in Benedetti et al. [15]. For a sake of clarity, the relevant equations are discussed in the following.

The prediction of the damaged breathing frequency f_B as a reduction of the original frequency f₀ indicated by Eq. (2) mainly depends upon the factor η quantifying the bending rigidity loss due to the damage $\left(\frac{{EJ}_{0}}{{EJ}_{T}}-1\right)$, where EJ₀ and EJ_T are the rigidity of the undamaged bridge deck and the tangential rigidity associated with the cracked concrete section. Then, the ratio α between the cracking moment M_cr and the maximum bending moment M_max achieved during the test is strictly related both to the damaged length of the beam and the amplification factor λ as the ratio between M_max and the yielding bending moment M_y.

Equation (2) is as follows:

$$f_{B} = f_{0} \cdot \sqrt {\frac{1}{{1 + 6\eta \cdot \frac{{\left( {1 - \alpha } \right)^{2} \left( {1 + \alpha } \right)}}{12 - 4\alpha }}}} .$$

(2)

Considering the energetic equivalence between the vibrating mode kinetic energy and the potential energy of one equivalent deflected shape of the beam under a concentrated load, the fundamental frequency can be written in terms of the maximum displacement occurring under that force [52]. Equation (2) is simply based on the average of the mid-span deflection of the deformed shapes associated with opened δ_o and closed δ_c cracks where g is the gravity acceleration leading to the following formula:

$$f_{B} = \sqrt {\frac{2g}{{\delta_{c} + \delta_{o} }}} = \sqrt {\frac{{2\mathop f\nolimits_{c}^{2} \mathop f\nolimits_{o}^{2} }}{{\mathop f\nolimits_{c}^{2} \mathop { + f}\nolimits_{o}^{2} }}} .$$

(3)

Then, considering f_c as the frequency associated with closed cracks and remarking the calculation f_o as the frequency of Eq. (4) associated with opened cracks as follows:

$$f_{o} = f_{c} \left[ {1 + 12\frac{{_{{L_{D} }} }}{L}\frac{{2L - L_{D} }}{{8L + 4L_{D} }}\left( {\frac{{EJ_{0} }}{{EJ_{D} }} - 1} \right)} \right]^{ - 1/2} .$$

(4)

It includes the loss in bending rigidity, the span length L and the damaged length L_D, which is a function of the amount of the bending moment exceeding the cracking one from the parameter α. In conclusion, by expanding f_o and f_c in Eq. (3) and considering the secant rigidity EJ_D as a function of the tangent rigidity EJ_T associated with the fully cracked section [15, 53], the formula (2) has been obtained.

Even if in a simply supported beam, the value of the average stiffness can be easily computed from the fundamental frequency, in general disregarding the so-called “crack breathing effect” due to the crack closure during the dynamic vibration, the analysis can lead to large errors in estimating the stiffness change.

All the data of the three increasing damage phases were processed, by recording the deviations of the lowest frequency for each step. The resulting frequency decay over the ratio λ is illustrated in Fig. 18, highlighting the three damage states by red stars. The first step of damage (D1) produced a deviation of 5% from the reference value, while the subsequent drops fit with the formula of breathing cracks developed by Benedetti et al. [15]; the resulting errors remain lower than 5% for each damage condition.

Fig. 18

Frequency decay due to the presence of damage

Starting from the original bending rigidity EJ₀, the rigidities associated with the three increasing damage states resulted in a stiffness decrease, based on the breathing crack theory, of 9%, 33%, and 38% for the damage conditions D1, D2, and D3, respectively.

This is consistently far from the frequency decay calculation based on the stiffness reduction identified by the red square in Fig. 18 since stabilised cracking, considering a fully cracked section, suggested a stiffness drop of 51% with a frequency shift of 28%. The frequency calculations which involve analytical values of bending stiffness do not consider the effect of crack closures on the modal behaviour of the bridge. This is the reason why the red square representing the damaged frequency computed with the cracked section rigidity is more similar to the black dashed line describing the condition in which the cracks remain open.

4 Conclusions

This paper addresses the problem of assessing the residual load-bearing capacity of a damaged concrete bridge deck through frequency data. Six vibration modes were clearly detected in the range up to 100 Hz in the dynamic investigation carried out on the undamaged deck. The MAC computed convolving the two sets of numerical and identified modal shapes showed high cross-correlation values, suggesting the good agreement of the natural frequencies given by the FE model and those detected experimentally.

The typical crack pattern of diffused damage along the main beams produced significant shifts in the values of the lowest frequencies, especially for the fundamental frequency, strictly associated with the stiffness of the deck. Concerning the observed decay in terms of frequency, the “breathing cracks” theory and the analytical formulation provided by Benedetti et al. [15] predicted the λ value quite closely, representing the ratio of the bending moment producing on the bridge a given damage scenario, to the yielding moment. Thus, the straightforward calculation of the loss in terms of carrying capacity is given as a fraction of this limit moment.

The theory was originally proposed on a concrete beam which is a quite simple structure, and then experimentally proved considering only one level of damage. The present work extends the field of application to the mesoscale and three different levels of damage, looking for the real-scale application of existing structures. Thus, the theory is proved even for a structure that is more complex than a simple beam (e.g., geometry, types of supports, and materials). In addition, the paper shows that the use of fully cracked bending stiffness is not suitable for the frequency calculation associated with the damage, because the resulting value does not consider the effect of crack closures in the modal behaviour of the bridge.

At this moment, the damaged bridge is exposed to environmental actions and we plan to monitor it for some more years. Then, further steps of the study will concern the retrofit of the damaged bridge and the dynamic investigation of the strengthened bridge response.