1 Introduction

The management and the safeguard of existing buildings are actual tasks for structural engineering. The development of non-invasive structural monitoring technologies [1] can significantly improve the management process and safety assessments of the existing structures, reducing the impact of disturbances on their functionality. In particular, structural monitoring technologies are extremely useful for reinforced concrete buildings and infrastructures that, built in the last century, have reached or even overcome their ultimate life, urgently demanding ongoing safety analysis [2].

Among the several monitoring techniques, satellite data applications are increasingly used, under different approaches. Many applications are based on using multi-temporal differential synthetic aperture radar (SAR) interferometry (DInSAR) techniques based on the exploitation of satellite data for performing analyses of ground deformations with reference to single buildings. A focus, through a case study, on the building deformation assessment by means of persistent scatterer interferometry analysis is developed in [3]. The application of DInSAR techniques for the assessment of the damage induced by slow-moving landslides in Moio della Civitella (Salerno province, Italy) urban settlement on the existing buildings [4, 5], also in combination with seismic actions [6], is presented. In [7] an overview of the results of diagnostic and monitoring activities carried out through satellite radar interferometry and in-situ measurements of two historic buildings is reported. Drougkas et al. [8] proposed a methodology for assessing the development of damage in building structures subjected to differential settlement and uplift. More recently, Cusson et al. [9] proposed the use of radar satellite data as an early warning system for the detection of unexpected bridge displacements and a decision-support tool.

The case study of buildings located in Rome is deepen in [10], through the integration of the results of a multi-temporal DInSAR analysis with a semi-empirical model for the assessment of the structural damage induced by subsidence, in [11], through the joint exploitation of long-term DInSAR deformation time series with geological information and structural characteristics of some heritage buildings, and in [12] focussing the implications for the heritage preservation of the Vittoriano monument in the Rome historical city centre, using the deformation profile monitored with satellite data.

In this research scenario, this study focuses on a methodological approach based on the application of satellite data for the structural analysis of existing buildings, via the joint exploitation of the historical investigation and accurate 3D modelling, through some case studies relevant to two twentieth century buildings in Rome: the residential buildings Torri Stellari in Valco San Paolo (1951–1953) and the housing complex known as Corviale (1967–1983). Referring to these case studies, the paper presents and compares three different approaches, with different levels of approximation, to study the active deformative processes of the examined buildings and the related damages assessment. The ground deformation derived by DInSAR measurements can be used to carry out a preliminary damage assessment by means of literature empirical evidences (e.g. [13,14,15,16,17,18,19]), or to provide a full structural assessment by impressing the displacements at the base of the building in an analytical structural model (e.g. [5, 6]).

The paper is structured as follows: the proposed work methodology is deeply discussed in Sect. 2; in Sect. 3 the DInSAR data analysis is outlined; the adopted 3D modelling process of the building under monitoring, together with the positioning of the identified pixels, hereinafter referred to as persistent scatterers (PSs), on the building’s volumes, are presented in Sect. 4; the DInSAR data analysis and the interpretation of the displacements for damage assessment are developed in Sect. 5; an application of the proposed methodology to two case studies is given in Sect. 6. Discussion and conclusions are presented in Sect. 7.

2 Work methodology

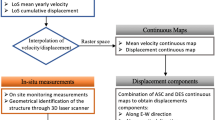
This work follows a three phases methodology: (i) large-scale analysis of multi-temporal differential SAR interferometry results, achieved by applying the full resolution SBAS-DInSAR approach to the whole Stripmap COSMO-SkyMed satellite dataset collected over the city of Rome during the 2011–2019 time interval; (ii) accurate 3D geometrical modelling of the external volume of the buildings under monitoring and consistent positioning of the identified and investigated PSs; (iii) analysis of the displacements of the structure under monitoring, through different strategies, and interpretation of the displacements for damage assessment.

A brief description of the above three steps follows, referring to the main different Sections of this paper, while a schematic graphic flowchart of the whole procedure is shown in Fig. 1:

  1. (i)

    Processing of COSMO-SkyMed satellite SAR data to generate displacement time series and mean yearly Line of Sight (LOS) deformation velocity maps along the satellite LOS, with the following retrieval of velocity maps of the monitored buildings, in terms of their components along the vertical and East–West (E–W) directions (Sect. 3);

  2. (ii)

    Accurate 3D geometrical modelling of the external volume of the buildings under monitoring, via the historical documentary sources investigations, in-situ surveys and parametric modelling; positioning of the investigated PSs, consistent to the actual geometry of the buildings (Sect. 4);

  3. (iii)

    Analysis of the vertical and horizontal components of the displacement of the PSs through different strategies, useful for the structural analysis of the building and characterized by different approximation levels; interpretation of the displacements for the damage assessment, through procedures available in literature (Sect. 5).

Fig. 1
figure 1

Flowchart of the presented methodology

Full size image

3 Remote sensing data

In the framework of the existing multi-temporal DInSAR techniques, the well-established Small BAseline Subset (SBAS) approach [20, 21] allows obtaining displacement measures for targets located on the ground surface. The spatial and temporal trend of the displacements associated with each single pixel measured along the sensor LOS—i.e. the direction joining the satellite sensor with the target on the ground—is given through deformation time series and mean velocity maps with sub-centimetric accuracy. To this aim, a large number of SAR images, acquired by satellite sensors over the investigated area, during a certain time period, are collected and properly selected to generate a multi-temporal sequence of differential interferograms, representing the phase differences between two SAR images. Small temporal and spatial separations between the acquisition orbits (referred to as temporal and perpendicular baseline) characterize the selected interferometric SAR data pairs, thus allowing to minimize noise effects and maximize the spatial pixel density. The generated interferograms, unwrapped to solve for the 2π ambiguities [22], are thus the starting point for the computation of the deformation time series, obtained through the solving of a linear system of equations in a least squares sense, by applying a minimum norm energy constraint (in some cases, the singular value decomposition (SVD) method is applied). The computational process finally ends with a filtering operation, for detecting and removing possible atmospheric artefacts from the displacement time series. As reported in [23,24,25], the mean deformation velocity and the single displacement measurements are characterized by a precision of about 1–2 mm/year and 5–10 mm, respectively. One key point of the SBAS-DInSAR approach is the possibility to generate displacement time series and corresponding velocity maps at different spatial scales, referred to as regional and local scale analysis. The first one is aimed to investigate natural or anthropic deformation phenomena associated with large areas, whereas the latter allows detecting spatially localized displacements related to full resolution pixels, particularly suitable to investigate and monitor over time deformation phenomena associated with single buildings and/or infrastructures [26, 27]. When operating at local scale, such as for investigating the structural assessment of single building [12] or detecting critical infrastructure behaviour [28], full resolution differential interferograms, generated from the single-look data with the full spatial resolution of the sensor ranging from 3 to 10 m, are used [21, 27].

For each coherent (from an electromagnetic point of view) PS, associated to a resolution cell size of about 3 × 3 m (for the COSMO-SkyMed -CSK- Stripmap mode), and identified by means of its geographical coordinates (latitude and longitude), and altitude with respect to a global reference system, measures of both LOS displacements and LOS mean velocity are given, over the acquisition period. The LOS direction is identified by its directional cosines, given for each PS. Furthermore, a temporal coherence parameter ranging between 0 and 1 is associated to each PS, expressing the quality and reliability of the measurement [21, 27]. A proper selection of the final PSs of the interferometric analysis is achieved by setting a threshold on the temporal coherence to exclude not reliable pixels; typically, this value is about 0.5 but, although in some specific cases (e.g., very good temporal sampling and distribution of the acquisitions, analysis on urban areas) we can also reach down 0.35. It is worth noting that the displacement measurements are always spatially referred to a point, i.e. the reference pixel, usually selected in a stable and coherent area; accordingly, the displacement of a generic PS is computed by subtracting the corresponding one of the reference point to the recorded measure.

Due to the combination of the orbits of satellites, namely ascending (ASC) and descending (DES) orbits, and rotational motion of the Earth around its axis, radar images of the same geographical area from different perspectives are available. The independent SBAS-DInSAR processing of both the ASC and DES acquisitions collected over the same area permits generating LOS ASC and DES full resolution deformation time series and velocity maps, which contribute to the reconstruction of the real deformation process. Accordingly, two independent sets of deformation measurements are concerned, referring to ASC and DES DInSAR products, eventually subdivided in sub-quadrants (different for ASC and DES datasets), for convenience’s sake. A time lag between measures of the two datasets can be found, due to the difference of their first acquisition dates.

With reference to the precision and accuracy of the PSs georeferencing on a planimetric scale, the height reconstruction of each PS is strictly dependent on the accuracy of the estimation of the residual topographic phase component with respect to the used DEM within the interferometric processing, which is on the order of 1–2 m. Consequently, by taking into account the full resolution CSK SBAS-DInSAR analysis, the precision of the PSs georeferencing is about 1–2 m, 2–3 m and 1–2 m along the North–South (N–S), the East–West (E–W) and the Vertical directions, respectively, which corresponds to about one standard deviation. It is worth noting that an error in the georeferencing of the reference point can affect the position of all PSs of the examined area.

The information of the ASC and DES SAR data measurements, usually provided as ASCII text files, can be combined to trace back to the actual direction of the displacement vector of each PS of the whole investigated area. The generic measure X—i.e. the displacement or the mean deformation velocity measurement—along the LOS of the sensor can be expressed in terms of its E–W (XE–W), N–S (XN–S) and Vertical (XV) components and of the LOS directional cosines nE–W,i, nN–S,i and nV,i (with i = A, D, where A and D refer to ASC and DES orbits, respectively), according to Eq. (1):

$$\left\{ {\begin{array}{*{20}c} {X_{{{\text{LOS}},{\text{A}}}} = X_{{{\text{E}} - {\text{W}}}} \cdot n_{{{\text{E}} - {\text{W}},{\text{A}}}} + X_{{{\text{N}} - {\text{S}}}} \cdot n_{{{\text{N}} - {\text{S}},{\text{A}}}} + X_{{\text{V}}} \cdot n_{{{\text{V}},{\text{A}}}} } \\ {X_{{{\text{LOS}},{\text{D}}}} = X_{{{\text{E}} - {\text{W}}}} \cdot n_{{{\text{E}} - {\text{W}},{\text{D}}}} + X_{{{\text{N}} - {\text{S}}}} \cdot n_{{{\text{N}} - {\text{S}},{\text{D}}}} + X_{{\text{V}}} \cdot n_{{{\text{V}},{\text{D}}}} } \\ \end{array} } \right.$$
(1)

Since the ASC and DES satellite orbits are quasi-polar ones, i.e. both ASC and DES LOS are nearly perpendicular to the N–S direction, the cosine terms \({n}_{\text{N}-\text{S},\text{ A}}\) and \({n}_{\text{N}-\text{S},\text{D}}\) are almost negligible, so a very small percentage of the deformation component in the N–S direction can be detected. More specifically, even in presence of a deformation component along the N–S direction, we can assume that it has very little influence on the LOS deformation values due to the very low sensitivity when retrieving the N–S deformation component, which is around 5%. Accordingly, this component can be neglected in Eq. (1) with a good approximation, and then the system of Eqs. (1) simplifies in:

$$\left\{ {\begin{array}{*{20}c} {X_{{{\text{LOS}},{\text{A}}}} = X_{{{\text{E}} - {\text{W}}}} \cdot n_{{{\text{E}} - {\text{W}},{\text{A}}}} + X_{{\text{V}}} \cdot n_{{{\text{V}},{\text{A}}}} } \\ {X_{{{\text{LOS}},{\text{D}}}} = X_{{{\text{E}} - {\text{W}}}} \cdot n_{{{\text{E}} - {\text{W}},{\text{D}}}} + X_{{\text{V}}} \cdot n_{{{\text{V}},{\text{D}}}} } \\ \end{array} } \right.$$
(2)

It is worth to highlight that, due to the geometrical properties of the acquisition system and to the different electromagnetic and geometrical properties of the scattering surfaces, it is not easy to find a direct correspondence between the ASC and DES LOS displacement information along the same observed target. Especially when analysing buildings, it is almost unrealistic to have coincident ASC and DES PSs within the same position on the object under investigation, since satellites, running along the two different orbits, investigate one or more fronts or portions of the building, but never the same ones, and, in case of the same front, never from the same point of view. Excluding the possibility of operativity using instruments, such as the corner reflectors, able to identify the scattering object and its position very precisely, it is not possible to a priori define where the PSs concretely are located within a structure or a building and is rather unusual to find a biunivocal spatial correspondence between points of the two datasets. However, it is possible to assume that ASC and DES PSs nearby, within the accuracies of the planimetric and altimetric positioning, can be representative with a good approximation of the same reflective target.

For this reason, in most applications which make use of advanced DInSAR measurements, a spatial resampling of the data obtained in the two acquisition geometries is usually required, to decompose the measured displacement along the vertical and E–W directions [5, 10].

To this aim, the PSs can be spatially interpolated, providing two continuous LOS mean velocity maps, one from the ASC and one from the DES original dataset. Subsequently, these continuous LOS mean velocity maps can be projected on a defined grid, making thus possible to compute the vectors of the mean interpolated LOS velocities VLOS,A and VLOS,D in each vertex of the grid. In this way, the vertical and E–W components (VV and VE–W, respectively), associated to each point of the above-mentioned grid, can be evaluated with Eq. (2).

Following this approach, an accurate 3D model of the buildings under monitoring is crucial to have a straight correspondence between PSs and the geometry of the structure. Assuming the correct positioning of the PSs on the building volumes, different techniques can be adopted to combine data from ASC and DES datasets. In this paper, three different approaches, characterized by different approximation levels, are presented to evaluate the vertical and horizontal components of the displacements of the structure, via two case studies of twentieth century buildings in Rome.

The used interferometric SAR products are obtained by applying the full resolution SBAS-DInSAR approach [21, 27] to SAR images collected from ASC and DES orbits by the sensors of the Italian CSK constellation, over the investigated area during the last decade. The images are acquired through the standard Stripmap mode with HH polarization and a ground spatial resolution of about 3 m in both azimuth (along-track) and range (cross-track) directions. The full resolution deformation time series and corresponding LOS mean velocity measurements of each PS have been computed using the 1-arcsec Shuttle Radar Topography Mission (SRTM) DEM of the study area, to remove the topographic phase component. Table 1 summarizes the main parameters of the exploited datasets.

Table 1 Main parameters of ASC and DES datasets
Full size table

As an example, Fig. 2 shows a view of the area of Rome in which the buildings of the Torri Stellari and Corviale complexes fall, indicated by a white and a black benchmark, respectively. Superimposed on the same figure are the achieved PSs, for the ASC and DES orbits, whose colour refers to the LOS mean velocity, expressed in mm/year.

Fig. 2
figure 2

View of the examined area with superimposed the LOS mean deformation velocity map for the identified PSs (white and black benchmarks indicate the Torri Stellari and Corviale complexes) (colour figure online)

Full size image

4 Accurate PSs positioning: from historical-based 3D to GIS

The accurate 3D modelling, via historical sources, and the accurate PSs positioning on the building’s volumes feature a three steps procedure.

Step 1:

Archival investigation In this step, written documents and graphic/iconographic sources of the original project and the subsequent maintenance interventions are crosschecked, to extract consistent technical and geometrical data of the buildings under monitoring. The historical investigation based on archival sources can prove particularly helpful in support base technical knowledge of the structure under monitoring: the crosscheck of all the associated written (e.g., design and calculation reports, load test results, construction materials characterization) and iconographic sources (e.g., execution drawings, construction site pictures), provides information about the geometry of the load-bearing structure, and the buildings materials and details.

Step 2:

3D modelling In this step the technical information derived from Step 1 are used as input data for the 3D model reconstruction via Rhinoceros 7 [29] plus Grasshopper [30] parametric modelling. The historical data allow the 3D modelling of the building volumes, limiting the on-site survey (e.g., in-situ measuring and laser scanning) to specific building details.

Step 3:

Georeferencing 3D models The 3D surface model, elaborated in Step 2, is georeferenced. Exploiting interoperability with GIS environment, through interchange file format, the 3D surface model is merged with the positioning of the PSs in the ArcGIS Pro 2.7.0 environment [31].

5 Analysis and interpretation of the displacements for damage assessment

Assuming the correct positioning of the PSs on the building 3D volume, different techniques are proposed to analyse the possible displacements of the structure, based on the combination of the ASC and DES DInSAR datasets, under the assumptions explained in Sect. 3. Three different approaches, with different approximation levels, are presented to study the active deformative processes of the single building. The first approach consists in the direct application of Eq. (2) for the evaluation of the maximum vertical and E–W displacements components, through the selection of couples of PSs belonging to ASC and DES datasets, sufficiently close to be assumed representative of the same reflecting target, unless the positioning error. The second procedure, also based on the selection of a couple of sufficiently close ASC and DES PSs, exploits the evaluation and combination of the mean LOS velocities in the two datasets, to compute the maximum displacement components, by multiplying the vertical and E–W velocity components for the duration of the acquisition period. A third procedure, characterized by a reduced computational effort, starts from the analysis of the mean velocity components associated to an auxiliar grid defined for the area of interest, multiplied by the numbers of acquisition years.

For the choice of the more appropriate strategy, a preliminary check on the LOS mean deformation velocity of the PSs is first needed, to provide an overview of the available data. In the following, an application of the described techniques for the analysis of the displacements is deepened through two case studies.

The information derived by the DInSAR measurements can highlight the existence of trends in the evolution of the ground deformation in time. The presence of trends can be associated with possible damage found on the structure. Moreover, a preliminary damage assessment related to cumulative differential deformations ongoing under a selected side of the considered building, can be implemented using limit thresholds of foundation distortions derived by literature evidences. The parameter most used in literature to determine the structural damage level is the angular distortion, given by the differential settlement between two extremes of the deformation profile, on the distance between them. Poulos et al. [32] summarized the limiting values of the significative parameters, for different types of damage or concern, in function of the type of structure. In Table 2, the literature limiting values referring to buildings, for angular distortion and total settlement, are reported. Clearly, Table 2 refers only to the framed buildings such as the two considered case studies, presented in Sect. 6. Analogously, other limiting values can be found in literature, for other different structural typologies (e.g., masonry walls, tall buildings, bridges, etc.).

Table 2 Summary of limiting value(s) for damage parameters of framed buildings and reinforced load-bearing walls by literature sources
Full size table

It is important to highlight that the differential settlement is cumulative, referring to the monitoring period. It is a part of the cumulative displacement occurred since the construction age of the building. If the building was built before the beginning of the monitoring period, the entity of the total cumulative displacement affecting the structure from its birth cannot be known through DInSAR technique. To make a global damage assessment, specific information on the building condition at that beginning of the monitoring are needed, otherwise only the relative damage can be undoubtedly estimated. Then, if the damage limit threshold is attained considering the cumulated differential displacement rescued from DInSAR measurements, it should be expected almost that relative damage condition on the structure.

Exploiting the obtained differential settlements, also a more detailed structural damage assessment can be done starting from DInSAR measurements and assigning them as imposed displacements at the base of the structural elements. This is meaningful only if enough information about the selected structure, almost an in-situ survey, and the output of the preliminary assessment are available.

6 The case studies of the Torri Stellari in Valco San Paolo and the Corviale housing quarter

6.1 Historical overview of the case studies

The Torri Stellari buildings, included in the Valco San Paolo housing quarter [33], built between 1949 and 1952 within the INA-Casa National programme [34], are part of the twentieth century architecture of Rome. The housing district is, indeed, characterized by four 8-floors tower buildings, which feature a star-shaped plan. The load-bearing structure of the four towers is a reinforced concrete frame with brick walls and hollow block slabs [35]. Due to these building characteristics, the towers can be considered a very representative model of the Italian construction trends in post-war years [36].

The Corviale housing complex was designed by a team and coordinated by architect Mario Fiorentino (1919–1982) in 1967. The final execution design was approved in 1974; the construction began in 1975 and the complex was completed in 1983. The Corviale is internationally known as an existing example of the 1970s urban planning theories and reinforced concrete industrialization [37]. The main block is 968 m long, 33 m wide and features 11 stories: 8 housing-floor, 1 open floor, 1 garage floor and 1 cellar floor. The huge block is divided into 7 sectors, with 5 entrances, 27 stairs-block, and 74 lifts. The building is entirely reinforced concrete, combining cast in situ and industrialized elements. Foundations were cast on site, as are the load-bearing partitions walls of the basement. Load-bearing walls, which vary in thickness from 35 to 75 cm, are placed each 6 m. Every 36 m there is an expansion joint and the load-bearing wall doubles. From the first floor, load-bearing walls were prefabricated reinforced concrete panels, 15 to 25 cm in thickness. The slab between the garage floor and the cellar floor is cast on site. The upper slabs feature a 3 cm thick prefabricated predalles, a ribbed cast-in-situ slab with 13 cm thick expanded polystyrene blocks. The external facades of the building were built in prefabricated reinforced concrete panels 8 cm thick; panels were of 5 types, differing in the design of the external surface and the presence of the insulating layer. The balconies of the upper block feature reinforced concrete prefabricated parapets, 12 cm thick.

6.2 Available historical sources and in-situ surveys of the case studies

The historical investigation of the two analysed housing complexes was based on different archival sources. In particular, the study of the Torri Stellari in Valco San Paolo focussed on the available original design drawings and documentation collected in the archive of the architect Mario De Renzi (1897–1967), who elaborated the general plan and the execution design of the tower n. 1 (Fig. 3a), conserved in the Accademia Nazionale di San Luca historical archive in Rome. The study of the Corviale based on the execution design documentation conserved in the ATER (Public Housing Agency) historical archive in Rome, focussing on one building block (Fig. 3b).

Fig. 3
figure 3

Original design drawings of a Valco San Paolo INA-CASA housing district (1949–1952): M. De Renzi, Star-shaped plan tower, plan of the first floor and section AA, 27 June 1950, 1: 50 (courtesy of Accademia Nazionale di San Luca), b Corviale complex, sector F (ATER Archive)

Full size image

In both cases, the original design drawings allowed the accurate knowledge concerning the geometry, the load-bearing structure and the execution details. For the Torri Stellari, some dimensional checks of the external volumes were performed on site on the tower n. 1, together with a photographic survey of the actual conservation state of the building.

6.3 3D modelling and PSs positioning

The correct positioning of the PSs on the building volumes is a crucial task for the structural interpretation of DInSAR data. The 3D modelling process, explained in Sect. 4, provides an accurate geometry for the PSs positioning. As an example, Fig. 4 shows the comparison between the PSs positioning (representing ASC and DES PSs with red and green colours, respectively) on the accurate 3D model and on the open-source Regional Technical Numerical Map (CTR) [38] schematic volumes, considering the Torri Stellari case study. It can be noted that only in the accurate 3D volume of the towers, the PSs are properly aligned along the external volumes of the buildings, considering the pitched roof, and the balconies.

Fig. 4
figure 4

PSs localization on the Torri Stellari accurate volumes (a) and CTR volumes (b), in ascending (red triangles) and descending (green circles) orbits (colour figure online)

Full size image

Figure 5 shows the same comparison for the Corviale complex. It can be noticed that, in the simplified CTR volume, the typical cross section of the building—featuring a larger top volume and a sloped basement—is not represented, with the consequent incorrect localization of the PSs into the building volume.

Fig. 5
figure 5

PSs localization in ascending (red triangles) and descending (green circles) orbits, on the Corviale block B accurate volume: from a East and b West sides; on the Corviale block B CTR volume: from c East and d West sides (colour figure online)

Full size image

6.4 Analysis of the displacements

The analysis of the displacements focuses on the Torri Stellari case study, considered representative of a significant displacement scenario. Indeed, looking at the Corviale complex area, the LOS mean velocities of its ASC and DES PSs do not reveal significant displacement trends, indicating a general stability of the area (Fig. 6).

Fig. 6
figure 6

LOS mean velocity of the PSs identified in the area of the Corviale complex (colour figure online)

Full size image

In the following Subsections, the analysis of displacements is deepened through the three approaches, introduced in Sect. 5 and characterized by an increasing accuracy level.

6.4.1 Approach 1

The first proposed procedure, named Approach 1, allows to accurately investigate the maximum displacement components, over the satellite data acquisition period. The Approach 1 starts with the selection of couples of PSs belonging to ASC and DES datasets, sufficiently close to be assumed representative of the same reflecting target, unless the positioning error. The acquisition instants of ASC and DES datasets can be different, since a time lag of a few days generally exists. Moreover, the first and last acquisition times may not be temporally coincident. For this reason, a temporal resampling is essential, taking care to ensure the overlapping of the acquisition periods of the two datasets, cutting previous or subsequent acquisitions, compared to the common acquisition period. Because of the low existing time lag between measures and the quasi-static feature of the monitored phenomena, a linear interpolation of the DES displacement measurements with respect to the acquisition moments related to the ASC dataset, and vice versa, can be done. Clearly, the initial time instant must be the same in the two datasets. Thus, in some cases, an identification of the period of interest of the time series could be required, with a cutting of the initial part of the data of one of the two datasets. The displacement value measured at the cutting time has to be subtracted from the remaining time history, allowing a null measure in the first instant common to ASC and DES datasets. In this way, since the two time series refer to the same time instants, a combination of the LOS displacements can be done with Eq. (2), to evaluate the vertical and E–W components, DV and DE–W (see Sect. 3). Through the Approach 1, it is thus possible to evaluate the maximum values of these displacement components, with reference to points spatially uniquely determined, starting from the combination of the selected PSs couple.

As an example, Fig. 7 shows a couple of ASC and DES points (represented with triangular and circular symbols, respectively), selected in proximity of the ground level of the South facade of the Tower n.1. As it can be noted from Fig. 7, the selection of points can be performed in several ways and must comply with the following criteria:

  1. (i)

    The distance between the PSs and the building must be lower than the planimetric positioning error;

  2. (ii)

    The planimetric (E–W and N–S) and altimetric distances between points must be lower than the error of the SAR data positioning;

  3. (iii)

    Being the first and second conditions satisfied, among all identified couples of points, the selected couple is the one characterized by the highest coherence value.

Fig. 7
figure 7

Selection of a couple of ascending (triangles) and descending (circles) PSs of the Tower n.1 (colour figure online)

Full size image

Then, two temporal resampling have been performed, one keeping fixed the acquisition times of the ASC dataset, the other with the ones of the DES dataset. It is worth to highlight that a cutting of the initial part of the displacement history of the ASC dataset has been required, to consider a period of acquisition common to both datasets.

Since the described selection of the couples of points, for each building facade, is computationally onerous, alternative approaches can be adopted, exploiting the slopes of the regression lines of the LOS displacement–time series of the PSs, representing the yearly LOS mean velocity for ASC and DES orbits. In these approaches, the temporal resampling can be avoided, especially in case of similar first measurement instants in the two datasets, since the mean velocity is little affected by a low difference in the number of the measurement points, over a long and consistent time series.

6.4.2 Approach 2

The second procedure, named Approach 2, is also based on the selection of the couples of ASC and DES PSs, close enough to be considered representative of the same reflecting target, as described in Sect. 6.4.1 and shown in Fig. 7. Then, the mean LOS velocities VLOS,A and VLOS,D of the selected PS are combined with Eq. (2), to evaluate the components of the velocity along the vertical and E–W directions, VV and VE–W, respectively. An estimation of the maximum displacement components DV and DE–W can be obtained by multiplying the latter velocity components for the duration of the acquisition period. For the applicability of the Approach 2, the same condition of the Approach 1 stands, based on the availability of couples of ASC and DES PSs sufficiently close to each other.

6.4.3 Approach 3

A third procedure, named Approach 3, is presented with the aim to reduce the computational effort required by the two procedures previously described. The vertical and E–W components of the displacement can be simply evaluated starting from the values of the mean velocities VV and VE–W associated to each point of the auxiliar grid, defined for the area of interest (see Sect. 3), and multiplying them for the duration of the acquisition period. It is worth to highlight that, with reference to a building, the spatial interpolation of the points can be performed at ground level or at different altitudes, for example at roof level.

As an example, the velocity maps along the LOS, vertical and E–W directions, related to the Torri Stellari area at ground level, are shown in Fig. 8. Superimposed in Fig. 8a and Fig. 8b are the PSs located at the ground level, belonging to ASC and DES orbits, respectively. The points have been selected considering the ground profile of the area and choosing a confidence band around the specific ground level of ± 2 m, equal to the altimetric error in positioning of the PSs. Moreover, if a precise information about the height of the construction is available, for example through historical sources and/or in-situ surveys, the distance between the bands of the points belonging to the roof and ground levels can be more exactly defined. This information can be useful also to compute velocity maps at different levels.

Fig. 8
figure 8

Mean velocity maps of the Torri Stellari area: a ASC and b DES data, with EBK interpolation; c vertical and d E–W components of the mean velocity (colour figure online)

Full size image

A spatial resampling of both ASC and DES ground data has been implemented, using an Empirical Bayesian Kriging (EBK) method [39], thus obtaining continuous maps of the mean LOS velocity (Fig. 8), with reference to the acquisition period, covering the years 2011–2019. To analyse the area at the scale of the single building, the continuous velocity maps have been projected on a defined grid with a cell size set at 5 m (Fig. 9), not exceeding the 3 × 3 m2 resolution of the COSMO-SkyMed products and at the same time representing a value comparable with the distance between the columns of a RC building. Adopting a deterministic approach, no information can be derived for cells characterized by the absence of PSs belonging to both datasets. In this case, an improvement can be given by the adopting of probabilistic resampling techniques, especially if the overall area results to be characterized by many points, well-spaced and belonging to both datasets.

Fig. 9
figure 9

Adopted grid in the Torri Stellari area, with superimposed ascending (red) and descending (green) PSs (colour figure online)

Full size image

For each point of the grid, the values of the velocity along the vertical and E–W directions can be thus evaluated, as shown in Fig. 8c and d, respectively, for the examined case study.

This type of graphical representation immediately highlights the presence of zones affected by substantial values of the velocity, along the vertical or E–W directions, and zones characterized on the contrary by a more stable behaviour. In the adopted convention, negative values represent downwards and West-directed displacements, while positive values represent upwards and East-directed displacements. Areas covered by green points are characterized by a stable deformative behaviour along the specific direction, presenting values of the vertical and/or E–W velocity, ranging around zero.

By observing Fig. 8c, it can be noted that there is an evidence of a pretty vertical deformational phenomenon ongoing, which can be connected to the subsidence of the area close to the Tiber River, already studied in literature [40, 41]. In particular, the four towers are in an orange zone of the vertical mean velocity map (Fig. 8c) with values ranging between − 5 and − 3 mm/year, while falling in a green zone of the E–W map (Fig. 8d), with values ranging between − 3 and − 1 mm/year.

6.4.4 Comparison of the three proposed approaches

The three proposed approaches for the evaluation of the components of the displacement of the PSs along the vertical and E–W directions are here practically implemented and compared. Because of the stable displacement trend of the area of the Corviale complex, characterized by low values of displacement, the Valco San Paolo area is examined. The three procedures are applied to the couple of points shown in Fig. 6, belonging to the ground level of the building n.1 of the Torri Stellari.

According to the Approach 1, Fig. 10 shows the trend of the vertical and E–W components of the displacement of the selected couple of points over the acquisition period, with cyan and red circles, respectively. For each displacement component, two series exist, because of the two temporal resampling previously described in Sect. 6.4.1 (Fig. 10a–d). The higher values among the two series give the vertical and E-W components corresponding to the Approach 1.

Fig. 10
figure 10

Comparison of the vertical (DV) and E–W (DE–W) displacement components for the three approaches: a and b DES data resampled on ASC ones; c and d ASC data resampled on DES ones

Full size image

Adopting the Approach 2, the maximum displacement components of the selected couple of points have been evaluated by multiplying the mean velocity components (superimposed in Fig. 10a–d with continuous grey lines) for the duration of the acquisition period. The values of the mean velocity components relative to the Approach 2 are also indicated in the figure.

With reference to the Approach 3, the displacement values are evaluated considering the nearest point of the auxiliar grid (see Sect. 6.4.3) to the selected couple of points. Similarly to the Approach 2, the values of VV and VE–W obtained through the maps have been multiplied by the duration of the acquisition period. The values of the mean velocity components relative to the Approach 3 are also reported in Fig. 10a–d and superimposed with black dashed line.

Two important clarifications are herein reported:

  1. (i)

    The continuous grey line and the violet dashed line represent the components of the mean velocity along the considered direction for the Approaches 2 and 3, respectively. In general, these latter can be different from the regression line of the time series of the resampled displacements of Approach 1;

  2. (ii)

    The initial instant is coincident among the three approaches: if the acquisition period used in the Approach 1 is reduced due to resampling issues, the same interval time should be considered also for Approaches 2 and 3 for the calculation of the displacements.

Observing the results of the examined couple of points, it can be noted that the horizontal displacement component presents a high oscillation, vice versa a linear decreasing trend over the acquisition period is obtained for the vertical displacement component. In all analysed cases, similar values of the maximum vertical displacement component are provided by the three approaches. With reference to the horizontal displacement component, an almost negligible magnitude is found, with a measurement oscillation around zero. The maximum displacements in this direction are comparable with the measure error for the single deformation measurement, as highlighted in Sect. 3. A well-defined trend cannot be identified for the horizontal displacement components and, from a statistical point of view, the applicability of Approaches 2 and 3 is lost, due to the low values of the gradient of the regression line and determination coefficients. This is confirmed by the very low value of the regression slopes, equal to 0.036 and 0.008 for curves in Fig. 10b, d respectively. Under these assumptions, the most effective procedure is represented by Approach 1.

As a final remark, Approach 1 represents a very suitable procedure for the evaluation of the maximum values of the displacement components. Nevertheless, a significant computational effort is required for its proper implementation, that can be reduced through the adoption of both Approach 2 and Approach 3. The existence of a well-defined trend of the displacement–time series is required to guarantee the applicability of Approach 2. In addition to this condition, Approach 3 provides good results if many points exist in the examined area, well-spaced and belonging to both datasets, necessary for a proper evaluation of the velocity maps along the LOS, vertical and E–W directions. Approach 3 is the simplest procedure to be implemented, since the selection of couple of points in the two datasets, close enough to be representative of the same target, is not required.

As an example, to compare the different computational effort required by the three approaches, the operations necessary to obtain the displacement profile at the ground level of a 15 m square plan building are herein reported:

  • Approach 1, procedure to be implemented for all facades of the building:

    (i) Choice of three couples of close enough points on the selected facade;

    (ii) Cutting of the initial part of the data of one of the two datasets, if necessary;

    (iii) Execution of the double temporal resampling for each couple of points;

    (iv) Evaluation of the vertical and horizontal displacement components, for each couple of points and resampled series;

    (v) Evaluation of the maximum displacement components over the acquisition period, for each couple of points.

  • Approach 2, procedure to be implemented for all facades of the building:

    (i)Choice of three couples of close enough points on the selected facade;

    (ii) Cutting of the initial part of the data of one of the two datasets, if necessary;

    (iii) Evaluation of the LOS mean velocity for both ASC and DES datasets, for each couple of points;

    (iv) Evaluation of the vertical and horizontal velocity components, for each couple of points;

    (v) Evaluation of the maximum displacement components over the acquisition period, for each couple of points.

  • Approach 3:

    (i) Spatial resampling of both ASC and DES points at ground level on the auxiliary grid, using an interpolation technique;

    (ii) Evaluation of the LOS mean velocity for both ASC and DES datasets, for all points of the resampled grid;

    (iii) Evaluation of the vertical and horizontal velocity components, for all points of the resampled grid;

    (iv) Evaluation of the maximum displacement components over the acquisition period, for all examined points.

6.4.5 Limits in the applicability of the three proposed approaches

This paragraph discusses about limits in the applicability of the three proposed approaches, presenting some practical cases. One of the main concerns refers to the distribution of the available points in the ASC and DES datasets.

In this framework, the case study of the Corviale complex is very useful to practically show some limits in the applicability of Approach 3. As an example, Fig. 11 shows the distribution of ASC and DES PSs at ground level, for the Corviale complex. An alignment of the ASC and DES points, respectively along the western and eastern sides of the building, is found (see also Fig. 5). Moreover, a larger view of the area surrounding the Corviale complex, reported in Fig. 6, shows the existence of wide zones characterized by a low number of PSs at ground level, or even by the lack of PSs. In such a case, the use of interpolation techniques for the definition of velocity maps presents severe limitations and particular attention should be paid.

Fig. 11
figure 11

Upper view of the Corviale complex: distribution of ascending (red triangles) and descending (green circles) PSs at ground level (colour figure online)

Full size image

With reference to Approaches 1 and 2, limits in their applicability usually refer to the difficulties encountered in the selection of couples of points, sufficiently close each to the other to be considered representative of the same reflecting target. Examples of these situations can be the inclined roof of the Buildings 2 and 4 of the Torri Stellari (Fig. 4a, b), and the sides at the ground level of the Corviale complex (Figs. 5 and 11), both characterized by the presence of points belonging to one dataset, only. Another interesting case concerning the applicability of Approaches 1 and 2 refers to areas of the building with a different number of ASC and DES points. It can be assumed that points belonging to different datasets can be considered sufficiently close each to the other, if their planimetric and altimetric distances are lower than 2 times the PS positioning error. Approaches 1 and 2 can be thus properly adopted for the evaluation of the maximum displacement components, only if the distance between selected PSs does not exceed the above limit value. As an example, this condition is found at the inclined roof level of the Buildings 1 and 3 of the Torri Stellari, presenting many points belonging to the ASC dataset and one point only to DES dataset (Fig. 4a, b). For the Building 1, the lower distance between ASC and DES PSs exceeds the limit value, making not applicable both Approaches 1 and 2. Vice versa for the Building 3, being the distance between ASC and DES points included in the recommended range.

6.4.6 Interpretation of the displacements for damage assessments

The three illustrated Approaches can be used, with different difficulties levels, to outline the base settlement profiles on the building sides. In particular, Approaches 1 and 2 are not always implementable and have the highest computational burden to rebuild the settlement profiles. The main obstacle, for the first two procedures, consists in finding couples of ASC and DES PSs, close enough to be considered representative of the same reflecting target, at least at each end of every building facade. This is very difficult, because of the lateral and inclined sensor acquisition system. It is usual to observe sides of the same building characterized by the presence of points belonging to one dataset only, as discussed in Sect. 6.4.5. When applicable, Approach 3 is the easier procedure to exploit to create the displacement profiles, having continuous mean velocity maps along the vertical and E–W directions. Taking the velocity values in the desired direction, along the examined alignment, they can be multiplied by the number of years in which that mean velocity trend can be extended. In the specific, for framed buildings, the mean velocity values can be taken in correspondence of the columns.

An example is given, for the Torri Stellari building number 2. The settlement profiles in the vertical and E–W directions for the South side of the tower (Fig. 12a), obtained starting from the velocity maps shown in Sect. 6.4.3 (Fig. 8c, d), are represented in Fig. 12b and c, respectively.

Fig. 12
figure 12

a Structural scheme of tower number 2 with the position of the three considered columns; example of settlement profiles of one short side of the Torri Stellari building number 2, in b vertical and c E–W direction

Full size image

The displacement values, obtained considering a time interval of 8 years, are marked in correspondence of the three columns (1, 2 and 3) highlighted in Fig. 12a, assuming that the structural scheme is the same for the four towers. This side of the tower number 2 is representative because of the existence of an evident differential displacement phenomenon between the two ends of the considered facade, both from vertical (Fig. 12a) and E–W (Fig. 12b) settlement profiles. Starting from the represented profiles, a preliminary damage assessment can be performed with respect to the monitored period, associating the maximum differential displacement or the angular distortion to limiting thresholds given in the classical literature, based on empirical evidence, as presented in Sect. 5.

The displacement profiles obtained from the DInSAR technique can also be used as action affecting the structure in an analytical model, allowing to perform more accurate analysis.

7 Conclusive remarks

This paper presents a work methodology for the use of DInSAR measurements for the structural analysis of buildings under monitoring. DInSAR-based displacements time series and mean deformation velocity values allow to identify possible critical situations. The work presents different Approaches, with increasing accuracy levels, to study the active deformative processes of the examined buildings and deals with the related damage assessments, which can be performed according to literature evidences or more detailed procedure based on analytical structural models. The combined use of historical investigations, accurate 3D modelling and consistent positioning of the PSs in the GIS environment is described and then applied to two case studies, the Torri Stellari in Valco San Paolo and the Corviale housing complex in Rome. The case studies analysis provides an insight into the three interpretative approaches of the DInSAR products, starting from the available data in terms of PS positioning and mean LOS velocity.

The study highlights the need of an accurate 3D model to provide a consistent positioning of the PSs in the GIS environment. In this sense, the proposed 3D modelling via the historical sources is a solid base to achieve accurate information on the real geometry and characterization of the structure under monitoring, with lower effort in terms of in-situ investigations. The interoperability with different modelling software, via exchange file format, allows automatizing the process from the 3D modelling to the GIS environment for the correct positioning of the PSs with low effort.

Furthermore, the correct positioning of the PSs allows to improve the study of the three proposed interpretative approaches, whose final aim is the performing of a civil structural health monitoring of single or more buildings and/or infrastructures. Clearly, the evaluation of the maximum displacement components, as well as the calculation of the maximum differential settlement, related to a building facade, represents a critical issue in the identification of possible critical situations for the building to be monitored.

In this framework, it is fundamental to set out the typology of external actions, whose effects can be potentially detected using SAR data. According to current literature, good results can be obtained with DInSAR measurements, in case of pseudo-static actions, such as actions related to ground deformations (e.g. subsidence settlements, excavations execution, landslides), hydraulics actions (e.g. infiltrations and flooding), thermal variations, shrinkage and viscous phenomena of concrete, long duration vertical loads.

The presented methodology is proved to be useful for a structural health monitoring of buildings, since the previously described approaches allow to identify the ongoing of potentially critical phenomena. The examined technique enables to understand if the building is in a stable area or is subjected to dangerous settlements and the direction along which they are active. Moreover, a preliminary assessment procedure, based on the combination of DInSAR data with basic information concerning the construction geometry (e.g. through historical sources), can be implemented, to obtain a damage classification, according to literature damage scales, by comparing deformation limits with the monitoring outcomes. The damage classification can help establish a list of priorities of the more vulnerable constructions, for a better planning of more in-depth evaluations.

Furthermore, a complete process of structural assessment and monitoring can be performed for an examined construction, supporting the DInSAR measurements with additional information obtained from in-situ inspections (for example for the definition of the material mechanical properties), required to establish a structural model and to perform accurate verification.

Within its limits of applicability, Approach 3 is shown to be the most adequate procedure for performing a pre-structural damage classification, because of its low computational effort and the ease to check the trend of the displacements in the examined area.