Abstract
Skewed masonry arch railway bridges are common, yet their structural behaviour under typical working loads, along with gradual changes in behaviour due to degradation, can be difficult to determine. This paper aims to address this problem through detailed monitoring of a damaged, skewed masonry arch railway bridge in the UK, which was recently repaired. A comprehensive Structural Health Monitoring system was installed, including an array of fibre-optic Fibre Bragg Grating (FBG) sensors to provide distributed sensing data across a large portion of the bridge. This FBG monitoring data is used, in this paper, to investigate the typical dynamic structural response of the skewed bridge in detail, and to quantify the sensitivity of this response to a range of variables. It is observed that the dynamic bridge response is sensitive to the time of day, which is a proxy for passenger loading, to the train speed, and to temperature. It is also observed that the sensitivity of the response to these variables can be local, in that the response can differ throughout the bridge and be affected by existing local damage. Identifying these trends is important to distinguish additional damage from other effects. The results are also used to evaluate some typical assumptions regarding bridge behaviour, which may be of interest to asset engineers working with skewed masonry arch bridges.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Masonry arch bridges feature significantly on the road and rail networks of the United Kingdom and other countries. Across Europe, railway networks alone contain an estimated 200,000 masonry arch bridges. In the UK, roughly 40–50% of bridge spans on the rail and road networks are masonry arches, resulting in an approximate overall total of 70,000 of these structures [1]. Many of these are located at important points on passenger and freight routes, meaning that their continued smooth operation carries considerable social and economic significance. At the same time, many of these bridges are ageing structures, which have typically been in continuous operation for between 100 and 150 years. The length of their working lives and the changing nature of modern vehicular loading—particularly for rail—has led to damage [2].
The Ultimate Limit State (ULS) behaviour of masonry arch bridges, when these structures are close to collapse, is relatively well understood. A range of established theoretical approaches exists to study these structures in varying levels of detail, from simplified limit analysis tools [3, 4]—which are commonly used in practice to establish a first estimate of a structure’s capacity—through to advanced computational approaches such as the Finite Element Method (FEM) and Discrete Element Method (DEM)—which can be applied to study complex aspects of bridge behaviour such as the interactions of different structural components or soil-structure interaction within a bridge, which may affect its ULS performance [5, 6]. These computational studies offer valuable contributions to our knowledge of masonry arch bridges. However, these approaches are sometimes too simple to account for extensive uncertainties, and sometimes may be too complex, considering both the underlying uncertainties as well as the required cost and time, for regular application in asset management practice.
For this reason, quick, simplified assessment approaches are still in use for asset management purposes, except for certain highly significant, unusual, or damaged structures which warrant an increased scale of analysis. Frequently, simplified assessments will suggest that masonry arch bridges do not have sufficient capacity to carry higher ratings of train loading, leaving asset managers with little choice but to implement speed or weight restrictions. This is despite the fact that the full impact of speed restrictions on masonry arch bridges remains unclear. Increasing our understanding of the real behaviour of masonry arch bridges under working conditions, i.e. at the Serviceability Limit State (SLS), will allow such decisions to be made in greater context, and may even allow for some simplified assessment procedures to be revisited and revised based on field measurement data.
SLS behaviour is more complex and less well understood than the ULS case, yet it is behind a substantial majority of the observed defects requiring intervention and repair. A lack of proper understanding of SLS behaviour creates a major challenge for asset managers, and when a bridge exhibits signs of damage or deterioration there may be little choice other than to use blunt instruments, such as speed and weight restrictions or extensive repair works. There is the risk that inappropriate asset management decisions may be made, with potential consequences such as repair works not being properly tailored to the structures they seek to benefit. Such interventions may introduce changes in the stiffness profile of a masonry bridge, giving rise to new load paths that either exacerbate current damage or lead to new damage arising in another location. Even when interventions do not actively harm a bridge, uncertainty remains as to how long these may remain effective.
The SLS behaviour of masonry arch bridges remains an active research area. Some computational studies have investigated the SLS behaviour of masonry arch bridges, e.g. [1]. However, the study of SLS behaviour is also a prime opportunity to deploy Structural Health Monitoring (SHM). Monitoring can provide useful insights into the real-world behaviour of these structures, improving our fundamental understanding of this behaviour and offering validation to complex analyses, where uncertainty in the results may otherwise persist.
This paper presents results from a detailed field monitoring project carried out at a case study bridge: a single span, skewed, masonry arch bridge in North Yorkshire, UK. This bridge shows signs of past damage, which were the target of repair work in 2016. To validate the success of this intervention, and track the bridge’s structural condition over time, monitoring of its live load response under working (i.e. SLS) loads was commissioned by the asset owners, Network Rail. This monitoring has been carried out in collaboration between the Cambridge Centre for Smart Infrastructure and Construction (CSIC) and AECOM [7], although, with the exception of ambient temperature data, only results from CSIC sensors are presented here.
1.1 The impact of skew angle on masonry arch bridges
A subgroup of masonry arch bridges is those which are skewed, meaning that the longitudinal and transverse axes of the bridge are not perpendicular to one another. For instance, in the case study structure that is considered in this paper, the presence of skew was necessary so that the railway tracks above the bridge could span over an existing road. The bridge crosses this road at an angle of 64°, meaning that the skew angle of this particular bridge is 26°.
The impact of skew on a masonry arch bridge’s structural behaviour can be unclear and increase its complexity. The planform of a skewed arch is no longer a rectangle, as it would be for a square-spanning arch; instead, it is a parallelogram. Whereas the span direction for a square-spanning arch can intuitively be seen to follow the arch’s longitudinal axis, the preferred load path in a skewed arch is not as clear. The bridge width can influence whether a skewed arch spans along its square or its skew span direction, and rules of thumb to account for skew are offered in guidance documents [8, 9]. It is generally considered that the behaviour of skewed arches can be significantly more three-dimensional than may be the case for square-spanning arches and that for even modest skew angles it is sensible to perform a full 3D analysis for skewed bridges [8]. This three-dimensionality of structural response has been observed in computational analyses [10, 11], while previous monitoring of skewed masonry arch bridges does exist [12] but is very limited. In this paper, detailed fibre-optic sensing data is analysed to offer new insights into the three-dimensional response of skewed masonry arch bridges to their working loads.
1.2 Structural health monitoring of masonry arch bridges
Asset owners sometimes commission Structural Health Monitoring of their masonry arch bridges to observe and track metrics describing their structural behaviour. The aim is not necessarily to gain a deep understanding of each structure through monitoring, but rather to identify any changes in behaviour which could be emblematic of the onset or progression of damage in the bridge, thus warranting a bridge inspection. The actual identification of specific damage, and prescription of remedies such as repair works, is more likely to be based on visual inspection of a bridge. For this reason, SHM strategies to date in the UK have tended to be centred on simplified, single-point measurements that can be taken to be representative of the overall condition of a larger portion of a structure or even its entirety.
Network Rail commonly uses a deflection pole measurement system to record vertical displacement of the arch crown as a train goes over the bridge. It is assumed that, as damage progresses, the dynamic response will increase. However, by the time this damage, which may be occurring far from the arch crown, has progressed sufficiently to influence the crown vertical deflections, it may already be quite significant and require an appreciable intervention to remedy. Furthermore, the deflection pole method is not practical for bridges in inaccessible locations, such as those spanning rivers or deep valleys. It may also necessitate costly and disruptive road closures and therefore does not lend itself to continuous long-term monitoring.
Alternatively, remote sensing technologies typically only require access to the bridge for installation and maintenance. Conventional point sensors such as strain gauges and LVDTs can be deployed in this way, as well as a range of more emergent sensing technologies such as fibre-optic monitoring. This study uses Fibre Bragg Gratings (FBGs), a type of fibre-optic monitoring technology which enables efficient dynamic monitoring at numerous points across a structure [2]. FBGs can be used in isolation, or in conjunction with other sensing technologies as part of a complementary monitoring system. A number of SHM studies have made use of FBGs but these have only recently been applied to monitor masonry structures [2, 13, 14]. The project described in this paper is believed to be the first application of FBGs to study a skewed masonry arch bridge.
FBGs offer the possibility of a large number of measurement locations across a structure, enabling monitoring of local behaviour in increased detail. Local measurements allow for more localised damage detection and the ability to track damage in more detail, but also provide the information needed to build up a picture of the overall behaviour of the structure. The broader adoption of such schemes, however, will ultimately require improvements in automated data processing, visualisation, and presentation, so that the interpretation of monitoring data can still be performed quickly and intuitively by asset managers.
1.3 Introduction to the monitoring case study
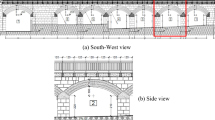
The bridge considered in this study is a single span, skewed masonry arch railway bridge in North Yorkshire, UK. Completed in 1868, it carries a range of passenger and freight rail traffic, on two tracks. Its construction is a brick masonry arch barrel, with the bricks laid helicoidally following the skew span direction, supported by stone blockwork skewbacks, abutments, and wing walls. The spandrel walls and parapets are also built using stone blocks. An elevation view of this bridge is shown in Fig. 1.
The main signs of damage at this bridge are separation cracks between the brick arch barrel and stone spandrel walls, and an additional longitudinal crack in the south-eastern quadrant of the arch soffit. This crack is located roughly underneath the centreline of the southern track and extends from the arch springing by just over 3 m, approximately following the skewed span direction. In addition to these cracks, some cracking and bulging of the spandrel walls has been reported, as well as bulging of the south-western and north-eastern wing walls, adjacent to the acute corners of the skewed arch. In 2016, soil anchors were fitted in these wing walls, ten new tie rods were installed through the spandrel walls to constrain the arch in its transverse direction, and the cracks were comprehensively stitched using steel rods. Visible signs of this damage and intervention work are shown in Fig. 2, and the extent of the tie rods can also be seen in the elevation view of Fig. 1. The new tie rods were installed to replace previous ones, which had been found to be ineffective in preventing further expansion of the spandrel separation cracks. Pattress plates for the previous tie rods can also be seen in Fig. 2; these are smaller and a lighter colour than those for the new tie rods.
Based on visual observations from before and after this repair work, the 2016 intervention was successful in reducing the growth of cracks and the liveliness of the bridge response. In particular, the arch barrel had previously displayed visible vertical deflections under train loading, relative to the spandrel wall. This “pumping” response was believed to cause progressive deterioration of the bridge over time, and so preventing this response was a key objective of the intervention. However, the extensive nature of these repairs, in which the cracks were stitched at frequent intervals, was motivated by significant uncertainty regarding the bridge’s structural response to live loads. It is therefore unclear to what extent this intervention was proportionate to the scale of the problems at this bridge, and for how long it will continue to remain effective. This led to a desire from the asset managers to instigate regular condition monitoring of the bridge. Specifically, this monitoring should track any increases in the magnitude of the bridge response under its SLS loads, which could indicate the return or progression of damage. The bridge crosses a busy road, so continuous deflection pole monitoring was not feasible.
FBGs were installed in a variety of innovative configurations at this bridge, as previously reported in [7, 15, 16]. In particular, the installation included monitoring of both in-plane and out-of-plane crack displacements, which was used to measure “pumping” between the arch barrel and the south spandrel wall.
In this paper, the FBG implementations used at the case study bridge will be introduced and explained, followed by analysis and interpretation of 6 months of monitoring data recorded between September 2018 and February 2019. The high sensitivity of the FBG measurements is used to explore the statistical variability of the dynamic strain response and its sensitivity to variables such as temperature, date, train speed, and time of day, the latter of which is used as a proxy for passenger loading.
2 Methodology
The FBGs used in this installation were manufactured by FBGS, and a model sm130 FBG interrogator manufactured by Micron Optics was used to record measurements. Custom-made clamps, designed by CSIC and manufactured by L&C Precision Engineering, were used to install the fibre-optic cables on the bridge. The measurement noise achieved by this monitoring system was 1 με, ideal for capturing the small magnitudes of movements at this masonry arch bridge. By pre-straining the FBGs during installation, so that they are under tension when the bridge is unloaded, both compressive and tensile strains can be measured. This pre-strain was applied by hand and was of the order of several hundred microstrain, an order of magnitude above the compressive strains to be measured.
A combination of thermal and mechanical strain will make up the overall total measured strain and, furthermore, changes in temperature can cause the refractive index of the glass core inside the fibre to vary. Therefore, the true mechanical strain is related to the measured shift in Bragg wavelength by Eq. (1), in which \(\Delta \in_{m}\) is the change in mechanical strain, \(k\) is a strain calibration coefficient for the fibre, \(\frac{{{\Delta }\lambda }}{{\lambda_{0} }}\) is the ratio of the measured change in wavelength to the original Bragg wavelength for the grating, \({\Delta }T\) is the change in temperature, and \(\alpha\) is a coefficient accounting for thermal effects. In reality, \(\alpha\) captures a range of thermal and thermo-optic effects which influence the fibre-optic cable and the structure being monitored [17].
Consequently, it is necessary to compensate for thermal strains in static FBG monitoring. However, when only short dynamic events are being measured, changes in thermal strain can be neglected. In this study, temperature variation during dynamic events was assumed to be negligible, but temperatures were still recorded to account for possible thermal effects within the bridge. This ambient temperature data was measured by separate points sensors, distributed across the bridge, and then averaged to give a single value for each train event.
The total allowable number of FBGs is limited by the wavelength range of the FBG interrogator. Each FBG is etched to have its own Bragg wavelength. These wavelengths need to be sufficiently separated so that the individual gratings can always be distinguished during monitoring. In this study, four fibre-optic cables, each with a maximum of 20 FBGs, were used. The sampling frequency was 1 kHz.
74 FBGs were ultimately installed on the arch soffit of the case study bridge, of which 34 are discussed in this paper. Preliminary results for the remainder of the FBG installation were presented in [15, 16] and detailed analysis of data from these other sensors will be carried out in future work.
The FBG sensors which will be discussed in this paper were fixed to the case study bridge in accordance with the installation plan in Fig. 3. Key accompanying dimensions are given in Table 1. Values for the thickness of the arch barrel and the depth of ballast and fill material are based on inspection reports and could not be independently verified in this study. The FBGs in Fig. 3 monitor three key regions of the bridge:
-
1.
FBGs L1 to L20 are installed in two longitudinal lines of ten FBGs each along the arch intrados, directly underneath the centreline of the north track and the overall bridge centreline. There are no clear visible signs of damage in this region of the bridge, and so these sensors are used to investigate the general structural behaviour of a skewed masonry arch railway bridge. It was previously reported by the authors in [13, 14], that the skewed span direction appears to offer a preferential load path for the arch to transmit applied train loading to its abutments. In this paper, the sensitivity of this longitudinal response to various parameters is investigated in detail. These FBGs are installed with gauge lengths of 1 m.
-
2.
FBGs SE1 to SE8 are installed to measure the in-plane crack opening of the south-eastern longitudinal crack. These FBGs are installed with gauge lengths of 0.5 m, and at 0.5 m intervals along the length of the crack. In this way, FBG SE1 is located at the crack root, FBG SE7 is located at the crack tip, and FBG SE8 is located just ahead of the crack tip in masonry that is not currently visibly cracked.
-
3.
FBGs SS1 to SS6 are installed in pairs, in three locations along the south spandrel separation crack. These locations were either side of the arch crown, at the \({\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 {12}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${12}$}}\) and \({\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {12}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${12}$}}\) points of the arch span, as well as the eastern \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}\) point. A schematic of a typical FBG pair is shown in Fig. 4. It can be seen that one fibre is installed in the in-plane transverse direction of the arch, to measure the pure crack opening, while the second fibre is inclined so that it measures both crack opening and crack shearing, or “pumping”, in the vertical direction. With the data from both sensors, it is possible to calculate the relative vertical movement across the crack, i.e. movements parallel to \(c\) in Fig. 4. These readings were validated against other measurement technologies which recorded the relative vertical displacements directly [7].
Using the notation in Fig. 4, the fibre measuring pure crack opening has a gauge length of \(a = 1 {\text{ m}}\). This fibre is parallel to the transverse direction of the arch barrel, while one end of the second fibre in this pair is displaced by \(c = 150 {\text{ mm}}\). As a result, the gauge length of this second fibre is \(b = \sqrt {a^{2} + c^{2} } = 1.011 {\text{ m}}\). Relative movements across this spandrel separation crack are known to be small in magnitude, such that there is a negligible change to the interior angles of this triangle. Therefore, as movements across the crack occur, the new side lengths of this triangle are given by Eq. (2).
Here, \({\Delta }c\) corresponds to the vertical, out-of-plane, displacements of the arch barrel relative to the spandrel wall. This is of interest but cannot be directly measured. \({\Delta }a\) and \({\Delta }b\) correspond to the axial extensions of the fibres in these two directions (see Fig. 4) and can hence be related to the measured FBG strains \(\in_{a}\) and \(\in_{b}\) using Eq. (3). \({\Delta }a\) is also the in-plane component of the crack opening movements.
Rearranging Eq. (2) and substituting for \({\Delta }a\) and \({\Delta }b\) results in Eq. (4), a quadratic in \({\Delta }c\) in which all else is known. Solving this for each instance in time yields the dynamic “pumping” displacements of the arch barrel relative to the spandrel wall.
FBGs L1 to L20, installed in the longitudinal direction of the bridge, are clamped to the bridge such that their gauge length, along the fibre axis, is 1 m. Note that the arch barrel is elliptical in the skew span direction, which means that the corresponding arc length between two adjacent clamps is slightly greater than 1 m. However, this was estimated to cause only a 0.07% difference in the strain measurements, and so was neglected. Additionally, it is more important to emphasize that the patterns and variability of strain across the arch, and any changes in these over time, are of primary interest rather than the absolute values of strain.
Monitoring data were recorded for a range of passenger trains, on each monthly monitoring shift between September 2018 and February 2019. The data was categorised by train class and direction, which corresponded to the track on which the train had passed over the bridge. Information was then assigned to each data file to represent the date and time of the measurement, the ambient temperature (measured by other point sensors), and the train speed (calculated using the FBG data itself). This allowed different groupings of data to be analysed, to better investigate the sensitivity of the strain response to individual variables while minimising the influence of other variables. The variables considered in this analysis were train speed, ambient temperature (to investigate the impact of any seasonality on the response, through thermal expansion or contraction of the bridge), time of day (which was used as a proxy for passenger loading, by differentiating between peak and off-peak trains), and date (to investigate any potential long-term trends or deterioration of the bridge over time).
In this paper, results for Class 185 trains are studied. These have been chosen as representative of the SLS loading case, since they are the most common train class to pass over this bridge.
3 Results
3.1 Typical strain and displacement distribution time histories
3.1.1 Arch intrados: distributions of longitudinal strains
A typical distribution of longitudinal strains along the arch intrados, as a Class 185 train passes over the bridge on the northern track, is shown in Fig. 5. In this figure, plots for the individual FBG responses are arranged so that the direction of travel of the train is from the top to the bottom of the overall figure, with the train travelling directly above the FBGs in the left-hand column. Thus, the train passes first over FBG L1 and last over FBG L10, as it travels east. Note that, after FBG L10, the fibre-optic cable returns westward along the centreline of the bridge, so that FBG L20 is the first to detect the passage of a train on the northern track and FBG L11 is the last. This sequence can also be seen in the FBG installation plan in Fig. 3.
The FBG strain data shown in Fig. 5 onwards has been processed using a low-pass filter, to remove high-frequency noise in the signals. For FBGs close to the arch crown – such as FBGs L5, L6, L15, and L16 where there is less potential for load distribution to occur through the backfill before loads are transmitted into the arch, it is still possible to identify the individual axles on each bogie of the train. For FBGs in other locations, these axles tend to merge into a single peak. In such locations, the time history of the strain response is composed of single peaks at the start and end of the response, corresponding to the first and last bogies of the train, with intermediate double peaks in which the rear and leading bogies of adjacent carriages are both visible.
Throughout the figures in this paper, tensile strains are plotted as positive while compressive strains are negative. Note that the measured strains are purely the result of dynamic train loading and do not include the substantial, pre-existing compressive strains caused by the dead load of the bridge.
Using the monitoring data for this typical train event, the instantaneous strain distributions across all longitudinal FBGs can be plotted for times of interest. Examples are shown in Fig. 6, with distributions included that correspond to the critical axle load of the train from Fig. 5 being applied above FBGs: (a) L18, the western third point, (b) L16, just west of the arch crown, (c) L15, just east of the arch crown, and (d) L13, the eastern third point. These responses—corresponding to progressive instances in time during the passage of this train—are plotted, respectively, as dotted, dot-dashed, dashed, and solid lines, whose colour varies progressively from black to light grey.
The instantaneous longitudinal strain responses observed at the arch intrados when the leading axle of a typical Class 185 train passes above key locations along the arch span, and schematics of the anticipated thrust lines in the arch bridge for point loads applied in these locations, namely a the western third point, b west of the arch crown, c east of the arch crown, and d the eastern third point
In each case, a bulb of positive, tensile strains is observed in the vicinity of the applied load, with compressive strains either side of this bulb. This observation supports the notion that a potential load path for these applied forces is through arching action in this longitudinal direction. Furthermore, the instantaneous intrados strain distributions in Fig. 6 are consistent with the anticipated thrust lines for concentrated loads applied at locations (a–d) along the span, which are also shown schematically in Fig. 6. Close to the applied load the thrust line will pass nearer to the arch extrados so that strains at the intrados are tensile. Outside of this region, the thrust line will be nearer to the intrados, and intrados strains will, therefore, tend to become compressive.
The distributions in Fig. 6 also demonstrate that the largest tensile strains occur close to the arch crown when loads are applied directly overhead: the symmetric loading case. This is to be expected because close to the crown there is the least backfill material between the arch and the track and therefore the least opportunity for load distribution to occur before the load path enters the arch. The largest compressive strains, meanwhile, are observed on either side of the arch at times when loads are applied on the opposite side: the asymmetric loading case. Again, this is to be expected, as the asymmetric loading case will cause the thrust line to pass closer to the intrados in the locations where peak compressive strains are observed (see schematic thrust lines (a) and (d) in Fig. 6).
The largest peak-to-peak strains are observed at the arch \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) points. This is consistent with later observations in Sect. 3.2, in which the statistical distribution of peak-to-peak strains for all recorded data is presented.
When trains pass on the northern track, the largest magnitude response is observed in FBGs L1 to L10, located directly underneath the active track. Although the pattern of strains along the bridge centreline is very similar, the strain magnitudes here are reduced; they are in the range of 50–90% of the values observed in corresponding FBGs under the north track centreline.
3.1.2 South-eastern longitudinal crack: distribution of crack opening displacements
Figures 7a and 8a show typical time histories of crack opening displacements at the south-eastern longitudinal crack, as a Class 185 train passes on the south and north track respectively. Figures 7b and 8b show schematics of these crack opening distributions overlaid on photographs of the crack. The schematics show the relative shapes of these distributions while the magnitudes of movements have been exaggerated, although the schematics in Figs. 7b and 8b are plotted at the same scale.
In Figs. 7a and 8a, crack opening is positive and crack closing is negative. In both of these figures, a “football-shaped” distribution is observed along the crack length, with the response being largest over the central portion of the crack. FBGs SE1 and SE7 are located at the root and tip of the crack respectively, while FBG SE8 is located ahead of the crack tip. Magnitudes of peak-to-peak movements are similar at FBGs SE1 and SE8, and only slightly larger at FBG SE7, although the ratio of tension to compression is higher at the crack tip than it is at the crack root.
The crack opening movements occur relatively simultaneously along the crack length, as trains pass over the bridge. The largest crack opening responses take place when train axles are at the eastern \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) point, above the crack. This gives rise to the distributions shown with black bars in Figs. 7b and 8b, for trains travelling on the south and north tracks respectively. Conversely, when axles reach the western \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) point, peaks in crack closing are observed. For trains on the south and north tracks, these take the form of the distributions shown with white bars in Figs. 7b and 8b respectively. While, in both cases of crack opening and closing, the peak response is observed over the central region of the crack, it is also observed in Figs. 7b and 8b that crack opening results in generally larger movements over the top half of the crack, while crack closing leads to larger movements over the lower half of the crack.
Comparing each FBG between Figs. 7 and 8, the magnitudes of peak-to-peak crack opening remain similar regardless of the track on which trains are travelling. However, in Fig. 7, for a train travelling on the south track directly above the crack, movements over the upper half of the crack are primarily tensile and the crack is opening, while movements over the lower half of the crack are primarily compressive and the crack is closing. When trains pass on the northern track, as in Fig. 8, movements at the crack are almost entirely compressive, at all points along its length.
It is of interest that the lower half of the crack displays primarily compressive movements regardless of whether a train is passing directly overhead or on the other side of the bridge. This could suggest that compressive thrusting into the abutment and obtuse corner of the arch dominates the response in this region, where the fill depth is large and therefore local transverse bending is negligible. It is also interesting that tensile movements ahead of the crack tip are not negligible when trains are passing directly overhead, as seen for FBG SE8 in Fig. 7. For these load locations, the response in this region of the arch is consistent with transverse sagging bending. Tracking the evolution of these movements over the long term will provide insight into whether the crack is stable or still growing, with the potential for any changes to be detected before they are observable in visual inspections of the bridge.
3.1.3 South spandrel separation crack: distributions of crack opening and pumping displacements
In each of the measurement locations across the southern spandrel wall crack, monitored by FBGs SS1/SS2, SS3/SS4, and SS5/SS6, strains have been converted to give relative displacements of the arch barrel compared to the spandrel wall. Here, these are presented in two orthogonal directions: in-plane crack opening in the transverse direction of the arch barrel, and out-of-plane vertical “pumping” displacements (i.e. crack shearing). Crack opening and upwards vertical movements are plotted as positive, while crack closing and vertical downwards movements are plotted as negative. The high stiffness of the spandrel walls limits their vertical deflection. This was confirmed by the fact that the relative vertical displacements of the arch barrel compared to the spandrels agree very well with overall vertical displacements of the arch compared to the ground [7].
Figures 9 and 10 show typical crack opening and relative vertical displacements at the three monitoring locations, for Class 185 trains passing on the southern and northern tracks respectively. The top rows of these Figs. 9a and 10a show that the separation crack always opens, in the transverse direction, when trains pass on the southern track and closes when trains pass on the northern track. The magnitudes of these movements are very small, below 0.1 mm for trains on the southern track and below 0.05 mm for trains on the northern track.
The magnitudes of the vertical pumping displacements—shown in the second rows of Figs. 9a and 10a—are always substantially larger, with peak-to-peak pumping displacements of approximately 1 mm for trains on the southern track and 0.15 mm for trains passing on the northern track.
These patterns of response are visualised in Figs. 9b and 10b, which are schematics showing the positive and negative components of the peak-to-peak displacements. The convention for plotting these displacements is shown in the top-left of Figs. 9b and 10b: crack opening displacements, which occur in the transverse direction of the bridge, are shown with horizontal bars, while the relative pumping displacements are shown with vertical bars. For crack opening displacements, as with Figs. 7b and 8b, these schematics show crack opening in black and crack closing in white. For relative vertical displacements, peak upwards movements of the barrel compared to the spandrel are shown in black while peak downwards movements are shown in white. The monitored points along the crack are indicated by grey circles. Note that the schematics in Figs. 9b and 10b use two distinct scaling factors, because of the significant difference between the magnitudes of response for the two cases. The figures are internally consistent; however, bar lengths between figures should not be directly compared.
For trains passing on the southern track, as in Fig. 9, the vertical component of the response at the separation crack is dominated by downwards movement of the arch barrel relative to the spandrel wall. However, small upwards movements are seen in the responses at all three monitored points on the crack, corresponding to instances in time when axle loads are applied to the opposite side of the arch span. Magnitudes of movement are largest in the central region of the crack, peaking for FBG SS4 to the east of the arch midspan, although interestingly the response is not symmetric on the two sides of the crown (at FBGs SS2 and SS4).
A different pattern is observed when trains pass on the northern track. In this case, shown in Fig. 10, movements at FBG SS4, just to the east of the arch crown, are notably smaller than those observed on either side, at SS2 and SS6, and there are appreciable upwards movements of the southern edge of the arch barrel relative to the spandrel wall. The response to the west of the arch crown (at FBG SS2, shown in the bottom-left subplot of Fig. 10a) demonstrates that application of axle loads at a corresponding point along the arch span still leads to downwards movement of the arch relative to the spandrel wall, but upwards movements occur in the “troughs” between these peaks. The response at the eastern quarter point (at FBG SS6) is more notably dominated by upwards movements, at the same times as the peak downwards movements are observed at the arch crown (particularly at FBG SS2).
The crack does not shear simultaneously along its length. With the exception of FBG SS6 for trains on the north track, as described above, the peak vertical response is a downwards deflection occurring when an axle load is applied at a corresponding point along the arch span. Peak vertical deflections at each monitored location, for the trains in Figs. 9 and 10, are given in Table 2.
The values in Table 2 highlight that the response is not symmetric on either side of the arch crown, and that different patterns of responses arise depending on the track on which the train is travelling. When trains pass on the southern track and loading is applied close to the midspan of the arch, this causes asymmetric downwards movement of the points on either side of the arch crown and either a modest downwards deflection or a small uplift of the eastern quarter point, depending on which side of the arch crown the axle load is applied. Loads applied at the eastern quarter point cause a peak downwards deflection at the corresponding point along the crack (SS6), decreasing downwards deflections towards the arch crown (SS4), and some uplift of the opposite side of the crown (SS2).
For trains on the northern track, loading close to the midspan causes an asymmetric response at the southern arch crown (SS2 and SS4) but a consistent uplift at the eastern quarter point (SS6). The magnitude of this uplift is approximately double that of the observed downwards deflection when axle loads are applied to the eastern side of the north track. Furthermore, this asymmetric loading case causes upwards movement at the arch midspan, with larger upwards deflections observed on the opposite side of the crown (SS2).
3.2 Statistical overview of the longitudinal strain distributions
This section provides a statistical summary of all longitudinal strain data recorded for Class 185 trains passing on the northern track. Figure 11 summarises the peak compressive, peak tensile, and peak-to-peak strain responses at each longitudinal FBG. Note that, in keeping with earlier figures, compressive strains are plotted as negative while tensile strains are positive. Figure 12 summarises the variation of the instantaneous strain responses as the leading axles of each train reach certain key locations along the arch span. These locations are the same as those for which a typical instantaneous strain response was plotted in Fig. 6.
In both Figs. 11 and 12, the top rows plot the strains measured by FBGs L1 to L10 underneath the north track centreline, while the bottom rows plot strains for FBGs L11 to L20 along the bridge centreline.
These figures use boxplots [18, 19] to represent the statistical distribution of strains at each FBG. Median values of strain are shown as black dots in white circles. These circles are within solid boxes which represent the interquartile ranges, although for data sets with very low statistical dispersion these boxes are not always visible. Whiskers extend beyond the boxes by a distance of 1.5 times the interquartile range. The few outliers beyond these whiskers have been omitted for clarity. Solid lines between adjacent boxplots connect the median values.
In Fig. 11, the left-hand plots show the statistical distribution of peak compressive strains, in black, and peak tensile strains, in light grey. The right-hand plots show the statistical distribution of peak-to-peak strains. Peak tensile strains reach their maximum values close to the arch crown, while peak compressive strains reach theirs close to the two \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) points of the arch. These observations match those made earlier, during discussion of Fig. 6, regarding the two critical loading cases for a point load applied to an arch. Peak-to-peak strains, dominated by the higher magnitudes of the peak compressive strains, also reach their maximum values close to the arch \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) points.
In most cases in Fig. 11, the median strains are close to the centres of their respective boxes. This indicates that these data sets have low sample skewness and that the median and mean strains are likely to coincide. There is also a general trend that the amount of dispersion increases as the strain magnitude rises. At most, the magnitude of the interquartile range reaches approximately 4% of the median strain magnitude, with an absolute value of roughly 5 με.
In Fig. 12, the statistical distributions of the instantaneous strain responses also show reasonable agreement between different train events, for most FBGs. Here, strain responses are considered at times when the leading axle of a Class 185 train is positioned above the western and eastern third points of the arch, as well as either side of the arch crown. In each case, these plots maintain the pattern observed for typical instantaneous strains in Fig. 6a. Again, the spread in the strain data is typically low in absolute terms, although this can be up to 15% of the median strain magnitude in some cases.
Sorting the FBG data into groups, corresponding to fast or slow trains travelling during commuter or off-peak times, does not substantially affect the distribution of median strains, or the spread in this data. This is the case for both peak-to-peak and instantaneous strain responses. For brevity, plots showing the statistical distributions of subgroups of data are not included here.
Each strain response summarised in Fig. 12 corresponds to a distinct thrust line, adopted by the arch under instantaneous loading, and therefore the median strain distribution represents a typical thrust line for the arch under this load. Variation in the adopted thrust line gives rise to dispersion in the statistical strain distribution.
There is often considerable skew in this dispersion, which is evident in Fig. 12 in those boxplots for which the median is clearly not centred in its interquartile range. A consequence of this skew is that the mean strain cannot be presumed to give an accurate measure of typical, instantaneous behaviour. The median, conversely, is more resistant to the influence of outliers, which are themselves also useful since they represent the largest deviations from typical behaviour over the sample period.
Therefore, when comparing arch behaviour over time, to search for any long-term changes in this behaviour, one potential approach is to track the median and extreme outliers of the instantaneous strain response for various positions of applied loading. For the monitoring data currently available, covering the period of September 2018 to February 2019, the remarkable consistency of the strain responses, as visualised by the low statistical spread in this data, suggests that there is very little variation in the load path being adopted by the arch when it is subjected to train loading. This is despite the variation in passenger loading, which is discussed in the next section. Over time, however, damage or deterioration of the arch may cause the load path to change; such changes could be detected using this statistical approach.
Statistical representations of monitoring data, therefore, have useful asset management applications, in the form of identifying changes in behaviour which could indicate damage or deterioration of the structure. The ability of FBGs to measure statistical changes in the strain response, when these strains are themselves very small in magnitude, offers considerable practical benefits. Although there have not been significant changes in the bridge response over the 6-month monitoring period presented here, these results nevertheless demonstrate that FBGs are capable of identifying such changes.
3.3 Variation of the longitudinal strain distributions
Figures 13 and 14 plot peak-to-peak strains for a subset of the longitudinal FBGs against time of day and train speed, for which trends have been observed. The data that is plotted corresponds to all Class 185 trains passing on the northern train, and a subset of FBGs underneath the north track and along the bridge centreline. These include FBGs L3 and L18, underneath the western \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) point; FBGs L5, L6, L15, and L16, close to the arch crown; and FBGs L8 and L13 underneath the eastern \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\) point.
In both Figs. 13 and 14, data is plotted for all recorded trains, including trains travelling at any speed. The entire 6-month monitoring period is included in these, and in the following plots. Data are coloured in clusters based on train speed, as can be seen clearly in Fig. 14. Fast trains with speeds above 82 mph are plotted as solid black dots; slow trains below 72 mph are plotted as white dots with black borders; and trains with intermediate speeds (i.e. 72–82 mph) are coloured grey with black borders.
In Fig. 13, time of day is used as a proxy for passenger loading. The actual axle loads applied to the bridge are not known a priori; although the train weights are known, the overall axle loads can vary significantly depending on passenger levels. Information obtained from Network Rail, the asset managers, suggests that the axle loads applied by a Class 185 train may increase by as much as 10–16% between typical and maximum, termed “crush,” passenger loading scenarios. Furthermore, “crush” loadings can be 27% higher than those applied by an empty train. These increases are not uniform across all axles.
Despite the spread in the data, a clear increase in the peak strain responses of the longitudinal FBGs can be seen in Fig. 13 around the evening commute, between 5 and 7 pm, before decreasing later in the evening to a lower level than is observed during the day. Qualitatively, this trend matches well with anticipated passenger behaviour. Although the precise increases between off-peak and peak conditions are obscured by the remaining scatter in the data, especially for off-peak trains, the changes observed are broadly consistent with those anticipated. Furthermore, the amount of scatter is generally observed to decrease during peak times of travel, suggesting more consistent levels of passenger loading at these times.
Considering only the fast trains plotted in Fig. 13, Table 3 presents bounds on the increase in strain magnitude that is observed during peak travel times. These are calculated by comparing the largest strains recorded during peak travel times with the largest and smallest strains recorded during off-peak times, excluding extreme outliers. The uppers limits of these bounds generally agree well with the 10–16% estimate above: the loading increase due to full passenger capacity, relative to typical passenger levels. The lower limits of these bounds may be explained by the large variation in strain measurements for trains recorded during off-peak times; passenger levels are expected to vary significantly during these times and it is not unreasonable to expect some of these trains to approach full capacity.
The upper limits on the strain increases for FBGs L5 and L16, close to the arch crown, exceed this estimated load increase for full capacity trains relative to typical passenger levels. Although the bounds in Table 3 have been calculated only considering fast trains travelling at over 82 mph, the strain increase at these FBGs could be due in part to a residual impact of train speed. As is seen in Fig. 14, strain amplification due to high train speed is only observed close to the arch crown. Further sub-dividing the FBG data by train speed may help to fully decouple this effect. However, to do this, more data will be required to reliably characterise each group.
Nonetheless, the findings in Table 3 suggest that uncertainty regarding precise train and passenger loading can be mitigated if repeat measurements are taken at the same time of day over a long period of time. In particular, data recorded during weekday commuter times is likely to give the best repeatability. Loading at this time can be assumed to correspond to well-defined “crush” scenarios, while the precise loading during other times of day is more uncertain. Using this approach, time of day could be employed as a simple framework to classify railway traffic loading, instead of bridge weigh-in-motion techniques.
For FBGs L5, L6, L15, and L16, close to the arch crown, variation of the strain response based on train speed can be observed, with an increase in measured strains for the fast trains. In Fig. 13, the subplots for these FBGs contain bands of black and white dots corresponding to the separate time-of-day variation for both fast and slow trains respectively. The increase in strain response for fast trains can be seen in Fig. 14 for FBGs close to the arch crown, most clearly for FBGs L5, L6, and L15. Here, there is a marked increase in peak-to-peak strains for fast trains relative to slow trains.
It is important to note that variation of the strain response with train speed is not observed at FBGs further away from the arch crown. The variation is also more pronounced for FBGs L5 and L6 underneath the northern track, on which the trains are passing than it is for FBGs L15 and L16 along the bridge centreline. This suggests that the impact of train speed is localised, primarily affecting regions of the bridge with relatively little backfill, and which are also close to the point of application of the load.
In Fig. 14, the crown FBGs under the north track centreline show an increase of up to 15% in the magnitude of the strain response for fast (> 82 mph) trains relative to slow (< 72 mph) trains. The corresponding value for crown FBGs at the bridge centreline is 10%. For FBGs further away from the crown, no variation of the peak-to-peak strains with train speed can be observed, although more data for slow trains are needed to confirm these observations and identify the precise nature of any trends with speed below 72 mph, which are currently obscured by scatter. Nevertheless, from this data, the pronounced increase in strain response and reduction in scatter for trains travelling above 82 mph is clear.
The current Network Rail guidance [9] prescribes a dynamic factor of 1.8, to be applied to the critical axle loading; this is significantly higher than the strain amplification measured at this bridge and reported above. The guidance states that this factor may be reduced where the depth of ballast and fill, between the sleeper and arch crown extrados, exceeds 600 mm, but gives no suggestions on how to calculate this reduction and does not allow for the increase in fill at locations other than the arch crown. The depth of ballast and fill at the crown, for this case study bridge, is approximately 350 mm according to record drawings. The findings here suggest that continued monitoring of multiple bridges could enable revisions to the current dynamic amplification factor used by Network Rail for the assessment of masonry arch rail bridges.
Separate guidance on dynamic amplification factors for traffic loading, such as rail, is given in Eurocode EN 1991–2. This guidance is founded on the use of simplified beam models, resulting in expressions for dynamic amplification factors that depend on a determinant length for the structure, its first natural frequency, and the vehicle speed. These expressions were not derived with masonry arches specifically in mind, and it has been demonstrated that they produce results which are too conservative for masonry rail bridges [20]. Attempts to improve this guidance are an active area of research (see, for example, [21]).
Longitudinal strain variation was also studied for ambient temperature and date, to investigate any seasonal and long-term trends respectively. However, no discernible trends could be identified for the data available over this 6-month monitoring period. Further study of any long-term changes in this behaviour will form a part of future research, once more data has been recorded by a new logging system deployed at the bridge in July 2020.
3.4 Variation of crack opening displacements
Figures 15a and b show the variation of peak-to-peak crack opening displacements at the south-eastern longitudinal crack with time of day and temperature respectively. The data that is plotted corresponds to Class 185 trains travelling on the south track. In Fig. 15a, all fast Class 185 trains travelling above 82 mph are plotted, while in Fig. 15b only fast Class 185 trains travelling between 5 and 7 pm, i.e. at evening commute times, are plotted. All data in Fig. 15 is coloured by temperature, as can be seen more clearly in Fig. 15b. Data for which the ambient temperature was between 0 and 5 °C are plotted as white dots with black borders; data for ambient temperatures between 5 and 10 °C are plotted as grey dots with black borders; and data for higher temperatures are plotted as solid black dots. “Black” data was recorded in September and October 2018, “grey” data was recorded in November 2018 and February 2019, and “white” data was recorded in December 2018 and January 2019.
Variation of peak-to-peak crack opening displacements at the south-east longitudinal crack with a time of day, only plotting data for fast Class 185 trains passing on the southern track, and b temperature, only plotting data for fast, evening commuter Class 185 trains passing on the southern track (data coloured by temperature)
In Fig. 15a, the increase in response magnitude around the evening commute can be observed but it is less notable than it was for the longitudinal strains in the previous section. In the subplots for FBGs SE5 to SE8, over the upper half of the crack, the peak for evening commuter trains appears to be larger and more pronounced for data recorded during cold ambient conditions than it is for the subplots corresponding to FBGs SE1 to SE4 over the lower half of the crack. For these FBGs, there is no clear relationship with temperature over the evening commuter period. Additionally, the time of day plots are now dominated by a significant decrease in the magnitudes of peak-to-peak crack opening displacements between approximately 08:30 and 13:30. This corresponds to a steady, approximately linear increase in the recorded ambient temperature, which also occurred between these times.
In Fig. 15b, a notable decrease in the magnitudes of peak-to-peak displacements as the ambient temperature rises is observed for FBGs SE5 to SE8, located over the upper half of the crack where the response is primarily tensile (i.e. crack opening). However, this is not observed for FBGs SE1 to SE4 over the lower half of the crack, where the response is primarily compressive (i.e. crack closing). For FBGs SE5 to SE8, the decrease in peak-to-peak displacements is approximately 10% over a rise in temperature of 15.5 °C.
No clear relationships between crack opening displacements and either temperature or time of day were observed for data corresponding to trains passing on the northern track. Note that in this case the crack opening displacements are always primarily compressive, while in Fig. 15 the only significant observed relationships are for crack opening displacements that are primarily tensile.
In summary, for the south-eastern longitudinal crack, there is some sensitivity to temperature observed when crack movements are tensile. The peak-to-peak crack opening magnitudes decreased as the ambient temperature rose. However, when crack movements were compressive, no relationship with temperature was observed. This could be explained by thermal expansion causing cracks to partially close. In other words, crack widths are larger when the bridge is cold, so dynamic tensile strains across these open cracks are also larger.
Furthermore, this sensitivity to temperature appears to match the anticipated increase in response for evening commuter trains, when these peak-to-peak displacements are plotted against time of day. Therefore, it could be that a lower ambient temperature, and corresponding thermal contraction of the masonry, simply leads to tensile movements of this crack becoming more sensitive to the precise magnitude of the applied loading, while compressive movements remain less sensitive to this.
It is worth noting that the general observation of an inverse relationship between the magnitude of dynamic deformation and ambient temperature, in certain circumstances, agrees with the findings of a recent study into a masonry viaduct of similar construction [22, 23]. In that study, a clear inverse relationship was identified. However, it is likely that the large number of masonry spans at that viaduct affects its sensitivity to temperature, in contrast to the single-span bridge studied here which has different boundary conditions at the arch abutments. In future work, data will be gathered at this bridge over a greater range of temperatures, to further investigate the impact of thermal effects.
No relationship between crack movements and train speed was observed, in keeping with the earlier observation that the impact of train speed on the strain response is highly localised to the regions in which loading is applied to the arch, and to places where little backfill is present. For brevity, plots of the crack strains against train speed are not included here.
Variation of crack opening and pumping displacements was also investigated for the south spandrel separation crack. However, no relationships were identified. The spread in the magnitudes of peak-to-peak crack displacements was significantly higher for this crack, and it is possible that this obscured any underlying trends in the data.
4 Conclusions
In this study, high sensitivity FBGs have been utilised to monitor a damaged, skewed masonry arch railway bridge in unprecedented levels of detail, at a wide range of points across its extent. Data for Class 185 trains, the most common SLS train loading for this bridge, has been analysed, and a comprehensive overview of the typical structural response of this bridge has been presented. This has covered the longitudinal strain distributions over the undamaged northern half of the arch, and the behaviour across cracked interfaces of interest. At the southern spandrel separation crack, a novel implementation of FBGs has been deployed to allow this technology to measure both in-plane crack opening and out-of-plane relative vertical displacements across the crack, for the first time.
By capturing the structural response in these regions in detail and visualising the monitoring data in a range of ways, it has been possible to relate the measured bridge movements to expectations of its anticipated structural behaviour. In the case of the longitudinal strain distributions, accurate measurements allowed meaningful statistical representations to be created; even when peak strains only reach tens of microstrain and the interquartile range of measurements was at most 6 με and frequently much lower. The simple statistical approach described in this paper has the potential to be of benefit to asset managers who wish to identify the early onset of changes in the behaviour of similar masonry structures, potentially before these changes become visible to coarser monitoring techniques or visual inspections.
The ability of FBGs to accurately measure microstrain-scale movements has also been leveraged to study the sensitivity of the structural response of this bridge to various parameters of interest. Trends in the longitudinal strain distributions were identified with the time of day, which was observed to be an approximate indicator of passenger loading, and with train speed. In the first instance, this opens up the potential for the time of day to be used as a proxy for the magnitude of train loading, instead of using complex bridge weigh-in motion systems.
Secondly, the results regarding train speed suggest that, pending further data for slow trains, it may be appropriate for current Network Rail guidance on the impact of train speed on the structural response of masonry bridges to be revisited. It was found that the sensitivity of the arch’s longitudinal strain response to train speed is localised, only being observed in regions of the arch with low cover of backfill and ballast above the arch extrados, and is most notable close to the point at which train loads are applied. A dynamic amplification factor of approximately 1.15 was observed in the FBGs directly underneath the active track on which the train was passing, with the corresponding factor for FBGs 1.5 m to the side of these, at the bridge’s longitudinal centreline, being approximately 1.10. These factors describe a relative increase in strain response for trains travelling above 82 mph, compared to those travelling below 72 mph. More data will be gathered to refine these factors, based on a more precise understanding of the response for slower trains. The current Network Rail recommendation for this dynamic factor is significantly higher, at 1.8.
At the south-eastern longitudinal crack, tensile crack openings were similarly found to be sensitive to a combination of temperature and time of day. However, it may simply be that the effects of thermal contraction of the masonry, under cold conditions, allowed these displacements to become more sensitive to the precise applied loading on the bridge, in the manner described above for the longitudinal strains.
The sensitivity of the bridge response to ambient temperature and date, representing, respectively, seasonal variation and potential deterioration over time, was also investigated. However, no other clear trends in the response were identified for these variables.
In general, this study demonstrates the potential for fibre-optic FBG monitoring to be applied in the Structural Health Monitoring of masonry railway bridges, in which the desired measurements may be expected to be very small and it may be wished to monitor a range of behavioural types with one system. More broadly, it also demonstrates the benefits of distributed monitoring, since the findings of this study were made possible, in part, because of the high number of measurement locations afforded by an FBG monitoring installation.
Availability of data
The data used in this paper originate from work carried out by the Centre for Smart Infrastructure and Construction on behalf of Network Rail. Because of the commercial nature of this project, the data is covered by a Non-Disclosure Agreement. Any questions or requests regarding the data in this paper should be directed to the corresponding author.
Code availability
Not applicable.
References
Cocking S, Acikgoz S, DeJong M (2020) Interpretation of the dynamic response of a masonry arch rail viaduct using finite-element modeling. J Archit Eng 26(1):05019008. https://doi.org/10.1061/(ASCE)AE.1943-5568.0000369
Acikgoz S, DeJong MJ, Kechavarzi C, Soga K (2018) Dynamic response of a damaged masonry rail viaduct: measurement and interpretation. Eng Struct 168:544–558. https://doi.org/10.1016/j.engstruct.2018.04.054
Harvey WJ (1988) Application of the mechanism analysis to masonry arches. Struct Eng 66(5):77–84
Gilbert M, Melbourne C (1994) Rigid-block analysis of masonry structures. Struct Eng 72(21):356–361
Forgacs T, Rendes S, Adany S, Sarhosis V (2019) Mechanical role of spandrel walls on the capacity of masonry arch bridges. Proc ARCH Int Conf Arch Bridges. https://doi.org/10.1007/978-3-030-29227-0_21
Sarhosis V, Forgacs T, Lemos JV (2019) Modelling backfill in masonry arch bridges: a DEM approach. Proc ARCH Int Conf Arch Bridges. https://doi.org/10.1007/978-3-030-29227-0_16
Cocking S, Thompson D, DeJong M (2019) Comparative evaluation of monitoring technologies for a historic skewed masonry arch railway bridge. Proc ARCH Int Conf Arch Bridges. https://doi.org/10.1007/978-3-030-29227-0_46
McKibbins LD, Melbourne C, Sawar N, Gaillard CS (2006) Masonry arch bridges: condition appraisal and remedial treatment (CIRIA C656). CIRIA, London
Network Rail (2006) The structural assessment of underbridges. Network Rail, London
Forgacs T, Sarhosis V, Bagi K (2018) Influence of construction method on the load bearing capacity of skew masonry arches. Eng Struct 168:612–627. https://doi.org/10.1016/j.engstruct.2018.05.005
Forgacs T, Sarhosis V, Adany S (2018) Discrete element modeling of skew masonry arch bridges taking into account arch ring-backfill interaction. In: Proceedings of 10IMC, the 10th International Masonry Conference, pp 337–346
Harvey B (2013) A spatial view of the flow of force in masonry bridges. Proc Instit Civil Eng 166(1):51–58. https://doi.org/10.1680/bren.11.00026
Acikgoz S, Alexakis H, Ye C, Franza A, DeJong M (2019) The marsh lane railway viaduct: 2 years of monitoring with combined sensing and surveying technologies. Proc ARCH Int Conf Arch Bridges. https://doi.org/10.1007/978-3-030-29227-0_44
Alexakis H, Franza A, Acikgoz S, DeJong MJ (2019) A multi-sensing monitoring system to study deterioration of a railway bridge. In: Proceedings of SHMII-9, the 9th International Conference on Structural Health Monitoring of Intelligent Infrastructure.
Cocking S, Alexakis H, DeJong MJ (2019) Measurement of the flow of force in a skewed masonry arch bridge using fibre optic sensing. In: Proceedings of SHMII-9, the 9th International Conference on Structural Health Monitoring of Intelligent Infrastructure.
Cocking SH, Ye C, DeJong MJ (2019) Damage assessment of a railway bridge using fibre optic sensing and LIDAR data. Proc ICSIC Int Conf Smart Infrastruct Constr. https://doi.org/10.1680/icsic.64669.701
Majumder M, Gangopadhyay TK, Chakraborty AK, Dasgupta K, Bhattacharya DK (2008) Fibre Bragg gratings in structural health monitoring: present status and applications. Sens Actuators A Phys 147(1):150–164. https://doi.org/10.1016/j.sna.2008.04.008
Tukey JW (1977) Exploratory data analysis. Addison-Wesley, Reading
McGill R, Tukey JW, Larsen WA (1978) Variations of box plots. Am Stat 32(1):12–16. https://doi.org/10.2307/2683468
Gibbons N (2014) Modelling and assessment of masonry arch bridges. PhD Thesis, University College Dublin.
Smith J, Acikgoz S (2019) Dynamic amplification of curved beams subjected to a moving point load. Proc ARCH Int Conf Arch Bridges. https://doi.org/10.1007/978-3-030-29227-0_20
Alexakis H, Lau FDH, DeJong M (2021) Fibre optic sensing of ageing railway infrastructure enhanced with statistical shape analysis. J Civ Struct Heal Monit 11:49–67. https://doi.org/10.1007/s13349-020-00437-w
Alexakis H, Franza A, Acikgoz S, DeJong MJ (2019) Monitoring bridge degradation using dynamic strain, acoustic emission and environmental data. Proc ICSIC Int Conf Smart Infrastruct Constr. https://doi.org/10.1680/icsic.64669.523
Acknowledgements
The work presented here is part of a monitoring collaboration between the Cambridge Centre for Smart Infrastructure and Construction (CSIC), AECOM, and the asset owners Network Rail, who have funded the installation. The authors are grateful for the help and support of both organisations throughout this project. In particular, they express their thanks to Sam De’Ath (Network Rail), and to David Kite, Daniel Thompson, Andrew Mercer, Nathan Lander, and Harry Lineker (AECOM). The monitoring has been performed with support from CSIC, and the authors remain grateful to Jason Shardelow for his assistance with the FBG installation.
Funding
The monitoring project described in this paper has been funded by Network Rail, the asset owners of the bridge. This study also forms part of a PhD, which is funded by an EPSRC Doctoral Training Partnership (Grant Number EP/M506485/1). The monitoring installation was performed with assistance from the Cambridge Centre for Smart Infrastructure and Construction, which is supported by EPSRC, Innovate UK, and industry funding (including Grant Numbers EP/I019308/1, EP/K000314/1, EP/L010917/1, and EP/N021614/1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cocking, S., Alexakis, H. & DeJong, M. Distributed dynamic fibre-optic strain monitoring of the behaviour of a skewed masonry arch railway bridge. J Civil Struct Health Monit 11, 989–1012 (2021). https://doi.org/10.1007/s13349-021-00493-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13349-021-00493-w