1 Introduction

Autonomous vehicles (AVs) are expected to play a key role in future transportation systems. They will have a global impact that will change society and the safety of roadways and transportation systems. For the final introduction of AVs on public roads, the technological perspective is only one aspect. It is assumed that AVs will have to make decisions which would be morally difficult for humans, and to which industry and research have not yet provided solutions. Policymakers as well as car manufacturers currently focus on the inclusion of ethical considerations into the software of AVs. Therefore, the aim of this paper is to derive a mathematical formulation for the decision-making of AVs. This is a first necessary step to bring ethical theories into the software of AVs one day.

While the public discourse mainly deals with thought experiments like the trolley problem, solutions are actually needed to consider ethical principles in the software of AVs. In the following, we want to take up the widely discussed trolley problem and develop the public discourse towards the actual problems of AVs.

There are many different versions of the trolley problem, all aimed at a moral dilemma (Foot, 1967; Thomson, 1985). A simple and widely used version is as follows:

Imagine you are standing at a switch and a trolley is speeding towards five people tied up on the rails. It is certain that these people will definitely die if you do not intervene. There is the possibility to change the switch. On the other rail, however, there is also a person tied up on the tracks who will surely die if the trolley takes this path. You can either do nothing and five people will die, or you can pull the switch and a single person will be killed. What will you do?

The trolley problem represents a dilemma, which has mainly two dimensions that create a moral conflict. The first dimension is about outweighing human lives. The question here is, whether five lives are worth more than a single one. The second dimension addresses the degree of intervention: Whether one lets a person die (i.e., does not evade) or kills a person actively makes a big difference not only from a legal point of view. From a moral point of view, it is increasingly difficult for people to actively decide in favor of saving more lives the stronger the necessary intervention is (Greene, 2013; Rehman & Dzionek-Kozłowska, 2018).

The main problem from the trolley dilemma that can be transferred to autonomous driving and that we would like to investigate in this paper is the outweighing of human lives. In contrast to a trolley, the trajectory planning of AVs does not have any initial setting, but the algorithm actively computes all calculated trajectories. Figure 1 visualizes the trajectory planning of an AV. The blue area represents the quantity of all possible trajectories. The question of outweighing human lives becomes relevant for AVs, as algorithms are able to decide within the fraction of a second, whereas human drivers become panicked and act on their instinct (Nyholm & Smids, 2016).

Fig. 1
figure 1

Schematic visualization of the trajectory planning of an AV. Physically possible trajectories are represented by the blue area within the boundaries of the road. The dotted lines are exemplary discrete trajectories within the possible area

Full size image

However, the comparison of the trolley problem with real scenarios of autonomous driving reveals some shortcomings. Firstly, the consequences in the trolley problem, namely the death of the victims, are postulated as certain events, which cannot be assumed in real-life scenarios. Secondly, the dilemma offers only two options, while the AV can draw on a continuous solution space for trajectories (Fig. 1). Thirdly, depending on the version of the trolley problem, there is a lack of important prior information about how the situation occurred. This information may be necessary to enable a morally well-founded decision to be made. Nyholm & Smids, (2016) draw a comprehensive comparison between the trolley problem and autonomous driving. According to our third point, they see a lack of information regarding the question of whom we can justifiably hold morally and legally responsible for the dilemma situation. Kauppinen, (2020) argues that when an accident becomes inevitable, the degree of moral responsibility that people bear for creating risky situations must be taken into account. Himmelreich, (2018) identifies further issues around the trolley problem, and argues that solutions to trolley cases are likely to be only of limited help in informing decisions in novel and uncertain situations. Therefore, one objective of this work is to establish a connection between the public discussion about moral dilemmas and relevant ethical problems around autonomous driving, as well as to provide a possible solution approach to such problems.

The next section presents a selection of approaches facing the problem of unavoidable accidents. We identify need for further research in deploying ethical behavior in the trajectory planning of an AV. Section 3 deals with this topic in detail and compares different ethical theories. Based on this analysis, great potential in the area of ethics of risk is recognized, and a risk-based framework is proposed in Section 4.

2 Unavoidable Accidents and the Need for Ethics

As already highlighted by the trolley dilemma, unavoidable accidents involving AVs are one of the main research topics in autonomous driving ethics. Previous works deal with different fields at very different degrees of abstraction: from theoretical considerations to implemented software. The literature largely agrees that AVs will be involved in accidents (Goodall, 2014; Shalev-Shwartz et al., 2017). Goodall, (2014) concludes that the decision of automated vehicles preceding certain crashes will have a moral component. The Moral Machine experiment shows that there is no easy way to encode complex human morals in software, as moral values strongly differ by culture for example (Awad et al., 2018). In literature, there is so far no known way of addressing unavoidable accidents that meets all ethical requirements. Davnall, (2019) looks at the problem of fatal accidents independently of ethical considerations, and argues from a vehicle dynamics perspective. Due to the dynamics of braking and tire traction, it is always least risky for the car to brake in a straight line rather than swerve in the case of the trolley dilemma. However, Lin, (2016) argues against purely physical approaches, as they do not satisfy the need of an ethical decision. In addition, this physical approach has other limitations. The approach no longer pays off if the obstacles in the dilemma are not equidistant from the ego vehicle, so the shortest braking distance is not necessarily the best solution. Therefore, ethical approaches known in literature, which tackle these kinds of moral problems, are presented in Section 3. Kumfer and Burgess, (2015) examine a simple programming thought experiment to demonstrate the AVs behavior in a moral dilemma based on utilitarianism, respect for persons, and virtue ethics. They find that utilitarian ethics reduces the total number of fatalities, but conclude that some drivers may object to being potentially sacrificed to protect other drivers. Leben, (2017) presents a way of developing Rawls’, (1971) Contractarian moral theory into an algorithm for crash optimization. Accordingly, the AV calculates a chance of survival for every individual. The action that is considered fair is the one every player would agree not knowing his own position in this situation. He argues that according to this veil of ignorance, every self-interested player will follow the Maximin criterion, which results in maximizing the minimum payoffs. Keeling, (2018), however, shows the weaknesses of this approach and therefore argues not to use this decision strategy presented by Leben, (2017). He formulates three challenges based on scenarios that an ethical AV has to overcome. We will address these challenges in the further development of our framework in Section 4.

In the literature, the focus is on finding decision metrics in crash situations. However, it is still unclear how these metrics can one day be used in real vehicles. We propose a holistic framework for ethical trajectory planning in all kinds of driving situations in Section 4 and focus on the practical applicability of our approach. We want to transfer knowledge from thought experiments with mostly binary outputs to algorithms with real applications in public road traffic.

The deployment of ethical theories to the problem of unavoidable accidents means to also consider whether we should implement a mandatory ethics setting for the whole of society, or whether every driver should have the choice to select his own personal ethics setting (Gogoll & Müller, 2017). Mandatory in the sense of Gogoll & Müller, (2017) means that this particular ethics setting would not be self-determined or adjustable by drivers but rather imposed by manufacturers that implement a universal industry standard for autonomous vehicles. Traditionally, moral considerations are always mandatory, meaning that they impose a moral duty on an agent to act in a certain way so that diverging personal ethical considerations cannot emerge in the first place. However, according to Gogoll & Müller, (2017), a disintegration of personal and mandatory ethics settings can arise when assuming a situation that does not require one specific action but instead permits a plethora of different beliefs, moral stances, and hence actions. For example, when an autonomous vehicle enters a dilemma situation “an old couple might decide that they have lived a fulfilled life and thus are willing to sacrifice themselves” while “a family father might decide […] that his car should never be allowed to sacrifice him” (Gogoll & Müller, 2017, p. 688). This question of mandatory versus personal ethics settings can be related to a social conflict between self-determination and protection. In the literature, we find arguments for both approaches: Gogoll & Müller, (2017) use a game theoretical thought experiment and argue that ethical settings should be mandatory, as this would be in the best interest of society as a whole. Contissa et al., (2017) argue for the use of personal settings achieved by an “ethical knob.” Via this knob, users can input their personal ethical setting on a scale between altruist and egoist. The authors further suggest that an adjustment in the direction to the passenger’s benefit should lead to a higher insurance premium, as the chances of accidents will be increased (Contissa et al., 2017). Since the literature does not yet have a clear answer here, it would be of great advantage if the framework leaves space for both options.

3 Practical Requirements and Ethical Theories

The literature agrees that there is more research required in the area of ethics of unavoidable accidents involving AVs. In order to implement ethical algorithms for dealing with unavoidable accidents, which can be used in a real AV, some requirements have to be satisfied. We would like to introduce these five requirements here: representation of the reality, technical feasibility, universality, social acceptance, explainability, and transparency. In the further course of the section, we want to review existing approaches from different ethical theories for these requirements. We focus on the implementations derived from theory in the software with special attention to the problem of unavoidable accidents. Rather than looking at ethical theories as a whole, we focus on implementations and algorithms from the literature that emerge from different theories. In particular, we will deal with approaches originating from deontology, utilitarianism, virtue ethics, and ethics of risk. Based on this analysis, we will argue to develop our proposal based on ethics of risk in Section 4 regarding our motion planning framework.

One of the most important requirements is the representation of the reality within a specific framework. The real world is characterized by complex correlations, while ethical theories can only consider a simplification of these correlations. In the field of autonomous vehicles, there are important circumstances in reality, which must be represented by an ethical framework. For application in the vehicle, the technical feasibility is also of great importance, i.e., the ability to transfer tenets from ethical theories into software. Ethical implications must be captured in software code, which ultimately determines the behavior of AVs. The literature already contains suggestions for the implementation regarding various theories, which we will discuss briefly in this section.

To enable the widest possible use of ethical driving software in the future, universality is an essential requirement with the objective to enable general applicability. As already described, it is not enough to give answers in critical situations. Since it is often not even possible to predict exactly when a critical situation will occur or which kind of situation applies, it is advantageous if the framework has general applicability.

The literature shows that trust is a major construct for the adoption of autonomous vehicles on road traffic one day (Choi & Ji, 2015). Therefore, social acceptance (i.e., society’s inclination towards a particular theory) represents a further requirement. Moreover, to increase user’s trust in algorithmic decisions, explainability and transparency play an important role (Kizilcec, 2016). This also ensures that the parties affected by a decision are provided with sufficient information to exercise their rights properly and may challenge the decision if necessary (Data Ethics Comission, 2018).

3.1 Deontological Approaches

In general, deontological theories judge the morality of choices by criteria different from the states of affairs the choice brings about (Alexander & Moore, 2020). For example, such criteria may be the underlying intention for pursuing a particular action, or for its compatibility with a certain formal principle (Bartneck et al., 2019). According to deontic ethics, ethically right actions should generally conform to a moral norm. The philosopher Immanuel Kant is regarded as central to deontological moral theories, thanks to his introduction of the Categorical Imperative as a fundamental principle for human’s moral duties: Act only according to that maxim whereby you can at the same time will that it should become a universal law (Kant, 1981). Similarly, contractualist deontological theorists seek principles, which individuals in a social contract would agree to (e.g., Rawls, 1971) or which none could reasonably reject (e.g., Scanlon, 2003). Regarding the field of AVs, maxims such as the Kant’s Categorical Imperative seem too broad and unspecific to be directly adopted. Therefore, scholars have recently proposed rule-based ethical theories in the form of a cluster (e.g., “forbidden, permissible, obligatory actions” (Powers, 2006)) or hierarchy of constraints that are tailored to the programming of machines or AVs, to guide them towards desirable behavior in dilemma situations. An example of such a hierarchy is the Three Laws of Robotics by Asimov that prioritizes the non-maleficence (i.e. avoidance of injury or harm) of human beings by robots, whereas the obedience of robots to humans and the robot’s own protection is only subordinate (Asimov, 1950). Gerdes & Thornton, (2015) translated such a hierarchy to collision-situations in traffic. In general, such rule-based ethical theories may represent promising application possibilities for machine/AV ethics, since they offer a computational structure for judgment and thus, at least from a practical perspective, are achievable (Powers, 2006). However, it can be argued that such rule-based approaches ignore context-specific information (Loh, 2017) such as the probability of occurrence of current and future conditions. Hence, the AV may undertake dangerous behaviors in order to adhere to its strict rules (Goodall, 2016). According to this, the representation of reality is only possible to a limited extent. This may also lead to a lower level of social acceptance of implementing rule-based approaches since moral decisions and obligations are not absolute but dependent on context (Karnouskos, 2020). Although rule-based approaches can be implemented very well in software (technical feasibility), the number of rules needed that can conflict with each other arbitrarily represents an enormous complexity. The universality of such approaches is also poor since each so-called corner case must be covered by a rule in advance. Only the explainability is given by the representation of rules with different prioritization. Therefore, from a technical and functional perspective, implementing a deontic approach in the systems of AVs seems to exhibit many complications.

3.2 Utilitarian Approaches

Utilitarianism is a prominent form of consequentialism, which was introduced by philosopher Jeremy Bentham and promotes the maximization of human welfare (Crimmins, 2019). The theory determines the ethical correctness of an act or norm solely on the basis of its (foreseeable) consequences (Bartneck et al., 2019) by maximizing the expected overall utility. Such a theory may permit and advocate the sacrifice of one person in order to save a greater amount of people overall. Therefore, such an ethical theory could be adopted to AVs by designing cost function algorithms that calculate the expected costs (i.e., personal damages) for various possible options, selecting the one that involves the lowest cost (Lin, 2016), e.g., the one that minimizes the number of victims in car crashes (Johnsen et al., 2018). Therefore, utilitarian approaches for AVs may enable an improved representation of reality as many situational factors could be considered in its calculation. A cost function with the goal of maximizing benefits can also be potentially used in numerous traffic situations, depending on the exact definition of the benefit being maximized. Therefore, the objective of general applicability in terms of universality is given. Similar to the deontological ethics, the programming of utilitarianism in AVs is appealing to engineers due to machines’ inherent ability to maximize functions for the sake of optimization (technical feasibility), which is ultimately the underlying logic of utilitarianism (Gogoll & Müller, 2017). However, calculating the benefits or burden of all accident participants represents a great challenge from a technical point of view. Compared to a deontological AVs that act according to fixed constraints, a utilitarian vehicle that pursues unrestricted optimization may be less transparent (Hübner & White, 2018) or at least less foreseeable before the underlying logic is inspected to explain why a certain decision was made by the AV. Furthermore, when confronted with trolley scenarios, laypersons generally express a tendency for utilitarian solutions, which may promote the social acceptance of AVs that follow such a logic (Bonnefon et al., 2016). However, the central question here is whether it is right and permissible to actively inhibit the utility of an individual to achieve greater utility for other individuals. Therefore, from an ethical and legal perspective implementing a utilitarian approach in the system of AVs seems to exhibit many barriers. To approximate a compromisable approach, scholars advocate the combination of deontological ethics (e.g., some sort of imperative to avoid collisions and personal damage) and utilitarianism in the form of a relative weighing of costs and options (Gerdes & Thornton, 2015).

3.3 Approaches from Virtue Ethics

Virtue ethics go back as far as Plato and Aristotle, and tend to grasp morality as a question of character, meaning that virtues are central to a well-lived life. Corresponding cardinal virtues for mankind are prudence, courage, temperance, and justice (Bartneck et al., 2019). A cognitive machine should analogically exhibit such virtues (Berberich & Diepold, 2018), in the “hope for automation to allow us to care better and more readily” (Vallor, 2018). Therefore, the consideration of virtues—and thus virtue ethics—is becoming more essential than ever before in the digital age (Ess, 2015; Vallor, 2018). Such virtues or behavioral traits could relate to the type of role a vehicle is assigned to (e.g., ambulance versus passenger vehicle). This consideration of role morality may lend greater social acceptance of such AVs (Thornton et al., 2017). Virtues within machines cannot be preprogrammed, yet are due to the result of machine learning (Berberich & Diepold, 2018). Presently, the actual operating systems of autonomous vehicles demonstrate different variants of machine learning. For example, autonomous vehicles can be trained via reinforcement, where wrong acts are punished and right acts are rewarded. The technical feasibility is shown by a recent implementation of imitation learning for real-world driving called ChaffeurNet (Bansal et al., 2018). In this process, ethics in the form of a set of virtues can provide guidance as a pattern of the positive signals (Kulicki et al., 2019). Ultimately, machines or autonomous vehicles themselves should (learn to) recognize situations that require moral action, and decide to act accordingly. Depending on the number of trainable parameters, even complex correlations from reality can be represented, which would provide an adequate representation of reality. To enable a good universality, it is important that the machine learning models can generalize well. The problem with such models is that corner cases, which are poorly represented by the training data, lead to unwanted decisions. However, the most pressing challenge for a virtue-based autonomous vehicle is the explainability of its underlying logic and thus the attribution of responsibility. Namely, it should be made clear how the virtues of such cars have been formed through experience, and how a given car has been led to its particular action (Berberich & Diepold, 2018). In this regard, autonomous vehicles or driver assistance systems at present should and cannot be regarded as moral agents, but rather weak actors of responsibility (Loh, 2017). Observing people will not teach an AV what is ethical, but what is common (Etzioni & Etzioni, 2017). Therefore, truly applying virtue ethics to autonomous vehicles seems impermissible until questions of explainability and responsibility can be answered.

3.4 On the Basis of Ethics of Risk

Ethics of risk deal with the morally correct action in situations of risk. There are three established decision theories of ethics of risk: the Bayes’ rule, the Maximin principle, and the Precautionary principle. Firstly, the Bayes’ decision criterion demands—when confronted with different options of action—the selection of the particular action that yields the greatest expected utility. This expected utility is composed of the probability of occurrence for different events and a real number/rating for these consequences. Secondly, the Maximin principle can be described as a strategy to avoid the greatest damage when in a situation where information on the probability of occurrence for each consequence is not available. Accordingly, a decision-maker would choose an alternative action that yields the least bad consequence in the worst expected scenario. Thirdly, the Precautionary principle follows the motto “better safe than sorry” and advocates encountering new innovations that may prove disastrous with caution and risk aversion, by developing particular laws to proactively prevent potential future damage (Nida-Rümelin et al., 2012). Since these three decision theories are known, ethics of risk could generate more transparent (in the sense of more predictable) decisions that corresponding AV would make. For example, the Maximin principle states clearly that (the traffic participant facing) the greatest damage will be avoided while, in comparison, the utilitarian principle maximizes human welfare without giving particular information on what the worst outcome should or would be. Furthermore, the use of ethics of risk enables the consideration of probabilities and their associated consequences. Since all decisions of an AV are subject to certain uncertainties, the best representation of reality is achieved by this. This is also why AVs that follow an ethics of risk approach may be more acceptable to society: in fact, respondents have demanded to include uncertainties and risks about decision outcomes in future studies (Frison et al., 2016). Another advantage is the given universality. The consideration of risk enables an implementation independent of the situation. The applicability is therefore not limited to decision strategies in moral dilemmas or crash optimization. Compared to other approaches that are based on machine learning, the use of ethics of risk as top-down approach is explainable, and we have no black box behavior: In the case of an accident, investigators could access the vehicle’s calculations and logic to determine why the AV has behaved in a certain way.

However, to the best of the authors’ knowledge, there is no technical approach to implementing ethics of risk in trajectory planning. Theoretically, cumulative risk of certain outcomes could be easily calculated and compared (Goodall, 2016), thus reflecting its technical feasibility to be turned into a mathematical formula and subsequently into code. For this reason, we will devote Section 4 to such a technical implementation. A further challenge that we will address in Section 4 is the adaptability to different cultures or individuals. As a top-down approach, the risk for a fair distribution of risk would have to be answered anew for each case—for example, for each culture.

4 Proposed Framework

4.1 Motivation

Section 3 prompts the use of a risk-aware framework for the motion and behavior planning of AVs. With our framework, we build on the work of Bonnefon et al., (2019), who transform the trolley problem into a statistical thought experiment. We agree with the argument that AVs do not make decisions between the outright sacrificing of the lives of some, in order to preserve those of others. Instead, they decide implicitly about who is exposed to a greater risk of being sacrificed. Figure 2 illustrates this by means of an example: An AV drives precisely between a cyclist and a truck. The lateral position of the AV determines the risk posed by it. Reducing the distance to the cyclist shifts the risk towards the cyclist, as the consequences for the cyclist are assumed much greater in the event of a collision with a car. On the other hand, a reduction of the distance to the truck causes a shift of the risk towards the AV, under the assumption that due to the different masses, the consequences of an accident are mainly noticeable on the car. In general, it can be seen that minimizing the risk for the occupants of AVs is at the expense of vulnerable road users, such as cyclists or pedestrians.

Fig. 2
figure 2

The lateral distance of the AV in the middle influences the probability of a collision, and thus, the risks to which road users are exposed. Illustration according to Bonnefon et al., (2019)

Full size image

In 2014, Google described in a patent how an AV might position itself in a lane to minimize its risk exposure, similar to the left-hand illustration of Fig. 2 (Dolgov & Urmson, 2014). According to a user study by Bonnefon et al., (2016), a majority of the participants agree that utilitarian AVs were the most moral. Nevertheless, these people also tend to have a personal preference towards riding in AVs that will protect themselves at all costs. Accordingly, vehicle manufacturers may be incentivized—in line with the Google patent—to develop vehicles that always strive to minimize the passenger’s risk, with possibly devastating consequences for vulnerable road users. Mercedes Benz announced to program its self-driving cars to prioritize the safety of people inside the car over pedestrians (Taylor, 2016). These developments at the expense of vulnerable road users are alarming from an ethical perspective. Weighing up human lives or even prioritizing them deprives human beings of their subjectivity. This is not compatible with the human dignity based on Kant. According to this concept of human dignity, human beings are capable of autonomy. They set their own goals and as such are ends in themselves. Therefore, they must not be used solely as means. The German ethics commission follows this argumentation and classifies the sacrifice of innocent people for the benefit of other potential victims, as in a utilitarian approach, as inadmissible (Ethik-Kommission, 2017). However, minimizing the number of victims does not constitute a violation of human dignity according to the commission if it is a matter of a probability prognosis in which the identity of the victims has not yet been established (Ethik-Kommission, 2017). Lütge, (2017) underlines this in his analysis of the ethics commission’s report. The second ethical rule of the report suggests the further need for risk assessment. It describes that the registration of automated systems is only justifiable if these systems guarantee a reduction in damage, in the sense of a positive risk balance compared to human driving performance. This prompts the development of a motion planning framework with a fair assessment of risks.

The shifting of risks, although not intended, is not completely new to the automotive industry. Studies found that bull bars attached to vehicles increase the risk for vulnerable road users in road traffic (Desapriya et al., 2012). For this reason, the European Union decided to prohibit bull bars on road vehicles (Bonnefon et al., 2019). Developments to the detriment of vulnerable road users have therefore already been prohibited in the past. However, regulating the decision-making process in motion planning for AVs is much more complex than banning specific hardware components.

4.2 Mathematical Formulation of Risk

First, the aforementioned risk is to be formulated mathematically. In general, risk is defined as the product of a probability of occurrence and an estimated consequence (Rath, 2011). Thus, according to our case, we define the risk R as the product of collision probability p and estimated harm H. Both, p and H are functions of the trajectory u of the AV. This allows us to account for the two-dimensionality of risk resulting from a probability and the corresponding consequences. In contrast to Leben, (2017), who argues in favor of a probability of survival, extreme cases of high probabilities for minor harm and very low probabilities for major harm can thus be mapped separately. Therefore, unlike Leben, (2017), our approach overcomes the first challenge in dilemmatic situations formulated by Keeling, (2018).

$$R=p\left(u\right) H(u)$$
(1)

Figure 3 shows a high-level overview of the proposed framework for motion planning.

Fig. 3
figure 3

High-level structure of the proposed framework for the trajectory planning of an AV

Full size image

The collision probability is a result of uncertainties occurring during automated driving.

These uncertainties mainly originate from the vehicle sensors, the perception system, and the prediction algorithm. The uncertainties due to sensor technology are mainly related to noise, range limitations, and occluded areas. Uncertainties in the perception amount to the classification and localization of foreign road users, as well as the own localization. As third part, uncertainties in the prediction regarding the intention and exact trajectory of foreign road users contribute to overall uncertainty.

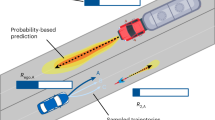
Previous research, such as by Hu, Zhan, and Tomizuka (2018), involved a probability-based prediction of external trajectories. Collision probabilities for trajectories can be determined on such a basis. Another major uncertainty that must be taken into account in a risk assessment is that caused by sensor occlusion (Nolte et al., 2018). Objects that may not yet be visible to the AV may be involved in a future collision. Thus, trajectories close to occluded areas have a slightly higher collision probability. An assessment of uncertainties through not yet known objects may finally reveal the need to adjust the AV’s velocity. Figure 4 schematically visualizes collision probabilities resulting from these uncertainties. The probabilities are visualized as a heat map, where red corresponds to a high probability and green to a low probability.

Fig. 4
figure 4

Visualization of two types of motion planning uncertainties. On the left, the prediction of the vehicle’s trajectory is based on a probabilistic distribution. On the right, an occluded area (red) causes a probability of an object appearing around it in the next time steps, from the AV’s point of view

Full size image

4.3 Harm Estimation

Harm has been an abstract quantity to date. One of the major challenges is the quantification of harm. The objective of a risk assessment is to map the expected accidental damage on a single scale to calculate according values for risk. From an ethical perspective, it is unclear how different types of harm should be quantified and weighed against each other. Especially when it comes to extreme accidents with potentially fatal consequences, this presents us with enormous difficulties. We cannot, for example, weigh up how a serious injury with lifelong disabilities relates to a death. From a moral point of view, it is even more difficult to compare property damage with personal injury. In research, we find approaches, for example, from economics, which attribute a certain monetary value to a human life (Murphy & Topel, 2006). However, this cannot be a basis for weighing up material damage and personal injury in the sense of a decision metric. According to the German Code of Ethics, this would constitute a violation of human dignity in the German Basic Law. As an alternative, for example, lives are not valued in monetary terms, but rather various measures are merely compared in terms of their effectiveness in statistically extending the lifetime of the population (e.g., in quality-adjusted life years) (Weinstein et al., 2009). This method is also controversial, as young and healthy people with a higher life expectancy would be systematically preferred. According to the German Ethics Code, however, age must not be a basis for decision-making (Ethik-Kommission, 2017).

These ethical considerations in relation to the quantification of harm require precise knowledge of the consequences of accidents. Indeed, in practice, the severity of an accident can only be predicted to a certain degree of accuracy. According to the current state of the art, it is not possible to differentiate, for example, whether a road user dies in an accident or suffers serious injuries. This makes the ethical problems of quantifying harm discussed at the beginning obsolete for our proposed motion planning framework. Particularly from the point of view of an autonomous vehicle, only a few factors are known to indicate the severity of an accident. For example, it is unknown how many people are in a vehicle or where the people are located inside the vehicle. Furthermore, vehicle-specific elements of passive safety such as airbags or seat belts are completely unknown. There are only a few characteristics that are known and on which a modeling of the accident damage must be based: The type of road user, such as a pedestrian or a passenger vehicle and therefore a general measure of vulnerability and an estimate of the mass; the differential speed of the accident participants at which a collision could occur; and an impact angle under which a collision could occur.

The severity of injury increases in proportion to the kinetic energy. Relevant studies show that the kinetic energy seems to be a good measure for the harm (Sobhani et al., 2011): The higher the kinetic energy exerted on a road user in an accident, the higher is the severity of injuries in general. Similarly, the probability of death in an accident increases with higher velocities and thus higher kinetic energies (Rosén & Sander, 2009). Given the AVs’ vehicle mass and the differential speed, the kinetic energy that will be impacted on a third-party road user can be calculated. Depending on the angle of impact, the kinetic energy actually acting on road users and the AV can be adjusted as part of a physical model. The exact modeling of harm can be done analogous to the so-called Injury Severity Score proposed by Sobhani et al. (2011). It should be noted that the calculation of the harms must be done at runtime, and therefore, the calculation time must be limited. Normalization can be achieved by means of an upper limit value, above which the severity of an accident is assumed as being maximum and thus cannot increase. Summarizing, we will not determine estimated harm by the rather subjective measure of quality of life but by quantifying the severity of injuries based on a few more objective factors such as the kinetic energy.

4.4 Risk Distribution

We can calculate a quantified risk \({R}_{\mathrm{ego}}\) for an automated ego vehicle according to Eq. (2). The subscriptions of p and H indicate a collision between two objects. While the two objects would be permutable in case of collision probability, the harm refers to the first index of harm H.

$$R_{\mathrm{ego}}=\sum p_{\mathrm{ego},\;\mathrm s\mathrm t\mathrm a\mathrm t.\mathrm{obst}.\;}H_{\mathrm{ego},\;\mathrm s\mathrm t\mathrm a\mathrm t.\mathrm{obst}.}+\sum p_{\mathrm{ego},\;\mathrm d\mathrm y\mathrm n.\mathrm{obst}.\;}H_{\mathrm{ego},\;\mathrm d\mathrm y\mathrm n.\mathrm{obst}.}$$
(2)

We distinguish between static obstacles (stat. obst.) and dynamic obstacles (dyn. obst.), in order to later consider only dynamic obstacles for the sake of simplification. With the focus on risk distribution between human road users, it seems to be a good assumption to focus only on dynamic objects. Furthermore, the uncertainties regarding static objects are significantly lower compared to dynamic objects. From the perspective of our ego vehicle, the risk for a third-party road user is presented in Eq. (3). It consists of one part, which the ego vehicle has influence on and one part \({R}_{\mathrm{own}}\), which is independent of the ego vehicle’s trajectory.

$${R}_{\mathrm{third party}}={p}_{\mathrm{third party,\;ego}}\:{H}_{\mathrm{third party,\;ego}}+{R}_{\mathrm{own}}$$
(3)

All the appearing risks, including the ego vehicle and all relevant third-party road users, are defined to be part of the set \({M}_{R}\). The corresponding harms \(H\) are assigned analogously in the set \({M}_{H}\).

$$\begin{array}{c}{M}_{R}=\left\{{R}_{1},\dots , {R}_{n}\right\}\\ {M}_{H}=\left\{{H}_{1},\dots , {H}_{n}\right\}\end{array}$$
(4)

The essential question now is how the calculated risks of road users can be distributed fairly in an ethical sense. The trajectory of the ego vehicle must then be selected accordingly. In literature, different principles for dividing risk are well-known and investigated, that can serve here as a model (Nida-Rümelin et al., 2012):

The Bayesian principle demands that the overall social benefit is maximized and corresponds to a utilitarian demand. According to this principle, the risk assessed to one person can be outweighed by the benefit done to another. This means choosing a trajectory that minimizes the total risk of all road users according to Eq. (5). \(J\) denotes the resulting costs to be minimized for a given trajectory \(u\).

$${J}_{B}(u)= {R}_{\text{total}}(u)= \sum_{i=1}^{|{M}_{R}|}{R}_{i}\left(u\right) , {R}_{i}\in {M}_{R}$$
(5)

However, only the overall risk is minimized here, which does not yet provide any information on the relation of the risks. Accordingly, the Bayesian principle does not take fairness into account. For reasons of fairness, the following Eq. (6) could be added to this cost function. This principle demands equality in the distribution of risk by minimizing the differences in the risks taken into account. We call this the Equality principle.

$${J}_{E}(u)= \sum_{i=1}^{\left|{M}_{R}\right|} \sum_{j=i}^{\left|{M}_{R}\right|}{|R}_{i}\left(u\right)-{R}_{j}\left(u\right)| , { R}_{i}, {R}_{j}\in {M}_{R}$$
(6)

Although minimizing the differences in risks taken seems to increase fairness, this principle has some weaknesses. Regardless of the outcome, the preferred option is one in which road users are treated as equally as possible. For example, it prefers a trajectory where two people are certain to die over a trajectory where one will die and one will survive unharmed. The example becomes even more apparent if in the second case one of the two road users receives a harm H of 0.01 with a probability of 0.01, so that no one will die in this case. As Fig. 5 shows with this example, even then the Equality principle would still prefer the two certain deaths.

Fig. 5
figure 5

There are two options for the AV: In a, two people will certainly die, while in option b, one person will receive a harm of 0.01 with a probability of 1% and the other person will certainly be unharmed. The Equality principle would choose option a here

Full size image

The Maximin principle requires that the option for action is chosen where the greatest possible damage is least, which is achieved by minimizing Eq. (7). For the worst of all possible cases, the best of all possible results should be achieved. In contrast to the Bayesian principle, the relation of risks is implicitly taken into account here.

$${J}_{M}(u)= {\text{argmax}}_{{H}_{i}(u)}\left({M}_{H}\right) , {H}_{i}\in {M}_{H}$$
(7)

The disadvantages of this principle are entirely highlighted by Keeling, (2018) in three exemplary thought experiments. Especially the second challenge shows that the Maximin principle gives undue weight to the moral claims of the worst-off (Keeling, 2018). Accordingly, only the greatest possible harm is considered regardless of its probability of occurrence. If there is a much higher probability that a slightly lower harm will occur, it does not influence the choice. The fact that only the harm of one person is taken into account also means that all other road users are not considered. Figure 6 shows an example that demonstrates the problem of the Maximin principle. In case A, one person will receive a harm of 1 with a probability of 1%, a group of n people will be unharmed for sure. In option B, one person and the group of n people will both certainly receive a harm of 0.99. No matter how large the quantity n is, which would certainly suffer high amount of harm, the Maximin principle would in any case prefer option B. Furthermore, it is not considered how likely or unlikely the largest possible harm of 1 will occur.

Fig. 6
figure 6

There are two options for the AV: In a, one person will receive a harm of 1 with a probability of 1% and a group of n people will be unharmed for sure. In option b, one person and the group of n people will both certainly receive a harm of 0.99. The Maximin principle would choose option B here

Full size image

All three principles presented in this paper thus have systematic shortcomings. However, we also realize that these three principles should be considered and taken into account in the choice of the trajectory. A combination of different moral principles is also proposed by Persad et al., (2009) in the field of allocation principles in terms of organ donation. Like the authors, we find here that a single principle cannot meet all the requirements for ethical risk assessment.

Therefore, we propose a cost function \({J}_{\mathrm{total}}\) considering all three principles in Eq. (8). \(w\) represents a weighting factor for the three terms being added. These weights can therefore be used to adjust how strongly each principle should be represented. From a perspective of risk assessment, we choose the trajectory that minimizes Eq. (8). The weights of the cost function provide an opportunity to compare different ethical settings as discussed in Section 2. Future work will focus on evaluating mandatory (in the sense of universal and imposed) ethics settings next to personal ethics settings with the ultimate aim of converging the two, meaning to reach consensus on required actions, functioning, and decisions of AVs in traffic scenarios. For personal ethics settings, weights can be derived from empirical studies that reflect the ethical intuitions of users. Combining these insights with considerations of fundamental principles and rules from the disciplines of law and ethics such as human dignity can serve as a starting point to move closer to a mandatory ethics setting for AVs (in the traditional sense, meaning the only allowed and required action). At this point, it should be noted that trajectory planning also has to consider other aspects in the form of an optimization problem, such as minimizing acceleration and jerk. Accordingly, the weighting of these factors must also be included. The question of the weighting factors within the proposed risk function can therefore not be answered separately. However, with the appropriate choice of weighting factors, all the challenges proposed by Keeling can be successfully overcome.

In addition to the three distribution principles, we also want to consider the time factor in the risk distribution function. The general approach is that imminent risk should be prioritized more than risk appearing further in the future. With increasing time horizon of a planned trajectory, the space for action increases (see Fig. 1) as well as the uncertainties. For example, the autonomous vehicle can usually avoid a risk that appears in 5 s by swerving or braking, whereas a risk appearing in 0.5 s represents a greater hazard. So we introduce a discount factor \(\gamma \le 1\), which reduces the risk with increasing time step \(t\in {\mathbb{N}}\).

$${J}_{\mathrm{total}}=\left({w}_{B} {J}_{B}+{w}_{E} {J}_{E}+{w}_{M} {J}_{M}\right) {\gamma }^{t}$$
(8)

When individual risks are compared, as in this case, the problem of information asymmetry arises. As an ego vehicle, the calculated risk contains potential collisions with all possible road users. However, the risk of third parties can only be calculated based on the collision with the ego vehicle. Hence, from the point of view of the ego vehicle, there are parts of third-party risks, namely the collisions with other third-party road users, we cannot quantify. We already described these parts with \({R}_{\mathrm{own}}\). Since the own risk is better quantifiable, it is correspondingly higher. This information asymmetry can be counteracted by normalizing the own risk with the number of potential collisions considered. However, dealing with this problem of information asymmetry that arises when transferring thought experiments to real applications will be part of future research.

4.5 Discussion

In our proposed motion planning framework with risk assessment, we create the possibility to combine the advantages of three risk distribution principles. Analogous to the distribution of scarce medical interventions proposed by Persad et al., (2009), we achieve priority for the worst-off, maximization of benefits, and equal treatment of people. Moreover, our approach does not only focus exclusively on decision-making in unavoidable accidents, but can be applied in any driving situation. This brings us significantly closer to an actual application in real vehicles, which is demanded by society and politics. Nevertheless, implicit answers are given also for situations of unavoidable accidents or dilemma situations.

In Section 2, we demanded that our motion planning framework should be able to represent both personal ethics settings and mandatory ethics settings. By defining weights in our risk cost function, we offer the possibility to represent both approaches. The representation of the knowledge learned in these three weight values limits the possible complexity of the model. On the other hand, the transparency and explainability of moral decisions are guaranteed by this. While the proposed model consists of sophisticated functions, a high-level explanation can be given, by which principle (Bayes, Equality or Maximin) the decision was dominated. Our proposed framework can thus be seen as a hybrid option of top-down and bottom-up approaches aiming to combine the advantages of both.

The topic of attributing responsibility to artificial agents is very important (Loh, 2019; Misselhorn, 2018). In Section 1, we showed that the moral responsibility must be taken into account in the case of unavoidable accidents (Kauppinen, 2020). A pedestrian who, contrary to the law, crosses the road when the pedestrian traffic lights are red brings risks into a traffic situation. Thus, it is reasonable that he/she must be assigned more risk. In point nine, the guidelines of the German ethics commission also distinguish between those involved in generating risks to mobility and those not involved (Ethik-Kommission, 2017). While we present a method for distributing risk among road users, the question of responsibility is not considered in our framework. In the future, to consider individual responsibility, a method must be found to quantify the level of risk for which a particular road user is responsible. Hence, responsibility cannot be related to individual road users to this date, but could be considered in terms of the road user type. Pedestrians in general, due to their lower mass and velocities, bring less risk into road traffic than motorized vehicles. On this basis, a representation of responsibility in this framework could be implemented by introducing a discount factor for vulnerable road users similar to the discount factor \(\gamma\) in the previous section.

4.6 Back to the Trolley Problem

In Section 1, we argued that the trolley problem does not reflect the ethical challenges of autonomous driving. However, some researchers claim that an answer to how the self-driving car would behave in that case must be given. Minx & Dietrich, (2015) state that AVs will only become established if it is possible to provide them a kind of decision ethics in dilemma situations. For this reason, we use our proposed framework and apply it to the trolley problem. Therefore, we calculate the risks for a limited number of two trajectories. As in autonomous driving, there is no initial setting, such as a preset switch: We have to omit this dimension of the trolley problem. Furthermore, as described in the dilemma, in the event of a collision, the AV does not take any consequences in terms of harm. The postulated death of a human is described by a harm of 1. The trolley dilemma leaves two options, which are killing a single human or killing five humans, as shown in Fig. 7. As a collision is also postulated as a certain event for both possible trajectories, the probabilities are set to 1. Risks for the ego AV and all humans as third-party road users are calculated according to Eqs. (2) and (3). The application of the Bayesian principle provides a total risk of 1 for all road users in the case of killing a single person; while in the case of five people being killed, the total risk is 5. As we see, applying the Bayesian principle to the trolley problem yields to a utilitarian procedure. While the Bayesian principle gives a straight answer to the trolley problem, the Equality principle does not. Applying Eq. (6) to the given scenario leads to the same cost value of five for both options. So both options are to consider equal in the sense of the Equality principle. Similarly, the Maximin principle does not provide a clear indication of how the autonomous vehicle should behave in this situation. The maximum risk in both cases is equal to 1. Thus, the Maximin principle does not provide a basis for a decision on the trolley problem, since the maximum risk is the same in both cases, and minimization, therefore, does not lead to a unique solution. Implemented in software, only a random generator could bring about a decision in this case. The proposed weighted combination of all three principles can be applied to the trolley problem without the definition of weight factors. Two cases must be distinguished: If the weighting factor for the Bayesian principle is equal to zero, no unique solution can be found, since only the unclear solutions of Maximin and Equality are summed up. However, as soon as this weighting factor takes on a value greater than zero, the decision is then to kill only one person. So, the decision in the case of the trolley problem is in line with human intuition using our proposed framework with \({w}_{B}>0\).

Fig. 7
figure 7

Our proposed framework applied to the commonly known trolley problem. Bayesian principle provides a decision to kill only one person instead of five because the total risk is lowest. The Equality and Maximin principles do not yield a decision criterion in this case. Our proposed combination of these free principles favors killing only one person in case of a weighting factor for the Bayesian principle greater than zero

Full size image

While in the case of the trolley problem, only the Bayesian risk term allows for an unambiguous decision, thought experiments are also conceivable in which the Maximin and Equality principles provide guidance. As an example, we modify the trolley problem slightly and postulate in the case of a collision with the 5 people that they all will not die (H = 1) but only suffer injuries corresponding to a relative harm value of 0.2. The rest of the trolley problem remains unchanged. Now, the Bayesian principle results in a cost value of 1 for both cases. Consequently, no decision can be made using the Bayesian principle in this slightly different case. Maximin and Equality principles both advocate a collision with the five persons (\({J}_{M}=0.2, {J}_{E}=1\)), as both costs are relatively lower than for the collision with a single human (\({J}_{M}=1, {J}_{E}=5\)). According to this, there are further examples conceivable in which the different distribution principles have different significance.

Although applying the proposed framework to the trolley problem means many simplifications, it is still possible to provide an answer to the widely discussed dilemma. However, as already mentioned, the trolley problem reveals some significant shortcomings and the challenges in the distribution of risk only become apparent in real traffic scenarios. Nevertheless, both cases emphasize that a single distribution principle is not sufficient to meet the demands of risk distribution from an ethical perspective and a combination of various principles is required.

5 Conclusions and Future Work

In order to bring AVs to the mass market one day, a variety of ethical problems still need to be clarified. The behavior of an AV in situations of unavoidable accidents raises ethical problems that need to be solved. Established ethical theories, such as deontology, utilitarianism, or virtue ethics, are discussed in this paper based on their applicability for deployment in AVs. We conclude that none of these theories alone provides satisfactory answers. In Germany, an ethics commission provides basic guidelines for the ethics of AVs. The development of AVs must consequently incorporate these guidelines. Especially against the background of these guidelines, we have argued to make use of ethics of risk. We define risk as the product of collision probability and estimated harm. Quantifying these variables enables risks to be taken into account in trajectory planning. The mathematical formulation of a risk cost function in trajectory planning establishes the basis for incorporating ethical considerations from ethics of risk into the software of an AV. We find that there is no ethical principle in ethics of risk that meets all the requirements of an ethical risk assessment alone. Therefore, we propose a combination of the Bayesian, Equality, and Maximin principles. This assessment method is able to overcome the challenges formulated by Keeling, (2018), although the weighting of the individual principles will be subject to future research. Furthermore, future work will address the question of how responsibility can be taken into account in a risk distribution. With our proposed framework, we form the basis for implementing ethical motion planning in real vehicles and at the same time provide an answer to the widely discussed trolley problem. However, the question of what constitutes a fair distribution of risk in road traffic cannot be answered here sufficiently. Therefore, this should be at the center of future research in order to move ahead in the endeavor of creating an ethical AV.