Abstract
In this paper, we prove bilinear sparse domination bounds for a wide class of Fourier integral operators of general rank, as well as oscillatory integral operators associated to Hörmander symbol classes \(S^m_{\rho ,\delta }\) for all \(0\le \rho \le 1\) and \(0\le \delta < 1\), a notable example is the Schrödinger operator. As a consequence, one obtains weak (1, 1) estimates, vector-valued estimates, and a wide range of weighted norm inequalities for these classes of operators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we study the bilinear sparse domination of oscillatory integral operators of the form:
where a is an amplitude of Hörmander type, and the phase function class will satisfy regularity conditions in \(\xi \) such that the operator is either a Fourier integral operator (FIO), or an oscillatory integral operator (OIO). See below for the definition of these two classes (see Sects. 2.3 and 2.4).
Recently, a significant advancement in pointwise estimates has been made with the development of the theory of sparse domination. This theory introduces the concept of sparse domination for operators T on function spaces, characterized by the following inequalities:
We call the first inequality sparse domination and the second one bilinear sparse domination. Moreover, the operators
are examples of sparse operators, which are positive averaging operators. See Sect. 2.2 for the full definitions of \({\Lambda }_{ {\mathcal {S}}, q}\) and \({\Lambda }_{{{\mathcal {S}}},q,p'}\).
The significance of proving sparse bounds extends well beyond their relationship to \(L^p\) bounds. These bounds are useful for establishing weighted and vector-valued inequalities. Importantly, the \(A_2\) conjecture, initially solved by Hytönen [14]. Lerner’s work [21] subsequently introduced sparse domination in a novel proof of the conjecture, emphasizing its foundational role before further developments in sparse operators. This approach has also been applied in many contexts, such as Bochner–Riesz multipliers [19], singular integrals [10, 20], various Hilbert transforms, multipliers and pseudodifferential operators [1, 25]. Recent advancements further developing the principles of sparse domination for \(L^p\)-improving operators in great generality include works by Beltrán et al. [2], Conde-Alonso et al. [7] and Hu [12], highlighting the ongoing innovation and application of these techniques across various mathematical disciplines.
Beltran and Cladek [1] showed that a sharp (up to the endpoint) bilinear sparse domination estimate for classical pseudodifferential operators, with amplitudes in \(S^m_{\rho ,\delta }({\mathbb {R}}^{n})\) for \(0<\delta \le \rho < 1\), holds. Building upon this result, our paper delves into the investigation of sparse domination for Fourier integral operators and other oscillatory integral operators with nonlinear phase functions associated to partial differential equations, like the Schrödinger equation. In the former case we focus on phase functions belonging to the Dos Santos Ferreira–Staubach classes \(\Phi ^2\). While in the latter case, we investigate the sparse domination of oscillatory integral operators with phase functions in the class  , which was initially introduced by Castro et al. [5].
, which was initially introduced by Castro et al. [5].
The sparse bounds established in our study yield a range of consequential results, including weighted and vector-valued inequalities for FIOs and OIOs. While some of the weighted norm inequalities have previously been established in the case of Fourier (see Dos Santos Ferreira and Staubach [9]) and oscillatory integral operators (see Bergfeldt and Staubach [3]), our work unveils new weighted norm inequalities, and gives quantitative control of the weighted operator norm. These new results, along with the previously known ones, are discussed in detail in Sect. 3. We choose to only discuss our main results about sparse domination in the introduction, beginning with the Fourier integral operators.
To this end, we define the following notation, set
and
This latter number is the sharp regularity exponent in the \(L^2\) boundedness of FIOs and also OIOs.
Theorem 1.1
(Fourier Sparse Domination) Assume that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\), and \(\varphi (x,\xi )\) is in the class \(\Phi ^2\) with rank \(0\le \kappa \le n-1\) and is SND. Then for any compactly supported bounded functions f, g on \({\mathbb {R}}^n\), there exist sparse collections \({\mathcal {S}}\) and \(\widetilde{{\mathcal {S}}}\) of dyadic cubes such that
for all pairs \((q, p')\) and \((p', q)\) such that
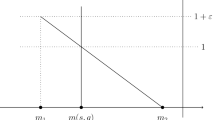
(See Fig. 1).
If the phase \(\varphi \) is linear (or \(\kappa =0\)), the FIOs reduce to the pseudodifferential case, this case was investigated by Beltran and Cladek [1]. Their sparse domination result suggests that the bilinear sparse domination estimates for the pseudodifferential operators could be improved in two ways. First, pseudodifferential operators are examples of Fourier integral operators with phase function of rank 0, secondly the order and type of the amplitude i.e. m, \(\rho \) and \(\delta \). The motivation for investigating Fourier integral operators with amplitude types different than \(\rho =1\) and \(\delta =0\), and ranks different than \(n-1\), comes from the theory of partial differential equations, scattering theory, inverse problems, and tomography, just to name a few. In this paper, we have made an attempt to investigate and achieve optimal results in all three of these directions.
We now turn to the oscillatory integral operators. Let \(\varkappa =\min (\rho ,1-k)\) and set
We also extend the class of the phase function to include nonlinear phase functions of the type \(x\cdot \xi +|\xi |^k\). This second class includes various oscillatory integral operators described in more detail below.
Theorem 1.2
(Oscillatory Sparse Domination) Let \(n\ge 1\), \(0<k<\infty \). Assume that  is SND, satisfies the LF\((\mu )\)-condition for some \(0<\mu \le 1\), and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then for any compactly supported bounded functions f, g on \({\mathbb {R}}^n\), there exist sparse collections \({\mathcal {S}}\) and \(\widetilde{{\mathcal {S}}}\) of dyadic cubes such that
is SND, satisfies the LF\((\mu )\)-condition for some \(0<\mu \le 1\), and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then for any compactly supported bounded functions f, g on \({\mathbb {R}}^n\), there exist sparse collections \({\mathcal {S}}\) and \(\widetilde{{\mathcal {S}}}\) of dyadic cubes such that
for all pairs \((q, p')\) and \((p', q)\) such that
(See Fig. 1).
The motivation behind investigating the OIOs in this paper stems from the theory of partial differential equations, specifically in the study of dispersive equations. These dispersive equations often involve phase functions \(\varphi (x, \xi ) = x \cdot \xi + \phi (\xi )\), where \(\xi \) represents the wave variable and x denotes the spatial variable. Different choices of \(\phi (\xi )\) lead to various important equations. For instance, when \(\phi (\xi ) = |\xi |^{1/2}\), it corresponds to the water-wave equation. When \(\phi (\xi ) = |\xi |^{2}\), it relates to the Schrödinger equation. Furthermore, in dimension one, \(\phi (\xi ) = |\xi |^{3}\) and \(\phi (\xi ) = \xi |\xi |\) correspond to the Airy and Benjamin–Ono equations, respectively.
This paper, and the method of obtaining sparse form bounds, is inspired by the work by Beltran and Cladek [1], Lacey and Spencer [20], and Lacey et al. [19]. The essential ingredients of this method are geometrically decaying \(L^p\)-improving estimates (i.e. \(L^q\rightarrow L^p\) estimates for \(p>q\)) on spatially and frequency localised pieces of the operator, as well as optimal \(L^p\) estimates on frequency localized pieces.
For \(m<-n(1-\rho )(1/q-1/2)\) in the range \(1\le q\le p\le 2\), and \(m<-n(1-\rho )(1/q-1/p)\) whenever \(1\le q\le 2\le p\le q'\), Beltran and Cladek obtained sharp up to the endpoint bilinear sparse domination estimates for the pseudodifferential operators with symbols in the Hörmander classes \(S^m_{\rho ,\delta }\) for \(0<\delta \le \rho <1\). In the corresponding ranges of p, q we obtain (1.2) for the Fourier integral operator with amplitudes in the Hörmander classes \(S^m_{\rho ,\delta }\) for \(0\le \delta <1\) and \(0\le \rho \le 1\). Thus, since Theorem 1.1 reduces to the sharp sparse domination result obtained for the pseudodifferential case in [1] whenever \(\rho \ge \delta \) and \(\kappa =0\), our result is also sharp in that range.
The trapezoid \({\textbf {T}}\) of Theorem 1.2. The thick lines are contained in the diagram while the dashed lines are not
We shall briefly describe the trapezoid associated with the admissible \((1/q,1/p')\)-points corresponding to the case of OIOs for \(m<0\). A similar description works to describe the numerology in Theorem 1.1. Let \({\textbf {T}}\) be the trapezoid with vertices,
where \(-n(1-\varkappa )\le m+\zeta \le -\frac{n(1-\varkappa )}{2}\). While if \(-\frac{n(1-\varkappa )}{2}-\zeta<m<0\) then we obtain the trapezoid
See Fig. 1 for a visualization of the trapezoid \({\textbf {T}}\). One may obtain similar trapezoids for the Fourier integral operators, e.g. just substitute \(\rho \) for \(\varkappa \) in \({\textbf {T}}\) to to obtain the corresponding trapezoid for the FIOs.
1.1 Organization and notation
In the first section of the paper (Sect. 2), we introduce the necessary fundamental concepts from microlocal analysis, weighted \(A_p\)-theory, and sparse domination theory. We also give the definitions of the various classes of amplitudes and phase functions regarding oscillatory integral operators and Fourier integral operators.
In Sect. 3 we derive all the corollaries of Theorems 1.1 and 1.2, these include weighted norm inequalities, weak (1, 1) estimates, and vector-valued inequalities. We also discuss how these estimates are new in relation to previously established results.
In Sect. 4 we provide the various decompositions that we employ in each case, along with various tools that we need in order to obtain the geometrically decaying \(L^q\)-improving estimates in Sect. 5. This section is concerned with the proof of \(L^q\)-improving estimates of oscillatory integral operators. This process is divided in two main steps. The first step is to use the various tools developed in the first section to obtain \(L^q\)-improving estimates which decay geometrically. In the second step we use the optimal global \(L^2\)-boundedness of OIOs shown in [16], along with the geometric decay of the first step to obtain \(L^2\) and estimate for the principal term of the decomposition. We do a similar procedure to obtain \(L^1\) and \(L^1\rightarrow L^\infty \) cases for the localized pieces and the principal term. By an interpolation procedure we then obtain the desired \(L^q\)-improving estimates.
In Sect. 6 we turn to the proof of the \(L^q\)-improving estimates pertaining to FIOs. We employ a similar strategy to the one in Sect. 5, the resulting analysis differs in the details more so than the overall strategy.
Finally in Sect. 7 we give the proof of the main results.
As for notation, in the subsequent analysis we will adopt the customary practice of denoting positive constants in inequalities by the symbol C. The specific value of C is not crucial to the current problem but can be determined based on known parameters, such as n, p, and q which are relevant in the given context. For instance, these parameters may be associated with the seminorms of various amplitudes or phase functions. While the value of C may vary from line to line, it can be estimated if required. In this paper, we refer to C as the “hidden constant”.
Additionally, we adopt the notation \(c_1 \lesssim c_2\) as a shorthand for \(c_1 \le Cc_2\). Moreover, we use the notation \(c_1 \sim c_2\) when both \(c_1 \lesssim c_2\) and \(c_2 \lesssim c_1\).
2 Preliminaries
We start by recalling the definition of the Littlewood–Paley partition of unity, which is the most basic tool in the frequency decomposition of the operators at hand.
Let \(\psi _0 \in {\mathcal {C}}_c^\infty ({\mathbb {R}}^n)\) be equal to 1 on B(0, 1) and have its support in B(0, 2). Then let
where \(j\ge 1\) is an integer and \(\psi (\xi ):= \psi _1(\xi )\). Then \(\psi _j(\xi ) = \psi \left( 2^{-(j-1)}\xi \right) \), and one has the following Littlewood–Paley partition of unity
for all \(\xi \in {\mathbb {R}}^n\). We also define the fattened Littlewood–Paley operators, set
with \(\psi _{-1}:=\psi _{0}\). Define the Littlewood–Paley operators by
In connection to the \(L^q\rightarrow L^p\) estimates for FIOs and OIOs below, we will encounter the well-known \(L^r\)-maximal function
where the supremum is taken over all balls B containing x. It is a classical result of Hardy and Littlewood that the \(L^r\)-maximal function \({\mathcal {M}}_rf(x)\) is bounded on \(L^p\) for \(p>r\).
The class of amplitudes considered in this paper was first introduced by Hörmander [11].
Definition 2.1
Let \(m\in {\mathbb {R}}\) and \(0\le \rho , \delta \le 1\). An amplitude \(a(x,\xi )\) in the class \(S^m_{\rho ,\delta }({\mathbb {R}}^{n})\) is a function \(a\in {\mathcal {C}}^\infty ({\mathbb {R}}^{n}\times {\mathbb {R}}^{n})\) for which
for all multi-indices \(\alpha \) and \(\beta \) and \((x,\xi )\in {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\), where \(\langle \xi \rangle := (1+|\xi |^2)^{1/2}.\)
In our subsequent discussion, we will refer to m as the order of the amplitude, while using \(\rho \) and \(\delta \) to denote its type. Specifically, we will refer to the class \(S_{\rho ,\delta }^m({\mathbb {R}}^n)\), where \(0<\rho \le 1\) and \(0\le \delta <1\), as the classical class. Similarly, the class \(S_{0,\delta }^m({\mathbb {R}}^n)\) with \(0\le \delta <1\) will be referred to as the exotic class, and we will denote the class \(S_{\rho ,1}^m({\mathbb {R}}^n)\), where \(0\le \rho \le 1\), as the forbidden class of amplitudes.
2.1 Tools from weighted function spaces
In deriving the weighted consequences of Theorems 1.1 and 1.2, we will make use of the classical \(A_p\) space and the reverse Hölder space \(RH_p\). We recall the definitions of these below for the convenience of the reader.
Definition 2.2
Let \(1<p< \infty \). A locally integrable and a.e. positive function w is called a weight. A weight is called a Muckenhoupt \(A_p\) weight if
while a weight is called a reverse Hölder \(RH_p\) weight if
The intersection of the \(A_s\) and the reverse Hölder classes can be characterized by the equivalence:
Definition 2.3
Let \(s \in {{\mathbb {R}}}\) and \(1\le p \le \infty \), \(1\le q \le \infty \) and \(w\in A_p\). The weighted Triebel–Lizorkin space is defined by
where \({\mathscr {S}}'({\mathbb {R}}^n)\) denotes the space of tempered distributions.
Later, in the discussion on vector-valued inequalities we shall need the following classical theorem due to de Francia [8].
Definition 2.4
An operator T defined in \(L^p\) is called linearizable if for any \(f_0\in L^p\), there exists a linear operator \({\mathcal {L}}\) such that
Theorem 2.5
Let \(T_j\) be a sequence of linearizable operators and suppose that for some fixed \(r\ge 1\), and all weights \(w\in A_r\) one has \(\Vert T_j f\Vert _{L^r_w}\lesssim \Vert f\Vert _{L^r_w}\). Then for \(1< p < \infty \) and \(w\in A_p\) one has
2.2 Background on sparse forms
Now, let us delve into some facts concerning sparse bounds.
Definition 2.6
Let \(0<\eta <1\). A collection \({\mathcal {S}}\) of cubes in \({\mathbb {R}}^{n}\) is called an \(\eta \)-sparse family if there are pairwise disjoint subsets \({\{ E_Q\}}_{Q \in {\mathcal {S}} }\) such that
-
(1)
\( E_{Q} \subset Q \)
-
(2)
and \(|E_{Q}|>\eta |Q|\).
If there is no confusion, we usually say sparse instead of \(\eta \)-sparse. By a cube Q in \({\mathbb {R}}^{n}\) we mean a half open cube such as
where l(Q) is the side length of the cube and \(x(Q)=(x_1,\ldots ,x_n)\) is a corner of the cube. Define a dyadic cube to be a cube Q with \(l(Q)=2^k\) for some \(k\in {\mathbb {Z}}\). Let v be vector in \(\{0,1,2\}^n\) and define the shifted dyadic grid \({\mathcal {D}}_v\) as the set
Definition 2.7
For any cube Q and \(1\le p <\infty \), we define \( {\langle f \rangle }_{p,Q}:= {|Q|}^{-\frac{1}{p}} {||f||}_{ L^p(Q)} \). Let \({\mathcal {S}}\) be an \(\eta \)-sparse family and \(1\le q <\infty \), then the (q, s)-sparse form operator \({\Lambda }_{{\mathcal {S}}, q,p}\) and q-sparse operator \( {\Lambda }_{ {\mathcal {S}},q}\) are defined by
for all \( f,g \in L^{1}_{loc} \).
If \(q<s<p\), we have
This inequality follows from the \(L^s\)-boundedness of the \(L^r\)-maximal operator \(M_r\), as detailed in [22]. In Sect. 7 we shall also make use of the following useful fact.
Lemma 2.8
Let \(1\le p,q\le \infty \). For bounded, compactly supported functions f, g, there exists a sparse form \({\Lambda }_{{\mathcal {S}}_0, q,p'}\) such that
(the hidden constant can be taken to only depend on the dimension n)
Obtaining (1, 1)-sparse bounds is the best scenario, while the quite trivial \((p,p')\)-sparse bounds are the weakest.
The following result due to Conde-Alonso et al. [6], shows that sparse form bounds are stronger than weak (1, 1) estimates.
Lemma 2.9
Suppose that a sublinear operator T has the following property: there exists \(C > 0\) and \(1 \le q < \infty \) such that for every f, g bounded with compact support there exists a sparse collection \({\mathcal {S}}\) such that
Then \(T: L^1({\mathbb {R}}^{n}) \rightarrow L^{1,\infty }({\mathbb {R}}^{n})\).
2.3 Basic definitions and results related to the Fourier integral operators
The phase functions that we shall use to define Fourier integral operators were first introduced in [9] by Dos Santos Ferreira and Staubach.
Definition 2.10
A phase function \(\varphi (x,\xi )\) in the class \(\Phi ^k\), \(k\in {\mathbb {Z}}_{>0}\), is a function \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^n \times {\mathbb {R}}^n {\setminus }\{0\})\), positively homogeneous of degree one in the frequency variable \(\xi \) satisfying the following estimate
for any pair of multi-indices \(\alpha \) and \(\beta \), satisfying \(|\alpha |+|\beta |\ge k.\)
Definition 2.11
One says that the phase function \(\varphi (x,\xi )\) satisfies the strong non-degeneracy condition (or \(\varphi \) is \(\textrm{SND}\) for short) if
Now, having the definitions of the amplitudes and the phase functions at hand, we define the FIOs as follows.
Definition 2.12
A Fourier integral operator \(T_a^\varphi \) with amplitude a and phase function \(\varphi \), is an operator defined (once again a-priori on \({\mathscr {S}}({\mathbb {R}}^n)\)) by
where \(\varphi \) is a member of \(\Phi ^k\) for some \(k\ge 1\). We say that \(\varphi \) is of rank \(\kappa \) if it satisfies \(\textrm{rank}\,\partial ^{2}_{\xi \xi } \varphi (x, \xi ) = \kappa \) for all \((x,\xi ) \in {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\setminus \{0\}\).
We will refer to a Fourier integral operator with amplitude in \(S^m_{\rho ,\delta }\) and phase function in \(\Phi ^2\) as a Fourier integral operator (or FIO for short). Taking \(\varphi (x,\xi )=x\cdot \xi \), one obtains the class of pseudodifferential operators associated to Hörmanders symbol classes.
2.4 Basic facts related to oscillatory integral operators
In this section, we aim to provide a concise overview of fundamental concepts about oscillatory integral operators that will serve as the foundation for the subsequent sections of our paper. We begin by introducing the definition of an oscillatory integral operator and exploring its essential properties.
When dealing with oscillatory integral operators, it is crucial to focus on the phase functions, as they play a central role in their classification. We consider nonlinear phase functions that go beyond the Fourier integral operators, in particular we are interested in phase functions of the following type, originally defined in [5]:
Definition 2.13
For \(0<k<\infty \), we say that a real-valued phase function \(\varphi (x,\xi )\) belongs to the class  , if \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^{n}\times {\mathbb {R}}^{n}{\setminus }\{0\})\) and satisfies the following estimates (depending on the range of k):
, if \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^{n}\times {\mathbb {R}}^{n}{\setminus }\{0\})\) and satisfies the following estimates (depending on the range of k):
-
for \(k \ge 1\),
$$\begin{aligned} \left| \partial ^\alpha _\xi (\varphi (x,\xi )-x\cdot \xi ) \right| \le c_{\alpha } |\xi |^{k-1}, \quad |\alpha | \ge 1, \end{aligned}$$ -
for \(0<k<1\),
$$\begin{aligned} \left| \partial ^\alpha _\xi \partial ^{\beta }_x (\varphi (x,\xi )-x\cdot \xi ) \right| \le c_{\alpha ,\beta } |\xi |^{k-|\alpha |}, \quad |\alpha + \beta | \ge 1, \end{aligned}$$
for all \(x\in {\mathbb {R}}^{n}\) and \(|\xi |\ge 1\).
A widely recognized and representative example of a phase in the space  is given by \(|\xi |^k + x \cdot \xi \). This particular type of phase is closely associated with the operator \(e^{i (\Delta )^{k/2}}\). Having the definitions of the amplitudes and the phase functions at hand, one has the following definition.
is given by \(|\xi |^k + x \cdot \xi \). This particular type of phase is closely associated with the operator \(e^{i (\Delta )^{k/2}}\). Having the definitions of the amplitudes and the phase functions at hand, one has the following definition.
Definition 2.14
An oscillatory integral operator \(T_a^\varphi \) with amplitude a in \( S^{m}_{\rho , \delta }({\mathbb {R}}^n)\) and a real-valued phase function \(\varphi \) is defined, initially on \({\mathscr {S}}({\mathbb {R}}^n)\), as follows:
where \(\varphi \) is a member of  for some \(k\ge 1\). We call k the order of the oscillatory integral operator.
for some \(k\ge 1\). We call k the order of the oscillatory integral operator.
In order to ensure the global \(L^2\)-boundedness of our operators, an additional condition must be imposed on the phase, which we will henceforth refer to as the \(L^2\)-condition for the sake of simplicity. This condition plays a crucial role in controlling the \(L^2\) behavior of the oscillatory integral operators under consideration.
Definition 2.15
One says that the phase function \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^{n}\times {\mathbb {R}}^{n})\) satisfies the \(L^2\)-condition if
for \(|\alpha |\ge 1\), \(|\beta |\ge 1,\) all \(x \in {\mathbb {R}}^{n} \) and \(|\xi |\ge 1\).
The following \(\textrm{LF}(\mu )\)-condition is an inherent requirement that, from the perspective of applications to PDEs, is typically satisfied and does not introduce any loss of generality. This condition is essential for analyzing the low-frequency components of the operators.
Definition 2.16
Let \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^n \times {\mathbb {R}}^n {\setminus } {0})\) be a real-valued function, and consider \(0<\mu \le 1\). We define the low-frequency phase condition of order \(\mu \), abbreviated as the \(\textrm{LF}(\mu )\)-condition, as follows: We say that \(\varphi \) satisfies the \(\textrm{LF}(\mu )\)-condition if it satisfies the inequality
for all \(x\in {\mathbb {R}}^n\), \(0<|\xi | \le 2\), and all multi-indices \(\alpha \) and \(\beta \).
3 Consequences of the main results
Sparse domination offers a notable advantage over classical \(L^p\) estimates by yielding weighted norm inequalities. In the subsequent subsections, we will delve into the discussion of several of these weighted estimates, as well as implications to weak (1, 1) estimates and vector-valued inequalities.
3.1 Weighted norm inequalities
In this section we derive bounds for \(T_a^\varphi \) of the form
with \(w\in A_q\), for some \(1<q,p<\infty \), and where
For weighted norm inequalities for FIOs the reader is referred to the work Dos Santos Ferreira and Staubach [9]. For weighted norm inequalities for oscillatory integral operators that go beyond FIOs the reader is referred to Bergfeldt et al. [3]. Note that in these papers the authors consider weighted norm inequalities for weights that belong to all \(A_p\)-classes, for \(1<p<\infty \) (see Eq. (3.1)), i.e. \(q=p\) in Eq. (3.1). In both cases they disregard the quantitative control on C.
Our corollary recovers all the previous known weighted estimates of Beltran and Cladek [1]. In the case of FIOs our result extends the weighted norm estimates in [3, 9] to phase functions with arbitrary rank \(0\le \kappa \le n-1\) (see item (2) below). In both the cases of FIOs and OIOs we obtain control of C, moreover we obtain new weighted norm inequalities for weights in the more general class \( A_{q/q_0} \cap RH_{(p_0/q)'}\), i.e. we extend to the case when p and q are not necessarily equal.
The following corollary is derived from [4, Proposition 6.4] (due to Bernicot, Frey and Petermichl) and Theorem 1.1 in the case of FIOs and Theorem 1.2 in the case of OIOs.
Corollary 3.1
Let \(a\in S^{m}_{\rho ,\delta }\) be an amplitude with \(m\le 0\) and \(0\le \rho \le 1\), \(0\le \delta < 1\). Let the phase functions \(\varphi \) be SND and satisfy either
-
(1)
\(\varphi \in \Phi ^2\), or
-
(2)
 , obeys the \(L^2\)-condition and is \(LF(\mu )\) for some \(0< \mu \le 1\).
, obeys the \(L^2\)-condition and is \(LF(\mu )\) for some \(0< \mu \le 1\).
If (1) holds, take m and all pairs \((q_0, p_0')\), \((p_0', q_0)\) such that (1.2) is satisfied. While if (2) holds, take \((q_0, p_0')\), \((p_0', q_0)\) and m such that (1.4) is satisfied. For \(w \in A_{q/q_0} \cap RH_{(p_0/q)'}\) and all \(q_0<p<p_0\), there exists a constant \(c_{p}\)
where
We define the class dependent number D as follows. Let
if \(T_a^\phi \) is an OIO, as in Theorem 1.2, and let
if \(T_a^\phi \) is an FIO, as in Theorem 1.1.
Remark 3.2
Observe that using the open property of \(A_p\) weights (see [13] or [23]) and that \(A_p\) classes increase in p, one can show the following two cases of corollary 3.1 for OIOs. For more details on proving this we refer the reader to [1].
-
(1)
Let \(-D-\zeta <m\le -D/2-\zeta \). Then \(T_a^\varphi \) is bounded on \(L^p_w\) for \(w \in A_{-\frac{p(m+\zeta )}{D}}\) and all \(-\frac{D}{m+\zeta }<p<\infty \).
-
(2)
Let \(m=-D/2-\zeta \). Then \(T_a^\varphi \) is bounded on \(L^p_w\) for \(w \in A_{p/2}\) and all \(2<p<\infty \).
These results only constitute some of the weighted estimates implied by corollary 3.1.
3.2 Weak-type estimates
For weighted norm inequalities for local FIOs the reader is referred to the work by Tao [24]. Note that in that paper the author consider FIOs with amplitudes in \(S^m_{1,0}\) (\(m=-(n-1)/2\)) and compact support in the spatial variable x, as well as phase functions which are smooth away from \(|\xi |=0\), satisfy the SND condition, and are homogeneous of degree 1. Our corollary extends this result to global FIOs, with phase functions that are in \(\Phi ^2\) and amplitudes in the \(S^m_{\rho ,\delta }\) for all \(0\le \rho \le 1\) and \(0\le \delta <1\) up to the end point. In particular when the phase has full rank, we obtain \(m<-(n-1)/2\) for \(a\in S^m_{1,0}\), recovering the result in [24] up to the end point.
For global oscillatory integral operators our corollary is entirely new, in particular the numerology in corollary 3.4 agrees with the \(L^p\) estimates obtained in [16] by Israelsson, Staubach and the author.
Combining Lemma 2.9 with Theorems 1.1 and 1.2 respectively, we obtain the following two corollaries.
Corollary 3.3
Assume that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\), and \(\varphi (x,\xi )\) is in the class \(\Phi ^2\) with rank \(0\le \kappa \le n-1\) and is SND. Then, for
it holds that
Corollary 3.4
Let \(n\ge 1\), \(0<k<\infty \). Assume that  is SND, satisfies the LF\((\mu )\)-condition for some \(0<\mu \le 1\), and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then, for \(m<-\frac{n(1-\varkappa )}{2}-\zeta \) it holds that
is SND, satisfies the LF\((\mu )\)-condition for some \(0<\mu \le 1\), and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then, for \(m<-\frac{n(1-\varkappa )}{2}-\zeta \) it holds that
3.3 Vector-valued inequalities
By leveraging the \(A_p\) weighted estimates obtained earlier and Lemma 2.4, we can derive new vector-valued estimates for OIOs and FIOs. Define \(\Vert \cdot \Vert _{L^q(\ell ^p)}\) to be the quasi-norm
Define the space \(L^q(\ell ^p)\) as the sequence space in which \(\Vert (f_k)\Vert _{L^q(\ell ^p)}<\infty \).
As we mentioned in the introduction there are important applications for FIOs and OIOs with simplified phase functions of the form \(x\cdot \xi +\phi (\xi )\). The following result is a weighted vector-valued estimate for FIOs and OIOs with simple phase functions. For weighted Triebel–Lizorkin estimates we refer the reader to [9]. Since the proof of the result below follows essentially in the same way as theirs, we omit the details and refer the reader to that paper.
Theorem 3.5
Let \(a\in S^{m}_{\rho ,\delta }\)be an amplitude with \(m\le 0\) and \(0\le \rho \le 1\), \(0\le \delta < 1\). Let the phase functions \(\varphi \) be SND and satisfy either
-
(1)
\(\varphi \in \Phi ^2\), or
-
(2)
 , and \(\varphi \) is \(LF(\mu )\) for some \(0< \mu \le 1\).
, and \(\varphi \) is \(LF(\mu )\) for some \(0< \mu \le 1\).
If (1) holds, take \(m=-n(1-\rho )-\zeta \), while if (2) holds take \(m=-n(1-\varkappa )-\zeta \). For all \(1<q,p<\infty \), and \((f_j)_{j\ge 0}\in L^q(\ell ^p)\) it holds that
Moreover, for \(s'\ge s\) it holds that
whenever the phase is simple. (See Definition 2.3 for the details on the space \(F^s_{p,q}(w)\).)
In the above result (3.2) is a direct consequence of Theorem 2.5, and item (2) in remark 3.2 applied to \(T_{a}^{\varphi }\). For the reader interested in the proof of estimate (3.3) we refer to [9]. The argument is rather short and is essentially an application of a variant of (3.2), and using that \([\psi _j,T_{a}^{\varphi }]=0\) for simple phase functions.
4 Decompositions and kernel estimates
In this section we provide the necessary tools used in the proofs of Theorems 1.1 and 1.2.
4.1 Decomposition of Fourier integral operators
In this section we introduce the spatial and frequency decompositions related to the FIOs, we refer the reader to [15] for the origin of this decomposition and details on the proofs of the Lemmas 4.2 and 4.3.
To start, one considers an FIO \(T^{\varphi }_{a}\) with amplitude \(a(x, \xi )\in S^{m}_{\rho , \delta }({\mathbb {R}}^n)\), \(0<\rho \le 1\), \(0\le \delta <1\), \(m\in {\mathbb {R}}\) and \(0 \le \kappa \le n-1\), \(\varphi \in \Phi ^2\), \(\textrm{rank}\,\partial ^{2}_{\xi \xi } \varphi (x, \xi ) = \kappa \), on the support of \(a(x, \xi )\) and its Littlewood–Paley decomposition
where the kernel \(K_j\) of \(T_j\) is given by
Here each \(\psi _j\) (for \(j\ge 1\)) is supported in a dyadic shell \(\left\{ 2^{j-1}\le \vert \xi \vert \le 2^{j+1}\right\} \).
The shells \(A_j\) will in turn be decomposed into truncated cones using the following construction. Since \(\varphi \) has constant rank \(\kappa \) on the support of \(a(x, \xi )\) we may assume that there exists some \(\kappa \)-dimensional submanifold \(S_\kappa (x)\) of \({{\mathbb {S}}}^{n-1}\cap \Gamma \) for some sufficiently narrow cone \(\Gamma \), such that \({{\mathbb {S}}}^{n-1}\cap \Gamma \) is parameterised by \(\overline{\xi }=\overline{\xi }_x(u,v)\), for (u, v) in a bounded open set \(U\times V\) near \((0,0)\in {\mathbb {R}}^{\kappa }\times {\mathbb {R}}^{n-\kappa -1}\), and such that \(\overline{\xi }_x(u,v)\in S_\kappa (x)\) if and only if \(v=0\), and \(\nabla _\xi \varphi (x,\overline{\xi }_x(u,v))=\nabla _\xi \varphi (x,\overline{\xi }_x(u,0))\).
Definition 4.1
For each \(j\in {{\mathbb {Z}}}_{>0}\), let \(\{u^{\nu }_{j} \} \) be a collection of points in U such that
-
(i)
\( | u^{\nu }_{j}-u^{\nu '}_{j} |\ge 2^{-j/2},\) whenever \(\nu \ne \nu '\).
-
(ii)
If \(u\in U\), then there exists a \(u^{\nu }_{j}\) so that \(\vert u -u^{\nu }_{j} \vert <2^{-j/2}\).
Moreover we set \(\xi ^{\nu }_{j}=\overline{\xi }_x(u^{\nu }_{j},0).\) One may take such a sequence by choosing a maximal collection \(\{\xi _{j}^{\nu }\}\) for which (i) holds, then (ii) follows. Now, denote the number of cones needed by \({\mathscr {N}}_j\).
Let \(\Gamma ^{\nu }_{j}\) denote the cone in the \(\xi \)-space given by
We decompose each \(A_j\) into truncated cones \(\Xi ^{\nu }_{j}:=\Gamma ^{\nu }_{j}\cap A_j.\) One also defines the partition of unity \(\{\chi _j^\nu (u)\}_{j,\nu }\) on \(\Gamma \) (a construction can be found in [15]). This homogeneous partition of unity \(\chi _j^\nu \) is defined such that \(\chi _j^\nu (s\overline{\xi }_x(u,v))=\tilde{\chi }_j^\nu (u),\) for \(v\in V\) and \(s>0\). Using this decomposition, we make a second dyadic decomposition of \(T_j\) as
where
Observe that \(T_j = \sum _{\nu =1}^{{\mathscr {N}}_j} T_j^\nu .\) We choose the coordinate axes in \(\xi \)-space such that \(\xi ''\in (T_{\xi ^{\nu }_j}S_\kappa (x))^\perp \) and \(\xi '\in T_{\xi ^{\nu }_j}S_\kappa (x)\), so that \(\xi =(\xi '',\xi ')\).
Lemma 4.2
The functions \(\chi _j^\nu \) belong to \({\mathcal {C}}^\infty ({\mathbb {R}}^n\setminus \{0\} )\) and are supported in the cones \(\Gamma _j^\nu \). They satisfy
for all multi-indices \(\alpha \).
We will also make us of the following slightly modified version of the partition of unity
for which
This partition of unity also satisfies the estimates in Lemma 4.2. In connection to this partition of unity we also define the fattened version of the second dyadic decomposition. We define these pieces by \({\mathcal {X}}_j^{\nu }(D):=\tilde{\chi }_j^\nu (D)\Psi _j(D)\). Observe that these have the nice property that they satisfy the equation
where \(f_j^\nu (x):={\mathcal {X}}_j^{\nu }(D) \Psi _j(D) f(x)\). Moreover, these pieces satisfy the following estimate
the proof of which follows using that \(\tilde{\chi }_j^\nu (D)\) satisfies lemma 4.2 and partial integration.
We will split the phase \(\varphi (x,\xi )-y\cdot \xi \) into two different pieces, \((\nabla _\xi \varphi (x,\xi _j^\nu )-y)\cdot \xi \) (which is linear in \(\xi \)), and \(\varphi (x,\xi ) - \nabla _\xi \varphi (x,\xi _j^\nu ) \cdot \xi \). The following lemma yields an estimate for the nonlinear second piece. For \(j\in {\mathbb {Z}}_{\ge 0}\), \(1\le \nu \le {\mathscr {N}}_j,\) define
Lemma 4.3
Let \(\varphi (x,\xi )\in {\mathcal {C}}^{\infty }({\mathbb {R}}^n \times {\mathbb {R}}^n{\setminus }\{0\})\) be positively homogeneous of degree one in \(\xi \). Then for \(\xi \) in \(\Xi ^{\nu }_{j}\), one has for \(\alpha \in {{\mathbb {Z}}}_{> 0}^{\kappa }\) that
Moreover, for \(\beta \in {{\mathbb {Z}}}_{> 0}^{n-\kappa }\) one has that
And finally one has the estimate
Define \(\widetilde{\psi }_{j,l}^{\nu }(x,y)\) as the characteristic function of the set
We further decompose each \(T_j\) into spatially localised operators \(T_{j, l}^\nu \) defined by
for \(l \in {\mathbb {Z}}\) and \(j>0\), and in an analogous manner for \(T_{0,l}\), so that
We further group the pieces \(T_{j,l}\) according to their spatial scale. Fix some \(\epsilon >0\) and write
In the next lemma we estimate the regularity of the kernel
of \(T_{j,l}^\nu \).
Lemma 4.4
Let \(0\le \rho ,\delta \le 1\), \(\rho \ne 0\), \(n\ge 1\). Assume that \(\varphi \in \Phi ^2\). Then if \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\), we have for \(1\le p\le \infty \) that
for all \(j\ge 0\) and all \(N,L\ge 0\), and where
Proof
For any \(j\ge 0\) we have
where
Observe that by Lemma 4.3 we have
on the support of \(\psi _j\). Using this and that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\) we can calculate that for any multi-index \(\gamma \), any \(j\ge 0\) and any \(\nu \) one has
If we now set \(h_j^\nu (x,\xi ):=\varphi (x,\xi )-\xi \cdot \nabla _\xi \varphi (x,\xi _j^\nu )\), then we can write
Now we estimate the derivatives of \(h_j^\nu \) in \(\xi \) on the support of \(\sigma _{j}^{\nu }(x,\xi )\). To this end, Lemma 4.3 yields
and
Next we introduce the operator L defined by
Then using the estimate (4.10) and (4.12) we obtain,
This estimate can be improved in terms of obtaining a decaying factor depending on \(\rho \), however for our purposes this is not necessary since we are looking for geometric decay, which will be achieved in a different manner below. We also have that
Therefore, partial integration and the trivial estimate \(|\Xi ^{\nu }_{j}|\lesssim 2^{jn}\) yields
The observation that
on the support of \(\widetilde{\psi }_{j,l}^\nu \) gives us for any \(N,L\ge 0\) and \(1\le p\le \infty \) that
for \(M>n+N+L\). Therefore we obtain,
\(\square \)
4.2 Decomposition of oscillatory integral operators
In this section we introduce the spatial and frequency decompositions related to the OIOs, we refer the reader to [16] for the origin of this decomposition. It is an adaption of the classical second dyadic decomposition introduced by C. Fefferman, to the case of nonlinear phases of the type  .
.
Let \(k>0\). We make the following decomposition of the integral kernel
Then for every \(j\ge 0\) we cover \({{\,\textrm{supp}\,}}\psi _j\) with open balls \(C_j^\nu \) with radii \(2^{j(1-k)}\) and centres \(\xi _j^\nu \), where \(\nu \) runs from 1 to \({\mathscr {N}}_j:=O(2^{njk})\). Observe that \(|C_j^\nu |\lesssim 2^{n j(1-k)}\), uniformly in \(\nu \). Now take \(u\in {\mathcal {C}}_c^{\infty }({\mathbb {R}}^{n})\), with \(0\le u\le 1\) and supported in B(0, 2) with \(u=1\) on \(\overline{B(0,1)}.\) Next set
and note that
Now we define the second order frequency localized pieces of the kernel above as
and define
We further decompose each \(T_j\) into spatially localised operators \(T_{j, l}^\nu \) defined by
for \(l \in {\mathbb {Z}}\) and \(j>0\), and in an analogous manner for \(T_{0,l}\), so that
We further group the pieces \(T_{j,l}\) according to their spatial scale. Fix some \(\epsilon >0\) and write
In the next lemma we estimate the kernel
of \(T_{j,l}^\nu \), to this end define the notation
Lemma 4.5
Let \(0\le \rho ,\delta \le 1\), \(n\ge 1\), and \(0<k<\infty \). Assume that  . Then if \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\), we have for \(1\le p\le \infty \) that
. Then if \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\), we have for \(1\le p\le \infty \) that
for all \(j\ge 0\) and all \(N,L\ge 0\).
Proof
From Lemma 3.2 in [16] we obtain the following inequality
for all \(j\ge 0\) and \(M\ge 0\). The observation that
on the support of \(\widetilde{\psi }_{j,l}^{\nu }\) gives us for any \(N,L\ge 0\) and \(1\le p\le \infty \) that
for \(M>n+N+L\). \(\square \)
4.3 A low frequency sparse domination result for Fourier and oscillatory integral operators
In this section we prove a low frequency sparse form bound, which yields the necessary boundedness for all the low frequency parts considered in this paper. Therefore, from now we only consider the high frequency portions of the operators at hand.
Theorem 4.6
Let \(a\in S^m_{\rho ,\delta }\) with \(m\in {\mathbb {R}}\) and \(0\le \rho ,\delta \le 1\) and let the phase function \(\varphi \) be SND and satisfy either
-
(1)
\(\varphi \in \Phi ^2\) or
-
(2)
 , obeys the \(L^2\)-condition and \(\varphi \) is \(LF(\mu )\) for some \(0< \mu \le 1\).
, obeys the \(L^2\)-condition and \(\varphi \) is \(LF(\mu )\) for some \(0< \mu \le 1\).
Let \(\chi \in C_c^\infty \) compactly supported around the origin, and define the OIO
Then for any compactly supported bounded functions f, g on \({\mathbb {R}}^n\), there exist sparse collections \({\mathcal {S}}\) and \({\mathcal {S}}'\) such that
for all pairs \((q, p')\) and \((p', q)\) such that
Proof
We begin by considering the case of FIOs. Fix a \(\xi _0\in S^{n-1}\), and define
We decompose \(T_\chi \) into spatially localised operators \(T_{\chi , l}\) defined by
with \(K_l(x,y)= \widetilde{\psi }_{\chi ,l}(x,y) K(x,y)\). Let \(b(x,\xi )=e^{i(\nabla _\xi \varphi (x,\xi )-\nabla _\xi \varphi (x,\xi _0)\cdot \xi )}a(x,\xi )\chi (\xi )\), then
Observe that for all \(\mu \in [0,1)\),
The proof of this estimate follows from the same arguments as Theorem 1.2.11 in [9] except one uses integration by parts with the differential operator given by \(L=(I-\Delta _{\xi ''})(I-\Delta _{\xi '})\) instead of just \(L=\partial _\xi \). The rest of the proof for FIOs follows in a very similar manner to that of Theorem 1.1.
Handling the OIOs: In the case of the OIOs, define
We decompose \(T_\chi \) into spatially localised operators \(T_{\chi , l}\) defined by
with \(K_l(x,y)= \widetilde{\psi }_{\chi ,l}(x,y) K(x,y)\). Observe that when  satisfies the \(LF(\mu )\)-condition then Lemma 4.3 in [5] yields
satisfies the \(LF(\mu )\)-condition then Lemma 4.3 in [5] yields
for any \(0\le \epsilon _1<1\). Thus, by continuing in the same way as was done for the FIOs above, one obtains the desired sparse form bound. \(\square \)
5 \(L^q\)-improving estimates for oscillatory integral operators
This section is devoted to showing the \(L^q\rightarrow L^p\) boundedness of OIOs. Recall that because of the low frequency sparse bound Lemma 4.6 it suffices to consider the high frequency part in this section, therefore we do not need the \(LF(\mu )\)-condition either, which is needed in Theorem 1.2.
Lemma 5.1
Let \(n\ge 1\), \(0<k<\infty \). Assume that  is SND, and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m(p)}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then for \(1\le q\le p\le 2\)
is SND, and the \(L^2\)-condition (2.6). Assume also that \(a(x,\xi )\in S^{m(p)}_{\rho ,\delta }({\mathbb {R}}^{n}),\) for \(0\le \rho \le 1\) and \(0\le \delta < 1\). Then for \(1\le q\le p\le 2\)
Moreover, for \(1\le q \le 2 \le p \le q'\) we have
Proof
We begin by proving the geometrically decaying \(L^q\rightarrow L^p\) estimates for \(T_{j, l}^\nu \) when \(1\le p \le 2\). Lemma 4.5 gives us that
for \(N>n/r\), \(l>j\epsilon \), and \(L(C,\epsilon )>\max \{C,\frac{\varkappa -w(k,\rho )n+C+C\epsilon +nk}{w(k,\rho )+\epsilon }\}.\) By the SND condition and the Hardy–Littlewood maximal theorem we have that
for \(1<r<p\le \infty \). If \(p=1\) then Young’s inequality for integral operators and Lemma 4.5 yields
Thus summing this in \(\nu \), we have for all \(1\le p\le 2\) that
We now lift the \(L^p\) estimate above to geometrically decaying \(L^q\rightarrow L^p\) bounds of \(T_{j, l}^\nu \) in the range \(1\le q\le p\le 2\). To this end, we use Bernstein’s inequality for \(1\le q\le p\le 2\) and estimate (5.2),
where \(\Psi _j\) is a fattened Littlewood–Paley piece.
The next step is to obtain geometrically decaying \(L^q\rightarrow L^p\) bounds of \(T_{j, l}^\nu \) in the range \(1\le q\le 2\le p<q'\). Observe that the pointwise estimate (5.1) yields that
By now interpolating this \(L^1\rightarrow L^\infty \) estimate and the \(L^2\rightarrow L^2\) estimate of \(T_{j, l}\) we obtain for \(1\le p\le 2\) that
Now interpolating this with (5.3) with \(p=2\) and using Bernstein’s inequality again we obtain
for \(1\le q\le 2\le p\le q'\).
The case of \(\sum _{l\le j\epsilon } T_{j, l}\):
In this case we leverage the geometrically decaying bounds on \(T_{j, l}^\nu \) and the \(L^2\) boundedness of \(T_j\) established in [16]. For a fixed j consider \(T_j\), defined as \(2^{j(-\zeta -m)}T_j = \sum _l 2^{j(-\zeta -m)}T_{j, l}\), which corresponds to a OIO associated with an amplitude in the class \(S_{\rho , \delta }^{\zeta }\) with \(L^p\) operator norm of
By the \(L^2\)-boundedness in [16] we establish the inequality
Using the decomposition
and the geometrically decaying estimate (5.2) we obtain
Similarly for \(L^1\rightarrow L^1\) we obtain
Interpolating these two bounds we obtain for \(1\le p\le 2\) that
As demonstrated in the previous case, this and Bernstein’s inequality for \(1\le q\le p\le 2\) yields
We do the \(L^\infty \) bound as before, by taking out the supremum of the kernel and summing over \(\nu \), this yields the estimate
which combined with the corresponding estimates for \(T_{j, l}\) and the rapid decay yields that
By interpolating the \(L^1\rightarrow L^\infty \) estimate and the \(L^2\rightarrow L^2\) estimate of \(\sum _{l\le j\epsilon } T_{j, l}\), we obtain for \(1\le p\le 2\) that
Moreover, (5.6) and Bernstein’s inequality yields
Now interpolating these last two estimates we obtain
for \(1\le q\le 2\le p\le q'\). \(\square \)
6 \(L^q\)-improving estimates for Fourier integral operators
This section is devoted to showing the \(L^q\rightarrow L^p\) boundedness of Fourier integral operators.
Lemma 6.1
Assume that \(a(x,\xi )\in S^{m}_{\rho ,\delta }({\mathbb {R}}^{n})\) for \(0< \rho \le 1\) and \(0\le \delta < 1\), and \(\varphi (x,\xi )\) is in the class \(\Phi ^2\) and is SND. Then for \(1\le q\le p\le 2\)
Moreover, for \(1\le q \le 2 \le p \le q'\) we have
Proof
The proof for the \(\sum _{l\le j\epsilon } T_{j, l}^\nu \) case is similar to the one above in Lemma 5.1, corresponding to the OIOs, with a few modifications. Mainly, one substitutes the use of the sharp \(L^2\)-boundedness result [16] for OIOs with a corresponding optimal \(L^2\)-boundedness result in [9, Theorem 2.7]. The rest of the changes to the argument involve simple numerical modifications.
We turn to proving the geometrically decaying \(L^q\rightarrow L^p\) estimates for \(T_{j, l}^\nu \).
Define \({\mathcal {M}}''\) as the Hardy–Littlewood maximal function acting on the function in the \(x''\) variable, i.e.
where \(x=(x'',x')\). We define \({\mathcal {M}}'\) in a similar manner.
Using (4.5) we can write \(T^\nu _{j,l}f(x)=T^\nu _{j,l}f^\nu _j(x)\), where \(f^\nu _j(x)=\chi _{j}^\nu (D)\Psi _j(D)f(x).\) Now using Lemma 2.22 in [17], take \(k=\nu \), \(n'=\kappa \) and \( r_1=r_2 = \frac{1}{2N} <p\) and note that the spectrum of \(f^\nu _j\) is
Moreover take \(c_{j,\nu }=2^{j}\) and \(d_{j,\nu }=2^{\frac{j}{2}}\). Then the conditions of Lemma 2.22 in [17] and Lemma 4.5 all hold for \(f_j^\nu \), and therefore we have
for \(l>j\epsilon \), \(L-N> n\) and \(L=L(C,\epsilon ,n)\) sufficiently large.
By the SND condition, the Hardy–Littlewood maximal theorem, and (4.6) we have
for \(1\le p\le \infty \). We also used that there are roughly \(2^{j(n-1)/2}\) terms in the sum over \(\nu \).
We now lift the \(L^p\) estimate above to geometrically decaying \(L^q\rightarrow L^p\) bounds of \(T_{j, l}^\nu \) in the range \(1\le q\le p<\infty \). To this end, we use Bernstein’s inequality for \(1\le q\le p\le 2\) and estimate (6.2),
where \(\Psi _j\) is a fattened Littlewood–Paley piece.
The next step is to obtain geometrically decaying \(L^q\rightarrow L^p\) bounds of \(T_{j, l}^\nu \) in the range \(1\le q\le 2\le p<q'\). Observe that
By interpolating this \(L^1\rightarrow L^\infty \) estimate and the \(L^2\rightarrow L^2\) estimate of \(T_{j, l}\) we obtain for \(1\le p\le 2\) that
Now interpolating this with (6.3) for \(p=2\) and using Bernstein’s inequality, again we obtain
for \(1\le q\le 2\le p\le q'\). \(\square \)
7 Proof of the main results
In this section we give a brief description of the proof of Theorem 1.1 and Theorem 1.2.
We distil the idea of [1, 18,19,20] to use geometrically decaying \(L^q\rightarrow L^p\) estimates of pieces of an operator to prove sparse form bounds. We attribute the subsequent lemma to the work of Beltran and Cladek [1], building on earlier work of Lacey [18], and Lacey and Spencer [20] and Lacey et al. [19]. Using the one-third trick and using shifted dyadic grids, they made calculations that have culminated in the following lemma. Notably, although their original paper did not cast it as a lemma, we have chosen to formalize it as such in our context.
Lemma 7.1
[1] Fix \(\epsilon >0\) and \(\delta > \epsilon \). Then for a sequence of operators \((T_{j,l})_{j,l\ge 0}\) we have
and
where the sums are taken over Q in some shifted dyadic grid \({\mathcal {D}}_v\).
Proof
The proof we give is a sketch, based on arguments appearing in [1], reproduced here for completeness. We begin with decomposing \(T_{j,l}\) using the shifted dyadic grid \({\mathcal {D}}_v\) in Sect. 2.2. For \(v\in \{0,1,2\}^n\), define
such that
Observe that this decomposition ensures that the support of \(T_{j,l} [f\chi _{\frac{1}{3}Q}]\) lies in Q. Because of (7.1), it now suffices to show the result for \(T_{j,l,v}\) for some specific choice of v. Thus
Next, we turn to deal with the second sum. This follows from the following calculation,
analogous to the first part. \(\square \)
Proposition 7.2
Let \(1\le q, p\le \infty \), \(\delta>\epsilon >0\) and \(m<(\delta -\epsilon )n(1/q-1/p)\) be given. Suppose that for all \(l,j\ge 0\) and all \(C\gg 1\) (not depending on l, j) such that
holds, then for any compactly supported bounded functions f, g on \({\mathbb {R}}^n\), there exist sparse collections \({\mathcal {S}}\) and \(\widetilde{{\mathcal {S}}}\) of dyadic cubes such that
Proof
Observe that estimate \(|\left<T f, g\right>|\le C(m, q, p)\Lambda _{\widetilde{{\mathcal {S}}}, p', q}(f, g)\) follows by duality from \(|\left<T f, g\right>|\le C(m, q, p)\Lambda _{{\mathcal {S}}, q, p'}(f, g)\). By Lemma 7.1, and the first estimate in (7.2), we have that
Both sums in j and l converge for sufficiently large C. The bound for \(\sum _{l \le j \epsilon } T_{j,l}\) follows from essentially the same arguments, except that we need to take \(m<(\delta -\epsilon )n(1/q-1/p)\). Finally Lemma 2.8 gives us the sparse form bound we desire. \(\square \)
We now turn to the proof of our main results.
Proof of Theorem 1.2
Note that for \(1\le q\le p\le 2\) we have by Lemma 5.1 that
By taking C large enough we have
for all \(1\le q\le p\le 2\). Moreover, to satisfy the hypothesis of Proposition 7.2 we need that
since we can take \(\epsilon >0\) arbitrarily small. Under this assumption on m, the case when \(1\le q\le p\le 2\) in Theorem 1.2 follows from Proposition 7.2. Moreover, for \(1\le q \le 2 \le p \le q'\) we have
The second inequality can be handled as above. For the first one we need that
since we can take \(\epsilon >0\) arbitrarily small. Under this assumption we then obtain Theorem 1.2 in the range \(1\le q \le 2 \le p \le q'\). \(\square \)
Proof of Theorem 1.1
The proof follows is very similar manner to the one above, the main modification is the following requirements:
\(\square \)
References
Beltran, D., Cladek, L.: Sparse bounds for pseudodifferential operators. J. Anal. Math. 140(1), 89–116 (2020)
Beltran, D., Roos, J., Seeger, A.: Multi-scale sparse domination. Mem. Am. Math. Soc. (2024)
Bergfeldt, A., Rodríguez-López, S., Staubach, W.: On weighted norm inequalities for oscillatory integral operators. Anal. Math. Phys. 12(6), 136 (2022)
Bernicot, F., Frey, D., Petermichl, S.: Sharp weighted norm estimates beyond Calderón–Zygmund theory. Anal. PDE 9(5), 1079–1113 (2016)
Castro, A.J., Israelsson, A., Staubach, W., Yerlanov, M.: Regularity properties of Schrödinger integral operators and general oscillatory integrals. arXiv:1912.08316 (2019)
Conde-Alonso, J.M., Culiuc, A., Di Plinio, F., Ou, Y.: A sparse domination principle for rough singular integrals. Anal. PDE 10(5), 1255–1284 (2017)
Conde-Alonso, J.M., Di Plinio, F., Parissis, I., Vempati, M.N.: A metric approach to sparse domination. Ann. Mat. Pura Appl 201(4), 1–37 (2022)
de Francia, J.L.R.: Vector valued inequalities for operators in \(L^p\) spaces. Bull. Lond. Math. Soc. 12(3), 211–215 (1980)
Dos Santos Ferreira, D., Staubach, W.: Global and local regularity of Fourier integral operators on weighted and unweighted spaces. Mem. Am. Math. Soc. 229(1074) (2014)
Grafakos, L., Wang, Z., Xue, Q.: Sparse domination and weighted estimates for rough bilinear singular integrals (2022)
Hörmander, L.: Pseudo-differential operators and hypoelliptic equations. Singul Integrals 138–183 (1967)
Hu, B.: Sparse domination of singular radon transform. J Math Pures Appl 139, 235–316 (2020)
Hytönen, T., Pérez, C., Rela, E.: Sharp Reverse Hölder property for \(A^\infty \) weights on spaces of homogeneous type. J. Funct. Anal. 263(12), 3883–3899 (2012)
Hytönen, T. P.: The sharp weighted bound for general Calderón–Zygmund operators. Ann Math 1473–1506 (2012)
Israelsson, A., Mattsson, T., Staubach, W.: Boundedness of Fourier integral operators on classical function spaces. J. Funct. Anal. 285(5), 110018 (2023)
Israelsson, A., Mattsson, T., Staubach, W.: Regularity of oscillatory integral operators. arXiv:2308.00973 (2023)
Israelsson, A., Rodríguez-López, S., Staubach, W.: Local and global estimates for hyperbolic equations in Besov–Lipschitz and Triebel–Lizorkin spaces. Anal. PDE 14(1), 1–44 (2021)
Lacey, M.T.: Sparse bounds for spherical maximal functions. J. Anal. Math. 139(2), 613–635 (2019)
Lacey, M.T., Mena, D., Reguera, M.C.: Sparse bounds for Bochner–Riesz multipliers. J. Fourier Anal. Appl. 25, 523–537 (2019)
Lacey, M. T., Spencer, S.: Sparse bounds for oscillatory and random singular integrals. arXiv:1609.06364 (2016)
Lerner, A.K.: A simple proof of the \(A_2\) conjecture. Int. Math. Res. Not. 2013(14), 3159–3170 (2013)
Lerner, A.K., Nazarov, F.: Intuitive dyadic calculus: the basics. Expo. Math. 37(3), 225–265 (2019)
Stein, E. M.: Harmonic Analysis: Real-variable Methods, Orthogonality, and Oscillatory Integrals, vol. 1. Princeton University Press, Princeton, NJ (1993)
Tao, T.: The weak-type \((1,1)\) of Fourier integral operators of order \(-(n-1)/2\). J. Aust. Math. Soc. 76(1), 1–21 (2004)
Yamamoto. R.: A sharp sparse domination of pseudodifferential operators. arXiv:2211.13840 (2022)
Acknowledgements
The author is supported by the Knut and Alice Wallenberg Foundation. The author is also grateful to Andreas Strömbergsson for his support and encouragement.
Funding
Open access funding provided by Uppsala University.
Author information
Authors and Affiliations
Contributions
T. M. is the sole author of this work and the only contributor.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A grant from the K. and A. Wallenberg foundation supports the author.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mattsson, T. Bilinear sparse domination for oscillatory integral operators. Anal.Math.Phys. 14, 37 (2024). https://doi.org/10.1007/s13324-024-00895-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-024-00895-1


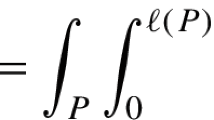
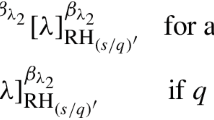

 , obeys the
, obeys the  , and
, and  , obeys the
, obeys the