Abstract
We present a geometrical construction of families of finite isospectral graphs labelled by different partitions of a natural number r of given length s (the number of summands). Isospectrality here refers to the discrete magnetic Laplacian with normalised weights (including standard weights). The construction begins with an arbitrary finite graph \({\varvec{G}}\) with normalised weight and magnetic potential as a building block from which we construct, in a first step, a family of so-called frame graphs \(({\varvec{F}}_a)_{a \in {\mathbb {N}}}\). A frame graph \({\varvec{F}}_a\) is constructed contracting a copies of G along a subset of vertices \(V_0\). In a second step, for any partition \(A=(a_1,\dots ,a_s)\) of length s of a natural number r (i.e., \(r=a_1+\dots +a_s\)) we construct a new graph \({\varvec{F}}_A\) contracting now the frames \({\varvec{F}}_{a_1},\dots ,{\varvec{F}}_{a_s}\) selected by A along a proper subset of vertices \(V_1\subset V_0\). All the graphs obtained by different s-partitions of \(r\ge 4\) (for any choice of \(V_0\) and \(V_1\)) are isospectral and non-isomorphic. In particular, we obtain increasing finite families of graphs which are isospectral for given r and s for different types of magnetic Laplacians including the standard Laplacian, the signless standard Laplacian, certain kinds of signed Laplacians and, also, for the (unbounded) Kirchhoff Laplacian of the underlying equilateral metric graph. The spectrum of the isospectral graphs is determined by the spectrum of the Laplacian of the building block G and the spectrum for the Laplacian with Dirichlet conditions on the set of vertices \(V_0\) and \(V_1\) with multiplicities determined by the numbers r and s of the partition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since Weyl’s seminal article in 1912 on the asymptotic distributions of eigenvalues of the Laplacian on a compact Riemannian manifold ([56], see also [31]) and, in particular, since Kac’s celebrated article “Can one hear the shape of a drum?” [33], the relation between the spectrum of the Laplacian and the geometric properties of the underlying space has been studied from many different perspectives. The problem was proposed by Kac for the usual Laplacian on two-dimensional bounded domains with Dirichlet condition at the boundary. The first negative answer to Kac’s original question for two-dimensional flat domains was presented in [26]. We refer to [24, 40, 57] for some surveys on different aspects of isospectrality and inverse spectral problems. An operator-theoretic point of view to the problem of finding non-isometric isospectral domains can be found in [2]. Also, the references [1, 36, 45] show the importance and timeliness of isospectrality in physics.
Recall that two linear operators with discrete spectrum are called isospectral (or cospectral), if their spectra coincide, i.e. they have the same eigenvalues with the same multiplicity. In order to avoid trivial cases, it is important that the underlying spaces are non-isomorphic (in the corresponding category). Sunada presented in [50] a systematic method for constructing non-isometric manifolds where the corresponding Laplacians have the same eigenvalues, answering negatively Kac’s original question. Sunada’s method is based on certain quotients of a Riemannian normal coverings and group theoretic properties of the covering groups. An application to discrete graphs and examples that do not arise from Sunada’s method can be found in [7]. We refer to Sect. 7 for further remarks and for a comparison of our method with Sunada’s method.
An extension of Sunada’s method is presented in [4] together with examples of isospectral quantum graphs (see also [25, 34, 54]). If one considers families of magnetic graphs with fixed underlying discrete graph and the magnetic potential as a parameter, then certain metric graphs that are isospectral for the entire family are isomorphic, cf. [48]. An approach using the Dirichlet-to-Neumann map of certain subgraphs is used in [34, Sect. 4] in order to construct isospectral quantum graphs leading to similar examples as ours (see also the last paragraph of Sect. 7). Additional references including the relation between isospectral metric and discrete graphs and the refinement of nodal or flip counts are, for example, [22, 32, 43]. In [14] it is shown that equilateral quantum graphs with only a few number of vertices are determinded by their spectrum; and in [47] isospectral equilateral quantum graphs are determined with the help of a computer algebra programme. Another systematic approach for constructing isospectral finite-dimensional operators using quotients is given in [3].
In the context of discrete graphs isospectral constructions refer to different operators: typically, to the adjacency matrix or the combinatorial Laplacian (and its signless version), see e.g. [7, 8, 15, 23, 27, 30, 41, 53, 55] or the normalised Laplacian (see e.g. [9,10,11,12,13, 17, 28, 53]). Since there is in general no simple relation between these spectra for non-regular graphs, isospectrality for discrete graphs strongly depends on the operator chosen. In this article we will focus on Laplacians with normalised weights (see Sect. 2.4 for a precise definition) and there are several reasons for itFootnote 1
-
First, standard Laplacians have a direct connection to spectral geometry and stochastic processes (cf. [16]) and their eigenvalues are sometimes called geometric (cf. [5]).
-
Second, there is an explicit relation between the eigenvalues of the standard (discrete) Laplacian and the Kirchhoff Laplacian of the corresponding compact equilateral metric graph (see e.g. [39, 54] and references therein; in [39] also the relation between Laplacians with Dirichlet conditions on subsets of vertices are described).
-
Third, the construction of isospectral graphs for normalised weights has been studied less than for other operators like the combinatorial Laplacian or the adjacency matrix (cf. [11]).
-
Finally, it seems that there is a relatively small number of isospectral graphs with normalised weights compared to other cases. Table 1 (taken from [11] and based on results for the combinatorial operators by [30]) shows the number of simple graphs of order at most 9 with an isospectral mate for different types of Laplacians: for the combinatorial Laplacian, the signless (combinatorial) Laplacian and for the standard (sometimes also called normalised or geometric) Laplacian.
Specific construction techniques of isospectral discrete graphs are presented in [11] where the gluing of certain blocks of graphs including some bipartite blocks resulted in pairs of isospectral graphs for the standard Laplacian. In [12] the authors present a technique based on toggling of three basic blocks to produce isospectral graphs with different number of edges, see also the construction technique presented in [10] using twin graphs and a scaling technique on general vertex and edge weights. Cavers shows in [13] that a variation of the Godsil-McKay switching also preserves the spectrum of the standard Laplacian. In [17] the authors give necessary conditions for a graph to be isospectral with a subgraph with one edge deleted; moreover, they give classes of graphs where this cannot happen. In [28] the authors construct isospectral graphs for the normalised Laplacian by partitioning the vertices into several blocks and allowing edges only between consecutive blocks in certain proportions.
Isospectrality of discrete graph Laplacians may be extended in several directions. Lim studies the Hodge Laplacian in [37, Example 4.1 and Sect. 5.3], a higher order generalisation of the graph Laplacian mentioned before, and considers isospectral graphs for this operator.
In this article we propose to extend the question of isospectrality to the discrete magnetic Laplacian with normalised weights on discrete graphs. Recall that the magnetic field is described in this context in terms of a magnetic potential function \(\alpha \) on the oriented edges (arcs) with values in \({\mathbb {R}}/2\pi {\mathbb {Z}}\) and we call these graphs simply magnetic graphs (see [49, 51] in the case of magnetic Laplacians on the lattice graph \({\mathbb {Z}}^2\)). Isospectrality of magnetic graphs refers to this operator. One important advantage of the use of the magnetic potential is that it interpolates between different types of Laplacians including the usual normalised Laplacian (if \(\alpha =0\)), the signless Laplacian (if \(\alpha _e=\pi \), \(e\in A\)) or the signed Laplacian (if \(\alpha _e\in \{0,\pi \}\)). Therefore, the graphs constructed here will be isospectral for these Laplacians and, also, for the Kirchhoff Laplacian of the corresponding equilateral graphs, see Sect. 2.6. We refer to [18, 21] for additional motivation and the use of the magnetic potential in periodic graphs and for the generation of spectral gaps. Moreover, we refer to [20] for the use of magnetic potentials to give spectral obstructions for the graph having Hamiltonian cycles or perfect matchings. In [19] we present a perturbative method using only spectral information (and no eigenfunctions) to construct isospectral graphs for the normalised Laplacian (for simplicity without magnetic field).
The construction of pairs of isospectral graphs: Top row from left to right: the building block \({\varvec{G}}\) (a so-called kite graph), the frame members \({\varvec{F}}_1={\varvec{G}}\), \({\varvec{F}}_2\) and \({\varvec{F}}_3\). Bottom row: The two graphs \({\varvec{F}}_{A,V_1}\) and \({\varvec{F}}_{B,V_1}\) are isospectral but not isomorphic. Note that this is the smallest possible choice of non-trivial partitions, namely the two different 2-partitions of  (left) and
(left) and  (right) (\(4=1+3=2+2\)). Note that the kite graph can also carry a magnetic potential; here given by three parameters, see Example 6.9
(right) (\(4=1+3=2+2\)). Note that the kite graph can also carry a magnetic potential; here given by three parameters, see Example 6.9
We illustrate first our general construction procedure through a motivating family of examples presented in Sect. 3. In Fig. 1 we show, and briefly explain, a concrete example of two isospectral graphs constructed from a kite graph as a building block \({\varvec{G}}\) and frame graphs \({\varvec{F}}_1={\varvec{G}}\), \({\varvec{F}}_2\) and \({\varvec{F}}_3\). In this example, the frame graphs are then glued together along certain vertices and according to the two partitionsFootnote 2 and
and  of the natural number \(r=4\) with length \(s=2\), i.e., gluing \({\varvec{F}}_1={\varvec{G}}\) with \({\varvec{F}}_3\) and \({\varvec{F}}_2\) with itself to produce the isospectral mates \({\varvec{F}}_A\) and \({\varvec{F}}_B\). Making contact with Kac’s original question, our construction shows that for any \(r\in {\mathbb {N}}\) one can hear the length of the partition s but not the particular decomposition summing up to r. In addition, our graphs will be isospectral for the the standard Laplacian, the signless standard Laplacian, the signature Laplacian corresponding to arbitrary signatures of the building block and, more generally, arbitrary magnetic potentials on the building block. Our construction also determines the spectrum of the isospectral graphs in terms of the spectrum of \({\varvec{G}}\) and the spectra of the Laplacian on \({\varvec{G}}\) with Dirichlet conditions of the selected sets of vertices \(V_0\) and \(V_1\). Nevertheless, we emphasise the geometrical construction leading to the families of mutually isospectral graphs rather than the determination of the corresponding spectra. Our isospectral graphs will have the same number of edges.
of the natural number \(r=4\) with length \(s=2\), i.e., gluing \({\varvec{F}}_1={\varvec{G}}\) with \({\varvec{F}}_3\) and \({\varvec{F}}_2\) with itself to produce the isospectral mates \({\varvec{F}}_A\) and \({\varvec{F}}_B\). Making contact with Kac’s original question, our construction shows that for any \(r\in {\mathbb {N}}\) one can hear the length of the partition s but not the particular decomposition summing up to r. In addition, our graphs will be isospectral for the the standard Laplacian, the signless standard Laplacian, the signature Laplacian corresponding to arbitrary signatures of the building block and, more generally, arbitrary magnetic potentials on the building block. Our construction also determines the spectrum of the isospectral graphs in terms of the spectrum of \({\varvec{G}}\) and the spectra of the Laplacian on \({\varvec{G}}\) with Dirichlet conditions of the selected sets of vertices \(V_0\) and \(V_1\). Nevertheless, we emphasise the geometrical construction leading to the families of mutually isospectral graphs rather than the determination of the corresponding spectra. Our isospectral graphs will have the same number of edges.
Let us finally mention that all our isospectral, but not isomorphic discrete graphs with standard weight (and no magnetic field) directly lead to equilateral metric graphs which are isospectral, but not isomorphic (see Corollary 5.9).
1.1 Structure of the article
The following section introduces the basic notions and results on multidigraphs and discrete magnetic Laplacians needed in this article. We also introduce here the two basic graph operations needed in our construction: vertex contraction and vertex virtualisation leading to the corresponding Dirichlet Laplacian. In Sect. 3 we present our construction first in a family of examples with a concrete building block graph and illustrate some of the key ideas of the general proof in these prototypes. The following section focuses on the notion of a frame obtained from a generic building block (magnetic graph) with some distinguished subset of vertices \(V_0\). We also calculate the spectrum of a frame member and give a group theoretical explanation of the different multiplicities that appear in the spectrum of the isospectral graphs. In Sect. 5 the general construction is presented and the main results on isospectrality (Theorem 5.8 and Corollary 5.9) are proved. In the next section we present many families of isospectral graphs exploiting systematically the combinatorial freedom in our construction procedure. In Appendix 1 we recall basic facts on partitions and multisets that will be used throughout the article.
2 Magnetic discrete graphs and their Laplacians
In this section, we introduce briefly the discrete structures and operations needed for the construction for families of isospectral graphs. We will consider discrete locally finite graphs having normalised weights on vertices and edges. We will also consider a magnetic potential on the graph in terms of an \({\mathbb {R}}/2\pi {\mathbb {Z}}\)-valued function \(\alpha \) on the edges. Finally we will specify the discrete normalised magnetic Laplacian as a second order discrete analogue of the usual Laplace operator on a Riemannian manifold with magnetic potential.
2.1 Discrete graphs
In this subsection, we fix the notation for discrete graphs following the notation of Sunada (cf. [52, Chapter 3]), see also our previous articles [18, 21], where certain aspects are explained in more detail.
A (discrete multidi-)graph \(G=(V,E,\partial )\) is given by two disjoint and (in this article) finite sets V and E (the set of vertices and of (directed) edges or arcs) together with an incidence map \( \partial :E \longrightarrow V \times V\), \(\partial e=(\partial _-e,\partial _+e)\), where \(\partial _-e\) is the initial, and \(\partial _+e\) the terminal vertex of \(e \in E\). The order of \(G\) is \(|G|:=|V(G)|\).
An inversion map \( \overline{\cdot } :E \longrightarrow E\) is a map fulfilling \(\overline{\overline{e}} =e\), \(\overline{e} \ne e\), \(\partial _+ (\overline{e})=\partial _-e\) and \(\partial _-(\overline{e})=\partial _+e\) for all \(e \in E\). The inversion map \(\overline{\cdot }\) introduces a \({\mathbb {Z}}_2\)-action on E, the orbits \(\{e,\overline{e}\}\) are called undirected edges; in the figures, we only plot the undirected edges; each comes with both directions e and \(\overline{e}\).
A loop is an edge e such that \(\partial _+e=\partial _-e\) (note that a loop also has two different directed edges e and \(\overline{e}\)). Two edges \(e_1\) and \(e_2\) are called parallel if \(e_1\ne e_2\) with \(\partial _+e_1=\partial _+e_2\) and \(\partial _- e_1 =\partial _- e_2\). A graph is simple if it has no loops or parallel edges.
For a vertex \(v\in V\), the set of directed edges with origin v is denoted as \(E_v(G)\) or simply \(E_v\), i.e.
The degree of a vertex v is the cardinality of \(E_v\), denoted by \(\deg v:= |E_v|\). Observe that loops are counted twice in each set \(E_v\) (as \(e \ne \overline{e}\)). We exclude isolated vertices and vertices with infinite degree, i.e., we assume that \(0<\deg _G v<\infty \) for all \(v \in V\). A vertex of degree 1 is called pendant. If the dependence of the graph \(G\) is important, we write \(V=V(G)\), \(E=E(G)\) or \(\deg _G\) etc. Let \(G\) be a graph with n vertices labelled \(v_1, v_2, \dots , v_n\). The multiset

is called the degree multiset of \(G\) (see see Appendix A.1 for more details on multisets). A graph \(G\) is connected if for any two vertices u, v there exists a path from u to v, i.e., there is a sequence of distinct vertices \((u,v_1,\dots ,v_{n-1},v)\) and of directed edges \((e_1,e_2,\dots ,e_n)\) with \(v_{i}=\partial _+ e_i=\partial _-e_{i+1}\) for \(1\le i\le n-1\) and \(\partial _-e_1=u\) and \(\partial _+ e_n=v\).
A graph homomorphism \( \varphi :G \longrightarrow G'\) between the graphs \(G=(V(G),E(G))\) and \(G'=(V(G'), E(G'))\) is given by two maps \( \varphi :V(G) \longrightarrow V(G')\) and \( \varphi :E(G) \longrightarrow E(G')\) respecting the incidence and inversion maps, i.e., they fulfil \(\partial _\pm (\varphi (e))=\varphi (\partial _\pm e)\) and \(\overline{\varphi (e)}=\varphi (\overline{e})\) for all \(e\in E(G)\). The map \(\varphi \) is a graph isomorphism if \(\varphi \) is a bijection on the vertex and edge sets; in this case, \(G\) and \(G'\) are called isomorphic (discrete) graphs. Note that the degree multiset (2.1) is a graph invariant, i.e., if the degree sequence or the degree multiset of two graphs differ, then the graphs cannot be isomorphic.
2.2 Graphs with normalised weights and magnetic potentials
We briefly define here discrete graphs with normalised weights. As before, details can be found in [18, 21] and references therein. An (edge) weight is a function \( w :E \longrightarrow (0,\infty )\) such that \(w_{\overline{e}}=w_e\) for all \(e\in E\), the associated weighted degree is defined by
The edge weight w and vertex weight \(\deg _G^w\) are called normalised in the terminology of [18, 21, Sect. 2.2]. A particular case is \(w_e=1\) for all \(e \in E\) and hence \(\deg ^w_Gv=\deg _Gv\) is the usual degree of v; this weight is called standard.Footnote 3 We extend w and \(\deg ^w_G\) naturally as discrete measures on \(E(G)\) and \(V(G)\).
Next, we define magnetic potentials on discrete graphs (see [18, 21] and references therein for details). A magnetic potential is a function \( \alpha :E \longrightarrow {\mathbb {R}}/2\pi {\mathbb {Z}}\) such that \(\alpha _{\overline{e}}=-\alpha _e\) for all \(e \in E\). We call \({\varvec{G}}=(G,\alpha ,w)\) a magnetic graph (with normalised weights). For the standard weight and no magnetic potential (i.e., \(w_e=1\) and \(\alpha _e=0\) for all \(e \in E\)) we simply write \(G\) for the corresponding magnetic graph \({\varvec{G}}=(G,0,1)\).
Two magnetic graphs \({\varvec{G}}=(G,\alpha ,w)\) and \({\varvec{G}}'=(G',\alpha ',w')\) are said to be isomorphic (as magnetic graphs) if there exists a graph isomorphism \( \varphi :G \longrightarrow G'\) such that \(w_e=w'_{\varphi (e)}\) and \(\alpha _e=\alpha '_{\varphi (e)}\) for all \(e\in E(G)\).
2.3 Contraction of vertices
An important operation we need in this article is the contraction of vertices (also called gluing or merging of vertices in the literature). We introduce the shrinking number s that quantifies the reduction of the number of vertices in the quotient graph.
Definition 2.1
(Contracting vertices and shrinking number) Let \(G=(V,E)\) be a graph and \(\sim \) an equivalence relation on the vertex set V. The graph \(G/{\mathord {\sim _{}}}=(V/{\mathord {\sim _{}}},E)\) obtained from \(G\) by contracting the vertices (with respect to \(\sim \)) is given by \(V/{\mathord {\sim _{}}}\) and incidence function \(\partial (e)=([\partial _-(e)],[\partial _+(e)])\). The shrinking number s of the equivalence relation \(\sim \) on \(V(G)\) is defined by \(s:=|G|-|G/{\mathord {\sim _{}}}|=|V|-|V/{\mathord {\sim _{}}}|\).
Note that if we contract two adjacent vertices \(v_1\) and \(v_2\), all edges joining \(v_1\) and \(v_2\) become loops in \(G/\mathord \sim \) (in contrast to some conventions in combinatorics where only simple graphs are allowed).
Given a discrete graph \(G=(V,E)\) with (edge) weight w, we choose w also as weight on the quotient graph \(G/{\mathord {\sim _{}}}=(V/{\mathord {\sim _{}}},E)\) (denoted by the same symbol w). For the quotient, we have
where \({{\,\mathrm{\sqcup }\,}}\) means that the union is disjoint. Hence the weighted degree is
It follows that the quotient map \( \pi :G \longrightarrow G/{\mathord {\sim _{}}}\) given by \(v \mapsto [v]\) is a measure preserving map, since the edge weights are the same (the edges are actually not changed) and since
for any \(\widetilde{V} \subset V(G/{\mathord {\sim _{}}})\). Similarly, a magnetic potential \(\alpha \) on \(G\) will be lifted to \(G/{\mathord {\sim _{}}}\).
2.4 Normalised magnetic Laplacians
For a graph \((G,w)\), we associate the following natural Hilbert space
as our graphs are finite, \(\ell _{2}^{}({V,\deg ^w})\) is a \(|G|\)-dimensional space.
Definition 2.2
(discrete (normalised) magnetic Laplacian and its spectrum) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph with normalised weights. The (normalised) magnetic Laplacian is the operator \( \Delta _{{{\varvec{G}}}}^{{}} :\ell _{2}^{}({V,\deg ^w}) \longrightarrow \ell _{2}^{}({V,\deg ^w})\) defined by
where the sum in Eq. (2.5) is taken over all edges starting at v and loops are counted twice; \(\deg ^w v=\sum _{e \in E_v}w_e\) is the weighted degree (see (2.2)). If \({\varvec{G}}\) has order n, then we write the spectrum of the corresponding Laplacian \(\Delta _{{{\varvec{G}}}}^{{}}\) as the multiset (see Appendix A.1 below)

where the eigenvalues \(\lambda _1({\varvec{G}}), \dots , \lambda _n({\varvec{G}})\) are written in ascending order and repeated according to their multiplicities.
For a definition using a discrete (twisted) exterior derivative, we refer to [18, Definition 2.3] or [21, Definition 3.1].
Remark 2.3
(matrix representation of the Laplacian) Note that the matrix representation of \(\Delta _{{{\varvec{G}}}}^{{}}\) with respect to the orthonormal basis \((\delta _v)_{v \in V}\) of \(\ell _{2}^{}({V,\deg ^w})\) (\(\delta _v(v')=1/\sqrt{\deg ^w(v)}\) if \(v=v'\) and \(\delta _v(v')=0\) otherwise) is
If the graph is simple and has no magnetic potential, we have
For a graph with loops and standard weight \(w_e=1\), we have \((\Delta _{{{\varvec{G}}}}^{{}})_{v,v}=1-2\ell (v)/\deg (v)\) if there are \(2\ell (v)\) loops at a vertex v (note that we distinguish between e and \({\bar{e}}\)), so a loop counts twice.
As an example the (non-simple) magnetic graph \({\varvec{G}}^\theta \) in Fig. 2 with three vertices has the matrix representation
Definition 2.4
(isospectral magnetic graphs) Let \({\varvec{G}}\) and \(\widetilde{\varvec{G}}\) be two finite magnetic graphs. We say that \({\varvec{G}}\) and \(\widetilde{\varvec{G}}\) are isospectral (or cospectral) if their spectra agree as multiset, i.e., if all eigenvalues agree including their multiplicities.
Remark 2.5
(multiple edges versus weighted graphs without multiple edges) A weighted graph \(G\) with multiple edges can be turned into a graph \(\widetilde{G}\) without multiple edges. On the other hand, a weighted graph with integer (edge) weights can be turned into a graph with multiple edges and standard weights. We discuss for simplicity only the case of graphs without loops and magnetic potential.
It turns out that both graphs (with or without multiple edges) have the same Laplacian. This leads us to the following definition: We say that two weighted graphs \({\varvec{G}}=(G,0,w)\) and \(\widetilde{\varvec{G}}=(\widetilde{G},0,\widetilde{w})\) on the same vertex set \(V({\varvec{G}})=V(\widetilde{\varvec{G}})\) are isolaplacian if \(\deg ^w_{{\varvec{G}}}=\deg ^{\widetilde{w}}_{\widetilde{\varvec{G}}}\) and \(\Delta _{{{\varvec{G}}}}^{{}}f= \Delta _{{\widetilde{\varvec{G}}}}^{{}} f\) for all \(f \in \ell _{2}^{}({V({\varvec{G}}),\deg ^w})\), or, equivalently, if the matrix representation of their Laplacians is the same.
Clearly, isomorphic magnetic graphs are isolaplacian, and isolaplacian magnetic graphs are isospectral (as the corresponding matrices are the same), but not vice versa.
-
a.
Assume that \({\varvec{G}}=(G,0,w)\) is a weighted graph without magnetic potential. If \(G\) has multiple edges, we define a weighted graph \(\widetilde{G}=(\widetilde{G},0,\widetilde{w})\) as follows: Denote by
$$\begin{aligned} E(v_-,v_+):=\{ \, e \in E(G) \, | \, \partial _-e=v_-, \partial _+ e=v_+ \, \} . \end{aligned}$$(2.8)Then \(|E(v_-,v_+)|\) denotes the number of edges starting at \(v_-\) and terminating at \(v_+\). We obtain a graph \(\widetilde{G}\) without multiple edges by identifying all edges in \(E(v_-,v_+)\) into a single edge \(\widetilde{e}\) provided \(|E(v_-,v_+)| \ge 2\) and keeping all other edges. As incidence function we set \( \widetilde{\partial } :E(\widetilde{G}) \longrightarrow V(G)\times V(G)\), \(\widetilde{\partial }(\widetilde{e})=(\partial _- e, \partial _+ e)\) for \(e \in E(v_-,v_+)\). The weight function of \(\widetilde{\varvec{G}}\) is defined as
$$\begin{aligned} \widetilde{w}_{\widetilde{e}}=\sum _{e \in \widetilde{e}} w_e. \end{aligned}$$Then the graphs \({\varvec{G}}\) and \(\widetilde{\varvec{G}}\) are isolaplacian. We call \(\widetilde{\varvec{G}}\) the underlying simple weighted graph. Note that the graphs \({\varvec{G}}\) and \(\widetilde{\varvec{G}}\) are not isomorphic (as a multiple edge changes the Betti number).
-
b.
On the other hand, a weighted graph \({\varvec{G}}\) with weights \(w_e \in {\mathbb {N}}\) can be turned into a graph with standard weights \({\varvec{G}}'\) by replacing an edge e by \(w_e\) multiple edges \(e'\) with weight \(w'_{e'}=1\). Again, it is easy to see that the graphs \({\varvec{G}}\) and \({\varvec{G}}'\) are isolaplacian, but again not isomorphic (if at least one weight fulfils \(w_e \ne 1\)).
Remark 2.6
(signed graphs as a special case of magnetic graphs) If the magnetic potential \(\alpha \) has values only in \(\{0,\pi \}\), then the magnetic potential is also called a signature and \({\varvec{G}}\) is called a signed graph (see e.g. [38] and references therein). The corresponding Laplacians (see below) are called signed Laplacian, including the so-called signless Laplacian, where \(\alpha _e=\pi \) for all \(e \in E\). In this sense the magnetic potential can be interpreted as a parameter interpolating different Laplacians.
The construction presented later shows isospectrality for magnetic Laplacians including signed and signless Laplacians.
The next proposition collects some well-know properties of the discrete magnetic Laplacian (for a proof, see e.g. [18, Sect. 3]):
Proposition 2.7
(magnetic Laplacians and cohomologous magnetic potentials) Let \({\varvec{G}}=(G,\alpha ,w)\) be a normalised magnetic graph and \(\Delta _{{{\varvec{G}}}}^{{}}\) its associated Laplacian.
-
a.
\(\Delta _{{{\varvec{G}}}}^{{}}\) is a non-negative and self-adjoint operator with spectrum contained in [0, 2].
-
b.
If \(\alpha \) and \(\alpha '\) are cohomologous (\(\alpha \sim \alpha '\), i.e., there is \( \xi :V \longrightarrow {\mathbb {R}}/2\pi {\mathbb {Z}}\) such that \(\alpha '_e=\alpha _e+\xi (\partial _+e)-\xi (\partial _-e)\) for all \(e \in E(G)\)), then \(\Delta _{{(G,\alpha ,w)}}^{{}}\) and \(\Delta _{{(G,\alpha ',w)}}^{{}}\) are unitarily equivalent and have the same spectrum, i.e., \((G,\alpha ,w)\) and \((G,\alpha ',w)\) are isospectral.
-
c.
In particular, if \(\alpha \sim 0\) then \(\Delta _{{(G,\alpha ,w)}}^{{}}\) is unitarily equivalent with the usual normalised Laplacian \(\Delta _{{(G,0,w)}}^{{}}\), i.e., \((G,\alpha ,w)\) and \((G,0,w)\) are isospectral.
-
d.
If the underlying graph of \({\varvec{G}}\) is a tree, then \(\alpha \sim 0\) and \(\Delta _{{(G,\alpha ,w)}}^{{}}\) and \(\Delta _{{(G,0,w)}}^{{}}\) are unitarily equivalent for any magnetic potential \(\alpha \).
-
e.
Let \(\alpha =\pi \) and \(G\) be connected. Then \(\alpha \sim 0\) if and only if \(G\) is bipartite.
Proof
Only (e) needs some comments: “\(\Rightarrow \)”: \(\alpha \sim 0\) implies the existence of \( \xi :V \longrightarrow {\mathbb {R}}/2\pi {\mathbb {Z}}\) such that \(\pi =\alpha _e=\xi (\partial _+e)-\xi (\partial _-e)\). Adding a constant to \(\xi \) if necessary, we can assume that \(\xi (V)=\{0,\pi \}\). The bipartite partition of vertices can be chosen as \(A=\xi ^{-1}(\{0\})\) and \(B=\xi ^{-1}(\{\pi \})\).
“\(\Leftarrow \)”: Let \(V=A{{\,\mathrm{\sqcup }\,}}B\) be a disjoint decomposition of the bipartite graph (i.e., there are no edges between vertices in A respectively B). We define \(\xi (v)=0\) if \(v \in A\) and \(\xi (v)=\pi \in {\mathbb {R}}/2\pi {\mathbb {Z}}\) if \(v \in B\). It can then be shown that \(\alpha _e=\pi =\xi (\partial _+e)-\xi (\partial _-e)\) for all \(e \in E\). \(\square \)
2.5 Dirichlet magnetic Laplacians
We define here the notion of a “Dirichlet boundary condition” on a subset \(V_0\) of vertices for a discrete graph. We call this process vertex virtualisation. Concretely, let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph and \(V_0 \subset V(G)\). The virtualisation of the vertices \(V_0\) specifies a partial subgraphFootnote 4\({\varvec{G}}^+_{V_0}=(G^+_{V_0},w^+,\alpha ^+)\), where \(V(G^+_{V_0})=V(G){\setminus } V_0\). Moreover, \(E(G^+)=E(G){\setminus } E(V_0)\), where \(E(V_0)\) is the set edges starting and ending in \(V_0\).
The weight function and the magnetic potential are defined as the restriction to \(E(G^+)\), namely \(w^+:=w {\restriction }_{E(G^+)}\) and \(\alpha ^+:=\alpha {\restriction }_{E(G^+)}\). For simplicity of notation we will not distinguish the restriction by the label \((\cdot )^+\), and use w resp. \(\alpha \) instead of \(w^+\) resp. \(\alpha ^+\). We denote the normalised magnetic partial subgraph with virtualised vertices \(V_0\) obtained from \({\varvec{G}}\) hence by \({\varvec{G}}^+_{V_0}=(G^+_{V_0},\alpha ,w)\). The order of \({\varvec{G}}^+_{V_0}\) is defined as \(|{\varvec{G}}^+_{V_0}| = |{\varvec{G}}|-|V_0| = |V({\varvec{G}})|-|V_0|\). For an example as matrix representation see the end of this subsection.
Definition 2.8
((normalised) magnetic Dirichlet Laplacian) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph and \(V_0 \subset V(G)\). The (normalised) magnetic Dirichlet Laplacian with Dirichlet conditions on \(V_0\) is defined as
where \( \iota _{V_0} :\ell _{2}^{}({V {\setminus } V_0,\deg ^w}) \longrightarrow \ell _{2}^{}({V,\deg ^w})\) is the natural extension by 0 on \(V_0\). If \(V_0=\{v_0\}\), we simply write \(\Delta _{{{\varvec{G}}^+_{v_0}}}^{{}}\). We denote the spectrum of \(\Delta _{{{\varvec{G}}^+_{V_0}}}^{{}}\) by \(\sigma _{\mathrm {}}({\varvec{G}}^+_{V_0})\).
Note that the k-th eigenvalue of the Dirichlet Laplacian (written in ascending order) is larger than the corresponding k-th eigenvalue of the Laplacian without restrictions, a consequence of the interlacing theorem for eigenvalues. This justifies the superscript \((\cdot )^+\) in the notation. The relation between both Laplacians is as follows: if both Laplacians are represented as a matrix, then the Dirichlet Laplacian corresponds to a principal submatrix of the original Laplacian.
As an example we consider again the graph \({\varvec{G}}^\theta \) in Fig. 2, now with \(V_0=\{v_1\}\) as Dirichlet vertex. The Dirichlet Laplacian \(\Delta _{{({\varvec{G}}^\theta )^+_{V_0}}}^{{}}\) is now the principal submatrix obtained from the original matrix (2.7) by deleting the row and column corresponding to the Dirichlet vertex \(v_1\), here the first one, i.e.,
Note that this graph is now independent of the magnetic potential \(\theta \) (see also Sect. 3).
2.6 Metric graph Laplacians and isospectrality
Given a discrete graph \(G\) we construct a corresponding equilateral metric graph \(\overline{G}\) as the topological graph as follows: We choose an orientation \(E^{\circ }\) of E, i.e., a partition \(E=E^{\circ } {{\,\mathrm{\sqcup }\,}}\overline{E^{\circ }}\). We consider the space \({{\,\mathrm{\bigsqcup }\,}}_{e \in E^{\circ }}[0,1] \times \{e\}\), where each edge \(e \in E^{\circ }\) is identified with the interval \([0,1] \times \{e\}\) and having length 1. We define \( \psi :{{\,\mathrm{\bigsqcup }\,}}_{e \in E^{\circ }}\{0,1\} \times \{e\} \longrightarrow V(G)\) by \(\psi (0,e)=\partial _-e\) and \(\psi (1,e)=\partial _+e\), mapping the endpoints of the intervals to the corresponding vertices.
The metric graph \(\overline{G}\) is then the quotient space \({{\,\mathrm{\bigsqcup }\,}}_{e \in E^{\circ }}[0,1] \times \{e\}/\psi \), where the interval endpoints are identified according to the graph \(G\). In particular, we consider V as subset of \(\overline{G}\), and it makes sense to speak of a continuous function at a vertex in \(\overline{G}\). We have a natural coordinate \(x_e \in [0,1]\) and a natural measure on \(\overline{G}\), the Lebesgue measure on each interval. For a function \( f :\overline{G} \longrightarrow {\mathbb {C}}\) we define \(f_e(x):= f(x,e)\) for \(e \in E^{\circ }\) and \(f_e(x):=f(1-x,\overline{e})\) for \(e \in \overline{E^{\circ }}\) and \(x \in [0,1]\). The corresponding natural Hilbert space is \({\textsf{L}}_{2}^{}({\overline{G}})\cong \bigoplus _{e \in E^{\circ }} {\textsf{L}}_{2}^{}({[0,1] \times \{e\}})\).
The Kirchhoff (sometimes also called standard or Neumann) Laplacian \(\Delta _{{\overline{G}}}^{{}}\) on \(\overline{G}\), acting on functions \(f=(f_e)_e \in {\textsf{L}}_{2}^{}({\overline{G}})\) is \((\Delta _{{\overline{G}}}^{{}}f)_e = -f''_e\) for functions \(f_e\) and their two weak derivatives in \({\textsf{L}}_{2}^{}({[0,1]})\) satisfying
for all \(v \in V\) (note that \(f_{\overline{e}}'(0)=-f_e'(1)\) for \(e \in E^{\circ }\)). For more details on metric graphs, we refer for example to [6]. For simplicity, we consider graphs without magnetic potentials here only.
We use a beautiful relation between the spectra of the standard Laplacian and the Kirchhoff Laplacian (see for example [54, Theorem 1], or [34, 35, 39] and references cited therein (recall that \(G\) refers here to the weighted graph \((G,0,\mathbb {1})\) with standard weights):
Proposition 2.9
Let \(G\) resp. \(G'\) be two (finite) discrete graphs and \(\overline{G}\) resp. \(\overline{G}'\) the corresponding equilateral metric graphs. Then the following are equivalent:
-
(a)
\(G\) and \(G'\) are isospectral (with respect to the discrete standard Laplacian), and \(G\) and \(G'\) have the same number of edges;
-
(b)
the metric Kirchhoff Laplacians on \(\overline{G}\) and \(\overline{G}'\) are isospectral.
Proof
The spaces \(\overline{N}_{\overline{\lambda }}=\ker (\Delta _{{\overline{G}}}^{{}}-\overline{\lambda })\) and \(N_\lambda =\ker (\Delta _{{G}}^{{}}-\lambda )\) are isomorphic for \(\lambda =1-\sqrt{\overline{\lambda }} \in (0,2)\) and \(\sqrt{\overline{\lambda }} \notin \pi {\mathbb {N}}_0\) (see e.g. [54, Theorem 1] or [39, Proposition 4.1]Footnote 5 and references therein). In particular, if \(G\) and \(G'\) are isospectral, then \(\overline{G}\) and \(\overline{G}'\) are isospectral up to the eigenvalues of the form \(\overline{\lambda }_n=n^2\pi ^2\) and \(n \in {\mathbb {N}}_0\). For \(n \in 2{\mathbb {N}}_0\), an eigenfunction constant on a connected component of the discrete graph (with value 1, say) corresponds to the eigenfunction \(\varphi _e(x)=\cos (n\pi x)\) on each edge of the same connected component in \(\overline{G}\). For \(n \in 2{\mathbb {N}}_0+1\), the multiplicity of the correspondent discrete eigenvalue \(\lambda =2\) counts the number of connected bipartite components (see e.g. [39, Proposition 2.3] and references therein), and each such eigenfunction (with values \(\pm 1\)) leads to an eigenfunction \(\varphi _e(x)=\cos (n \pi x)\) on each edge of the corresponding connected bipartite component.
The remaining eigenfunctions of \(\Delta _{{\overline{G}}}^{{}}\) corresponding to eigenvalues \(\overline{\lambda }_n=n^2\pi ^2\) are 0 on all vertices; we called them topological in [39, Definition 4.4]. They are entirely determined by the homology and the bipartiteness of the discrete graph ( [39, Lemma 5.1 and Proposition 5.2]). As the homology of the graph is determined by the number of vertices and edges, and as the number of bipartite connected component can be detected from the spectrum of \(\Delta _{{G}}^{{}}\), the stated equivalence follows. \(\square \)
3 A motivating family of examples
Before going into a formal description of the construction of isospectral magnetic graphs in Sect. 5 we illustrate the main idea of the construction with a class of examples. This motivating family of examples of isospectral graphs generalise those given by Butler and Grout in [11, Example 2] allowing multiple edges, a general magnetic potential and dropping the bipartiteness condition. The construction begins with the choice of a building block, out of which we will assemble the frame members. The building block \(G\) in the example is given by a graph with three vertices \(\{v_1,v_2,v_3\}\), and three edges, two of which are multiple joining \(v_1\) and \(v_2\) (see Fig. 2). For \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\) we add a magnetic potential \(\alpha _e^\theta =\theta \) on one of the two parallel edges e and \(\alpha ^\theta _e=0\) on the remaining two edges, and call the resulting magnetic graph \({\varvec{G}}^\theta =(G,1,\alpha ^\theta )\).Footnote 6 Examples with simple graphs (i.e. without multiple edges or loops) are given in Sect. 6
Let \(V_0=\{v_1,v_3\}\) be the set the two non-adjacent vertices of \(G\). For each \(a \in {\mathbb {N}}\) we contract a copies of \({\varvec{G}}\) by merging \(v_1\) (respectively \(v_3\)) in each copy to one vertex. The edge weight and the magnetic potential remains the same after identification on each copy. The resulting magnetic graph is called a-th frame member \({\varvec{F}}_a^\theta :={\varvec{F}}_a({\varvec{G}}^\theta , V_0)\), as in Fig. 2 (see also the general Definition 4.1). We denote by \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) the frame obtained by the building block G and the choice of merging vertices \(V_0\).
The frame \(({\varvec{F}}^\theta _a)_{a \in {\mathbb {N}}}\) given by the frame members \({\varvec{F}}^\theta _a\) for \(a\in {\mathbb {N}}\). Each graph \({\varvec{F}}^\theta _a\) has a so-called distinguished bottom vertex (outlined); it will be used in the next step for the contracted frame union
Note that the graphs in the family given in Fig. 2 have a high degree of symmetry, and this fact is reflected in the spectrum through eigenvalues with high multiplicity (see Remark 4.6). The idea of the construction is to use the frame \(({\varvec{F}}^\theta _a)_{a \in {\mathbb {N}}}\) to construct new non-isomorphic graphs that preserve most of the eigenvalues of the initial frame. The geometric procedure to assemble different frame members to specify the families of isospectral graphs are determined by s-partitions of a natural number \(r\in {\mathbb {N}}\) (cf. Definition 7.1 for a formal definition).
To be concrete, we construct two isospectral graphs using the family given in Fig. 2 as follows. Consider, for example, the two different 2-partitions of the number 4, namely  and
and  , i.e.,
, i.e.,
(here  is the multiset with one element 2 of multiplicity 2, see Appendix A.1). We choose the vertex \(v_1 \in V_0\) of degree 2 (due to the double edge) as distinguished vertex, and we construct a graph \({\varvec{F}}_{A,v_1}^\theta \) (called later \(v_1\)-contracted frame union, see Definition 5.5) associated with the first partition
is the multiset with one element 2 of multiplicity 2, see Appendix A.1). We choose the vertex \(v_1 \in V_0\) of degree 2 (due to the double edge) as distinguished vertex, and we construct a graph \({\varvec{F}}_{A,v_1}^\theta \) (called later \(v_1\)-contracted frame union, see Definition 5.5) associated with the first partition  as follows (see Fig. 3): contract the copies of the distinguished vertex \(v_1\) (outlined vertices) from the frame members \({\varvec{F}}_1^\theta \) and \({\varvec{F}}_3^\theta \) in Fig. 2. Similarly, define \({\varvec{F}}_{B,v_1}^\theta \) by contracting two copies of \({\varvec{F}}_2^\theta \) along the distinguished vertex \(v_1\).
as follows (see Fig. 3): contract the copies of the distinguished vertex \(v_1\) (outlined vertices) from the frame members \({\varvec{F}}_1^\theta \) and \({\varvec{F}}_3^\theta \) in Fig. 2. Similarly, define \({\varvec{F}}_{B,v_1}^\theta \) by contracting two copies of \({\varvec{F}}_2^\theta \) along the distinguished vertex \(v_1\).
An explicit computation of the eigenvalues of the corresponding standard Laplacians shows that both graphs \({\varvec{F}}^\theta _{A,v_1}\) and \({\varvec{F}}^\theta _{B,v_1}\) are isospectral with spectrum

where \(1^{(3)}\) means that 1 has multiplicity 3, but the corresponding discrete graphs are not isomorphic. We actually prove in Theorem 5.7 the general result that for an s-partition of r the spectrum of the normalised magnetic Laplacian is given by
where \(\uplus \) denotes the multiset union, see Appendix A.1. In our example we have \(r=4\) and \(s=2\) and the spectra of the building block \({\varvec{G}}^\theta \) and the magnetic graphs with vertices \(v_1\) and \(V_0=\{v_1,v_3\}\) virtualised are given respectively by

The three types of eigenfunctions (represented by dotted vertical lines with arrow pointing in a virtual third dimension); Dirichlet vertices are marked outlined with a bigger circle: Top: The eigenfunctions of \({\varvec{G}}^\theta \) are copied symmetrically onto each copy of \({\varvec{G}}^\theta \) in \({\varvec{F}}^\theta _{A,v_1}\). Hence, the three eigenfunctions (in the picture, it is the constant one) become three eigenfunctions on \({\varvec{F}}^\theta _{A,v_1}\). Middle: each eigenfunction of \(({\varvec{G}}^\theta )^+_{v_1}\) becomes a symmetric copy on each member \(({\varvec{F}}_a^\theta )^+_{v_1}\) of \({\varvec{F}}^\theta _{A,v_1}\) for  . To make them orthogonal to the symmetric ones, we can choose only \(s-1=1\) one here for each of the two eigenfunctions of \(({\varvec{G}}^\theta )^+_{v_1}\), hence \(2(s-1)=2\) eigenvalues of \({\varvec{F}}^\theta _{A,v_1}\) are captured. Bottom: we consider the eigenfunctions of \(({\varvec{G}}^\theta )^+_{V_0}\) (here only one) onto each copy of \(({\varvec{G}}^\theta )^+_{V_0}\) in \(({\varvec{F}}_a^\theta )^+_{v_1}\) for
. To make them orthogonal to the symmetric ones, we can choose only \(s-1=1\) one here for each of the two eigenfunctions of \(({\varvec{G}}^\theta )^+_{v_1}\), hence \(2(s-1)=2\) eigenvalues of \({\varvec{F}}^\theta _{A,v_1}\) are captured. Bottom: we consider the eigenfunctions of \(({\varvec{G}}^\theta )^+_{V_0}\) (here only one) onto each copy of \(({\varvec{G}}^\theta )^+_{V_0}\) in \(({\varvec{F}}_a^\theta )^+_{v_1}\) for  . There are here \(r-s=(3-1)+(1-1)=2\) such eigenfunctions orthogonal to the previous ones, supported here only on \(({\varvec{F}}_3^\theta )^+_{v_1}\)
. There are here \(r-s=(3-1)+(1-1)=2\) such eigenfunctions orthogonal to the previous ones, supported here only on \(({\varvec{F}}_3^\theta )^+_{v_1}\)
Remark 3.1
(explanation of spectrum) We give here some heuristic reasons for the spectrum having the form as in (3.1) and will formalise them in the proofs of the main results of the following sections (see Proposition 4.5 and Theorem 5.7).
-
a.
Each eigenfunction of the building block \({\varvec{G}}^\theta \) carries over to \({\varvec{F}}^\theta _{A,v_1}\) by symmetrically extending it to each copy of \({\varvec{G}}^\theta \) with the same eigenvalue; hence each eigenvalue of \({\varvec{G}}^\theta \) contributes one time its original multiplicity. This gives three eigenvalues in our concrete example.
-
b.
Each eigenfunction of \(({\varvec{G}}^\theta )^+_{v_1}\) carries over to symmetric copies on each member \({\varvec{F}}_a^\theta \) of \({\varvec{F}}^\theta _{A,v_1}\) for \(a \in A\) with the same eigenvalue. We can suitably choose \(s-1\) copies of them being orthogonal to the symmetric ones constructed in the first item. This gives \(2 \cdot (s-1)=2\) eigenvalues in our case as \(s=2\).
-
c.
Finally, each eigenfunction of \(({\varvec{G}}^\theta )^+_{V_0}\) carries over to an eigenfunction on each \({\varvec{F}}_a^\theta \) for \(a \in A\) with the same eigenvalue. There are \(a-1\) of them on \({\varvec{F}}_a^\theta \) orthogonal to the symmetric ones. As they vanish on the contracted vertices \(V_0\), they remain eigenfunctions on \({\varvec{F}}^\theta _{A,v_1}\), and there are \(\sum _{a \in A}(a-1)=r-s\) of them, again orthogonal to the previously constructed ones. Therefore we obtain \(1 \cdot (r-s)=2\) new eigenvalues in our case.
One can see that all eigenvalues are captured via this procedure (here \(r+s+1=7=3+2+2\)). In addition, the two graphs are not isomorphic, as \({\varvec{F}}^\theta _{A,v_1}\) has a pendant vertex while \({\varvec{F}}^\theta _{B,v_1}\) has no vertex of degree 1.
The important feature for the construction of families of isospectral graphs in the preceding example is the partition of a natural number that selects members of a frame \(({\varvec{F}}_a^\theta )_{a \in {\mathbb {N}}}\) that will be contracted at the distinguished vertices (the outlined vertex \(v_1\) in our example). In fact, there is an infinite collection of (finite) families of isospectral graphs that can be constructed similarly. We illustrate this with all different 4-partitions of 8:

For each of the different s-partitions \(A_q\) (\(q \in \{1,2,3,4,5\}\)) (\(s=4\)) of \(r=8\) construct the graphs \({\varvec{F}}_{A_q,v_1}^\theta \) as before (see Fig. 5).
An explicit computation of the eigenvalues of the Laplacian of \({\varvec{F}}_{A_q,v_1}^\theta \) shows again that the five graphs are isospectral for \(q\in \{1,\dots ,5\}\) and with spectrum

in accordance with (3.1) for \(r=8\) and \(s=4\). Note that isospectrality is guaranteed for any constant value of the magnetic potential on one of the multiple edges. Finally, all graphs \({\varvec{F}}_{A_q,v_1}^\theta \) in Fig. 5 are mutually non-isomorphic, as their corresponding degree multisets (see (2.1)) contain the corresponding partition \(A_q\) (highlighted as bold numbers), and hence are different. In fact, the degree sequences of the graphs \({\varvec{F}}_{A_q,v_1}^\theta \) are given by
Graph | Degree multiset |
|---|---|
\({\varvec{F}}_{A_1,v_1}^\theta \) |
|
\({\varvec{F}}_{A_2,v_1}^\theta \) |
|
\({\varvec{F}}_{A_3,v_1}^\theta \) |
|
\({\varvec{F}}_{A_4,v_1}^\theta \) |
|
\({\varvec{F}}_{A_5,v_1}^\theta \) |
|
4 Frames constructed from a building block and their spectra
We construct formally in this section a family of magnetic graphs, called a frame, constructed from a given magnetic graph as a building block and a subset of its vertex set along which we identify copies of the given graph. In particular, the spectrum of this family depends only on the given magnetic graph and the subset of vertices.
Given a magnetic graph \({\varvec{G}}\) and a subset \(V_0\) of its vertices, we define a geometrical construction of graphs with a symmetric structure:
Definition 4.1
(frame members and frames) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph (which we call building block), \(V_0\subset V(G)\) and \(a \in {\mathbb {N}}\).
-
a.
Define the a-th frame member obtained from \(G\) identified along \(V_0\) by
$$\begin{aligned} F_a =F_a(G,V_0):=G^a/{\mathord {\sim _{V_0}}}, \qquad \text {where}\qquad G^a:= {{\,\mathrm{\bigsqcup }\,}}_{j \in \{1,\dots ,a\}} (G\times \{j\}) \end{aligned}$$is the disjoint union of a copies of \(G\) with vertex set \(V(G^a)=V(G)\times \{1,\dots ,a\}\) and edge set \(E(G^a)=E(G)\times \{1,\dots ,a\}\). The equivalence relation \(\sim _{V_0}\) on the vertex set \(V(G^a)\) of the disjoint union is given by
$$\begin{aligned} (v,i) \sim (v',j) \qquad \text {if and only if}\qquad v=v' \quad \text {and}\quad v \in V_0, \end{aligned}$$and all other pairs are equivalent only to itself, i.e., we contract each vertex \(v \in V_0\) of all copies to one vertex. Denote by [(v, j)] the corresponding class specifying a vertex in \(F_a\). Moreover, we call
$$\begin{aligned} {\varvec{F}}_a({\varvec{G}},V_0):=(F_a(G,V_0), \alpha ,w) \end{aligned}$$the a-th (\({\varvec{G}}\)-)frame member obtained from the magnetic graph \({\varvec{G}}\) identified along \(V_0\), where the weights and vector potentials are the same on each copy (and also denoted by the same symbol), i.e., \(w_{(e,j)}:=w_e\) and \(\alpha _{(e,j)}:=\alpha _e\) for all \(e \in E(G)\) and \(j \in \{1,\dots ,a\}\).
-
b.
The family \(({\varvec{F}}_a({\varvec{G}}, V_0))_{a \in {\mathbb {N}}}\) is called a (\({\varvec{G}}\)-)frame identified along \(V_0\).
If the dependence on \(G\) and \(V_0\) are clear from the context we will denote a frame member and a frame simply by \({\varvec{F}}_a\) and \(({\varvec{F}}_a)_{a \in {\mathbb {N}}}\), respectively.
Remark 4.2
It is easily seen that for a simple graph \({\varvec{G}}\) and \(a \ge 2\), the frame \({\varvec{F}}_a({\varvec{G}},V_0)\) is simple if and only if there are no edges inside the identified vertex set \(V_0\).
Remark 4.3
(frames with virtualised vertices) We also allow that \({\varvec{G}}\) has virtualised vertices \(V_1 \subset V({\varvec{G}})\), i.e., vertices on which we impose Dirichlet boundary conditions (see Definition 2.8). We write \(({\varvec{F}}_a)^+_{V_1}:={\varvec{F}}_a({\varvec{G}}^+_{V_1},V_0)\) for the a-th \({\varvec{G}}^+_{V_1}\)-frame member identified along \(V_0\). Note that the case \(V_1=\emptyset \) is just the case described in Definition 4.1.
The following result is a direct result of the preceding definitions.
Lemma 4.4
(order and degree multiset of frame members) Let \({\varvec{G}}^+_{V_1}\) be a magnetic graph with virtualised vertices \(V_1 \subset V(G)\). Moreover, let \(V_0\) be a subset of vertices such that \(V_1 \subset V_0 \subset V\). Then the order and the number of edges of the a-th frame member \((F_a)^+_{V_1}:=F_a(G^+_{V_1},V_0)\) are given respectively by
Moreover, the degree multiset of \((F_a)^+_{V_1}\) is given by

We prove next, that the spectrum of the magnetic graph \({\varvec{F}}_a({\varvec{G}}^+_{V_1},V_0)\) with building block \({\varvec{G}}^+_{V_1}\) identified along \(V_0 \subset V(G)\) depends on the spectrum of \({\varvec{G}}^+_{V_1}\) and \({\varvec{G}}^+_{V_0}\) only. Basically, we use the cyclic symmetry of the a-th frame member.
Proposition 4.5
(spectrum of frame members) Let \({\varvec{G}}^+_{V_1}\) be a magnetic graph with virtualised vertices \(V_1 \subset V(G)\). Moreover, let \(V_0\) be a subset of vertices such that \(V_1 \subset V_0 \subset V\). Then the spectrum of the a-th \({\varvec{G}}^+_{V_1}\)-frame member \({\varvec{F}}_a({\varvec{G}}^+_{V_1},V_0)\) identified along \(V_0\) (\(a\in {\mathbb {N}}\)) is given by
Proof
We assume for ease of notation that \(V_1=\emptyset \), i.e., \({\varvec{G}}^+_{V_1}={\varvec{G}}\), the general case can be treated exactly in the same way.
Let \(n=|{\varvec{G}}|=|V|\) and  be eigenvalues of \(\Delta _{{{\varvec{G}}}}^{{}}\) with corresponding orthonormal eigenfunctions given by \(\{f_1,f_2,\dots ,f_n\}\). For each \(k \in \{1,\dots , n\}\), we extend first the eigenfunction \(f_k\) onto the disjoint union \({\varvec{G}}^a\) to a function \( \widetilde{f}_k :V({\varvec{G}}^a) \longrightarrow {\mathbb {C}}\) by \(\widetilde{f}_k(v,j)=f_k(v)\) for \(j \in \{1,\dots ,a\}\). With a little abuse of notation we write by \(\widetilde{f}_k\) also the corresponding function on the a-th frame member \({\varvec{F}}_a={\varvec{F}}_a({\varvec{G}},V_0)\), which is naturally defined since the functions have the same value on the contracted vertices \(V_0\). The proof of the multiset inclusion \(\sigma _{\mathrm {}}\bigl ({\varvec{G}}\bigr )\subset \sigma _{\mathrm {}}\bigl ({\varvec{F}}_a({\varvec{G}},V_0)\bigr )\) is then a special case of the first part of the proof in Theorem 5.7 (choose
be eigenvalues of \(\Delta _{{{\varvec{G}}}}^{{}}\) with corresponding orthonormal eigenfunctions given by \(\{f_1,f_2,\dots ,f_n\}\). For each \(k \in \{1,\dots , n\}\), we extend first the eigenfunction \(f_k\) onto the disjoint union \({\varvec{G}}^a\) to a function \( \widetilde{f}_k :V({\varvec{G}}^a) \longrightarrow {\mathbb {C}}\) by \(\widetilde{f}_k(v,j)=f_k(v)\) for \(j \in \{1,\dots ,a\}\). With a little abuse of notation we write by \(\widetilde{f}_k\) also the corresponding function on the a-th frame member \({\varvec{F}}_a={\varvec{F}}_a({\varvec{G}},V_0)\), which is naturally defined since the functions have the same value on the contracted vertices \(V_0\). The proof of the multiset inclusion \(\sigma _{\mathrm {}}\bigl ({\varvec{G}}\bigr )\subset \sigma _{\mathrm {}}\bigl ({\varvec{F}}_a({\varvec{G}},V_0)\bigr )\) is then a special case of the first part of the proof in Theorem 5.7 (choose  in the construction of the symmetric functions).
in the construction of the symmetric functions).
To show that also the eigenvalues of \({\varvec{G}}^+_{V_0} \) with Dirichlet conditions on \(V_0\) lift to eigenvalues on the frame member \({\varvec{F}}_a\) put \(n' = |{\varvec{G}}^+_{V_0}| = n-|V_0|\). Let \(\lambda _1,\lambda _2,\dots ,\lambda _{n'}\) be the eigenvalues of \({\varvec{G}}^+_{V_0}\) with corresponding orthonormal eigenfunctions \(h_1,h_2,\dots ,h_{n'}\). Moreover, let \(\eta \in {\mathbb {C}}\) be a non-trivial a-th root of unity, i.e., \(\eta \ne 1\) and \(\eta ^a=1\). For each such \(\eta \) we extend the eigenfunction \(h_{k'}\) to an eigenfunction \(\widetilde{h}_{k',\eta }\) onto \({\varvec{F}}_a\) by
Note that this choice is also well-defined on the quotient as \(h_{k'}(v)=0\) for \(v \in V_0\). We now show that \(\widetilde{h}_{k',\eta }\) is an eigenfunction of \(\Delta _{{{\varvec{F}}_a}}^{{}}\) with eigenvalue \(\lambda _{k'}\): If \(v \in V_0\), we have \(h_{k'}(v)=0\) and
as \(\sum _{j=1}^a \eta ^j=0\) since \(\eta \ne 1\).
If \(v \in V\setminus V_0\), all equivalence classes [(v, j)] contain only one element, again denoted by (v, j). In this case, we have
This shows that \(\widetilde{h}_{k',\eta }\) is an eigenfunction of \(\Delta _{{{\varvec{F}}_a}}^{{}}\) with eigenvalue \(\lambda _{k'}\) as claimed.
Next we will show that the constructed eigenfunctions on the frame member are mutually orthogonal. First, recall that \(\sum _{j=1}^a \eta ^j=0\) since \(\eta \ne 1\). Therefore, we have
Second, the eigenfunctions corresponding to different non-trivial roots of unity are also orthogonal since
Here, \(\eta \ne 1\ne \eta '\) and \(\eta \ne \eta '\), so that the product \(\eta \eta '\) also determines a non-trivial root of unity. Therefore, we have shown that the functions \(\widetilde{f}_k\) and \(\widetilde{h}_{k',\eta }\) for \(k \in \{1,\dots ,n\}\), \(k' \in \{1,\dots ,n'\}\) and \(\eta ^a=1\) with \(\eta \ne 1\) are mutually orthogonal. In particular, we have shown that \(\sigma _{\mathrm {}}\bigl ({\varvec{G}}^+_{V_0}\bigr )^{(a-1)}\subset \sigma _{\mathrm {}}\bigl ({\varvec{F}}_a({\varvec{G}},V_0)\bigr )\), the multiplicity \(a-1\) coming from the fact that there are \(a-1\) solutions of \(\eta ^a=1\) with \(\eta \ne 1\). Altogether we have \(n+(a-1) n'\) mutually orthogonal eigenfunctions and by Lemma 4.4, the order of \(F_a\) is precisely
hence we have found all eigenvalues. \(\square \)
We next present several examples that illustrate how different choices of \(V_0\) of the same underlying graph \({\varvec{G}}\) lead to different families of graphs. We apply the preceding proposition to determine their spectra. We will mention examples with a tree as building block (hence the magnetic potential has no effect) and building blocks with cycles and a non-trivial magnetic potential.
Remark 4.6
(group-theoretical justification) There is an elegant group-theoretical justification for the multiplicities appearing in the spectrum of the magnetic Laplacian of a frame member. In fact, in the proof of Proposition 4.5 there is a cyclic group \({\mathbb {Z}}_a\) acting on the vertices of \({\varvec{F}}_a\) by shifting the label j, \(j \in {\mathbb {Z}}_a\), numbering the branches of the frame member. This induces naturally an action of \({\mathbb {Z}}_a\) on the corresponding \(\ell _2\) space which defines the regular representation U of \({\mathbb {Z}}_a\). Since \({\mathbb {Z}}_a\) is a finite Abelian group the unitary dual satisfies \({\widehat{{\mathbb {Z}}}}_a \cong {\mathbb {Z}}_a\) and U decomposes into a direct sum of one-dimensional representations which consist of multiplication with a-th root of unity (see e.g. [29, Sect. 23.27]). The arguments in the proof of Proposition 4.5 essentially show that the lifted \(\widetilde{f}\)- and \(\widetilde{h}\)-eigenfunctions not only reduce the Laplacian but also reduce the regular representation U. In fact, one has the following decomposition of the Laplacian
explaining the multiplicity \((a-1)\) of the eigenvalues of \(\Delta _{{{\varvec{G}}^+_{V_0}}}^{{}}\) in the spectrum of the Laplacian on the frame \({\varvec{F}}_a\). Note that the first summand arises from the trivial representation and recall that the constant function is excluded as eigenfunction of the Dirichlet Laplacian due to the Dirichlet conditions on \(V_0\).
We start with a simple building block; here a tree, hence any magnetic potential is cohomologous to 0.
Example 4.7
(complete bipartite graphs) Let \(G=K_{m,1}\) be the complete bipartite graph with \(m+1\) vertices and m edges (it is also called a star graph). We draw \(m-1\) of the pendant vertices on the bottom and one vertex on top. Let \(V_0\) be the set of vertices of degree 1 (the bottom and top ones). Again we choose standard weights. The spectrum of \(\Delta _{{G}}^{{}}\) and \(\Delta _{{G^+_{V_0}}}^{{}}\) is given respectively by

Note that the frame member \(F_a=F_a(G,V_0)\) is obtained from the complete bipartite graph \(K_{m-1,a}\) by decorating each of the a vertices on top with a pendant vertex, and that the pendant a vertices are all identified into a single vertex.
Proposition 4.5 implies that the spectrum of the standard Laplacian on \(F_a\) is given by \(\sigma _{\mathrm {}}(F_a)=\sigma _{\mathrm {}}(K_{m,1}) \uplus \sigma _{\mathrm {}}((K_{m,1})^+_{V_0})^{(a-1)}\), i.e.,

Actually, \(F_a\) is just the complete bipartite graph \(K_{m+1,a}\) if one draws the top vertex also on the bottom. Nevertheless, we draw \(F_a\) in this way as we will use only the \(m-1\) bottom vertices (outlined) as distinguished ones in Sect. 5.
Example 4.8
(a diamond-like graph with magnetic potential) We start with a path graph with three vertices and add a loop with magnetic potential to the middle vertex \(v_2\). For \(\theta \in {\mathbb {R}}/2\pi {\mathbb {Z}}\), we let \({\varvec{G}}^\theta := (G,\alpha ^\theta ,1)\) be the magnetic graph with standard weights \((w_e=1\) for all \(e \in E(G)\)), where \(G\) is the path graph \(P_3\) with a loop \(e_0\) attached at the middle vertex \(v_2\). We set \(\alpha _{e_0}^\theta =\theta \) and \(\alpha _e^\theta =0\) for the other two edges. In this case, the spectrum of \({\varvec{G}}^\theta \) is given by the eigenvalues of
namely we have

Now, we let \(V_0=\{v_1,v_3\}\) be the set of the two vertices of degree 1 (see Fig. 7)
Here, the spectrum of \(({\varvec{G}}^\theta )^+_{V_0}\) is given by

The spectrum of the frame member \({\varvec{F}}_a^\theta = {\varvec{F}}_a({\varvec{G}}^\theta ,V_0)\) is hence given by

Example 4.9
(kite graphs) Let \(G\) be the complete graph on four vertices with one pendant vertex added (so \(G\) has five vertices). The vertex set \(V_0\) consists now of the pendant vertex and one of the remaining four vertices (see Fig. 8). Let \({\varvec{G}}\) be the corresponding weighted graph with standard weights. We then have

for the standard Laplacian without magnetic potential. As building block \({\varvec{G}}=(G,\alpha ,1)\) one can also choose an arbitrary magnetic potential \( \alpha :E \longrightarrow {\mathbb {R}}/2\pi {\mathbb {Z}}\). Note that as the Betti number of the building block is 3, it can be seen that it is enough to consider magnetic potentials only which are supported on three edges only, leading to three parameters in \({\mathbb {R}}/2\pi {\mathbb {Z}}\); any other magnetic potential leads to a unitarily equivalent Laplacian by Proposition 2.7 (b).
5 Graphs constructed from frames and partitions
In this section we present the construction of an infinite collection of families of magnetic graphs, where all the elements in each family are isospectral, but non-isomorphic graphs for the magnetic Laplacian with normalised weights. Each family consists of finitely many graphs. Given a frame \((F_a)_{a \in {\mathbb {N}}}\) constructed as in the previous section we will determine these families by assembling the members of the frame according to different s-partitions of the natural number r (see Definition 7.1 and Sect. 3). We present the construction in two steps.
5.1 Disjoint frame unions
We start with a simple construction of isospectral, but non-isomorphic graphs. Note that these graphs are not connected. The construction in this subsection is a special case of the one in Sect. 5.2, namely when \(V_1=\emptyset \).
Definition 5.1
(disjoint frame unions) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph (building block) and choose a subset \(V_0\subset V(G)\). Consider the frame \(({\varvec{F}}_a({\varvec{G}},V_0))_{a\in {\mathbb {N}}}=({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) as specified in Definition 4.1 and let  be an s-partition of the natural number r. The disjoint A-union of the frame \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) is defined as
be an s-partition of the natural number r. The disjoint A-union of the frame \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) is defined as
Note that disjoint frame unions associated to a partition A can be similarly defined for building block graphs that have Dirichlet conditions on some vertices, say \(V_0\). We denote the corresponding disjoint frame union by \({\varvec{F}}_A ({\varvec{G}}^+_{V_0},V_0)\).
In fact, in the proof of Theorem 5.7 we will consider disjoint A-unions of frames constructed from building block graphs that have Dirichlet conditions on \(V_0\). Note that \({\varvec{F}}_A ({\varvec{G}}^+_{V_0},V_0)\) is actually also the disjoint union of r copies of \({\varvec{G}}^+_{V_0}\), but we need the grouping into the partition members \(a \in A\) in the proof of Theorem 5.7.
We need the order and degree multiset of the disjoint union of frames.
Lemma 5.2
(order and degree multiset of disjoint frame unions) Let A be an s-partition of r and consider the disjoint A-union of frames \(F_A\) defined before. Its order is given by
The degree multiset of \(F_A\) is given by

Proof
The first result follows from Lemma 4.4 since \(F_A\) is a disjoint union of frames. In particular, \(|F_a|=a(|G|-|V_0|)+(|V_0|)\), hence
where we used (7.1). The second statement follows similarly. \(\square \)
As the map \(A \mapsto \deg F_A\) is injective, graphs with different s-partitions A and B of r cannot be isomorphic. Note that in order to have two different s-partitions of r, we need \(r \ge 4\) and \(2 \le s \le r-2\).
Lemma 5.3
Let A and B be two different s-partitions of r with \(r \ge 4\) and \(2 \le s \le r-2\). Then the graphs \(F_A\) and \(F_B\) are not isomorphic.
As a prelude (or a special case) of the main theorem (Theorem 5.7) we mention next a first family of isospectral non-isomorphic graphs labelled by different s-partitions of r. Note that these graphs are not connected.
Proposition 5.4
The spectrum of \({\varvec{F}}_A\) is given by
In particular, for two different s-partitions A and B of r with \(r \ge 4\) and \(s \ge 2\), the graphs \({\varvec{F}}_A\) and \({\varvec{F}}_B\) are isospectral, but not isomorphic.
Proof
The spectrum of a disjoint union of graphs is the multiset sum of its spectra, hence the first equality holds. For the second, we use Proposition 4.5 and (7.1). As only r and s enter in \(\sigma _{\mathrm {}}({\varvec{F}}_A)\), we have \(\sigma _{\mathrm {}}({\varvec{F}}_A)=\sigma _{\mathrm {}}({\varvec{F}}_B)\). By Lemma 5.3, the graphs are not isomorphic. \(\square \)
5.2 Contracted frame unions
Next, we construct contracted frame unions by merging a subset of distinguished vertices \(V_1\subset V_0\).
Definition 5.5
(contracted frame union) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph (building block) and choose a subset \(V_0\subset V(G)\). Consider the frame \(({\varvec{F}}_a({\varvec{G}},V_0))_{a\in {\mathbb {N}}}=({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) as specified in Definition 4.1 and let  be an s-partition of the natural number r. For a subset \(V_1 \subset V_0\), called the set of distinguished vertices, we define the \(V_1\)-contracted A-union of the frame \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) by
be an s-partition of the natural number r. For a subset \(V_1 \subset V_0\), called the set of distinguished vertices, we define the \(V_1\)-contracted A-union of the frame \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) by
where \({\sim }_{V_1}\) contracts the vertices \(([v_1],i) \in {\varvec{F}}_{a_i} \times \{i\}\) (\(i \in \{1,\dots ,s\}\)) for each \(v_1 \in V_1\) into a single vertex, denoted again by \(v_1\) for simplicity.
The next result establishes the order of the graphs constructed before. It follows directly from the definition.
Lemma 5.6
(order and degree multiset of contracted frame union) The order of \(F_{A,V_1} = F_A/{\mathord {\sim _{V_1}}}\) is
and the degree multiset is

We now calculate the spectrum of the \(V_1\)-contracted A-union of the frame \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) in terms of its building block \({\varvec{G}}\) and certain Dirichlet conditions.
Theorem 5.7
(Spectrum of contracted frame unions) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph, with underlying discrete graph \(G=(V,E,\partial )\), \(V_0\subset V\), and let \(({\varvec{F}}_a)_{a\in {\mathbb {N}}}\) with \({\varvec{F}}_a={\varvec{F}}_a({\varvec{G}},V_0)\) be a frame constructed from the building block \(G\) by identifying vertices along \(V_0\). Moreover, let A be an s-partition of the natural number r, and choose a subset of distinguished vertices \(V_1 \subset V_0\). Then the spectrum of the normalised Laplacian of the \(V_1\)-contracted A-union \({\varvec{F}}_{A,V_1} = {\varvec{F}}_{A,V_1}({\varvec{G}},V_0)\) (cf. Definition 5.5) is given by
Proof
The graphs given in (5.2) come from two successive vertex contractions; we hence denote a generic vertex by
where \(v\in V\) is a vertex in the building block graph \(G\), j labels the branch in the frame member \(F_{a_i}\) and i numerates the frame member determined by the partition  .
.
Symmetric eigenfunctions. We start with the “symmetric” functions obtained from eigenfunctions of \({\varvec{G}}\) extended symmetrically to \(F_{A,V_1}\): Let \(n=|{\varvec{G}}|\) and denote by \(\{f_1,f_2,\dots ,f_n\}\) the orthonormal eigenfunctions of \(\Delta _{{{\varvec{G}}}}^{{}}\) with eigenvalues \(\{\rho _1,\dots ,\rho _n\}\), respectively. For each \(k \in \{1,\dots , n\}\), we extend the eigenfunction \(f_k\) onto the disjoint union \({\varvec{F}}_A\) to a function
With a little abuse of notation we write by \(\widetilde{f}_k\) also the corresponding function on the quotient \({\varvec{F}}_{A,V_1}\), which is well-defined since \(\widetilde{f}\) takes the same value on all contracted vertices. We show that \(\widetilde{f}_k\) is an eigenfunction of \(\Delta _{{{\varvec{F}}_{A,V_1}}}^{{}}\) with the same eigenvalue \(\rho _k\) considering three different cases for the vertex v.
If \(v \in V_1\), then the equivalence class \(\widetilde{v}\) consists of \(r=\sum _{i=1}^s a_i\) vertices all contracted into a single vertex, while the adjacent edges remain. In particular, \(\deg _{F_{A,V_1}}^w (\widetilde{v}) = r \deg _Gv\) which gives
If \(v \in V_0 \setminus V_1\) the equivalence class \(\widetilde{v}=[([(v,j)],i)]\) consists of \(a_i\) elements, denoted for simplicity by (v, i). Moreover, we have \(\deg _{F_{A,V_1}} (v,i) = a_i \deg _G^w v\), and hence
Finally, if \(v \in V \setminus V_0\), the equivalence class \(\widetilde{v}=[([(v,j)],i)]\) has just one element which is denoted simply by (v, j, i). In this case we have \(\deg _{F_{A,V_1}}^w(v,j,i)=\deg _G^w v\) which gives
This shows that \(\sigma _{\mathrm {}}({\varvec{G}})\) is contained in \(\sigma _{\mathrm {}}\bigl ({\varvec{F}}_{A,V_1}\bigr )\) as a multiset.
Eigenfunctions with Dirichlet conditions on \(V_1\). Dirichlet conditions on \(V_1\) will disconnect the graph \({\varvec{F}}_{A,V_1}\) into s frame member components determined by the partition A. Let \(n'= |{\varvec{G}}^+_{V_1}|=|V| - |V_1|\) and denote by \(\{g_1, \dots , g_{n'}\}\) the eigenfunctions of \(\Delta _{{{\varvec{G}}^+_{V_1}}}^{{}}\) with eigenvalues \(\{\mu _1,\dots , \mu _{n'}\}\). We will lift the eigenfunctions \(g_{k'}\) to eigenfunctions of \(\Delta _{{{\varvec{F}}_{A,V_1}}}^{{}}\) supported on each frame member \(F_{a_i}\). Denote now by \(\varepsilon \) a non-trivial s-th root of unity, i.e., \(\varepsilon \not =1\) and \(\varepsilon ^{s}=1\). For \(\widetilde{v}=[([(v,j)],i)]\) we define
Note that now the function value of a vertex [(v, j)] on \({\varvec{F}}_{a_i}\) is the same for all \(j \in \{1,\dots ,a_i\}\) as the root of unity takes the same value on each frame member. It can be seen similarly as before (and as in the proof of Proposition 4.5) that
for all \(\widetilde{v} \in V({\varvec{F}}_{A,V_1})\). Moreover, since \(\varepsilon \ne 1\) we have \(\sum _{i=1}^s \varepsilon ^i=0\) and, therefore, the functions \(\widetilde{f}_k\) and \({\widetilde{g}_{k',\varepsilon }}\) are mutually orthogonal, as we have
In particular, the eigenfunctions \(\widetilde{f}_k\) are orthogonal to the eigenfunctions \(\widetilde{g}_{k',\varepsilon }\) with \(k=1,\dots ,n\), \(k'=1,\dots ,n'\) and \(\varepsilon \ne 1\) with \(\varepsilon ^s=1\).
Eigenfunctions with Dirichlet conditions on \(V_0\). Since \(V_1\subset V_0\) we have by construction that eigenfunctions on \({\varvec{F}}_{A,V_1}\) with Dirichlet conditions on \(V_0\) are eigenfunctions of the disjoint union \({\varvec{F}}_A({\varvec{G}}^+_{{V_0}},V_0)\) (see Definition 5.1). In fact, we have
Exploiting the symmetry of the frame members we will construct next a family of eigenfunctions which are lifted from eigenfunctions of the Laplacian on \({\varvec{G}}\) with Dirichlet conditions on \(V_0\) and which are orthogonal to the symmetric eigenfunctions \(\widetilde{f}_k\) constructed in the first step. Let \(n''=|{\varvec{G}}^+_{V_0}| =|V| - |V_0 |\) and denote by \(\{h_1, \dots , h_{n''}\}\) the eigenfunctions of \(\Delta _{{{\varvec{G}}^+_{V_0}}}^{{}}\) with eigenvalues \(\{\lambda _1,\dots , \lambda _{n''}\}\). For each \(i\in \{1,\dots ,s\}\) we will lift the eigenfunctions \(h_k\) to eigenfunctions of \(\Delta _{{{\varvec{F}}_{A,V_1}}}^{{}}\) supported on each frame member \(F_{a_i}\). Denote by \(\eta \) a non-trivial \(a_i\)-th root of unity, i.e., \(\eta \not =1\) and \(\eta ^{a_i}=1\). For \(\widetilde{v}=[([(v,j)],i)]\) we define
and extend by 0 if the label of the frame member is different from i. Since the functions \(\widetilde{h}_{k'',\eta , i}\) are supported on each frame member the proof that the preceding functions are eigenfunctions of \(\Delta _{{{\varvec{F}}_{A,V_1}}}^{{}}\) with eigenvalue \(\lambda _{k''}\) can be reduced to the analysis on each frame \({\varvec{F}}_{a_i}\). This was shown in the proof of Proposition 4.5, and the inclusion of multisets \(\sigma _{\mathrm {}}\bigl ({\varvec{G}}^+_{V_0}\bigr )^{(a_i-1)}\subset \sigma _{\mathrm {}}\bigl ({\varvec{F}}_{a_i}( {\varvec{G}}^+_{V_0})\bigr )\) follows. Since this inclusion holds for each \(i\in \{1,\dots ,s\}\) and since \(a_1+\dots +a_s=r\) we conclude that
As in the proof of Proposition 4.5 we also see that the functions \(\widetilde{f}_k\) and \(\widetilde{h}_{k'',\eta ,i}\) are mutually orthogonal since the functions \(\widetilde{h}\) are supported on each frame member. Moreover, the eigenfunctions \(\widetilde{g}_{k',\varepsilon }\) constructed in the second step and \(\widetilde{h}_{k'',\eta ,i}\) turn out to be also mutually orthogonal with a similar computation with the root of unity as in the second step. This shows that
Finally, we have to check that we identified all eigenvalues. In fact, we have identified \(|G|\) symmetric eigenfunctions and
eigenfunctions from \({\varvec{G}}^+_{V_0}\). Moreover, the remaining eigenfunctions are \(\widetilde{g}_{k',\varepsilon }\) for \(k' \in \{1,\dots , |G|- |V_1|\}\) and \(\varepsilon ^s=1\) with \(\varepsilon \ne 1\) determine \((s-1)(|G|-|V_1|)\) additional eigenvalues. Altogether, we have specified
eigenvalues corresponding to a mutually orthogonal set of eigenfunctions. Since, according to Lemma 5.6, the order of \(F_{A,V_1}\) is precisely \(r(|{\varvec{G}}|-|V_0|) + s(|V_0|-|V_1|) + |V_1|\) we conclude that we found all eigenvalues and the spectrum of the magnetic Laplacian is determined. \(\square \)
We can now formulate our main result on the construction of isospectral, non-isomorphic and, now, connected graphs.
Theorem 5.8
(main theorem) Let \({\varvec{G}}=(G,\alpha ,w)\) be a magnetic graph, \(V_0\subset V(G)\) and let \(V_1 \subset V_0\) be a set of distinguished vertices. For any different pair A and B of s-partitions of a natural number \(r \ge 4\) the graphs \({\varvec{F}}_{A,V_1}\) and \({\varvec{F}}_{B,V_1}\) (the \(V_1\)-contracted A- respectively B-union of \(({\varvec{F}}_a({\varvec{G}},V_0))_{a\in {\mathbb {N}}}\), cf. Definition 5.5) are isospectral and not isomorphic.
Proof
In the calculation of the spectrum in Theorem 5.7, only the natural number r and the length s of the partition are relevant and not the concrete partitions A and B. Therefore different s-partitions of r lead to isospectral graphs. Moreover, the fact that two graphs determined by different partitions are not isomorphic follows from Lemma 5.6 since the corresponding degree multisets are different. \(\square \)
Corollary 5.9
(isospectral equilateral metric graphs) Let \(G\) be a discrete graph (with standard weights), \(V_0\subset V(G)\) and let \(V_1 \subset V_0\) be a set of distinguished vertices. For any different pair A and B of s-partitions of a natural number \(r \ge 4\) the corresponding equilateral metric graphs \(\overline{F}_{A,V_1}\) and \(\overline{F}_{B,V_1}\) constructed according to the corresponding discrete graphs are isospectral and not isomorphic.
Proof
The proof follows from Theorem 5.8 and Proposition 2.9, as in our construction, \(F_{A,V_1}\) and \(F_{B,V_1}\) have the same number of edges. \(\square \)
6 Examples of isospectral magnetic graphs
In this section we give more examples of isospectral magnetic graphs constructed as contracted frame union from various building blocks. Let \({\varvec{G}}=(G,\alpha ,w)\) be such a general building block, i.e., a discrete weighted magnetic graph. From \({\varvec{G}}\), we construct a frame \(({\varvec{F}}_a)_{a \in {\mathbb {N}}}\), where the frame members \({\varvec{F}}_a={\varvec{F}}_a({\varvec{G}},V_0)\) are identified along \(V_0 \subset V:=V(G)\), cf. Definition 4.1. Moreover, let A be an s-partition of \(r \in {\mathbb {N}}\). As we need at least two different s-partitions of r we restrict ourselves to \(r \in \{4,5,6,\dots \}\) and \(s \in \{2,3,\dots ,r-2\}\). Our isospectral and non-isomorphic graphs will be given by the \(V_1\)-contracted frame unions \({\varvec{F}}_{A,V_1}\) and \({\varvec{F}}_{B,V_1}\), where \(V_1\) is some subset of \(V_0\).
6.1 Special cases and very small contracted frame unions
We start with some extreme or trivial cases for the choice of merging vertex sets \(V_0\) and \(V_1\).
Examples 6.1
(no distinguished vertex) If \(V_1=\emptyset \) in Definition 5.5, then \({\varvec{F}}_{A,\emptyset }={\varvec{F}}_A (:={{\,\mathrm{\bigsqcup }\,}}_{a \in A} {\varvec{F}}_a(G,V_0))\), i.e., \({\varvec{F}}_{A,\emptyset }\) is the disjoint frame union of Definition 5.1. Note that the graph \({\varvec{F}}_{A,\emptyset }\) is not connected. In particular, for different s-partitions of r, we obtain two isospectral, non-isomorphic, but non-connected graphs \({\varvec{F}}_A\) and \({\varvec{F}}_B\).
Examples 6.2
(all vertices are distingued) If \(V_1=V_0\), then \({\varvec{F}}_{A,V_1}={\varvec{F}}_r\) is the r-th frame member. In particular, it depends only on r, but not on s any more, hence we will not obtain non-isomorphic graphs for different partitions of r.
We will hence assume in the sequel that \(V_1\) is a non-trivial subset of \(V_0\), i.e., that \(V_1 \ne \emptyset \) and \(V_1 \ne V_0\).
 ,
, 
 ,
, 
Examples 6.3
If \(V_0=V(G)\), then \({\varvec{F}}_a({\varvec{G}},V(G))\) is the r-fold edge copy of \({\varvec{G}}\), i.e., the vertex set is the same, but each edge is copied r times keeping its original weight and magnetic potential. Examples are the graphs from the building blocks labelled 2.1, 3.3, 3.3’, 3.4, 3.4’, 3.6, 3.6’ in Tables 2 and 3.
Moreover, the order of the \(V_1\)-contracted frame union \({\varvec{F}}_{A,V_1}\) for some \(V_1 \subset V_0\) now is
i.e., it does not depend on r. In particular, we obtain an infinite family of isospectral graphs, as an s-partition for any \(r \in \{s+2,s+3, \dots \}\) leads to another non-isomorphic graph (isomorphy as multigraph, of course). We have another class of examples in Example 6.11.
Remark 6.4
(frames identified along all vertices, weighted graphs) If \({\varvec{G}}=(G,0,1)\) has standard weight, then the frames for \(V_0=V(G)\) as in the previous example are the r-fold edge copy of \(G\) (i.e., each edge with standard weight is repeated r times). Note that \(G\) and its r-fold edge copy are isolaplacian (as the common factor r cancels out in the matrix representation of the Laplacian).
Moreover, each frame member and also the \(V_1\)-contracted frame union \(F_{A,V_1}\) for some proper subset \(V_1 \subset V_0\) can be turned into a simple graph (called underlying simple weighted graph) with edge weights now given by the number of parallel edges in the original graph, see Remark 2.5. Note that as weighted graphs, two contracted frame unions for different s-partitions are still non-isomorphic (as weighted graphs), as the weights are given by the partition A.
A special case of the last example is the following:
Examples 6.5
(the smallest non-trivial example) Let \(G\) be the graph on two vertices and one edge joining them with standard weight. Let \(V_0=V=\{v_1,v_2\}\) and \(V_1=\{v_1\}\) (see the first row in Table 2). Moreover, let  be an s-partition of r. Then \({\varvec{F}}_{A,v_1}\) is a star graph with \(s+1\) vertices and multiple edges according to the partition A (\(a_1\) edges joining the first non-central vertex, \(a_2\) the second etc.). Note that for two different s-partitions, the corresponding contracted frame unions are not isomorphic (as multigraphs).
be an s-partition of r. Then \({\varvec{F}}_{A,v_1}\) is a star graph with \(s+1\) vertices and multiple edges according to the partition A (\(a_1\) edges joining the first non-central vertex, \(a_2\) the second etc.). Note that for two different s-partitions, the corresponding contracted frame unions are not isomorphic (as multigraphs).
The spectrum of \({\varvec{F}}_{A,v_1}\) is  for any s-partition A. For \(s=2\), the underlying simple weighted graph is a path graph with three vertices. Actually, it can be seen that the spectrum of this graph is always
for any s-partition A. For \(s=2\), the underlying simple weighted graph is a path graph with three vertices. Actually, it can be seen that the spectrum of this graph is always  for any weights on the two edges.
for any weights on the two edges.
6.2 Other small contracted frame unions
We now list all possible cases with standard weights leading to isospectral and non-isomorphic examples starting from building blocks \(G\) with two, three or four vertices. We start with a certain graph \(G\) as building block, and draw the vertices in \(V_0\) on top and bottom; while the vertices in \(V_1\) (the “distinguished” vertices, along the frames are contracted) are drawn on bottom and outlined). For one graph \(G\) one might hence have several possibilities of frames and contracted frame unions.
If \(G\) has two or three vertices, we allow that the isospectral graphs have parallel edges (see Tables 2 and 3). If \(G\) has four vertices, we restrict ourselves to examples leading only to simple graphs, see Remark 4.2. Table 4 contains all examples with a building block being a tree with four vertices while Table 5 lists all remaining cases.
As simplest non-trivial partitions in Tables 2, 3, 4, 5 we choose  and
and  . Moreover, C denotes an arbitrary s-partition of r.
. Moreover, C denotes an arbitrary s-partition of r.
Examples 6.6
(all examples with building blocks with three vertices) Examples of building blocks with three vertices and standard weights can be seen in Tables 2 and 3 (labels starting with 3). Only one building block leads to simple isospectral examples (label 3.1); this example class was already presented in [11, Example 2] under the name inflated stars there.
All other examples leads to graphs with parallel edges. Note that one can always replace parallel edges by a single weighted edge with the number of parallel edges as weight, see Remark 2.5. The corresponding Laplacians are the same, hence we also obtain isospectral, but non-isomorphic examples; these examples are not isomorphic as weighted graphs as their lists of weights are different.
Examples 6.7
(all examples with building blocks with four vertices) For simplicity, we list here only those cases leading to simple isospectral examples. Table 4 contains all cases where the building block \(G\) is a tree while Table 5 contains the remaining cases with building blocks not being a tree.
Note that only the cases with label 4.2’, 4,4 and 4.4’ can be treated using Theorem 1 of [11]. In all other cases, the graphs \(G_j[A',B]\) (in the notation of [11]) are not complete bipartite graphs as required by [11, Thm .1].
The case with label 4.4 can also be treated with the perturbative technique described in [19, Sect. 4.2], where we used the name fuzzy complete bipartite graph. With the method in the present paper, it is based on the frames used in Example 4.7.
6.3 Some other examples with possible non-trivial magnetic potential
Here, we give examples where the underlying building block is not a tree, hence there exist magnetic potentials having an effect on the spectrum.
Example 6.8
(a diamond-like graph with magnetic potential) Taking as building block the magnetic graph \({\varvec{G}}^\theta \) of Example 4.8, and choosing as set \(V_1=\{v_1\}\) just the bottom (outlined) vertex, then the spectrum of \(({\varvec{G}}^\theta )^+_{V_1}\) is given by

For  and
and  , we have the isospectral magnetic graphs as in Fig. 9.
, we have the isospectral magnetic graphs as in Fig. 9.
Example 6.9
(kite graphs) Let \(G\) be the complete graph on four vertices with one pendant vertex added (so \(G\) has five vertices) as in the frame construction of Example 4.9. The vertex set \(V_0\) consists now of the pendant vertex and one of the remaining four. The set of distinguished vertices \(V_1\) consists just of the pendant vertex. Let \({\varvec{G}}\) be the corresponding weighted graph with standard weights and no magnetic potential, then

An example of isospectral graphs is given in Fig. 1 (right hand side). Note that this construction also works for any magnetic potential, see Example 4.9.
Example 6.10
(all non-trivial magnetic graphs with building block with four vertices) Note that all examples of Table 5 can carry also a magnetic potential on the building block leading to a non-trivial family with one parameter (labels 4.5, 4.5’ and 4.6) respectively two parameters (label 4.7) in \({\mathbb {R}}/2\pi {\mathbb {Z}}\).
6.4 A class of weighted isospectral graphs
Example 6.11
(contracted along all but one vertex) Let \(G\) be a graph with standard weights and \(V_0=V(G)\). Then the frame members \(F_a({\varvec{G}},V_0)\) are the r-fold edge copy of \(G\) as in Example 6.3 and in particular isolaplacian with \(G\) (see second and third graph in Fig. 10). Note that Butler [10] also uses the idea of changing weights. Special cases are actually the graphs with label 2.1, 3.3’, 3.4’ and 3.6’ in Tables 2 and 3 where \(G\) is a path graph with two or three vertices or a cycle graph with three vertices.
Let now \(F_{A,V_1}=F_{A,V_1}(G,V(G))\) be the contracted frame union for \(V_1=V(G) \setminus \{v^*\}\) and some s-partition of r. Here, \(v^* \in V(G)\) is one chosen vertex. Its order is \(|F_{A,V_1}|=s+|V_1|=|{\varvec{G}}|+s-1\) independently of r as in Example 6.3. The spectrum of \(G^+_{V_1}\) is just  , as \(V(G) \setminus V_1=\{v^*\}\) contains just one point. From Theorem 5.7 we conclude that
, as \(V(G) \setminus V_1=\{v^*\}\) contains just one point. From Theorem 5.7 we conclude that

Note that the matrix representation of Laplacian on \(F_{A,V_1}\) (with standard weights) has the matrix representation of \(G^*\) as principal submatrix, where \(G^*\) denotes the graph \(G\) with \(v^*\) and all adjacent edges removed. It could also be observed that passing to the corresponding simple weighted graphs (with weights r on all edges in \(G^*\)) and weights \(a \in A\) on the edges joining the s copies of \(v^*\). Dividing the weights by the common factor 1/r (this does not change the Laplacian), we end up with an isolaplacian graph \(G_{A,v^*}\) with standard weights (\(w_e=1\)) for all edges inside \(G^*\), and weights a/r (\(a \in A\)) for the remaining edges joining the extra s copies of \(v^*\) (see Fig. 10). In particular, we have a way of keeping the spectrum of \(G\) and adding eigenvalues 1.
7 Conclusions
Sunada’s method [50] as well as some of its generalisations [3, 4, 46] use representation theory as a key ingredient to construct the isospectral manifolds or graphs which appear as quotient graphs. It is worth to point out differences and similarities between the method presented here and the one given, for example, in [4] even if we think that both methods are different in nature. We do not exclude though that both approaches may be combined.
In [4] the metric graph considered first carries the action of a finite (in general non-commutative) group. Two different subgroups are chosen which will determine the isospectral quotient graphs provided the corresponding induced representations are equivalent. Neumann and Dirichlet conditions on the metric graph appear naturally.
The method presented in this article has a more combinatorial nature even if the underlying symmetry is, of course, expressed in terms of cyclic (commutative) groups acting on the copies of the building block as mentioned in Remark 4.6. But the construction of the quotient here goes through for any choice of the pair of subsets \(V_0\), \(V_1\), and we see no way to implement this freedom through subgroups of \({\mathbb {Z}}_a\). Another instance is that the action of the cyclic groups is not free on the quotient, as the vertices in \(V_0\) are fixed points. An additional difference is the importance of the eigenfunctions with Dirichlet conditions on the vertices \(V_0\) and \(V_1\) and the specific form of the partition that appears explicitly in the degree lists of the different quotients but not in the corresponding spectra. Nevertheless, Brooks result on isospectral (regular) graphs not arising from Sunada’s method (cf. [7]) as well as a theory of groups acting not freely on graphs might give a hint how to understand our examples in the spirit of representation theory.
Last but not least the approach using Dirichlet-to-Neumann maps of subgraphs of quantum graphs in [34] produces some of our examples of isospectral graphs using different methods; and it may also apply to discrete graphs. Moreover, as the authors also write in [34] it is not obvious how their approach can be linked with representation theory.
Data availibility
No datasets were generated or analysed during the current study.
Notes
For the multiset notation we refer to Appendix 1.
For a partial subgraph, the incidence function \( \partial :E(G) \longrightarrow V(G) \times V(G)\) may not map all initial or final vertices into \(V(G) {\setminus } V_0\) (see Sect. 2 of [18] for additional results and motivation). Mohar [42] also calls edges with one vertex not in the graph also “free edges”.
In [39], we assumed that the underlying graphs are connected. The results there extend straightforward to the case of several connected components.
Note that if \(\theta =\pi \), then the entry in the matrix of \(\Delta _{{{\varvec{G}}^\theta }}^{{}}\) corresponding to the edges joining \(v_1\) and \(v_2\) (cf. (2.6)) is actually 0, due to the two parallel edges, one of them with magnetic potential \(\pi \), the other one 0, hence \(\mathrm e^0 + \mathrm e^{\mathrm i\pi }=0\). In particular, \({\varvec{G}}^\pi \) is isolaplacian (see Remark 2.5) with the disjoint union of a graph with one isolated vertex (having spectrum 1 by definition), and \(G^+_{v_1}\); in accordance with the spectrum
 given in (3.2) for \(\theta =\pi \). This special case is hence a procedure to “delete” edges while keeping the original degrees.
given in (3.2) for \(\theta =\pi \). This special case is hence a procedure to “delete” edges while keeping the original degrees.
References
Angelone, G., Facchi, P., Marmo, G.: Hearing the shape of a quantum boundary condition. Modern Phys. Lett. A 37, 2250114 (2022)
Arendt, W.: Does diffusion determine the body? J. Reine Angew. Math. 550, 97–123 (2002)
Band, R., Berkolaiko, G., Joyner, C.H., Liu, W.: Quotients of finite-dimensional operators by symmetry representations, arXiv:1711.00918 (2017)
Band, R., Parzanchevski, O., Ben-Shach, G.: The isospectral fruits of representation theory: quantum graphs and drums. J. Phys. A 42, 175202 (2009)
Banerjee, A., Jost, J.: On the spectrum of the normalized graph Laplacian. Linear Algebra Appl. 428, 3015–3022 (2008)
Berkolaiko, G., Kuchment, P.: Introduction to quantum graphs, Mathematical Surveys and Monographs, vol. 186. American Mathematical Society, Providence (2013)
Brooks, R.: Non-Sunada graphs. Ann. Inst. Fourier (Grenoble) 49, 707–725 (1999)
Brouwer, A.E., Haemers, W.H.: Spectra of Graphs, Universitext. Springer, New York (2012)
Butler, S.: A note about cospectral graphs for the adjacency and normalized Laplacian matrices. Linear Multilinear Algebra 58, 387–390 (2010)
Butler, S.: Using twins and scaling to construct cospectral graphs for the normalized Laplacian. Electron. J. Linear Algebra 28, 54–68 (2015)
Butler, S., Grout, J.: A construction of cospectral graphs for the normalized Laplacian. Electron. J. Comb. 18, 231 (2011)
Butler, S., Heysse, K.: A cospectral family of graphs for the normalized Laplacian found by toggling. Linear Algebra Appl. 507, 499–512 (2016)
Cavers, M.S.: The Normalized Laplacian Matrix and General Randić Index of Graphs, ProQuest LLC, Ann Arbor, MI, Thesis (Ph.D.)–The University of Regina (Canada) (2010)
Chernyshenko, A., Pivovarchik, V.: Recovering the shape of a quantum graph. Integr. Equ. Oper. Theory 92, 23 (2020)
Cvetković, D.M., Doob, M., Sachs, H.: Spectra of graphs, Theory and applications. 3rd edn., Johann Ambrosius Barth, Heidelberg, (1995)
Chung, F.: Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, vol. 92, Published for the Conference Board of the Mathematical Sciences, Washington, DC (1997)
Das, K.C., Sun, S., Gutman, I.: Normalized Laplacian eigenvalues and Randić energy of graphs. MATCH Commun. Math. Comput. Chem. 77, 45–59 (2017)
Fabila-Carrasco, J.S., Lledó, F., Post, O.: Spectral gaps and discrete magnetic Laplacians. Linear Algebra Appl. 547, 183–216 (2018)
Fabila-Carrasco, J.S., Lledó, F., Post, O.: Isospectral graphs via spectral bracketing, arXiv:2207.03924 (2022)
Fabila-Carrasco, J.S., Lledó, F., Post, O.: Matching number, Hamiltonian graphs and magnetic Laplacian matrices. Linear Algebra Appl. 642, 86–100 (2022)
Fabila-Carrasco, J.S., Lledó, F., Post, O.: Spectral preorder and perturbations of discrete weighted graphs. Math. Ann. 382, 1775–1823 (2022)
Gnutzmann, S., Smilansky, U., Sondergaard, N.: Resolving isospectral ‘drums’ by counting nodal domains. J. Phys. A Math. Gen. 38, 8921–8933 (2005)
Godsil, C.D., McKay, B.D.: Constructing cospectral graphs. Aequationes Math. 25, 257–268 (1982)
Gordon, C., Perry, P., Schueth, D.: Isospectral and isoscattering manifolds: a survey of techniques and examples, geometry, spectral theory, groups, and dynamics, Contemp. Math., vol. 387, Amer. Math. Soc., Providence, pp. 157–179 (2005)
Gutkin, B., Smilansky, U.: Can one hear the shape of a graph? J. Phys. A 34, 6061–6068 (2001)
Gordon, C., Webb, D., Wolpert, S.: Isospectral plane domains and surfaces via Riemannian orbifolds. Invent. Math. 110, 1–22 (1992)
Halbeisen, L., Hungerbühler, N.: Generation of isospectral graphs. J. Graph Theory 31, 255–265 (1999)
Hu, M., Li, S.: Cospectral graphs for the normalized Laplacian. AIMS Math. 7, 4061–4067 (2022)
Hewitt, E., Ross, K.A.: Abstract Harmonic Analysis, vol. 1, 2nd edn. Springer-Verlag, Berlin (1979)
Haemers, W.H., Spence, E.: Enumeration of cospectral graphs. Eur. J. Comb. 25, 199–211 (2004)
Ivrii, V.: 100 years of Weyl’s law. Bull. Math. Sci. 6, 379–452 (2016)
Juul, J.S., Joyner, C.H.: Isospectral discrete and quantum graphs with the same flip counts and nodal counts. J. Phys. A 51, 245101 (2018)
Kac, M.: Can one hear the shape of a drum? Am. Math. Mon. 73, 1–23 (1966)
Kurasov, P., Muller, J.: On isospectral metric graphs, arXiv:2112.04230 (2021)
Kuchment, P.: Quantum graphs: an introduction and a brief survey, In: Exner, P., Keating, J.P., Kuchment, P., Sunada, T., Teplayaev, A. (eds.) Analysison Graphs and its Applications (Providence, R.I.), Proc. Symp. Pure Math., vol. 77, Amer. Math. Soc., pp. 291–312 (2008)
Ławniczak, M., Kurasov, P., Bauch, S., Białous, M.G., Akhshani, A., Sirko, L.: A new spectral invariant for quantum graphs. Nat. Sci. Rep. 11, 15342 (2021)
Lim, L.-H.: Hodge Laplacians on graphs. SIAM Rev. 62, 685–715 (2020)
Lange, C., Liu, S., Peyerimhoff, N., Post, O.: Frustration index and Cheeger inequalities for discrete and continuous magnetic Laplacians. Calc. Var. Partial Differ. Equ. 54, 4165–4196 (2015)
Lledó, F., Post, O.: Eigenvalue bracketing for discrete and metric graphs. J. Math. Anal. Appl. 348, 806–833 (2008)
Lu, Z., Rowlett, J.: The sound of symmetry. Am. Math. Mon. 122, 815–835 (2015)
Merris, R.: Large families of Laplacian isospectral graphs. Linear Multilinear Algebra 43, 201–205 (1997)
Mohar, B.: A domain monotonicity theorem for graphs and Hamiltonicity. Discrete Appl. Math. 36, 169–177 (1992)
Oren, I., Band, R.: Isospectral graphs with identical nodal counts. J. Phys. A Math. Theor. 45, 135203 (2012)
Osborne, S.P.: Cospectral bipartite graphs for the normalized Laplacian, ProQuest LLC, Ann Arbor, MI, Thesis (Ph.D.)–Iowa State University (2013)
Park, S., Lee, I., Kim, J., et al.: Hearing the shape of a drum for light: isospectrality in photonics. Nanophotonics 11, 2763–2778 (2022)
Parzanchevski, O., Band, R.: Linear representations and isospectrality with boundary conditions. J. Geom. Anal. 20, 439–471 (2010)
Pistol, M. E.: Generating isospectral but not isomorphic quantum graphs, https://arxiv.org/pdf/2104.12885.pdf v12 (2023)
Rückriemen, R.: Recovering quantum graphs from their Bloch spectrum. Ann. Inst. Fourier (Grenoble) 63, 1149–1176 (2013)
Shubin, M.A.: Discrete magnetic Laplacian. Comm. Math. Phys. 164, 259–275 (1994)
Sunada, T.: Riemannian coverings and isospectral manifolds. Ann. Math. 121, 169–186 (1985)
Sunada, T.: A discrete analogue of periodic magnetic Schrödinger operators, Geometry of the spectrum (Seattle, WA, 1993) Contemp. Math., vol. 173, Amer. Math. Soc. Providence, pp. 283–299 (1994)
Sunada, T.: Topological Crystallography, Surveys and Tutorials in the Applied Mathematical Sciences. With a view towards discrete geometric analysis, vol. 6. Springer, Tokyo (2013)
Tan, J.: On isospectral graphs. Interdiscip. Inform. Sci. 4, 117–124 (1998)
von Below, J.: Can one hear the shape of a network?, Partial differential equations on multistructures (Luminy, 1999), Lecture Notes in Pure and Appl. Math., vol. 219, Dekker, New York, pp. 19–36 (2001)
van Dam, E.R., Haemers, W.H.: Which graphs are determined by their spectrum? Linear Algebra Appl. 373, 241–272 (2003). (Special issue on the Combinatorial Matrix Theory Conference (Pohang, 2002))
Weyl, H.: Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen (mit einer Anwendung auf die Theorie der Hohlraumstrahlung). Math. Ann. 71, 441–479 (1912)
Zelditch, S.: Survey on the inverse spectral problem. ICCM Not. 2, 1–20 (2014)
Acknowledgements
It is a pleasure to thank an anonymous referee for a careful reading of the manuscript and many useful suggestions and remarks on the first version of the manuscript.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors wrote, read, and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
JSFC was supported by the Leverhulme Trust via a Research Project Grant (RPG-2020-158). FLl was supported by the Severo Ochoa Programme for Centres of Excellence in R &D (SEV-2015-0554) and from the Spanish National Research Council, through the Ayuda extraordinaria a Centros de Excelencia Severo Ochoa (20205CEX001) and by the Madrid Government under the Agreement with UC3M in the line of Research Funds for Beatriz Galindo Fellowships (C &QIG-BG-CM-UC3M), and in the context of the V PRICIT.
Appendix A: Multisets and partitions
Appendix A: Multisets and partitions
1.1 A.1 Multisets
Multisets will be a convenient tool to deal with spectra and degree lists of graphs.
-
A multiset is an ordered pair (A, m) where A is a set and \( m :A \longrightarrow {\mathbb {N}}_0=\{0,1,2,\dots \}\) is a map on A. We say that \(x \in A\) appears m(x)-times in A. In order to simplify notation, we set \(m_A(x)=0\) whenever \(x \notin A\).
-
We often simply refer to A as a multiset without mentioning the map m, and hence refer to the multiplicity map of A as \(m_A\). Sets A can be considered as multisets by setting \(m_A(x)=1\) whenever \(x \in A\) and 0 otherwise.
-
The cardinality of the multiset A is the sum of the multiplicities of all its elements, i.e., \(|A| =\sum _{x\in A} m_A(x)\).
-
When A is finite (i.e., \(|A| < \infty \)) we write \(A=\{a_1,a_2,\dots ,a_s\}\), and a multiset (A, m) will then also be written as

Multisets with elements in \({\mathbb {N}}\) or \({\mathbb {R}}\) (or any other linearly ordered set) can be also seen as ordered lists and sometimes it will be convenient for the exposition to take this point of view.
-
The sum of two multisets A and B denoted as \( A \uplus B\) is the set \(A \cup B\) with multiplicity map \(m_{A_\uplus B}(x):=m_A(x)+m_B(x)\) for all \(x \in A \cup B\).
-
The difference of two multisets, denoted by \(A \ominus B\) is the set \(A \setminus B\) with multiplicity map \(m_{A \ominus B}(x):= \max \{m_A(x)-m_B(x),0\}\).
-
The k-th multiple of a multiset A (with multiplicity map \(m_A\)), denoted by \(A^{(k)}\), is the multiset A with multiplicity map \(m_{A^{(k)}}(x)=km_A(x)\) for all \(x\in A\), i.e., the multiplicity of each element in \(A^{(k)}\) is multiplied by k.
1.2 A.2 Partitions of a natural number
The notion of a partition of a natural number will be important for our construction of isospectral graphs.
Definition 7.1
(partition of a number) A partition of a natural number r of length s (or an s-partition r for short) is a multiset A of natural numbers with sum r, i.e.,

The number s is called the length of the partition.
We frequently use the following equations
where A is understood as a multiset.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fabila-Carrasco, J.S., Lledó, F. & Post, O. A geometric construction of isospectral magnetic graphs. Anal.Math.Phys. 13, 64 (2023). https://doi.org/10.1007/s13324-023-00823-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-023-00823-9



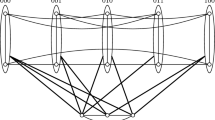



 and
and  of 4 are isospectral, but not isomorphic for each value
of 4 are isospectral, but not isomorphic for each value 

 ,
,  ,
,  ,
,  and
and  of
of 



 .
.




 given in (
given in (