Abstract
Recently a spectral Favard theorem for bounded banded lower Hessenberg matrices that admit a positive bidiagonal factorization was presented. These type of matrices are oscillatory. In this paper the Lima–Loureiro hypergeometric multiple orthogonal polynomials and the Jacobi–Piñeiro multiple orthogonal polynomials are discussed at the light of this bidiagonal factorization for tetradiagonal matrices. The Darboux transformations of tetradiagonal Hessenberg matrices is studied and Christoffel formulas for the elements of the bidiagonal factorization are given, i.e., the bidiagonal factorization is given in terms of the recursion polynomials evaluated at the origin.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we will analyze some aspects for the tetradiagonal Hessenberg matrix of the form

where we assume that \(a_n>0\), and its bidiagonal factorization
with bidiagonal matrices given by

If the requirement
is fulfilled, we say that we have a positive bidiagonal factorization (PBF). In [5], this factorization was shown to be the key for a Favard theorem for bounded banded Hessenberg semi-infinite matrices and the existence of positive measures such that the recursion polynomials are multiple orthogonal polynomials and the Hessenberg matrix is the recursion matrix from this set of multiple orthogonal polynomials. We also gave a multiple Gauss quadrature together with explicit degrees of precision. Then, in [6] we studied for the tetradiagonal case when such PBF, in terms of continued fractions, for oscillatory matrices exists. Oscillatory tetradiagonal Toeplitz matrices were shown to admits a PBF. Moreover, it was proven that oscillatory banded Hessenberg matrices are organized in rays, with the origin of the ray not having the positive bidiagonal factorization and all the interior points of the ray having such positive bidiagonal factorization.
In the next section of this paper we succinctly discuss two cases that appear in the literature, the Jacobi–Piñeiro [11, 16] and the hypergeometric [3, 12] families. In the final section, the Darboux and Christoffel transformations [4] are connected with the PBF factorization, the coefficients \(\alpha \) in the PBF are reconstructed in terms of the values of the type II and I polynomials at 0, see Theorem 2 and the Darboux transformations are discussed at the light of the spectral Christoffel perturbations [1], see Theorem 3.
1.1 Preliminary material
For multiple orthogonal polynomials see [1, 11, 14].
Let us denote by \( T^{[N]}=T[\{0,1,\ldots ,N\}]\in \mathbb {R}^{(N+1)\times (N+1)}\) the \((N+1)\)-th leading principal submatrix of the banded Hessenberg matrix T:

Definition 1
(Recursion polynomials of type II) The type II recursion vector of polynomials

is determined by the following eigenvalue equation
Uniqueness is ensured by taking as initial condition \(B_0=1\). We call the components \(B_n\) type II recursion polynomials. One obtains that \(B_1=x- c_0\), \(B_2=(x-c_0)(x-c_1)-b_1\), and higher degree recursion polynomials are constructed by means of the 4-term recurrence relation
Definition 2
(Recursion polynomials of type I) Dual to the polynomial vector B(x) we consider the two following polynomial dual vectors

that are left eigenvectors of the semi-infinite matrix J, i.e.,
The initial conditions, that determine these polynomials uniquely, are taken as
with \(\nu \ne 0\) being an arbitrary constant. Then, from the first relation
we get \(A^{(1)}_2=\frac{x}{a_2}-\frac{c_0+b_1\nu }{a_2}\) and \(A^{(2)}_2=-\frac{b_1}{a_2}\). The other polynomials in these sequences are determined by the following four term recursion relation
For example, one finds
Second kind polynomials are also relevant in the theory of multiple orthogonality.
Definition 3
(Recursion polynomials of type II of the second kind) Let us consider the recursion relation (6) in the form
set \(b_0=a_0=a_1=-1\) and \(n\in \mathbb {N}_0\). The values, initial conditions, for \(B_{-2}, B_{-1}, B_0\) are required to get the values \(B_n\) for \(n\in \mathbb {N}\). The polynomials of type II correspond to the choice
Two sequences of polynomials of type II of the second kind \(\big \{B_n^{(1)}\big \}_{n=0}^\infty \) and \(\big \{B_n^{(2)}\big \}_{n=0}^\infty \) are defined by the following initial conditions
Proposition 1
(Determinantal expressions)
-
(i)
For the recursion polynomials we have the determinantal expressions
 (12)
(12)Hence, they are the characteristic polynomials of the leading principal submatrices \(T^{[N]}\).
-
(ii)
For the recursion polynomials of type II of the second kind, \(B^{(1)}_{N+1} \) and \(B^{(2)}_{N+1} \), we have the following adjugate and determinantal expressions

Finite truncations of this matrices having this positive bidiagonal factorization are oscillatory matrices. In fact, we will be dealing in this paper with totally non negative matrices and oscillatory matrices and, consequently, we require of some definitions and properties that we are about to present succinctly.
Further truncations are, for \(k \in \{0,1,..., N\}\),


notice that \(T^{[N]}=T^{[N,0]}\). Corresponding characteristic polynomials are:

Totally nonnegative (TN) matrices are those with all their minors nonnegative [8, 9], and the set of nonsingular TN matrices is denoted by InTN. Oscillatory matrices [9] are totally nonnegative, irreducible [10] and nonsingular. Notice that the set of oscillatory matrices is denoted by IITN (irreducible invertible totally nonnegative) in [8]. An oscillatory matrix A is equivalently defined as a totally nonnegative matrix A such that for some n we have that \(A^n\) is totally positive (all minors are positive). From Cauchy–Binet Theorem one can deduce the invariance of these sets of matrices under the usual matrix product. Thus, following [8, Theorem 1.1.2] the product of matrices in InTN is again InTN (similar statements hold for TN or oscillatory matrices). We have the important result:
Theorem 1
(Gantmacher–Krein Criterion).[9, Chapter 2, Theorem 10]. A totally non negative matrix A is oscillatory if and only if it is nonsingular and the elements at the first subdiagonal and first superdiagonal are positive.
The Gauss–Borel factorization of the matrix \(T^{[N]}\) in (4) is the following factorization
with banded triangular matrices given by

Proposition 2
The Gauss–Borel factorization exists if and only if all leading principal minors \(\delta ^{[N]}\) of \(T^{[N]}\) are not zero.
For \(n\in \mathbb {N}\), the following expressions for the coefficients hold

where \(\delta ^{[-1]}=1\) and \(a_1=0\), and we have the following recurrence relation for the determinants
is satisfied.
For oscillatory matrices the Gauss–Borel factorization exits and both triangular factors belong to InTN. See [13] for a modern account of the role of Gauss–Borel factorization problem in the realm of standard and non standard orthogonality.
2 Hypergeometric and Jacobi–Piñeiro examples
Now we discuss two cases of tetradiagonal Hessenberg matrices that appear as recurrence matrices of two families of multiple orthogonal polynomials. For each of them we consider bidiagonal factorizations and its positivity.
2.1 Hypergeometric multiple orthogonal polynomials
In [12] a new set of multiple hypergeometric polynomials were introduced by Lima and Loureiro. The corresponding recursion matrix \(T_{LL}\) was used in [7] to construct stochastic matrices and associated Markov chains beyond birth and death. For the hypergeometric case the \(T_{LL}=L_1L_2U\) bidiagonal factorization is provided in [12, Equations 107-110], that ensures the regular oscillatory character of the matrix \(T_{LL}\) for this hypergeometric case. Notice the correspondence between Lima–Loureiro’s \(\lambda _n\) and our \(\alpha _n\) is \( \lambda _{3n+2}\rightarrow \alpha _{3n+1}\), \(\lambda _{3n+1}\rightarrow \alpha _{3n}\) and \(\lambda _{3n}\rightarrow \alpha _{3n-1}\). These coefficients were gotten in [12] from [15, Theorem 14.5] as the coefficients of a branched-continued-fraction representation for \(_{3}F_{2}\). For more on this see the recent paper [17]. This sequence is TP, so that \(T_{LL}\) is a regular oscillatory banded Hessenberg matrix.
2.2 Jacobi–Piñeiro multiple orthogonal polynomials
Jacobi–Piñeiro multiple orthogonal polynomials, associated with weights \(w_1=x^{\alpha }(1-x)^\gamma , w_2=x^{\beta }(1-x)^\gamma \) with support on [0, 1] \(\alpha ,\beta ,\gamma >-1\), \(\alpha -\beta \not \in \mathbb {Z}\), is a well study case. This system is an AT system and the corresponding orthogonal polynomials and linear forms interlace its zeros, see [11], even though, as we will discuss now, the recursion matrix \(T_{JP}\) is not oscillatory. The corresponding monic recursion matrix \(T_{JP}\) was considered in [7, Section 4.3] and we show that this recursion matrix was a positive matrix whenever the parameters \(\alpha ,\beta \) lay in the strip given by \(|\alpha -\beta |<1\).
Lemma 1
(Jacobi–Piñeiro’s recursion matrix bidiagonal factorization). The Jacobi–Piñeiro’s recursion matrix has bidiagonal factorizations as in Eq. (2) with at least the following two set of parameters:
here \(n\in \mathbb {N}_0\).
Proof
We have \( \alpha _1 = c_0\) and  and \(\alpha _4\) are gotten from
and \(\alpha _4\) are gotten from  and
and  . Then,
. Then,  ,
,  , \(\alpha _{3(n-1)+1}\), \(n = 2,3,\ldots \), are determined recursively according to
, \(\alpha _{3(n-1)+1}\), \(n = 2,3,\ldots \), are determined recursively according to  ,
,  and \( m_n + \alpha _{3n+1} = c_n\) (from the first relation we get
and \( m_n + \alpha _{3n+1} = c_n\) (from the first relation we get  , from the second \(m_n\) and from the third \(\alpha _{3(n-1)+1}\)). Now, these expressions for
, from the second \(m_n\) and from the third \(\alpha _{3(n-1)+1}\)). Now, these expressions for  ’s and
’s and  ’s lead to the remaining \(\alpha \)’s. Indeed, we have
’s lead to the remaining \(\alpha \)’s. Indeed, we have  and
and  (we get \(\alpha _3\) and \(\alpha _5\), respectively) and then we apply the recursion, \(n \in \mathbb {N}\),
(we get \(\alpha _3\) and \(\alpha _5\), respectively) and then we apply the recursion, \(n \in \mathbb {N}\),  ,
,  (in each iteration we obtain \(\alpha _{3(n+1)}\) and \(\alpha _{3(n+1)+2}\), respectively). \(\square \)
(in each iteration we obtain \(\alpha _{3(n+1)}\) and \(\alpha _{3(n+1)+2}\), respectively). \(\square \)
Remark 1
The bidiagonal factorization \(\{{\tilde{\alpha }}_n\}_{n=1}^\infty \) was found in [2, Section 8.1], that is why we refer to it as the Aptekarev-Kalyagin-Van Iseghem (AKV) bidiagonal factorization.
For \(n\in \mathbb {N}_0\), given these two bidiagonal factorizations, the entries of the corresponding lower unitriangular factor \(L=L_1L_2={\tilde{L}}_1{\tilde{L}}_2\) of the lower factor L in the Gauss–Borel factorization of the Jacobi–Piñeiro’s Hessenberg transition matrix, can be expressed in the following two manners

To better understand the dependence on the set of Jacobi–Piñeiro’s parameters \((\alpha ,\beta )\) we define some regions in the plane. Let us denote by \({\mathscr {R}}{:=}\{(\alpha ,\beta )\in \mathbb {R}^2, \alpha ,\beta >-1, \alpha -\beta \not \in \mathbb {Z}\}\), that we call the natural region –where the orthogonality is well defined, and divide it in the following four regions:
We show these regions in the following figure

Lemma 2
-
(i)
For the sequence \(\{\alpha _n\}_{n\in \mathbb {N}}\) of the first bidiagonal factorization, we have
-
(a)
In the region \({\mathscr {R}}\) the sequence in TN but for \(\alpha _5\) that is negative in \({\mathscr {R}}_4\) and \(\alpha _6\) that is negative in \({\mathscr {R}}_1\).
-
(b)
Is a TN sequence in the strip \({\mathscr {R}}_2\cup {\mathscr {R}}_3\). Excluding \(\alpha _2=0\), the sequence is TP.
-
(a)
-
(ii)
For the AKV sequence \(\{{\tilde{\alpha }}_n\}_{n\in \mathbb {N}}\), we have
-
(a)
In the region \({\mathscr {R}}\) the sequence in TP but for \({\tilde{\alpha }}_2\) that is negative in \({\mathscr {R}}_1\cup {\mathscr {R}}_2\), \({\tilde{\alpha }}_8\) that is negative in \({\mathscr {R}}_1\) and \({\tilde{\alpha }}_3\) that is negative in \({\mathscr {R}}_4\).
-
(b)
Is a TP sequence in the half strip \({\mathscr {R}}_3\).
-
(a)
Proof
For the first set of bidiagonal parameters \(\{\alpha _n\}_{n\in \mathbb {N}}\), we check that all are positive in \({\mathscr {R}}\), but for \(\alpha _2=0\) and \(\alpha _5,\alpha _6\). From direct inspection we get that \(\alpha _5<0\) when \(1+\alpha -\beta <0\), i.e. in region \({\mathscr {R}}_4\) and \(\alpha _6<0\) when \(1-\alpha +\beta <0\), i.e. in region \({\mathscr {R}}_1\). Hence, the sequence \(\{\alpha _n\}_{n=1}^\infty \) is a TN sequence, TP but for \(\alpha _2=0\), in region \({\mathscr {R}}_2\cup {\mathscr {R}}_3\), is TN in \({\mathscr {R}}\) but for \(\alpha _5\) in \({\mathscr {R}}_4\) and TN in \({\mathscr {R}}\) but for \(\alpha _6\) in \({\mathscr {R}}_1\). For theAKV parameters \(\{{\tilde{\alpha }}_n\}_{n\in \mathbb {N}}\), all are positive in \({\mathscr {R}}\), but for \({\tilde{\alpha }}_2,{\tilde{\alpha }}_8\) and \({\tilde{\alpha }}_3\). The entry \({\tilde{\alpha }}_2<0\) when \(\alpha >\beta \), that is in \({\mathscr {R}}_1\cup {\mathscr {R}}_2\), \({\tilde{\alpha }}_8<0\) when \(1-\alpha +\beta <0\) i.e. in \({\mathscr {R}}_1\) and \({\tilde{\alpha }}_3\) when \(1+\alpha -\beta <0\), i.e. in \({\mathscr {R}}_4\). \(\square \)
Lemma 3
For the two first subdiagonals of the lower triangular matrix L in the Gauss–Borel factorization of the Jacobi–Piñeiro’s Hessenberg recursion matrix \(T_{JP}\) we have
-
(i)
The sequence
 is TP in the definition region \({\mathscr {R}}\).
is TP in the definition region \({\mathscr {R}}\). -
(ii)
The sequence
 is TP but for
is TP but for  (
( ), that is negative in \({\mathscr {R}}_4\) (\({\mathscr {R}}_1\)).
), that is negative in \({\mathscr {R}}_4\) (\({\mathscr {R}}_1\)).
Proof
From (19) and the first bidiagonal factorization we get that the lower triangular L has all its entries in the two first subdiagonals TP but for  (
( ), that is negative in \({\mathscr {R}}_4\) (\({\mathscr {R}}_1\)), and maybe
), that is negative in \({\mathscr {R}}_4\) (\({\mathscr {R}}_1\)), and maybe  . Looking now at the AKV factorization we see that
. Looking now at the AKV factorization we see that  . \(\square \)
. \(\square \)
Proposition 3
The Jacobi–Piñeiro’s recursion matrix satisfies:
-
(i)
Is oscillatory if and only if the parameters \((\alpha ,\beta )\) belong to the strip \({\mathscr {R}}_2\cup {\mathscr {R}}_3\).
-
(ii)
Admits a positive bidiagonal factorization at least if the parameters belong to the lower half strip \({\mathscr {R}}_3\).
-
(iii)
The retraction of the complementary matrix \(T_{JP}^{(4)}\) ( \(T_{JP}^{(5)}\)), described in [6, Theorem 11] is oscillatory in the region \({\mathscr {R}}_2\cup {\mathscr {R}}_3\cup {\mathscr {R}}_4\) (\({\mathscr {R}}\)).
Proof
-
(i)
It follows from Lemma 2.
-
(ii)
The AKV bidiagonal factorization sequence is TP in \({\mathscr {R}}_3\).
-
(iii)
We use the Gauss–Borel factorization of these retractions described in [6, Theorem 11], that we know have a bidiagonal factorization with TP sequences.
\(\square \)
Remark 2
From the previous discussion of the Jacobi–Piñeiro’s recursion matrix it becomes clear that demanding the matrix to have a positive bidiagonal factorization is sufficient but not necessary to have spectral measures. In the natural region \({\mathscr {R}}\) the Jacobi–Piñeiro’s weights exist, are positive with support on [0, 1]. However, we know that it is an oscillatory matrix only in the strip \({\mathscr {R}}_2\cup {\mathscr {R}}_3\). The associated matrix that is regular oscillatory in the natural region \({\mathscr {R}}\) is the retracted complementary matrix \(T_{JP}^{(5)}\). This observation leads to the question: Is it enough to have a spectral Favard theorem and positive measures that a retracted complementary matrix of the banded Hessenberg matrix is oscillatory?
3 Applications to Darboux transformations
3.1 Darboux transformations of oscillatory banded Hessenberg matrices
We now show how our construction connects with those of the seminal paper [2] by Aptekarev, Kalyagin and Van Iseghem on genetic sums, vector convergents, Hermite–Padé approximants and and Stieltjes problems, and with the Darboux–Christoffel transformations discussed in [4]. We identify the Darboux transformations of the oscillatory banded Hessenberg matrices with Christoffel transformations of the spectral measures. Recall that \(\nu \) is the initial condition given in Definition 2.
Definition 4
(Darboux transformed Hessenberg matrices). Given an oscillatory banded lower Hessenberg matrix T and its bidiagonal factorization as in (2), we consider the semi-infinite matrices
We will refer to these matrices as the first and second Darboux transformations of the banded Hessenberg matrix T.
Remark 3
These auxiliary matrices \({\hat{T}}^{[N]}\) are not the m-th leading principal submatrix of the matrix \({\hat{T}}{:=}L_2UL_1\). The difference is in the last diagonal entry. The entries of \({\hat{T}}\) are
All the entries of the \((N+1)\)-th leading principal submatrix of \(\,{\hat{T}}\) coincide with those of \({\hat{T}}^{[N]}\) but for the last diagonal entry, as \(({\hat{T}}^{[N]})_{N+1,N+1}=\alpha _{3N}+\alpha _{3N+1}\) while \({\hat{c}}_{N+1}=\alpha _{3N}+\alpha _{3N+1}+\alpha _{3N+2}\).
Remark 4
-
i)
From definition it is immediately checked that both Darboux transformed Hessenberg matrices has the same banded structure as T.
-
ii)
For coefficients of the second Darboux transform \(\hat{{\hat{T}}} \) we have
$$\begin{aligned} \left\{ \begin{aligned} \hat{{\hat{c}}}_n&= \alpha _{3n+3} + \alpha _{3n+2} + \alpha _{3n+1}, \\ \hat{{\hat{b}}}_n&= \alpha _{3n+1} \alpha _{3n}+ \alpha _{3n+2} \alpha _{3n}+ \alpha _{3n+1}\alpha _{3n-1} , \\ \hat{{\hat{a}}}_n&=\alpha _{3n+1}\alpha _{3n-1} \alpha _{3n-3}. \end{aligned}\right. \end{aligned}$$ -
iii)
If \(\,T\) has a positive bidiagonal factorization, so that we can take \(\alpha _2>0\), then the Darboux transforms \({\hat{T}}, \hat{{\hat{T}}}\) are oscillatory.
Associated with these Hessenberg matrices we introduce the vectors of polynomials
Notice that \({\hat{B}}_n\) and \( \hat{{\hat{B}}}_n\) are monic with \(\deg {\hat{B}}_n= \deg \hat{{\hat{B}}}_n= n+1\).
Lemma 4
We have
Proof
Equations (21) imply \( L_1 {\hat{B}}=L_1L_2 U B=TB=xB\). \(\square \)
Proposition 4
The eigenvalue properties \( {\hat{T}} {\hat{B}}=x {\hat{B}}\) and \(\hat{{\hat{T}}}\hat{{\hat{B}}}= x\hat{{\hat{B}}}\) are satisfied.
Proof
Equations (21) and (22) lead by direct computation to
\(\square \)
Let us denote by if \({\tilde{T}}^{[n]}\) and \(\tilde{{\tilde{T}}}^{[n]}\) the \((n+1)\)-th leading principal submatrices of \({\hat{T}}\) and \(\hat{{\hat{T}}}\).
Lemma 5
The polynomials \({\hat{B}}_n\) and \(\hat{{\hat{B}}}_n\) can be expressed as \( \hat{B}_n=x{\tilde{B}}_n\) and \( \hat{{\hat{B}}}_n=x \tilde{{\tilde{B}}}_n\), with the monic polynomials \({\tilde{B}}_n, \tilde{{\tilde{B}}}_n\) having degree n.
Proof
One has that \(\hat{{\hat{B}}}_0={\hat{B}}_0=\alpha _1+B_1=\alpha _1+x-c_0=x\). Then, as the sequences of polynomials are found by the recurrence determined by the banded Hessenberg matrices \({\hat{T}}\) and \(\hat{{\hat{T}}}\), respectively, we find that the desired result. \(\square \)
We call these polynomials \({\tilde{B}}_n\) and \( \tilde{{\tilde{B}}}_n\) as Darboux transformed polynomials of type II.
Proposition 5
The entries of the Darboux transformed polynomial sequences of type II
read
were we take \(\alpha _k=0\) for \(k\in \mathbb {Z}_-\). The following determinantal expressions hold
Proof
Equation (24) appears as the entries of the defining equations. The determinantal expressions follow from the fact that its expansions along the last row satisfy the recursion relations with adequate initial conditions. \(\square \)
Following definitions given in (13) and (15) we consider similar objects in this context. That is, we denote by \({\tilde{T}}^{[n,k]}\) (\(\tilde{{\tilde{T}}}^{[n,k]}\)) the matrix obtained from \({\tilde{T}}^{[n]}\) (\(\tilde{{\tilde{T}}}^{[n]}\)) by erasing the first k rows and columns. The corresponding characteristic polynomials are
These polynomials \({\tilde{B}}_{n}^{[k]}\) (\(\tilde{{\tilde{B}}}_n^{[k]}\)) satisfy the same recursion relations, determined by \({\tilde{T}}\) (\(\tilde{{\tilde{T}}}\)) as do \({\tilde{B}}_{n}\) (\(\tilde{{\tilde{B}}}_n\)) but with different initial conditions. Following ii) in Proposition 1 we have the transformed recursion polynomials of type II
Then we consider the following vectors of polynomials
Proposition 6
(Vector Convergents) These recursion polynomials correspond to the vector convergent \(y^1_n=(A_{n,0},A_{n,1},A_{n,2})\) discussed in [2] as follows
Proof
It follows from the fact that they satisfy the recursion relation [2, Equation (23)] and adequate initial conditions. \(\square \)
Then, following this dictionary the important [2, Lemma 5] states for \(x\geqslant 0\) that

Remark 5
Using these facts, Aptekarev, Kalyagin and Van Iseghem in [2, Lemmata 6 & 7] deduce the degree of polynomials, simplicity of zeros and interlacing properties of \(B_n\) with \(B_{n-1}\), \(B_n^{(1)}\) and \(B^{(2)}_n\). Notice that we derive the same result by just using the spectral properties of regular oscillatory matrices.
For recursion polynomials of type I, we introduce the following polynomials \( {\hat{A}}^{(2)}{:=}A^{(1)}L_1\), \({\hat{A}}^{(1)}{:=}A^{(2)}L_1\), \(\hat{ {\hat{A}}}^{(1)}{:=}A^{(1)}L_1L_2\) and \(\hat{{\hat{A}}}^{(2)}{:=}A^{(2)}L_1L_2\).
Proposition 7
Vectors \( {\hat{A}}^{(1)}\), \( {\hat{A}}^{(2)}\) are left eigenvectors of \({\hat{T}}\) and \(\hat{ {\hat{A}}}^{(1)}\), \(\hat{ {\hat{A}}}^{(2)}\) are left eigenvectors of \(\hat{{\hat{T}}}\).
Proof
A direct computation shows that \( {\hat{A}}^{(2)}{\hat{T}}=A^{(1)}L_1 L_2UL_1= A^{(1)}T L_1=xA^{(1)}L_1= x {\hat{A}}^{(2)}\). The other cases are proven similarly. \(\square \)
Lemma 6
Let us assume that \(1+\alpha _{2}\nu =0\). Then, \({\hat{A}}^{(2)}_0=0\) and \({\hat{A}}^{(2)}_1=\frac{1}{\alpha _3\alpha _1}x\).
Proof
Let us consider the vector \( {\hat{A}}^{(2)}=A^{(1)} L_1\) with components \( {\hat{A}}^{(2)}_n=A^{(1)}_n+\alpha _{3n+2}A^{(1)}_{n+1}\), \(n\in \mathbb {N}_0\). The first two entries are
Here we have used Definition 2 and \(c_0=\alpha _1\), \(b_1=(\alpha _3+\alpha _2)\alpha _1\) and \(a_2=\alpha _5\alpha _3\alpha _1\). Then, as \(1+\alpha _{2}\nu =0\), we find the stated result. \(\square \)
Proposition 8
If \( 1+\nu \alpha _2=0\), we can write \({\hat{A}}^{(2)}_n= x {\tilde{A}}^{(2)}_n\) and \(\hat{{\hat{A}}}^{(1)}_n= x \tilde{{\tilde{A}}}^{(1)}_n\), for some polynomials \( {\tilde{A}}^{(2)}_n,\tilde{{\tilde{A}}}^{(1)}_n\).
Proof
The recursion relation \({\hat{c}}_0 {\hat{A}}^{(2)}_0+{\hat{b}}_1{\hat{A}}^{(2)}_1+{\hat{a}}_2 {\hat{A}}^{(2)}_2=x{\hat{A}}^{(2)}_0\) and Lemma 6 gives \({\hat{A}}^{(2)}_2=-\frac{{\hat{b}}_1}{{\hat{a}}_2 \alpha _3\alpha _1}x\). Hence, induction leads to the conclusion that \({\hat{A}}^{(2)}_n=x{\tilde{A}}^{(2)}_n\), for some polynomial \({\tilde{A}}^{(2)}_n\). \(\square \)
Lemma 7
We have \(\hat{\hat{A}}^{(2)}_0=0\) and \(\hat{\hat{A}}^{(2)}_1=\frac{1}{\alpha _4}x\).
Proof
Let us consider the vector \( {\hat{A}}^{(1)}=A^{(2)} L_1\) with components \( {\hat{A}}^{(1)}_n=A^{(2)}_n+\alpha _{3n+2}A^{(2)}_{n+1}\), \(n\in \mathbb {N}_0\). The first three entries are
Then, we consider \( \hat{ \hat{A}}^{(2)}=\hat{A}^{(1)} L_2\) with components \(\hat{{\hat{A}}}^{(2)}_n={\hat{A}}^{(1)}_n+\alpha _{3n+3}{\hat{A}}^{(1)}_{n+1}\), \(n\in \mathbb {N}_0\). The first two components being
and the result follows. \(\square \)
Proposition 9
There are polynomials \(\tilde{{\tilde{A}}}^{(2)}_n \) such that \(\hat{{\hat{A}}}^{(2)}_n =x\tilde{{\tilde{A}}}^{(2)}_n \).
Proof
It holds for the two first entries \(\hat{{\hat{A}}}^{(2)}_0\) and \(\hat{{\hat{A}}}^{(2)}_1\). Hence, from the recursion relation \(\hat{{\hat{A}}}^{(2)}\hat{{\hat{T}}}= x\hat{{\hat{A}}}^{(2)}\) we get that it holds for any natural number n. \(\square \)
We name the polynomials \({\hat{A}}^{(1)}_n\), \(\tilde{{\tilde{A}}}^{(1)}_n \), \({{\tilde{A}}}^{(2)}_n\) and \(\tilde{{\tilde{A}}}^{(2)}_n \) as Darboux transformed polynomials of type I.
Proposition 10
Let us assume that \(1+\nu \alpha _2=0\). The entries of the Darboux transformed polynomials sequences of type I
are given by
3.2 Spectral representation and Christoffel transformations
We identify the entries in the bidiagonal factorization (2) with simple rational expressions in terms of the recursion polynomials valuated at the origin.
Theorem 2
(Parametrization of the bidiagonal factorization) The \(\alpha \)’s in the bidiagonal factorization (2) can be expressed in terms of the recursion polynomials evaluated at \(x=0\) as follows:
The relations

are satisfied as well.
Proof
Equation (21) and the fact that \({\hat{B}}(0)=0\) gives that \(UB(0)=0\). Hence, we get \(\alpha _{3n+1}B_n(0)+B_{n+1}(0)=0\) and (25) follow. Now, as \( {\hat{A}}^{(1)}= A^{(1)}L_1\) and \({\hat{A}}^{(1)}(0)=0\) implies \(A^{(1)}(0)L_1=0\). Hence, \(A_{n}^{(1)}(0)+A_{n+1}^{(1)}(0)\alpha _{3n+2}=0\) and we find (26). To prove (28) we observe that
so that

and Eq. (28) follows.
This equation implies component-wise the following relations
Thus, we get Eq. (27). \(\square \)
With the previous identification we are ready to show the complete correspondence of the described Darboux transformations of the oscillatory banded Hessenberg matrix T with Christoffel perturbations of the corresponding pair of positive Lebesgue–Stieltjes measures \(({\text {d}}\psi _1,{\text {d}}\psi _2)\).
Theorem 3
(Darboux vs Christoffel transformations) For \(\alpha _2=-\frac{1}{\nu }>0\), the multiple orthogonal polynomial sequences \(\big \{{ {\tilde{B}}}_n,{\hat{A}}^{(1)}_n,{\tilde{A}}^{(2)}_n\big \}_{n=0}^\infty \) and \(\big \{\tilde{ {\tilde{B}}}_n,\tilde{ {\tilde{A}}}^{(1)}_n, \tilde{ {\tilde{A}}}^{(2)}_n\big \}_{n=0}^\infty \) correspond to the Christoffel transformations given in [4, Theorems 4 & 6] of the multiple orthogonal polynomial sequence \(\{ B_n, A^{(1)}_n, A^{(2)}_n\}_{n=0}^\infty \). If the original couple of Lebesgue–Stieltjes measures is \(({\text {d}}\psi _1,{\text {d}}\psi _2)\), then the corresponding transformed pairs of measures are \(({\text {d}}\psi _2,x{\text {d}}\psi _1)\) and \((x{\text {d}}\psi _1,x{\text {d}}\psi _2)\), respectively.
Proof
Recalling (26), that \(c_n=\alpha _{3n+1}+\alpha _{3n}+\alpha _{3n-1}\) and that \(a_{n+1}=\alpha _{3n+2}\alpha _{3n}\alpha _{3n-2}\) we write
Then, using Theorem 2 and the first equation in (24) we get
These three equations are the Christoffel formulas in [4, Theorem 4] for the permuting Christoffel transformation \(({\text {d}}\psi _1,{\text {d}}\psi _2)\rightarrow ({\text {d}}\psi _2,x{\text {d}}\psi _1)\). Also, using again Theorem 2, the second equation in (24) and (28) we get

These three equations are the Christoffel formulas in [4, Theorem 6] for the Christoffel transformation \(({\text {d}}\psi _1,{\text {d}}\psi _2)\rightarrow (x{\text {d}}\psi _1,x{\text {d}}\psi _2)\). \(\square \)
4 Conclusions and outlook
In this paper we have discussed examples of structured tetradiagonal matrices of oscillatory type connected to two families of multiple orthogonal polynomials and the possibility of having a positive bidiagonal factorization. Moreover, it has been shown the relation of Darboux transformations of this matrix and Christoffel formulas for Christoffel perturbations of corresponding multiple orthogonal polynomials.
Other open questions are:
-
(i)
What happens when the banded recursion matrix has several superdiagonals as well as subdiagonals? What about the corresponding Darboux transformations?
-
(ii)
Chebyshev (T) systems appear in [9] in relation with influence kernels and oscillatory matrices. Is there any connection between the AT property and the oscillation of the matrix or some submatrix of it?
Availability of data and materials
This paper has no additional data or materials.
References
Álvarez-Fernández, C., Fidalgo, U., Mañas, M.: Multiple orthogonal polynomials of mixed type: Gauss-Borel factorization and the multi-component 2D Toda hierarchy. Adv. Math. 227, 1451–1525 (2011)
Aptekarev, A., Kaliaguine, V., Van Iseghem, J.: The genetic sums’ representation for the moments of a system of Stieltjes functions and its application. Constr. Approx. 16, 487–524 (2000)
Branquinho, A., Fernández-Díaz, J.E., Foulquié-Moreno, A., Mañas, M.: Hypergeometric multiple orthogonal polynomials and random walks. arXiv:2107.00770
Branquinho, A., Foulquié-Moreno, A., Mañas, M.: Multiple orthogonal polynomials: Pearson equations and Christoffel formulas. Anal. Math. Phys. 12, 129 (2022)
Branquinho, A., Foulquié-Moreno, A., Mañas, M.: Oscillatory banded Hessenberg matrices, multiple orthogonal polynomials and random walks. arXiv:2203.13578
Branquinho, A., Foulquié-Moreno, A., Mañas, M.: Positive bidiagonal factorization of Tetradiagonal Hessenberg matrices. arXiv:2210.10728
Branquinho, A., Foulquié-Moreno, A., Mañas, M., Carlos, Á.-F., Fernández-Díaz, J.E.: Multiple orthogonal polynomials and random walks. arXiv:2103.13715
Fallat, S.M., Johnson, C.R.: Totally Nonnegative Matrices. Princeton Series in Applied Mathematics. Princeton University Press, Princeton (2011)
Gantmacher, F.P., Krein, M.G.: Oscillation and Kernels and Small Vibrations of Mechanical Systems, revised 2nd edn, AMS Chelsea Publishing, American Mathematical Society, Providence, Rhode Island
Horn, R.A., Johnson, C.R.: Matrix Analysis, Corrected reprint, 2nd edn. Cambridge University Press, Cambridge (2018)
Ismail, M.E.H.: Classical and Quantum Orthogonal Polynomails in One Variable, Encyclopedia of Mathematics and its Applications, vol. 98. Cambridge University Press, Cambridge (2009)
Lima, H., Loureiro, A.: Multiple orthogonal polynomials with respect to Gauss’ hypergeometric function. Stud. Appl. Math. 148, 154–185 (2022)
Mañas, M.: Revisiting biorthogonal polynomials. An LU factorization discussion in orthogonal polynomials: current trends and applications. In: Huertas, E., Marcellán, F. (eds.) SEMA SIMAI Springer Series, vol. 22, pp. 273–308. Springer, Berlin (2021)
Nikishin, E.M., Sorokin, V.N.: Rational Approximations and Orthogonality. Translations of Mathematical Monographs, vol. 92. American Mathematical Society, Providence (1991)
Pétréolle, M., Sokal, A.D., Zu, B.-X.: Lattice paths and branched continued fractions: an infinite sequence of generalizations of the Stieltjes–Rogers and Thron–Rogers polynomials, with coefficient wise Hankel-total positivity. To appear in Memoirs of the American Mathematical Society (2023). arXiv:1807.03271v2 [math.CO] (2021)
Piñeiro, L. R.: On simultaneous approximations for a collection of Markov functions, Vestnik Moskovskogo Universiteta, Seriya I (2) (1987) 67–70 (in Russian); translated in Moscow University Mathematical Bulletin 42 (2) (1987) 52–55
Zhu, B.-X.: Coefficientwise Hankel-total positivity of row-generating polynomials for the m-Jacobi-Rogers triangle. arXiv:2202.03793v1 [math.CO] (2022)
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. Amílcar Branquinho thanks Centre for Mathematics of the University of Coimbra–UIDB/00324/2020 (funded by the Portuguese Government through FCT/MCTES) and co-funded by the European Regional Development Fund through the Partnership Agreement PT2020
Ana Foulquié acknowledges Center for Research & Development in Mathematics and Applications, supported through the Portuguese Foundation for Science and Technology (FCT– Fundação para a Ciência e a Tecnologia), references UIDB/ 04106/2020 and UIDP/04106/2020. Manuel Mañas: Thanks financial support from the Spanish “Agencia Estatal de Investigación” research project [PGC2018-096504-B-C33], Ortogonalidad y Aproximación: Teoría y Aplicaciones en Física Matemática and [PID2021- 122154NB-I00], Ortogonalidad y Aproximación con Aplicaciones en Machine Learning y Teoría de la Probabilidad.
Author information
Authors and Affiliations
Contributions
All the authors have contribute equally.
Corresponding author
Ethics declarations
Conflict of interest
The authors hereby declare to have no conflict of interest.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Branquinho, A., Foulquié-Moreno, A. & Mañas, M. Bidiagonal factorization of tetradiagonal matrices and Darboux transformations. Anal.Math.Phys. 13, 42 (2023). https://doi.org/10.1007/s13324-023-00801-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-023-00801-1
Keywords
- Tetradiagonal Hessenberg matrices
- Oscillatory matrices
- Totally nonnegative matrices
- Multiple orthogonal polynomials
- Favard spectral representation
- Darboux transformations
- Christoffel formulas



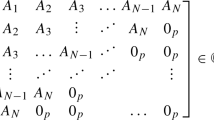


 is TP in the definition region
is TP in the definition region  is TP but for
is TP but for 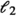 (
( ), that is negative in
), that is negative in