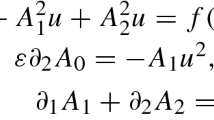Abstract
In this paper we investigate the following nonlinear Chern–Simons–Schrödinger system
where \(\lambda >0\), the Chern–Simons term \(h(s)=\int _0^s\frac{r}{2}u^2(r)dr=\frac{1}{4\pi }\int _{B_s}u^2(x)dx\) and V(|x|) is an external potential. Under some suitable conditions on the external potential, we prove the existence of a positive ground state solution for \(p\in (6,+\infty )\) via the Pohožaev–Nehari manifold method and the global compactness lemma. The novelty of this works with respect to some recent results is that we establish a key lemma which is analogous to the Br\(\acute{e}\)zis–Lieb convergence lemma. Furthermore, we also prove concentration of these ground state solutions. As its supplementary results, we give the several nonexistence results of nontrivial solutions.
Similar content being viewed by others
References
Brézis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88, 486–490 (1983)
Byeon, J., Huh, H., Seok, J.: Standing waves of nonlinear Schrödinger equations with the gauge field. J. Funct. Anal. 263, 1575–1608 (2012)
Byeon, J., Huh, H., Seok, J.: On standing waves with a vortex point of order N for the nonlinear Chern–Simons–Schrödinger equations. J. Differ. Equ. (2016). https://doi.org/10.1016/j.jde.2016.04.004
Chen, Z., Tang, X., Zhang, J.: Sign-changing multi-bump solutions for the Chern–Simons–Schrödinger equations in \({\mathbb{R}}^2\). Adv. Nonlinear Anal. 9, 1066–1091 (2020)
Cunha, P., d’Avenia, P., Pomponio, A., Siciliano, G.: A multiplicity result for Chern–Simons–Schrödinger equation with a general nonlinearity. Nonlinear Differ. Equ. Appl. 22, 1831–1850 (2015)
DAvenia, P., Pomponio, A., Watanabe, T.: Standing waves of modified Schrödinger equations coupled with the Chern–Simons gauge theory. Proc. A Roy. Soc. Edin. 150, 1915–1936 (2020)
Huh, H.: Blow-up solutions of the Chern–Simons–Schrödinger equations. Nonlinearity 22, 967–974 (2009)
Huh, H.: Standing waves of the Schrödinger equation coupled with the Chern–Simons gauge field. J. Math. Phys. 53, 063702 (2012)
Jackiw, R., Pi, S.Y.: Soliton solutions to the gauged nonlinear Schrödinger equations. Phys. Rev. Lett. 64, 2969–2972 (1990)
Jackiw, R., Pi, S.Y.: Classical and quantal nonrelativistic Chern–Simons theory. Phys. Rev. D. 42, 3500–3513 (1990)
Jeanjean, L.: On the existence of bounded Palais–Smale sequence and application to a Landesman–Lazer type problem set on \(\text{ R}^3\). Proc. Roy. Soc. Edinb. Sect. A 129, 787–809 (1999)
Li, G., Ye, H.: Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in \(\text{ R}^3\). J. Differ. Equ. 257, 566–600 (2014)
Li, Y., Li, X., Ma, S.: Groundstates for Kirchhoff-Type equations with Hartree-type nonlinearities. RM 74, 1–26 (2019)
Lions, P.: The concentration compactness principle in the calculus of variations: the locally compact case. Part 1. Ann. Inst. H. Poincar Anal. Non Linéaire 1, 109–145 (1984)
Liu, B., Smith, P., Tataru, D.: Local wellposedness of Chern-Simons-Schrödinger. Int. Math. Res. Notices. https://doi.org/10.1093/imrn/rnt161
Liu, Z., Ouyang, Z., Zhang, J.: Existence and multiplicity of sign-changing standing waves for a gauged nonlinear Schrodinger equation in \({\mathbb{R}}^2\). Nonlinearity 32, 3082–3111 (2019)
Luo, X.: Multiple normalized solutions for a planar gauged nonlinear Schödinger equation. Z. Angew. Math. Phys. 69, 17 (2018)
Pomponio, A., Ruiz, D.: A variational analysis of a gauged nonlinear Schrödinger equation. J. Eur. Math. Soc. 17, 1463–1486 (2015)
Pomponio, A., Ruiz, D.: Boundary concentration of a gauged nonlinear Schrödinger equation on large balls. Calc. Var. Partial. Differ. Equ. 53, 289–316 (2015)
Ruiz, D.: The Schrödinger–Poisson equation under the effect of a nonlinear local term. J. Funct. Anal. 237, 655–674 (2006)
Seok, J.: Infinitely many standing waves for the nonlinear Chern–Simons–Schrödinger equations. Adv. Math. Phys. (2015). https://doi.org/10.1155/2015/519374
Tang, X., Zhang, J., Zhang, W.: Existence and concentration of solutions for the Chern–Simons–Schrödinger system with general nonlinearity. RM 71, 643–655 (2017)
Tolksdorf, P.: Regularity for some general class of quasilinear elliptic equations. J. Differ. Equ. 51, 126–150 (1984)
Trudinger, N.: On Harnack type inequalities and their applications to quasilinear elliptic equations. Comm. Pure Appl. Math. 20, 721–747 (1967)
Wan, Y.Y., Tan, J.G.: Standing waves for the Chern–Simons–Schrödinger systems without (AR) condition. J. Math. Anal. Appl. 415, 422–434 (2014)
Wan, Y., Tan, J.: The existence of nontrivial solutions to Chern–Simons–Schrödinger system. Discrete Cont. Dyn. Syst. 37, 2765–2786 (2017)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Zhang, N., Tang, X., Chen, Z., Qin, L.: Ground state solutions for the Chern–Simons–Schödinger equations with general nonlinearity. Complex Var. Elliptic Equ. https://doi.org/10.1080/17476933.2019.1667337 (2019)
Zhao, L., Zhao, F.: On the existence of solutions for the Schrödinger–Poisson equations. J. Math. Anal. Appl. 346, 155–169 (2008)
Acknowledgements
Both authors are grateful to editor and referees for their critical and helpful comments.
Funding
Research supported by National Natural Science Foundation of China (Grant No. 12071486).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Xu, L., Chen, H. Positive ground state solutions for the Chern–Simons–Schrödinger system. Anal.Math.Phys. 12, 45 (2022). https://doi.org/10.1007/s13324-022-00656-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-022-00656-y
Keywords
- Chern–Simons–Schrödinger system
- Pohožaev–Nehari manifold
- A Br\(\acute{e}\)zis–Lieb type convergence lemma
- Positive ground state solutions
- Concentration
- Nonexistence