Abstract
We prove a generalized Kac-Rice formula that, in a well defined regular setting, computes the expected cardinality of the preimage of a submanifold via a random map by expressing it as the integral of a density. Our proof starts from scratch and although it follows the guidelines of the standard proofs of Kac-Rice formula, it contains some new ideas coming from the point of view of measure theory. Generalizing further, we extend this formula to any other type of counting measure, such as the intersection degree. We discuss in depth the specialization to smooth Gaussian random sections of a vector bundle. Here, the formula computes the expected number of points where the section meets a given submanifold of the total space, it holds under natural non-degeneracy conditions and can be simplified by using appropriate connections. Moreover, we point out a class of submanifolds, that we call sub-Gaussian, for which the formula is locally finite and depends continuously with respect to the covariance of the first jet. In particular, this applies to any notion of singularity of sections that can be defined as the set of points where the jet prolongation meets a given semialgebraic submanifold of the jet space. Various examples of applications and special cases are discussed. In particular, we report a new proof of the Poincaré kinematic formula for homogeneous spaces and we observe how the formula simplifies for isotropic Gaussian fields on the sphere.



Similar content being viewed by others
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
Stands for “Kac Rice OK”.
Actually a better analogy is with the sine of the angle.
A Borel measure that is finite on compact sets.
Meaning that G acts on the left on both E and M and the action commutes with the projection: \(\pi (g\cdot x)=g\cdot \pi (x)\), for any \(x\in E\) and \(g\in G\). Thus, the function \(gXg^{-1}\) such that \(p\mapsto g\cdot X(g^{-1}\cdot p)\) is a section.
Note that the Riemannian volume density is defined independently from the orientability of the manifold \(S_{p}\). Roughly speaking, it is the absolute value of a volume form, see “Appendix 1”.
i.e. continuous at every point of \({\mathscr {M}}\).
The argument is exactly the same as that used to prove Lemma 1.1
We are implicitly making the identification \(\varDelta _{(p,q)}{\mathscr {M}}\cong \varDelta _q(S_p\cap W)\otimes \varDelta _pM\). By the KROK hypotheses 2.1, \({\mathscr {M}}\) is a smooth submanifold of \(M\times N\). However, \(\delta {{\mathscr {M}}}\) is not the volume density of the metric induced by inclusion in the product Riemannian manifold \(M\times N\).
Such pair of metrics, always exists. To construct them, first define any metrics on M and N. Then consider the subbundle \(H\subset TN\) given by the orthogonal complement of the vertical one, namely \(H_q=\ker (d_q\pi )^\perp \) (alternatively, take H to be any Ehresmann connection). Now modifiy the metric on \(H_q\) by declaring the map \(d_q\pi :H_q\rightarrow T_pM\) a linear isometry.
A connection \(H\subset E\) is linear if \(H_{\lambda q}=d_qL_{\lambda }(H_q)\) for every \(\lambda \in {\mathbb {R}}\), where \(L_\lambda \) denotes the scalar multiplication. in this case, the operator \(\nabla :{\mathscr {C}}^\infty (M|E)\rightarrow {\mathscr {C}}^{\infty }(M|E\otimes T^*M)\) satisfies the Leibnitz rule and thus it defines a covariant derivative.
Since \(W\subset N\) is cooriented, there exists a Thom class \(\tau \in H^m(N,N\smallsetminus W)\). By definition, \(\text {deg}(f|_U,W)=\int _Uf^*\tau \) in the case
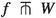 , but now this identity remains true for any continuous f such that \(f(\partial U)\subset N\smallsetminus W\). Looking at the long exact sequence for the pair \((N,N\smallsetminus W)\), we see that \(\tau \mapsto e\) maps to the Poincaré dual of W, so that if \(e=0\) then there exists an element \(\alpha \in H^{m-1}(N\smallsetminus W)\) that maps to \(\tau \) (i.e. \(d^*\alpha =\tau \)), therefore \(\int _Uf^*\tau =\int _{\partial U} f^*\alpha \) by naturality (or Stokes theorem from De Rham’s point of view). In such case, \(\text {link}(f|_U,W)=\int _{\partial U}f^*\alpha \). If N is a tubular neighborhood of W, then \(e,\tau ,\alpha \) are respectively the Euler class, the Thom class and the class of a closed global angular form (Compare with [6]).
, but now this identity remains true for any continuous f such that \(f(\partial U)\subset N\smallsetminus W\). Looking at the long exact sequence for the pair \((N,N\smallsetminus W)\), we see that \(\tau \mapsto e\) maps to the Poincaré dual of W, so that if \(e=0\) then there exists an element \(\alpha \in H^{m-1}(N\smallsetminus W)\) that maps to \(\tau \) (i.e. \(d^*\alpha =\tau \)), therefore \(\int _Uf^*\tau =\int _{\partial U} f^*\alpha \) by naturality (or Stokes theorem from De Rham’s point of view). In such case, \(\text {link}(f|_U,W)=\int _{\partial U}f^*\alpha \). If N is a tubular neighborhood of W, then \(e,\tau ,\alpha \) are respectively the Euler class, the Thom class and the class of a closed global angular form (Compare with [6]).Actually here the connection is not needed, since if \(X(p)=0\) then \((\nabla X)_p\) is independent from \(\nabla \).
In particular, this implies that y is a Morse function, almost surely.
A consequence of this trick is that \(\mu (A\times B):={\mathbb {E}}\#_{X\in W\cap B}(A)\) defines a Borel measure on the product space \(M\times W\). We are going to develop this idea properly later, in Sect. 8.1.
Let M be a nonempty set; a Dynkin class \({\mathscr {D}}\) is a collection of subsets of M such that:
-
1.
\(M\in {\mathscr {D}}\);
-
2.
if \(A, B\in {\mathscr {D}}\) and \(A\subset B\), then \(B\backslash A\subset {\mathscr {D}};\)
-
3.
given a family of sets \(\{A_k\}_{k\in {\mathbb {N}}}\) with \(A_k\in {\mathscr {D}}\) and \(A_k\subset A_{k+1}\), then \(\bigcup _{k}A_k\in {\mathscr {D}}\).
The Monotone Class Theorem (see [9, p. 3]) says that if a family \({\mathscr {D}}\) is a Dynkin class which contains a family \({\mathscr {P}}\) closed by intersection, then it contains also the \(\sigma \)-algebra generated by \({\mathscr {P}}\).
-
1.
See point (ii) of Definition 2.1.
The set \(W_{t}\) might be empty for some non negligible set of values of \(t\in {\mathbb {R}}^{m}\). This is not a contradiction: for such t we will have that \(\delta _{X\in W_{t}}=0\) and \({\mathbb {E}}\#_{X\in W_{t}}=0\).
It corresponds to the set function \({\mathscr {H}}_\varepsilon ^0(S)\) used in the construction of the Hausdorff measure.
It is possible because the functions involved are positive and measurable.
S is called the Schur complement of the block \(G_{22}\) in \(G=\begin{pmatrix} G_{11} &{} G_{12} \\ G_{21} &{} G_{22} \end{pmatrix}\).
Here \(\delta _p\) denotes the \(\delta -\)measure on the point p.
It is a strict inclusion, when \(\rho _{X(p)}(q)= 0\) on a not negligible set of points p, q.
After a rescaling of the coordinate y, we can assume that \({\mathbb {D}}^s\times {\mathbb {D}}^s\subset \phi (N_0)\).
This is why we defined the continuous functions \(\alpha _{s,\eta }\), instead of simply using the characteristic functions \(\mathbb {1}_{{{\mathscr {A}}_s}}\).
They are the Christoffel symbols of the corresponding covariant derivative: given a smooth section \(s(u)=(u,s_v(u))\), the vertical projection of \(d_us\) is given by
$$\begin{aligned} (\nabla s)_u=d_us_v+\varGamma (u,s_v(u))\in {\mathbb {R}}^{m\times s}.\end{aligned}$$Notice that \(T_{(u,x)}W\) is a well defined m dimensional subspace of \({\mathbb {R}}^m\times {\mathbb {R}}^s\) even if \(u\in \partial {\mathbb {D}}^m\). In such case the transversality
 is still meant in the space \({\mathbb {R}}^m\times {\mathbb {R}}^s\).
is still meant in the space \({\mathbb {R}}^m\times {\mathbb {R}}^s\).
References
Adler, R.J., Taylor, J.E.: Random Fields and Geometry. Springer Monographs in Mathematics, Springer, New York (2007)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Science Publications, Clarendon Press (2000)
Arnold, V.I., Gusein-Zade, S.M., Varchenko, A.N.: Singularities of Differentiable Maps, Volume 1: Classification of Critical Points, Caustics and Wave Fronts. Modern Birkhäuser Classics. Birkhäuser, Boston (2012)
Azais, J.-M., Wschebor, M.: Level Sets and Extrema of Random Processes and Fields. Wiley, Hoboken (2009)
Billingsley, Patrick: Convergence of Probability Measures. Wiley Series in Probability and Statistics: Probability and Statistics, 2nd edn. John Wiley and Sons, Inc., New York (1999)
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Graduate Texts in Mathematics, Springer, New York (1995)
Breiding, P., Keneshlou, H., Lerario, A.: Quantitative singularity theory for random polynomials. Int. Math. Res. Not. 10, rnaa274 (2020)
Chavel, I.: Riemannian Geometry: A Modern Introduction. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2006)
Çınlar, E.: Probability and Stochastics. Graduate Texts in Mathematics, Springer, New York (2011)
Dudley, R.M.: Real Analysis and Probability. Cambridge Studies in Advanced Mathematics, 2nd edn. Cambridge University Press, Cambridge (2002)
Federer, H.: Geometric Measure Theory. Springer, Grundlehren der mathematischen Wissenschaften (1996)
Fyodorov, Y.V., Lerario, A., Lundberg, E.: On the number of connected components of random algebraic hypersurfaces. J. Geom. Phys. 95, 1–20 (2015)
Gayet, D., Welschinger, J.-Y.: Lower estimates for the expected Betti numbers of random real hypersurfaces. J. Lond. Math. Soc. 90(1), 105–120 (2014)
Gayet, D., Welschinger, J.-Y.: Expected topology of random real algebraic submanifolds. J. Inst. Math. Jussieu 14(4), 673–702 (2015)
Gayet, D., Welschinger, J.-Y.: Betti numbers of random real hypersurfaces and determinants of random symmetric matrices. J. Eur. Math. Soc. (JEMS) 18(4), 733–772 (2016)
Goresky, M., MacPherson, R.: Stratified Morse Theory. Springer-Verlag, Ergebnisse der Mathematik und ihrer Grenzgebiete (1988)
Hirsch, M.W.: Differential Topology, volume 33 of Graduate Texts in Mathematics. Springer-Verlag, New York, (1994). Corrected reprint of the 1976 original
Howard, R.: The kinematic formula in Riemannian homogeneous spaces. Mem. Am. Math. Soc. 106(509), vi+69 (1993)
Jordan, C.: Essai sur la géométrie à \(n\) dimensions. Bull. Soc. Math. Fr. 3, 103–174 (1875)
Kac, M.: On the average number of real roots of a random algebraic equation. Bull. Am. Math. Soc. 49, 314–320 (1943)
Kostlan, Eric: On the distribution of roots of random polynomials. In From Topology to Computation: Proceedings of the Smalefest (Berkeley, CA, 1990), pp. 419–431. Springer, New York (1993)
Lerario, A.: Random matrices and the average topology of the intersection of two quadrics. Proc. Am. Math. Soc. 143(8), 3239–3251 (2015)
Lerario, A., Lundberg, E.: Statistics on Hilbert’s 16th problem. Int. Math. Res. Not. IMRN 12, 4293–4321 (2015)
Lerario, A., Lundberg, E.: On the geometry of random lemniscates. Proc. Lond. Math. Soc. 113(5), 649–673 (2016)
Lerario, A., Stecconi, M.: Maximal and typical topology of real polynomial singularities (2019)
Lerario, A., Stecconi, M.: Differential topology of gaussian random fields (2021)
Marinucci, D., Peccati, G.: Random Fields on the Sphere: Representation. Limit Theorems and Cosmological Applications. London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge (2011)
Miao, J., Ben-Israel, A.: On principal angles between subspaces in rn. Linear Algebra Appl. 171, 81–98 (1992)
Milnor, J.W., Stasheff, J.D.: Characteristic classes. Princeton University Press, Princeton, N. J.; University of Tokyo Press, Tokyo, (1974). Annals of Mathematics Studies, No. 76
Nazarov, F., Sodin, M.: Asymptotic laws for the spatial distribution and the number of connected components of zero sets of Gaussian random functions. Zh. Mat. Fiz. Anal. Geom. 12(3), 205–278 (2016)
Nazarov, F., Sodin, M.: On the number of nodal domains of random spherical harmonics. Am. J. Math. 131(5), 1337–1357 (2009)
Nicolaescu, L.I.: A stochastic gauss-bonnet-chern formula. Probab. Theory Relat. Fields 165(1), 235–265 (2016)
Park, C., Pranav, P., Chingangbam, P., Van De Weygaert, R., Jones, B., Vegter, G., Kim, I., Hidding, J., Hellwing, W.A.: Betti numbers of Gaussian fields (2013)
Parthasarathy, K.R.: Probability Measures on Metric Spaces. Ams Chelsea Publishing, Academic Press (2005)
Rice, S.O.: Mathematical analysis of random noise. Bell Syst. Tech. J. 23(3), 282–332 (1944)
Sarnak, P., Wigman, I.: Topologies of nodal sets of random band-limited functions. Commun. Pure Appl. Math. 72(2), 275–342 (2019)
Shub, M., Smale, S.: Complexity of Bezout’s theorem. II. Volumes and probabilities. In Computational algebraic geometry (Nice, 1992), volume 109 of Progr. Math., pp. 267–285. Birkhäuser Boston, Boston (1993)
Wigman, I.: Fluctuations of the nodal length of random spherical harmonics. Commun. Math. Phys. 298(3), 787–831 (2010)
Wigman, Igor: On the expected betti numbers of the nodal set of random fields. Anal. pde 14(6), 1797–1816 (2020)
Zhu, P., Knyazev, A.V.: Angles between subspaces and their tangents. J. Numer. Math. 21(4), 325–340 (2013)
Acknowledgements
The author wishes to thank Antonio Lerario for his useful suggestions indicating the most interesting directions; Léo Mathis and Riccardo Tione for being “the one with the answer” and ready to help on multiple occasions. Also, thanks to the anonymous referee for her/his helpful observations and comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was initiated while the author was a PhD student at SISSA, Trieste, Italy, supported by the SISSA PhD Fellowship in Geometry and Mathematical Physics, and it was completed while he was a postdoctoral researcher at Nantes University, funded by the ANR project ENUMGEOM NR-18-CE40-0009-02 and the grant TROPICOUNT of Région Pays de la Loire.
Appendices
Densities
Let M be a smooth manifold. The density bundle or, as we call it, the bundle of density elements \(\varDelta M\) is the vector bundle:
where L is the orientation bundle (see [6, Sect. 7]); \(\varDelta M\) is a smooth real line bundle and the fiber can be identified canonically with
We call an element \(\delta \in \varDelta _pM\), a density element at p.
Given a set of coordinates \(x^1,\dots ,x^m\) on U, we denote
Using the language of [6], dx is the section \((dx_1\wedge \cdots \wedge dx_m)\otimes e_U\), where \(e_U\) is the section of \(L|_{U}\) which in the trivialization induced by the chart \((x_1, \ldots , x_m)\) corresponds to the constant function 1.
We have, directly from the definition, that
for any other set of coordinates \(y^1,\dots ,y^m\). It follows that an atlas for M with transition functions \(g_{a,b}\) defines a trivializing atlas for the vector bundle \(\varDelta M\), with transition functions for the fibers given by \(|\det (Dg_{a,b})|\).
Each density element \(\delta \), is either positive or negative, respectively if \(\delta =|{\omega }|\) or \(\delta =-|{\omega }|\), for some skew-symmetric multilinear form \(w\in \wedge ^mT^*_pM\). In other words, the bundle \(\varDelta M\) is canonically oriented and thus trivial (but not canonically trivial) and we denote the subbundle of positive elements by \(\varDelta ^+ M\cong M\times [0,+\infty )\) (again, not canonically).
The modulus of a density element is defined in coordinates, by the identity \(|({\omega }(x)dx)|=|{\omega }(x)|dx\). This defines a continuous map \(|\cdot |:\varDelta M\rightarrow \varDelta ^+ M\).
The sections of \(\varDelta M\) are called densities and we will usually denote them as maps \(p\mapsto \delta (p)\). We define \({\mathscr {D}}^r(M)\) to be the space of \({\mathscr {C}}^r\) densities and by \({\mathscr {D}}^r_c(M)\) the subset of the compactly supported ones. For smooth densities, we just write \({\mathscr {D}}={\mathscr {D}}^\infty \). From the formula for transition functions it is clear that there is a canonical linear function
If N is Riemannian and \(f:M\rightarrow N\) is a \({\mathscr {C}}^1\) map with \(\dim M\le \dim N\), we define the jacobian density \(\delta f\in {\mathscr {D}}(M)\) by the following formula, in coordinates:
In particular \(\delta (\text {id}_M)\) is the Riemannian volume density of M and we denote it by dM. Similarly, if f is a Riemannian inclusion \(M\subset N\), then \(\delta f=dM\).
Given any Riemannian metric on the manifold M, one can make the identification \(\varDelta _p M= {\mathbb {R}}(dM(p))\) and treat densities as if they were functions. Moreover this identification preserves the sign, since dM is always a positive density: \(dM(p)\in \varDelta _p^+M\), for every \(p\in M\). We denote by B(M) the set of all Borel measurable functions \(M\rightarrow [-\infty ,+\infty ]\) and by \(L(M)=B(M)dM\) the set of all measurable, not necessarily finite, densities (the identification with B(M) depends on the choice of the metric). Let \(B^+(M)\) be the set of positive measurable functions \(M\rightarrow [0,+\infty ]\) and \(L^+(M)\) be the set of densities of the form \(\rho dM\), for some \(\rho \in B^+(M)\). In other words
is the set of all nonnegative, non necessarily finite measurable densities. The integral can be extended in the usual way (by monotone convergence) to a linear function \(\int _M:L^+(M)\rightarrow {\mathbb {R}}\cup \{\infty \}\). Similarly, we define the spaces \(L^1(M),L^\infty (M),L^1_{loc}(M),L^\infty _{loc}(M)\) and their respective topologies by analogy with the standard case \(M={\mathbb {R}}^m\).
Definition A.1
We say that a real Radon measure (see [2]) \(\mu \) on M is absolutely continuous if \(\mu (A)=0\) on any zero measure subset \(A\subset M\). In other words \(\mu \) is absolutely continuous if and only if \(\varphi _*\left( \mu |_{U}\right) \) is absolutely continuous with respect to the Lebesgue measure \({\mathscr {L}}^m\) for any chart \(\varphi :U\subset M\rightarrow {\mathbb {R}}^m\).
In this language, the Radon-Nikodym Theorem takes the following form.
Theorem A.2
Let \(\mu \) be an absolutely continuous real Radon measure on M. Then there is a density \(\delta \in L^1_{loc}(M)\) such that, for all Borel subsets \(A\subset M\),
Angle between subspaces
Let \(E, \langle \cdot ,\cdot \rangle \) be a euclidean vector space (i.e. a finite dimensional real Hilbert space).
Definition B.1
Let \(f=(f_1,\dots ,f_k)\) be a tuple (in row) of vectors \(f_i\in E\). We define its volume as
If the vectors \(f_1,\dots ,f_k\) are independent, then f is called a frame. The span \(\text {span}(f)\) of the tuple f is the subspace of E spanned by the vectors \(f_1,\dots ,f_k\). A tuple f is a basis of a subspace \(V\subset E\) if and only if it is a frame and its span is V. Given two frames v, w, we can form the tuple (v, w).
Definition B.2
Let \(V,W\subset E\) be subspaces. Let v and w be frames in E such that:
-
\(\text {span}(v)=V\cap (V\cap W)^\perp \);
-
\(\text {span}(w)=W\cap (V\cap W)^\perp \).
We define the angle between V and W as
It is easy to see that the definition is well posed, independently from the choices of the frames. This definition corresponds to Howard’s [18] in the case when \(V\cap W=\{0\}\). Observe that \(\sigma \) is symmetric and that we have \(\sigma (V,W)=1\) if and only if \(V=A\oplus _\perp B\) and \(W=A\oplus _\perp C\) with and \(B\perp C\).
When V and W are one dimensional, \(\sigma (V,W)=|\sin \theta |\), where \(\theta \) is the angle between the two lines. In general \(\sigma (V,W)\in [0,1]\) is equal to the product of the sines of the nontrivial principal angles between V and W (see [19, 28, 40]). In particular, notice that \(\sigma (V,W)>0\) always.
It is important to notice that \(\sigma :\text {Gr}_k(E)\times \text {Gr}_h(E)\rightarrow [0,1]\) is not a continuous function. However the restriction to the subset of the pairs of subspaces (V, W) such that \(\dim (V+W)=n\) is continuous.
Proposition B.3
Assume that \(W\not \subset V\). Let w be a basis for \(W\cap (V\cap W)^\perp \), as in Definition B.2, then
Proof
First, observe that the projected frame \(\varPi _{V^\perp }(w)\) is a basis of the space \((V+W)\cap V^\perp \). Let \(\nu \) be an orthonormal basis of the same space, let v be an orthonormal basis for \(V\cap (V\cap W)^\perp \) and let \(\tau \) be a basis for \(V\cap W\). It follows that \((\tau , v,\nu )\) is a basis for \(V+W\). Therefore, there is an invertible matrix B and a matrix A such that
Then, by Definition B.2, we have
\(\square \)
Proposition B.4
\(\sigma (V^\perp ,W^\perp )=\sigma (V,W).\)
Proof
The statement is trivially true if \(V\subset W\) or \(W \subset V\), so let us assume that this is not the case. Let \(\nu \) be an orthonormal basis of the space \((V+W)\cap V^\perp \) and v be an orthonormal basis of \(V\cap (V\cap W)^\perp \). Besides, let \((\tau ,w)\) be an orthonormal basis of W, such that \(\tau \) is a basis for \(V\cap W\). We have
\(\square \)
Area and Coarea formula
Definition C.1
Let \(\varphi :M\rightarrow N\) be a \({\mathscr {C}}^1\) map between \({\mathscr {C}}^1\) Riemannian manifolds. The Jacobian (often called normal Jacobian when f is a submersion) of \(\varphi \) at \(p\in M\) is
where \(e=(e_1,\dots , e_k)\) is any basis of \(\ker (d_p\varphi )^\perp \subset T_pM\).
If \(L:V_1\rightarrow V_2\) is a linear map between metric vector spaces, then we write \(J L:=J_0L\) (Clearly \(J_p\varphi =Jd_p\varphi \)). If \(V_1,V_2\) have the same dimension, then, to stress this fact, we may write \(|\det L|:=JL\), although the sign of \(\det L\) is not defined, unless we specify orientations.
In particular, let \(\varphi :({\mathbb {R}}^m;g_1)\rightarrow ({\mathbb {R}}^n;g_2)\) with differential \(\frac{\partial \varphi }{\partial u}(u)=A\) having maximal rank, then
Remark C.1
In the case \(m\le n\), the density induced on M by a map \(\varphi \), defined in (A.1) corresponds to \(\delta _p\varphi =(J_p\varphi ) dM\).
Theorem C.2
(Area formula) Let \(f:M\rightarrow N\) be a Lipschitz map between \({\mathscr {C}}^1\) Riemannian manifolds, with \(\dim M=\dim N\). Let \(g:M\rightarrow [0,+\infty ]\) be a Borel function, then
Proof
See [11, Theorem 3.2.3]. \(\square \)
The Area formula is actually much more general than this, in that it holds for \(\dim M\le \dim N\) and with the Hausdorff measure instead of dN. However, this simplified statement is all that we need in this paper. It also can be thought as a generalization of the following, in the case \(\dim M=\dim N\).
Theorem C.3
(Coarea formula) Let \(f:M\rightarrow N\) be a \({\mathscr {C}}^1\) submersion between smooth Riemannian manifolds, with \(\dim M\ge \dim N\). Let \(g:M\rightarrow [0,+\infty ]\) be a Borel function, then
Proof
See [8] or deduce it from [11, Theorem 3.2.12]. \(\square \)
Rights and permissions
About this article
Cite this article
Stecconi, M. Kac-Rice formula for transverse intersections. Anal.Math.Phys. 12, 44 (2022). https://doi.org/10.1007/s13324-022-00654-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-022-00654-0



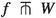 , but now this identity remains true for any continuous f such that
, but now this identity remains true for any continuous f such that  is still meant in the space
is still meant in the space