Abstract
The Funk–Radon transform, also known as the spherical Radon transform, assigns to a function on the sphere its mean values along all great circles. Since its invention by Paul Funk in 1911, the Funk–Radon transform has been generalized to other families of circles as well as to higher dimensions. We are particularly interested in the following generalization: we consider the intersections of the sphere with hyperplanes containing a common point inside the sphere. If this point is the origin, this is the same as the aforementioned Funk–Radon transform. We give an injectivity result and a range characterization of this generalized Radon transform by finding a relation with the classical Funk–Radon transform.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The reconstruction of a function from its integrals along certain submanifolds is a key task in various mathematical fields, including the modeling of imaging modalities, cf. [18]. One of the first works was in 1911 by Funk [6]. He considered what later became known by the names Funk–Radon transform, Minkowski–Funk transform or spherical Radon transform. Here, the function is defined on the unit sphere and we know its mean values along all great circles. Another famous example is the Radon transform [22], where a function on the plane is assigned to its integrals along all lines. Over the last more than 100 years, the Funk–Radon transform has been generalized to other families of circles as well as to higher dimensions.
In this article, we draw our attention to integrals along certain subspheres of the \((d-1)\)-dimensional unit sphere
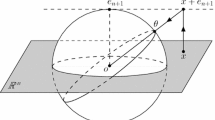
Any subsphere of \({\mathbb {S}}^{d-1}\) is the intersection of the sphere with a hyperplane. In particular, we consider the subspheres of \({\mathbb {S}}^{d-1}\) whose hyperplanes have the common point \( (0,\dots ,0,z)^\top \) strictly inside the sphere for \(z\in [0,1)\). We define the spherical transform \({\mathcal {U}}_z f\) of a function \(f\in C({\mathbb {S}}^{d-1})\) by
which computes the mean values of f along the subspheres
where \(V({\mathscr {C}}_z^{\varvec{\xi }}) \) denotes the \((d-2)\)-dimensional volume of \({\mathscr {C}}_z^{\varvec{\xi }}\).
The spherical transform \({\mathcal {U}}_z\) on the two-dimensional sphere \({\mathbb {S}}^2\) was first investigated by Salman [25] in 2016. He showed the injectivity of this transform \({\mathcal {U}}_z\) for smooth functions \(f\in C^\infty ({\mathbb {S}}^2)\) that are supported inside the spherical cap \(\{\varvec{\xi }\in {\mathbb {S}}^2 \mid \xi _3 < z \}\) as well as an inversion formula. This result was extended to the d-dimensional sphere in [26], where also the smoothness requirement was lowered to \(f\in C^1({\mathbb {S}}^d)\). A different approach was taken in [20], where a relation with the classical Funk–Radon transform \({\mathcal {U}}_0\) was established and also used for a characterization of the nullspace and range of \({\mathcal {U}}_z\) for \(z<1\).
In the present paper, we extend the approach of [20] to the d-dimensional case. We use a similar change of variables to connect the spherical transform \({\mathcal {U}}_z\) with the Funk–Radon transform \({\mathcal {F}} = {\mathcal {U}}_0\) in order to characterize its nullspace. However, the description of the range requires some more effort, because the operator \({\mathcal {U}}_z\) is smoothing of degree \({({d-2})/{2}}\).
In the case \(z=0\), we have sections of the sphere with hyperplanes through the origin, which are also called maximal subspheres of \({\mathbb {S}}^{d-1}\) or great circles on \({\mathbb {S}}^2\). We obtain the classical Funk–Radon transform \({\mathcal {F}} = {\mathcal {U}}_0\). The case \(z=1\) corresponds to the subspheres containing the north pole \((0,\dots ,0,1)^\top \). This case is known as the spherical slice transform \({\mathcal {U}}_1\) and has been investigated since the early 1990s in [1, 4, 10]. However, unlike \({\mathcal {U}}_z\) for \(z<1\), the spherical slice transform \({\mathcal {U}}_1\) is injective for \(f\in L^\infty ({\mathbb {S}}^{d-1})\), see [23]. The main tool to derive this injectivity result of \({\mathcal {U}}_1\) is the stereographic projection, which turns the subspheres of \({\mathbb {S}}^{d-1}\) through the north pole into hyperplanes in \({\mathbb {R}}^{d-1}\) and thus connecting the spherical slice transform \({\mathcal {U}}_1\) to the Radon transform on \({\mathbb {R}}^{d-1}\). For \(z\rightarrow \infty \), we obtain vertical slices of the sphere, i.e., sections of the sphere with hyperplanes that are parallel to the north–south axis. This case is well-known for \({\mathbb {S}}^2\), see [7, 12, 24, 30]. In 2016, Palamodov [19, Section 5.2] published an inversion formula for a certain nongeodesic Funk transform, which considers sections of the sphere with hyperplanes that have a fixed distance to the point \((0,\dots ,0,z)^\top \). This contains both the transform \(\mathcal U_z\) as well as for \(z=0\) the sections with subspheres having constant radius previously considered by Schneider [27] in 1969.
A key tool for analyzing the stability of inverse problems are Sobolev spaces, cf. [15] for the Radon transform and [11] for the Funk–Radon transform. The Sobolev space \(H^{s}({\mathbb {S}}^{d-1})\) can be imagined as the space of functions \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) whose derivatives up to order s are square-integrable, and we denote by \(H^{s}_{\text {even}}({\mathbb {S}}^{d-1})\) its restriction to even functions \(f(\varvec{\xi })=f(-\varvec{\xi })\). A thorough definition of \(H^s({\mathbb {S}}^{d-1})\) is given in Sect. 5.2. The behavior of the Funk–Radon transform was investigated by Strichartz [28, Lemma 4.3], who found that the Funk–Radon transform \({\mathcal {F}}:H^s_{\text {even}}({\mathbb {S}}^{d-1})\rightarrow H^{s+({d-2})/{2}}_{\text {even}}({\mathbb {S}}^{d-1})\) is continuous and bijective. In Theorem 6.4, we show that basically the same holds for the generalized transform \({\mathcal {U}}_z\), i.e., the spherical transform \({\mathcal {U}}_z:H^s_{z}({\mathbb {S}}^{d-1})\rightarrow H^{s+({d-2})/{2}}_{\text {even}}({\mathbb {S}}^{d-1})\) is bounded and bijective and its inverse is also bounded, where \(H^s_{z}({\mathbb {S}}^{d-1})\) contains functions that are symmetric with respect to the point reflection in \((0,\dots ,0,z)^\top \).
This paper is structured as follows. In Sect. 2, we give a short introduction to smooth manifolds and review the required notation on the sphere. In Sect. 3, we show the relation of \({\mathcal {U}}_z\) with the classical Funk–Radon transform \({\mathcal {F}} = {\mathcal {U}}_0\). With the help of that factorization, we characterize the nullspace of the spherical transform \({\mathcal {U}}_z\) in Sect. 4. In Sect. 5, we consider Sobolev spaces on the sphere and show the continuity of certain multiplication and composition operators. Then, in Sect. 6, we prove the continuity of the spherical transform \({\mathcal {U}}_z\) in Sobolev spaces. Finally, we show an explicit inversion formula of the spherical transform in Sect. 7.
2 Preliminaries and definitions
2.1 Manifolds
In this section, we summarize some facts about smooth manifolds. Most of the material in extended form can be found in [2]. We denote by \({\mathbb {R}}\) and \({\mathbb {C}}\) the real and complex numbers, respectively. We define the d-dimensional Euclidean space \({\mathbb {R}}^{d}\) equipped with the scalar product \(\left\langle \varvec{\xi },\varvec{\eta }\right\rangle = \sum _{i=1}^{d}\xi _i\eta _i\) and the norm \(\left\Vert \varvec{\xi } \right\Vert =\left\langle \varvec{\xi },\varvec{\xi }\right\rangle ^{1/2}\). We denote the unit vectors in \({\mathbb {R}}^{d}\) with \(\varvec{\epsilon }^i\), i.e. \(\epsilon ^{i}_j = \delta _{i,j}\), where \(\delta \) is the Kronecker delta. Every vector \(\varvec{\xi }\in {\mathbb {R}}^{d}\) can be written as \(\varvec{\xi }=\sum _{i=1}^{d}\xi _i \varvec{\epsilon }^i\).
A diffeomorphism is a bijective, smooth mapping \({\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) whose inverse is also smooth. We say a function is smooth if it has derivatives of arbitrary order. An n-dimensional smooth manifold M without boundary is a subset of \({\mathbb {R}}^{d}\) such that for every \(\varvec{\xi }\in M\) there exists an open neighborhood \(N(\varvec{\xi })\subset {\mathbb {R}}^{d}\) containing \(\varvec{\xi }\), an open set \(U\subset {\mathbb {R}}^{d}\), and a diffeomorphism \(m:U \rightarrow N(\varvec{\xi })\) such that
We call \(m:V\rightarrow M\) a map of the manifold M, where \(V=U\cap ({\mathbb {R}}^n\times \{0\}^{d-n})\). An atlas of M is a finite family of maps \(m_i:V_i\rightarrow M\), \(i=1,\dots ,l\), such that the sets \(m_i (V_i)\) cover M. We define the tangent space \(T_{\varvec{\xi }} M\) of M at \(\varvec{\xi }\in M\) as the set of vectors \(\varvec{x}\in {\mathbb {R}}^{d}\) for which there exists a smooth path \(\gamma :[0,1]\rightarrow M\) satisfying \(\gamma (0) = \varvec{\xi }\) and \(\gamma '(0)=\varvec{x}\).
A k-form \(\omega \) on M is a family \((\omega _{\varvec{\xi }})_{\varvec{\xi }\in M}\) of antisymmetric k-linear functionals
where \((T_{\varvec{\xi }} M)^k = T_{\varvec{\xi }} M \times \dots \times T_{\varvec{\xi }} M\). Let \(f:M \rightarrow N\) be a smooth mapping between the manifolds M and N and let \(\omega \) be a k-form on N. The pullback of \(\omega \) is the k-form \(f^*(\omega )\) on M that is defined for any \(\varvec{v}^1,\dots ,\varvec{v}^k \in T_{\varvec{\xi }} M\) by
where \(\gamma _i:[0,1]\rightarrow M\) are smooth paths satisfying \(\gamma _i(0) = \varvec{\xi }\) and \(\gamma _i'(0)=\varvec{v}^i\). If the smooth function \(f:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}^{d}\) extends to the surrounding space, the pullback can be expressed as
where \(J_f\) denotes the Jacobian matrix of f.
An atlas \(\{m_i:V_i \rightarrow M\}_{i=1}^l\) is called orientation of M if for each i, j the determinant of the Jacobian of \(m_i^{-1} \circ m_j\) is positive wherever it exists. A basis \(\varvec{e}^1,\dots ,\varvec{e}^n\) of the tangent space \(T_{\varvec{\xi }} M\) is oriented positively if for some i with \(\varvec{\xi }\in m_i(V_i)\) the determinant of the matrix \([J_{m_i^{-1}}\, \varvec{e}^1,\dots ,J_{m_i^{-1}}\, \varvec{e}^n]\) is positive. Up to the multiplication of a constant real number depending only on \({\varvec{\xi }}\), there exists only one n-form on an n-dimensional manifold. Let \(\varvec{e}^1,\dots ,\varvec{e}^n\) be a positively oriented, orthonormal basis of the tangent space \(T_{\varvec{\xi }} M\). Then the volume form \(\mathrm {d}M\) is the unique n-form on M satisfying \(\mathrm {d}M(\varvec{e}^1,\dots ,\varvec{e}^n) = 1\).
A set \(\{\varphi _i\}_{i=1}^l\) of functions \(\varphi _i\in C^\infty (M)\) is a partition of unity of the manifold M with respect to an atlas \(\{m_i:V_i \rightarrow M\}_{i=1}^l\) if \({\text {supp}}(\varphi _i)\subset m_i(V_i)\) for all i and \(\sum _{i=1}^{l} \varphi _i \equiv 1\) on M. Then the integral of a k-form \(\omega \) on M is defined as
where the latter is the standard volume integral \(\mathrm {d}{\mathbb {R}}^n\) on \(V_i\subset {\mathbb {R}}^n\) and the functions \(c_i:V_i\rightarrow {\mathbb {R}}\) are uniquely determined by the condition \(m_i^*(\varphi _i\cdot \omega ) = c_i \, \mathrm {d}{\mathbb {R}}^n\).
Let \(f:M\rightarrow N=f(M)\) be a diffeomorphism between the n-dimensional manifolds M and f(M), and let \(\omega \) be an n-form on N. Then the substitution rule [14, p. 94] holds,
2.2 The sphere
Let \(d\ge 3\). The \((d-1)\)-dimensional unit sphere
is a \((d-1)\)-dimensional manifold in \({\mathbb {R}}^{d}\) with tangent space
for \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\). We define an orientation on \({\mathbb {S}}^{d-1}\) by saying that a basis \([\varvec{x}^i]_{i=1}^{d-1}\) of \(T_{\varvec{\xi }} {\mathbb {S}}^{d-1}\) is oriented positively if the determinant \(\det [\varvec{\xi }, \varvec{x}^1, \dots , \varvec{x}^{d-1}]>0\). We denote the volume of the \((d-1)\)-dimensional unit sphere \({\mathbb {S}}^{d-1}\) with
2.2.1 The spherical transform
Every \((d-2)\)-dimensional subsphere of the sphere \({\mathbb {S}}^{d-1}\) is the intersection of \({\mathbb {S}}^{d-1}\) with a hyperplane, i.e.
where \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\) is the normal vector of the hyperplane and \(t\in [-1,1]\) is the signed distance of the hyperplane to the origin. We define an orientation on the subsphere \(S(\varvec{\xi },t)\) by saying that a basis \([\varvec{e}^i]_{i=1}^{d-2}\) of the tangent space \(T_{\varvec{\eta }} S(\varvec{\xi },t)\) is oriented positively if
In the following, we consider subspheres of \({\mathbb {S}}^{d-1}\) whose hyperplanes have a common point located in the interior of the unit ball. Because of the rotational symmetry, we can assume that this point lies on the positive \(\xi _{d}\) axis. For \(z\in [0,1)\), we consider the point
The \((d-2)\)-dimensional subsphere that is located in one hyperplane together with \(z\varvec{\epsilon }^{d}\) can be described by \(S(\varvec{\xi },t)\) with \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\) and \(t = \left\langle \varvec{\xi }, z\varvec{\epsilon }^{d}\right\rangle = z\xi _{d}\). We define the subsphere
The \((d-2)\)-dimensional sphere \({\mathscr {C}}_z^{\varvec{\xi }}\) has radius \(\sqrt{1-z^2\xi _{d}^2}\) and volume
For a continuous function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\), we define its spherical transform \({\mathcal {U}}_z f\) by
which computes the mean values of f along the subspheres \({\mathscr {C}}_z^{\varvec{\xi }}\).
Remark 2.1
The subspheres \({\mathscr {C}}_z^{\varvec{\xi }}\), along which we integrate, can also be imagined in the following way. The centers of the subspheres \({\mathscr {C}}_z^{\varvec{\xi }}\) are located on a sphere that contains the origin and \(z\varvec{\epsilon }^{d}\) and is rotationally symmetric about the North–South axis. This can be seen as follows. The center of the sphere \({\mathscr {C}}_z^{\varvec{\xi }}\) is given by \(z\xi _{d}\varvec{\xi }\). Then the distance of \(z\xi _{d}\varvec{\xi }\) to the point \(\frac{z}{2}\,\varvec{\epsilon }^{d}\) reads
which is independent of \(\varvec{\xi }\). So, the centers of \(\mathscr {C}_z^{\varvec{\xi }}\) are located on a sphere with center \(\frac{z}{2}\varvec{\epsilon }^{d}\) and radius \(\frac{z}{2}\).
2.2.2 The Funk–Radon transform
Setting the parameter \(z=0\), the point \(0\varvec{\epsilon }^d=(0,\dots ,0)^\top \) is the center of the sphere \({\mathbb {S}}^{d-1}\). Hence, the spherical transform \({\mathcal {U}}_0\) integrates along all maximal subspheres of the sphere \({\mathbb {S}}^{d-1}\). This special case is called the Funk–Radon transform
which is also known by the terms Funk transform, Minkowski–Funk transform or spherical Radon transform, where the latter term occasionally also refers to means over \(({d-1})\)-dimensional spheres in \({\mathbb {R}}^{d}\), cf. [21].
3 Relation with the Funk–Radon transform
In this section, we show a connection between the spherical transform \({\mathcal {U}}_z\) and the Funk–Radon transform \({\mathcal {F}}\).
3.1 Two mappings on the sphere
Let \(z\in (-1,1)\). We define the transformations \(\varvec{h}_z, \varvec{g}_z:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1}\) by
and
Remark 3.1
The definitions of both \(\varvec{h}_z\) and \(\varvec{g}_z\) rely only on the d-th coordinate. The values in the other coordinates are just multiplied with the same factor in order to make the vectors stay on the sphere. Furthermore, the transformations \(\varvec{h}_z\) and \(\varvec{g}_z\) are bijective with their respective inverses given by
and
The computation of the inverses is straightforward and therefore omitted here.
The following lemma shows that the inverse of \(\varvec{h}_z\) applied to the subsphere \({\mathscr {C}}_z^{\varvec{\xi }}\) yields a maximal subsphere of \({\mathbb {S}}^{d-1}\) with normal vector \(\varvec{g}_z(\varvec{\xi })\).
Lemma 3.2
Let \(z\in (-1,1)\) and \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\). Then
Proof
Let \(\varvec{\eta }\in {\mathbb {S}}^{d-1}\). Then \(\varvec{\eta }\) lies in \(\varvec{h}_z^{-1} ({\mathscr {C}}_z^{\varvec{\xi }})\) if and only if \(\varvec{h}_z(\varvec{\eta }) \in {\mathscr {C}}_z^{\varvec{\xi }}\), i.e.,
By the definition of \(\varvec{h}_z\) in (3.1), we have
After subtracting the right-hand side from the last equation, we have
Multiplication with \((1+z\eta _{d})(1-z^2)^{-1/2}(1-z^2\xi _{d}^2)^{-1/2}\) yields
which is equivalent to \(\langle \varvec{\eta }, \varvec{g}_z(\varvec{\xi })\rangle =0\), so we obtain that \(\varvec{\eta }\in {\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\). \(\square \)
Lemma 3.3
Let \(z\in (-1,1)\) and \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\). Denote by \(\mathrm {d}{\mathscr {C}}_z^{\varvec{\xi }}\) and \(\mathrm {d}{\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\) the volume forms on the manifolds \( {\mathscr {C}}_z^{\varvec{\xi }}\) and \(\mathscr {C}_0^{\varvec{g}_z(\varvec{\xi })}\), respectively. Then the following relation between the pullback of the volume form \(\mathrm {d}{\mathscr {C}}_z^{\varvec{\xi }}\) over \(\varvec{h}_z\) and \(\mathrm {d}{\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\) holds. For \(\varvec{\eta }\in {\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\), we have
Furthermore, we have for the volume form \(\, \mathrm {d}{\mathbb {S}}^{d-1}\) on the sphere
Proof
We compute the Jacobian \(J_{\varvec{h}_z}\) of \(\varvec{h}_z\), which comprises the partial derivatives of \(\varvec{h}_z\). For all \(l,m \in \{1,\dots ,d-1\}\), we have
Let \([\varvec{e}^i]_{i=1}^{d-2}\) be an orthonormal basis of the tangent space \(T_{\varvec{\eta }} {\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\). Then \(J_{\varvec{h}_z} \varvec{e}^i\in T_{\varvec{h}_z(\varvec{\eta })} {\mathscr {C}}_z^{\varvec{\xi }}\) for \(i=1,\dots ,d-1\) is given by
Hence, we have for all \(i,j \in \{1,\dots ,d-2\}\)
Expanding the sum, we obtain
Since the vectors \(\varvec{e}^i\) and \(\varvec{e}^j\) are elements of an orthonormal basis, we have \(\left\langle \varvec{e}^i,\varvec{e}^j\right\rangle = \sum _{l=1}^{d} e^i_l e^j_l = \delta _{i,j}\). Furthermore, we know that \(\left\langle \varvec{e}^i,\varvec{\eta }\right\rangle =\left\langle \varvec{e}^j,\varvec{\eta }\right\rangle = 0\) because \(\varvec{e}^i\) and \(\varvec{e}^j\) are in the tangent space \(T_{\varvec{\eta }} \mathscr {C}_0^{g(\varvec{\xi })} \subset T_{\varvec{\eta }} {\mathbb {S}}^{d-1}\), and also \(\left\Vert \varvec{\eta } \right\Vert ^2=1\). Hence, we have
The above computation shows that the vectors \(\{J_{\varvec{h}_z} \varvec{e}^i\}_{i=1}^{d}\) are orthogonal with length \(\left\Vert J_{\varvec{h}_z} \varvec{e}^i \right\Vert = {\sqrt{1-z^2}}/({1+z\eta _{d}})\). By the definition of the pullback in (2.1) and the fact that the volume form \(\mathrm {d}{\mathscr {C}}_z^{\varvec{\xi }}\) is a multilinear \((d-2)\)-form, we obtain
If we set \([\varvec{e}^i]_{i=1}^{d-1}\) as a basis of the tangent space \(T_{\varvec{\eta }}({\mathbb {S}}^{d-1})\) in order to obtain (3.7), the previous calculations still hold except that the exponent \(d-2\) is replaced by \(d-1\) in equation (3.9).
Finally, we prove that the basis \(\left[ J_{\varvec{h}_z}\varvec{e}^1,\dots , J_{\varvec{h}_z}\varvec{e}^{d} \right] \) of \(T_{\varvec{h}_z(\varvec{\eta })}\mathscr {C}^{\varvec{\xi }}_z\) is oriented positively, i.e., that
By the formula (3.8) of \(J_{\varvec{h}_z}\), the function \(d:[0,1)\rightarrow {\mathbb {R}}\) is continuous, and it satisfies
since both \(\varvec{h}_0\) and \(\varvec{g}_0\) are equal to the identity map and we assumed the orthonormal basis \(\left[ \varvec{e}^1,\dots , \varvec{e}^{d-2} \right] \) be oriented positively. By the orthogonality of the vectors \(\varvec{\xi }\), \(\varvec{h}_z(\varvec{\eta })\) and \(J_{\varvec{h}_z}\varvec{e}^i\), we see that d(z) vanishes nowhere and, hence, we obtain that \(d(z)>0\) for all \(z\in [0,1)\). The assertion follows by the uniqueness of the volume form \(\mathrm {d}{\mathscr {C}}_0^{\varvec{g}_z(\varvec{\xi })}\). \(\square \)
3.2 Geometric interpretation
In this section, we give geometric interpretations of the mappings \(\varvec{g}_z\) and \(\varvec{h}_z:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1}\). The mapping \(\varvec{g}_z\) consists of a scaling with the factor \(\sqrt{1-z^2}\) along the \(\xi _{d}\) axis, which maps the sphere to an ellipsoid, which is symmetric with respect to rotations about the \(\xi _{d}\) axis. Then a central projection maps this ellipsoid onto the sphere again.
In order to give a description of the mapping \(\varvec{h}_z\), we define the stereographic projection
and its inverse
The following corollary states that, via stereographic projection, the map \(\varvec{h}_z\) on the sphere \({\mathbb {S}}^{d-1}\) corresponds to a uniform scaling in the equatorial hyperplane \({\mathbb {R}}^{d-1}\) with the scaling factor \(\sqrt{\frac{1+z}{1-z}}\).
Corollary 3.4
Let \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\) and \(z\in (0,1)\). Then we have
Proof
We are going to show that
holds. We have on the one hand
and the other hand
The assertion follows by canceling \(\sqrt{1-z}\). \(\square \)
3.3 Factorization
Let \(z\in (-1,1)\) and \(f\in C({\mathbb {S}}^{d-1})\). We define the two transformations \({\mathcal {M}}_z,\, {\mathcal {N}}_z: C({\mathbb {S}}^{d-1})\rightarrow C({\mathbb {S}}^{d-1})\) by
and
Remark 3.5
The transformation \({\mathcal {M}}_z\) is inverted by
which expands to
Furthermore, the inverse of \({\mathcal {N}}_z\) is given by
Now we are able to prove our main theorem about the factorization of the spherical transform \({\mathcal {U}}_z\).
Theorem 3.6
Let \(z\in [0,1)\). Then the factorization of the spherical transform
holds, where \({\mathcal {F}}\) is the Funk–Radon transform (2.5).
Proof
Let \(f\in C({\mathbb {S}}^2)\) and \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\). By the definition of \({\mathcal {U}}_z\) in (2.4), we have
Then we have by the substitution rule (2.2)
By the definition of \({\mathcal {M}}_z\) in (3.10), we see that
The definition of the Funk–Radon transform (2.5) shows that
which implies (3.15). \(\square \)
Theorem 3.6 for the three-dimensional case on \({\mathbb {S}}^2\) becomes Theorem 3.1 in [20].
The factorization theorem 3.6 enables us to investigate the properties of the spherical transform \(\mathcal U_z\). Because the operators \({\mathcal {M}}_z\) and \({\mathcal {N}}_z\) are relatively simple, we can transfer many properties from the Funk–Radon transform, which has been studied by many authors already, to the spherical transform \({\mathcal {U}}_z\).
4 Nullspace
With the help of the factorization (3.15) obtained in the previous section, we can show the following characterization of the nullspace of the spherical transform \({\mathcal {U}}_z\).
Theorem 4.1
Let \(z\in [0,1)\) and \(f\in C({\mathbb {S}}^{d-1})\). Then \({\mathcal {U}}_zf=0\) if and only if
where \(\varvec{r}_z:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1}\) is given by
Proof
Let \(f\in C({\mathbb {S}}^{d-1})\). Since the operator \({\mathcal {N}}_z\) is bijecive by Remark 3.1, we see that \({\mathcal {U}}_zf = {\mathcal {N}}_z {\mathcal {F}} {\mathcal {M}}_z f = 0\) if and only if \({\mathcal {F}} {\mathcal {M}}_z f=0\). The nullspace of the Funk–Radon transform \({\mathcal {F}}\) consists of the odd functions, cf. [8, Proposition 3.4.12], so we obtain
By the definition of \({\mathcal {M}}_z\) in (3.10), we have
We substitute \(\varvec{\omega }=\varvec{h}_z(\varvec{\eta })\) and obtain
In order to show that \(\varvec{r}_z = \varvec{h}_z(-\varvec{h}_z^{-1})\), we compute the d-th component
For \(i\in \{1,\dots ,d-1\}\), we have
\(\square \)
For the three-dimensional case of \({\mathbb {S}}^2\), the Theorem 4.1 becomes Theorem 4.4 in [20].
Remark 4.2
The map \(\varvec{r}_z\) from (4.2) is the point reflection of the sphere \({\mathbb {S}}^{d-1}\) about the point \(z\varvec{\epsilon }^{d}\). This can be seen as follows. Let \(\varvec{\omega }\in {\mathbb {S}}^{d-1}\). The vectors \(\varvec{\omega }-z\varvec{\epsilon }^{d}\) and \(\varvec{r}_z(\varvec{\omega })-z\varvec{\epsilon }^{d}\) are parallel if for all \(i\in \{1,\dots ,d\}\)
We have
provided all denominators are nonzero.
5 Function spaces on the sphere
Before we can state the range of the spherical transform \(\mathcal U_z\), we have to introduce some function spaces on the sphere \({\mathbb {S}}^{d-1}\). The Hilbert space \(L^2({\mathbb {S}}^{d-1})\) comprises all square-integrable functions with the inner product of two functions \(f,g:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\)
and the norm \(\left\Vert f \right\Vert _{L^2({\mathbb {S}}^{d-1})}={\left\langle f,f\right\rangle _{L^2({\mathbb {S}}^{d-1})}^{1/2}}\).
5.1 The space \(C^s({\mathbb {S}}^{d-1})\) and differential operators on the sphere
For brevity, we denote by \(\partial _i = \frac{\partial }{\partial x_i}\) the partial derivative with respect to the i-th variable. We extend a function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) to the surrounding space \({\mathbb {R}}^{d} \setminus \{\varvec{0}\}\) by setting
The surface gradient \(\varvec{\nabla }^\bullet \) on the sphere is the orthogonal projection of the gradient \(\varvec{\nabla }=(\partial _1,\dots ,\partial _{d})^\top \) onto the tangent space of the sphere. For a differentiable function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\), we have
In a similar manner, the restriction of the Laplacian
to the sphere is known as the Laplace–Beltrami operator [17, (§14.20)]
For a multi-index \(\varvec{\alpha }=(\alpha _1,\dots ,\alpha _{d}) \in {\mathbb {N}}_0^{d}\), we define its norm \(\left\Vert \varvec{\alpha } \right\Vert _1 = \sum _{i=1}^{d}\left| \alpha _i\right| \) and the differential operator \(D^{\varvec{\alpha }} = \partial _1^{\alpha _1} \cdots \partial _{d}^{\alpha _{d}}\). Let \(s\in {\mathbb {N}}_0\). We denote by \(C^s({\mathbb {S}}^{d-1})\) the space of functions \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) whose extension \(f^\bullet \) has continuous derivatives up to the order s with the norm
The space \(C^0({\mathbb {S}}^{d-1}) = C({\mathbb {S}}^{d-1})\) is the space of continuous functions with the uniform norm. The definition implies for \(f\in C^{s+1}({\mathbb {S}}^{d-1})\)
We define the space \(C^s({\mathbb {S}}^{d-1}\rightarrow {\mathbb {R}}^{d})\) of vector fields \(\varvec{f}:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {R}}^{d}\) with the norm as the Euclidean norm over its component functions, i.e., for \(\varvec{f}(\varvec{\xi }) = [f_i(\varvec{\xi })]_{i=1}^{d}\) we set
We see that for \(f\in C^{s+1}({\mathbb {S}}^{d-1})\)
5.2 Sobolev spaces
We give a short introduction to Sobolev spaces on the sphere based on [3] (see also [5, 16]). We define the Legendre polynomial \(P_{n,d}\) of degree \(n\in {\mathbb {N}}_0\) and in dimension d by [3, (2.70)]
For \(f\in L^2({\mathbb {S}}^{d-1})\) and \(n\in {\mathbb {N}}_0\), we define the projection operator
where
Note that \({\mathcal {P}}_{n,d}\) is the \(L^2({\mathbb {S}}^{d-1})\)-orthogonal projection onto the pairwise orthogonal spaces \( {\mathcal {P}}_{n,d} (L^2({\mathbb {S}}^{d-1}))\) of harmonic polynomials that are homogeneous of degree n restricted to the sphere \({\mathbb {S}}^{d-1}\).
Let \(\{Y_{n,d}^k \mid k=1,\dots ,N_{n,d}\}\) be an orthonormal basis of the space \( {\mathcal {P}}_{n,d} (L^2({\mathbb {S}}^{d-1}))\) for \(n\in {\mathbb {N}}_0\). The functions \(Y_{n,d}^k\) are commonly known as the spherical harmonics of degree n and order k. Every function \(f\in L^2({\mathbb {S}}^{d-1})\) can be written as the spherical Fourier series
with the spherical Fourier coefficients
The spherical harmonics \(Y_{n,d}^k\) are eigenfunctions of the Laplace–Beltrami operator \(\Delta ^\bullet \) satisfying [3, Proposition 3.5]
With this equation, we can define the following fractional powers of the Laplace–Beltrami operator acting on spherical harmonics \(Y_{n,d}^k\) for \(s\in {\mathbb {R}}\) by
We define the Sobolev space \(H^s({\mathbb {S}}^{d-1})\) of smoothness \(s\ge 0\) as the space of all functions \(f\in L^2({\mathbb {S}}^{d-1})\) with finite Sobolev norm [3, (3.98)]
Similarly to (5.2), we define the Sobolev norm of a vector field \(\varvec{f}:{\mathbb {S}}^{d-1} \rightarrow {\mathbb {R}}^{d}\) as the Euclidean norm over its component functions \(\varvec{f}(\varvec{\xi }) = (f_1(\varvec{\xi }),\dots ,f_{d}(\varvec{\xi }))\), i.e.,
Since the negative Laplace–Beltrami operator \(-\Delta ^\bullet \) is self-adjoint, we can write the Sobolev norm (5.6) as
We have for \(s\in {\mathbb {N}}_0\)
Then the Green–Beltrami identity [17, §14, Lemma 1]
implies that
Since the gradient \(\varvec{\nabla }^\bullet \) and the Laplacian \(\Delta ^\bullet \) commute by Schwarz’s theorem, we obtain the recursion
5.3 Sobolev spaces as interpolation spaces
The norm of a bounded linear operator \({\mathcal {A}}:X\rightarrow Y\) between two Banach spaces X and Y with norms \(\left\Vert \cdot \right\Vert _X\) and \(\left\Vert \cdot \right\Vert _Y\), respectively, is defined as
The following proposition shows that the boundedness of linear operators in Sobolev spaces \(H^s({\mathbb {S}}^{d-1})\) can be interpolated with respect to the smoothness parameter s. This result is derived from a more general interpolation theorem in [29].
Proposition 5.1
Let \(0\le s_0\le s_1\), and let \({\mathcal {A}}:H^{s_0}({\mathbb {S}}^{d-1})\rightarrow H^{s_0}({\mathbb {S}}^{d-1})\) be a bounded linear operator such that its restriction to \(H^{s_1}({\mathbb {S}}^{d-1})\) is also bounded. For \(\theta \in [0,1]\), we set \(s_\theta = (1-\theta )s_0 + \theta s_1\). Then the restriction of \({\mathcal {A}}\) to \(H^{s_\theta }({\mathbb {S}}^{d-1})\) is bounded with
Proof
For \(n\in {\mathbb {N}}_0\), let \(\{Y_{n,d}^k \mid k=1,\,\dots ,\,N_{n,d}\}\) be an orthonormal basis of \({\mathcal {P}}_{n,d} (L^2({\mathbb {S}}^{d-1}))\), and let \(f\in L^2({\mathbb {S}}^{d-1})\). We can write f as the spherical Fourier series (5.4). On the index set
we define for \(s\ge 0\) the weight function
Then the Sobolev space \(H^s({\mathbb {S}}^{d-1})\) is isometrically isomorphic to the weighted \(L^2\)-space
that consists of the Fourier coefficients
on the set I with the counting measure. By [29, Theorem 1.18.5], the complex interpolation space between \(L^2(I;w_{s_0}) \cong H^{s_0}({\mathbb {S}}^{d-1})\) and \(L^2(I;w_{s_1}) \cong H^{s_1}({\mathbb {S}}^{d-1})\) is
where
Hence, \(L^2(I;w) \cong H^{s_\theta }({\mathbb {S}}^{d-1})\). The assertion is a property of the interpolation space. \(\square \)
5.4 Multiplication and composition operators
The following two theorems show that multiplication and composition with a smooth function are continuous operators in spherical Sobolev spaces \(H^s({\mathbb {S}}^{d-1})\).
Theorem 5.2
Let \(s\in {\mathbb {N}}_0\). The multiplication operator
is continuous. In particular, for all \(f\in H^s({\mathbb {S}}^{d-1})\) and \(v\in C^{s}({\mathbb {S}}^{d-1})\), we have
where
Proof
We use induction over \(s\in {\mathbb {N}}_0\). For \(s=0\), we have
Let the claimed equation (5.10) hold for \(s\in {\mathbb {N}}_0\), and let \(f\in H^{s+1}({\mathbb {S}}^{d-1})\) and \(v\in C^{s+1}({\mathbb {S}}^{d-1})\). Then the decomposition (5.9) of the Sobolev norm yields
By the triangle inequality and since \((a+b)^2\le 2(a^2+b^2)\) for all \(a,b\in {\mathbb {R}}\), we obtain
By the induction hypothesis, we have
where we made use of the decomposition (5.9) of the Sobolev norm. Furthermore, we apply (5.3) and obtain
Because the involved norms are non-decreasing with respect to s, we see that
which shows (5.10). \(\square \)
Theorem 5.3
Let \(s\in {\mathbb {N}}_0\), and let \(\varvec{v}:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1}\) be bijective with \(\varvec{v}\in C^s({\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1})\) and \(\varvec{v}^{-1}\in C^1({\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1})\). Then there exists a constant \(b_{d,s}(\varvec{v})\) such that for all \(f\in H^s({\mathbb {S}}^{d-1})\), we have
Proof
We have for \(s=0\)
The substitution \(\varvec{\eta }=\varvec{v}(\varvec{\xi })\) yields with the substitution rule (2.2)
Since \(\varvec{v}^{-1}\in C^1({\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1})\), there exists a continuous function \(\nu :{\mathbb {S}}^{d-1}\rightarrow {\mathbb {R}}\) such that the pullback satisfies \((\varvec{v}^{-1})^*(\mathrm d{\mathbb {S}}^{d-1}) = \nu \, \mathrm {d}{\mathbb {S}}^{d-1}\). Hence, we have
which shows the claim for \(s=0\).
We use induction on \(s\in {\mathbb {N}}_0\). By the decomposition (5.9) of the Sobolev norm, we have
By the induction hypothesis, the second summand of (5.11) is bounded by
Furthermore, by (5.7) and the chain rule, we have for the first summand of (5.11)
Applying the triangle inequality for the sum over j and Jensen’s inequality \((\sum _{j=1}^{d} x_j)^2 \le d\,\sum _{j=1}^{d} x_j^2\), we obtain
By Theorem 5.2, we have
where the last line follows from (5.3). By the induction hypothesis, we see that
By (5.7) and the fact that \(\left\Vert v_j \right\Vert _{C^{s+1}({\mathbb {S}}^{d-1})}^2 \le \left\Vert \varvec{v} \right\Vert _{C^{s+1}({\mathbb {S}}^{d-1}\rightarrow {\mathbb {R}}^{d})}^2\) for all \(j=1,\dots ,d\), we obtain
Inserting the last equation and (5.12) into (5.11), we obtain
where we have made use of (5.9). \(\square \)
Remark 5.4
The last theorem resembles a similar result found in [13, Theorem 1.2]: Let M be a smooth, closed and oriented d-dimensional manifold and, for \(s>\frac{d}{2}+1\), let \(\varphi \in H^s(M\rightarrow M)\) be an orientation-preserving \(C^1\)-diffeomorphism. Then the composition map
is continuous. However, Theorem 5.3 is not a special case of this result because Theorem 5.3 requires only \(s\ge 0\) but imposes stronger assumptions on \(\varphi \).
6 Range
In this section, we show that for \(s\ge 0\) the spherical transform
is continuous. To this end, we separately investigate the parts of the decomposition obtained in Theorem 3.6,
6.1 Continuity of \({\mathcal {F}}\)
The following property of the Funk–Radon transform in Sobolev spaces was shown by Strichartz [28, Lemma 4.3] using an asymptotic analysis of its eigenvalues.
Proposition 6.1
Denote by \(H^s_{\mathrm{even}}({\mathbb {S}}^{d-1})\) the restriction of the Sobolev space \(H^s({\mathbb {S}}^{d-1})\) to even functions \(f(\varvec{\xi })=f(-\varvec{\xi })\). The Funk–Radon transform
is continuous and bijective.
6.2 Continuity of \({\mathcal {M}}_z\) and \({\mathcal {N}}_z\)
Theorem 6.2
Let \(z\in [0,1)\) and \(s \in {\mathbb {R}}\) with \(s\ge 0\). The operators
and
as defined in (3.10) and (3.11), are continuous and open.
Proof
We first perform the proof for \({\mathcal {M}}_z\). Initially, we consider only the situation \(s\in {\mathbb {N}}_0\). Let \(f\in H^s({\mathbb {S}}^{d-1})\) and \(z\in (-1,1)\). We write
where
and \(\varvec{h}_z\) is given in (3.1). We see that the extension
is smooth except in the origin, i.e., \(w_z^\bullet \in C^\infty ({\mathbb {R}}^{d}\setminus \{\varvec{0}\})\). Hence, \(w_z\in C^\infty ({\mathbb {S}}^{d-1})\). Then Theorem 5.2 implies that
Moreover, the extension of \(\varvec{h}_z\),
is also smooth, so \(\varvec{h}_z\in C^\infty ({\mathbb {S}}^{d-1}\rightarrow {\mathbb {S}}^{d-1})\). This implies that also the inverse \(\varvec{h}_z^{-1} = \varvec{h}_{-z}\), see (3.3), is smooth. So \(\varvec{h}_z\) is a diffeomorphism and Theorem 5.3 together with (6.1) implies that
Thus, the operator \({\mathcal {M}}_z:H^s({\mathbb {S}}^{d-1})\rightarrow H^s({\mathbb {S}}^{d-1})\) is continuous.
Now let \(s\in {\mathbb {R}}\) with \(s\ge 0\). The above proof shows that both the restrictions of \({\mathcal {M}}_z\) to \(H^{\lfloor s\rfloor }\) and to \(H^{\lfloor s\rfloor +1}\) are continuous, where \(\lfloor s\rfloor \) denotes the largest integer that is smaller than or equal to s. The continuity of \({\mathcal {M}}_z\) on \(H^s({\mathbb {S}}^{d-1})\) follows by the interpolation result Proposition 5.1.
In order to prove the openness of \({\mathcal {M}}_z\), we show that the inverse \({\mathcal {M}}_z^{-1}\) restricted to \(H^s({\mathbb {S}}^{d-1})\) is continuous. However, we have already done this because \(\mathcal M_z^{-1} = {\mathcal {M}}_{-z}\) by (3.12).
The same argumentation as above also works for the operator \({\mathcal {N}}_z\) as follows. Let \(z\in [0,1)\) and \(s\in {\mathbb {N}}_0\). We write
where
We see that the extension
is smooth and hence \(v_z\in C^s({\mathbb {S}}^d)\). Theorem 5.2 yields
Since the extensions of both
and its inverse (3.4)
are smooth functions on \({\mathbb {R}}^{d}\setminus \{\varvec{0}\}\), we see that \(\varvec{g}_z\) is a smooth diffeomorphism in \(C^s({\mathbb {S}}^{d-1})\). By Theorem 5.3, there exists a constant \(b_{d,s} (\varvec{g}_z)\) independent of f such that
Hence, \({\mathcal {N}}_z\) is a bounded operator on \(H^s({\mathbb {S}}^{d-1})\). An analogue computation shows that the inverse operator (3.14)
is also bounded on \(H^s({\mathbb {S}}^{d-1})\). The assertion for general s follows by the same interpolation argument as for \({\mathcal {M}}_z\). \(\square \)
Remark 6.3
In the case \(d=3\) and \(s=0\), Theorem 6.2 for the operator \({\mathcal {M}}_z\) becomes Lemma 4.1 in [20]. However, the operator \({\mathcal {M}}_z:L^2({\mathbb {S}}^2)\rightarrow L^2({\mathbb {S}}^2)\) is unitary only on \({\mathbb {S}}^2\), but not on \({\mathbb {S}}^{d-1}\) for \(d>3\). In the case \(d=3\), Theorem 6.2 for the operator \({\mathcal {N}}_z\) was shown by the author [20] in Lemma 4.2 for \(s=0\) and in Lemma 4.5 for \(s=\frac{1}{2}\).
6.3 Continuity of \({\mathcal {U}}_z\)
Theorem 6.4
Let \(z\in (0,1)\) and \(s\in {\mathbb {R}}\) with \(s\ge 0\). We set \(H^s_z({\mathbb {S}}^{d-1})\) as the subspace of all functions \(f\in H^s({\mathbb {S}}^{d-1})\) that satisfy
almost everywhere, where the point reflection \(\varvec{r}_z\) about the point \(z\,\!\varvec{\epsilon }^d\) is given in (4.2). Then the spherical transform
is continuous and bijective and its inverse operator is also continuous.
Proof
In Theorem 3.6, we obtained the decomposition
We are going to look at the parts of this decomposition separately. By Theorem 6.2, we obtain that
is continuous and bijective. The same holds for the restriction
which follows from the characterization of the nullspace in Theorem 4.1. By Proposition 6.1, the Funk–Radon transform
is continuous and bijective. Finally, Theorem 6.2 and the observation that any function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) is even if and only if \({\mathcal {N}}_zf\) is even show that
is continuous and bijective. The continuity of the inverse operator of \({\mathcal {U}}_z\) follows from the open mapping theorem. \(\square \)
Theorem 6.4 is a generalization of Proposition 6.1 for the Funk–Radon transform \(\mathcal F\); the main difference is that the space \(H^s_{\text {even}}({\mathbb {S}}^{d-1})\) is replaced by \(H^s_z({\mathbb {S}}^{d-1})\), which contains functions that satisfy the symmetry condition (6.2) with respect to the point reflection in \(z\,\varvec{\epsilon }^d\). Furthermore, the spherical transform \({\mathcal {U}}_z\) is smoothing of degree \(\frac{d-2}{2}\), which comes from the fact that \({\mathcal {U}}_z\) takes the integrals along \((d-2)\)-dimensional submanifolds. Moreover, Theorem 6.4 in the special case of \(s=0\) and dimension \(d=3\) becomes Theorem 4.6 in [20].
7 An inversion formula
In this section, we are going to show an explicit inversion formula of the spherical transform \({\mathcal {U}}_z\). The idea is to use the decomposition theorem 3.6 of the spherical transform and apply it to the following well-known inversion formula of the Funk–Radon transform \({\mathcal {F}}\).
We define the more general transform \({\mathcal {F}}^\star _v\) for some \(v\in (-1,1)\) and a function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) by
where \(\mathrm {d}S(\varvec{\eta })\) denotes the volume form on \(S(\varvec{\xi },v) = \{\varvec{\eta }\in {\mathbb {S}}^{d-1}\mid \langle \varvec{\xi },\varvec{\eta }\rangle =v \}\), cf. (2.3). The transform \({\mathcal {F}}^\star _vf\) computes the mean value of the function f along the subsphere \(S(\varvec{\xi },v)\). An even function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) can be reconstructed from its Funk–Radon transform \(\mathcal Ff\) by
The inversion formula (7.2) was shown by Helgason [9, Theorem 3.2]. We note that Helgason’s work does not use the normalization factor \(\left| {\mathbb {S}}^{d-2}\right| ^{-1}\) of the Funk–Radon transform as in (2.5).
Based on (7.2), we obtain the following inversion formula of the spherical transform \({\mathcal {U}}_z\).
Theorem 7.1
Let \(z\in (-1,1)\), and let the function \(f:{\mathbb {S}}^{d-1}\rightarrow {\mathbb {C}}\) fulfill the symmetry condition (6.2). Then f can be reconstructed from its spherical transform \({\mathcal {U}}_zf\) for any \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\) by
Proof
By the factorization (3.15) of the spherical transform \({\mathcal {U}}_z\), we have
Let \(\varvec{\xi }\in {\mathbb {S}}^{d-1}\). With (3.13) for \(\mathcal M_z^{-1}\), we obtain
Since \({\mathcal {U}}_zf\) is always even and hence also \(\mathcal N_z{\mathcal {U}}_zf\) is even, we can apply Helgason’s inversion formula (7.2). Then we have
Inserting the definition (7.1) of \({\mathcal {F}}^\star _v\), we have
With (3.14), we obtain
\(\square \)
Remark 7.2
In dimension \(d=3\), the inversion formula of the spherical transform \({\mathcal {U}}_z\) from Theorem 7.1 can be simplified for \(\varvec{\xi }\in {\mathbb {S}}^2\) to
where we made use of the simplification \(\frac{\mathrm {d}}{\mathrm {d}(u^2)} = \frac{1}{2u}\, \frac{\mathrm {d}}{\mathrm {d}u}\). This was obtained in a slightly different form in [20, Theorem 5.1]. For \(z=0\), the inversion formula from Theorem 7.1 becomes the inversion formula (7.2) of the Funk–Radon transform.
References
Abouelaz, A., Daher, R.: Sur la transformation de Radon de la sphère \(S^d\). Bull. Soc. Math. France 121(3), 353–382 (1993)
Agricola, I., Friedrich, T.: Global Analysis. Graduate Studies in Mathematics, vol. 52. American Mathematical Society, Providence, RI (2002)
Atkinson, K., Han, W.: Spherical Harmonics and Approximations on the Unit Sphere: An Introduction. Lecture Notes in Mathematics, vol. 2044. Springer, Heidelberg (2012)
Daher, R.: Un théorème de support pour une transformation de Radon sur la sphère \(S^d\). C. R. Acad. Sci. Paris 332(9), 795–798 (2001)
Dai, F., Xu, Y.: Approximation Theory and Harmonic Analysis on Spheres and Balls. Springer Monographs in Mathematics. Springer, New York (2013)
Funk, P.: Über Flächen mit lauter geschlossenen geodätischen Linien. Dissertation. Dietrich, Göttingen, (1911)
Gindikin, S., Reeds, J., Shepp, L.: Spherical tomography and spherical integral geometry. In: Quinto, E.T., Cheney, M., Kuchment, P. (eds.) Tomography, Impedance Imaging, and Integral Geometry, volume 30 of Lectures in Appl. Math, pp. 83–92. American Mathematical Society, South Hadley, Massachusetts (1994)
Groemer, H.: Geometric Applications of Fourier Series and Spherical Harmonics. Encyclopedia of Mathematics and its Applications, vol. 61. Cambridge University Press, Cambridge (1996)
Helgason, S.: The totally-geodesic Radon transform on constant curvature spaces. In: Integral geometry and tomography (Arcata, CA, 1989), volume 113 of Contemp. Math., pages 141–149. Amer. Math. Soc., Providence, RI, (1990)
Helgason, S.: Integral Geometry and Radon Transforms. Springer, New York (2011)
Hielscher, R., Quellmalz, M.: Optimal mollifiers for spherical deconvolution. Inverse Prob. 31(8), 085001 (2015)
Hielscher, R., Quellmalz, M.: Reconstructing a function on the sphere from its means along vertical slices. Inverse Probl. Imaging 10(3), 711–739 (2016)
Inci, H., Kappeler, T., Topalov, P.: On the regularity of the composition of diffeomorphisms. Mem. Amer. Math. Soc., 226(1062):vi+60, (2013)
Jänich, K.: Vector Analysis. Undergraduate Texts in Mathematics. Springer, New York (2001)
Jonas, P., Louis, A.K.: A Sobolev space analysis of linear regularization methods for ill-posed problems. J. Inverse Ill-Posed Probl. 9(1), 59–74 (2001)
Michel, V.: Lectures on Constructive Approximation: Fourier, Spline, and Wavelet Methods on the Real Line, the Sphere, and the Ball. Birkhäuser, New York (2013)
Müller, C.: Analysis of Spherical Symmetries in Euclidean Spaces. Applied Mathematical Sciences, vol. 129. Springer, New York (1998)
Natterer, F., Wübbeling, F.: Mathematical Methods in Image Reconstruction. SIAM, Philadelphia, PA (2000)
Palamodov, V.P.: Reconstruction from Integral Data. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton, FL (2016)
Quellmalz, M.: A generalization of the Funk-Radon transform. Inverse Prob. 33(3), 035016 (2017)
Quinto, E.T.: Null spaces and ranges for the classical and spherical Radon transforms. J. Math. Anal. Appl. 90(2), 408–420 (1982)
Radon, J.: Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Ber. Verh. Sächs. Akad. Wiss. Leipzig. Math. Nat. Kl. 69, 262–277 (1917)
Rubin, B.: Radon transforms and Gegenbauer-Chebyshev integrals. II; examples. Anal. Math. Phys. 7, 349–375 (2017)
Rubin, B.: The vertical slice transform in spherical tomography. ArXiv e-prints, (2018). arXiv:1807.07689 [math.NA]
Salman, Y.: An inversion formula for the spherical transform in \(S^2\) for a special family of circles of integration. Anal. Math. Phys. 6(1), 43–58 (2016)
Salman, Y.: Recovering functions defined on the unit sphere by integration on a special family of sub-spheres. Anal. Math. Phys. 7(2), 165–185 (2017)
Schneider, R.: Functions on a sphere with vanishing integrals over certain subspheres. J. Math. Anal. Appl. 26, 381–384 (1969)
Strichartz, R.S.: \(L^p\) estimates for Radon transforms in Euclidean and non-Euclidean spaces. Duke Math. J. 48(4), 699–727 (1981)
Triebel, H.: Interpolation Theory, Function Spaces, 2nd edn. Differential Operators. Barth, Heidelberg, Leipzig (1995)
Zangerl, G., Scherzer, O.: Exact reconstruction in photoacoustic tomography with circular integrating detectors II: Spherical geometry. Math. Methods Appl. Sci. 33(15), 1771–1782 (2010)
Acknowledgements
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quellmalz, M. The Funk–Radon transform for hyperplane sections through a common point. Anal.Math.Phys. 10, 38 (2020). https://doi.org/10.1007/s13324-020-00383-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-020-00383-2