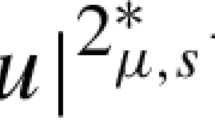Abstract
The aim of this paper is to investigate the multiplicity of solutions to the following nonlocal fractional Choquard–Kirchhoff type equation involving critical exponent,
where \(a\ge 0, b>0\), \(0<s<\min \{1,N/2p\}\), \(2sp\le \mu <N\), \((-\Delta )_p^s\) is the fractional p-Laplace operator, \(\lambda >0\) is a parameter, \(p_{\mu ,s}^*=\frac{(N-\frac{\mu }{2})p}{N-sp}\) is the critical exponent in the sense of the Hardy–Littlewood–Sobolev inequality, \(1<q<p_s^*=\frac{Np}{N-sp}\) and \(h\in L^{\frac{p_s^*}{p_s^*-q}}(\mathbb {R}^N)\). Under some suitable assumptions, we obtain the multiplicity of nontrivial solutions by using variational methods. In particular, we get the existence of infinitely many nontrivial solutions for the degenerate Kirchhoff case by using Krasnoselskii’s genus theory.
Similar content being viewed by others
References
Ambrosetti, A., Rabinowitz, P.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Applebaum, D.: Lévy processes—from probability to finance quantum groups. Not. Am. Math. Soc. 51, 1336–1347 (2004)
Autuori, G., Pucci, P.: Elliptic problems involving the fractional Laplacian in \(\mathbb{R}^N\). J. Differ. Equ. 255, 2340–2362 (2013)
Autuori, G., Fiscella, A., Pucci, P.: Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal. 125, 699–714 (2015)
Caffarelli, L.: Nonlocal diffusions, drifts and games. Nonlinear Part. Differ. Equ. Abel Symp. 7, 37–52 (2012)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Part. Differ. Equ. 32, 1245–1260 (2007)
Caponi, M., Pucci, P.: Existence theorems for entire solutions of stationary Kirchhoff fractional \(p\)-Laplacian equations. Ann. Mat. Pura Appl. 195, 2099–2129 (2016)
Chang, K.C.: Critical Point Theory and Applications. Shanghai Scientific and Technology Press, Shanghai (1986)
Chen, C.S., Wei, Y.F.: Existence, nonexistence, and multiple results for the fractional \(p\)-Kirchhoff-type equation in \(\mathbb{R}^N\). Mediterr. J. Math. 13, 5077–5091 (2016)
Clarke, D.C.: A variant of the Lusternik–Schnirelman theory. Indiana Univ. Math. J. 22, 65–74 (1972)
Corrêa, F.J.S.A., Figueiredo, G.M.: On a \(p\)-Kirchhoff equation via Krasnoselskii’s genus. Appl. Math. Lett. 22, 819–822 (2009)
d’Avenia, P., Siciliano, G., Squassina, M.: On fractional Choquard equations. Math. Models Methods Appl. Sci. 25, 1447–1476 (2015)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2012)
Dipierro, S., Palatucci, G., Valdinoci, E.: Existence and symmetry results for a Schrödinger type problem involving the fractional Laplacian. Matematiche 68, 201–216 (2013)
Felmer, P., Quaas, A., Tan, J.: Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian. Proc. R. Soc. Edinb. Sect. A 142, 1237–1262 (2012)
Figueiredo, G.M., Molica Bisci, G., Servadei, R.: On a fractional Kirchhoff-type equation via Krasnoselskii’s genus. Asymptot. Anal. 94, 347–361 (2015)
Fiscella, A.: Infinitely many solutions for a critical Kirchhoff type problem involving a fractional operator. Differ. Integral Equ. 29, 513–530 (2016)
Fiscella, A., Valdinoci, E.: A critical Kirchhoff type problem involving a nonlocal operator. Nonlinear Anal. 94, 156–170 (2014)
Fiscella, A., Pucci, P.: \(p\)-fractional Kirchhoff equations involving critical nonlinearities. Nonlinear Anal. Real World Appl. 35, 350–378 (2017)
Gao, F., Yang, M.: On the Brezis-Nirenberg type critical problem for nonlinear Choquard equation (2016), preprint, arxiv:1604.00826
Kichenassamy, S., Veron, L.: Singular solutions of the \(p\)-Laplace equation. Math. Ann. 275, 599–615 (1985)
Kilbas, A. A., Srivastava, H. M., Trujillo, J. J.: Theory and applications of fractional differential equations. In: North-Holland Mathematics Studies, vol. 204. Elsevier Science BV, Amsterdam (2006)
Laskin, N.: Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268, 298–305 (2000)
Laskin, N.: Fractional Schrödinger equation. Phys. Rev. E 66, 056108 (2002)
Lieb, E.H.: Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Stud. Appl. Math. 57, 93–105 (1977)
Lieb, E., Loss, M.: Analysis, Gradute Studies in Mathematics. AMS, Providence (2001)
Lions, P.-L.: The Choquard equation and related questions. Nonlinear Anal. 4, 1063–1072 (1980)
Liu, J., Liao, J.F., Tang, C.L.: Positive solutions for Kirchhoff-type equations with critical exponent in \(\mathbb{R}^N\). J. Math. Anal. Appl. 429, 1153–1172 (2015)
Mawhin, J., Willem, M.: Critical Point Theory and Hamiltonian Systems. Springer, New York (1989)
Menzala, G.P.: On regular solutions of a nonlinear equation of Choquard’s type. Proc. R. Soc. Edinb. Sect. A 86, 291–301 (1980)
Metzler, R., Klafter, J.: The restaurant at the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 37, 161–208 (2004)
Mingqi, X., Molica Bisci, G., Tian, G.H., Zhang, B.L.: Infinitely many solutions for the stationary Kirchhoff problems involving the fractional \(p\)-Laplacian. Nonlinearity 29, 357–374 (2016)
Mingqi, X., Pucci, P., Squassina, M., Zhang, B.L.: Nonlocal Schrodinger–Kirchhoff equations with external magnetic field. Discret. Contin. Dyn. Syst. A 37, 1631–1649 (2017)
Molica Bisci, G., Rǎdulescu, V.D.: Ground state solutions of scalar field fractional Schrödinger equations. Calc. Var. Partial Differ. Equ. 54, 2985–3008 (2015)
Moroz, V., van Schaftingen, J.: Ground states of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265, 153–184 (2013)
Moroz, I.M., Penrose, R., Tod, P.: Spherically-symmetric solutions of the Schrödinger–Newton equations. Class. Quantum Gravity 15, 2733–2742 (1998)
Naimen, D.: The critical problem of Kirchhoff type elliptic equations in dimension four. J. Differ. Equ. 257, 1168–1193 (2014)
Nyamoradi, N.: Existence of three solutions for Kirchhoff nonlocal operators of elliptic type. Math. Commun. 18, 489–502 (2013)
Pekar, S.: Untersuchungüber die Elektronentheorie der Kristalle. Akademie, Berlin (1954)
Perera, K., Squassina, M., Yang, Y.: Bifurcation and multiplicity results for critical fractional \(p\)-Laplacian problems. Math. Nachr. 289, 332–342 (2016)
Perera, K., Squassina, M., Yang, Y.: Critical fractional \(p-\)Laplacian problems with possibly vanishing potentials. J. Math. Anal. Appl. 433, 818–831 (2016)
Pucci, P., Saldi, S.: Critical stationary Kirchhoff equations in \(\mathbb{R}^N\) involving nonlocal operators. Rev. Mat. Iberoam. 32, 1–22 (2016)
Pucci, P., Xiang, M.Q., Zhang, B.L.: Multiple solutions for nonhomogeneous Schrödinger–Kirchhoff type equations involving the fractional \(p\)-Laplacian in \(\mathbb{R}^N\). Calc. Var. Partial Differ. Equ. 54, 2785–2806 (2015)
Pucci, P., Xiang, M.Q., Zhang, B.L.: Existence and multiplicity of entire solutions for fractional \(p\)-Kirchhoff equations. Adv. Nonlinear Anal. 5, 27–55 (2016)
Pucci, P., Xiang, M.Q., Zhang, B. L.: Existence results for Schrödinger–Choquard–Kirchhoff equations involving the fractional \(p-\)Laplacian (2016), preprint
Rabinowitz, P.: Minimax method in critical point theory with applications to differential equations. In: CBMS Reg. Conf. Ser. Math., vol. 65. American Mathematical Society, Providence, RI (1986)
Servadei, R., Valdinoci, E.: Variational methods for non-local operators of elliptic type. Discret. Contin. Dyn. Syst. 33, 2105–2137 (2013)
Shen, Z.F., Gao, F.S., Yang, M.B.: Groundstates for nonlinear fractional Choquard equations with general nonlinearities. Math. Methods Appl. Sci. (2016). doi:10.1002/mma.3849
Wang, F.L., Xiang, M.Q.: Multiplicity of solutions to a nonlocal Choquard equation involving fractional magnetic operators and critical exponent. Electron. J. Differ. Equ. 2016, 1–11 (2016)
Xiang, M.Q., Zhang, B.L., Ferrara, M.: Existence of solutions for Kirchhoff type problem involving the non-local fractional \(p\)-Laplacian. J. Math. Anal. Appl. 424, 1021–1041 (2015)
Xiang, M.Q., Zhang, B.L., Rǎdulescu, V.: Existence of solutions for perturbed fractional \(p\)-Laplacian equations. J. Differ. Equ. 260, 1392–1413 (2016)
Xiang, M.Q., Zhang, B.L., Rǎdulescu, V.: Multiplicity of solutions for a class of quasilinear Kirchhoff system involving the fractional \(p\)-Laplacian. Nonlinearity 290, 3186–3205 (2016)
Xiang, M. Q., Zhang, B. L., Zhang, X.: A nonhomogeneous fractional \(p\)-Kirchhoff type problem involving critical exponent in \({\mathbb{R}}^{N}\), Adv. Nonlinear Stud. doi:10.1515/ans-2016-6002
Acknowledgements
M. Xiang was supported by the National Natural Science Foundation of China (No. 11601515) and the Fundamental Research Funds for the Central Universities (No. 3122017080).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Wang, F., Xiang, M. Multiplicity of solutions for a class of fractional Choquard–Kirchhoff equations involving critical nonlinearity. Anal.Math.Phys. 9, 1–16 (2019). https://doi.org/10.1007/s13324-017-0174-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13324-017-0174-8