A dispersive model for undular bores

Abstract

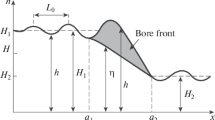
In this article, consideration is given to weak bores in free-surface flows. The energy loss in the shallow-water theory for an undular bore is thought to be due to upstream oscillations that carry away the energy lost at the front of the bore. Using a higher-order dispersive model equation, this expectation is confirmed through a quantitative study which shows that there is no energy loss if dispersion is accounted for.

Appendix A: The numerical scheme

The numerical discretization used to find approximate solutions of the system (1.1) is briefly presented. First, it should be noted that mathematical aspects of the system (1.1) have been studied in [9, 11, 28]. In these works, a theory of well posedness for the Cauchy problem and various boundary-value problems has been developed. In [10], a finite-element method for the periodic problem was constructed. Here, we consider a finite-difference method. We begin by writing $\zeta (x,t) = \eta (x,t) - \eta _0(x)$, and $\xi (x,t) = w(x,t) - w_0(x)$, so that the functions $\zeta$ and $\xi$ satisfy homogeneous Dirichlet boundary conditions. Next, we use the transformation

$$\begin{aligned} \left( \begin{array}{l} \displaystyle u\\ \displaystyle v \end{array}\right)=\left( \begin{array}{ll} \displaystyle \root 4 \of {\frac{g}{h_0}}&\displaystyle \root 4 \of {\frac{h_0}{g}} \\ \displaystyle \root 4 \of {\frac{g}{h_0}}&\displaystyle - \root 4 \of {\frac{h_0}{g}} \end{array}\right)\left( \begin{array}{l} \displaystyle \zeta \\ \displaystyle \xi \end{array} \right) \end{aligned}$$

(5.1)

to obtain a system which is diagonal in the highest derivative. The new variables $u$ and $v$ satisfy the equations

$$\begin{aligned} \displaystyle u_t + \frac{1}{6} c_0 h_0^2 u_{xxx}&= - \left( \root 4 \of {\frac{g}{h_0}} \frac{\partial _x(u-v)}{2} + w_0^{\prime } \right) \left( u + \root 4 \of {\frac{h_0}{g}} w_0 + \root 4 \of {\frac{g}{h_0}} \eta _0 + \root 4 \of {\frac{g}{h_0}} h_0 \right) \\&\displaystyle - \left(\root 4 \of {\frac{h_0}{g}} \frac{\partial _x(u+v)}{2} + \eta _0^{\prime } \right) \left(\sqrt{\frac{g}{h_0}} \frac{u-v}{2} + \root 4 \of {\frac{g}{h_0}}w_0 + \root 4 \of {\frac{h_0}{g}} g \right) \\&\displaystyle - \root 4 \of {\frac{h_0}{g}} \frac{g h_0^2}{6} \eta _0^{\prime \prime \prime } - \root 4 \of {\frac{g}{h_0}} \frac{h_0^3}{6} w_0^{\prime \prime \prime } \\&\displaystyle \equiv \lambda _u (u,v,\partial _x),\\ v_t-\frac{1}{6} c_0 h_0^2 v_{xxx}&= \left( \root 4 \of {\frac{g}{h_0}} \frac{\partial _x(u-v)}{2} + w_0^{\prime } \right) \left( -v + \root 4 \of {\frac{h_0}{g}} w_0 - \root 4 \of {\frac{g}{h_0}} \eta _0 - \root 4 \of {\frac{g}{h_0}} h_0 \right) \\&\displaystyle - \left(\root 4 \of {\frac{h_0}{g}} \frac{\partial _x(u+v)}{2} + \eta _0^{\prime } \right) \left(\sqrt{\frac{g}{h_0}} \frac{u-v}{2} + \root 4 \of {\frac{g}{h_0}}w_0^{\prime } - \root 4 \of {\frac{h_0}{g}} g \right) \\&\displaystyle + \root 4 \of {\frac{h_0}{g}} \frac{g h_0^2}{6} \eta _0^{\prime \prime \prime } - \root 4 \of {\frac{g}{h_0}} \frac{h_0^3}{6} w_0^{\prime \prime \prime } \\&\displaystyle \equiv \lambda _v (u,v, \partial _x). \end{aligned}$$

The functions $u$ and $v$ also satisfy homogeneous Dirichlet boundary conditions at the endpoints $x_1$ and $x_2$ of the computational domain. In addition, we require the Neumann conditions $u_x(x_2,t)=0$ and $v_x(x_1,t)=0$. The first and third spatial derivatives are approximated by the matrices $D_{N,1}$ and $D_{N,3}^u$, $D_{N,3}^v$, respectively. The matrix $D_{N,1}$ arises from a standard finite-difference approximation of the first derivative. The matrix $D_{N,3}^u$ is given by

$$\begin{aligned} D_{N,3}^u=\frac{1}{2(\delta x)^3} \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 10&-12&6&-1&\,&\\ 2&0&-2&1&\,&\\ -1&2&0&-2&1&\,&\\&\ddots&\ddots&\ddots&\ddots&\ddots&\\&\,&-1&2&0&-2&1 \\&\,&-1&2&0&-2 \\&\,&\,&-1&2&1 \\ \end{array} \right). \end{aligned}$$

(5.2)

This matrix arises from the use of one-sided Taylor approximations on the left side of the domain, since only one boundary conditions is required there. Since a Neumann condition is given on the right side of the domain, a simpler pattern is seen in the right lower half of the matrix. Similar considerations are applied to construct $D_{N,3}^v$.

The system of ordinary differential equations resulting from the spatial discretization is integrated with a combined Crank-Nicholson Adams-Bashforth method. The linear terms are treated with a Crank-Nicholson method, while the nonlinear terms are treated using an Adams-Bashforth method. This combination of time discretizations is explicit, but treats the highest-order spatial derivatives implicitly. Using the notation $U_N^m$ to denote the $N$-vector approximating $u(\cdot , m \, \delta t)$ at the $m$-th time step, and respectively for $V_N^m$, the equations to be solved at the $m$-th time step are

$$\begin{aligned} U_N^{m+1}&= (I+c_0h_0^2 {\textstyle \frac{\delta t}{12}}D_{N,3}^u)^{-1} [(I-c_0h_0^2{\textstyle \frac{\delta t}{12}}D_{N,3}^u)U_N^{m}\\&+{\textstyle \frac{\delta t}{2}}\{ 3\lambda _u(U_N^m,V_N^m,D_{N,1}) -\lambda _u(U_N^{m-1},V_N^{m-1},D_{N,1})\}]\\ V_N^{m+1}&= (I-c_0h_0^2{\textstyle \frac{\delta t}{12}}D_{N,3}^v)^{-1} [(I+c_0h_0^2{\textstyle \frac{\delta t}{12}}D_{N,3}^v )V_N^{m}\\&+{\textstyle \frac{\delta t}{2}}\{ 3\lambda _v(U_N^m,V_N^m,D_{N,1})-\lambda _v(U_N^{m-1},V_N^{m-1},D_{N,1})\}] \end{aligned}$$

As two previous time steps are required to compute the next time step, the very first time step is done using a simple forward Euler method. The Euler method is locally of second order, and a single time step does not lead to instability problems. In Table 4, a convergence study is presented, using an exact solution found in [19]. In non-dimensional variables, where both $g=1$ and $h_0=1$ are set to unity, this solution is given by

$$\begin{aligned} \eta (x,t)&=-\frac{6+\kappa }{12}+\frac{\kappa }{4}\ \text{ sech}^2\left(\frac{1}{2}\sqrt{\kappa }(x+x_0-ct)\right),\\ w(x,t)&=\frac{\mp \sqrt{2}(6+\kappa )+12c}{12}\pm \frac{\kappa }{2\sqrt{2}}\ \text{ sech}^2\left(\frac{1}{2}\sqrt{\kappa }(x+x_0-ct)\right), \end{aligned}$$

(5.3)

for positive $\kappa$ and $c$. This exact traveling wave is integrated in time, and it can be seen that second-order convergence is obtained for both the spatial and the temporal discretization. Figure 5 shows both the initial profile $\eta (x,0)$ and the computed profile $\eta (x,t)$ at $t=10$.

Table 4 Convergence of time and space discretization

Fig. 5

Plots of $\eta$ of the exact traveling wave defined in (A-3) with $\kappa =\frac{1}{2}$ and $c=1$, shown at time $t=10$. The computed profile was obtained with a resolution $\delta x= 0.01$ and $\delta t=0.01$