Introduction

Semaglutide is a receptor agonist of the naturally occurring peptide hormone glucagon-like peptide-1 (GLP-1). As with native GLP-1, semaglutide acts to stimulate insulin secretion and inhibit glucagon release depending on the blood glucose concentration, leading to improved blood glucose levels together with a reduced risk of hypoglycaemia [1, 2]. Semaglutide is approved for the treatment of type 2 diabetes mellitus, using the subcutaneous route of administration. With 94% amino acid sequence homology to native GLP-1, semaglutide has three structural modifications that make it less susceptible to degradation by dipeptidyl peptidase-4 (DPP-4) enzymes and prolong its half-life to approximately 1 week [1, 3]. Semaglutide is thereby appropriate for once-weekly administration.

The prolonged exposure of semaglutide as compared with native GLP-1 is mainly driven by slow systemic elimination and, to a lesser extent, by delayed absorption [4], in line with the observation that more than 99% of the semaglutide is bound to plasma albumin [5]. In a metabolism trial, semaglutide was the primary component circulating in plasma and, prior to excretion, it was metabolised by proteolytic cleavage of the peptide backbone and sequential beta-oxidation of the fatty acid side chain [4]. Semaglutide metabolites are primarily excreted in the urine and faeces [4].

Semaglutide population pharmacokinetics (PK) and exposure in terms of average concentration in the dosing interval have been previously investigated for subcutaneous dosing using phase 3 steady-state data from subjects with type 2 diabetes [6]. Of the covariates investigated, only body weight had a relevant effect on the exposure of semaglutide at either once-weekly maintenance dose of 0.5 or 1.0 mg [6].

In addition to an assessment of semaglutide exposure levels, the aim of the present analysis was to provide additional details of the PK properties of semaglutide in terms of absorption, distribution and elimination and their relationships to covariate factors, in order to develop a novel disposition model that would be generally applicable across different routes of administration. This was achieved by means of population PK models using frequently sampled PK profiles from nine clinical pharmacology trials. Inclusion of data from intravenous administration provided information about the structural two-compartment disposition model, allowing for separate estimation of clearance and bioavailability.

The analysis was applied to identify and validate the use of a one-compartment model previously applied to analyse sparsely sampled phase 3 data [6], and subsequently to investigate the consistency between PK data from phase 1 and phase 3 trials.

Methods

Clinical Data Included in the Analysis

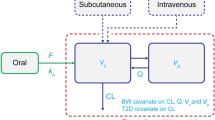
A two-compartment PK model was estimated using data from nine clinical pharmacology trials employing single as well as multiple semaglutide doses and conducted in subjects with type 2 diabetes or obesity, or in healthy volunteers (Table 1). The included trials were those with administration of recombinant semaglutide in which PK samples, assessed via liquid chromatography and tandem mass spectrometry (LC–MS/MS) [3], were available at the time of the analysis. One trial provided data for the intravenous administration of semaglutide and also used different drug product strengths (see further descriptions in the “Methods” section of the Electronic supplementary material, ESM).

Table 1 Overview of clinical trials included in the analysis
Full size table

In order to compare the current analysis with the analysis conducted using phase 3 data, a one-compartment model was estimated using data from seven of the clinical pharmacology trials (Table 1) which employed multiple doses of the semaglutide drug product used in the phase 3 trials. Data from the two trials with single dose administration were not included in this comparison.

Population Pharmacokinetic Modelling

Datasets containing plasma concentration and covariate data from each trial were converted to a format compatible with the nonlinear mixed-effects modelling (NONMEM) software (ICON Development Solutions, Ellicott City, MD, USA), version 7.1.2. Out of a total of 10,573 concentration values, 43 values (i.e. < 1%) were excluded because the subjects had an inadequate dosing history. Conditional weighted residuals (CWRES) were used as a diagnostic tool to identify outliers, and an additional 24 concentration values (23 in the one-compartment model) were excluded from the final dataset as they were associated with CWRES greater than 6 in order to limit bias from influential data items. The software package R (version 3.2.3, obtained from the R Foundation: http://www.r-project.org/foundation) was used for data file processing, explorative data analysis and to plot figures.

Model Development

Model development was conducted in NONMEM as follows:

  1. 1.

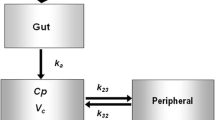
    The structural disposition model, which was supported by graphical analysis, in particular of intravenous data, was a two-compartment model with first-order elimination. Different absorption models were investigated, including parallel absorption, but a simpler first-order absorption model for subcutaneous administration was found to adequately describe the data, and no significant improvement was obtained based on other absorption models.

  2. 2.

    An additive residual error model on log-transformed concentration values was assessed to adequately describe the data.

  3. 3.

    Inter-individual variability in the absorption rate (ka), clearance (CL), intercompartmental clearance (Q), central volume (Vc), and peripheral volume (Vp) was explored using a log normal distribution in a model that included covariates with clear effects: drug product strength on the absorption rate constant and body weight as a covariate factor on CL, Vc and Vp. A correlation between the central volume and CL was significant and included in the model. Due to the limited amount of intravenous data, less information was available for individual estimation of Q and for the separation of Vc and Vp. Various implementations for these parameters were investigated and selected based on objective function values; i.e. using individual (eta) values for CL to identify differences across subjects for Q, as well as for Vc and Vp.

  4. 4.

    The covariate effects of sex, race, ethnicity, age, hepatic impairment and glycaemic status were investigated for CL, Vc and ka based on a graphical analysis of individual parameter estimates versus body weight, and glycaemic status was identified as a covariate factor for CL and ka. Similarly, injection site was investigated with respect to F and ka. Covariates with 90% confidence intervals which were within the 80–125% equivalence interval were not considered important.

  5. 5.

    Covariate effects were investigated using a full model approach with inclusion of all investigated covariates in one step (Table 2). The final model included only those covariates that were significant (10% alpha level). To assess the amount of variability explained by covariate factors, a base model was investigated, including only covariates for the effects of drug product strength on the absorption rate constant.

    Table 2 Covariates included in the full two-compartment model
    Full size table

Model Description

The full model for subcutaneous administration was a model with first-order absorption, two-compartment disposition and first-order elimination, whereas intravenous data were modelled as a bolus injection into the central compartment. Inter-individual variability was estimated for ka, and CL/Q (with a common factor), and for Vc/Vp (with a common factor).

The covariate models were parameterised as follows for the ith individual:

$$ {\text{CL}}_{i} = {\text{CL}}_{\text{ref}} \cdot E_{\text{weight, CL}} \cdot E_{\text{sex}} \cdot E_{\text{race}} \cdot E_{\text{ethnicity}} \cdot E_{\text{glycaemic status}} \cdot E_{\text{age group}} \cdot { \exp }(\eta_{{{\text{CL}},i}} ) $$
$$ Q_{i} = Q_{\text{ref}} \cdot E_{\text{weight, CL}} \cdot { \exp }(\eta_{{{\text{CL}},i}} ) $$
$$ V_{{{\text{c}},i}} = V_{\text{c,ref }} \cdot E_{\text{weight,V}} \cdot { \exp }(\eta_{{{\text{V,}}i}} ) $$
$$ V_{{{\text{p,}}i}} = V_{\text{p,ref}} \cdot E_{\text{weight,V}} \cdot { \exp }(\eta_{{{\text{V}},i}} ), $$

and the effect of drug product strength on the rate of absorption was described as

$$ k_{\text{a}} = \left( {\left( {k_{\text{a,ref}} } \right)^{{1.34\;{\text{mg}}}} \cdot \left( {\theta_{{{\text{k}}_{\text{a}} ,\; 1 \;{\text{mg}}}} } \right)^{{ 1 {\text{mg}}}} \cdot \left( {\theta_{{{\text{k}}_{\text{a}} , 3 {\text{mg}}}} } \right)^{{ 3 {\text{mg}}}} \cdot \left( {\theta_{{{\text{k}}_{\text{a}} , 1 0 {\text{mg}}}} } \right)^{{ 1 0 {\text{mg}}}} } \right) \cdot {\theta_{{{\text{k}}_{\text{a}}, {\text{T2D}}}}}^{\text{T2D}} \cdot \exp \left( {\eta_{{{\text{k}}_{\text{a}} . {\text{i}}}} } \right). $$

Covariate relationships were described as follows:

$$ F = F_{\text{ref}} \left( {\theta_{\text{thigh}} } \right)^{\text{thigh}} $$
$$ E_{\text{weight,CL}} = \left( {\frac{{{\text{weight}}_{i} }}{{85\; {\text{kg}}}}} \right)^{{\theta_{\text{weigth,CL}} }} $$
$$ E_{\text{weight,V}} = \left( {\frac{{{\text{weight}}_{i} }}{{85\; {\text{kg}}}}} \right)^{{\theta_{\text{weight, V}} }} $$
$$ E_{\text{sex}} = \left( {\theta_{\text{male}} } \right)^{\text{male}} $$
$$ E_{\text{race}} = \left( {\theta_{\text{black}} } \right)^{\text{black}} \cdot \left( {\theta_{\text{Asian}} } \right)^{\text{Asian}} $$
$$ E_{\text{ethnicity}} = \left( {\theta_{\text{Hispanic}} } \right)^{\text{Hispanic}} $$
$$ E_{\text{glycaemic status}} = \left( {\theta_{\text{T2D}} } \right)^{\text{T2D}} $$
$$ E_{\text{age group}} = \left( {\theta_{\text{ > 65 years}} } \right)^{\text{ > 65 years}}. $$

In the above equations, θ represents an estimated value for a covariate and η represents between-subject variability. The other exponents are indicator variables assigned a value of 1 for the specific covariate values and 0 otherwise. CLref, Qref, Vc,ref, Vp,ref, Fref and ka, ref are parameter values for the reference subject profile, which is a healthy, white, non-Hispanic female aged ≤ 65 years with a body weight of 85 kg, using the abdomen as the injection site and dosed with a 1.34 mg/mL semaglutide drug product. The residual error model was additive for log-transformed observations.

Steady-State Exposure Evaluation for Subcutaneous Semaglutide

A one-compartment model, similar to the one used to evaluate phase 3 data, was investigated using steady-state data from subcutaneous dosing only in clinical pharmacology trials; hence, the fraction absorbed (F) could not be estimated separately in this model. Therefore, the model was parameterised by the apparent clearance (CL/F), volume of distribution (V/F) and the absorption rate constant (ka). The inter-individual variability was estimated for each of these. The residual error model was additive for log-transformed observations.

The one-compartment model contained three covariate relationships: body weight and glycaemic status (healthy, type 2 diabetes) on CL, and body weight on volume of distribution. These were parameterised as for the two-compartment model.

Compliance with Ethics Guidelines

This article is based on previously conducted studies and does not contain any studies with human participants or animals performed by any of the authors.

Results

Population Characteristics

A total of 353 subjects with 10,573 semaglutide concentrations were included in the population PK model analysis. For the comparison to the phase 3 modelling approach, 267 subjects contributed with 8292 semaglutide concentration values. The demographic characteristics for the subjects included in each of the analyses are summarised in Table 3.

Table 3 Demographic characteristics of subjects included in the two- and one-compartment models
Full size table

Semaglutide Pharmacokinetics

The final population PK model provided an accurate description of the PK time course across the nine clinical pharmacology trials. Figure 1 shows the consistency between the model and data across the eight trials which employed both single and multiple doses of marketed semaglutide with a drug product strength of 1.34 mg/mL. Figure 2 shows that the biphasic PK profile obtained from the two-compartment model is consistent with intravenous data and, furthermore, that the rate of absorption as well as the maximum concentration following subcutaneous doses of different strengths were well captured by the model.

Fig. 1
figure 1

Observed and model-predicted semaglutide pharmacokinetic profiles from eight clinical pharmacology trials. All trials employed semaglutide doses of up to 1.0 mg, except trial 3, which was a single dose (0.5 mg) trial, and trial 4, which used a supratherapeutic dose of 1.5 mg. Data points with error bars are observed geometric means and 95% CIs. Model predictions (lines) are population predictions from the final two-compartment model of semaglutide PK. CI confidence interval, PK pharmacokinetics, SD single dose, SS steady state

Full size image
Fig. 2a–b
figure 2

Observed and model-predicted subcutaneous and intravenous semaglutide PK profiles over 7 days (a) and 30 days (b). Data are from trial 7 with semaglutide doses of up to 0.5 mg. Data points with error bars are observed geometric means and 95% CIs. Model predictions (lines) are population predictions from the final two-compartment model of semaglutide PK. In b, two values above the lower limit of quantification obtained at day 35 were not included in the figure. CI confidence interval, i.v. intravenously, PK pharmacokinetic(s), s.c subcutaneously

Full size image

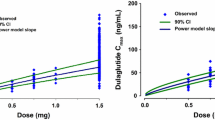
The model-based analysis suggested that drug product strength influences the rate of absorption but not the bioavailability (Table 4), indicating that the total exposure of semaglutide is not affected by the product strength. These model-based results are consistent with the noncompartmental results for trial 7 (see Table S1 in the ESM), in which equivalence was demonstrated for exposure (AUC0–∞) for all pairwise comparisons between the three strengths of semaglutide. For Cmax, the comparison between 1 mg/mL and 3 mg/mL met the equivalence criterion but equivalence was not shown for 1 mg/mL relative to 10 mg/mL or for 3 mg/mL relative to 10 mg/mL, as Cmax increased with increasing strength.

Table 4 Parameter estimates obtained from the final two-compartment model
Full size table

All parameters were successfully estimated (relative standard error ≤ 11%) in the final model using data from the nine clinical trials (Table 4). In accordance with findings based on phase 3 semaglutide data investigating covariate effects on CL/F [6], body weight was found to be the only important covariate with respect to CL and, hence, average semaglutide concentrations under steady-state conditions with 90% CIs outside the equivalence interval. There were also clear relationships between body weight and the Vc and Vp, whereas the ka was independent of body weight (Table 4 and Fig. S1c in the ESM). Less important though statistically significant effects included an effect on semaglutide CL of glycaemic status, with a 12% higher CL (95% CI 9–16%) observed in subjects with type 2 diabetes compared to healthy subjects (Table 4 and Fig. S1a in the ESM). Moreover, ka was reduced in subjects with type 2 diabetes compared to healthy subjects (Table 4 and Supplementary Fig. S1c in the ESM). For a typical subject with type 2 diabetes and a body weight of 85 kg, clearance was estimated to be 0.0348 L/h (95% CI 0.0327–0.0369 L/h) and the total volume of distribution was estimated to be 7.7 L (Vc + Vp; Table 4). A small effect of injection site was found with respect to the bioavailability, which was 12% lower when using the thigh compared with the abdomen (95% CI 0.84–0.92). The effects of other covariates were not relevant as they were found to lie within the 80–125% equivalence interval. No effects of sex, race, ethnicity, age, or hepatic impairment on CL were found, and these covariates were excluded from the final model.

Trial 7, which provided data from both subcutaneous and intravenous administration, allowed the absolute bioavailability for subcutaneous administration of semaglutide to be estimated. Using noncompartmental analysis, the absolute bioavailability after the subcutaneous administration of semaglutide was estimated to be 89% (95% CI 0.83–0.94). This was captured well in the final model, which estimated the bioavailability to be 85% (95% CI 0.80–0.90) (Table 4).

Inclusion of covariates in the final two-compartment model explained 58%, 56% and 24% of the interindividual variance of CL, volume of distribution and ka, respectively.

Model Qualification

Parameter estimates (Table 4) were estimated with a low (≤ 11%) relative standard error in the final model; shrinkage values were all below 10%, supporting the accuracy of the individual parameter estimates.

The standard visual predictive checks indicated that the model was able to reproduce the data used for estimation in terms of both median concentrations and variability between subjects (Fig. S2 in the ESM). In addition, an illustration of variability in a dosing interval was included for the dose-normalised steady-state concentrations from the target semaglutide doses 0.5 and 1.0 mg (Fig. 3a). Subjects at other dose levels and those who did not complete the study were excluded from this analysis. Thus, the figure was limited to include data from the last PK profile in each trial to illustrate the variability at steady-state conditions.

Fig. 3a–b
figure 3

Variability of semaglutide PK under steady-state conditions (a) and model fits to dose-normalised semaglutide concentration–time profiles at steady state for different body weight quantiles (b). For a, points with error bars are observed steady-state PK data (geometric mean and 90% range) for 173 completing subjects at selected time points with PK sampling across trials. Overlaid are 58 simulated replicates of data (n = 10,034) in a dosing interval after the latest treatment dose. The light blue line represents the geometric mean of the observed data and the shaded area represents the 90% prediction interval. The figure includes data from six trials with steady-state PK and subjects treated with 0.5 mg and 1.0 mg semaglutide as well as the model from nine clinical pharmacology trials of semaglutide. For b, data points with error bars are observed geometric means and 95% CIs from seven clinical pharmacology trials with semaglutide at steady state concentrations after weekly dosing of 0.5 or 1.0 mg. Model predictions are population predictions from the final two-compartment model of semaglutide PK. CI confidence interval, PK pharmacokinetic(s)

Full size image

The dose-normalised time profiles across body weight in 10-kg intervals (Fig. 3b) spanned a similar range to the overall 90% range, illustrating that body weight does explain most of the variability. Furthermore, the close fit of the model to data in each of the 10-kg intervals illustrates that the influence of body weight on the different parameters was adequately described by the model.

The above findings indicate that the two-compartment PK model provided an accurate description of the PK of semaglutide across clinical pharmacology trials, including different populations, administration routes and drug product strengths, and was found suitable for predictive purposes, i.e. for the simulation of semaglutide concentration–time profiles in various populations. Moreover, the low interindividual variation of ~ 15% for both CL and Vc as well as the low residual error (< 5%; Table 4) indicate that the PK of semaglutide is highly predictable.

Estimation of a One-Compartment Model for Steady-State Evaluation of Subcutaneous Data

The population PK model was compared to a one-compartment model similar to the one used in the phase 3 analysis. The two models provided almost identical apparent exposure estimates for individual subjects (Fig. S3a in the ESM). In addition, mean simulated PK profiles during subcutaneous administration were almost identical, with similar exposure levels as well as peak-to-trough fluctuations (Fig. S3b in the ESM). The PK parameter estimates in the one-compartment model used for comparison were similar to those obtained with the two-compartment model (Table S2 in the ESM).

Comparison with the Model Estimated with Phase 3 Data

Parameter values obtained in the present analysis for a reference subject profile were compared to the corresponding parameter values obtained with phase 3 data [6] (Table 5). Due to limitations in the phase 3 data, that analysis applied a fixed value of ka. Although the total volume of distribution was lower in the present analysis than in the phase 3 analysis, profiles from these models were similar (Fig. 4), indicating that the higher volume of distribution in the phase 3 model had a relatively small impact on the overall PK profile. High consistency between the simulated profiles indicate that the PK in the phase 3 trials could be predicted using the two-compartment model that was developed using clinical pharmacology data, supporting the overall predictability of semaglutide PK. Furthermore, the estimated inter-individual variability in clearance (15.2%; Table 4) was consistent with phase 3 data (12.9%) [6].

Table 5 Comparison of pharmacokinetic parameter values from different semaglutide models
Full size table
Fig. 4
figure 4

Simulated PK profiles under steady-state conditions for a reference subject profile based on the final two-compartment model developed from clinical pharmacology data and the one-compartment model developed from phase 3 data

Full size image

Discussion

The PK of semaglutide were well characterised by a two-compartment model with first-order absorption and elimination, and were shown to be predictable across clinical pharmacology and phase 3 trials and across subjects with low interindividual variation and low residual error. This model provided a joint description of semaglutide PK across clinical pharmacology trials in both healthy subjects and those with type 2 diabetes with frequently sampled PK profiles following subcutaneous and intravenous administration in well-controlled settings.

The total volume of distribution (Vc + Vp) was approximately 8 L, similar to the volume of extracellular water in the body and supporting the idea that semaglutide distributes into plasma and peripheral tissues to the same extent as albumin [7, 8]. The terminal half-life was driven by the disposition parameters rather than the rate of absorption. The population PK model for semaglutide was similar overall to that developed for dulaglutide [9], whereas liraglutide had much faster elimination [10], and exenatide extended-release had nonlinear disposition and a substantially slower absorption [11]. Compared to semaglutide, dulaglutide has approximately 50% greater CL and a 20% lower volume of distribution, as well as approximately threefold slower absorption [9]. The interindividual variability was, however, greater for dulaglutide (40.5% coefficient of variation (CV) for CL) compared to semaglutide (CV for CL was 15.2% in the present analysis and 12.9% in the phase 3 analysis [6]). Similarly, both exenatide extended-release and liraglutide had large variabilities between subjects compared to semaglutide [10, 11].

Based on the present steady-state data, we compared the developed population PK model to a one-compartment PK model similar to the one estimated in the phase 3 analysis [6] with almost identical results. Moreover, we verified that the typical steady-state profiles obtained from phase 3 data [6] were consistent with those predicted based on clinical pharmacology data, and similar estimates for clearance CV% also verified that variability was consistent compared to phase 3 trial results.

In the phase 3 population PK analysis, only body weight had a relevant effect on the exposure of semaglutide, a finding which did not warrant dose adjustment [12]. No effects of sex, age, race, ethnicity, renal function or injection site used on semaglutide exposure were observed [6]. The present analysis confirmed the finding that only body weight was a relevant covariate for exposure. Compared to the phase 3 evaluation, the current analysis provides a more general description of semaglutide PK that is applicable across different administration routes, and informs on covariate relationships not only for exposure, but also for absorption, distribution and elimination. Additional covariate effects were identified for body weight on the Vc and Vp and glycaemic status on CL and the ka. Other investigated covariates (sex, race, ethnicity, age group, hepatic impairment) were not found to be influential and were not included in the final model. The impact of covariates on the PK of semaglutide support previous findings [6, 12] that no adjustment of the dose is needed across population subgroups.

With once-daily liraglutide, another GLP-1 receptor agonist approved for the treatment of type 2 diabetes at doses of up to 1.8 mg, body weight and sex were found to be the most important covariates for exposure which, however, did not influence liraglutide PK to any clinically relevant degree [13]. Similarly, neither age, body weight, sex, race, ethnicity nor injection site influenced once-weekly semaglutide or dulaglutide PK to any clinically relevant extent [6, 9]. For twice-daily exenatide and once-weekly exenatide extended-release, body weight was also found to have a significant relationship with the volume of distribution, and a significant relationship between renal function and elimination was found [11, 14].

The slightly higher CL of semaglutide in subjects with type 2 diabetes compared to healthy subjects has also been seen previously with liraglutide 1.8 mg [10] and with liraglutide for weight management at a higher 3.0 mg dose [15]. The mechanism behind this difference is not known.

The present analysis showed that injection site had a small effect on the bioavailability of semaglutide, which was lower following injection in the thigh compared to abdominal injection. This observation was in accordance with previous findings that the injection site has a minor and not clinically relevant effect on the CL/F of semaglutide [6]. Similarly, the bioavailability of liraglutide was found to be slightly lower after administration in the thigh versus the abdomen [16]. Differences between injection sites are generally considered to be of no clinical relevance across GLP-1 receptor agonists [9, 17]. A limitation of the present analysis is that we cannot exclude the possibility that other demographic factors that we did not evaluate were influential in the target patient population.

Conclusions

In summary, semaglutide PK was shown to be predictable across clinical pharmacology and phase 3 trials, with limited interindividual variability that was primarily influenced by body weight. A novel two-compartment model provided a general characterisation of semaglutide absorption following subcutaneous administration and of distribution and elimination across administration routes. A one-compartment model structure was found to be suitable for conducting covariate analyses of exposure levels based on sparse PK sampling in late-stage trials for subcutaneous semaglutide.