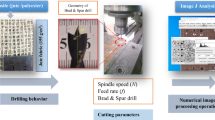
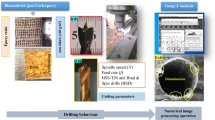
Abstract
This study analyses the interior-two-flange (ITF) web crippling strength of roll-formed aluminum alloy lipped channels (RA channels) with web holes employing experimental testing, numerical modeling, and deep neural network (i.e., Deep belief Network, DBN). A total of 30 experimental tests on web crippling behavior were carried out, with the results utilized to validate a finite element (FE) model, developed in this study. The experimental results were compared to the data produced by the validated FE model, which was then used to train the DBN model. The results of the DBN prediction were shown to be around 5% more conservative than the FE results. In order to evaluate the effects of associated factors on the ITF web crippling strength of RA channels, a comprehensive parametric study was conducted using the DBN. The design guidelines that are currently available in the American Iron and Steel Institute (AISI 2016), the Australian and New Zealand Standards (AS/NZS 1997; AS/NZS (2018)), and the Eurocode (CEN 2007) were found to be unreliable while determining the ITF web crippling strength of RA channels. The DBN's predictions developed new formulae for calculating the web crippling strength reduction factors. After conducting a reliability study, it was found that the developed strength reduction factor equations are reliable when calculating the ITF web crippling strength of such perforated roll-formed aluminium alloy channels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Aluminum alloy (RA) structural members are increasingly employed as load-bearing components in structural engineering applications (Liu et al. (2015), Hiyama et al. (2000), Kim et al. (2018), Nanda and Behera (2005), Seo et al. (2016)); they frequently require web openings for convenience of service installation. Web crippling is actually local buckling that often occurs when the web is slender, and thus the research on web crippling behaviour of RA channels is becoming a focus in structural engineering. However, in current design standards (AISI (2016), AS/NZS (1997a, b, 2018), CEN (2007)), there are no guidelines on (reduced) web crippling strength of RA perforated channels. Therefore, this paper intends to analyse the interior-two-flange (ITF) web crippling behaviour of RA perforated channels (see Fig. 1). The analysis was carried out with the help of experimental testing, finite element (FE) modelling, and deep learning methods.
Few studies on web crippling behaviour of RA sections could be found in the literature. Zhou and Young (2008, 2009) investigated web crippling behaviour of tubular sections using experimental tests, and they found that AS/NZS (1997a, b, 2018), CEN (2007) are unreliable in determining the web crippling strength. Mclntosh et al. (2021) investigated two-flange web crippling of RA lipped channel sections, and conducted a comprehensive parametric analysis to study the effects of related factors. They also proposed design approach for the RA channels under such loading cases. Alsanat et al. (2019, 2020) investigated two-flange web crippling behaviour of RA channels experimentally and numerically, and the design guidelines from AS/NZS (1997a, b), AS/NZS (2018), and CEN (2007) were proven to be unreliable by comparing design strengths with the test results. The findings of the comparison demonstrate that the design strengths are unreliable, hence new design rules based on AS/NZS (1997a, b), AS/NZS (2018), and CEN (2007) have been recommended. Only a few investigations on web crippling strength of perforated sections have been conducted. Fang et al. (2022a, b) used experimental testing, numerical simulations, and machine learning approaches to examine the two-flange web crippling behaviour of RA unlipped perforated channels. The developed machine learning technique was proven to be accurate in determining the two-flange web crippling strength of RA channels, however the objective is unlipped channels. Similarly, Fang et al. (2022c) studied the lip effects on web crippling behaviour in RA lipped channel sections. However, the research objectives in Fang et al. (a, b, c) do not include the ITF web crippling performance of the RA lipped channel sections.
Deep Belief Network (DBN) (Hinton (2006)) could be used to do data regression and prediction work, has been applied in multiple research (Qureshi et al. (2017), Wang et al. (2017)). Besides, DBN is a quick approach for establishing optimal settings that may be learned to reflect high-dimensional data features. DBN has also been shown to be a valuable method for studying thin-walled structures Fang et al. (2022a, b, c).
A DBN framework is employed in this research to analyse the mechanism of ITF web crippling in RA perforated channels. The experimental results on RA perforated channels when loaded under ITF are presented, and the test results were used to verify the FE models. The DBN was trained using the data points that were obtained from the validated finite element models. The prediction accuracy of DBN, as well as the design recommendations from AISI (2016), AS/NZS (1997a, b), AS/NZS (2018), and CEN (2007), was evaluated by comparing the web crippling strength calculated from those approaches with the results of the tests. After that, the result of the DBN was used in the process of developing the design equations on the (reduced) web crippling strength of RA perforated channels under ITF loading circumstances. Notably, Fang et al. (2022b) investigated the ITF web crippling behavior of unlipped channel sections using the similar methodology. Similar methodologies and test data from Fang et al. (2022b) have been applied in the present study.
2 Laboratory Tests (Fang et al. 2022b)
2.1 Test specimen
A total of 30 RA perforated channels were tested. The test specimens are divided into two categories: unfastened and fastened parts. Three bearing lengths (N) are considered in the tests: 50, 75, and 100 mm. Instead of 1.5 times the web's flat section, the distance between the bearing plate's edge and both ends of the members was 1.5 times the web's entire depth (h). For the tested channels, the hole diameter to web depth (a/h) ratios were 0.2 and 0.6, respectively.
The specimens were labelled with information on the section dimensions, web hole size and location, bearing length and flange type. The label "ITF240-N50-DH-A0.6-FR" (see Fig. 1) can be explained as follows: "ITF" stands for loading condition; "240" stands for the web depth in millimeters (d = 240 mm); "N50" stands for bearing length in millimeters (N = 50 mm), and in the tests, three bearing lengths are considered: 50, 75, and 100 mm; "NH," "DH," and "OH" reflect the state of the web hole. "NH" denotes plain channel, whereas "DH" and "OH" denote the channel with a down hole and an offset hole, respectively; "A0.6" denotes the ratio of a/h, which is equal to 0.6; and "FR" and "FX" stand for unfastened channel and fastened channel, respectively.
2.2 Test-setup and loading procedure
Tensile coupons were cut longitudinally from the centre of web plates of untested specimens. It is noted that the tensile coupons were cut from the same aluminium alloy coil group as Fang et al. (2022a, b, c, d) and Roy et al. (2021, 2022). In the current investigation, the yield stress was determined to be 150.50 MPa from the typical tested coupon based on multiple coupon tests (see Fig. 2). The stress–strain curve was shown in Fig. 2. A hydraulic actuator was used to apply loading to the RA channels (see Fig. 3). For all test specimens, the hydraulic actuator was operated at a constant and low speed at 0.01 mm/s utilizing displacement control, and the displacement of specimen was read from the linear variable differential transformer (LVDT).
2.3 Test Results
The deformed shapes of several RA channels are presented in Fig. 4. The out-of-plane deformation of web was visible from the start of the loading and persisted until failure. The failure was caused by the formation of a local yield zone underneath the bearing plate, which resulted in symmetrical failure patterns. The load–displacement curves are presented in Fig. 4.
FE modelling and FEA results (Fang et al. 2022b)
From the Table 1, the web crippling strength was improved by 12.1% and 5.5% for unfastened and fastened channels, respectively, when the bearing lengths were raised from 50 to 100 mm.
The size and position of the web hole affect the web crippling behaviour significantly. In terms of hole size, increasing the a/h ratio from 0 to 0.6 reduced web crippling strengths by 27% and 33.2%, respectively, for unfastened channels with down hole and offset hole (see Table 1). Similarly, the strengths of fastened channels with a centred hole and an offset hole were lowered by 33.5% and 22.4%, respectively, for fastened channels with a centred hole and an offset hole (see Table 1). In terms of hole location, the web crippling strength decrease percentages of unfastened channels with centred and offset web holes were 15.4 and 20%, respectively. Fastened channels with centred and offset web holes had values of 20.0 and 14.2%, respectively.
On average, the web crippling strength of fastened channels is 31.6% higher than that of unfastened channels. The initial stiffness of fastened channels is higher than that of unfastened channels, as shown in Fig. 4.
3 Advanced Finite Element Analysis
3.1 FE Modelling
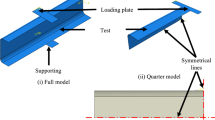
ABAQUS (2021) was used to create the finite element model (FE model), which was then used to predict the structural behaviour of RA lipped channels. The tensile coupon tests were performed in order to get the material parameters that were then input into the FE models. In the FE modelling, the non-linear behaviour of the aluminium alloy material was taken into account. In order to accurately represent the channels, a mesh sensitivity analysis was performed, and the results showed that the S4R shell element with a size of 5 mm x 5 mm worked well. Based on Fang et al. (2023), the mesh number per radius was adjusted to 1.2 in the FE models for the corner section mesh size. This mesh size can enable the FE model perform well in terms of computational time and prediction accuracy to match the experimental results. Figure 4 shows the comprehensive FE meshing that was performed.
Regarding the modelling of interactions, the surface contact is taken into account, and the prevention of penetration between two touched surfaces is ensured. In the experimental testing, the FE modelling used displacement control in order to replicate the application of vertical force loading. In terms of the boundary conditions, the top bearing plate was constrained in all directions save from the vertical ones. The specifics of the modelling are shown in Fig. 4. Ye et al. (2016, 2018a, b), Li et al. (2019, 2022), and Fang et al. (2022a, b, c) all use the similar FE modelling approaches that are quite similar to one another.
Normally the initial geometric imperfections and residual stresses are important in modeling the light gauge steel columns (Craveiro et al. 2022; Fang et al. 2021a, b; Rahnavard et al. 2021) and beams (Chen et al. 2021). However, in FE model of light gauge steel sections susceptible to web crippling, the effects of initial geometric imperfections and residual stresses can be ignored. In the web crippling study, the predicted buckling modes demonstrate stable post-buckling behavior, which considerably minimizes their impacts on imperfection sensitivity, while the stocky channel sections with restraints at both ends similarly diminish their effects. A lot of research investigations have previously proved this (Fang et al. 2022a, b, c; Li & Young, 2019; Uzzaman et al. 2012a, 2012b). In these studies, experimental and numerical investigations were conducted on the web crippling behavior of thin-walled structures where the ratio of channel length to web depth was around 3. This ratio has been used in the parametric analysis of the current study. The FE models developed for this investigation did not account for the impact of initial geometric imperfections and residual stresses.
3.2 FE Validation
Web crippling strength and failure mechanisms were evaluated through experimental and FEA. The failure modes of the sections, as indicated by the FE analysis, are shown in Fig. 4, and they are quite similar to the experimental failure modes. Both the testing and the FEA yielded the load–displacement characteristics seen in Fig. 4. Except for a few instances in which the beginning stiffness of the FE curves deviated significantly from the experimental curves, the bulk of the load–displacement curves obtained from testing and FEA were in fair agreement. This is due to the localized slip observed between bearing plates and test specimens in several experiments. This explains why certain load–displacement curves exhibit inconsistencies between numerical and experimental results. Regarding web crippling capacity and deformed shapes, most of the numerical simulation results matched well with the experimental results. The mean values of the ratio of experimental to FEA strengths (PEXP/PFEA) for unfastened channels and fastened channels are 1.06 and 1.04, respectively. The FEA strengths are quite close to the experimental values, as indicated in Table 1. For all specimens, FEA results are slightly conservative when compared to experimental data. In conclusion, the FEA results matched the experimental results well, and the validated FE models could be employed in the follow-up research of this paper.
4 Design Guidelines
4.1 Equations for Web Crippling Strength
Equations (1) and (2) from AS/NZS (1997a, b) were used to determine the ITF and ETF web crippling strengths (PAS/NZS1997), respectively.
where, Cw1 = 140 mm; Cw2 = 33 mm; Cw3 = 10 mm; θ = 90°.
Equation (3) from CEN (2007) was used to determine two-flange web crippling strength (PCEN).
where, α denotes the coefficient from CEN (2007).
For RA plain sections with different coefficient values, the AISI 2016 and AS/NZS (2018) provide unified web crippling strength (PAISI&AS/NZS) formulae:
where, C denotes a coefficient; CR, CN and Cw denote the coefficients in AISI (2016) and AS/NZS (2018).
4.2 Equations for Web Strength Reduction Factor
Uzzaman et al. (2012a, 2012b) offers equations for RA perforated channels, and the limitation for the equations is: h/t ≤ 156, N/t ≤ 84, N/h ≤ 0.63 and a/h ≤ 0.8. The equations given by Uzzaman et al. (2012a, 2012b) were used and assessed in current study because there were no design requirements for ITF web crippling strength reduction factor of RA channels.
5 Deep Belief Network (DBN)
5.1 Overview
The DBN used in this study integrated the unsupervised pretraining as well as the supervised fine-tuning procedures. The DBN has been employed by Fang et al. (2022b) to investigate the web crippling of unlipped channels under ITF loading case. Normalization was applied to both the input and output layers. Every 50 epochs, the cross-validation error was checked, and training process was stopped when the error did not improve or the 50,000-epoch limit was reached. Some training parameters are adopted to assess the performance of the DBN training:
where ti and yi represent the real and prediction output values, respectively, while \(\overline{{t_{i} }}\) and \(\overline{{y_{i} }}\) represent average values of both outputs respectively, and N represents the amount of data set; R*, MSE, MAE, and Erri denote the correlation coefficient, mean squared error, mean absolute error, and absolute error, respectively.
5.2 Data Feature Extraction and Hyper-Parameter Optimization
Denoising Auto Encoder (DAE) is an unsupervised neural network that operates on unlabelled training data. DAE-derived data features preserve the majority of the information, and the data features are learnt without the addition of label information. There are significant links between feature extraction and label information for supervised learning tasks like regression prediction on small amounts of data. As a consequence, by including label information in the DAE output layer, the model's features can be more stable for regression analysis. The Stacked Denoising Auto Encoder (SDAE) was used in this study to examine more complex data characteristics. Unsupervised layer-wise pre-training and supervised fine-tuning are the two steps of SDAE training. The DBN's hyperparameters were optimized using Block Changing Grid Search (BCGS), and the BCGS was developed based on Block Grid Search.
5.3 Data Training
To avoid over-fitting, the early stopping technique is used in this study. In this technique, the available data developed from the validated FEA is randomly divided into three groups: training (50%), validation (25%), and testing (25%) sets. The input and output of the neural network training are given:
where L stands for the channel's length, x for the distance between the holes and the bearing block. The predicted web crippling strength is Pp.
The DBN used nine distinct channel section characteristics as input variables and a single normalized output (Pp) for the RA channel as output. The R* values of DBN were 0.996, 0.993, and 0.988 for the training, validation, and testing data sets, respectively.
5.4 DBN Assessment
The performance of DBN was assessed by using the target parameters (R*, MSE, and MAE). When compared to AS/NZS (1997a, b), CEN (2007), AISI (2016), and AS/NZS (2018), the deep-learning methodology (DBN) has the ability to offer accurate results, as illustrated in Table 2. When comparing the design strengths obtained from AS/NZS (1997a, b), CEN (2007), AISI (2016)&AS/NZS (2018), the average absolute percentage errors for unfastened channels obtained from DBN results were 95.5, 34.1, 65.3, and 4.8%, respectively (see Table 2). The average absolute percentage errors for fastened channels were 34.9, 7.3, 21.7, and 6.4%, respectively. The findings demonstrate that the design strengths of AS/NZS (1997a, b), CEN (2007), AISI (2016), and AS/NZS (2018) are around 10% lower than the FEA and DBN predictions. The web crippling strength of RA perforated channels is calculated with acceptable accuracy using both FEA and DBN data.
6 Parametric Analyses on the Qualitative Effect of Related Parameters
Using the validated DBN model, a comprehensive parametric analysis was conducted to assess the qualitative effects of hole size, hole position, section thickness, and bearing plate length on the ITF web crippling strength of the perforated RFA lipped channel. The a/h ratio was modified in increments of 0.2 between 0 and 0.8. The section thickness (t) was changed between 1 and 4 mm, while the corner radius (r) was modified between 2 and 6 mm. The bearing lengths (N) of 50, 75, and 100 mm were considered.
6.1 Effects of r/t, N/t, h/t and Flange Type
The r/t ratio has a negative effect on the (dimensionless) web crippling strength of RA plain channels, as demonstrated in Fig. 5a. The (dimensionless) web crippling strength fluctuated as the r/t ratio increased from 1.0 to 1.5. Overall, as the ratio increased from 0.5 to 6, the (dimensionless) web crippling strength of unfastened changes and fastened channels decreased by 50% and 8%, respectively.
As the N/t ratio went from 8.3 to 100, the (dimensionless) web crippling strength dropped. From Fig. 5b, the enhanced percentages of (dimensionless) web crippling strength for unfastened channels and fastened channels, respectively, are 48% and 88%.
The (dimensionless) web crippling strengths reduced as the h/t ratio was raised, as seen in Fig. 5c. The average (dimensionless) web crippling strengths of unfastened channels and fastened channels were lowered by 67% and 59%, respectively, as the h/t ratio was increased from 21 to 295.
The Pn of fastened channels is generally higher than unfastened channels, according to Fig. 5d, with an average difference of 19.22.
6.2 Effect of Web Holes on the Web Crippling Strength Reduction Factor (R)
When the ratio of a/h grows from 0.2 to 0.8, there is a general steady decline in the web crippling strength reduction factors, as shown in Fig. 6a–b. The web crippling strength reduction factors for both unfastened and fastened channels were comparable.
When N/h grows from 0.2 to 0.75, there will be an increase in web crippling strength reduction factor. For instance, the web crippling strength reduction factors of unfastened and fastened RA channels with offset web holes varied from 0.73 to 0.75 and 0.80 to 0.86 for unfastened and fastened channels, respectively (see Fig. 6c–f).
The average value of web crippling strength reduction factors for unfastened and fastened RA channels was 0.51 to 0.94 and 0.85 to 0.99, respectively, when the x/h ratio was changed from 0.01 to 0.50. As seen in Fig. 6g–h, the trend of web crippling strength reduction factors for each group varies considerably, with varying a/h ratios across various sections.
The average value of web crippling strength reduction factor for RA channels varies considerably, as can be shown in Fig. 6i–j and Table 3. For the channels with offset web holes, the web crippling strength reduction factor for fastened channels is higher than unfastened channels by 11.1% on average.
7 Development of Design Equations
As a result of the DBN results, new design formulas for (reduced) web crippling strength were proposed for RA perforated channels. The newly developed formulas have limitations of h/t ≤ 295, N/t ≤ 100, R/t ≤ 6.0, N/h ≤ 0.75 and a/h ≤ 0.8. The range of parameters included in the design equations given in this study was increased to include the ratios of h/t, N/t, and N/h, in contrast to the equations developed by Uzzaman et al. (2012a, b).
7.1 Design Equations
The web crippling strength (Pprop) and strength reduction factor (Rprop) design equations are given next.
RA channels with a centred web hole,
RA channels with an offset web hole,
where the values for coefficients in Eqs. 11–13 are shown in Table 4.
To evaluate the performance of the developed formulas, comparisons were done between the design strengths and the experimental failure strengths, as well as between the design strengths and the failure strengths supplied by the developed equations of Uzzaman et al. (2012a, b). The results presented in Table 5(a) demonstrate that the (reduced) web crippling strengths predicted by employing the developed formulas are considerably predictive of the experimental failure loads. Additionally, the average values of the ratios P/Pprop and R/Rprop are both close to 1, which confirms the accurate prediction capability of the developed formulas for calculating ITF web crippling strengths of RA perforated channels.
7.2 Reliability Analysis
To assess the predictive performance of developed formulas, a reliability study was performed. The approach that was used was one that was provided by Hsiao et al. (1988). According to the American standard (AISI (2016)), the equation is regarded trustworthy if its reliability index (β') is more than or equal to the goal reliability index of 2.50.
AISI (2016) outlines the procedures for determining the resistance factor (φ) for load and resistance factored design (LRFD). Since the actual distributions of resistance (R) and demand (Q) are unknown, it is reasonable to assume that the distribution of resistance to demand (R/Q) is log-normal, using the mean value and coefficient of variation of R and Q to estimate. Using this distribution approach and first-order probabilistic theory, the reliability index can be represented as given in Eq. 14, where Rm and Qm are the mean values of resistance and load effects, and VR and VQ are the respective coefficients of variance. From the ratios of the tested load to the anticipated load, the mean values and coefficients of variation of variables are calculated. Using the specified factors and associated reliability index, the resistance factor for a given design equation can be calculated. The similar method has been employed by Rahnavard et al. (2022a, b).
As can be shown in Table 5(b), the results that are predicted by the developed equations are more accurate than the goal reliability index specified by the American standard (AISI (2016)). This is true for both unfastened and fastened RA channels. This demonstrates that the recommended design formulae are capable of determining with a high degree of precision the ITF web crippling strength of RA perforated channels.
8 Conclusions
This study analyses the interior-two-flange (ITF) web crippling behaviour of roll-formed aluminium alloy lipped channels (RA channels) with web holes by means of experimental testing, numerical modelling, and deep neural network (i.e., Deep belief Network, DBN). The experimental data and FEA results were found to be in fair agreement. On the basis of experimental and FEA data, it was determined that the existing design recommendations for evaluating the ITF web crippling strength of investigated channels are inaccurate.
For training DBN with the validated elasto-plastic FE model, a total of 1,080 data points were gathered. When the DBN predictions were compared with test data, it was discovered that they are quite similar to the test results, being just 5% conservative for unfastened channels and 6% conservative for fastened channels. By comparing the absolute percentage inaccuracy of different approaches, including DBN, FEA, and current design criteria, the accuracy of numerous processes was determined. The accuracy of DBN prediction was compared to design strengths estimated using AS/NZS 1997, AISI 2016, AS/NZS (2018), and CEN 2007, showing that the DBN exceeded these design standards. The AS/NZS 1997, AISI 2016, AS/NZS (2018), and CEN 2007 design strengths for unfastened channels are highly conservative by 95.5, 65.3, and 34.1%, and conservative by 34.9, 21.7, and 7.3%, respectively.
In addition, DBN output were utilised to evaluate the effect of web hole, geometric dimensions, and bearing length on the web crippling strength of RA perforated channels. Based on the findings of the parametric analysis, design modifications on (reduced) web crippling strength were provided. The developed design's strengths corresponded rather well with the test results. In addition, a reliability analysis shown that the developed design equations could accurately estimate the ITF web crippling strength of RA perforated channels.
Abbreviations
- a :
-
Hole diameter
- ANN:
-
Artificial neural network
- b f :
-
Flange length
- b w :
-
Web depth
- C w 1, C w 2, C w 3 :
-
Coefficients in AS/NZS (1997)
- CC R, CN, Ch :
- DBN:
-
Deep belief network
- E :
-
Young’s modulus
- ETF:
-
End-two-flange
- Err :
-
Absolute percentage error
- FEA:
-
Finite element analysis
- f y :
-
Yield stress
- h :
-
Web flat depth
- k 1, k 2, k 3 :
-
Coefficients in CEN (2007)
- MAE:
-
Mean absolute error
- MSE:
-
Mean squared error
- N :
-
Bearing length
- Num :
-
Number of specific data character
- P AS/NZS1664 :
-
Web crippling strength determined by AS/NZS (1997)
- P CEN :
-
Web crippling strength determined by CEN (2007)
- P EXP :
-
Web crippling strength from experimental tests
- P n :
-
Web crippling strength
- P p :
-
Prediction web crippling strength from trained DBN
- P prop :
-
Web crippling strength from proposed equation
- r :
-
Corner radius
- R :
-
Web crippling strength reduction factor
- RFA:
-
Roll-formed aluminium alloy
- RFCS:
-
Roll-formed carbon steel
- R prop :
-
Web crippling strength reduction factor from proposed equation
- R * :
-
Correlation coefficient
- t :
-
Section thickness
- t i, \(\overline{{t }_{i}}\) :
-
Real, average real value of output for DBN training
- x :
-
Hole distance to bearing block
- X :
-
Variable in data series for DBN training
- y i, \(\overline{{y }_{i}}\) :
-
Predicted, average predicted output for DBN training
- ω :
-
Coefficients in CEN (2007)
- α, γ, λ, β, μ, ζ, ξ :
-
Coefficients for proposed equation
- β' :
-
Reliability index
References
ABAQUS (2021). Analysis User’s Manual-Version. ABAQUS Inc
AISI (American Iron and Steel Institute). (2016). North American Specification for the Design of Cold-formed Steel Structural Members. AISI S100–16
Alsanat, H., Gunalan, S., Guan, H., Keerthan, P., & Bull, J. (2019). Experimental study of aluminium lipped channel sections subjected to web crippling under two flange load cases. Thin-Walled Structures, 141, 460–476.
Alsanat, H., Gunalan, S., Poologanathan, K., Guan, H., & Baniotopoulos, C. (2020). Fastened aluminum-lipped channel sections subjected to web crippling under two-flange loading conditions: Experimental study. Journal of Structural Engineering, 146(4), 04020023.
AS/NZS (Australian/New Zealand Standard). (1997a). Aluminium Structures Part 1: Limit State Design. AS/NZS 1664
AS/NZS (Australian/New Zealand Standard). (1997b). Aluminium Structures Part 2: Allowable stress design. AS/NZS 1664
AS/NZS (Australian/New Zealand Standard). (2018). Cold-Formed Steel Structures. AS/NZS 4600
CEN (European Committee for Standardization). (2007). Design of Aluminium Structures - Part 1.4 vol. 9, Cold-formed structural sheeting
Chen, B., Roy, K., Fang, Z., Uzzaman, A., Raftery, G., & Lim, J. B. (2021). Moment capacity of back-to-back cold-formed steel channels with edge-stiffened holes, un-stiffened holes, and plain webs. Engineering Structures, 235, 112042.
Craveiro, H. D., Rahnavard, R., Laím, L., Simões, R. A., & Santiago, A. (2022). Buckling behavior of closed built-up cold-formed steel columns under compression. Thin-Walled Structures, 179, 109493.
Fang, Z., Roy, K., Chen, B., Sham, C. W., Hajirasouliha, I., & Lim, J. B. (2021a). Deep learning-based procedure for structural design of cold-formed steel channel sections with edge-stiffened and un-stiffened holes under axial compression. Thin-Walled Structures, 166, 108076.
Fang, Z., Roy, K., Mares, J., Sham, C. W., Chen, B., & Lim, J. B. (2021b). Deep learning-based axial capacity prediction for cold-formed steel channel sections using Deep Belief Network. Structures, 33, 2792–2802.
Fang, Z., Roy, K., Dai, Y., & Lim, J. B. (2022a). Effect of web perforations on end-two-flange web crippling behaviour of roll-formed aluminium alloy unlipped channels through experimental test, numerical simulation and deep learning. Thin-Walled Structures, 179, 109489.
Fang, Z., Roy, K., Xu, J., Dai, Y., Paul, B., & Lim, J. B. (2022b). A novel machine learning method to investigate the web crippling behaviour of perforated roll-formed aluminium alloy unlipped channels under interior-two flange loading. Journal of Building Engineering, 51, 104261.
Fang, Z., Roy, K., Ingham, J. M., & Lim, J. B. (2022c). Assessment of end-two-flange web crippling strength of roll-formed aluminium alloy perforated channels by experimental testing, numerical simulation, and deep learning. Engineering Structures, 268, 114753.
Fang, Z., Roy, K., Chen, B., Xie, Z., & Lim, J. B. (2022d). Local and distortional buckling behaviour of aluminium alloy back-to-back channels with web holes under axial compression. Journal of Building Engineering, 47, 103837.
Fang, Z., Roy, K., Padiyara, S., Chen, B., Raftery, G. M., & Lim, J. B. (2023). Web crippling design of cold-formed stainless steel channels under interior-two-flange loading condition using deep belief network. Structures, 47, 1967–1990.
Hinton, G. E., & Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Sci., 313(5786), 504–507.
Hiyama, Y., Ishikawa, K., & Kato, S. (2000). Experiments and analysis of the post-buckling behaviors of aluminum alloy double layer space grids applying ball joints. Structural Engineering and Mechanics, 9(3), 289–304.
Hsiao, L., Yu, W., & Galambos, T. V. (1988). Load and resistance factor design of cold formed steel, calibration of the AISI design provisions, Ninth progress report, civil engineering study 88–2. University of Missouri-Rolla, Rolla, Missouri.
Kim, S.-H., Woo, H., Choi, G.-G., & Yoon, K. (2018). A new concept for blast hardened bulkheads with attached aluminum foam. Structural Engineering and Mechanics, 65(3), 243–250.
Li, H. T., & Young, B. (2019). Behaviour of cold-formed high strength steel RHS under localised bearing forces. Engineering Structures, 183, 1049–1058. https://doi.org/10.1016/j.engstruct.2018.11.079
Li, H. T., & Young, B. (2022). Cold-formed stainless steel RHS members undergoing combined bending and web crippling: Testing, modelling and design. Engineering Structures, 250, 113466.
Liu, H., Chen, Z., Xu, S., & Bu, Y. (2015). Structural behavior of aluminum reticulated shell structures considering semi-rigid and skin effect. Structural Engineering and Mechanics, 54(1), 121–133.
McIntosh, A., Gatheeshgar, P., Poologanathan, K., Gunalan, S., Navaratnam, S., & Higgins, C. (2021). Web crippling of cold-formed carbon steel, stainless steel, and aluminium channels: Investigation and design. Journal of Constructional Steel Research, 179, 106538. https://doi.org/10.1016/j.jcsr.2021.106538
McIntosh, A., Gatheeshgar, P., Gunalan, S., Kanthasamy, E., Poologanathan, K., Corradi, M., & Higgins, C. (2022). Unified approach for the web crippling design of cold-formed channels: Carbon steel, stainless steel and aluminium. Journal of Building Engineering, 51, 104134.
Nanda, B. K., & Behera, A. K. (2005). Study on structural damping of aluminium using multi-layered and jointed construction. Structural Engineering and Mechanics, 20(6), 631–653.
Qureshi, A. S., Khan, A., Zameer, A., & Usman, A. (2017). Wind power prediction using deep neural network based meta regression and transfer learning. Applied Soft Computing, 58, 742–755.
Rahnavard, R., Craveiro, H. D., Laím, L., Simões, R. A., & Napolitano, R. (2021). Numerical investigation on the composite action of cold-formed steel built-up battened columns. Thin-Walled Structures, 162, 107553.
Rahnavard, R., Craveiro, H. D., Lopes, M., Simões, R. A., Laím, L., & Rebelo, C. (2022a). Concrete-filled cold-formed steel (CF-CFS) built-up columns under compression: Test and design. Thin-Walled Structures, 179, 109603. https://doi.org/10.1016/j.tws.2022.109603
Rahnavard, R., Craveiro, H. D., Simões, R. A., Laím, L., & Santiago, A. (2022b). Buckling resistance of concrete-filled cold-formed steel (CF-CFS) built-up short columns under compression. Thin-Walled Structures, 170, 108638.
Roy, K., Chen, B., Fang, Z., Uzzaman, A., Chen, X., & Lim, J. B. (2021). Local and distortional buckling behaviour of back-to-back built-up aluminium alloy channel section columns. Thin-Walled Structures, 163, 107713.
Roy, K., Chen, B., Fang, Z., Uzzaman, A., & Lim, J. B. P. (2022). Axial capacity of back-to-back built-up aluminum alloy channel section columns. Journal of Structural Engineering, 148(2), 04021265.
Seo, J. K., Park, D. K., Jo, S. W., Park, J. S., Koo, J. B., Ha, Y. S., & Jang, K. B. (2016). A numerical and experimental approach for optimal structural section design of offshore aluminium helidecks. Structural Engineering and Mechanics, 59(6), 993–1017.
Uzzaman, A., Lim, J. B., Nash, D., Rhodes, J., & Young, B. (2012a). Web crippling behaviour of cold-formed steel channel sections with offset web holes subjected to interior-two-flange loading. Thin-Walled Structures, 50(1), 76–86.
Uzzaman, A., Lim, J. B., Nash, D., Rhodes, J., & Young, B. (2012b). Cold-formed steel sections with web openings subjected to web crippling under two-flange loading conditions—Part II: Parametric study and proposed design equations. Thin-Walled Structures, 56, 79–87.
Wang, H., Li, G., Wang, G., Peng, J., Jiang, H., & Liu, Y. (2017). Deep learning based ensemble approach for probabilistic wind power forecasting. Applied Energy, 188, 56–70.
Ye, J., Hajirasouliha, I., Becque, J., & Pilakoutas, K. (2016). Development of more efficient cold-formed steel channel sections in bending. Thin-Walled Structures, 101, 1–13.
Ye, J., Mojtabaei, S. M., Hajirasouliha, I., Shepherd, P., & Pilakoutas, K. (2018a). Strength and deflection behaviour of cold-formed steel back-to-back channels. Engineering Structures, 177, 641–654.
Ye, J., Becque, J., Hajirasouliha, I., Mojtabaei, S. M., & Lim, J. B. (2018b). Development of optimum cold-formed steel sections for maximum energy dissipation in uniaxial bending. Engineering Structures, 161, 55–67.
Zhou, F., & Young, B. (2008). Aluminum tubular sections subjected to web crippling—Part I. Thin-Walled Structures, 46(4), 339–351.
Zhou, F., Young, B., & Zhao, X. L. (2009). Tests and design of aluminum tubular sections subjected to concentrated bearing load. Journal of Structural Engineering, 135(7), 806–817.
Acknowledgements
The authors sincerely thank Mark Byrami and Yuanyi Ji for helping to conduct the experimental tests at the “Structures test hall” of the University of Auckland.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I would like to confirm that the authors (Zhiyuan Fang, Krishanu Roy, and James B.P. Lim) have no conflict of interest in publishing this manuscript in the International Journal of Steel Structures.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fang, Z., Roy, K. & Lim, J.B.P. Structural Design for Roll-Formed Aluminium Alloy Perforated Channels Subjected to Interior-Two-Flange Web Crippling: Experimental Tests, Numerical Simulation, and Neural Network. Int J Steel Struct 23, 692–708 (2023). https://doi.org/10.1007/s13296-023-00722-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13296-023-00722-6