1 Introduction

A deadly and unprecedented heatwave occurred across the Pacific Northwest in June 2021. From a meteorological perspective, the causes of the heat wave are quite clear. The intensity of the heatwave involved several complex meteorological factors. A system of high atmospheric pressure occurred in a relatively common meteorological pattern called an “omega block” (McKinnon and Simpson 2022) and was enhanced by atmospheric heating due to clouds and precipitation over the Pacific several days earlier (Mo et al. 2022), a split in the Arctic polar vortex (Wang et al. 2022), and enhanced solar heating at the surface due to cloud-free skies (Mo et al. 2022). Additional details on the meteorology of the event, including an explanation of associated meteorological jargon, are included in Online Appendix A. Despite this complicated meteorology, the unprecedented temperatures and other heat indices experienced during the 2021 PNW heatwave were well predicted several days in advance by forecast centers (Emerton et al. 2022). Although the meteorology of the event is reasonably well understood at this point, statistical understanding remains elusive. Undoubtedly, anthropogenic climate change also played a role in the 2021 PNW heatwave but its far outlier temperatures challenge extreme value analyses to confidently predict the event’s rarity from previous observations (Bercos-Hickey et al. 2022; Philip et al. 2021). In these two previous studies, the upper bound of a generalized extreme value (GEV) distribution fitted to observed maximum summer daily maximum temperatures, from station data prior to 2021, was lower than the hottest observed 2021 temperatures. As a result, it is impossible to explain the true abnormality of this event or quantify the probability of a similar event in the future using the univariate GEV models, although they incorporated time-dependent covariates in the GEV location parameter to permit return levels which are nonstationary in time.

Alternatively, Bercos-Hickey et al. (2022) performed a storyline hindcast attribution study using two regional climate models (the Weather Research and Forecasting model, WRF, and RegCM) to attempt to quantify the magnitude of the human influence without addressing the question of the changes in rarity. Their study found that human-induced climate change increased the 2021 PNW heatwave temperature by approximately 1 \(^\circ \)C. While the hindcast simulations in Bercos-Hickey et al. (2022) are in agreement with their imposed initial and boundary condition datasets, they resulted in cooler simulated gridded temperatures than station observations during the most intense part of the heatwave because of biases in the input dataset. Because an out-of-sample GEV distribution failed to include the 2021 values, Philip et al. (2021) included the 2021 values in a fitted GEV distribution and used that information along with summer annual maximum temperatures from long climate model simulations to find a human increase in the 2021 PNW heatwave temperature of about 2 \(^\circ \)C. Furthermore, based on their in-sample GEV analysis, Philip et al. (2021) concluded that the event was “virtually impossible” without anthropogenic climate change. However, Bercos-Hickey et al. (2022) found that including the 2021 temperatures decreases the p values of the \(\chi ^2\) goodness-of-fit tests from greater than 0.2 in general to less than 0.05 at many stations, implying that the 2021 seasonal maxima are generated from a different underlying distribution than the previous years. McKinnon and Simpson (2022) used a large climate model ensemble simulation to examine gridboxes across the global land where simulated maximum temperatures exhibited similar skewness and kurtosis to the observed station temperatures in the PNW region. They found that while the model could produce temperatures that exceed 4.5 standard deviations above average temperatures (similar to the 2021 PNW observations), such occurrences are extremely rare with return periods of about 100,000 years. Finally, Heeter et al. (2023) examined tree ring records finding that the 2021 summer temperatures in the PNW regions were unprecedented in the last millennium.

In this paper, our objective is to examine the statistical difficulties of estimating the probability of far outlier temperatures along with human- and naturally-driven changes to such quantities. Such estimates are required to make the attribution statements that advance our understanding of how anthropogenic forcing and natural climate variability affected the rarity of the PNW heatwave, similarly to those in Philip et al. (2021) and Bercos-Hickey et al. (2022). The primary challenge is represented by the fact that the out-of-sample GEV analyses in Philip et al. (2021) and Bercos-Hickey et al. (2022) both yielded estimated upper bounds for temperature extremes that were exceeded by the observed 2021 daily maxima. In other words, using station data-based statistical models, the PNW heatwave was impossible to anticipate in advance of its occurrence. Consequently, the human influence on these “impossible” events cannot be attributed with these models, either in likelihood or severity because they are not within the bounds (i.e., support) of the out-of-sample model fits. This unexplainability is largely due to the fact that analyses in Philip et al. (2021) and Bercos-Hickey et al. (2022) represent simplified approaches to the problem of estimating the spatial extent of an event like the PNW heatwave: Philip et al. (2021) analyzed the spatial average of annual maxima from all weather stations in a fixed latitude-longitude box (which both aggregates over important topographical variability in the PNW domain and ignores the fact that historical events may have been offset geographically from this box), while Bercos-Hickey et al. (2022) utilize single-station analyses (which ignore both autocorrelation in the climatology of temperature extremes and the fact that individual heatwave events will impact multiple weather stations). As outlined in Zhang et al. (2022), failing to account for the spatial coherence of individual events results in underestimation of the risks associated with weather extremes (Davison et al. 2012; Saunders et al. 2017). Our hypothesis is that extreme value analysis methods that more appropriately account for both climatological and event-based autocorrelation (e.g., Huser et al. 2017; Huser and Wadsworth 2019; Zhang et al. 2021, ) can better characterize temperature extremes in the PNW such that the 2021 temperatures are less “unexplainable” in an out-of-sample statistical sense. Importantly, these methods should also improve the predictive power of the out-of-sample analysis on the 2021 PNW heatwave so that we can construct well-defined attribution statements.

To test this hypothesis, we analyze the summertime maxima of homogenized Pacific Northwest U.S. temperature station data from 1950 to present using a statistical model that flexibly accounts for spatial variability in the climatology of extreme temperatures and yields data-driven measures of the spatial extent of heatwave events in the PNW. Our statistical framework can account for both secular trends due to anthropogenic and naturally forced year-to-year variability while robustly quantifying uncertainty via Bayesian hierarchical modeling. We explicitly quantify the individual effect of including physical covariates versus accounting for the spatial coherence of heatwave events on the corresponding GEV upper bounds and whether or not the 2021 temperature extremes could have been anticipated in an out-of-sample sense. We then revisit the climate change attribution question, using a statistical counterfactual (following Risser and Wehner 2017) invoking Granger causal inference (Granger 1969) to isolate the effect of anthropogenic forcing on both the predictability of the 2021 temperatures and their probabilities.

The paper proceeds as follows. Section 2 describes all input data sources for our analysis, while Sect. 3 outlines our methodological innovations, including our Bayesian hierarchical model (Sect. 3.1), an attribution framework for isolating the human influence on the heatwave (Sect. 3.2), and descriptions of alternative statistical models (Sect. 3.3). Our main results are provided in Sects. 4 and 5 concludes the paper.

2 Data

2.1 Long-Term Temperature Records for Trend Analysis

In order to assess secular trends over time and year-to-year variability that are unaffected by inhomogeneities from nonclimatic influences (such as changes to measurement devices and the local effects of the built environment), we analyze a homogenized version of the Global Historical Climatology Network-Daily (GHCN-D) over the contiguous United States (Rennie et al. 2019). While the homogenized records extend back to the early 20th century, we focus our analysis on the last 71 years (1950–2020) due to the high density of nonmissing measurements from weather stations during this period. Focusing our attention on the 487 gauged locations from this database within a longitude-latitude box defined by \([125^\circ \text {W},116.5^\circ \text {W}]\times [40^\circ \text {N},49^\circ \text {N}]\) (see Fig. 1a), we extract the summertime (June/July/August or JJA) maximum daily maximum temperature measurement, denoted “TXx,” from each station in each year so long as there are no more than 40% missing daily measurements in each JJA season. Stations with less than ten non-missing JJA TXx from 1950–2020 are excluded; this results in \(n=438\) gauged locations with sufficient temperature records. The seasonal maxima from these locations are used in the statistical analysis described in Sect. 3; note that we do not include any measurements from 2021 in our analysis of the historical record (i.e., the 2021 event is considered out-of-sample).

Fig. 1
figure 1

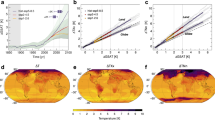
a The maximum daily maximum temperature between June 25 and July 4 (i.e., TXx) at each of the \(n=470\) high-quality Global Historical Climatology Network gauged locations in the Pacific Northwest region with the World Weather Attribution (WWA; Philip et al. 2021) region overlaid in black, b area-averaged June/July/August (JJA) TXx time series from 1950–2021 for the PNW and WWA regions

Full size image

2.2 Estimation of the 2021 PNW Temperature Extremes

Homogenized temperature records are used for trend analysis because they explicitly modify the raw station measurements to account for known, non-natural shifts in the distribution of daily temperatures. However, to quantify the extreme daily temperatures that actually occurred during the heatwave period (defined as June 25 to July 4, 2021), we prefer to use the available non-homogenized GHCN-D (Menne et al. 2012) records from the longitude-latitude box shown in Fig. 1. From the GHCN-D records with available daily maximum temperatures over these ten days, we see that a large majority of the maximum daily measurements (the 2021 TXx) occurred between June 26 and July 1 (see Supplemental Fig. B.2); there are \(n=470\) GHCN-D gauged locations with six non-missing daily maximum temperatures over these six days (see Supplemental Fig. B.3). Unfortunately, there is a mismatch in the \(n = 438\) homogenized sites used to estimate historical trends and the \(n = 470\) GHCN-D sites used to define the 2021 event (see Supplemental Fig. B.5a).

To ensure that we can report results for all gauged locations in the homogenized records, we apply the spatial statistical model proposed in Eq. (5), wherein we use thin plate splines and topographical covariates to conduct interpolation to a regular 800 m grid over the PNW domain. Supplemental Fig. B.4 shows the GHCN-D TXx used as input data as well as the results of this interpolation for the \(n=470\) GHCN-D sites (Fig. B.4b), the \(n=438\) homogenized sites (Fig. B.4c; these values are identical to the ones shown in Fig. 1), and the 800 m grid (Fig. B.4d). As shown in Fig. B.5b, c, the interpolated TXx measurements compare favorably with the GHCN-D input data (\(R^2=0.94\)), and furthermore provide a better reconstruction than corresponding measurements from the nearest-neighbor ERA5 grid box. Note ERA5 is a state-of-the-art atmospheric reanalysis product widely used in climate analysis (Hersbach et al. 2020; Bell et al. 2021).

2.3 Anthropogenic and Natural Drivers of Temperature Change

One benefit of our methodology is that we can include physical covariates in GEV distributions to account for spatio-temporal nonstationarity and model their coefficients as spatial random effects. This way of modeling spatial nonstationarity is less standard in the related literature (e.g., Paciorek and Schervish 2006; Risser and Calder 2015; Castro-Camilo and Huser 2020), which often does not assume second-order stationarity and employs a nonstationary covariance function that is locally isotropic. However, in Online Appendix D, we show that the covariance from our model, as detailed in Sect. 3, is still not a function of the lag (i.e., is not weakly stationary) after marginalizing out the random coefficients associated with the covariates. In addition, the time-varying covariates describe both long-term trends in the distribution of temperature extremes as well as year-to-year variability due to modes of natural climate variability (see Sect. 3).

Secular trends. Dating back to seminal work by Arrhenius (1897), it is well-established that anthropogenic greenhouse gas (GHG) emissions drive increases to global mean temperature via radiative forcing of the climate system. Following Risser et al. (2022), we use the sum-total forcing time series of the five well-mixed greenhouse gases (CO\(_2\), CH\(_4\), N\(_2\)O, and the CFC-11 and CFC-12 halocarbons) to describe long-term, human-induced secular trends in the distribution of extreme temperature measurements. The radiative forcing time series (see Fig. B.1a) is calculated from reconstructed atmospheric concentrations of each greenhouse gas (Meinshausen and Vogel 2016; Meinshausen and Nicholls 2018) via the forcing formulae given in Etminan et al. (2016) and Hodnebrog et al. (2013); a time lag is also included to account for the lagged response of sea surface temperatures to these forcings (see, for further details, Risser et al. 2022). Thus, the greenhouse gas forcing time series, denoted by \(\text {GHG}(t)\), \(t=1950,\ldots , 2021\), characterizes a nonlinear trend over 1950–2021, and is applied uniformly across space.

Large-scale modes of oceanic variability. The El Niño-Southern Oscillation (ENSO) is a coupled ocean–atmosphere mode of natural climate variability that cycles between positive (El Niño) and negative (La Niña) phases every two to seven years (Philander 1985). While the effect of ENSO on winter climate in the Pacific Northwest is robust (Whan and Zwiers 2017), it also influences the large-scale circulation in the region during the summer (Stuecker et al. 2015). On this account, we use the ENSO Longitude Index (ELI, Williams and Patricola 2018) as a covariate to represent this influence. ELI is a sea surface temperature-based index that summarizes the average longitude of deep convection in the Walker Circulation and accounts for the different spatial patterns of ENSO. The JJA seasonally-averaged ENSO time series is applied uniformly across space and is denoted by \(\text {ELI}(t)\), \(t=1950,\ldots , 2021\); see Fig. B.1b.

Palmer Drought Severity Index. Heatwave temperatures are strongly influenced by evapotranspirative cooling from the surface soil moisture content and the local vegetation (Domeisen et al. 2023). Dry soil conditions reduce this surface moisture feedback compared to moist soil conditions. To capture this feedback in our statistical model we use the Palmer drought severity index (PDSI) as another physically motivated covariate (Palmer 1965). PDSI quantifies the relative surface dryness through moisture supply and demand by calculating the cumulative departure in water balance using monthly precipitation and temperature data. While the PDSI evapotranspiration terms are temperature dependent, in general there is a separation of time scales between long-term drought metrics and short-term heatwaves. In our analysis, we use the PRISM monthly PDSI data from the West Wide Drought Tracker (Abatzoglou et al. 2017), and flip the sign of their indices so that PDSI ranges from about -10 (wet) to +10 (dry) with values above 3 representing severe to extreme drought. We then calculate the JJA average for each year \(t=1950,\ldots , 2021\) at each spatial location \(\varvec{s}\), which is denoted by \(\text {PDSI}(\varvec{s},t)\). Just prior to the 2021 heatwave, much of Washington State and Oregon were in pre-existing severe drought conditions; see Fig. B.1c.

Urbanization Binary Index. The urban heat island effect is another well-known anthropogenic factor influencing temperature distributions within urban and suburban environments (e.g., Chen and Dirmeyer 2019) due to differences in heat fluxes (both sensible and latent) and momentum fluxes (e.g., surface roughness) that impact the evolution of daily temperatures (Oleson et al. 2011). To account for the effects of urbanization in a parsimonious manner, we treat urbanization as a binary covariate. Markley et al. (2022) developed a reliable “urbanization year” indicator, based on United State census data, that denotes if and when census tracts became “urbanized” during 1940–2021; see Fig. B.7. They define a region as urbanized if its housing density exceeds 200 housing units per square mile. To model the potential urban heat island effect, we use the dataset of Markley et al. (2022) to create a binary variable \(\text {Urban}(\varvec{s},t)\) for each year \(t=1950,\ldots , 2021\) to indicate whether the census tract surrounding the station \(\varvec{s}\) has been urbanized in year t by finding the corresponding census tract and its urbanization year.

2.4 Characterizing Spatial Nonstationarity in GEV Climatology

The anthropogenic and natural drivers described in Sect. 2.3 are used to account for nonstationarity over space and time in the distribution of extreme temperature measurements (see Eq. (4)). However, we use an additional set of covariates to statistically model spatial nonstationarity in the parameters of the extreme temperature distributions (described in Eq. (5)). Along with thin plate splines, the following spatial-only covariates are used to statistically model spatial variability in distributional parameters:

  • The natural logarithm of the average monthly precipitation over January, 1950, to December, 2020, as estimated from the PRISM data set (Daly et al. 1994). This covariate is used to discriminate between wet and dry regimes of the PNW.

  • Topographical aspect, slope, and elevation. Elevation (meters above sea level) accounts for the fact that extreme temperatures tend to decrease with increasing altitude (via lapse rate theory). Topographical aspect describes the direction in which each location faces (ranging from zero to \(2\pi \)), while topographical slope is an index that describes the steepness; collectively, slope and aspect account for the effect of solar radiation and exposure on extreme temperatures. Elevation is obtained from the 800 m digital elevation map used to generate the PRISM data product; slope and aspect are calculated using the raster package for R (Hijmans 2022).

  • Distance-to-coast (km) to account for the fact that stations closer to the ocean tend to have cooler temperatures. This variable is calculated by NASA’s Ocean Biology Processing Group (2009) at a global grid of \(1/16^\circ \) using the Generic Mapping Tools package (Wessel and Smith 1998). They did not consider the landlocked bodies of water (e.g., Lake Tahoe) to be oceans with a coast.

Maps of each of these quantities are shown in Supplemental Fig. B.6. Since a \(1/16^\circ \) degree grid is very high resolution, we simply interpolate them to the GHCN locations to obtain the values for model fitting.

3 Methods

3.1 Spatial Extreme Value Analysis

To assess the effect of statistical assumptions on the failure of previous studies to characterize a nonzero probability in an out-of-sample context as described in Sect. 1, we describe a more refined nonstationary statistical model that flexibly accounts for spatial coherence in both the climatology of temperature extremes and individual heatwave events. Grounded in extreme value theory, the methodology is comprised of three building blocks:

Nonstationary marginal Generalized Extreme Value analysis. The first innovation of our methodology involves incorporating of a broad range of external information (also known as “covariates”) to characterize spatially- and temporally-varying changes in the estimated distribution of extreme temperature. Based on classical extreme value theory (see Theorem 3.1.1 of Coles 2001), the JJA maxima in year t at a generic weather station \(\varvec{s}\) from PNW, denoted by \(Y(\varvec{s},t)\), can be considered as arising from a generalized extreme value (GEV) distribution with the cumulative distribution function (CDF)

$$\begin{aligned} \mathbb {P}(Y(\varvec{s},t) \le y) = \exp \left\{ -\left[ 1 + \xi (\varvec{s},t)\left( \frac{y - \mu (\varvec{s},t)}{\sigma (\varvec{s},t)}\right) \right] ^{-1/\xi (\varvec{s},t)} \right\} , \end{aligned}$$
(1)

which is defined for \(\{ y: 1 + \xi (\varvec{s},t)(y - \mu (\varvec{s},t))/\sigma (\varvec{s},t) > 0 \}\). The GEV distribution is characterized by the location parameter \(\mu (\varvec{s},t) \in \mathbb {R}\), the scale parameter \(\sigma (\varvec{s},t)>0\) and the shape parameter \(\xi (\varvec{s},t) \in \mathbb {R}\). While the three GEV parameters provide useful information about the marginal behavior of temperature extremes over time, we are often more interested in summaries of the fitted GEV distribution. For the purposes of this analysis, we are interested in the so-called risk probability for the 2021 heatwave, which summarizes the probability of exceeding the location-specific 2021 TXx temperature threshold (see Fig. 1a; denoted by \(u(\varvec{s})\)) in a given year t. Based on the form of the GEV distribution, we can calculate the risk probability as a direct function of the GEV parameters:

$$\begin{aligned} {p}_t(\varvec{s}, u(\varvec{s})) = \left\{ \begin{array}{ll} 1 - \exp \left\{ - \left[ 1+ {\xi }(\varvec{s},t)\left[ ({\mu }(\varvec{s},t) - u(\varvec{s})\right] /{\sigma }(\varvec{s},t) \right] ^{-1/{\xi }(\varvec{s},t)} \right\} , &{} {\xi }(\varvec{s},t) \ne 0, \\[1ex] 1 - \exp \left\{ - \exp \big \{ \left[ ({\mu }(\varvec{s},t) - u(\varvec{s})\right] /{\sigma }(\varvec{s},t) \big \} \right\} , &{} {\xi }(\varvec{s},t) = 0. \end{array} \right. \end{aligned}$$
(2)

Additionally, when the shape \(\xi (\varvec{s},t)\) is negative, the GEV distribution has a finite, time-varying upper bound, which can also be written in terms of the GEV parameters as

$$\begin{aligned} b(\varvec{s},t) = {\mu }(\varvec{s},t) - {\sigma }(\varvec{s},t)/\xi (\varvec{s},t). \end{aligned}$$
(3)

The fact that the GEV distribution has a finite bound when \(\xi (\varvec{s},t)<0\) has important implications for analyzing temperature extremes; see Sect. 4 for further discussion.

Specific to analyzing temperature extremes in the Pacific Northwest, the spatio-temporal variability in GEV parameters are modeled as:

$$\begin{aligned} \mu (\varvec{s},t)&= \mu _0(\varvec{s})+\mu _1(\varvec{s})\text {GHG}(t) + \mu _2(\varvec{s})\text {PDSI}(\varvec{s},t) + \mu _3(\varvec{s})\text {ELI}(t) +\mu _4(\varvec{s}) \text {Urban}(\varvec{s},t), \nonumber \\ \log \sigma (\varvec{s},t)&= \sigma _0(\varvec{s})+\sigma _1(\varvec{s})\text {GHG}(t) + \sigma _2(\varvec{s})\text {ELI}(t), \nonumber \\ \xi (\varvec{s},t)&\equiv \xi (\varvec{s}), \end{aligned}$$
(4)

in which \(\text {GHG}(t)\), \(\text {PDSI}(\varvec{s},t)\), \(\text {ELI}(t)\) and \(\text {Urban}(\varvec{s},t)\) are anthropogenic and natural drivers defined in Sect. 2.3. Given the difficulty in estimating the shape parameter (Cooley et al. 2007; Opitz et al. 2018), \(\xi (\varvec{s},t)\) is fixed constant over time, which is a common practice in spatial extremes (see, e.g., Risser et al. 2019). We tested different combinations in a series of pointwise analyses and determined that this combination of covariates gives the maximum likelihood assuming independence among stations, and thus the set of \(\{\mu _0(\varvec{s}), \dots , \mu _4(\varvec{s}), \sigma _0(\varvec{s}), \ldots , \sigma _2(\varvec{s}), \xi (\varvec{s})\}\) is denoted as the so-called GEV coefficients; note that these coefficients describe the climatological behavior of temperature extremes. Statistically modeling spatio-temporal variability in the GEV parameters in this manner implies a nonstationary model for extremes, and furthermore means that the risk probabilities in Eq. (2) can be calculated as a function of the GEV coefficients and the drivers.

Accounting for climatological dependence. The second important innovation of our modeling framework accounts for the fact that the climatology of temperature extremes exhibits spatial dependence. This is accounted for by forcing the climatological GEV coefficients to vary smoothly over the domain of interest. To this end, we suppose each marginal GEV coefficient is a function of thin plate splines (Wood 2003) and topographical features. In other words, for \(\gamma \in \{\mu _0,\mu _1,\mu _2,\mu _3, \mu _4, \sigma _0,\sigma _1,\sigma _2,\xi \}\), we statistically model

$$\begin{aligned} \gamma (\varvec{s})\mid \beta ^{\gamma }_0,\beta ^{\gamma }_1,\ldots , \beta ^{\gamma }_B = \beta ^{\gamma }_0+\sum _{i=1}^{99} \beta ^{\gamma }_i \underbrace{b_i(\varvec{s})}_{\mathrm{T.P. splines}} + \sum _{j=1}^{5} \alpha ^{\gamma }_j \underbrace{g_j(\varvec{s})}_{\textrm{topography}}, \end{aligned}$$
(5)

where the thin plate splines \(b_i(\cdot )\) are smooth functions of longitude and latitude and the \(g_j(\varvec{s}), j = 1, \dots , 5\) are the spatial-only covariates described in Sect. 2.4 (log average precipitation, elevation, slope, aspect, and distance-to-coast; see Supplemental Fig. B.6). We included 99 thin plate spline functions in order to flexibly model fine-scale spatial variability; however, to guard against over-fitting we furthermore included a regularization prior for the \(\{\beta ^\gamma _i:i=1,\dots ,99\}\) (see, e.g., Hans 2009). The climatological dependence in Eq. (5) and the subsequent individual event dependence are modeled in one Bayesian hierarchical model. In comparison, Richards et al. (2022) model the marginal GEV parameters using a basis of smoothing B-splines, which is done separately from the further individual event dependence modeling. In our approach, we substitute physical covariates for B-splines, representing a small methodological adjustment. However, this change leads to truly large gains for our application.

Accounting for the spatial coherence of individual events. While enforcing spatial coherence in the GEV coefficients following Eq. (5) is useful for describing climatological dependence, we must further account for the fact that individual heatwave events (aggregated over the course of a JJA season) will simultaneously affect multiple gauged locations. The third innovation of our methodology is that we account for this so-called data-level dependence in the maxima using a flexible method from the spatial extremes literature called a Gaussian scale mixture; see Zhang et al. (2021) for a full treatment of the theory and Zhang et al. (2022) for an application of the methodology to an analysis of extreme precipitation. At each time t, we assume the spatial field of JJA maxima \(\{Y(\varvec{s},t)\}\) has a copula defined by

$$\begin{aligned} X(\varvec{s},t)=R_t \cdot W(\varvec{s},t)+\epsilon (\varvec{s}), \end{aligned}$$
(6)

where \(R_t\sim \text {Pareto}\{(1-\delta )/\delta \}\), \(W(\varvec{s},t)\) is a standard isotropic and stationary Gaussian process with standard Pareto margins and \(\epsilon (\varvec{s})\) is a white Gaussian noise process with variance \(\tau ^2\). The covariance function of \(W(\varvec{s},t)\), \(C_{\theta _W}(h)\), describes the covariance of \(W(\varvec{s},t)\) at pairs of locations separated by a distance h and is indexed by \(\theta _W=(\rho ,\nu )\), in which \(\rho \) is the range parameter and \(\nu \) is the smoothness parameter.

The reason why the copula model (6) accounts for the spatial coherence of individual events is that it obviates the need for an independence assumption across sites conditioning on the marginal distributions defined by Eqs. (1) and (4). Instead, (6) directly considers the extreme events that occur simultaneously at a certain time. Specifically, \(R_t\) at time t acts as a scaling factor that amplifies the simultaneous large but not yet extreme values in \(\{W(\varvec{s},t)\}\). In the meantime, larger \(\delta \) induces heavier-tailed \(R_t\) and thus the amplifying effect from \(R_t\) will tend to be more evident. Consequently, the Gaussian scale mixture \(\{X(\varvec{s},t)\}\) exhibits asymptotic independence when \(\delta \in (0,1/2]\) and asymptotic dependence when \(\delta \in (1/2,1)\). Larger \(\delta \) values also induce higher sub-asymptotic dependence strength, and in the case of \(\delta \in (0,1/2]\) there is still weakening yet nonzero dependence at the sub-asymptotic levels. Using a well-defined dependence measure, we verified empirically in Online Appendix F that this copula model accurately quantifies the spatial dependence between stations during individual extreme heatwave events.

Given that we have one measurement per year at each station, we assume that any long-term autocorrelation or year-to-year variability in the maxima at each station is fully described by the time-varying location and scale parameters and any residual variability is temporally independent. For simplicity, we henceforth write \(X_{tj} = X_t(\varvec{s}_j)\), \(\varvec{X}_t=(X_{t1},\ldots ,X_{t,438})^T\) and so forth, in which \(\varvec{s}_j\) denotes the location of jth station, \(j=1,\ldots , 438\). In order to connect the copulas of the observed process \(\{Y(\varvec{s},t)\}\) and the Gaussian scale mixture \(\{X(\varvec{s},t)\}\), we define the following marginal transformation:

$$\begin{aligned} F_{Y\vert \gamma (\varvec{s}),t}\{Y(\varvec{s},t)\}=F_{X\vert \delta ,\tau ^2}\{X(\varvec{s},t)\}, \end{aligned}$$
(7)

where \(F_{Y\vert \gamma (\varvec{s}),t}\) is the GEV distribution function with parameters \(\{\mu (\varvec{s},t), \sigma (\varvec{s},t),\xi (\varvec{s},t)\}\) defined in Eq. (4) and \(F_{X\vert \delta ,\tau ^2}\) is the marginal CDF for \(X(\varvec{s},t)\) in Eq. (6). This marginal transformation allows us to examine the heterogeneity in the spatial characteristics of extremes. Conditioning on \(\gamma (\varvec{s})\) and the latent Gaussian process \(\varvec{W}_t\), the likelihood for \(\varvec{Y}_t\) is independent between locations due to the presence of the white noise process \(\{\epsilon (\varvec{s})\}\) and can be described by

$$\begin{aligned} \varphi \left( Y_{tj}\mid R_t, \varvec{W}_t,\delta ,\varvec{\theta }_j,\tau ^2\right) = \frac{1}{\tau ^2}\phi \left( \frac{X_{tj}- R_tW_{tj}}{\tau }\right) \frac{f_{Y\vert \varvec{\theta }_j, t}(Y_{tj})}{f_{X\vert \delta ,\tau ^2}\left( X_{tj}\right) }, \end{aligned}$$
(8)

in which \(X_{tj}=F_{X\vert \delta ,\tau ^2}^{-1}\circ F_{Y\vert \varvec{\theta }_j, t}(Y_{tj})\), \(f_{Y\vert \varvec{\theta }_j, t}\) and \(f_{X\vert \delta ,\tau ^2}\) are the density functions of \(F_{Y\vert \varvec{\theta }_j, t}\) and \(F_{X\vert \delta ,\tau ^2}\), and \(\phi \) is the probability density function of the standard Normal distribution. The likelihoods for all locations from different time replicates are simply multiplied together; see Online Appendix C for detailed specification of the hierarchical model. It is worth noting that many papers in the spatial extremes literature, such as Huser et al. (2017), Huser and Wadsworth (2019) and Zhang et al. (2021), use empirical or approximate marginal transformations instead of modeling the marginal distributions formally like we do in Eq. (7).

3.2 Statistical Counterfactual for Quantifying Human Influence

As discussed in Sect. 1, a major limitation of existing analyses of the PNW heatwave (e.g., Philip et al. 2021; Bercos-Hickey et al. 2022) is that they were unable to estimate nonzero risk probabilities for the observed temperatures, meaning they could not draw any conclusions regarding the human influence on the probability of experiencing temperatures at least as extreme as those that occurred in June, 2021. Such statements are the focus of the broader field of Extreme Event Attribution (EEA; see, e.g., National Academies of Sciences, Engineering, and Medicine 2016), which seeks to quantify the human influence on individual extreme weather and climate events. Traditional approaches to EEA are based on the concept of Pearl causality (Hannart et al. 2015), which uses counterfactual methods where an “intervention” can be applied and assessed. However, in cases where dynamical models are either not able to adequately simulate the extreme events of interest or cannot generate the requisite simulations fast enough (e.g., for rapid attribution statements), an alternative is to utilize a Granger-causal framework (Granger 1969) using observations only (see, e.g., Risser and Wehner 2017; Philip et al. 2021). Granger-causal attribution statements are subject to the usual caveats regarding the effect of hidden covariates (i.e., “correlation does not imply causation”) but are useful since they both motivate dynamical studies (e.g., the Hurricane Harvey study provided motivation for Patricola and Wehner 2018; Wang et al. 2018) and enhance confidence in attribution statements by using multiple analysis techniques to explore the causes of climate change.

The statistical framework for extreme value analysis outlined in Eqs. (1) and (4) uses covariates to describe long-term trends and year-to-year variability in temperature extremes in the Pacific Northwest and can therefore be used to generate Granger-causal attribution statements similar to Risser and Wehner (2017) and Philip et al. (2021). Specifically, the statistical model specified by Eq. (4) implies that risk probabilities and upper bounds (in the case of \(\xi (\varvec{s})<0\)) are all functions of the input covariates. As such, we can use the fitted model to estimate risk probabilities and upper bounds for two different climate scenarios (summarized in Supplemental Table B.1): the “factual” quantities represent our best estimates for the conditions present when the heatwave occurred, and the “counterfactual” summarizes the isolated effect of GHG forcing while holding all other quantities fixed.

Exploring the counterfactual scenario in this way allows us to identify the individual effect of GHG forcing under consistent “background” conditions as specified by ELI, PDSI and urbanization. We refer to the counterfactual scenario as “statistical” since it leverages the underlying statistical model to predict the distribution of temperature extremes for a setting of climate variables that did not actually occur (i.e., 1950 levels of GHG forcing and present-day ELI, PDSI, and urbanization). Finally, in a Bayesian framework the posterior samples of all unknown quantities in Eq. (1) and (4) allow us to propagate all statistical uncertainty to yield posterior distributions of the GEV upper bounds and risk probabilities.

In addition to summarizing the inferred GEV upper bounds and risk probabilities for each scenario, we furthermore use the risk probabilities to construct an attribution statement for the anthropogenic drivers. Specifically, we compare the factual probability of the 2021 heatwave event with corresponding probabilities from the counterfactual scenario, commonly referred to as probabilistic event attribution. One way to summarize the anthropogenic influence on an event of interest is via the “risk ratio” (Paciorek et al. 2018):

$$\begin{aligned} RR(\varvec{s}) = p_F(\varvec{s})/p_{C}(\varvec{s}). \end{aligned}$$

Here, \(p_F\) represents the risk probability for the factual scenario and \(p_{C}\) represents the risk probability for counterfactual; see Eq. (2) for the definition of risk probability. The risk ratio is thus a unitless quantity that attributes the isolated effect of anthropogenic GHG forcing on the probability of the heatwave occurring at location \(\varvec{s}\). A risk ratio of greater than one indicates that anthropogenic influence caused the 2021 PNW heatwave to become more likely, while a risk ratio of less than one indicates that anthropogenic influence caused the event to become less likely. We summarize best estimates and uncertainties in the risk ratios via their posterior distributions, which are obtained from the posterior distributions of the risk probabilities.

3.3 Alternative Statistical Models

The statistical model proposed in Sect. 3.1 represents three improvements upon the methodology used in, e.g., Philip et al. (2021) and Bercos-Hickey et al. (2022): (1) inclusion of additional spatio-temporal covariates (characterizing the influence of ELI, PSDI, and urbanization in addition to GHG forcing), (2) accounting for climatological dependence by including wet/dry regimes and orographic properties, and (3) accounting for spatial dependence in the tail of copula. In order to explicitly assess which aspect(s), if any, of our proposed model address the challenges of estimating out-of-sample probabilities related to an extremely rare heatwave, we consider three additional statistical models that can be viewed as special cases of the more general approach outlined in Sect. 3.1:

M1:

Pointwise, GHG only: this represents the approach used to analyze in situ records in Bercos-Hickey et al. (2022). Marginally, we simplify Eq. (4) such that the location parameter is a linear function of GHG forcing and the scale and shape parameters are time-invariant. Then, GEV estimates are obtained independently for each weather station record such that both climatological and data-level dependence are ignored.

M2:

Pointwise, all covariates: this approach generalizes M1 by using the full suite of covariates (in both location and scale) described by Eq. (4); however, like M1, both climatological and data-level dependence are ignored.

M3:

Climatological dependence only, all covariates: this approach generalizes M2 by again using the full suite of covariates (in both location and scale) described by Eq. (4); however, we now account for climatological dependence only and ignore data-level dependence. This is equivalent to the GEV-GP model in Cooley et al. (2007).

M4:

All spatial, all covariates: this approach denotes the full model described in Sect. 3.1 that includes all covariates and accounts for both climatological and data-level dependence.

These models are furthermore summarized in Supplemental Table B.2. Fitting each of these models in a Bayesian framework allows us to calculate best estimates and uncertainties for 2021 GEV upper bounds, risk probabilities, and risk ratios, which are all implemented in python. The code along with the temperature observations are publically available at https://github.com/likun-stat/scalemixture_temp.

Fig. 2
figure 2

Posterior means of the maximum effects of GEV coefficients \(\{\mu _0(\varvec{s}),\ldots , \mu _1(\varvec{s}),\sigma _0(\varvec{s}), \ldots , \sigma _2(\varvec{s}), \xi (\varvec{s})\}\) under M4; see Sect. 3.3 for the definition of M4 and see Eq. (9) to learn how to calculate the maximum effects

Full size image

4 Results

4.1 GEV Coefficients

From each MCMC update of basis coefficients \(\{\beta ^{\gamma }_0,\beta ^{\gamma }_1,\ldots , \beta ^{\gamma }_B\} \), \(\gamma \in \{\mu _0,\ldots ,\mu _4,\sigma _0,\ldots , \sigma _2,\xi \}\), we plug each quantity into Eq. (5) and generate the GEV coefficient values \(\{\gamma (\varvec{s})\}\) on an unobserved \(\sim 4\)km \(\times \sim 4\)km (\(1/16^\circ \) degree) grid over the PNW region. Here we use the thin plate splines and topographical bases values calculated on the grid a priori, and we update \(\{\gamma (\varvec{s})\}\) for each MCMC iteration. Figure 2 displays the pointwise posterior medians of GEV coefficients (denoted by \(\{\tilde{\gamma }(\varvec{s})\}\)). In order to directly compare the effect of each covariate, we multiply \(\tilde{\mu }_j(\varvec{s})\) and \(\tilde{\sigma }_j(\varvec{s})\) by the range of the time series over 1950–2021 (i.e., converting units from \(^\circ \)C per unit increase in covariate to just \(^\circ \)C). First, for \(\tilde{\mu }_1(\varvec{s})\) we show

$$\begin{aligned} \tilde{\mu }_1(\varvec{s})\times \left[ \max _{t}\{\text {GHG}(t)\}-\min _{t}\{\text {GHG}(t)\}\right] . \end{aligned}$$
(9)

Figure 2b indicates that an increase in GHG forcing led to a slight decrease of temperature near the Elliot Bay of Seattle and along the Pacific coast. However, a temperature increase of at least 1\(^\circ \)C is observed in the majority of the PNW region, while the increase is more evident in the Yakima Valley of Washington (\(\sim 4^\circ \)C) and the Willamette Valley of Oregon(\(\sim 8^\circ \)C). This in and of itself could be an attribution statement even if a few observed temperatures are out of bounds, since the human influence on extreme temperatures is insensitive to rarity (see Fig. 6 in Wehner et al. 2018, and later discussion in Sect. 4.2). To show the maximum effect of PDSI, we examine the maximum effect on a pointwise basis and multiply \(\tilde{\mu }_2(\varvec{s})\) by the range of the time series \(\{\text {PDSI}(\varvec{s},t): t=1950,\ldots , 2021\}\) at each location \(\varvec{s}\), i.e.,

$$\begin{aligned} \tilde{\mu }_2(\varvec{s})\times \left[ \max _{t}\{\text {PDSI}(\varvec{s},t)\}-\min _{t}\{\text {PDSI}(\varvec{s},t)\}\right] . \end{aligned}$$

Recall that PDSI \(>0\) indicates dry conditions. From Fig. 2b, PDSI has a consistently positive effect on the GEV location, driving a \(\approx 1^\circ \)C increase uniformly across the domain except for the lower right corner where there are no GHCN stations included in the analysis.

Similarly to Eq. (9), we multiply \(\mu _3(\varvec{s})\) and \(\sigma _2(\varvec{s})\) by the range of the series \(\{\text {ELI}(t): t=1950,\ldots , 2021\}\). The effect of ELI on the GEV location is generally weaker than GHG and PSDI, and (like GHG forcing) its effect on typical extreme temperatures is varied over the PNW. The effect of ELI on the GEV scale is also heterogeneous, with an evident decrease in the Shasta Valley of California and west of the Cascade Mountains in Washington.

For the urban heat island effect, we multiply \(\mu _4(\varvec{s})\) by 1 to assess the potential temperature increase brought by urbanization. If \(\text {Urban}(\varvec{s},t)\equiv 0\) for all t at location \(\varvec{s}\), the urban heat island effect is non-existent even though \(\mu _4(\varvec{s})\) might be positive in Fig. 2; if \(\text {Urban}(\varvec{s},t)\equiv 1\) for all t, there is some urbanization effect but it stays constant over 1950–2021. It is more interesting to look into locations where \(\text {Urban}(\varvec{s},t)\) starts out as 0 but changes to 1 before 2020. For example, there are large areas near the Portland and Seattle metropolitan regions that were urbanized in between 1950 and 2020; see Supplemental Fig. B.7.

4.2 2021 Upper Bounds

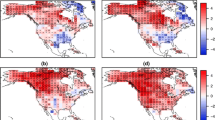
In Fig. 3, we calculate the GEV distributional upper bounds using Eq. (3) and the out-of-sample MCMC updates of the marginal parameters under the four modeling settings outlined in Sect. 3.3. The top row presents the pointwise medians of the posterior upper bounds in year 2021 using the factual conditions, in which the pointwise analyses (M1 and M2) produced relatively low upper bounds such that over 38% and 28%, respectively, of the stations had 2021 TXx values that exceed their corresponding theoretical upper bounds. In comparison, accounting for spatial dependence, even only at the climatological level, greatly improved the predictability of the 2021 heatwave event while increasing the GEV upper bounds consistently across PNW region: under M3, only 10.3% of stations have 2021 TXx that exceed the posterior median upper bound. Interestingly, the GEV shape parameters at many coastal stations changed from being positive in M1 to being negative but close to zero in M3 and M4 such that the upper bounds are finite but very large. In particular, the cluster of inexplicable 2021 TXx values near the Portland and Seattle-Tacoma metropolitan area in M1-M3 disappeared in M4 due to the incorporation of the urbanization index and extremal copula modeling. Further accounting for extremal dependence in M4 reduced the number of unexplainable events to just 3.4% of stations, demonstrating that accounting for both climatological and extremal dependence are critical for making the PNW heatwave event more predictable in an out-of-sample sense. Additionally, in one of our previous analyses in which we basically followed the M4 settings but excluded the urban binary index from the model, the proportion of stations with a 2021 TXx value exceeding the posterior median of upper bound was 9.4%, compared to 3.4% under M4 with the urban binary index in upper right panel of Fig. 3. Nonetheless, there are still some observations that exceed the posterior median GEV upper bound in spite of using a more sophisticated statistical model with the urbanization index, albeit the upper limits of our 95% credible intervals of the upper bounds from M4 contain the 2021 TXx at all stations.

Fig. 3
figure 3

The posterior median of the GEV upper bound under four statistical models (M1–M4; see Sect. 3.3). The first and second rows show upper bound estimates under the factual and counterfactual scenarios, respectively. For these rows, the ‘\(\triangle \)’ signifies an infinite upper bound (corresponding to \(\xi >0\)), and ‘+’ signifies stations for which the observed 2021 TXx exceeded the posterior median of the upper bound. The inset text in each panel displays the fraction of stations where the upper bound is exceeded. See Supplemental Fig. B.8 for the differences in the upper bounds for each scenario

Full size image

The bottom row of Fig. 3 examine the isolated effect of GHG forcing under the counterfactual scenario, which show that many more stations in Washington and Oregon (between 8–12% more) would have failed to contain the 2021 TXx values if the GHG stayed at the 1950 level. Particularly under M3 and M4, differences in the posterior medians of the upper bounds exceeds 3 \(^\circ \)C in majority of the stations in Oregon; i.e., increases in GHG forcing drive increases in GEV upper bounds by more than 3 \(^\circ \)C; see Supplemental Fig. B.8. Although M2 under the factual conditions failed to contain a large fraction of the 2021 TXx measurements, the differences in upper bounds are much higher than M1 and even comparable to spatial analyses. This indicates that including more covariates will augment the anthropogenic effects and increase the factual upper bounds but not enough to contain significantly more 2021 TXx values compared to M1. Interestingly, under all modeling settings and factual/counterfactual conditions, there are practically no stations in northern California and eastern Oregon whose 2021 TXx values exceeded the upper bounds, indicating a not-so-extreme heatwave in that region.

4.3 Attribution: Counterfactual Risk Probabilities and Risk Ratios

In order to assess whether or not anthropogenic factors had a meaningful influence on the probability of the 2021 heatwave in a Granger sense (Granger 1969; Risser and Wehner 2017), we calculate both location-specific estimates of the risk probabilities and risk ratios for the PNW region; see Fig. 4. For attribution results we now focus on the estimates obtained from the full model (labeled M4 in Sect. 3.3) since this approach best accounts for known relationships in the data and minimizes the fraction of stations for which the GEV upper bounds are exceeded by the 2021 extreme temperatures.

Fig. 4
figure 4

Subfigure a shows the station-specific posterior medians of the risk probabilities calculated from statistical model M4 for the Counterfactual (left) and Factual (right) climate scenarios, and subfigure b shows their ratio. For the risk probabilities, solid black triangles indicate gauged locations for which the risk probability best estimate is zero; for the risk ratios, solid black circles denote \(RR(\varvec{s}) = \infty \) (wherein the counterfactual risk probability is zero but the factual risk probability is nonzero) and yellow ‘\(+\)’ shows where the risk ratios are undefined (wherein both counterfactual and factual risk probabilities are zero). In the rightmost panel, points that are plotted with additional ‘\(\circ \)’ sign indicates that risk ratio estimates are statistically significantly different from 1

Full size image

First, consider the posterior median estimates of the risk probabilities for the factual \(p_F(\cdot )\) and counterfactual \(p_C(\cdot )\) scenarios, shown in Fig. 4a. Recall that \(p_F(\cdot )\) and \(p_C(\cdot )\) quantify the probability of experiencing an extreme daily maximum temperature measurement at least as large as what was observed during the heatwave under each climate scenario; furthermore, these probabilities represent the best seasonal forecast for extreme daily temperatures in advance of the 2021 summer using a statistical model given the values of the covariates in Eq. (4). The counterfactual risk probabilities are generally quite small: for a large majority of stations, the event had a probability of less than 0.1 and in many cases less than 0.01. For the factual scenario, risk probability estimates are also small, but not as small as for the counterfactual scenario: factual risk probabilities are generally between 0.05 and 0.3. As would be expected from the discussion around upper bounds in Sect. 4.2, there are cases where the posterior medians of the risk probability are zero (denoted by black triangles in Fig. 4), meaning that the 2021 heatwave temperatures would have been considered impossible in the counterfactual or factual scenario. However, there are many stations for which the 2021 temperatures were quite “normal,” even in the counterfactual scenario: across Nevada and much of northwest California, the observed heatwave temperatures had more than a 0.5 probability. In the meantime, there are still a small number of stations for which the factual risk probability estimates are exactly zero—in other words, for several stations we would have concluded that the 2021 temperatures were impossible even with increases to GHG forcing. However, it is the case that \(p_F(\varvec{s}) = 0\) if and only if \(p_C(\varvec{s}) = 0\), i.e., if the event was considered impossible in the factual scenario than it would also have been considered impossible in the counterfactual scenario.

Next, consider the posterior median estimates of the risk ratios, shown in Fig. 4b. Across the PNW, the dominant color in Fig. 4b is purple/magenta (i.e., \(RR(\varvec{s})>1\)), indicating that the 2021 heatwave event was made more likely by increases to GHG forcing. The risk ratios are often larger than 3, indicating that increases to GHG forcing resulted in a threefold increase in the probability of the extreme temperatures associated with the heatwave (and often much more than a threefold increase). In many cases, these increases in risk probability are statistically significant, in the sense that the lower bound of the 95% credible interval for the risk ratio is also greater than 1 (indicated by black circles around points in Fig. 4b). This is a powerful result: using a more refined statistical model, we can both quantify nonzero probabilities for the PNW heatwave event as well as determine statistically significant changes to this probability in an out-of-sample sense—this was previously impossible (again, see Philip et al. 2021; Bercos-Hickey et al. 2022). The presence of zeros in the best estimates of the counterfactual risk probability means that in many cases the risk ratio is infinite; however, there are a still \(\sim 7\)% of stations for which the risk ratio is undefined (i.e., both risk probabilities are zero, such that \(RR = 0/0\)), even using our best statistical model. (Note that the 7.5% of stations with undefined risk ratios differs from the 3.4% of stations for which the factual GEV upper bounds were exceeded due to the nonlinearity of posterior calculations.) Notably, there are some cases where the risk ratio is less than one (very few stations significantly so). The locations of these stations coincides with the regions where the GHG coefficient is negative; see Fig. 2b. They also correspond to the stations that have very low risk probabilities under both factual and counterfactual scenarios.

In summary, we now have a solution to the original problem posed by the severity of the heatwave event for existing attribution methods: while naïve statistical methods fail to quantify nonzero probabilities of the event (with or without climate change) and hence cannot make confident attribution statements, by using a sophisticated statistical model that more appropriately accounts for known features of the data (i.e., covariates, climatological dependence, and extremal dependence in the copula), we are able to robustly quantify the extent to which anthropogenic GHG emissions increased the likelihood of the observed extreme temperatures in 2021.

5 Conclusion

In this paper, we built a novel statistical model that accounts for the spatial coherence of both the climatological coefficients while also considering the natural and anthropogenic drivers for extreme temperatures. Using a Bayesian hierarchical framework, our method improves on the results from both Philip et al. (2021) and Bercos-Hickey et al. (2022) as more than 38% of the in situ 2021 TXx values could not be anticipated in their out-of-sample analyses, compared to 3.4% from our best model fit. As a result, we were able to estimate risk probabilities and make attribution statements for most GHCN stations while also quantifying the uncertainties for the estimates of the risk ratios. We showed that the increases in GHG forcing resulted in at least 3-fold increase in the probability of the extreme temperatures associated with the heatwave at the majority of the PNW locations in the US. Furthermore, we performed analyses under a set of simpler models to isolate the contributions from each component of the model to the improvements over predicting the 2021 PNW heatwave. We found that borrowing strength from neighboring stations, even only at the climatological level, maximizes the information contained in the historical data which sheds more light on the extreme events.

It should be noted here that while our analyses focus on the PNW region in the USA, the most intense part of the heatwave occurred in British Columbia because the associated heat dome was centered there. However, we confined our analyses to the PNW region within the USA due to a lack of the homogenized temperature data in Canada from GHCN. McKinnon and Simpson (2022) increased the spatial coverage of British Columbia by including station data archived by the Government of Canada (2022) and the sub-daily measurements in the Integrated Surface Database (Smith et al. 2011). In future work, we plan to include in situ observations from both Canada and the USA and re-run the analysis to get a more complete picture of the heatwave and to evaluate the anthropogenic and natural contributions to the event for the larger spatial domain.

Bercos-Hickey et al. (2022) argued that the failure to contain the 2021 TXx values using the GEV upper bounds resulted from a violation of the “IID” assumption in the univariate extreme value theory, which requires the samples from each block (season in our case) to be independent and identically distributed. As explained in the introduction, the underlying meteorological conditions responsible for the extreme temperatures are truly unique and different in 2021, indicating that the observed TXx from 2021 do not arise from the same distribution as the TXx values from the preceding 71 years. Including covariates to model year-to-year changes in the marginal GEV distribution relaxes this assumption such that we only require the “residuals” to be IID. Nonetheless, using covariates in the GEV parameters alone within a single-station analysis framework is not enough to characterize the extreme 2021 temperatures (as shown in both Bercos-Hickey et al. 2022 and models M1 and M2; see Fig. 3). Instead, the real difference-maker is accounting for spatial dependence in extreme temperatures: even accounting for just climatological dependence in the GEV covariates drastically reduces the fraction of “unexplainable” 2021 temperatures (28.1% to 10.3% for the factual scenario). However, incorporating physical covariates and accounting for climatological dependence in these quantities is also not enough: it is only when additionally accounting for data-level dependence via the copula that we can provide the best characterization of the 2021 extreme temperatures.

In Sect. 4, we focused on posterior median summaries for determining exceedance of upper bounds and assessing the risk ratios between the factual and counterfactual scenarios. A principal benefit of using a Bayesian framework is that one can summarize uncertainty robustly via either 95% credible intervals or non-binary probabilities of upper bound exceedance. As noted previously, it is the case that the upper limits of 95% credible intervals of the upper bounds for statistical model M4 contain the 2021 TXx at all stations! As such, it could be more informative to instead summarize the rarity of the 2021 TXx values with probabilities related to the upper bound failing to contain the event at each station using the posterior samples of our model parameters. However, for simplicity of presentation, in this manuscript we opted to show results for the upper bound posterior medians.

Finally, it is noteworthy that the flexible scale mixture model described in Sect. 3.1 concluded that TXx measurements in the PNW are asymptotically independent (AI; see Fig. F.1 in Online Appendix F). A similar property emerged for measurements of extreme precipitation (Zhang et al. 2022); however, extreme precipitation events are generally more localized than extreme temperature events, such that we might expect the analysis in this paper to yield asymptotic dependence (AD). As discussed in Zhang et al. (2022), one reason for extreme temperatures exhibiting AI is the size of the spatial domain considered in this analysis: analyzing smaller spatial domains may cause extreme temperatures to become asymptotically dependent. This sheds light on the importance of building a more flexible model that exhibits nonstationary tail dependence; we are currently pursuing such methodology in related work.