Inference for New Environmental Contours Using Extreme Value Analysis

Abstract

Environmental contours are often used in engineering applications to describe risky combinations of variables according to some definition of an exceedance probability. These contours can be used to both understand multivariate extreme events in environmental processes and mitigate against their effects, e.g. in the design of structures. Such ideas are also useful in other disciplines, with the types of extreme events of interest depending on the context. Despite clear connections with extreme value modelling, much of this methodology has so far not been exploited in the estimation of environmental contours; in this work, we provide a way to unify these areas. We focus on the bivariate case, introducing two new definitions of environmental contours. We develop techniques for their inference which exploit a non-standard radial and angular decomposition of the variables, building on previous work for estimating limit sets. Specifically, we model the upper tails of the radial distribution using a generalised Pareto distribution, with adaptable smoothing of the parameters of this distribution. Our methods work equally well for asymptotically independent and asymptotically dependent variables, so do not require us to distinguish between different joint tail forms. Simulations demonstrate reasonable success of the estimation procedure, and we apply our approach to an air pollution data set, which is of interest in the context of environmental impacts on health.

Supplementary materials accompanying this paper appear online.

1 Introduction

In environmental, engineering, financial and health contexts, it is the exposure to extreme values of prevailing conditions that cause the most risk. When these prevailing conditions relate to a univariate random variable, the extreme values correspond to observations from either its lower or upper tail, depending on the context, e.g. human health responds differently to cold weather or heatwaves, with such events being linked to respective tails of the temperature variable. When the prevailing conditions are described by a multivariate random variable $\varvec{X}\in {\mathbb {R}}^d$, for $d \in {\mathbb {N}}\backslash \{1\}$, there is still a need for the identification of sets of variable combinations that are the ‘riskiest’, as judged for the given class of problems.

For such a set of risky combinations of $\varvec{X}$ to be useful, a probability needs to be associated with the set, where this probability is small given the rarity of the events of interest. Hence, empirical methods to identify such sets are infeasible, as typically the probability will be smaller than $n^{-1}$, where n is the sample size. In the reverse set-up, any set in ${\mathbb {R}}^d$ is not uniquely defined by the probability of its occurrence alone, so additional criteria need to be imposed. These criteria could lead to sets being defined such that they have a small probability of being exceeded, or by a contour of points representing the boundaries of different regions, each with some specified shape and equal occurrence probabilities.

This paper aims to formalise these statements, in the case where $\varvec{X}$ has a joint density function $f_{\varvec{X}}$, to provide an inference framework for extreme sets related to combinations of $\varvec{X}$, which are typically called environmental contours; see discussion in the engineering (Mackay and Haselsteiner 2021) and statistical (Hafver et al. 2022) literature. In engineering, these contours are critical to the practical design of complex, multifaceted, structures that need to withstand environmental multivariate extreme events (Huseby et al. 2015). Similar ideas can be applied in environmental settings, e.g. to specify safety standards relating to combinations of pollutants, for mitigation against a range of health issues, as used as the motivating example in Heffernan and Tawn (2004), or in finance when studying risk across portfolios with different combinations of investments (Poon et al. 2004; Castro-Camilo et al. 2018).

The key complication with identifying such risky combinations is the lack of a natural ordering in multivariate problems. Barnett (1976) addressed this problem by identifying four possible ordering strategies: componentwise maxima, concomitants, convex hulls and structure variables. Subsequent extreme value theory and/or methodology has been developed for these four strategies in Tawn (1990); Ledford and Tawn (1998); Eddy and Gale (1981), Brozius and de Haan (1987) and Davis et al. (1987); and Coles and Tawn (1994), respectively. In the context of the convex hull, the asymptotic shape and number of points contributing to the convex hull are studied, and links are drawn with multivariate extreme value theory, but for environmental contours, interest lies additionally in events beyond the observed data. In contrast, the recent study of a new basis for ordering, linked to the limiting shape of a scaled sample cloud (Balkema et al. 2010; Nolde 2014; Nolde and Wadsworth 2022), seems to address these concerns.

For well-defined practical problems, it is the structure variable approach that is the most relevant for identifying sets of risky values of $\varvec{X}$. Coles and Tawn (1994) present a statistical framework to study extremes of structure variables. For a d-dimensional vector $\varvec{x}=(x_1, \dots ,x_d)$, they consider the structure function $\Delta (\varvec{x}): {\mathbb {R}}^d \rightarrow {\mathbb {R}}$, which is entirely determined by the context of the problem. For example, $\Delta$ could be the stress on an offshore structure with $\varvec{x}$ being wave height and wind speed at that structure. The function $\Delta$ captures information about the impact under different values of $\varvec{x}$; as the value of $\Delta$ increases, the severity of the impact also increases. Similarly, in a health context $\Delta$ could be the effect of air pollutants on human lungs, with $\varvec{x}$ representing levels of the different air pollutants. In these contexts, interest lies in the probability of occurrence of large structure variables, i.e.

$$\begin{aligned} \Pr \{\Delta (\varvec{X})>v\}=\Pr (\varvec{X}\in A_v) =\int _{\varvec{x}\in A_v} f_{\varvec{X}}(\varvec{x}) \textrm{d}\varvec{x}, \end{aligned}$$

(1)

where $A_v=\{\varvec{x}\in {\mathbb {R}}^d: \Delta (\varvec{x})>v\}$ is termed the failure region. If v is sufficiently large to be above any observations of the univariate variable $\Delta (\varvec{X})$, Bruun and Tawn (1998) show that there are substantial advantages that can be achieved in estimating $\Pr \{\Delta (\varvec{X})>v\}$ using a multivariate approach building out of the right hand side of expression (1), over analysing univariate realisations of $\Delta (\varvec{X})$; this is essentially because knowledge of the structure function beyond the observations can be exploited. However, these findings are subject to having a good inference method for multivariate joint tails, which is not always straightforward. The method from Coles and Tawn (1994) only considered asymptotically dependent models for $f_{\varvec{X}}$, whereas Heffernan and Tawn (2004) and Wadsworth and Tawn (2013) extended these models to also cover asymptotic independence, i.e. allowing for the possibility that only some subsets of the components of $\varvec{X}$ can be simultaneously extreme.

The structure variable approach provides an extreme set of risky combinations of $\varvec{X}$ via the set $A_v$, with an associated joint probability p of occurrence given by (1). For a single structure function $\Delta$, then the boundary of the failure region gives the required environmental contour, ${\mathcal {C}}_p:= \{\varvec{x}\in {\mathbb {R}}^d: \Delta (\varvec{x})=v_p\}$, where $v_p$ is the $(1-p)$th quantile of the structure function $\Delta$. For structure functions of interest, ${\mathcal {C}}_p$ will be a connected subset of ${\mathbb {R}}^d$ and a continuous function of p. As an illustration, consider the sub-class of this framework when $\Delta (\varvec{x})=\min _{i=1, \ldots ,d}(\phi _ix_i)$ for known constants $\phi _i>0~(i=1, \ldots ,d)$, so interest lies in the joint survivor function on a given ray determined by the $\phi _i$ constants. Here, the risky set is $A_{v_p}=\{\varvec{x}\in {\mathbb {R}}^d: x_i>v_p/\phi _i, i=1, \ldots ,d \}$, and ${\mathcal {C}}_p=\{\varvec{x}\in {\mathbb {R}}^d: \min _{i=1, \ldots ,d}(\phi _ix_i)=v_p\}$ is its lower boundary, so that ${\mathcal {C}}_p$ is continuous over ${\mathbb {R}}^d$ and changes smoothly with p.

However, the structure variable formulation is overly simplistic in practice as it assumes that $\Delta$ is entirely known. To illustrate this, consider again the structure function $\Delta (\varvec{x})=\Delta (\varvec{x}; \varvec{\phi })=\min _{i=1, \ldots ,d}(\phi _i x_i)$, where $\varvec{\phi }=(\phi _1, \ldots ,\phi _d)$ but now with the $\phi _i>0$ all unknown. In this case, both $A_{v_p}$ and ${\mathcal {C}}_p$ vary with $\varvec{\phi }$ as well as p. This means that either additional criteria are needed to optimise $\varvec{\phi }$, or a broader definition of an environmental contour is required than one based on the approach of Coles and Tawn (1994) with known $\Delta$. For this particular class of structure function, when $d=2$ and for a fixed probability p, Murphy-Barltrop et al. (2023) estimate environmental contours corresponding to all combinations of $(x_1(p),x_2(p))$ with $\Pr \{X_1>x_{1}(p), X_2>x_{2}(p)\}=p$, i.e. the contour of equal joint survivor functions. The fact that Murphy-Barltrop et al. (2023) need only to find a two-dimensional solution, whereas our set up above suggested it should be three-dimensional over $(\phi _1,\phi _2, v_p)$, illustrates that to get identifiability in our solution when using the $\Delta$-approach, we need to impose that $\phi _2=1-\phi _1$ and $\phi _1,\phi _2\in [0,1]$, say.

There is a need for techniques to estimate environmental contours in more general settings than Murphy-Barltrop et al. (2023) and which scale better with dimension, as the following examples illustrate. First, consider the scenario where $\Delta (\varvec{x})=\Delta (\varvec{x}; \varvec{\phi })$, for unknown $\varvec{\phi }$, occurs in an engineering design phase, e.g. for an oil rig. It is possible that the general form of $\Delta$ is known from previous constructions, but that there are features of the design, determined by $\varvec{\phi }$, which are specific to the location of the oil rig. In this case, it is not possible to evaluate $\Delta (\varvec{x}; \varvec{\phi })$ for all possible $\varvec{\phi }$, as numerical evaluation of $\Delta (\varvec{x}; \varvec{\phi })$ can be computationally demanding. Similarly, in health risk assessments for air pollutants in setting legal maximum levels, there are a range of structure functions to assess, i.e. $\Delta _i(\cdot ; \varvec{\phi }_i)$ for $i\in {\mathcal {I}}$, where the set ${\mathcal {I}}$ corresponds to a collection of different health risks as a consequence of the pollutants $\varvec{x}$.

Ross et al. (2020) and Haselsteiner et al. (2021) provide recent reviews on environmental contours from an engineering perspective. The earliest methods in that literature go back to the IFORM (Hasofer and Lind 1974; Winterstein et al. 1993), which is based on the implicit assumption of a Gaussian copula and a range of approximations. Since then, there have been a series of extensions to the definitions; these reduce the number and impact of various assumptions in different ways. Such extensions include the direct sampling approach of Huseby et al. (2013), the high density contour approach of Haselsteiner et al. (2017) and the ISORM (Chai and Leira 2018), all of which are discussed in Mackay and Haselsteiner (2021). If an environmental contour cannot be defined according to a known structure function, there are a number of ways these ideas may be used and implemented in practice. Critically, these will depend on the specific application and require knowledge from domain experts, so that statisticians have only a limited role to play at such a stage. To illustrate this, we return again to our engineering and air pollution motivating examples. In engineering contexts, if environmental contours are derived at an initial design stage, then different points on the contour can be used to test a range of possible structures and narrow down the specification to a known structure function $\Delta$; from here, the previously described structure function approach could be used to finalise a specific design. In contrast, in health contexts, practitioners may be able to identify the combinations of pollutants on the contour of interest that are the most likely to lead to adverse health effects, possibly relating to a range of different symptoms. Contours in this setting provide vital information about the most likely dangerous combinations of air pollutants and so help guide the setting of new environmental air quality standards.

Environmental contours can be seen as an application of multivariate extremes, yet they have not been studied systematically from a methodological perspective. In multivariate settings, statistical extreme value methods have primarily focused on dependence characterisations and inference, rather than following this through to implications for practitioners. For example, for any bivariate pair $(X_i,X_j)\subseteq \varvec{X}$, with $i\ne j$, much focus is given to determining the value of

$$\begin{aligned} \chi _{ij}=\lim _{u\rightarrow 1} \Pr \{F_{X_j}(X_j)>u\mid F_{X_i}(X_i)>u\}\in [0,1], \end{aligned}$$

(2)

where $F_{X_i}$ and $F_{X_j}$ are the marginal distribution functions of $X_i$ and $X_j$, respectively. When $\chi _{ij}>0$ ($\chi _{ij}=0$), the variables $(X_i,X_j)$ are said to be asymptotically dependent (asymptotically independent), respectively (Coles et al. 1999). The key difference between these two forms of extremal dependence is that under asymptotic dependence (asymptotic independence) it is possible (impossible) for both variables to take their largest values simultaneously. The asymptotically independent limit can occur for widely used dependence models, such as for all Gaussian copulas with non-perfect dependence, and distinguishing between these extremal dependence classes can be a non-trivial task in practice.

Some previous progress has been made in deriving contours linked to multivariate extreme value methods. Specifically, Cai et al. (2011) estimate equal joint density contours in the tail of the joint distribution. However, they make restrictive assumptions about the marginal and dependence structures; they assume multivariate regular variation, which imposes identically distributed marginal distributions that must be heavy tailed, and that the variables are either asymptotically dependent or completely independent, meaning more general forms of asymptotic independence are excluded. Einmahl et al. (2013) also focus on equal joint density contours, but select the contour such that the probability of $\varvec{X}$ being outside the contour is of a small target level. Although they allow different (though still heavy tailed) marginal distributions, they also assume asymptotic dependence and conditions such that the spectral measure is nonzero across all interior directional rays, for which no practical test currently exists.

The current methods have the potential to be improved using more advanced statistical techniques that can be applied in both asymptotic dependence and asymptotic independence settings, and crucially, which remove the need to determine in advance whether the variables are asymptotically dependent. Extensions of these approaches should also remove the restriction that the estimated contours must correspond to joint density contours. We aim to address all three of these gaps in current methodology in this paper.

We introduce two new environmental contour definitions and provide procedures for their estimation. We build on the methods of Simpson and Tawn (2022) for estimating the limiting boundary shape of bivariate sample clouds under some appropriate scaling. Following the strategy from copula modelling, where dependence features are considered separately to the marginal distributions, we define our contours on a standardised scale, with the variables first transformed to have common Laplace marginal distributions, and the resulting estimated contours then back-transformed to the original margins.

We end our introduction with an overview of the paper. In Sect. 2, we introduce two new environmental contour definitions and explain how the approach of Simpson and Tawn (2022) is adapted to estimate these contours in Sect. 3. The results of a simulation study are presented in Sect. 4, demonstrating across a range of examples that our estimation procedure provides contours are close to the truth, as well as being reasonably successful in obtaining regions with the desired proportion (probability) of observations lying outside them for within sample (out of sample) contours, respectively. An application to modelling air pollution, considering differences in behaviour due to season, is presented in Sect. 5. We conclude with a discussion in Sect. 6.

2 An outline of new contour definitions

2.1 Overview of the strategy

We make two key decisions when defining our new environmental contours. Firstly, we work on a marginal Laplace scale, and secondly, the contours are defined in terms of radial–angular coordinates. Before providing the contour definitions in Sect. 2.2, we discuss the motivation for these two choices.

It is common in the literature on both environmental contours and multivariate extremes to work on standardised margins. For instance, with the IFORM, one transforms to independent, standard Gaussian margins, before estimating a circular contour and then back-transforming to the original marginal scale. In the theoretical work of Nolde and Wadsworth (2022) and the methodological implementation of Simpson and Tawn (2022), standard exponential margins are used, but this choice comes with the drawback of only being able to capture positive dependence or independence. In order to additionally handle negative dependence, as well as lower tails on the marginal scale, we define our contours for variables $(X_L,Y_L)$ having standard Laplace margins (Keef et al. 2013), i.e. with marginal distribution functions

$$\begin{aligned} F_{X_L}(z) = F_{Y_L}(z) = {\left\{ \begin{array}{ll} \frac{1}{2}\exp (z), &{}z\le 0,\\ 1-\frac{1}{2}\exp (-z), &{}z>0, \end{array}\right. } \quad z\in {\mathbb {R}}. \end{aligned}$$

(3)

As the Laplace marginal distribution has both upper and lower exponential tails, the probabilistic structural relationship between $(X_L,Y_L)$ is the same as between the associated variables on exponential variables, i.e. $(X_E,Y_E)$, in the joint upper region. However, only with Laplace margins do these relationships hold, in a similar form, when considering joint tail regions involving both upper and lower tail events. So, the benefit of using Laplace over exponential margins is that they automatically cover all joint tails in a unified way, whilst being able to exploit existing theory derived using exponential variables.

In practice, as with the IFORM, we can apply a transformation to ensure the correct margins as a preliminary step and then back-transform to obtain a contour on the original marginal scale if required; this is discussed further in Sect. 3. We also demonstrate in Sect. 4.3 that estimation on a standardised Laplace scale has benefits over an equivalent approach applied on the scale of the observed data.

The radial and angular components of $(X_L,Y_L)$ are defined as

$$\begin{aligned} R_L=\sqrt{X_L^2+Y_L^2}>0, \quad W_L=\tan ^{-1}(Y_L/X_L)\in (-\pi ,\pi ], \end{aligned}$$

respectively. Here, large values of $R_L$ can be thought of as corresponding to ‘extreme events’ in both the Laplace and original space, with the value of $R_L$ defining the level of extremity; we exploit this in our contour definitions and estimation procedures. In particular, both contours are defined in terms of quantiles of $R_L\mid (W_L=w)$ with $w\in (-\pi ,\pi ]$, and this polar coordinate setting allows us to treat $W_L$ as a covariate when modelling $R_L$. This will be achieved by exploiting methods from univariate extreme value analysis, with smoothing over $W_L$ realised using the framework of generalised additive models.

Finally, the setting of Laplace margins and polar coordinates results in contours ‘centred’ on the marginal median values after back-transformation to the original scale. Even so, parallels with the setting considered in Simpson and Tawn (2022) mean that much of their methodology can be applied and extended here for estimation purposes, as discussed in Sect. 3.

2.2 Contour definitions

We obtain contours where the probability of lying outside these is $p\in (0,1)$, where in our extreme setting p is taken to be small. The first contour type uses the same quantile level for the radial variable across each angle, while the second allows the quantile level to vary with the density of the angular component.

Contour definition 1 If the angular density $f_{W_L}(w)$ exists, for $w\in (-\pi ,\pi ]$, define $r_p(w)$ such that

$$\begin{aligned} \Pr \left\{ R_L>r_p(w)\mid W_L=w\right\} = {\left\{ \begin{array}{ll} p, &{} \text {if } f_{W_L}(w)>0,\\ 0, &{} \text {if } f_{W_L}(w)=0,\\ \end{array}\right. } \end{aligned}$$

(4)

and the corresponding contour as ${\mathcal {C}}^1_p:=\left\{ r_p(w): w\in (-\pi ,\pi ]\right\}$. It is straightforward to show that the probability of lying outside the contour ${\mathcal {C}}^1_p$ is p, since

$$\begin{aligned} \int _{-\pi }^\pi \Pr \left\{ R_L>r_p(v)\vert W_L=v\right\} \textrm{d}F_{W_L}(v) = p \int _{-\pi }^\pi f_{W_L}(v)\textrm{d}v=p. \end{aligned}$$

When only a subset of the joint tail region is of practical concern, the definition of ${\mathcal {C}}_p^1$ can be adapted to reflect this. Specifically, in our Laplace marginal setting, interest may lie only with extreme values of $(X_L,Y_L)$ having angles $W_L\in \Omega \subset (-\pi ,\pi ]$. For example, if only the joint upper tail of both variables is of interest, we could consider $\Omega =[0,\pi /2]$. In this context, we suggest the contour ${\mathcal {C}}_p^1(\Omega ):= \left\{ r_p(w;\Omega ): w\in \Omega \right\}$, with $r_p(w;\Omega )$ such that $\Pr \left\{ R_L>r_p(w;\Omega )\mid W_L=w\right\} = p/\Pr (W_L\in \Omega )$, for $w\in \Omega$. As we are interested in $\Omega$, it follows that $\Pr (W_L\in \Omega ) =\int _{\Omega } f_{W_L}(v)\textrm{d}v >0$, and for $W_L\in \Omega$, the probability of lying outside the contour ${\mathcal {C}}^1_p(\Omega )$ is p.

Contour definition 2 Assume that $f_{W_L}(w)>0$ for all $w\in (-\pi ,\pi ]$, define $r^*_p(w)$ such that

$$\begin{aligned} \Pr \left\{ R_L>r^*_p(w)\mid W_L=w\right\} = \frac{c_p}{\max \left\{ f_{W_L}(w),p/(2\pi )\right\} }, \end{aligned}$$

(5)

with the constant $c_p$ chosen so that the probability of lying outside the contour ${\mathcal {C}}^2_p:=\left\{ r^*_p(w): w\in (-\pi ,\pi ]\right\}$ is p. This required value of $c_p$ is the solution to

$$\begin{aligned} \int _{-\pi }^\pi \Pr \left\{ R_L>r^*_p(v)\vert W_L=v\right\} \textrm{d}F_{W_L}(v)= & {} c_p\int _{-\pi }^\pi \frac{f_{W_L}(v)}{\max \left\{ f_{W_L}(v),p/(2\pi )\right\} }\textrm{d}v\\= & {} c_p\int _{-\pi }^\pi \min \left\{ 1, \frac{2\pi f_{W_L}(v)}{p}\right\} \textrm{d}v=p. \end{aligned}$$

That is,

$$\begin{aligned} c_p = p\left[ \int _{-\pi }^\pi \min \left\{ 1,\frac{2\pi f_{W_L}(v)}{p}\right\} \textrm{d}v\right] ^{-1}. \end{aligned}$$

(6)

The definition of ${\mathcal {C}}^2_p$ is chosen so that the probability of lying outside the contour is smaller on angles where the density is larger. We cannot take $f_{W_L}(w)$ as the denominator in the right-hand side of (5), since $c_p$ would simplify to $p/(2\pi )$, leading to the probability in (5) being greater than 1 if $f_{W_L}(w)<p/(2\pi )$, for any $w\in (-\pi ,\pi ]$; see Section A of the Supplementary Material. In the Supplementary Material, we also justify the choice to take the scaling function as $\max \left\{ f_{W_L}(w),p/(2\pi )\right\}$. We note that as more extreme contours are considered, i.e. as $p\rightarrow 0$, scaling via the density only is recovered and $c_p\sim p/(2\pi )$.

2.3 Contour examples

Fig. 1

Examples of ${\mathcal {C}}_p^1$ (solid lines) and ${\mathcal {C}}_p^2$ (dashed) for the case of independence, two Gaussian copulas and three bivariate extreme value copulas with logistic or asymmetric logistic models. For $p\in \{0.1,0.05,0.01,0.005,0.001\}$, the contours lie progressively further from (0, 0). The grey dashed lines show $X_L=0$, $Y_L=0$, $Y_L=X_L$ and $Y_L=-X_L$

Figure 1 demonstrates our two new contour definitions at varying probability levels for a range of copulas; their upper tail dependence features cover both asymptotic dependence and asymptotic independence, as defined by limit (2). We first present examples for the independence setting (case (i)) and two bivariate Gaussian copulas (cases (ii) and (iii)) with correlation matrices having off-diagonal elements $\rho =0.25,0.75$, respectively. We then consider some common bivariate extreme value distributions having copula function

$$\begin{aligned} C(u,v) = \exp \left\{ -V\left( -1/\log u,-1/\log v\right) \right\} ,\quad u,v\in [0,1], \end{aligned}$$

with the exponent measure V satisfying certain constraints; see Coles et al. (1999). The joint distribution of the corresponding variables $(X_L,Y_L)$ on standard Laplace scale is given by $F_{X_L,Y_L}(x,y) = C\left\{ F_{X_L}(x), F_{Y_L}(y)\right\}$, with $F_{X_L}(x)$, $F_{Y_L}(y)$ defined as in (3). In Fig. 1, examples (i) and (iv)–(vi) are all variants of the bivariate asymmetric logistic model of Tawn (1988), having exponent measure

$$\begin{aligned} V(x,y) = \frac{\theta _1}{x} + \frac{\theta _2}{y} + \left\{ \left( \frac{1-\theta _1}{x}\right) ^{1/\alpha }+\left( \frac{1-\theta _2}{y}\right) ^{1/\alpha }\right\} ^\alpha , \end{aligned}$$

with $x,y>0$, $\alpha \in (0,1]$ and $\theta _1,\theta _2\in [0,1]$. Setting $\theta _1=\theta _2=1$ gives independence, as in case (i); case (iv) is the logistic model (Gumbel 1960), where $\theta _1=\theta _2=0$; in case (v), we set $\theta _1=0$ and $\theta _2=0.5$, leading to a mixture structure where $X_L$ can only be large when $Y_L$ is also large, but $Y_L$ can be large independently of $X_L$; and in case (vi), we take $\theta _1=\theta _2=0.5$, which has features of both the independence and logistic models. Where the value of $\alpha$ is relevant, i.e. in cases (iv)–(vi), its value controls the strength of dependence in the upper tails and therefore the width of the pointed section along the upper-right diagonal; the closer $\alpha$ is to zero, the narrower this section of the contour. Having $\alpha \in (0,1)$ corresponds to asymptotic dependence, as defined by limit (2), while $\alpha =1$ recovers complete independence.

The independence and Gaussian examples all exhibit asymptotic independence in both the upper and lower joint tails. In contrast, while cases (iv)–(vi) have asymptotic dependence in their joint upper tails, they exhibit asymptotic independence in their joint lower tails. Another commonly considered copula in extreme value analysis is the inverted logistic model (Ledford and Tawn 1997); we note that such examples are not necessary here, since working on Laplace margins means that the contours ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ for any inverted logistic copula are equivalent to its logistic counterpart (i.e. where both have the same dependence parameter $\alpha$) up to a rotation about the origin.

For any copula and p, contours ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ differ due to the angular density $f_{W_L}(w)$. For the copulas in Fig. 1, plots of the $f_{W_L}(w)$ values are shown in Fig. 2. For independence and the Gaussian copula with $\rho =0.25$, the range of values taken by $f_{W_L}(w)$ for $w\in (-\pi ,\pi ]$ is relatively small, meaning that ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ are quite similar. For the logistic model and the Gaussian copula with $\rho =0.75$, $f_{W_L}(w)$ takes its largest values around $w=\pi /4$ and $w=-3\pi /4$, meaning that ${\mathcal {C}}_p^2$ appears to be more stretched along the diagonal $Y_L=X_L$ compared to ${\mathcal {C}}_p^1$; this is also true of the two asymmetric logistic cases, but to a lesser extent. The theory to derive contours such as those presented in Fig. 1, for $(X_L,Y_L)$ having some joint density $f_{X_L,Y_L}(x,y)$, is presented in Section B of the Supplementary Material. We will revisit these copula examples in Sect. 4, where we demonstrate the efficacy of our estimation procedure.

3 Contour estimation

3.1 Overview of the inferential approach and our new contribution

We now introduce our approach to estimating the new contours ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ by adapting the approach of Simpson and Tawn (2022), whose work focuses on limit sets, to allow for inference of sub-asymptotic contours. We begin by outlining the main ways we adapt the existing methodology for our new purpose. We then present our estimation approach for ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ in Sects. 3.2 and 3.3, respectively, before discussing tuning parameter selection in Sect. 3.4 and marginal modelling in Sect. 3.5.

An important difference between this work and that of Simpson and Tawn (2022) is that the latter considers variables having standard exponential marginal distributions, while we work on standard Laplace scale. As mentioned in Sect. 2.1, this allows for positive and negative associations between the variables, as well as flexibility in modelling both tails of each marginal distribution. In exponential margins, the angular variable is restricted to $[0,\pi /2]$, whereas in Laplace margins $W_L\in (-\pi ,\pi ]$; since results at these endpoints should coincide, we must now carefully consider the cyclic nature of the angular distribution in our inferential procedure by updating our modelling choices to ensure this feature is preserved.

The definition of ${\mathcal {C}}_p^2$ in (5) depends on the value of the angular density $f_{W_L}$; estimation of this function was not previously required, but must be considered in the present work. The cyclic nature of $f_{W_L}(w)$ over $w\in (-\pi ,\pi ]$ is again a key feature that needs to be considered in our estimation approach. In addition, having the exceedance probabilities in (5) depend on $f_{W_L}$ means that some of the radial quantiles required to estimate the contour may not be ‘extreme’; we must therefore introduce a way to estimate non-extreme radial quantiles (as well as extreme ones) into our contour estimation procedure.

A final adaptation comes in the estimation of the marginal distributions. The results in Simpson and Tawn (2022) only required contours estimated on exponential scale, which was achieved via a rank transformation approach, but here we need to transform the estimated contours on Laplace margins back to the original scale. Reversing the rank transformation is not possible for extreme contours beyond the largest observed value in a one or both margins. To overcome this, we now model each marginal distribution via a combination of the empirical distribution function and generalised Pareto distributions in the upper and lower tails, as outlined in Sect. 3.5.

3.2 Estimation of ${\mathcal {C}}_p^1$

Parametric estimation of a contour ${\mathcal {C}}_p^1$ requires a model for $R_L\mid (W_L=w)$ for each $w\in (-\pi ,\pi ]$, from which we can extract high quantiles. Since we are interested in values in the upper tail of the distribution of $R_L\mid (W_L=w)$, a natural model is provided by the generalised Pareto distribution (GPD) (Davison and Smith 1990). Following Simpson and Tawn (2022), for each $w\in (-\pi ,\pi ]$, and for $R_L$ exceeding some angle-dependent threshold $u_w>0$, we propose to have

$$\begin{aligned} \Pr \left( R_L<r\mid R_L>u_w,W_L=w\right) = 1 -\left[ 1+\xi (w)\left\{ \frac{r-u_w}{\sigma (w)}\right\} \right] ^{-1/\xi (w)}_+, \end{aligned}$$

(7)

for $x_+=\max (x,0)$, $r>u_w$, $\sigma (w)>0$ and $\xi (w)\in {\mathbb {R}}$. Once an appropriate threshold $u_w$ has been selected, and estimates ${\hat{\sigma }}(w)$ and ${\hat{\xi }}(w)$ of the scale and shape parameters have been obtained, the value of $r_p(w)$ in (4) can be estimated by extracting the relevant quantile of (7), namely

$$\begin{aligned} {\hat{r}}_p(w) = u_w + \frac{{\hat{\sigma }}(w)}{{\hat{\xi }}(w)}\left[ \left\{ \frac{{\hat{\zeta _u}}(w)}{p}\right\} ^{{\hat{\xi }}(w)}-1\right] , \end{aligned}$$

(8)

with ${\hat{\zeta _u}}(w)$ denoting an estimate of $\zeta _u(w)=\Pr (R>u_w\mid W=w)$, often taken to be empirical. A corresponding estimate of the contour ${\mathcal {C}}_p^1$ is given by $\hat{{\mathcal {C}}}^1_p:=\left\{ \hat{r}_p(w): w\in (-\pi ,\pi ]\right\}$.

Applying the GPD requires us to select thresholds $u_w$ and derive estimates of $\sigma (w)$ and $\xi (w)$ for $w\in (-\pi ,\pi ]$, using observations $(r_{L,1},w_{L,1}),\dots ,(r_{L,n},w_{L,n})$ of $(R_L,W_L)$. There will not be sufficiently many equal observations of any given w value to be able to fit the generalised Pareto distribution in (7) directly for $R_L\mid (W_L=w)$. Instead, following Simpson and Tawn (2022) by assuming that the parameters $u_w$, $\sigma (w)$ and $\xi (w)$ in (7) vary smoothly with w, we employ a generalised additive modelling (GAM) framework, which was adapted for use with the generalised Pareto distribution by Youngman (2019).

The thresholds $u_w$ are selected via quantile regression at some quantile level $(1-p_u)$ with $p_u>p$, i.e. such that ${\hat{\zeta _u}}(w)=p_u$ for all $w\in (-\pi ,\pi ]$. This is achieved by fitting an asymmetric Laplace (Yu and Moyeed 2001) GAM to $\log R_L$, with cyclic P-splines (see Wood, 2017) used for the model parameters with $W_L$ as a covariate, before back-transforming to obtain quantile estimates of $R_L$.

For exceedances above the threshold function, we again propose using cyclic P-splines for the parameter $\log \sigma (w)$. A spline approach could also be used to model $\xi (w)$, but taking this to be constant has shown to produce less variable estimates in our experiments, which was also found by Simpson and Tawn (2022); we therefore fix $\xi (w)=\xi$ for all $w\in (-\pi ,\pi ]$. Estimation for the GPD-GAM framework is carried out in the R package evgam (Youngman 2020). Once all of these parameters have been calculated/estimated, equation (8) can again be used to extract radial quantiles at the required level.

The degree of the splines used within this modelling framework can impact the success of the approach. Following Simpson and Tawn (2022), we choose a spline degree $d\in \{1,2,3\}$, denoting the resulting radial quantile estimates by ${\hat{r}}_p^{(d)}(w)$, for $w\in (-\pi ,\pi ]$, in each case. Choice of d is discussed further in Sect. 3.4, along with the selection of the other necessary tuning parameters. Once the appropriate degree, denoted $d^*$, has been selected, our final estimate of ${\mathcal {C}}_p^1$ is $\hat{{\mathcal {C}}}^1_p:=\left\{ \hat{r}^{(d^*)}_p(w): w\in (-\pi ,\pi ]\right\}$.

3.3 Estimation of ${\mathcal {C}}_p^2$

The main difference between the definitions of ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ is that the latter requires radial quantiles to be extracted at different probability levels, while for the former this level is constant. This requires us to estimate the angular density $f_{W_L}(w)$ and to take into account that some of the quantiles required in (5) may fall below the GPD threshold, such that we also require a model for non-extreme events.

We propose to use kernel density estimation for $f_{W_L}(w)$. We have adapted the standard approach implemented in the density base function of R to account for $W_L$ being cyclic. To enforce this cyclicity, we first use data $\{(w_{L,1}-2\pi ),\dots , (w_{L,n}-2\pi ),w_{L,1},\dots ,w_{L,n},(w_{L,1}+2\pi ),\dots , (w_{L,n}+2\pi )\}$, resulting in a kernel density estimate ${\hat{f}}_{W_L}^*(w)$ over $(-3\pi ,3\pi ]$. We then take ${\hat{f}}_{W_L}(w) = 3{\hat{f}}_{W_L}^*(w)$ for $w\in (-\pi ,\pi ]$. Default selections of the kernel bandwidth often rely on the standard deviation of the observations, but this will be affected by our choice to artificially replicate the data. Instead, we use the approach of Sheather and Jones (1991), which is a non-default option in R, that appears to work well in our setting. Estimation of $f_{W_L}(w)$ is demonstrated in Fig. 2 for the six examples in Fig. 1.

Fig. 2

Angular density $f_{W_L}(w)$ for each of the models in Fig. 1 (black). The red lines correspond to estimates using our cyclic kernel density approach, for 100 different samples of size $n=10,950$

The required probability in (5) can be calculated for any angle w by substituting ${\hat{f}}_{W_L}(w)$ for $f_{W_L}(w)$; the required scaling constant $c_p$ in (6) is calculated numerically. At any angle where the required exceedance probability in (5) is less than the threshold exceedance probability $p_u$, the appropriate radial quantile can be extracted from the GPD-GAM model, giving us an estimate ${\hat{r}}_p^*(w)$ of $r_p^*(w)$. However, for exceedance probabilities greater than $p_u$, the GPD is not appropriate. At any such levels, we adopt the same quantile regression model as for the threshold, using an asymmetric Laplace GAM for $\log R_L \mid (W_L=w)$ at this quantile level, and extract the appropriate estimate ${\hat{r}}_p^*(w)$ of $r_p^*(w)$. The overall estimate of ${\mathcal {C}}_p^2$ is $\hat{{\mathcal {C}}}^2_p:=\left\{ \hat{r}^*_p(w): w\in (-\pi ,\pi ]\right\}$.

3.4 Tuning parameter selection

The estimation procedures introduced in Sects. 3.2 and 3.3 require the selection of several tuning parameters: the threshold exceedance probability $p_u$; the number and location of knots in the cyclic P-splines; and the degree of the basis functions. We now discuss each of these choices in turn.

Simpson and Tawn (2022) propose to set $p_u=0.5$, and while this does seem to provide quite a low choice for the threshold of the GPD, we have also found it to work well in our setting (see Section C of the Supplementary Material for simulation results that support this choice). We therefore adopt this as our default tuning parameter. The plots in Fig. 1 demonstrate that there are important angles in particular settings, which it may be wise to consider when selecting spline knot locations. Under independence, the angles $w\in \{-\pi /2, 0, \pi /2, \pi \}$ correspond to the largest radial values on any given contour and the contours also exhibit a pointed shape here. If we are to capture such features using splines, it would be useful to have knots placed at these angles. For similar reasons, in the symmetric models exhibiting positive asymptotic dependence (cases (ii) and (iv)), the angle $w=\pi /4$ is particularly important. Angles $w\in \{3\pi /4,-\pi /4,-3\pi /4\}$ would also be important under negative asymptotic dependence or asymptotic dependence with one variable large while the other is small. All together, this suggests knots should be placed at all angles $w=-\pi +j\pi /4$, $j=1,\dots ,8$. However, this is generally not a sufficient number of knots, so we propose to add additional, equally spaced knots between these angles, so the knot locations are $w=-\pi +2j\pi /\kappa$, $j=1,\dots ,\kappa$, with $\kappa$ a multiple of eight; our default choice is $\kappa =24$.

For ${\mathcal {C}}_p^1$, to choose the spline degree $d^*$, we again adopt the approach of Simpson and Tawn (2022) to derive local estimates of $r_p(w)$ and use these to inform the value of $d^*$; the procedure is summarised here. For a given angle w, a ‘local estimate’ is obtained by defining a neighbourhood of radial values corresponding to the m nearest points to w. Maximum likelihood estimation is then used to fit the generalised Pareto distribution in (7) using these radial values. This is repeated over k angles $w^*_j = -\pi + j\pi /100$, $j=1,\dots ,k$, with the desired radial quantiles extracted and denoted by ${\hat{r}}^{\text {local}}_p(w_1^*),\dots ,{\hat{r}}^{\text {local}}_p(w_k^*)$. As in Simpson and Tawn (2022), our default tuning parameter choices are $m=100$ and $k=200$. Figure 1 shows that some contours have smooth, curved shapes, while others are quite ‘pointy’; this suggests that in some cases, linear basis functions may be appropriate, while in others, quadratic or cubic splines will perform better. We therefore estimate three different versions of the quantiles in (8) via the GAM-GPD approach, using degree $d=1,2,3$ basis functions for both the $\log u_w$ model and $\log \sigma (w)$. We denote the resulting estimates by ${\hat{r}}_p^{(d)}(w)$, for $w\in (-\pi ,\pi ]$, $d=1,2,3$. To select the spline degree, we find

$$\begin{aligned} d^* = \mathop {\mathrm {arg\,min}}\limits _{d=1,2,3}\sum _{j=1}^k \left| {\hat{r}}_p^{(d)}(w^*_j) - {\hat{r}}_p^{\text {local}}(w^*_j)\right| , \end{aligned}$$

i.e. the choice of basis function degree that allows the estimates to be as close to the local estimates as possible, but with the added benefit of smoothness in the resulting contour estimate. An equivalent approach is used to choose the spline degree in the estimation of ${\mathcal {C}}_p^2$, but at angles where a non-extreme radial quantile is required, an empirical quantile is used as the local estimate.

3.5 Marginal model

We end by describing the approach used to transform the original margins to Laplace scale. This is applied separately to each of the variables X and Y to obtain standard Laplace margins $X_L$ and $Y_L$, from where the contour estimation procedure can be implemented. We focus on the model for X in this section, but an analogous approach is used for Y. Supposing that X has distribution function $F_X$, transformation to Laplace scale can be achieved through application of the probability integral transform, defining

$$\begin{aligned} X_L = {\left\{ \begin{array}{ll} \log \left\{ 2F_X(X)\right\} , &{}F_X(X)\le 1/2,\\ -\log \left[ 2\{1-F_X(X)\}\right] , &{}F_X(X)>1/2, \end{array}\right. } \end{aligned}$$

(9)

so that the distribution function of $X_L$ is as in (3). In practice, the distribution of X is unknown, so we use a combination of the empirical distribution function, denoted by ${{\tilde{F}}}_X$, and generalised Pareto models for both tails. That is, for $v^L$ and $v^U$ denoting lower and upper thresholds, respectively, we take

$$\begin{aligned} F_X(x)= {\left\{ \begin{array}{ll} \lambda ^L\left\{ 1+\frac{\xi ^L(v^L-x)}{\sigma ^L}\right\} ^{-1/\xi ^L}_+, &{}x\le v^L,\\ {\tilde{F}}_X(x), &{}v^L<x<v^U,\\ 1 - \lambda ^U\left\{ 1+\frac{\xi ^U(x-v^U)}{\sigma ^U}\right\} ^{-1/\xi ^U}_+, &{}x\ge v^U, \end{array}\right. } \end{aligned}$$

(10)

where $\sigma ^L>0,\sigma ^U>0$, $\xi ^L\in {\mathbb {R}},\xi ^U\in {\mathbb {R}}$, $\lambda ^L=\Pr \left( X<v^L\right)$ and $\lambda ^U=\Pr \left( X>v^U\right)$. This is the two-tailed extension of the marginal modelling approach presented by Coles and Tawn (1991).

Model (10) requires the selection of two thresholds, which we choose such that $\lambda ^L=\lambda ^U=0.05$. More sophisticated threshold selection techniques are available (see Scarrott and MacDonald (2012) for an overview, and Wadsworth (2016) or Northrop et al. (2017) for examples of recent developments), but we choose this approach for ease. Estimation of the scale $(\sigma ^L,\sigma ^U)$ and shape $(\xi ^L,\xi ^U)$ parameters is carried out via maximum likelihood estimation, as implemented in the R package ismev (Heffernan and Stephenson 2018). Once all parameters in (10) are estimated, transformation (9) can be applied to each observation to provide the marginal observations on Laplace scale. Inversion of the transformation is also possible if the final results are required on the original scale; when inverting the empirical distribution function, we linearly interpolate where values between available X observations are required.

4 Simulation study

4.1 Overview

We now demonstrate how well the inferential procedure we introduced in Sect. 3 estimates the two types of contour defined in Sect. 2. We consider two scenarios: in Sect. 4.2, we work directly with data on Laplace margins; in Sect. 4.3 we allow the data to have more general, unknown margins. In the latter case, we compare our approach of estimating the contours on the transformed Laplace marginal scale before back transforming to the data scale, with an equivalent approach applied directly on the original scale of the data, which we demonstrate can lead to undesirable results.

Before presenting our results, we first detail the different tools and metrics that are used in our simulation study. We assess our methods based on how well the true contours are estimated, given data sampled from a range of different copula models (based on those presented in Fig. 1). Throughout this section, we simulate data sets of size $n=10,950$ (corresponding to a realistic scenario of daily observations over 30 years) and we use 100 replicates for each setting.

Our first strategy is to compare our estimated contours to the truth pictorially, allowing us to assess the estimation procedures by eye. We formalise this assessment by using two metrics for comparison. In the first, we count the number of points in the sample lying outside the estimated contour, denoting this by ${\hat{n}}_p$, so that the proportion of points outside the contour is ${\hat{n}}_p/n$. We then quantify the relative error from p, the target contour exceedance probability, to this empirical proportion by calculating the empirical relative error ${\hat{n}}_p/(np)-1$. When ${\hat{n}}_p/(np)-1=0$, we have correctly recovered the true probability.

The empirical relative error measure is suitable when the exceedance level p and the sample size n are such that a reasonable number of points is expected to lie outside the true contour. To cover more extreme cases, we also adopt the symmetric difference metric $\triangle$, used by Einmahl et al. (2013), which measures the difference between a true contour ${\mathcal {C}}$ and its estimate $\hat{{\mathcal {C}}}$ via

$$\begin{aligned} {\mathcal {C}}~\triangle ~ \hat{{\mathcal {C}}}=\int _{\{E_{\mathcal {C}}\backslash E_{\hat{{\mathcal {C}}}}\}\cup \{E_{\hat{{\mathcal {C}}}}\backslash E_{\mathcal {C}}\}} f_{X,Y}(x,y)\textrm{d}x\textrm{d}y, \end{aligned}$$

where $E_{\mathcal {C}}$ denotes the set of $(x,y)\in {\mathbb {R}}$ that are more extreme than ${\mathcal {C}}$, with $E_{\hat{{\mathcal {C}}}}$ defined similarly, and $f_{X,Y}(x,y)$ is the joint density under the true marginal and copula specification. In our setting, we calculate this in Laplace space using the polar coordinates $(R_L,W_L)$ with associated joint density $f_{R_L,W_L}(r,w)$. Here, $E_{\hat{{\mathcal {C}}}}$ and $E_{{\mathcal {C}}}$ are given by $\{(r,w): r>\hat{r}(w), -\pi <w\le \pi \}$ and $\{(r,w): r>r_{true}(w), -\pi <w\le \pi \}$, respectively, with $\hat{r}(w)$ and $r_{true}(w)$ given implicitly by the forms of $\hat{{\mathcal {C}}}$ and ${\mathcal {C}}$, and

$$\begin{aligned} {\mathcal {C}}~\triangle ~ \hat{{\mathcal {C}}}&=~ \int _{-\pi }^{\pi } \int _{r_{\min }(w)} ^{r_{\max }(w)}f_{R_L,W_L}(r,w)\textrm{d}r\textrm{d}w \nonumber \\&\quad ~\approx ~ \sum _{i=1}^{k} (2\pi /k) \int _{r_{\min }(-\pi + \frac{2\pi i}{k})} ^{r_{\max }(-\pi + \frac{2\pi i}{k})}f_{R_L,W_L}\left( r, -\pi + \frac{2\pi i}{k}\right) \textrm{d}r, \end{aligned}$$

(11)

where $r_{\min }(w)=\min \{\hat{r}(w), r_{true}(w)\}$ and $r_{\max }(w)=\max \{\hat{r}(w), r_{true}(w)\}$, for each $w\in (-\pi ,\pi ]$. Symmetric difference results for contours ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$ can be deceptive when comparing across different probability levels p. We instead present a scaled symmetric difference, i.e. $({\mathcal {C}}_p^1~\triangle ~ \hat{{\mathcal {C}}}_p^1) /p$ for contour definition 1.

4.2 Estimation on Laplace margins

Fig. 3

Top two rows: estimated contours $\hat{{\mathcal {C}}}_{0.1}^1$ (purple), $\hat{{\mathcal {C}}}_{0.01}^1$ (blue) and $\hat{{\mathcal {C}}}_{0.001}^1$ (red) for 100 data sets sampled under independence, from two Gaussian copulas, and from three bivariate extreme value copulas with logistic or asymmetric logistic models. Bottom two rows: equivalent estimated contours $\hat{{\mathcal {C}}}_{p}^2$, $p\in \{0.1,0.01,0.001\}$. The true contours are shown in black in all cases, for $p=0.1$ (dotted lines), $p=0.01$ (dashed lines) and $p=0.001$ (solid lines)

Figure 3 shows visual assessments of our estimators where we have known Laplace marginal distributions and the dependence structure is given by the six copula models shown in Fig. 1, covering both asymptotic independence and asymptotic dependence examples for the joint upper tail. Here, we produce estimates of ${\mathcal {C}}^1_p$ and ${\mathcal {C}}^2_p$ at probabilities $p\in \{0.1,0.01,0.001\}$. These plots show that our approach gives reasonably limited bias, but with increasing variability as p decreases, i.e. as we extrapolate further into the tails of the radial distributions at each angle. The performance appears to be equally good over all angles, for all six copulas and for both contour types. The methods pick up the contour shape whether it is pointed on the diagonal, or more rounded and flat in that region, for asymptotically dependent and asymptotically independent cases, respectively. The contours that are estimated for the asymmetric logistic models are especially impressive, given their very different levels of smoothness. The key to us achieving such flexibility comes from our selection of appropriate degrees of smoothing in the splines of the GPD parameters.

For a subset of the estimated contours in Fig. 3, results for the empirical relative error metric ${\hat{n}}_p/(np)-1$ are presented in Figs. 4 and 5 for ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$, respectively. For clarity, we omit results for one of the Gaussian copulas (case (ii)) and one of the asymmetric logistic copulas (case (v)), but these are similar to those that are shown. Results are shown for both the estimated and true contours, with the same simulated data sets used in each case. We include these empirical relative errors for the truth to demonstrate the base level of sampling variability for this metric; we cannot expect to improve on this level of performance with the estimated contours. The empirical relative errors for the true contours naturally show no bias but exhibit increasing variability with decreasing p.

Fig. 4

Boxplots of the empirical relative errors in the probability of lying outside the estimated contours $\hat{{\mathcal {C}}}^1_p$ (top row) and true contours ${\mathcal {C}}^1_p$ (bottom row) for 100 data sets sampled under independence (i), from a Gaussian copula with $\rho =0.75$ (iii), and from two bivariate extreme value copulas with a logistic (iv) or asymmetric logistic (vi) model, with $p\in \{0.1,0.01,0.001\}$. Here, the numbering of the copulas is chosen to be consistent with Figs. 1, 2 and 3, but with cases (ii) and (v) omitted

Fig. 5

These boxplots are equivalent to those in Fig. 4, but for $\hat{{\mathcal {C}}}^2_p$

In Figs. 4 and 5, there is no discernible difference between the performance of our estimators across the two different contour types, indicating that the additional complexity of estimating the angular density in ${\mathcal {C}}^2_p$ does not appear to have had an adverse effect. The performance, as judged by this metric, is very similar across the copula choices, with no evidence that contours for complex copulas are any more difficult to estimate than for the independence copula. Our estimation procedure is generally successful and unbiased, particularly for the $p=0.1$ and $p=0.01$ contours. For further extrapolation, i.e. the $p=0.001$ contours, the empirical relative errors tend to be positive, but are less than one, suggesting the bias is small. Importantly, over all combinations of copula, p and contour type, the variability of the empirical relative error for our estimated contours is similar to that of the true contours, indicating that much of the variability in our estimators is due to sampling variability rather than from our inference.

With a larger sample size, we would expect improved contour estimates for the $p=0.001$ cases, but we can see from the results for the true contour that given this sample size, the empirical relative error metric has limitations at such small levels of p. In Fig. 6, we therefore present a scaled symmetric difference $({\mathcal {C}}_p^1~\triangle ~ \hat{{\mathcal {C}}}_p^1) /p$ for $p\in \{0.1,0.01,0.001\}$. We only show results for the contour ${\mathcal {C}}_p^1$, given the similarity of results for the contour types seen in Figs. 4 and 5. Although the symmetric differences naturally decrease with decreasing p, the scaled versions instead increase, in a similar pattern to the empirical relative errors. However, for the smallest p, they reveal that the asymmetric logistic with $\alpha =0.25$ has the most difficult contour to estimate of the copulas we have considered, with both the largest mean and variance in the scaled symmetric differences over replicated samples.

Fig. 6

Boxplots of the scaled symmetric difference $({\mathcal {C}}_p^1~\triangle ~ \hat{{\mathcal {C}}}_p^1) /p$ for 100 data sets sampled under independence (i), from two Gaussian copulas (ii-iii), and from three bivariate extreme value copulas with logistic or asymmetric logistic models (iv-vi), with $p\in \{0.1,0.01,0.001\}$. We used $k=800$ in (11)

4.3 Estimation on original margins

Fig. 7

Left: example of data simulated from a bivariate extreme value copula with an asymmetric model, where X and Y have marginal GEV distributions with $-0.1$ and $+0.1$ shape parameters, respectively. Centre: 100 examples of contour estimates analogous to ${\mathcal {C}}_{0.01}^1$ but having polar coordinates defined on the original (X, Y) scale. Right: 100 examples of contour estimates of ${\mathcal {C}}_{0.01}^1$ calculated on Laplace margins and then transformed back to the original (X, Y) scale

A natural question is why we choose to define the contours on Laplace scale rather than considering (X, Y) as generic random variables, and defining the polar coordinates as $R=\sqrt{X^2+Y^2}$ and $W=\tan ^{-1}(Y/X)$ to construct the corresponding contours directly on the original (X, Y) scale. We considered this approach during development of this work, but found it often didn’t work well, particularly when the dependence exhibited some mixture structure (e.g. in the asymmetric logistic model). We now provide additional simulations to demonstrate this issue.

One issue when working on the general (X, Y) scale is that the variables do not necessarily have a natural centre at (0, 0), as they do in the Laplace case. To overcome this, we considered defining the marginal medians as $m_X$ and $m_Y$ for X and Y, respectively, and the polar coordinates as

$$\begin{aligned} R = \sqrt{(X-m_X)^2+(Y-m_Y)^2},\qquad W=\tan ^{-1}\left\{ \frac{Y-m_Y}{X-m_X}\right\} . \end{aligned}$$

Contours can be defined analogously to ${\mathcal {C}}_p^1$ and ${\mathcal {C}}_p^2$, but using these radial-angular coordinates. Estimation can be carried out in a similar way to the approach described in Sect. 3, but with $m_X$ and $m_Y$ added marginally to the resulting contour estimates as a final step, to obtain a contour centred on $(m_X,m_Y)$.

Figure 7 presents results for the asymmetric logistic copula model from case (iv) of Fig. 1 with margins following generalised extreme value (GEV) distributions. For X, the GEV location, scale and shape parameters are $(0,1,-0.1)$, and for Y they are (0, 1, 0.1), so Y has the heavier upper tail. In Fig. 7, we show a sample of size $n=10,950$ from this model, as well as estimated contours at the 0.01 probability level from 100 samples of size n, using both approaches. Visually, Fig. 7 clearly shows that the approach of transforming to Laplace margins before estimating the contours gives more consistent results, and there is no need to use the metrics introduced in Sect. 4.1 to see the distinct improvement using our proposed method. Specifically, our method is better at identifying the non-convex shape of the distribution. For these reasons, we prefer to define and estimate the contours on Laplace scale.

5 Air pollution application

We now apply our approach to air pollution data collected at a site in Bloomsbury, London, between 1 January 1993 and 31 December 2020. These data were provided by the Department for Environment Food and Rural Affairs (Defra) and are available to download from https://uk-air.defra.gov.uk,¹. We focus on daily maximum concentrations for two components of air pollution (nitric oxide NO and particulate matter $\text {PM}_{10}$) for the full year and also for summer (June, July, August) and winter (December, January, February) seasons. Values in the data set are rounded to the nearest whole number, so we add random noise simulated independently from a Uniform$(-0.5,0.5)$ distribution (or Uniform(0, 0.5) if the value is zero, to preserve non-negativity of concentration) to each observation, to mitigate issues with over-rounding. Approximately 9% of the NO values and 10% of the $\text {PM}_{10}$ values are missing; we assume that they are missing at random and proceed with estimating our contours. Retaining only those instances where both pollutants are available leaves us with 8,865 complete observations.

Fig. 8

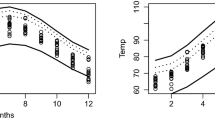
Estimates of ${\mathcal {C}}_p^1$ (top row) and ${\mathcal {C}}_p^2$ (bottom row) for nitric oxide and $\text {PM}_{10}$ across the full year (left), summer only (centre) and winter only (right). Estimated contours (solid lines) are shown for $p\in \{0.1, 0.01, 0.001\}$, lying progressively further from (0, 0), alongside pointwise 95% bootstrapped confidence intervals (dotted lines). The grey points represent the data in each case

Fig. 9

Data, estimated contours and confidence intervals from Fig. 8 shown after back-transformation to the original margins of the data

In Fig. 8, we present our estimated contours $\hat{{\mathcal {C}}}_p^1$ and $\hat{{\mathcal {C}}}_p^2$ for $p\in \{0.1,0.01,0.001\}$, using data from each of the three time periods (full year, summer, winter). The results are shown on Laplace scale, with the marginal transformations applied separately in each time period. We also provide pointwise 95% confidence intervals for the estimated radial quantiles at each angular value. This uncertainty is quantified using 200 bootstrapped samples via the block bootstrap scheme of Politis and Romano (1994); the samples are taken from the data after transformation to Laplace margins with the missing values retained. As the time series of NO and $\text {PM}_{10}$ observations both exhibit strong auto-correlation, we fix the average block-length in the bootstrapping procedure to be 14 in all cases. Carrying out bootstrapping after marginal transformation means that only uncertainty in the dependence features is taken into account in the confidence intervals, but allows for equivalent contours and confidence intervals to be obtained on the original scale by reversing the marginal transformations; these results are given in Fig. 9.

From Figs. 8 and 9, we can see that the dependence properties of the data vary between season. In particular, there is much stronger extremal dependence in both the upper and lower tails of NO and $\text {PM}_{10}$ in the winter than in the summer; this feature is visible in the data and successfully captured by our contour estimates. Further, our contours are able to capture the mixture of dependence features that is present when considering data for the full year. The maximum value across NO concentrations is 336 in summer and 1251 in winter, while $\text {PM}_{10}$ has a smaller variation between seasons, with a maximum of 399 in summer and 243 in winter. Since the winter months dominate the upper tail of the NO values, the feature from the summer months that NO can be large while $\text {PM}_{10}$ takes values close to its median is obscured when considering data across the full year. On the other hand, features corresponding to the upper tail of $\text {PM}_{10}$ in both summer and winter are preserved when considering the full year, i.e. NO and $\text {PM}_{10}$ can be simultaneously large but $\text {PM}_{10}$ can also be large when NO takes values around its median.

Focusing only on the separate summer and winter plots in Fig. 9, we now consider the implications that these estimated environmental contours have for potentially setting environmental controls. Given that large values of each pollutant have impacts on health, the key segments of the environmental contours in this case are where either of PM$_{10}$ and NO are large. Large values of NO only occur in winter, whereas very similar large levels of PM$_{10}$ occur in both seasons, so if there are implications on health from jointly large values of these two pollutants, winter is the period of most risk. However, it is these segments of the environmental contours that are most uncertain, particularly in winter, with approximate 95% confidence intervals differing up to $\pm 25$% from the point estimates, even without accounting for the marginal estimation uncertainty. For these two pollutants, there are relatively small differences in the estimates of the two different environmental contours in the key segments; this is due to the angular distributions on Laplace margins being reasonably uniform here. Here, we have focused on the contour ${\mathcal {C}}_p^1$ but equally, given interest in large values of the pollutants, we could have focused instead on the contour ${\mathcal {C}}_p^1([0,\pi /2])$ proposed in Sect. 2.2.

Having estimated the environmental contours, contributions from domain experts are now essential. Although in this pollutant example they may not have a formally defined structure function, they should be able to identify combinations of pollutants on the contours that are the most likely to lead to adverse health effects, possibly relating to a range of different symptoms. Likewise, the pollutant regulatory bodies can use this information to see if certain combinations of pollutants they have concerns about are likely to occur too often. If this is the case, they could look to set new control limits, or aim to remove or reduce the sources of these air pollutants so that future extreme combination levels are lowered.

6 Discussion

In some application areas, there may be only a subset of angles $W_L$ that are of interest. If this were the case, the contour definitions could be adapted to only consider radial exceedance probabilities for angles in a subset of $(-\pi ,\pi ]$. The estimation procedure we present could still be used, but with radial quantiles at a different set of levels extracted from the final estimates.

An area where our approach could be improved is in the construction of the splines used in the GPD threshold model and log-scale parameter. We use basis functions of the same degree across all knots, with this degree chosen as described in Sect. 3, irrespective of whether the copula is asymptotically independent or asymptotically dependent. However, in some cases, it may be more appropriate to allow different types of basis function at different knots. An example of this is the asymptotically dependent logistic model, where in case (ii) of Fig. 1, we can see that the contours are ‘pointy’ in the upper-right quadrant (so that linear basis functions may be more appropriate) and smooth in the lower-left quadrant (so that quadratic or cubic basis functions may perform better). Considering such bespoke spline constructions would add a significant level of complexity to our modelling procedure, so we did not pursue this idea here, but it does present a possible avenue for future work. Critically, our proposed method does not require us to pre-specify whether or not the copulas are asymptotically dependent, and this is a feature that it would be desirable to retain in any extension of the methodology.

Although the primary motivation for developing these novel environmental contours was for applications to engineering safety design and for setting environmental standards, an alternative potential use for these methods is in bivariate outlier or anomaly detection. Of course, multivariate outlier detection is a very widely studied topic, which goes well beyond simply using extreme value methods (see, for example, Hubert et al. 2015), although they are highly relevant for some problems (Dupuis and Morgenthaler 2002). Unlike the latter paper, we use univariate extreme value methods without needing to adopt a copula model, so adapting our approach to the anomaly detection setting may have the advantage of additional flexibility over existing methods.

We have focused on developing methodology for estimating bivariate contours, but the contour definitions can be extended to higher dimensions. With more than three dimensions, visualising the contours is impossible, and care would be needed to present the results in a usable format that offers easy interpretation. An option may be to project the contours onto lower dimensional subsets of interest.

Finally, the approach we have taken in this paper involves a combination of extending previous work related to limit set estimation and gauge functions (Simpson and Tawn 2022), and exploiting an alternative radial-angular representation for a given, common marginal distribution (here, Laplace). This appears to be a profitable line of future research; specifically, while our paper has been in the review process, two independently developed papers (Mackay and Jonathan 2023; Papastathopoulos et al. 2023) have been uploaded to arXiv that consider aspects linked to these strategies, though with different objectives.