1 Introduction

Estimating the density of wildlife populations is essential in ecology for management and conservation. Camera trapping is increasingly becoming a preferred monitoring tool for sampling animal populations due to their non-invasive nature and efficiency (Srbek-Araujo and Chiarello 2005; O’Connell et al. 2011). When individual animals are able to be uniquely identified capture–recapture (CR) methods are commonly applied to obtain estimates of population size (McCrea and Morgan 2015). CR models often incorporate different sources of heterogeneity such as individual, behavioural and/or temporal heterogeneity (Otis et al. 1978). The development of spatial capture–recapture (SCR), using an array of traps, permits spatial heterogeneity to be incorporated and spatial density to be estimated over the study region (Efford 2004; Borchers and Efford 2008; Royle and Young 2008; Borchers et al. 2014; Efford et al. 2016; Stevenson et al. 2021). SCR models account for the spatial heterogeneity of observations by specifying the associated capture probability of an individual at a given trap to be a function of the distance of that trap from the individual’s (unobserved) “activity centre” (Borchers and Efford 2008). The activity centre is defined such that it describes the centre of an animal’s movement activity (i.e. locations where an animals traverses) and is a latent variable.

Standard CR-type approaches that require individuals to be uniquely identified are often infeasible in practice, e.g. many species may be difficult to identify from camera trap images due to similar markings and/or poor quality images. Individuals not uniquely identifiable are often referred to as unmarked individuals, with the associated data corresponding to total counts of the number of encounters (Rowcliffe et al. 2008; Nakashima et al. 2018). Extending to the spatially explicit case leads to data of the form of the number of total counts of encounters for each individual camera location. Spatially explicit models for unmarked individuals have been introduced by Chandler and Royle (2013). These models consider two underlying sources of heterogeneity: detectability and spatial heterogeneity. Conditional on the number of individuals in the study area, and their associated activity centres, the number of animals observed at each camera trap in a given time interval is assumed to be Poisson, with some specified mean. Fitting this model faces two challenges due to (i) the unobserved activity centres; and (ii) the total unknown number of individuals. A Bayesian data augmentation approach is often used to address these challenges, which involves imputing the unknown activity centres and applying a super-population approach to deal with the unknown number of individuals (Chandler and Royle 2013; Ramsey et al. 2015; Evans and Rittenhouse 2018; Connor et al. 2022). However, this approach does not readily scale to large populations, and can exhibit (very) slow and poor mixing within the Markov chain Monte Carlo (MCMC) algorithm. A similar data augmentation approach has also been applied for marked capture–recapture data; but also an alternative trans-dimensional algorithm to more efficiently update the total population size (Fienberg et al. 1999; King and Brooks 2008; Durban and Elston 2005; McLaughlin 2019). See, for example, Schofield and Barker (2014) for further discussion and a review of these, and other, approaches.

In this paper, we consider a large unmarked SCR dataset relating to barking deer (Muntiacus muntjak) from Ujung Kulon National Park, Indonesia. A total of 1095 camera trap sightings over 77 cameras are recorded over a period of four months. The size of the population (in the thousands) is such that a super-population approach is computationally very demanding. We develop a new efficient Bayesian model-fitting approach, which also removes the necessity of a priori setting an upper bound on the population size, and directly specifies a prior on the total population size, by considering a trans-dimensional algorithm approach.

The paper is organised as follows. In Sect. 2, we describe the motivating study; and the unmarked SCR model in Sect. 3. In Sect. 4, we describe the different model-fitting approaches. In particular we propose a reversible jump (RJ)MCMC algorithm and an additional computationally efficient calculation that can be applied within bespoke code for a substantial improvement in the computational efficiency. For a proof-of-concept test, we perform a simulation study and consider a (small) dataset relating to the northern Parula (Setophaga americana), and directly compare the super-population approach with the new RJMCMC algorithm. In Sect. 5, we return to the motivating barking deer case study, where there are additional covariates considered relating to habitat. Finally, we conclude with a discussion in Sect. 6.

2 Survey Area

Ujung Kulon National Park (UKNP) is the largest lowland rainforest in Java with a total area of approximately 120,551 ha of which about 44,337 ha is a marine zone. The UKNP is a triangular peninsula located at the southwest end of Java island, Indonesia, lying approximately at \(6^{\circ }\,45'\) S by \(105^{\circ } \, 20'\) E. The study area is approximately 32,900 ha. Habitat structures of the study area can be divided into four typical vegetation corresponding to primary forest, secondary forest, mangrove-swamp forest and beach forest. The primary and secondary forests account for 90% of the total area, with all of the camera traps located in these two habitat types. There are two seasons corresponding to (i) the wet season occurring between October and April, with an average of approximately 400 mm of rainfall per month and (ii) the dry season between the May and September, with approximately 100 mm rainfall per month (Rahman et al. 2017).

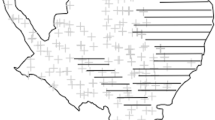
The study area was gridded into \(1 \times 1\) km sites, providing a total of 329 sites. A total of 77 motion-sensor cameras (Bushnell Tropy Cam 119,467 and 119,405) were distributed across the study region: 35 cameras in the primary forest; 42 cameras in the secondary forest. The spatial grid and camera trap locations are shown in Fig. 1. The camera traps were placed 170 cm above ground and fixed to a tree with a 10–20\(^{\circ }\) angle. The survey was conducted from March to June, 2014. Cameras were checked once a month (approximately every 21–30 days) and the battery and/or memory card replaced if necessary. Poor quality photographs, where identification was uncertain were discarded. Further, repeat photographs of individuals within 1 h were considered to be a single photographic event (Karanth and Nichols 1998).

A total of 1095 barking deer detections were recorded during the sampling period; with 540 detections during the wet season and 555 detections during the dry season. For the wet season, 344 detections were recorded in the primary forest and 196 in the secondary forest; corresponding to 64%/36% for the primary/secondary forest detections. For the dry season, 231 detections were recorded in the primary forest and 324 detections in the secondary forest; corresponding to 42%/58% for the primary/secondary forest.

Fig. 1
figure 1

The study area in Ujung Kulon National Park, Java with \(1\times 1\) \(\hbox {km}^2\) spacing grid. The points represent the camera trap locations distributed within the state space ensuring the sufficient spatial correlation between traps over different habitat. The black triangle represents Mt. Payung which is later excluded from the modelling

Full size image

3 Spatially Explicit Models

We consider the model proposed by Chandler and Royle (2013). We assume there are T sampling periods, and within each sampling period there are J camera detectors (their locations are assumed fixed over time, but this can be relaxed). The location of the camera traps is denoted by coordinates, \(\varvec{X}= \{\varvec{X}_j\} \in {\mathbb {R}}^2\) for \(j=1,\dots ,J\). Individuals observed by the cameras are not uniquely identifiable, so that the data correspond to the number of sightings on camera j in sampling period t, denoted, \(n_{jt}\), for \(j=1,\dots ,J\); \(t=1,\dots ,T\). The observed data are denoted by \(\varvec{n}=\{n_{jt}:j=1\,\dots ,J; t=1,\dots ,T\}\). Camera traps are assumed to be sufficiently close to each other such that individuals may be detected at multiple camera locations at each sampling period \(t=1,\dots ,T\). Finally, we define the latent variables \(\varvec{S}_i \in {\mathbb {R}}^2\), corresponding to the activity centre for individual \(i=1,\dots ,N\), representing the individual spatial heterogeneity.

We do not observe the individual encounter histories due to the nature of unmarked populations (i.e. animals are not uniquely identifiable), but only the total trap-count data, \(\varvec{n}\). The aggregate count-trap data are modelled by assuming a Poisson distribution:

$$\begin{aligned} n_{jt}|N, \varvec{S}\sim \text {Poisson} (\Lambda _j(\varvec{S})), \end{aligned}$$

where \(\Lambda _j(\varvec{S}) = \sum _{i=1}^N \lambda _{ij}(\varvec{S}_i)\) and \( \lambda _{ij}(\varvec{S}_i)\) denotes the encounter rate. The encounter rate, \(\lambda _{ij}(\varvec{S}_i)\), is specified to account for the correlation in counts from neighbouring detectors and spatial heterogeneity over individuals. In particular, we specify the encounter rate for individual i at trap j to be a function of the distance from the associated activity centre of the individual \(\varvec{S}_i\) and the trap location, \(\varvec{X}_j\). Specifying the encounter rate to be of half-normal form (Efford 2004) we have that,

$$\begin{aligned} \lambda _{ij}(\varvec{S}_i) = \lambda _0 \exp {\left( -\frac{||\varvec{X}_j-\varvec{S}_i||^2}{2\sigma ^2}\right) }, \end{aligned}$$

where \(\lambda _0\) denotes an underlying baseline detection parameter and \(\sigma \) the scale parameter controlling the rate of decay in the detection rate. Here, the \(\Lambda _j\) term does not depend on the sampling periods t since we assume a time-invariant model. Thus, we can simplify the model specification by considering the total trap counts over all times, \(n_{j.} = \sum _{t=1}^T n_{jt}\), for each trap \(j=1,\dots ,J\). Then,

$$\begin{aligned} n_{j.} | N, \varvec{S}, \sim \text{ Poisson }\left( T \Lambda _{j}(\varvec{S})\right) , \end{aligned}$$

independently for each \(j=1,\dots ,J\). Covariate information can be incorporated in the model parameters. For example, trap or activity centre level covariates can be specified in the baseline detection rate to account for variability due to environmental factors at either the trap level (affecting detectability of individuals given trap location) or activity centre level (to represent differences in detectability of individuals due to environment factors summarised by activity centre location). See Chandler and Royle (2013), Evans and Rittenhouse (2018), Connor et al. (2022) for further discussion. To complete the model specification, we assume the unobserved activity centres, \(\varvec{S}_i\), for \(i=1,\dots ,N\) are independent and uniformly distributed over the region, \({\mathbb {S}}\), (and do not change over the sampling period), so that \({\varvec{S}}_i \sim \text {Uniform}({\mathbb {S}})\). The corresponding (conditional) joint likelihood function of the data and (unobserved) activity centres is given by,

$$\begin{aligned} f(\varvec{n},\varvec{S}|N,\lambda _0,\sigma ^2)= & {} f(\varvec{n}|N,\lambda _0,\sigma ^2, \varvec{S}) f(\varvec{S}) \nonumber \\= & {} \left[ \prod _{j=1}^J \left( \frac{\exp (-T\Lambda _{j}(\varvec{S})) (T\Lambda _{j}(\varvec{S}))^{n_{j.}}}{n_{j.}!}\right) \right] |{\mathbb {S}}|^{-N}, \end{aligned}$$
(1)

where \(|{\mathbb {S}}|\) denotes the area over the region \({\mathbb {S}}\). The observed data likelihood is obtained by integrating out \(\varvec{S}\). However, this integration is very high dimensional and analytically intractable.

4 Model Fitting

The observed data likelihood is analytically intractable, so we consider a Bayesian data augmentation (or complete data likelihood) approach (Tanner and Wong 1987). In particular, we form the joint posterior distribution over the model parameters and unknown activity centres,

$$\begin{aligned} \pi (N, \varvec{S}, \lambda _0, \sigma ^2 | \varvec{n}) \propto f(\varvec{n}, \varvec{S}|N,\lambda _0,\sigma ^2) p(\lambda _0) p(\sigma ^2) p(N), \end{aligned}$$
(2)

where the joint likelihood of the observed data and activity centres is given in Equation (1) and p(.) denotes the prior distribution of the corresponding parameters. The posterior distribution is no longer of a fixed dimension, as it is a function of the parameter N, so that traditional MCMC algorithms cannot be applied. This has led to the use of the super-population approach, which uses a further data augmentation step, defining an upper limit for the population size, returning to the fixed dimension case (Chandler and Royle 2013). An alternative approach is to use reversible jump (RJ)MCMC (Green 1995), permitting trans-dimensional moves. We initially describe the super-population approach and associated challenges, particularly for large datasets, before proposing an alternative (and more computationally efficient) RJMCMC algorithm.

4.1 Super-Population Approach

The super-population approach (SPA) has been applied to unmarked SCR (Royle et al. 2009; Chandler and Royle 2013; Ramsey et al. 2015; Evans and Rittenhouse 2018; Connor et al. 2022). The idea is to use a fixed-dimensional parameter-expanded data augmentation approach by initially defining some upper limit for the population, M, typically referred to as the super-population. Each individual in the super-population has an associated activity centre and additional auxiliary variable to indicate whether or not it is a member of the population of interest.

Although this approach leads to a fixed parameter dimension and so implementable using standard MCMC and software, there are drawbacks in relation to the scalability of the algorithm and the prior specification on N. In particular, the super-population limit M needs to be specified a priori potentially leading to a large parameter space (see King et al. 2016 for further discussion); and the prior specification on N is now an induced prior (via the prior specified on \(\phi \)). In the next section, we describe an alternative RJMCMC model-fitting approach removing the need to specify an upper population limit and directly specifies a prior on N.

4.2 Reversible Jump MCMC

We propose a RJMCMC algorithm (Green 1995) for exploring the posterior distribution in Equation (2). RJMCMC is a generalisation of the Metropolis–Hastings (MH) algorithm that permits moves between different dimensions, required when updating the total population size N, due to the associated activity centres, \(\varvec{S}\). A similar updating algorithm was considered by King and Brooks (2008) in the presence of individual random effects; and by McLaughlin (2019) for a marked SCR model. The implementation of the RJMCMC algorithm can be separated into two distinct move types: (i) MH-update for model parameters \(\{\sigma , \lambda _0, \varvec{S}\}\); (ii) RJMCMC update for N. We describe only the RJMCMC update of N here.

Updating the total population size N involves a change in dimension (as \(|\varvec{S}| = N\)). We propose a new value for N, denoted \(N'\), using a random walk approach, such that \(N' = N + \epsilon \), where \(\epsilon \) is a discrete uniform distribution over \(\{-\delta ,\dots ,-1,1,\dots ,\delta \}\), with \(\delta \in {\mathbb {N}}\) chosen via pilot-tuning. If \(N' > N\), we propose \(\epsilon \) new activity centres \(\varvec{S}'\), using an independent proposal distribution (uniform over \({\mathbb {S}}\)); else if \(N' <N\) we remove \(\epsilon \) activity centres. We consider two proposal distributions for updating the activity centres: (a) “fixed”; and (b) “stochastic”.

Case (a) Fixed proposal distribution: For \(N' > N\), we propose new activity centres, \(\varvec{S}_{N+1},\dots ,\varvec{S}_{N'}\), such that for \(i=N+1,\dots ,N'\) each \(\varvec{S}_i\) are simulated uniformly over the region, \({\mathbb {S}}\) (i.e. are simulated from the prior distribution). The reverse move is subsequently defined such that for \(N' < N\), we simply remove the \(N-N'+1\) activity centres, \({\textbf{S}}_{N'+1},\dots ,{\textbf{S}}_{N}\).

Case (b) Stochastic proposal distribution: The stochastic proposal follows very similarly to the fixed proposal, with an added step of reordering the labels of the activity centres. For \(N' > N\), we initially propose new activity centres, \(\varvec{S}_{N+1},\dots ,\varvec{S}_{N'}\), simulated uniformly over the region, \({\mathbb {S}}\). We then randomly reorder the labels of the activity centres. In the reverse move, when \(N' < N\), we initially randomly reorder the labels of the N activity centres, before subsequently removing the final \(N-N'+1\) activity centres, \({\textbf{S}}_{N'+1},\dots ,{\textbf{S}}_{N}\). This is equivalent to adding the new activity centres randomly within the ordered set of activity centres (when \(N' > N\)); and removing activity centres chosen randomly from all current activity centres (when \(N' < N\)).

The acceptance probability reduces to the same for both the fixed and stochastic proposal distributions. In particular, let \(\varvec{S}'\) denote the set of proposed activity centres associated with the \(N'\) individuals. The acceptance probability reduces to \(\min (1,A)\), where,

$$\begin{aligned} A = \frac{f(\varvec{n}| N', \varvec{S}', \lambda _0, \sigma ^2)}{f(\varvec{n}|N, \varvec{S}, \lambda _0, \sigma ^2)}. \end{aligned}$$

The proposal densities for the parameters being added or removed from the model are equal to the associated prior densities, so that these terms cancel in the acceptance probability (A) and are hence omitted. Similarly the Jacobian term (i.e. determinant of the partial derivatives of the transition function defined in Green 1995) is equal to unity, as the transition function is equal to the identity function. Thus, the acceptance probability reduces to the ratio of the conditional likelihood evaluated at the proposed and current parameter values of the Markov chain.

4.3 Bespoke Code

For the SPA, there are several MCMC black-box packages that can be used, such as nimble (de Valpine et al. 2017) and jags (Plummer et al. 2022). However, in addition to the computational cost of the population limit, M, and indicator variables, \(\varvec{z}\), there is another hidden and considerably high computational cost in relation to the likelihood term. This is due to the structure of the likelihood function in terms of a summation over all individuals/activity centres for the Poisson means for each camera trap. However within the MH updating step, we can use an efficient likelihood calculation for updating the activity centre location, \(\varvec{S}_i\), or indicator variable \(z_i\). In particular, we calculate the new Poisson means required by considering only the change in the mean values for the proposed \(\varvec{S}_i\) or \(z_i\) values (compared to their current values), as opposed to the full summation over all individuals for each trap. To implement this approach, we simply need to store the Poisson mean values in the algorithm. These efficient implementational steps can be immediately incorporated within bespoke code (but typically not within general black-box MCMC packages), providing significant improvements in computational efficiency for both the SPA and RJMCMC algorithms. Thus, for meaningful computational comparisons between these approaches we implement each using similar bespoke code, using the same MH updating steps for parameters common to both approaches (\(\varvec{S}, \lambda _0, \sigma ^2\)).

4.4 Prior Specification on N

The prior specification on N in the SPA is specified implicitly via the indicator variables \(z_i\sim \text {Bern}(\phi )\) for \(i=1,\dots ,M\), and associated prior on \(\phi \). Chandler and Royle (2013) consider the prior, \(\phi \sim \text {Beta}(a,b)\) which induces a \(\text {Beta-Binomial}(M,a,b)\) prior on N. A common choice is to set \(a = 0.001\) and \(b=1\) which is a very close approximation to the scale (Jeffreys’) prior on N (Link 2013); or \(a=1\) and \(b=1\) (Chandler and Royle 2013). However, within the RJMCMC algorithm, a prior is specified explicitly on the total population size, N, leading to greater flexibility and interpretability in the prior specification. In general, common choices for N may include Jeffreys’ prior, a uniform prior or Poisson prior. Specifying an informative prior on N is particularly useful for unmarked models, where there may be limited information regarding the population size. For example, for (non-spatial) unmarked models, identifiability has been raised as an issue where the data are only weakly informative on N (Dennis et al. 2015; Barker et al. 2018). Alternatively, we note that N and \(\sigma \) are highly correlated and so specifying an informative prior on \(\sigma \) inferred from information relating to the size of individuals’ home ranges also leads to an improved precision of N. In all cases, a prior sensitivity analysis should be undertaken to assess the impact of the prior on the posterior distribution.

4.5 Simulation Study

We consider a simulation study with \(T=10\) sampling occasions; \(\lambda _0=0.6\); \(J=100\) traps. The traps are specified as a regular (square) design with a grid spacing of 20. To ensure sufficient spatial correlation between traps, we set the radius of the activity centres to be 30 units which provides \(\sigma = 12.26\) (see Chandler and Royle 2013 for the conversion between the radius and \(\sigma \)). We simulate 100 datasets for \(N=\{100, 500, 1000\}\), with the activity centre locations uniformly distributed over the study region; and independent uniform priors on \(\sigma \), \(\lambda _0\) and N.

Table 1 provides the statistical summaries, i.e. average relative bias (RB) and coverage probabilities (CP) for the simulation study. The results suggest that the model is generally able to estimate the parameters reasonably well, but this appears to be more challenging in the estimation of N as N increases. Notably, the posterior distribution for N is right-skewed, with a reduced RB for the posterior median/mode for \(N=1000\).

Table 1 Simulation results in terms of averaged relative bias (RB) and 95% coverage probabilities (CP) for 100 simulated datasets fitted via the RJMCMC algorithm assuming stochastic removal proposal distribution for 100,000 iterations
Full size table

4.6 Example: Parula Dataset

To compare the performance of the different algorithms on a small population, we consider the northern Parula (Parula americana) data. The data consist of 226 sightings detected by 105 trap stations over three survey periods. See Chandler and Royle (2013) for more details and associated SPA applied to the data. We used \(M=300\) for the upper limit for the SPA and \(\delta =10\) for the proposal distribution on N. We considered two priors on \(\sigma \): (i) uniform prior, \(\sigma \sim \text {Uniform}(0,\infty )\) and (ii) an informative prior, \(\sigma \sim \text {Gamma}(13,10)\). For \(\lambda _0\), we specify the Uniform prior, i.e. \(\lambda _0 \sim \text {Uniform}(0,\infty )\). Finally, for the total population size, we specify \(N\sim \text {Uniform}(0, 300)\) for the RJMCMC algorithm (the same upper limit population as for SPA); while for the SPA we set \(\phi \sim \text {Beta}(1,1)\). We ran each MCMC algorithm for 300,000 iterations following an initial 10,000 burn-in using three separate and independent chains.

Table 2 presents the posterior estimates for the different algorithms (SPA; fixed RJMCMC; stochastic RJMCMC), using bespoke code (see Sect. 4.3). As would be expected, the posterior estimates are similar allowing for Monte Carlo error (and minor differences in prior specification). However, there are noticeable differences in terms of computational performance and efficiency. In particular, the effective sample sizes (ESS) are generally slightly higher for SPA compared to the RJMCMC algorithms (except for \(\lambda _0\) for the uniform prior); and slightly higher for the stochastic RJMCMC algorithm compared to the fixed algorithm. However, the computational time is substantially greater for SPA (1.3 h per chain) compared to the RJMCMC algorithms (0.2 h per chain). Overall, the stochastic RJMCMC approach was substantially more efficient compared to SPA with an averaged ESS/s between 3 and 20 higher.

Table 2 Posterior summary estimates of model parameters, corresponding to the posterior mean, standard deviation (SD), median and 95% symmetric credible interval (CI) for the northern Parula data using super-population approach (SPA) and RJMCMC algorithms (fixed proposal; stochastic proposal) for the two different priors considered: \(\sigma \sim \text {Uniform}(0,\infty )\) and (ii) the informative prior, \(\sigma \sim \text {Gamma}(13,10)\)
Full size table

5 Case Study: Barking Deer

We consider the barking deer case study described in Sect. 2. The data are collected across two different seasons: wet and dry. We consider these separately due to the different weather conditions that may affect animal behaviour and/or detectability (Rowcliffe et al. 2011; Rahman 2019). The data relate to two-month periods for each of season: March–April (wet) and May–June (dry). We assume the population is (approximately) closed for these periods (Silver et al. 2004; Soria-Díaz and Monroy-Vilchis 2015; Rahman 2016) and consider a 7-day period for each sampling occasion, leading to nine sampling occasions for each of the dry and wet seasons.

We extend the baseline model presented in Sect. 3 to incorporate the environmental covariate relating to habitat into the baseline detectability rate, such that,

$$\begin{aligned} \log (\lambda _{0j}) = \beta _0 + \beta _{1} I(\text {habitat}_{j} = \text {primary}), \end{aligned}$$

where \(\beta _{1}\) corresponds to the difference between the baseline detectability associated with the primary forest, relative to the secondary forest; and we let \({\varvec{\beta }}=\{\beta _0, \beta _{1}\}\). The baseline rate for each forest is \(\lambda _\textrm{pri}=\exp {(\beta _0)}\) and \(\lambda _\textrm{sec} = \exp {(\beta _0 + \beta _1)}\) for primary and secondary forest, respectively. We let \(M_0\) denote the standard no-covariate dependence model, as described in Sect. 3 (i.e. where \(\beta _1 = 0\), so that \(\lambda _\textrm{pri} = \lambda _\textrm{sec}\)); and \(M_h\) the model where the baseline detection rate is a function of the habitat (at the given trap location).

We focus on the RJMCMC algorithm with stochastic proposal distribution given its performance in Sect. 4.6. For model \(M_0\), we specify \(\log (\lambda _0) \sim \text {N}(0, 10)\); and for model \(M_h\), \(\beta _k \sim \text {N}(0, 10)\) independently for \(k=1,2\). We consider the same priors on the remaining parameters for both models, setting \(\sigma \sim \text {U}(0, \infty )\) and specify a weakly informative prior on the total population size, using previous information relating to the barking deer in another national park combined with information provided by park staff in UKNP. In particular the previous study for Baluran National Park, Indonesia, suggested a barking deer density of \(\approx \) 25 per \(\hbox {km}^2\), with 95% confidence interval (15, 47), though this was from fairly limited data (Tyson 2007), with the density for the given barking deer in UKNP thought to be (potentially substantially) lower. Thus, we assume a prior density of \(\approx \) 40% of the previous study (i.e. 10 per \(\hbox {km}^2\)), but with a wide uncertainty interval of (5, 17) per \(\hbox {km}^2\) to represent significant prior uncertainty. This corresponds to a total number of 3290 and interval of (1645, 5593). We consider the prior of the form \(N|\mu \sim \text {Poisson}(\mu )\), where \(\mu \sim \Gamma (\alpha ,\beta )\) (equivalent to a Neg-Bin(\(\alpha ,\beta \)) prior distribution; King and Brooks 2001; Royle 2004). From the prior information, we derive the prior \(N \sim \text {Neg-Bin}(10, 0.0032)\), with associated mean of 3115, and 95% interval of (1491, 5325). We consider a prior sensitivity analysis, to investigate the influence of the weakly informative prior. In particular we consider two additional priors on N assuming a lower prior mean given the expected substantially lower density compared to the previous study: (i) Neg-Bin(1, 0.001) with a substantially lower mean of 999 and 95% interval (25, 3687); and (ii) Neg-Bin(5, 0.002) with slightly reduced mean of 2495 but still assuming a large 95% interval (808, 5113).

The RJMCMC algorithm was run for 500,000 iterations, following an initial burn-in of 10,000 iterations, using three independent chains for models \(M_0\) and \(M_h\). The simulations took approximately 22 h to run for each chain (N was updated 15 times per iteration to improve mixing; Gilks et al. 1995). Convergence was checked using the Brooks–Gelman–Rubin statistic for each model parameter via the R coda package (Plummer et al. 2020). The corresponding posterior summary statistics of the parameters for each model and for each season: \(M_0 \text {(dry)}, M_0 \text {(wet)}, M_{h} \text {(dry)}, M_h \text {(wet)}\) are given in Table 3.

First, we focus on \(M_0\). The posterior mean of the density of barking deer in the study area is approximately 11.7 animals per \(\hbox {km}^2\) in the dry season and 12.9 animals per \(\hbox {km}^2\) in the wet season. The 95% credible intervals are highly overlapping between seasons with 95% credible intervals of (6.4, 18.3) and (7.2, 20.1) individuals per \(\hbox {km}^2\) for the dry and wet season, respectively. The density of barking dear varies substantially from other areas including the previously considered estimated 25 per \(\hbox {km}^2\) in the Baluran National Park, Indonesia (Tyson 2007); to between 2.1 and 3.4 animals per \(\hbox {km}^2\) in Nepal (Wegge and Storaas 2009; Wegge and Mosand 2015); 2.9 animals per \(\hbox {km}^2\) in Sarawak (Dahaban et al. 1996); and 3.1 animals per \(\hbox {km}^2\) in Thailand (Srikosamatara 1993). The population density estimates remained relatively robust for the alternative prior specifications considered for the population size, with significantly overlapping credible intervals, though with some variability in the upper limits for the population size/density. For further discussion, see Appendix A of the Supplementary Material.

Despite similar population density estimates across the two seasons, the associated estimates for \(\lambda _0\) and \(\sigma \) are noticeably different. For the wet season, the estimated scale parameter \(\sigma \) is considerably smaller than the dry season; while the baseline detection rate is substantially larger (a posterior mean \(>2\) times) than in the dry season. The scale parameter is related to the movement of barking deer, i.e. the smaller \(\sigma \) in the wet season may indicate a smaller movement range due to closer water sources and/or food availability, while the larger value of \(\sigma \) for the dry season may be a result of larger movement to search for water and/or food availability (Tyson 2007). Similarly, the larger value of \(\lambda _0\) for the wet season indicates an increase in detectability, compared to the dry season (Rowcliffe et al. 2011). This may be potentially explained by animals having a smaller range due to plentiful resources during the wet season, resulting in smaller movements and higher frequency of cameras within their search/activity patterns.

Table 3 Posterior summary estimates, corresponding to the mean, standard deviation, 2.5%, 50% and 97.5% quantiles, effective sample size (ESS) and ESS per minute (ESS/m) of the model parameters fitted on the barking deer data for models \(M_0\) and \(M_h\) for data corresponding to each of the wet and dry seasons using 500,000 iterations
Full size table

We now consider model \(M_h\). The inclusion of habitat type in the detection parameter in the model does not lead to any substantial change in the estimate of the total population size (and hence density estimates) and \(\sigma \). These are again fairly consistent when considering the prior sensitivity analysis on N (see Appendix A). However, there does appear to be a substantial change in the estimates of the detection functions when considering the different habitats (primary and secondary forest) for the wet season; while similar estimates are obtained for the dry season for each habitat (which are comparable with the secondary forest in the wet season). The posterior mean for \(\beta _1\) for the dry season (corresponding to the difference in detection between the primary and secondary forests) is equal to \(-\) 0.24 with 95% credible interval \((-1.04, 0.48)\), suggesting no significant difference between the seasons in relation to detectability. However, for the wet season, the posterior mean for \(\beta _1\) is 2.94 with 95% credible intervals of (1.12, 5.86), indicating a much greater detection in traps in the primary forest habitat for barking deer in the wet season. This difference in detection between habitats in the wet season may again be related to the different usage of primary and secondary forests. For example, habitat preference is known to change seasonally which may be related to food availability, resting or nesting sites and predator avoidance (Yokoyama et al. 2020). To consider a more formal model selection approach in relation to the habitat covariate, a further RJMCMC step can be added to the algorithm, in order to obtain posterior model probabilities for \(M_0\) and \(M_h\). Implementing such an approach (and assuming a prior probability of 0.5 for each model, \(M_0\) and \(M_h\)) provides the associated posterior probabilities for model \(M_h\) of 0.54 for the dry season and 0.997 for the wet season, suggesting strong evidence of a habitat effect for the wet season.

Figure 2 provides the corresponding spatial distribution of relative population densities for two fitted models, \(M_0\) and \(M_h\) for each of the dry and wet seasons, respectively. We note that there appears to be a visible difference in spatial density across the region between the two seasons (e.g. a higher density area in the south-east during the wet season changing to being low density during the dry season; and higher density patches in the centre and further north west in the dry season compared to the wet season). As expected, given the similarity in parameters for the dry season, there is little discernible contrast in the estimated densities between two models for the dry season. However, there are some minor differences observable for the wet season, most notably a small increase in the densities near traps in the primary forest areas.

Fig. 2
figure 2

The estimated relative spatial densities of the barking deer for models \(M_0\) (A and B) \(M_h\), (C and D), corresponding to the wet (left) and the dry (right) seasons, respectively. The dots represent camera trap locations for primary forest (red) and secondary forest (blue). The black triangle represents Mt. Payung which is later excluded from the modelling (Color figure online)

Full size image

Finally, we compare the RJMCMC model-fitting approach with that of SPA. Fitting the SPA algorithm using black-box MCMC software was computationally infeasible (e.g. in nimble 10,000 iterations took approximately 50 h). Thus, we use bespoke code to take advantage of the efficient coding practice (see Sect. 4.3), and set the upper population limit to be \(M=\) 10,000. Due to the increased computational expense (86 h for 500,000 iterations), we consider only model \(M_0\) for the dry season. Appendix B of the Supplementary Material provides further details and construction of the weakly informative induced prior of N.

Table 4 provides the associated posterior estimates of the model parameters and associated ESS. Despite the slight difference in prior specification for the total population size, N, the posterior estimates are very similar. This would be expected given the previous investigations in relation to the limited sensitivity of the posterior on the prior for N, and fairly similar prior distributions. The SPA algorithm demonstrates both lower ESS for each parameters and also slower computational times (\(\approx 4\) times slower); such that the RJMCMC algorithm has >4 times higher ESS/m for all parameters, and >7 times higher for N.

Table 4 Posterior summary estimates, corresponding to the mean, standard deviation, median (Q50), 2.5% (Q2.5) and 97.5% (Q97.5) quantiles, effective sample size (ESS) and averaged ESS per minute (ESS/m) of the model parameters fitted on \(M_0\) (dry) using the SPA assuming \(M=\) 10,000 and using 500,000 iterations
Full size table

6 Discussion

We propose a scalable Bayesian model-fitting algorithm for fitting spatial count models for unmarked individuals when the size of population presents computational challenges. An efficient trans-dimensional RJMCMC approach is developed, which also immediately permits a direct prior specification on the total population size, for which there may often be external prior information. Bespoke code is required for implementing the RJMCMC algorithm, but this also provides the ability to include additional substantial computational savings within the updating of the activity centre parameters due to the particular structure of the likelihood. In particular, considering only differences in summations required (for the Poisson mean component) within the required likelihood calculations as opposed to a full recalculation of the likelihood term, providing a substantial computational saving, not possible in standard black-box MCMC packages. The use of black-box software (we used nimble) was rendered infeasible for the motivating barking dear case study using the SPA algorithm. The improved comparative performance (in terms of ESS/s) of the proposed RJMCMC algorithm compared to the alternative SPA, when both use the computationally efficient coding practice, is noticeable even on a relatively small dataset. The improvement depends on the exact model specification but for our studies the savings ranged from 3 to 20 fold. The RJMCMC algorithm considered assumed constant proposal parameters. Adaptive proposals may be considered to further improve the efficiency of the algorithm, for example, when updating N, proposing new locations for the associated activity centres in areas of higher density areas (Diana et al. 2022). In general, there is a trade-off between the additional computational expense and improved mixing.

For the case study, the density estimate of the barking deer in UNKP is estimated to be substantially higher than many other regions (approximately 2\(-\) 3.5 animals per \(\hbox {km}^2\)), but substantially less than for the study at Baluran National Park, Indonesia, with an estimated density of 25 per \(\hbox {km}^2\). There are several possible factors which may influence barking deer density (or equivalently population size) in UNKP. A previous study found that there is a relatively balanced sex ratio between adult males and females of 1.37:1 suggesting evidence of regular recruitment into the population (Rahman 2016). In addition, the specific habitat within the national park may be a factor. The primary and secondary forest occupies >90% of the park, with primary forest dominated by emergent plants and tree species while palms and other fruit trees are mainly dominant in the secondary forest (Rahman et al. 2017). Although there is no record or data regarding food choices of barking deer at UKNP, a study at Baluran park, Indonesia, found that trees, shrubs, grasses, forbs and climbers are frequently consumed by these species (Tyson 2007), thus suggesting an abundant food supply for barking deer within the park. However, not all these foods are available throughout the whole year. There may also be further factors such as poaching and predators that affect the spatial density of the deer. Differences in spatial and temporal food availability and predation risk can influence how herbivores use landscapes (Whittingham et al. 2006). As a result, trade-offs between costs and benefits can influence habitat, patch selection and density (Stears and Shrader 2015).

As for traditional (marked) SCR, the unmarked spatial count model requires a number of assumptions including population closure, independence and homogeneous activity centres (Chandler and Royle 2013). It has been shown in SCR that population density estimates are robust to low-moderate violations of these assumptions (Efford et al. 2016; Efford 2019; Bischof et al. 2020; Theng et al. 2022). The closure assumption can be easily violated for longer study periods, typically longer than three months for mammals (Silver et al. 2004; Soria-Díaz and Monroy-Vilchis 2015; Rahman 2016). Depending on the ecological questions of interest, the model may be extended by relaxing some of the assumptions, such as where the population may change over time (Dail and Madsen 2011; Chandler et al. 2011). The assumption of independent movement of individuals may be easily violated when animals move in (small or large) groups/herds. A recent research suggested that low to moderate levels of aggregation of individuals (group sizes <8) introduce small biases in density estimation and the scale parameter \(\sigma \) in SCR (Bischof et al. 2020; Theng et al. 2022). Current research focuses on investigating unmarked spatial models for deviations to such modelling assumptions.