1 Introduction

Sound experimentation techniques help to reduce the variation in a study. These may involve creating blocking factors in randomized block and Latin square designs or constructing covariate efficient designs to account for the heterogeneity among experimental units. The role of blocking factors and covariates in the design of experiments is well understood. Blocking aims to create homogeneous groups of experimental units before undertaking the experiment. On the other hand, covariance analysis uses a modeling approach, and requires a stronger linearity assumption between the response and covariates. It accounts for the heterogeneity in the data at the analysis stage after the experiment has been completed. The ultimate goal in both approaches is to account for the sources of variation in an experiment.

In this paper, a new blocking criterion is introduced based on ranks of within-block units to construct an additional blocking factor in a randomized block design. The ranking process attempts to rank the units in the order the results are most likely to occur in the absence of treatment effects. Hence, it can use all relevant information related to inherent variation among within-block units. For example, in a field experiment, one can rank within-block units based on the texture and color of the soil, elevation and wind pattern of the field, a yield map of the plots, or a combination of all of these factors. Ranking is performed separately in each block. So the ranks in one block are independent of the ranks of the units in any other block. Hence, the ranks within each block are correlated but those in different blocks are not.

This ranking process has previously been used in the design of experiments to draw inference on contrast parameters. We now provide a brief overview of this earlier work. The role of order restricted randomization is considered in Ozturk and MacEachern (2004) in a distribution-free control versus treatment multiple comparison test. The test compares the confidence intervals of the pairwise contrast parameters by controlling the overall coverage probability of simultaneous confidence intervals. The authors show that grouping experimental units in ranking blocks provides higher efficiency than a completely randomized design. Ozturk and MacEachern (2007) constructed order restricted randomization (ORR) for a completely randomized design with two treatments and constructed an approximate t-test for inference. Ozturk and MacEachern (2013) extended the two-sample ORR procedure to the one-way analysis of variance model. Du and MacEachern (2008) developed inference for the two-sample problem using judgment post stratification with order restricted randomization. Gao and Ozturk (2017) used ORR design in a regression setting and constructed an inference based rank regression model.

A ranking process was used in ranked set sampling (RSS) in rank regression in Ozturk (2002), which can be extended to the design of experiments in a special case. The main difference between the ranking processes of RSS and ORR design is that even though both procedures rank the units in a set of size H, the RSS uses only one and discards the other \(H-1\) units while the ORR design uses all of the H ranked units in the experiment. Conducting an experiment using the RSS procedure would create logistical challenges in settings where recruitment of experimental units for a study is expensive or limited. The ORR design does not suffer from this restriction since it does not discard any potential experimental units. For further details of the RSS procedure, readers are referred to Dell and Clutter (1972), Frey and Feeman (2013), Stokes (1995), Wolfe (2012), Kasprzak (2021), and references therein.

As an example, consider a randomized block design (RBD) of H blocks each with H treatments. An additive model for this design indicates that the observation \(Y_{ij}\) for treatment i in block j can be modeled as

$$\begin{aligned} Y_{ij}= \mu +\tau _i+b_j +\sigma \epsilon _{ij}, i=1, \ldots , H; j=1, \ldots , H, \end{aligned}$$
(1)

where \(\mu \) is the overall mean, \(\tau _i\) is the treatment effect, \(b_j\) is the block effect, and \(\epsilon _{ij}\) are independent identically distributed random variables from a standard normal distribution. The block effect \(b_j\) is assumed to be a random variable from a normal distribution with mean zero and variance \(\sigma ^2_b\), but if the block is a fixed effect, the main results of the paper will be still true with a slight modification in the expected values of mean squared errors. The treatment effect will be considered as fixed. We use the usual constraint \(\sum _{i=1}^H \tau _i=0\).

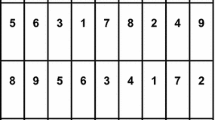
When variation between blocks is large relative to the within block variation, randomized block designs are highly effective at reducing the error variation and hence improving the precision of treatment estimates. If, however, within block variation is still large, there may be some other knowledge that would allow the plots within each block to be ranked prior to the application of treatments. This ranking information leads to a new criterion to create another blocking variable through the ranks of within-block units. Experimental units in each of the H blocks are ranked separately based on inherent variation among the within-block units using all relevant information for that block. A new blocking factor based on ranking groups is then created by grouping the experimental units having the same rank across all blocks. Ranking group 1 would consist of all experimental units (EU) having the assigned rank 1 in their blocks, ranking group 2 would consist of all EUs having the assigned rank 2, etc. The experimental units are then organized in an H by H row-column structure, indexed by ranks in the rows and blocks in the columns. The H treatments are then allocated to \(H^2\) units with the restriction that each treatment level appears only once in each row (ranking group) and column (block). Since the treatment allocation is constrained by the order of ranking groups, the new design is called order restricted randomized design (ORRD). Table 1 illustrates RBD and ORRD for a particular randomization scheme for each design when \(H=4\).

Table 1 Randomized block and order restricted randomized block designs with \(H=4\) treatments
Full size table

For ORRD, the observation \(Y_{ij}\) from the i-th row, j-th column can be modeled as

$$\begin{aligned} Y_{ij}=\mu +b_j+\tau _h+ \sigma \xi ^*_{ij}, \ i,j=1,\ldots , H, \end{aligned}$$
(2)

where h is the treatment applied to the (i, j)th cell, and \({\varvec{\xi }^*}^\top _{j}=(\xi ^*_{[1j]}, \ldots , \xi ^*_{[Hj]})\) are the judgment order statistics from a standard normal distribution. Judgment order statistics are the order statistics induced by the ranking process applied to within-block units. We assume that \(\xi ^*_{ij}\)’s are independent of \(b_j\). Other terms in model (2) are the same as the ones in model (1). A key difference between model (1) and (2) is the error structure. The errors in model (1) are all independent random variables from a standard normal distribution while the within-block errors in model (2) are the judgment order statistics with mean vector \(E({\varvec{\xi }^*}^\top _{j})= \varvec{\phi ^*}^\top =(\phi ^*_1,\ldots ,\phi ^*_H)\) and variance matrix \(\text{ var }({\varvec{\xi }^*}^\top _{j})=\varvec{\Sigma }^*\).

The ranking process in ORRD accounts for two types of variation, variation due to the separation between ranking groups through the expected values (\(\varvec{\phi }^* \)) of judgment order statistics, and variation among the judgment order statistics through their variances (\( \varvec{\Sigma }^*\)). To separate and model these two types of variation, we re-write model (2) by shifting the expected values of the judgment order statistics to ranking group effects

$$\begin{aligned} Y_{ij}=\mu +\sigma \phi ^*_{i}+b_j+\tau _h+ \sigma \epsilon ^*_{ij}, \ i,j=1,\ldots , H, \end{aligned}$$
(3)

where the \(\phi ^*_{i}\) is a fixed rank (row) effect with the constraint \(\sum _{i=1}^H \phi ^*_i=0\), and \(\epsilon ^*_{ij}\) \(=\xi ^*_{ij}-\phi ^*_i\) is now an error term having mean zero. The errors in column j, \({\varvec{\epsilon }^*}^\top _{j}=(\epsilon ^*_{1j}, \ldots , \epsilon ^*_{Hj})\) are judgment order statistics with shifted means \(E({\varvec{\epsilon }^*}_{j})=\varvec{0}\) and variance matrix \(\varvec{\Sigma }^*\). Hence, errors \(\varvec{\epsilon }^*_j\) in column j are correlated, but errors from different blocks are independent. It is clear that Eq. (3) defines a linear model. Hence, it provides an unbiased estimator for the ranking group effect (the expected value of judgment order statistics) \(\sigma \varvec{\phi }^*\).

Properties of a design are determined by the randomization principle of the treatment allocation. Hence, we highlight the difference between models (1) and (3) from the randomization perspective for the particular case \(H=4\). If we ignore the order restriction in model (3), the construction of the design in model (1) requires that the treatment sequence \(T_1,T_2,T_3,T_4\) be assigned at random to experimental units separately in each column. So the randomized block design in model (1) randomly selects one of the \((4!)^4=331776\) different possible treatment allocations in Table 1. The randomization scheme in model (3), however, has only \((4!)(3!)(2!)(1!)=288\) possible treatment allocations since each treatment regime can appear only once in each block and ranking group. The ORRD selects one of these 288 at random. This is reflected in the residual degrees of freedom in the analysis.

Before providing the detailed development of order restricted randomization for an arbitrary ranking scheme, we give an example to investigate the efficiency of RBD and ORRD under a perfect ranking procedure. We consider the estimation of the difference between the means of treatments \(T_1\) and \(T_2\), \( \mu _1-\mu _2\), for the designs in Table 1.

In design (a), the best linear unbiased estimator of the treatment effect \(\tau _1-\tau _2\) is \((Y_{11}+Y_{13}+Y_{34}+Y_{42})/4-(Y_{12}+Y_{21}+Y_{24}+Y_{33})/4 \) with the expected value \(\tau _1-\tau _2\), and variance \(0.5\sigma ^2\), while the corresponding estimate in design (b) is \((Y_{11}+Y_{24}+Y_{33}+Y_{42})/4-(Y_{12}+Y_{21}+Y_{34}+Y_{43})/4\) which has the same mean \(\tau _1-\tau _2\) but smaller variance \(\sigma ^2\left\{ \textrm{trace} (\varvec{\Sigma })- (2\sigma _{12}+\sigma _{14}+\sigma _{23})\right\} /8= 0.1095\sigma ^2\), where \(\sigma _{ij}\) is the covariance between the i-th and j-th order statistics from a standard normal distribution. In the case where ranking is perfect and the data are indeed normal, the variance is reduced to \(0.1095\sigma ^2\), which is 4.566 times smaller than the variance of the randomized block design.

This simple example shows that blocking the observations in ranking groups and using restricted randomization creates a better design than a randomized block design. In design (b) Table 1, the covariance between order statistics accounts for between ranking group variation within each column. This is an additional source of variation that design (a) does not account for. The magnitude of the between ranking group variation depends on the quality of ranking and also the natural variation among experimental units.

In this paper, we extend order restricted randomization to the randomized block design to account for the within-block variation using another blocking variable. Section 2 describes a consistent ranking procedure for ranking of within-block units. The consistency condition provides an unbiased estimator for the treatment effects regardless of the ranking quality. Section 3 provides a consistent ranking model for ORRD where the ranking structure of the error term is modeled with one parameter, \(\rho \), the correlation coefficient between the error and a ranking variable. Under any consistent ranking model, the ORRD outperforms a randomized block design of the same size. It is shown that for smaller block sizes error degrees of freedom of the ORRD are small. To increase the error degrees of freedom, the basic ORR design is replicated. Section 4 constructs estimators for the parameters of the ranking model to assess ranking quality using the restricted maximum likelihood estimator of the ranking model. This section also develops a testing procedure for the ranking group and treatment effects for the replicated design. Section 5 conducts a simulation study to investigate the empirical power of these tests. Section 6 provides an example to illustrate the use of the proposed design in a split-plot setting. Section 7 provides concluding remarks. Proofs of the expected mean squares are given in the Appendix.

2 A consistent ranking model for judgment order statistics

The effectiveness of ORRD will depend on how well the implicit ranking variable aligns with the actual errors achieved when the experiment is conducted. If that correlation is strong, there will be a large reduction in the experimental error and a consequent improvement in the precision of treatment estimates. However, in the worst case where the ranking is entirely ineffective, the ranking is random and the ORRD will have the same efficiency as the randomized block design.

In the formulation described here, the number of blocks in an ORRD is a multiple of the number of plots in a block. This creates an orthogonal design so that unbiased estimates of the treatment means can be obtained under a consistent ranking scheme as defined in Eq. (4). A subsequent paper generalizes the current design to order restricted randomized incomplete block designs.

The ranking procedure of within-block experimental units may be subjective, incomplete and in error, but it satisfies some consistency conditions. A ranking procedure is called consistent if it satisfies the following equality

$$\begin{aligned} G(y) = \frac{1}{H}\sum _{i=1}^H G_i(y) \end{aligned}$$
(4)

where \(G_i(y)\) are the cumulative distribution functions of the i-th judgment order statistics from a parent distribution G(y). Presnell and Bohn (1999) showed that the consistency Eq. in (4) holds for ranking procedures that rank all units in a set using the same ranking method regardless of its accuracy. Under consistency Eq. (4), the following equalities hold for standard normal distribution

$$\begin{aligned} \textrm{trace}(\varvec{\Sigma }^*)+ \varvec{\phi ^*}^\top \varvec{\phi ^*}=H \text{ and } \varvec{1}^\top \varvec{\Sigma }^* \varvec{1}=H. \end{aligned}$$
(5)

It is important to note that the condition in (4) implies that the average of the expected values of judgment order statistics is the same as the expected value of an unordered error term which is zero. Since each treatment level is applied to all judgment ranks, the consistency requirement is sufficient to have an unbiased estimator for the treatment effects for any imperfect ranking methods. The ORRD is robust against any departure from perfect ranking as long as ranking procedure is consistent. Hence, the parameter \(\varvec{\phi }^*\) is estimated from the data under an arbitrary but consistent ranking model without the requirement of the knowledge of the distribution of judgment order statistics.

The consistency Eq. (4) defines a very large class of judgment order statistics. Their distributions are in general unknown and depend on the ranking method. If a ranking model is provided, the distribution of the judgment order statistics can be determined. There have been a number of approaches in the literature to modeling the degree of imperfection in the rankings. Frey (2007) provides a general discussion of these approaches and presents a broad class of imperfect ranking models that can be used to construct the distribution of judgment order statistics. In Sect. 3, we introduce a one-parameter model for the judgment order statistics in model (2). In this paper, unless stated otherwise we use a consistent imperfect ranking model for the judgment order statistics.

The expected mean squares (EMS) for models (1) and (3) are developed in the Appendix and given in Tables 2(a) and (b), respectively. The EMS values of model (3) in Table 2(b) show that a test for treatment effects rejects the null hypothesis of no treatment effects for large values of the F-statistic

$$\begin{aligned} F_T=\frac{\text{ TreatMS }}{\text{ MSE }}, \end{aligned}$$

where TreatMS is the mean square of treatment and MSE is the error mean square. The null distribution of \(F_T\) can be approximated by an F-distribution with degrees of freedom \(df_1=H-1\) and \(df_2=(H-1)(H-2)\). Note that even though we have a linear model in Eq. (10), its error terms are not normal, they are rather mean-corrected judgment order statistics from a normal distribution. Hence, the null distribution of \(F_T\) would follow the exact F-distribution if the ranks are assigned completely at random in which case rank effect can be dropped from the analysis. Otherwise, it will only be an approximate F-distribution. Further discussion on the null distribution of \(F_T\) is given in Sect. 5.

Table 2 Expected mean squares for models (1), (8) and (10)
Full size table

Non-centrality parameters of the F-test for RBD and ORRD are given by

$$\begin{aligned} \kappa _{\text{ RBD }}= & {} \frac{H\varvec{\tau }^\top \varvec{\tau }}{E(\text{ MSE}_{\text{ RBD }})} \\ \kappa _{\text{ ORRD }}= & {} \frac{H\varvec{\tau }^\top \varvec{\tau }}{E(\text{ MSE}_{\text{ ORRD }})}, \end{aligned}$$

where \(E(\text{ MSE}_{\text{ RBD }})\) and \(E(\text{ MSE}_{\text{ ORRD }})\) are the expected value of the mean squared errors of the RBD and ORRD. The relative efficiency of the ORRD with respect to a randomized block design (RBD) with independent errors is defined as the ratio of the non-centrality parameters. The efficiency depends on the number of treatments (or set size) H and the expected values of the judgment order statistics of the consistent ranking model

$$\begin{aligned} \text{ RE(ORRD) }=\frac{\kappa _{\text{ ORRD }}}{\kappa _{\text{ RBD }}}= \frac{E(\text{ EMS}_{\text{ RBD }})}{E(\text{ EMS}_{\text{ ORRD }})}= \frac{1}{1-{\varvec{\phi }^*}^\top {\varvec{\phi }}^* /(H-1)}. \end{aligned}$$

This efficiency result holds for any consistent ranking scheme. While this expression offers a reasonable estimate for cases with a substantial number of error degrees of freedom in ORRD, it falls short in providing a comprehensive insight into the experiment’s sensitivity. This deficiency arises from its failure to account for the reduced error degrees of freedom within ORRD. For readers seeking alternative definitions of relative efficiency that address this issue, we recommend referring to Shieh and Shoe-Li (2004).

3 One parameter model for judgment order statistics

In this section, we suppose that there is a within-block correlation between the ranking variable and the error variable for the response of interest. Let \(\varvec{Y}_j\) be the response vector in block j in model (3). Since within-block units are ranked, the components of \(\varvec{Y}_j\) are not independent. The response vector in block j can be modeled as

$$\begin{aligned} \varvec{Y}_j = \varvec{\mu }_j + \sigma \varvec{\epsilon }^*_j, j=1, \ldots , H, \end{aligned}$$

where \(\varvec{\mu }_j\) contains the grand mean, judgment ranking group, block and treatment effects. Under perfect ranking, \(\varvec{\epsilon }^*_j \ (\varvec{\epsilon }^*_j=\varvec{\xi }^*_j-\varvec{\phi }_j)\) becomes the mean-corrected vector of the H order statistics \(\varvec{\xi }_j\) from a standard normal distribution. We denote its variance matrix by \(\varvec{\Sigma }\). Under imperfect ranking entries of \( \varvec{\epsilon }^*_j\) are not order statistics. Their distribution is unknown, and depends on the ranking model. The error terms \( \varvec{\epsilon }^*_j\) and \(\varvec{\epsilon }^*_{j'}\), \(j\ne j'\), are however independent since units are ranked separately within each block.

We now introduce a particular one-parameter consistent ranking scheme that yields an explicit expression for the distributions of judgment order statistics. Suppose that there exists a secondary variable Z which is used to rank the units in a block prior to the allocation of treatments. Let \(\varvec{\epsilon }_{j}\) and \( \varvec{z}_{j}\) be the unordered error terms and ranking variable, respectively, of the units that correspond to the response vector \(\varvec{Y}_{j}\). We assume that, for a given block j, the marginal distributions of \(\varvec{\epsilon }_{j}\) and \(\varvec{z}_{j}\) are normal with means zero and variance \(\varvec{I}\), but that their joint distribution has a correlation \(\rho \). The joint distribution of \( \varvec{\epsilon }_{j}\) and \( \varvec{z}_{j}\) of the unordered units in block j then has a variance-covariance matrix

$$\begin{aligned} \textrm{Var}\left( \begin{array}{l} \varvec{\epsilon }_{j} \\ \varvec{z}_{j} \end{array} \right) = \left( \begin{array}{ll} 1 &{} \rho \\ \rho &{} 1 \end{array} \right) \otimes \varvec{I}_H, \end{aligned}$$

where \(\otimes \) is the Kronecker product and \(\varvec{I}_H\) is an identity matrix of size H.

Suppose for the moment that variable Z can be measured. It can then be used as a covariate to obtain

$$\begin{aligned} E (\varvec{Y}_j| \varvec{z}_j)= & {} E \{(\varvec{\mu }_j+\sigma \varvec{\epsilon }_j)| \varvec{z}_j\}=\varvec{\mu }_j+\sigma \rho \varvec{z}_j \\ \textrm{Var}(\varvec{Y}_j| \varvec{z}_j)= & {} \sigma ^2(1-\rho ^2) \varvec{I}_H \end{aligned}$$

in which case the inclusion of the covariate \(z_{ij}\) (with slope \(\sigma \rho \)) and error term \(\epsilon _{ij}\) in model (3) in place of the terms \(\sigma \phi ^*_{i}\) and \(\epsilon _{ij}^*\) yields a covariance model, and would have the effect of reducing the residual variance from \(\sigma ^2\) (under independent error) to \(\sigma ^2(1-\rho ^2)\).

The error term \( \varvec{\epsilon }_{j}\) can be expressed as a weighted combination of \(\varvec{z}_j\) and a set of H standard Normal variates \(\varvec{u}_j\), namely

$$\begin{aligned} \varvec{\epsilon }_{j} = \sqrt{1- \rho ^2} \varvec{u}_j +\rho \varvec{z}_j, \end{aligned}$$
(6)

which captures the correlation structure between \(\varvec{\epsilon }_{j}\) and \(\varvec{z}_j \) for any \(\rho \). Since \( \varvec{u}_j\) and \(\varvec{z}_j\) are independent random vectors from a standard normal distribution, model (6) has only one unknown parameter \(\rho \). Hence, it provides a mechanism to capture a varying degree of within-block ranking quality for different values of \(\rho \). If we rank the units in each block based on the values of Z and record the corresponding values of \(\varvec{\epsilon ^*_j}\) as the within block error term for \(\varvec{Y}_j\):

$$\begin{aligned} \varvec{\epsilon }^*_j(\rho )=\sqrt{1-\rho ^2}\varvec{u}_j+\rho \varvec{z}^+_j- \rho \varvec{\phi }_j, \end{aligned}$$
(7)

where the entries of the vector \(\varvec{z}^+_j\) are the ordered values of \(\varvec{z}_j\) from smallest to largest. In this model, \(\varvec{u}_j\) is a noise variable. For small values of \(\rho \), \(\varvec{u}_j\) makes it harder to rank the entries of \(\varvec{\epsilon }^*_j(\rho )\). Hence, the quality of ranking is controlled by the magnitude of \(\rho \). If \(\rho =0\), the entries of \(\varvec{\epsilon }^*_j(\rho )\) are ranked at random. In the extreme case of \(\rho =1\), the entries of \(\varvec{\epsilon }^*_j(\rho )\) become order statistics in a sample of size H from a normal distribution. Other ranking qualities can be considered by selecting appropriate values of \(\rho \).

Following our earlier practice of removing the mean of the judgment order statistics from \(\varvec{\epsilon }^*_j(\rho )\), we now see that our original model (3) under the ranking model (7) can be revised to

$$\begin{aligned} Y_{ij}=\mu + \rho \sigma \phi _{i}+b_j+\tau _h+ \sigma \epsilon ^*_{ij}(\rho ), \ i,j=1,\ldots , H, \end{aligned}$$
(8)

where \(\phi _i\) is the mean of the ith order statistic for a sample of size H from N(0, 1) and, for a given block j, the error terms have mean zero and variance matrix

$$\begin{aligned} \textrm{Var}\{\varvec{\epsilon }^*_j(\rho )\}=(1-\rho ^2)\varvec{I}_H+\rho ^2 \varvec{\Sigma }. \end{aligned}$$

The EMS values for model (8) can be obtained from Table 2(b) by replacing \(\varvec{\phi }^*\) with \(\rho \varvec{\phi }\). The relative efficiency of the ORRD with respect to a randomized block design (RBD) with independent errors now becomes

$$\begin{aligned} \text{ RE(ORRD) }=\frac{E(\text{ MSE}_{\text{ RBD }})}{E(\text{ MSE}_{\text{ ORRD }})}= \frac{1}{1-\rho ^2\varvec{\phi }^\top \varvec{\phi } /(H-1)}. \end{aligned}$$
(9)

This efficiency result remains consistent both when \(\rho =1\) and when \(\rho =-1\). This consistency implies that employing either an ascending or descending perfect ranking yields an identical efficiency. This equivalence is contingent upon utilizing the same ranking procedure across all blocks.

We note, however, that this efficiency is only achievable by virtue of the fact that the design makes the treatment factor orthogonal to the ranks. The efficiency in Eq. (9) is no less than one, but is less than would be achieved if the values of Z were known, rather than just their ranks. In that case, the efficiency would have been \(1/(1-\rho ^2)\). This possible gain in efficiency diminishes with the size of the experiment, for example, the \(\varvec{\phi }^\top \varvec{\phi }/(H-1))\) increases from 0.72 for \(H = 3\), to 0.84 for \(H = 7\). There are no gains in efficiency if \(\rho =0\) since the ranking assignments within blocks are completely at random. However, under perfect ranking, the relative efficiencies for set sizes \(H=2, 3, 4, 5\) are 2.751, 3.523, 4.259, 4.969, respectively.

Figure 1 presents the relative efficiency in Eq. (9) with respect to a randomized block design for set sizes \(H=2,\ldots , 6\) and ranking correlation \(\rho =0,0.1, \ldots , 1\). It is clear that the efficiency is always greater than 1, but for a meaningful efficiency gain the ranking correlation \(\rho \) needs to be greater than about 0.4. As expected, the efficiency increases with the set size H since larger values of H allow us to explore the variation among a larger number of within-block experimental units.

The uppermost curve here is \(1/(1-\rho ^2)\), which is the efficiency that would be achieved if the actual values of the variable Z were known, rather than just the ranks in each block. However, using Z as a covariate in model (7) requires stronger assumptions than using a consistent ranking scheme based on any or all available ranking information of within block units. For example, to achieve this efficiency, we would need a randomization strategy that ensured treatment effects were orthogonal to the covariate Z, which is more difficult to achieve than the orthogonality obtained with the ranking procedure. Further, the model in Eq. (7) requires that the covariate Z be measurable. In many studies, there are several unmeasurable, but still observable factors that influence the within block variation. For example, color, texture, formation of the soil surface and visual assessment of vegetation cover of within block units may all influence the outcome of the experiment. The assessment of vegetation cover may be performed using smartphone based digital technologies in agricultural research (Heinonen and Mattila 2021). It may be difficult to translate this type of subjective information into a measurable covariate. On the other hand, it may be relatively easy to rank within block units from smallest to largest based on these factors. Even if Z is measurable, analysis of covariance may not be appropriate if linearity and normality of the responses on covariate Z are in doubt. Our procedure would be robust to this type of model violation.

Fig. 1
figure 1

Relative efficiency of ORRD with respect to randomized block designs for block sizes \(H=2,3,4,5,6\) and different values of \(\rho \), including the case where Z is known

Full size image

Table 2(b) indicates that model (3) yields smaller error degrees of freedom than the randomized block design, especially if the block size is small. For example, if \(H=4\), the error degrees of freedom drops from 9 for model (1) to 6 for model (3). The error degrees of freedom can be increased by repeating the basic design in model (3) m times. The model for the ORRD with m such arrays is given by

$$\begin{aligned} Y_{kij}= \mu + a_k+b_{kj}+ \sigma \phi ^*_{i}+\tau _h+ \sigma \epsilon ^*_{kij}, \ k=1,\ldots , m; \ i,j,=1,\ldots , H, \end{aligned}$$
(10)

where \(a_k\) is the array effect and \(b_{kj}\) is the jth block effect within array k. We assume that \(a_k\) has a normal distribution with mean zero and variance \(\sigma ^2_a\), and is independent of \(b_{kj}\) and \(\epsilon ^*_{kij}\). Note that the same treatment and ranking groups are used throughout. An analysis of variance (ANOVA) table of the data from model (10) is given in Table 2(c).

Because array and block effects are formed from block totals, which are unaffected by the ranking process, their mean squares remain the same whether we use RBD or ORRD. The impact of the ranking, however, is that the remaining \(mH(H-1)\) within block degrees of freedom each have their expected mean square reduced from \(\sigma ^2\) to \(\sigma ^2\{1-{\varvec{\phi }^*}^\top \varvec{\phi }^*/(H-1)\}\). The total reduction of \(mH(H-1)\sigma ^2{\varvec{\phi }^*}^\top \varvec{\phi }^*/(H-1)\) in the expected sum of squares achieved in this way is then shared between the \(H-1\) degrees of freedom for Ranks.

4 Estimation in the one-parameter ranking model

Ranking quality of the one-parameter ranking model can be assessed either by comparing variance components in the ANOVA table or by estimating the magnitude of the ranking correlation \(\rho \). One way to estimate \(\rho \) is to use restricted maximum likelihood estimator. In this section, we investigate both of these procedure.

The EMS values of model (10) in Table 2(c) show that a test for significant ranking effects rejects the null hypothesis of no ranking effects for large values of the F-statistic

$$\begin{aligned} F_R=\frac{\text{ RankMS }}{\text{ MSE }}, \end{aligned}$$

where RankMS is the mean squares of ranking group factor. Furthermore, under the consistency model (4) we can assess (estimate) the efficiency relative to the randomized block design as

$$\begin{aligned} \widehat{\text{ RE }}(\textrm{ORRD}) = 1+(F_R-1)/(mH). \end{aligned}$$

In the case where we replace \(\varvec{\phi }^*\) by the term \(\rho \varvec{\phi }\), the estimates of the two parameters \((\rho , \sigma ^2)\) are of some interest in assessing the ranking quality of the one-parameter ranking model. Looking at Table 2(c), we can consider an equivalent parameterisation, namely \(\gamma =\sigma \rho \) and \(\eta ^2=\sigma ^2\{1-\rho ^2{\varvec{\phi }}^\top \varvec{\phi }/(H-1)\}\). Estimates of these are available as follows.

Firstly, there is no effective information about \(\eta ^2\) in the RankMS without knowing \(\gamma \), because the EMS(Ranks) is just \(\eta ^2+mH\gamma ^2\varvec{\phi }^\top \varvec{\phi }/(H-1)\). It follows that the MSE ( \(\hat{\eta }^2\)) is an estimate of \(\eta ^2\) with variance approximated by \(v_\eta =2\eta ^4/\{(mH-2)(H-1)\}\), the approximation being due to the fact that the error terms are not independent.

Second, the minimum variance estimate of the slope \(\gamma \) comes from the row means in model (10), namely

$$\begin{aligned} \bar{Y}_{.i.}= \mu + a_.+b_{..}+ \gamma \phi _i+ \sigma \bar{\epsilon }^*_{.i.}, \ i=1,\ldots , H. \end{aligned}$$
(11)

If \({\bar{\varvec{\epsilon }}^*}=(\bar{\epsilon }^*_{.1.}, \ldots , \bar{\epsilon }^*_{.H.})^\top \) represents the vector of error terms for these row means, then \(\textrm{Var}(\bar{\varvec{\epsilon }}^*)=\sigma ^2 \varvec{Q}/(mH)\), where \(\varvec{Q}=(1-\rho ^2)\varvec{I}+\rho ^2\varvec{\Sigma }\). Let \(\varvec{w}\) be the vector of means \(\bar{Y}_{.i.} \). There are two choices for estimating the slope \(\gamma \). If \(\rho \) were known or estimated, the maximum likelihood estimator of \(\gamma \) would be

$$\begin{aligned} \tilde{\gamma } = \varvec{w}^\top \varvec{Q}^{-1}\varvec{\phi }/\varvec{\phi }^\top \varvec{Q}^{-1}\varvec{\phi }, \end{aligned}$$

with variance \(\sigma ^2/(mH\varvec{\phi }^\top \varvec{Q}^{-1}\varvec{\phi })\). Alternatively, an unweighted regression which does not require knowledge of \(\rho \) provides a slope estimate

$$\begin{aligned} \hat{\gamma }=\varvec{w}^\top \varvec{\phi }/\varvec{\phi }^\top \varvec{\phi }. \end{aligned}$$

This will have mean \(\sigma \rho \) and variance \(v_\gamma =\sigma ^2\varvec{\phi }^\top \varvec{Q}\varvec{\phi }/\{mH(\varvec{\phi }^\top \varvec{\phi })^2\}\), and will be independent of the estimate \(\hat{\eta }^2\). Now \(\varvec{Q}\varvec{1}=\varvec{1}\) and the next largest eigenvalue of \(\varvec{Q}\) corresponds to a vector which is very close to \(\varvec{\phi }\). Under these circumstances, these two parameter estimates are almost identical in value and in properties. We will use \(\hat{\gamma }\) since it does not require knowledge of \(\rho \). There remain \((H-2)\) degrees of freedom for departures from this linear regression, but it has a different expected mean square and, for values of m likely to be used, provides a small amount of information about \(\eta ^2\) relative to that provided by the residual mean square.

Estimates of \((\rho ,\sigma ^2)\) are obtained as

$$\begin{aligned} \hat{\rho }= & {} \hat{\gamma }/\sqrt{\hat{\eta }^2 + \hat{\gamma }^2 A}\nonumber \\ \hat{\sigma }^2= & {} \hat{\eta }^2 + \hat{\gamma }^2 A, \end{aligned}$$
(12)

where \(A = \varvec{\phi }^\top \varvec{\phi }/(H-1)\), and we can then use a first-order Taylor series expansion to determine approximate variances for these estimates. This is given by

$$\begin{aligned} \textrm{Var}\left[ \begin{array}{l} \hat{\rho } \\ \hat{\sigma }^2 \end{array} \right]= & {} \varvec{D}\varvec{V}\varvec{D}^\top \end{aligned}$$

where \(\varvec{V}=\textrm{diag}(v_\gamma ,v_\eta )\), and the matrix of derivatives is given by

$$\begin{aligned} \varvec{D} = \left[ \begin{array}{cc} \eta ^2/\sigma ^3 &{} -\gamma /(2\sigma ^3)\\ 2\gamma A &{} 1 \end{array} \right] \end{aligned}$$

The variance matrix is then given by

$$\begin{aligned} \textrm{Var}\left[ \begin{array}{l} \hat{\rho } \\ \hat{\sigma }^2 \end{array} \right]= & {} \left[ \begin{array}{cc} v_\gamma \eta ^4/\sigma ^6+v_\eta \gamma ^2/(4\sigma ^6) &{} 2v_\gamma \eta ^2\gamma A/\sigma ^3-v_\eta \gamma /(2\sigma ^3)\\ 2v_\gamma \eta ^2\gamma A/\sigma ^3-v_\eta \gamma /(2\sigma ^3) &{} 4v_\gamma \gamma ^2 A^2+v_\eta \end{array} \right] . \end{aligned}$$
(13)

For example, in the case \(m=3, H=4, \rho =\sqrt{0.5}\), this formula gives \(SD(\hat{\rho })=0.113\), whereas the results of 1000 simulations provide a standard deviation of 0.111.

5 Statistical inference for treatment effects

In this section we perform simulation studies to provide empirical evidence to evaluate the efficiency of the proposed design. The EMS values of model (10) in Table 2(c) show that a test for treatment effects rejects the null hypothesis of no treatment effects for large values of the F-statistic

$$\begin{aligned} F_T=\frac{\text{ TreatMS }}{\text{ MSE }}. \end{aligned}$$

The null distribution of \(F_T\) can be approximated by an F-distribution with degrees of freedom \(df_1=H-1\) and \(df_2=(H-1)(mH-2)\). Note that even though we have a linear model in Eq. (10), its error terms are not normal, they are rather mean-corrected judgment order statistics from a normal distribution. Hence, the null distribution of \(F_T\) would follow the exact F-distribution if \(\rho =0\), but it will only be an approximate F-distribution for \(\rho \ne 0\).

We performed a simulation study to investigate the null distribution of \(F_T\) for \(m=1,2,3\) and \(H=3,4,5\) under model (10) with no treatment effect. In the simulation, error terms are generated from a normal distribution with scale parameter \(\sigma =1\) under ranking model (7) with \(\rho =0,0.5,1\). The simulation size is taken to be 1000. Figure 2 presents the quantile plots of \(F_T\) against the F distribution with degrees of freedom \(H-1\) and \((H-1)(mH-2)\). All panels in Fig. 2 show a good fit to the F-distribution. Since the error terms are independent, \(F_T\) has an exact F-distribution when \(\rho =0\). The quantile plots for \(\rho =0.5\) and \(\rho =1\) are almost identical to the quantile plots of \(\rho =0\). This suggests that the null distribution of \(F_T\) can be approximated very well with the F-distribution when \(\rho \ne 0\). Part of the reason why this is so close is that each treatment mean is the average of equal numbers of each of the normal order statistics, albeit taken from different blocks.

Fig. 2
figure 2

Quantile plots of \(F_T \) with respect to the F-distribution with degrees of freedom \(H-1\) and \((H-1)(mH-2)\) for selected values of \(\rho \), m and H

Full size image

We performed another simulation study to investigate the empirical power of \(F_T\). Simulation parameters are selected as \(m=1, 2, 3, 4\), \(H=3, 4, 5\), \(\rho =0, 0.25, 0.5, 0.75, 1\), \(\mu =50\), \(\sigma _a=1\), \(\sigma _b=3\) and \(\sigma =5\). The empirical power is computed in the direction of the alternative hypothesis

$$\begin{aligned} H_A: \tau _1= -\Delta /2,\tau _2=0, \ldots , \tau _{H-1}=0, \tau _H=\Delta /2 \end{aligned}$$

for different values of \(\Delta \), where \(\Delta =\delta \sigma \), \(\delta =0,0.2, \ldots , 1\). The simulation size is taken to be 5000. The empirical power is computed as the fraction of \(F_T\) values exceeding the fifth-upper percentile of a central F-distribution with degrees of freedom \(df_1=H-1\) and \(df_2=(H-1)(mH-2)\). The empirical powers are given in Fig. 3. In all twelve panels, size of the test for all m, H and \(\rho \) values in the simulation study is approximately equal to nominal size of 0.05 for a five-percent test. Hence, the F-approximation to the null distribution of \(F_T\) holds reasonably well.

Fig. 3
figure 3

Empirical power of \(F_T\) for selected values of \(\rho \), m and H

Full size image

The power of the test \(F_T\) is affected by several factors. As expected, it increases with \(\Delta \). For fixed m and H, a good within-block ranking quality (large values of \(\rho \)) leads to power curves with steeper slopes than the ones with lower \(\rho \) values. For example, if the values of \(\rho \) are less than 0.5, there is not much improvement over a replicated Latin square design (also over RBD). This is consistent with the efficiency curves in Fig. 1, where we concluded that replicated ORRD is superior to RBD if \(\rho >0.4\). The set size H is also an important factor. For fixed values of m and \(\rho \), large values of H provide higher power since larger H makes it possible to facilitate a better restricted randomization in within-block experimental units. Finally, for fixed H and \(\rho \) large, values of \(m>1\) yield higher empirical power due to the increased sample size. If \(m=1\) the error degrees of freedom is small. Hence, the power of the test is not as high as those for \(m>1\).

Individual tests for treatment comparisons can be made by using differences between the row treatment means. The comparison \(\hat{\tau }_i-\hat{\tau }_j\) in the corresponding RBD would have variance \(2\sigma ^2/(mH)\) since each treatment has replication mH. We might then anticipate that the variance of each such comparison for an ORRD would reduce to \(2\sigma ^2\{1-\rho ^2\varvec{\phi }^\top \varvec{\phi }/(H-1)\}/(mH)\), and it is true that this is the average variance of such treatment comparisons. For example, in the ORRD shown in Table 1, the reduction would be from \(\sigma ^2/2\) to \(\sigma ^2(1-0.765\rho ^2)/2\). However, the variance matrix \(\sigma ^2\{(1-\rho ^2)\varvec{I}+\rho ^2\varvec{\Sigma }\}\) within blocks implies that these pairwise variances are not in general all equal. For example, suppose that \(\varvec{\Sigma }=(\sigma _{ij})\). Then, in the ORRD shown in Table 1, and taking account of the known symmetries in \(\varvec{\Sigma }\), the pairwise treatment comparisons for \(\hat{\tau }_i-\hat{\tau }_j\) have variance

$$\begin{aligned} \textrm{Var}(\hat{\tau }_i-\hat{\tau }_j) =\left\{ \begin{array}{ll} \sigma ^2[(1-\rho ^2)/2+\rho ^2\{ \textrm{trace}(\varvec{\Sigma })-(2\sigma _{12}+\sigma _{14}+ \sigma _{23})\}/8],&{} i-j=1 \text{ or } 3, \\ \sigma ^2[(1-\rho ^2)/2+\rho ^2\{ \textrm{trace}(\varvec{\Sigma })-4\sigma _{13}/8],&{} i-j=2. \end{array} \right. \end{aligned}$$

All pairwise variances for the ORRD in Table 1 are shown in Table 3. It transpires that there are 24 distinct Latin squares with the treatment numbers 1–4 in order across the top row. Among these, there are 4 distinct patterns for the variances of pairwise comparisons, all with the same average variance. In particular, if we choose any set of 3 Latin squares that form an orthogonal set, then any value of m which is a multiple of 3 can provide a balanced design in which all treatment comparisons have the same variance.

Table 3 Pairwise treatment variances for the ORRD in Table 1
Full size table

6 Example

The example is taken from the third of four uniformity trials described and analyzed by Clarke and Stefanova (2011). The Newdegate (ND) data are arranged in 25 rows and 12 columns.

In order to illustrate our procedure, we pair the rows, deleting the last row, and pretend that the odd-numbered rows represent “final” (post-treatment) yields, while the even-numbered rows represent “initial” (pre-treatment) values. The original data set had 8 missing values. In order to illustrate the current method, each of the missing “initial” values was replaced by its corresponding “final” value, and vice versa. This provides a data set with 12 row-pairs and 12 columns in which each (row-pair, column) combination has two values which we regarded as an initial (in the odd-numbered row) and a final (in the even-numbered row) yield. Given the likelihood of “local” variation, the initial and final yields so obtained are likely to be correlated, even after blocks are applied.

In their analysis, Clarke and Stefanova (2011) found strong column effects, small row effects and a strong auto-correlation in the row direction. In practice, this information would not generally be known beforehand. Designs can be placed onto such a field in a variety of ways, as Clarke and Stefanova have shown. To illustrate our methodology, however, we chose to break this \(12 \times 12\) array into nine \(4 \times 4\) arrays each consisting of 4 blocks (columns) of 4 units. Each unit then has an initial and a final value. The blocks within each array are then regarded as whole plots for the application of a factor A at 4 levels which is randomized to the whole plots in each array. A second factor B, also at 4 levels, is applied to the plots within each block. The factor B corresponds to the treatment term in the earlier Table 2. Table 4 then shows two alternative designs, as follows: (a) The four levels of B are applied in a Latin square arrangement in each of the \(4 \times 4\) arrays, while the four levels of A are applied at random to the columns in each array. This is a standard split plot design. (b) In this case, the four levels of A are again applied at random to the columns in each array. The four levels of B are then applied using order restricted randomization, where the 4 cells in a block are first ranked according to the “initial” values in that block, and then the levels of B applied according to a Latin square arrangement in each array with the rows being the ranks and the columns being the levels of A. Ideally, successive Latin squares are chosen so that each set of 4 arrays has a complete replicate of the 16 treatment combinations for each rank. In this case, with \(m=9, H=4\), there is necessarily some slight confounding of one set of 3 degrees of freedom from the AB interaction with the ranks because each rank occurs 36 times and cannot have all 16 treatment combinations equally often.

Table 4 Two designs applied to Clarke and Stefanova (2011)
Full size table

Table 5 shows the analysis of variance for each of the two designs. Terms for A and the AB interaction appear in addition to the terms shown in the earlier Table 2(c). These appear in the Block and Within Block strata, respectively. Rows in the first analysis are not effective in reducing the residual mean square, so these are dropped from the analysis, giving a residual mean square of 0.2072 for this particular randomization. The second design demonstrates that the use of ranks based on the pre-treatment values in this case provides a more efficient analysis, providing a residual mean square of 0.1603. Thus, the efficiency of the ORRD relative to the standard design is \(0.2072/0.1603=1.293\). In this case, the within-block correlation between initial values and their corresponding final residuals is estimated to be 0.496, with a standard error of 0.087, using Eq. (12) and (13), respectively. The standard error for comparing the estimates of any two levels of B is reduced from \(\sqrt{0.2072/18} = 0.107\) in the analysis without ranks to \(\sqrt{0.1603/18} = 0.094\) when the ORRD is used. The slight confounding of part of the AB interaction has no impact on standard errors for the main effects and less than half of 1% for standard errors of interaction comparisons. Analyses of this same data in ASReml-R (Butler et al. 2018) produced identical results. Any errors in the ranking due to the 6 missing “initial” readings will be absorbed into the accepted inaccuracies among the ranks. We therefore repeated the analyses with the two “final” missing values excluded, with the result that the residual variances with and without ranking both increased by about 2%, leaving our conclusions unchanged. Since this was a uniformity trial, we do not expect to see significant treatment effects for any of the factors.

Table 5 Analysis of two designs applied to Clarke and Stefanova (2011)
Full size table

7 Concluding remarks

One of the basic principles in designing an experiment in the field is to account for the sources of variation as much as possible and use appropriate randomization schemes to facilitate reduction of error terms. On many occasions, blocking and covariate variables are readily available to model the sources of variation in an experiment. Sometimes, however, blocking variables may be subjective or incomplete, while their values may possess a stochastic ordering. Hence, use of a blocking variable may require careful consideration in designing the experiment.

This paper considers ORRD, where within-block units are stochastically ordered using their ranks based on inherent variation among them. These within-block (pre-treatment) ranks are used as a second blocking factor. The ranking process induces a correlation structure for within-block units which can be used to reduce the variance of treatment comparisons. Randomization of treatments to blocks and ranking groups is facilitated using the randomization scheme of a Latin square design. The basic ORRD can be repeated m times to increase the error degrees of freedom.

The ranking process does not have to be accurate. As long as it provides a separation among ranking group means, it will be effective in accounting for at least some of the natural variation between experimental units within blocks.

The ORRD would be effective in a field experiment as long as there is a reasonable ranking mechanism to identify the relative positions (ranks) of experimental units within each block. An example, based on a uniformity trial, illustrates the use of the technique in a split-plot design setting. In the worst case, where ranking is completely at random, the ORRD would be equivalent to a replicated Latin square design in which one of the two block factors was ineffective. Hence there would be no loss of efficiency using the ORRD other than a slight reduction in error degrees of freedom. Further extensions to the ORRD for use in incomplete block designs will be considered in a subsequent paper.