1 Introduction

Comparative experiments continue to provide the foundation of agricultural research and thus underpin the improvement and optimisation of the productivity of agricultural systems. Over time, large-scale increases in productivity have become harder to achieve (Fischer and Connor 2018), resulting in greater pressure being placed on the humble comparative experiment to yield more comprehensive and detailed information on the biological processes underpinning the system. Often, the answer to this pressure is to ‘measure more’; more variables, more frequently or in more detail. An outcome of measuring more is that comparative experiments give rise to datasets of a greater size and detail than ever before. However, while sizes of datasets are growing, the size of experiments typically remains the same, leading to a situation where, in many experiments, the number of variables measured is greater than the number of experimental units.

With growing size and detail, the complexity of the datasets also often increases. This complexity can arise from relationships between measured traits or characteristics (Dreccer et al. 2020), structure implicit in or imposed on the experimental material by design, sampling or measurement protocols (Brien and Bailey 2006; De Faveri et al. 2017) or other physical or biological factors inherent to the treatments or material in the experiment (Oakey et al. 2006; Osama et al. 2021).

Comparative experiments conducted in the laboratory often facilitate a ‘measure more’ approach, enabling a detailed investigation of biological samples obtained from the field or other sources. When these samples arise from observational studies or designed experiments, a multi-phase experiment, conducted according to a multi-phase design, is possible (Brien et al. 2011). The simplest multi-phase experiment consists of two phases (McIntyre 1955), where units composing the first phase produce outcomes, such as material and/or response variable values, before material from the first phase is randomised to units in the second phase (Brien and Bailey 2006; Brien et al. 2011). A multi-phase design is then the implementation of an experimental design solution for a multi-phase experiment. Such designs have been applied to great effect in the agricultural domain, enabling the partitioning and investigation of extraneous variation across different phases of experimentation (Smith et al. 2006; Panozzo et al. 2007; Kelly and Forknall 2020).

The linear mixed model (LMM) provides a powerful and flexible framework for the analysis of data arising from comparative experiments, and continues to be relevant and applicable even as the size and complexity of the datasets arising from these experiments increase. In part, this is due to the ability to estimate variance structures of complex form, both between treatments and between residual errors (De Faveri et al. 2015; Verbyla et al. 2021).

In practice, the estimation of complex variance structures relies on sufficient independent pieces of information to reliably estimate the covariances and variances required. In situations where the number of variables exceeds the number of observations, the resulting variance structures can be of reduced rank, causing computational difficulties (Thompson et al. 2003). Structures that accommodate this reduced rank nature exist, for example, the factor analytic variance structure proposed by Smith et al. (2001b) and formulated for reduced rank estimation by Thompson et al. (2003). However, evidence suggests a degradation in the performance of this structure when the number of observations informing a variance parameter estimate is small (Macdonald 2018; Macdonald et al. 2019). In these situations, the modelling of covariance is often restricted to simplistic structures, such as that resulting from a variance components model (Patterson et al. 1977).

The LMM framework has also proven useful for the modelling of smooth trends in data arising from designed experiments. In cases where such trends display nonlinear forms, the LMM representation of the cubic smoothing spline has been formulated (Verbyla et al. 1999). This approach has been shown to be effective in modelling smoothly varying trends arising from designed agricultural experiments (Verbyla et al. 1999) and can be coupled with the estimation of complex covariance structures between residual errors (De Faveri et al. 2015, 2022).

There are multiple software solutions for the implementation of the LMM framework, both using standalone software or via statistical computing environments such as R (R Core Team 2019; Rogers and Taylor 2019). One of the more powerful and flexible options is the commercial asreml R package (Butler et al. 2017). This package implements variance component estimation via residual maximum likelihood (REML) (Patterson and Thompson 1971), using the average information algorithm (Gilmour et al. 1995), and supports the implementation of a wide range of complex variance–covariance structures, along with the LMM representation of the cubic smoothing spline.

While LMM software is well developed, currently, there is a distinct lack of software that supports the efficient implementation of highly complex variance–covariance structures. Despite the asreml package enabling the use of such structures, the time taken to fit models that include these structures, to even moderately sized datasets, is often prohibitive. Modelling run times are further exacerbated when the aim is to fit the models using a fully efficient single-stage analysis (Welham et al. 2010). An option to reduce computational issues and accelerate model fitting is to fit the LMM using a two-stage analysis (Smith et al. 2001a; Piepho et al. 2012).

A field of research in which laboratory-based comparative experiments are conducted, that produce large volumes of data from a limited number of samples, is mass spectrometry (MS)-based proteomics. Proteomics is the broad-scale investigation of the proteome of biological material, where the proteome is the set of proteins composing a biological sample (Yu et al. 2010). Standard modern proteomics workflows involve several sample processing steps to extract and digest the proteins composing a sample for measurement using MS (Osama et al. 2021). The data produced by these workflows have as their most fundamental building blocks the fragment ions linked to specific protein identities, along with their relative abundance (Gross 2011). Using knowledge of how ions comprise a peptide and how peptides comprise a protein enables the reconstruction of the abundance of each protein identified in a sample (Zhang et al. 2010).

In the context of field crops research, the application of MS-based proteomics is growing rapidly (Agrawal et al. 2013), with comparative experiments to test for differences in the proteome of plant tissues, as a result of treatments or plant developmental stages, becoming commonplace (Osama et al. 2021). Such experiments often result in the quantification of upwards of hundreds of proteins from the processing of an individual sample (Gross 2011), with the datasets generally characterised by complex relationships (correlations) between proteins (Agrawal et al. 2013; Robotti et al. 2015).

Mass spectrometry-based experiments can suffer from a lack of sound experimental design, with multiple authors reporting a need to improve the design of such studies (Hu et al. 2005; Oberg and Vitek 2009). Furthermore, the two-phase nature of MS studies is well suited for the implementation of multi-phase design solutions. Such solutions would facilitate the partitioning of variation associated with the collection of the biological material, from ‘technical’ variation that could arise during the subsequent processing of the material using MS techniques. However, we have found no reported occurrences in the literature of such a design solution being implemented in the conduct of an agriculturally motivated MS-based proteomics study.

Statistical methods for the exploration of proteomics datasets are dominated by pattern or cluster analysis and classification-based techniques (Robotti et al. 2015; Chen et al. 2020). Analysis methods to test for differences in proteome composition between treatments in MS-based proteomics experiments also vary and range from simple t-tests (Chen et al. 2020), to analysis of variance (Oberg et al. 2008), multivariate statistical techniques (Robotti et al. 2015) and machine learning approaches (Chen et al. 2020). Examples also exist of the LMM framework being used for the analysis of MS-based proteomics data (Oberg et al. 2008; Choi et al. 2014). However, these LMM frameworks are often simplistic (Osama et al. 2021), with likely advancements possible through estimation of complex covariance between proteins to characterise the nature of the relationships that exist within the proteome (Robotti et al. 2015).

Given the size and complexity of datasets now arising from the most simple of comparative experiments, exemplified by MS-based proteomics studies, the aim of this paper was to provide a parsimonious LMM framework for the analysis of designed experiments where datasets are characterised by a greater number of variables than experimental units, and for which the modelling of complex covariance structures between variables is desired. The proposed method is demonstrated through application to an MS-based proteomics experiment, the objective of which is to investigate changes in the proteome of barley grain during the malting process. We label our proposed method covariance clustering as, through extension of the traditional variance components model (Patterson et al. 1977), it allows for the modelling of covariance between variables by first clustering variables based on estimated effects and then introducing these covariance clusters into an LMM framework through an additional random term.

In order to address our aim, the paper proceeds as follows. To begin, the multi-phase MS-based proteomics experiment that forms the motivating example is introduced. Following this, the four-step procedure to implement the covariance clustering approach is given. The results from each step of the covariance clustering approach, as applied to the motivating experiment, are then presented. The paper concludes with a discussion of the proposed covariance clustering method.

2 Motivating Example

A recent multi-phase MS-based proteomics experiment, with components previously reported by Yousif and Evans (2020) and Osama et al. (2021), provides a motivating example. In this experiment, MS was used to quantify the proteome composition of barley grain and malt samples, where samples were collected at different times during a commercial malting process. The aims of the experiment were to identify proteins that demonstrated a change in abundance over time in the malting process and characterise the relationship between abundance and time for these proteins.

In what we believe to be a first report in the literature, the multi-phase MS-based proteomics experiment was conducted according to a multi-phase design. This multi-phase design enables an investigation of variation arising in both phases of the experiment, being the (i) malt sample collection phase and (ii) MS processing phase. Both phases are explored in more detail, following a brief overview of the particulars of the malting processes relevant to the motivating example.

2.1 Particulars of the Motivating Example

The malting process is typically conducted over approximately six days and involves the controlled and limited germination, then drying, of grain. The process initiates the expression and activation of enzymes that break down the complex carbohydrates and proteins contained within the grain endosperm for yeast utilisation in fermentation (Yousif and Evans 2020; Osama et al. 2021). The malting process is achieved through three stages; steeping, germination and kilning (Schwarz and Li 2010). Barley is the most commonly malted grain, as barley malt is a key ingredient in traditional beer brewing (Schwarz and Li 2010).

The barley samples considered in this study are a subset of those acquired from an Australian commercial malting plant, labelled as Plant Two in Yousif and Evans (2020).

2.2 Phase I: Malt Sample Collection

The collection of barley grain and malt samples constitutes the first phase of the motivating experiment. We consider the processing of two replicate batches of grain in the malting plant. For each replicate batch, grain was sampled a total of 12 times \((t=12)\), with the time at which each sample was collected consistent between the replicate batches (Table 1). Note that without the ability to randomise sampling times within replicate batches, this phase is observational in nature and not itself an experiment. Additionally, note that the sampling times presented in Table 1 do not correspond with those presented in Table 1 of Yousif and Evans (2020) due to an error in the measurement of kilning time previously reported. At each sampling time, samples were frozen and freeze-dried to less than 10% moisture if wet (Yousif and Evans 2020), before being stored for later processing using MS-based proteomics techniques.

Table 1 Times at which barley grain and malt samples were collected during Phase I of the motivating mass spectrometry-based proteomics experiment
Full size table

2.3 Phase II: Mass Spectrometry Processing

The individual grain and malt samples collected in the first phase of the experiment were subsequently processed using MS in the second phase of the experiment. Prior to processing, two subsamples were taken from each of the 24 grain samples. Together, this provides a total of 48 subsamples and four independent samples \((z=4)\) of each sampling time.

Each subsample was prepared and processed according to the workflow outlined in Osama et al. (2021). To briefly summarise, the preparation of individual subsamples involved first grinding them into a homogeneous powder, before a series of steps were undertaken to chemically extract the proteins composing each subsample (Osama et al. 2021). The processing of the extracted proteins from each subsample was achieved using a Sequential Window Acquisition of all THeoretical ions Mass Spectrometry (SWATH-MS) proteomic analysis technique (Osama et al. 2021), which facilitated the ionisation and measurement of the proteins composing the subsamples.

Due to the nature of the MS process, subsamples needed to be run through the mass spectrometer sequentially, and a design was applied to the order in which the subsamples were processed. Two replicate blocks were defined, with one subsample from each grain sample processed within each replicate block, and each replicate block was composed of 24 subsamples. Within each replicate block, subsamples were assigned to one of four processing groups according to an incomplete block design (processing groups correspond to incomplete blocks), with the order in which subsamples were processed randomised within each processing group. The blocking of subsamples into processing groups was performed to enable adjustment for potential extraneous variability or trend arising in the sequential MS processing of subsamples. The initial incomplete block design randomisation was optimised using the odw R package (Butler 2022), which searches for an optimal design given the specification of an associated LMM. Following this optimised design, all subsamples were processed using MS.

The proteins composing each subsample were identified and quantified using the methods described in Osama et al. (2021). This involved identifying the proteins by matching the measured protein signatures with those existing in a published proteomics database, before the abundance of the proteins was determined using proprietary software (Kerr et al. 2019; Osama et al. 2021).

Following this process, a consistent set of 617 proteins \((p=617)\) were identified from each subsample and the abundance of each protein i \((i=1,\ldots ,617)\) quantified. This resulted in the motivating dataset consisting of a total of \(n= t \, z \, p =\) 29,616 protein abundance observations. The proteins ranged in raw abundance, from 69 units per subsample to 4,687,460 units per subsample, with a median of 17,499, where the unit of measurement is related to MS intensity and the abundance of constituent ions composing a protein. The dataset arising from the motivating mass spectrometry-based proteomics experiment is available through the ProteomeXchange Consortium via the Proteomics Identifications Database (PRIDE) partner repository (Perez-Riverol et al. 2021), using the dataset identifier PXD019384 (https://www.ebi.ac.uk/pride/).

3 Statistical Methods

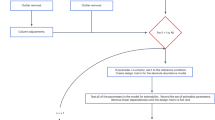
Methods for the implementation of covariance clustering are presented in the context of their application to the motivating example. The covariance clustering method is implemented using four steps; (1) fitting a baseline model, (2) forming a series of covariance clusters, (3) fitting a series of covariance cluster models, one for each of the plausible covariance clusters identified, and (4) locating the ‘optimal’ number of covariance clusters and fitting an ‘optimal’ covariance cluster model. Figure 1 presents these steps in the two alternate ways in which they are applied in the analysis of the motivating experiment; the first models residual covariance through forming what we label residual covariance clusters, and the second identifies similarly shaped response curves through forming what we label spline covariance clusters. In this case, a two-stage LMM framework is used to analyse the raw protein abundance data, with a different covariance clustering procedure implemented in each of the respective stages of the analysis (Fig. 1).

Fig. 1
figure 1

The four steps involved in the covariance clustering procedure (x.1 to x.4) are implemented in each of two stages (\(x=1,2\)) of a linear mixed model (LMM) framework, to analyse the motivating mass spectrometry-based proteomics experiment. In Stage 1, what we have labelled residual covariance clusters (RCCs) are formed to model residual covariance between proteins. In Stage 2, what we have labelled spline covariance clusters (SCCs) are formed to identify similarly shaped response curves describing the relationship between protein abundance and time in the malting process

Full size image

3.1 Stage 1

The first stage of the analysis involves the modelling of the raw protein abundance data for all p proteins. Protein abundance is log transformed \((\log (x/1000 + 1))\) including an offset of 1 as values of x/1000 are close to zero, and because diagnostics obtained from a preliminary analysis showed the LMM adhered better to the assumptions of normality and homogeneity of residual variance using this transformation. Note that the selection of this offset needs careful consideration in practice (Welham et al. 2014). Following transformation, the minimum, median and maximum of the log transformed data are, respectively, 0.067, 2.92, and 8.45. Notably, it is assumed the abundance observations are ordered as subsamples, within sampling times, within proteins.

Step 1.1: Fit baseline linear mixed model: The general form of the baseline LMM fit to the protein abundance data is written as

$$\begin{aligned} \textbf{y} = \textbf{X}\varvec{\tau } + \textbf{Z}_{\textrm{d}}\textbf{u}_{\textrm{d}} + \textbf{e}, \end{aligned}$$
(3.1)

where \(\textbf{y}\) is an \(n\times 1\) vector of (transformed) protein abundance observations and \(\varvec{\tau }\) is a \(p \,t\times 1\) vector containing fixed effects for each protein \(\times \) sampling time combination, with associated design matrix \(\textbf{X}\). The vector \(\textbf{u}_{\textrm{d}}\) contains random effects corresponding to the multi-phase experimental design structure, with associated design matrix \(\textbf{Z}_{\textrm{d}}\), and \(\textbf{e}\) is an \(n\times 1\) vector of residual error effects.

The random effects and residual error effects from (3.1) are assumed to follow a normal distribution with zero mean vector and variance–covariance matrix

$$\begin{aligned} \textrm{var}\left( \left[ \begin{array}{cc} \textbf{u}_{\textrm{d}} \\ \textbf{e} \end{array} \right] \right) = \left[ \begin{array}{cc} \textbf{G}_{\textrm{d}} &{} \textbf{0} \\ \textbf{0} &{} \textbf{R} \end{array} \right] . \end{aligned}$$

Of note is the form of \(\textbf{R}\), an \(n\times n\) matrix, which is defined using a three-way separable structure,

$$\begin{aligned} \textbf{R} = \textbf{R}_{\textrm{p}} \otimes \textbf{R}_{\textrm{t}} \otimes \textbf{I}_z, \end{aligned}$$
(3.2)

where \(\otimes \) is the Kronecker product, \(\textbf{R}_{\textrm{p}} = \oplus _{i=1}^p\sigma ^2_{e_{\textrm{p}_i}}\) is a \(p \times p\) diagonal matrix, enabling the estimation of heterogeneous residual variance for each protein i, \(\textbf{R}_{\textrm{t}} = \oplus _{j=1}^t\sigma ^2_{e_{\textrm{t}_j}}\) is a \(t \times t\) diagonal matrix, enabling the estimation of heterogeneous residual variance for each sampling time j, and \(\textbf{I}_z\) is a \(z \times z\) identity matrix. In practice, to ensure identifiability, \(\sigma ^2_{e_{\textrm{t}_j}}\) is replaced in the form of \(\textbf{R}_{\textrm{t}}\) with \(\gamma _{e_{\textrm{t}_j}}\), where \(\gamma _{e_{\textrm{t}_j}}\) is a scaling parameter and a single \(\gamma _{e_{\textrm{t}_j}}\) is constrained to equal 1.

The form of \(\textbf{R}\) presented in (3.2) enables the estimation of heterogeneous residual variance for each protein, while allowing for the differential scaling of these variances across sampling times. However, such a form assumes independence between proteins at the residual level, with any covariance built through the variance of the experimental design terms included in \(\textbf{G}_{\textrm{d}}\). This is a potentially restrictive and limiting assumption, given the complex relationships that are known to be present in the proteome (Robotti et al. 2015). As such, (3.1) can be extended to enable the modelling of additional and more complex covariance between proteins at the residual level.

Step 1.2: Form residual covariance clusters: Residual covariance clusters are formed by clustering proteins based on their estimated residuals \((\tilde{\textbf{e}})\) from (3.1). These residuals are obtained from (3.1) as empirical best linear unbiased predictors (e-BLUPs), before being studentised (Gilmour et al. 2015, p. 17).

A k-means clustering algorithm (Hartigan and Wong 1979) is used to generate a range of plausible residual covariance clusters. This involves the grouping of proteins into increasing numbers of residual clusters \((\upsilon _{\textrm{r}}=2, \ldots , q_{\textrm{r}})\), with the total number of potential cluster groupings labelled as \(\eta _{\textrm{r}}\). The k-means algorithm is repeated multiple times, each with a different starting seed for the randomisation process defining the initial cluster allocation. If the total number of seeds considered is labelled \(\phi _{\textrm{r}}\), then this results in the formation of \(k_{\textrm{r}} = \phi _{\textrm{r}} \times \eta _{\textrm{r}}\) plausible residual covariance cluster groupings \((l_{\textrm{r}}= 1, \ldots , k_{\textrm{r}})\), based on all seed \(\times \) number of cluster combinations.

Step 1.3: Fit residual covariance cluster linear mixed model: To incorporate a plausible residual covariance cluster, (3.1) is extended to include an additional random term containing effects corresponding to an individual seed \(\times \) number of cluster combination, \(h_{l_{\textrm{r}}}\). This model, referred to as the residual covariance cluster LMM, is repeatedly fit whereby the random cluster term is updated to consider each plausible residual covariance cluster. The general form of the model is

$$\begin{aligned} \textbf{y} = \textbf{X}\varvec{\tau } + \textbf{Z}_{\textrm{d}}\textbf{u}_{\textrm{d}} + \textbf{Z}_{\textrm{c}_{\textrm{r}}}\textbf{u}_{\textrm{c}_{\textrm{r}}} + \textbf{e}, \end{aligned}$$
(3.3)

where is an \((\upsilon _{\text {r}} \, t \, z \times 1)\) vector of random effects corresponding to the \(h_{l_{\textrm{r}}}^{\textrm{th}}\) residual covariance cluster \(\times \) sampling time combination, with design matrix \(\textbf{Z}_{\textrm{c}_{\textrm{r}}}\). All other terms are as defined for the model in (3.1).

The random effects and residual error effects from (3.3) are assumed to follow a normal distribution with zero mean vector and variance–covariance matrix

$$\begin{aligned} \textrm{var}\left( \left[ \begin{array}{cc} \textbf{u}_{\textrm{d}} \\ \textbf{u}_{\textrm{c}_{\textrm{r}}} \\ \textbf{e} \end{array} \right] \right) = \left[ \begin{array}{ccc} \textbf{G}_{\textrm{d}} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{G}_{\textrm{c}_{\textrm{r}}} &{} \textbf{0} \\ \textbf{0} &{} \textbf{0} &{} \textbf{R} \end{array} \right] , \end{aligned}$$

where \(\textbf{R}\) is as defined for the model in (3.2) and \(\textbf{G}_{\textrm{c}_{\textrm{r}}}\) is defined using the three-way separable form

$$\begin{aligned} {\textbf {G}}_{\text {c}_{\text {r}}} ={\textbf {G}}_{\text {g}} \otimes {\textbf {G}}_{\text {t}} \otimes {\textbf {I}}_z, \end{aligned}$$
(3.4)

where \(\textbf{G}_{\textrm{g}} =\oplus _{m=1}^{\upsilon _{\textrm{r}}}\sigma ^2_{\text {c}_{\textrm{r}_m}}\) is a \(\upsilon _{\textrm{r}} \times \upsilon _{\textrm{r}}\) diagonal matrix, enabling the estimation of heterogeneous variance for each residual covariance cluster m, and \(\textbf{G}_{\textrm{t}} = \oplus _{j=1}^t \gamma _{\textrm{c}_{{\textrm{r}}_{{\textrm{t}}_j}}}\) is a \(t\times t\) diagonal matrix, containing scaling parameters for the residual covariance cluster variances across sampling times.

The inclusion of the residual covariance cluster effects, with the associated variance model in (3.4), acts to induce greater covariance between proteins within a covariance cluster, along with providing greater heterogeneity of variance between clusters.

Step 1.4: Locate ‘optimal’ number of residual covariance clusters and fit ‘optimal’ residual covariance cluster linear mixed model: Upon fitting (3.3) for each seed \(\times \) number of cluster combination, the AIC based on the full log-likelihood (Verbyla 2019) is obtained for each model. For brevity, all further mentions of the AIC refers to that based on the full log-likelihood. The ‘optimal’ number of residual covariance clusters, labelled \(\upsilon ^{*}_{\textrm{r}}\), is that which minimises the AIC, on average across seeds, and thus provides the most parsimonious residual covariance structure.

Upon determining \(\upsilon ^{*}_{\textrm{r}}\), the AIC of the models fit for each seed is compared within \(\upsilon ^{*}_{\textrm{r}}\), to locate the seed which results in a clustering of proteins that further minimised the AIC. This ‘optimal’ seed is labelled \(\omega ^{*}_{\textrm{r}}\). The grouping of proteins into \(\upsilon ^{*}_{\textrm{r}}\) clusters, arising from seed \(\omega ^{*}_{\textrm{r}}\), are reintroduced into (3.3) and the model fit to obtain the ‘optimal’ residual covariance cluster LMM, (3.3\(^*\)).

Upon fitting (3.3\(^*\)), predictions of abundance for each protein at each sampling time \((\hat{\varvec{\tau }})\) are obtained from the model as empirical best linear unbiased estimators (e-BLUEs). Also obtained from (3.3\(^*\)) is \(\textbf{w}\), a \(p \, t \times 1\) vector of weights, corresponding to the diagonal elements of the inverse of the fixed effect variance–covariance matrix (Smith et al. 2001a). The e-BLUEs and associated weights are carried forward to the second stage of analysis.

3.2 Stage 2

The second stage of the analysis process involves the estimation of response curves to describe the response of proteins to time in the malting process (Fig. 1). In order to allow for nonlinearity in the response of protein abundance, the LMM representation of the cubic smoothing spline can be exploited (Verbyla et al. 1999). Note that the abundance e-BLUEs obtained from (3.3\(^*\)) are assumed to be ordered according to sampling times, within proteins.

Step 2.1: Fit baseline response curve linear mixed model: The general form of the model is

$$\begin{aligned} \hat{\varvec{\tau }} = \textbf{X}_{\textrm{s}_\textrm{o}}\varvec{\beta }_{\textrm{o}} + \textbf{Z}_{\textrm{s}_{\textrm{o}}}\textbf{u}_{\textrm{s}_{\textrm{o}}} + \textbf{Z}_{\textrm{f}}\textbf{u}_{\textrm{f}} + \textbf{X}_{\textrm{s}_{\textrm{p}}}\varvec{\beta }_{\textrm{p}} + \textbf{Z}_{\textrm{s}_{\textrm{p}}}\textbf{u}_{\textrm{s}_{\textrm{p}}} + \textbf{e}_{\textrm{s}}, \end{aligned}$$
(3.5)

where \(\hat{\varvec{\tau }}\) is a \(p\,t \times 1\) vector containing the abundance e-BLUEs for each protein \(\times \) sampling time combination obtained from (3.3\(^*\)). The terms \(\textbf{X}_{\textrm{s}_\textrm{o}}\varvec{\beta }_{\textrm{o}}\), \(\textbf{Z}_{\textrm{s}_{\textrm{o}}}\textbf{u}_{\textrm{s}_{\textrm{o}}}\) and \(\textbf{Z}_{\textrm{f}}\textbf{u}_{\textrm{f}}\) correspond to the fitting of an overall (main effect) spline to model the nonlinear response of abundance to sampling time, where \(\varvec{\beta }_{\textrm{o}}=\left[ \beta _{0} \, \beta _{1} \right] ^{\top }\), a \(2 \times 1\) vector, contains fixed regression coefficients, \(\textbf{u}_{\textrm{s}_{\textrm{o}}}\), a \((t-2) \times 1\) vector, contains random cubic smoothing spline coefficients and \(\textbf{u}_{\textrm{f}}\), a \(t \times 1\) vector, enables the estimation of random non-smooth effects that may arise due to replicated sampling at each sampling time (Verbyla et al. 1999). The design matrices accompanying these vectors are \(\textbf{X}_{\textrm{s}_\textrm{o}} = \textbf{1}_p \otimes \textbf{X}_{\textrm{s}_{\textrm{t}}}\), \(\textbf{Z}_{\textrm{s}_{\textrm{o}}}=\textbf{1}_p \otimes \textbf{Z}_{\textrm{s}_{\textrm{t}}}\) and \(\textbf{Z}_{\textrm{f}}\), respectively, where \(\textbf{X}_{\textrm{s}_{\textrm{t}}} = \left[ \textbf{1}_t \; \textbf{x}\right] \), \(\textbf{Z}_{\textrm{s}_{\textrm{t}}}\) is a \(t \times (t-2)\) spline design matrix as defined in Verbyla et al. (2018), \(\textbf{1}_p\) and \(\textbf{1}_t\) are vectors of ones of length p and t, respectively, and \(\textbf{x}\) is a \(t\times 1\) vector containing the t sampling times. The terms \(\textbf{X}_{\textrm{s}_{\textrm{p}}}\varvec{\beta }_{\textrm{p}}\) and \(\textbf{Z}_{\textrm{s}_{\textrm{p}}}\textbf{u}_{\textrm{s}_{\textrm{p}}}\) allow for the estimation of nonlinear protein specific spline responses. The vectors \({\varvec{\beta }}_{\text {p}}=\text {vec}\left( \left[ \begin{array}{cc} \varvec{\beta }^{\top }_{{\textrm{p}}_0} \\ \varvec{\beta }^{\top }_{{\textrm{p}}_1}\end{array}\right] \right) \), a \(2p\times 1\) vector, and \(\textbf{u}_{\textrm{s}_{\textrm{p}}}\), a \(p(t-2) \times 1\) vector, contain protein specific fixed regression and random spline coefficients, respectively, with associated design matrices \(\textbf{X}_{\textrm{s}_\textrm{p}} = \textbf{I}_p \otimes \textbf{X}_{\textrm{s}_{\textrm{t}}}\) and \(\textbf{Z}_{\textrm{s}_{\textrm{p}}}= \textbf{I}_p \otimes \textbf{Z}_{\textrm{s}_{\textrm{t}}}\), where \(\textbf{I}_p\) is a \(p \times p\) identity matrix. The vector \(\textbf{e}_{\textrm{s}}\), of length \(p \, t \times 1\), contains the residual error effects.

The random effects and residual error effects from (3.5) are assumed to follow a normal distribution with zero mean vector and variance–covariance given by

$$\begin{aligned} \textrm{var}\left( \left[ \begin{array}{cc} \textbf{u}_{\textrm{s}_{\textrm{o}}} \\ \textbf{u}_{\textrm{f}} \\ \textbf{u}_{\textrm{s}_{\textrm{p}}} \\ \textbf{e}_{\textrm{s}} \end{array} \right] \right) = \left[ \begin{array}{cccc} \textbf{G}_{\textrm{o}} &{} \textbf{0} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{G}_{\textrm{f}} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{0} &{} \textbf{G}_{\textrm{p}} &{} \textbf{0} \\ \textbf{0} &{} \textbf{0} &{} \textbf{0} &{} \textbf{R}_{\textrm{s}} \end{array} \right] , \end{aligned}$$

where \(\textbf{G}_{\textrm{o}} = \sigma _{\textrm{o}}^2\textbf{I}_{t-2}, \; \textbf{G}_{\textrm{f}}=\sigma ^2_{\textrm{f}}\textbf{I}_t, \; \textbf{G}_{\textrm{p}} = \sigma _{\textrm{p}}^2\textbf{I}_{p(t-2)},\) and \(\sigma _{\textrm{o}}^2\) and \(\sigma _{\textrm{p}}^2\) are inversely related to the smoothing parameters associated with the overall, and protein specific, nonlinear responses to time in the malting process, respectively. The matrix \(\textbf{R}_{\textrm{s}}\) has diagonal elements given by the weights vector \(\textbf{w}\).

Step 2.2: Form spline covariance clusters: Spline covariance clusters are formed by clustering proteins based on their estimated protein specific cubic smoothing splines coefficients (\(\tilde{\textbf{u}}_{\textrm{s}_{\textrm{p}}}\)), obtained from (3.5) as e-BLUPs. Using these effects, the procedure documented in Step 1.2 is performed to establish a range of plausible spline covariance clusters, where \(\upsilon _{\textrm{s}}=2, \ldots , q_{\textrm{s}}\) are the number of spline clusters formed, \(\eta _{\textrm{s}}\) and \(\phi _{\textrm{s}}\) are the total number of spline cluster groupings and random starting seeds considered, respectively, and \(k_{\textrm{s}}=\phi _{\textrm{s}} \times \eta _{\textrm{s}}\) is the total number of plausible spline covariance clusters \((l_{\textrm{s}}=1, \ldots , k_{\textrm{s}})\).

Step 2.3: Fit spline covariance cluster linear mixed model: To incorporate a plausible spline covariance cluster, (3.5) is extended to include an additional random term, allowing for the estimation of cluster specific nonlinear responses to time in the malting process, where the clusters correspond to a particular seed \(\times \) number of cluster combination \((h_{l_{\textrm{s}}})\). This model, labelled as the spline covariance cluster LMM, is repeatedly fit whereby the cluster random term is updated to consider each plausible spline covariance cluster. The general form of the model, assuming the data are ordered as sampling times, then proteins, then covariance clusters, is

$$\begin{aligned} \hat{\varvec{\tau }} = \textbf{X}_{\textrm{s}_\textrm{o}}\varvec{\beta }_{\textrm{o}} + \textbf{Z}_{\textrm{s}_{\textrm{o}}}\textbf{u}_{\textrm{s}_{\textrm{o}}} + \textbf{Z}_{\textrm{f}}\textbf{u}_{\textrm{f}} + \textbf{X}_{\textrm{s}_{\textrm{p}}}\varvec{\beta }_{\textrm{p}} + \textbf{Z}_{\textrm{s}_{\textrm{p}}}\textbf{u}_{\textrm{s}_{\textrm{p}}} + \textbf{Z}_{\textrm{c}_{\textrm{s}}}\textbf{u}_{\textrm{c}_{\textrm{s}}} + \textbf{e}_{\textrm{s}}, \end{aligned}$$
(3.6)

where \(\textbf{u}_{\textrm{c}_{\textrm{s}}}\) is a \(\upsilon _{\textrm{s}}(t-2) \times 1\) vector of random cubic smoothing spline coefficients for the \(\upsilon _{\textrm{s}}\) spline covariance clusters fitted, with spline design matrix \(\textbf{Z}_{\textrm{c}_{\textrm{s}}}=\oplus _{m=1}^{\upsilon _{\textrm{s}}}\textbf{1}_{p_m} \otimes \textbf{Z}_{\textrm{s}_{\textrm{t}}}\), where \(p_m\) is the number of proteins in spline covariance cluster m. All other terms are as defined for the model in (3.5).

The random effects and residual error effects from (3.6) are assumed to follow a normal distribution with zero mean vector and variance–covariance matrix

$$\begin{aligned} \textrm{var}\left( \left[ \begin{array}{cc} \textbf{u}_{\textrm{s}_{\textrm{o}}} \\ \textbf{u}_{\textrm{f}} \\ \textbf{u}_{\textrm{s}_{\textrm{p}}} \\ \textbf{u}_{\textrm{c}_{\textrm{s}}} \\ \textbf{e}_{\textrm{s}} \end{array} \right] \right) = \left[ \begin{array}{ccccc} \textbf{G}_{\textrm{o}} &{} \textbf{0} &{} \textbf{0} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{G}_{\textrm{f}} &{} \textbf{0} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{0} &{} \textbf{G}_{\textrm{p}} &{} \textbf{0} &{} \textbf{0} \\ \textbf{0} &{} \textbf{0} &{} \textbf{0} &{} \textbf{G}_{\textrm{c}_{\textrm{s}}} &{} \textbf{0} \\ \textbf{0} &{}\textbf{0} &{} \textbf{0} &{} \textbf{0} &{} \textbf{R}_{\textrm{s}} \end{array} \right] , \end{aligned}$$

where the forms of \(\textbf{G}_{\textrm{o}}\), \(\textbf{G}_{\textrm{f}}\), \(\textbf{G}_{\textrm{p}}\) and \(\textbf{R}_{\textrm{s}}\) are as defined for the model in (3.5), \(\textbf{G}_{\textrm{c}_{\textrm{s}}} = \sigma _{\textrm{c}_{\textrm{s}}}^2\textbf{I}_{\upsilon _{\textrm{s}}(t-2)}\) is a \(\upsilon _{\textrm{s}}(t-2) \times \upsilon _{\textrm{s}}(t-2)\) diagonal matrix and \(\sigma _{\textrm{c}_{\textrm{s}}}^2\) is inversely related to the smoothing parameter of the spline covariance cluster specific nonlinear responses to time in the malting process.

Step 2.4: Locate ‘optimal’ number of spline covariance clusters and fit ‘optimal’ spline covariance cluster linear mixed model: The procedure outlined in Step 1.4 is repeated to determine the ‘optimal’ number of spline covariance clusters, where \(\upsilon ^{*}_{\textrm{s}}\) is the number of covariance clusters which minimised the AIC, on average across seeds, and \(\omega ^{*}_{\textrm{s}}\) is the seed which further minimises the AIC within \(\upsilon ^{*}_{\textrm{s}}\). The protein groupings resulting from \(\omega ^{*}_{\textrm{s}}\) with \(\upsilon ^{*}_{\textrm{s}}\) clusters are then reintroduced into (3.6) and the model fit to obtain the ‘optimal’ spline covariance cluster LMM, (3.6*), being the model which results in the estimation of the most parsimonious set of ‘typical’ response profiles.

Following the implementation of (3.6*), e-BLUPs of protein abundance using the ‘typical’ protein response profiles are obtained as \(\textbf{X}^{*}_{\textrm{s}_{\textrm{o}}}\hat{\varvec{\beta }_{\textrm{o}}} + \textbf{Z}^{*}_{\textrm{s}_{\textrm{o}}}\tilde{\textbf{u}}_{\textrm{s}_{\textrm{o}}} + \textbf{X}^{*}_{\textrm{s}_{\textrm{p}}}\hat{\varvec{\beta }_{\textrm{p}}} + \textbf{Z}^{*}_{\textrm{c}_{\textrm{s}}}\tilde{\textbf{u}}_{\textrm{c}_{\textrm{s}}}\), where \(\textbf{X}^{*}_{\textrm{s}_{\textrm{o}}}\), \(\textbf{Z}^{*}_{\textrm{s}_{\textrm{o}}}\), \(\textbf{X}^{*}_{\textrm{s}_{\textrm{p}}}\) and \(\textbf{Z}^{*}_{\textrm{c}_{\textrm{s}}}\) are design matrices formed using the malting times for which protein abundance predictions are sought, with forms described in Verbyla et al. (2021). Additionally, the nonlinear relationships between abundance and time in the malting process at the spline covariance cluster, or ‘typical’ response profile, level can be explored by estimating the e-BLUPs \(\textbf{Z}^{*}_{\textrm{c}_{\textrm{s}}}\tilde{\textbf{u}}_{\textrm{c}_{\textrm{s}}}\).

3.3 Software

All models are fit using the asreml package (Butler et al. 2017) in the R statistical computing environment (R Core Team 2019). The AIC based on the full log-likelihood is derived using the icREML function (Verbyla 2019). The k-means clustering approaches are implemented using the kmeans package (R Core Team 2019). Functions used to implement the covariance clustering approach are available from https://github.com/ClaytonForknall/CovarianceClustering

4 Application of Method

The motivating MS-based proteomics experiment is used to illustrate the application of the covariance clustering method (Fig. 1). Throughout this section, a consistent subset of 25 proteins are presented. These proteins were selected to span the range of differential response types to time in the malting process. The extent of these differential responses is shown in Fig. 2, which presents the raw measured abundance for the selected subset of proteins, quantified in subsamples collected at each sampling time during the malting process (Table 1).

Fig. 2
figure 2

Raw abundance of a subset of 25 proteins quantified using mass spectrometry proteomics techniques from barley grain and malt samples. Samples were taken at different times during the malting process, as part of the motivating mass spectrometry-based proteomics experiment. Proteins are labelled using their unique identifier (HORVU code), followed by their common name

Full size image

Step 1.1: Fit baseline linear mixed model: The fitting of the baseline LMM revealed significant heterogeneity of residual variance, both between proteins and sampling times. Residual variances for proteins \((\sigma ^2_{e_{\text {p}_i}})\) ranged from 0.005 to 1.45, while the sampling time scaling parameters \((\gamma _{e_{\textrm{t}_j}})\) ranged from 0.88 to 1.17 relative to sampling time \(j=2\) which was constrained \((\gamma _{e_{\textrm{t}_2}}=1)\).

The baseline LMM also revealed non-negligible variation arising in both phases of the motivating experiment. Table 2 presents the variance component estimates of the terms included in the baseline LMM to account for the multi-phase experimental design structure (\(\tilde{\textbf{u}}_{\textrm{d}}\)). Terms describing the first phase of the experiment include MaltRep, labelling the replicate batches of malt processed in the malting plant, and MaltTime:MaltRep, indexing each unique grain sample collected during the malt sample collection phase. Terms describing the second phase of the experiment include LabRep, LabRep:LabBlock and MaltTime:MaltRep:Subsample, which describe the structured approach taken for the processing of the barley grain subsamples. All terms are fit separately and in combination with Protein, the latter terms included to capture potential variation between proteins in combination with these structural terms.

Table 2 Variance component estimates corresponding to the terms included in the baseline linear mixed model (Step 1.1) to account for the multi-phase experimental design structure of the motivating mass spectrometry-based proteomics experiment
Full size table

The two largest sources of extraneous variation arose during the MS processing phase and corresponded to variation between individual laboratory subsamples (MaltTime:MaltRep:Subsample), and variation between the processing groups of subsamples within a LabRep (LabRep:LabBlock), respectively (Table 2). Variation between proteins and the structural terms were of a smaller magnitude, with one of the four terms involving Protein estimated at the boundary of the variance parameter space (\(\sim 0\)), being Protein:MaltTime:MaltRep.

Step 1.2: Form residual covariance clusters: Proteins were grouped into \(\eta _{\text {r}}=28\) different cluster groupings, with the number of clusters considered ranging from 2 to 533 \((2 \le \upsilon _{\text {r}} \le 533)\) according to a geometric growth model, with a growth rate of 0.2. The grouping of proteins into clusters was repeated \(\phi _{\text {r}}=10\) times, each time with a different starting seed. This resulted in \(k_{\text {r}}=280\) plausible residual covariance cluster groupings, based on all seed \(\times \) number of cluster combinations.

Steps 1.3 & 1.4: Fit residual covariance cluster linear mixed model; Locate ‘optimal’ number of residual covariance clusters and fit ‘optimal’ residual covariance cluster linear mixed model: Fig. 3a presents the AIC for all \(k_{\text {r}}=280\) plausible residual covariance cluster models fit, along with the AIC from the baseline LMM. This shows that the AIC decreases sharply with the inclusion of more residual covariance clusters in the model, and is minimised with the inclusion of \(\upsilon ^*_{\text {r}}=147\) residual covariance clusters (vertical dashed line, Fig. 3a). Within \(\upsilon ^*_{\text {r}}=147\), the seed which further minimised the AIC was \(\omega ^*_{\text {r}}=16630\). Increasing the number of residual covariance clusters beyond 147 results in poorer model fit, demonstrated by the AIC increasing. This trend is apparent across all ten seeds, although there is some variability in individual model fits. When compared with the baseline LMM (red star, Fig. 3a), it is seen that the inclusion of any number of residual covariance clusters results in a substantial reduction in AIC.

Fig. 3
figure 3

Sample paths of AIC resulting from the fitting of the a residual and b spline covariance cluster linear mixed models, respectively, for each seed \(\times \) number of cluster combination (Steps 1.3 and 2.3, respectively). Coloured points and lines correspond to the result from each of the ten seeds considered, for each covariance cluster model. The AIC corresponds to the Akaike Information Criterion, derived from the full log-likelihood (Verbyla 2019). The dashed lines correspond to the number of covariance clusters that minimised the AIC, on average across the seeds considered, for each of the covariance cluster models (147 and 48, respectively). The red stars correspond to the AIC obtained from the a baseline linear mixed model and b baseline response curve linear mixed model, respectively (Color figure online)

Full size image

Using \(\upsilon ^*_{\text {r}}=147\) and \(\omega ^*_{\text {r}}=16630\), the ‘optimal’ residual covariance cluster LMM was fitted. This model revealed heterogeneity of variance between residual covariance clusters, with cluster variances \((\sigma ^2_{\text {c}_{{\text {r}}_m}})\) ranging from 0.005 to 0.21, while the accompanying sampling time scaling parameters \((\gamma _{\text {c}_{{\text {r}}_{{\text {t}_j}}}})\) ranged from 0.82 to 1.39 (relative to sampling time \(j=2\); \(\gamma _{\text {c}_{{\text {r}}_{{\text {t}_2}}}}=1\)). The inclusion of residual covariance clusters reduced the magnitude and range of residual protein variances, compared to the baseline LMM, with these variances ranging between \(4.08 \times 10^{-8}\) (estimated at the boundary of the parameter space) and 1.31, with the accompanying sampling time scaling parameters ranging from 0.88 to 1.07 (relative to sampling time \(j=2; \gamma _{e_{\text {t}_2}}=1\)).

Step 2.1: Fit baseline response curve linear mixed model: The baseline response curve LMM confirmed that there is non-negligible variation in the nonlinear responses of proteins to time in the malting process (Table 3), with the estimated variance component corresponding to the Protein:spl(malttime) term \((\tilde{\sigma }^2_{\text {p}})\) being nonzero.

Table 3 Variance component estimates corresponding to the terms included in the baseline response curve linear mixed model (Step 2.1). The use of spl() represents a term involving a cubic smoothing spline, as per the notation introduced in Verbyla et al. (1999)
Full size table

Step 2.2: Form spline covariance clusters: Proteins were grouped into \(\eta _{\text {s}}=28\) different cluster groupings, with the number of clusters considered spanning \(2 \le \upsilon _{\text {s}} \le 533\) according to a geometric growth model (growth rate of 0.2). The same ten starting seeds (\(\phi _{\text {s}}=10\)) used in Step 1.2 were used to explore the impact of starting conditions of the clustering procedure. This resulted in \(k_{\text {s}}=280\) plausible spline covariance cluster groupings, based on all seed \(\times \) number of cluster combinations.

Steps 2.3 & 2.4: Fit spline covariance cluster linear mixed model; Locate ‘optimal’ number of spline covariance clusters and fit ‘optimal’ spline covariance cluster linear mixed model: The AIC decreases rapidly with the inclusion of spline covariance clusters and is minimised when \(\upsilon ^*_{\text {s}}=48\) clusters are included in the model (vertical dashed line, Fig. 3b). Within \(\upsilon ^*_{\text {s}}=48\), the seed which resulted in the minimum AIC was \(\omega ^*_{\text {s}}=9157\). As the number of clusters increases beyond \(\upsilon ^*_{\text {s}}=48\), the AIC increases, indicating a reduction in quality of model fit, and approaches that of the baseline model (red star, Fig. 3b) as the number of clusters increase towards the number of proteins (\(p=617\)). This same trend is apparent across all ten seeds.

Using \(\upsilon ^*_{\text {s}}=48\) and \(\omega ^*_{\text {s}}=9157\), the ‘optimal’ spline covariance cluster LMM was fitted. Table 4 presents the variance component estimates from the model and shows that, with the inclusion of spline covariance clusters, the Protein:spl(malttime) term is estimated at the boundary of the parameter space, while the Cluster:spl(malttime) term is the dominate source of variation.

Table 4 Variance component estimates corresponding to the terms included in the ‘optimal’ spline covariance cluster linear mixed model (Step 2.4). The use of spl() represents a term involving a cubic smoothing spline, as per the notation introduced in Verbyla et al. (1999)
Full size table

The shape and magnitude of the ‘typical’ nonlinear response profiles (\(\textbf{Z}^{*}_{\textrm{c}_{\textrm{s}}}\tilde{\textbf{u}}_{\textrm{c}_{\textrm{s}}}\)) vary substantially, with some showing only small deviations from zero (spline covariance cluster 16), while others show larger departures (e.g. spline covariance clusters 45 and 11) (Fig. 4).

Fig. 4
figure 4

Estimated ‘typical’ response profiles, estimated using the spline covariance cluster (SCC) specific effects from the ‘optimal’ spline covariance cluster linear mixed model (Step 2.4). Labels in the top right-hand corner of each facet present the number of proteins belonging to each spline covariance cluster (\(p_m\)). Spline covariance clusters are ordered from largest number of proteins to smallest. Note the magnitude of the abundance axis varies from row to row in the figure

Full size image

The impact of the ‘typical’ response profiles is clear when investigating the estimated response curves (\(\textbf{X}^{*}_{\textrm{s}_{\textrm{o}}}\hat{\varvec{\beta }_{\textrm{o}}} + \textbf{Z}^{*}_{\textrm{s}_{\textrm{o}}}\tilde{\textbf{u}}_{\textrm{s}_{\textrm{o}}} + \textbf{X}^{*}_{\textrm{s}_{\textrm{p}}}\hat{\varvec{\beta }_{\textrm{p}}} + \textbf{Z}^{*}_{\textrm{c}_{\textrm{s}}}\tilde{\textbf{u}}_{\textrm{c}_{\textrm{s}}}\)) from the ‘optimal’ spline covariance cluster LMM (Fig. 5). For example, although the two proteins composing spline covariance cluster 45 vary in mean abundance, the shape of the respective response curves of the proteins is the same and is determined by the response profile they share by being in the same spline covariance cluster. Another example of this arises for the three proteins presented from spline covariance cluster 16, where, although the proteins demonstrate different responses to time in the malting process (constant, increasing and decreasing responses), all the proteins share a common nonlinear response profile.

Fig. 5
figure 5

Estimated response curves from the ‘optimal’ spline covariance cluster linear mixed model (Step 2.4), describing the relationship between abundance and time in the malting process, for a subset of 25 proteins. Proteins are labelled using their unique identifier (HORVU code), followed by their common name. Estimates obtained from the response curves are empirical best linear unbiased predictors. Solid black dots correspond to the empirical best linear unbiased estimators of protein abundance obtained from the ‘optimal’ residual covariance cluster linear mixed model (Step 1.4). Cluster labels in the top right-hand corner of each facet present the spline covariance cluster (SCC) to which each protein belongs

Full size image

5 Discussion and Conclusions

We have developed and deployed a method, labelled covariance clustering, that enables the analysis of designed experiments characterised by greater numbers of variables than experimental units, in an LMM framework. The method features a twist on the traditional variance component model (Patterson et al. 1977), building parsimonious covariance between variables by first clustering variables based on estimated effects, and then introducing these covariance clusters into the LMM through an additional random term. In this way, complex covariance between variables can be estimated parsimoniously. Additionally, the act of covariance clustering provides a model-based dimension reduction technique. This occurs when, through the inclusion of a suitable number of covariance clusters in the LMM, the variation originally arising between variables is fully accounted for by the variation arising between covariance clusters. In this way, variation between a large number of variables can potentially be reduced to a smaller set of covariance cluster effects.

Both outcomes of the covariance clustering method, being the estimation of parsimonious covariance between variables and model-based dimension reduction, have been demonstrated through application of the method to a multi-phase MS-based proteomics experiment. Typical of proteomics experiments, it was characterised by the measurement of a greater number of variables than experimental units; 617 proteins (variables) measured on a total of 48 subsamples (experimental units). Covariance clustering was implemented both at the residual level, to capture residual covariance between proteins, and at the treatment level, to cluster proteins displaying similar nonlinear responses to time in the malting process, in doing so demonstrating that the response of 617 proteins can be effectively reduced to 48 differential nonlinear forms.

We also present what we believe to be the first report of a multi-phase design for the conduct of an agriculturally motivated multi-phase MS-based proteomics experiment. Through the use of a multi-phase design, non-negligible variation was found to arise in both the malt sample collection phase and MS processing phase of the motivating experiment (Table 2). The two most dominant sources of variation were found to arise in the MS processing phase, and corresponded to variation between the processing of individual subsamples and batches of subsamples in the laboratory, respectively (Table 2). The potential for extraneous variation associated with processing order or batches in laboratory studies has been reported more generally (Cullis et al. 2003; Smith et al. 2006; Oakey et al. 2013) and also in the particular case of MS-based proteomics studies (Hu et al. 2005). In the case of the motivating experiment, the use of a multi-phase design prevented the introduction of potential bias in the experimental results, that would arise if samples had been processed in a systematic order. The findings of this experiment confirm the importance of sound experimental design in MS-based proteomics studies and demonstrate that multi-phase design is a robust design solution that is well suited for implementation in such studies into the future.

In the methods presented, a variance-component-model-like solution is used to induce covariance between variables. The traditional variance component model (Patterson et al. 1977) builds a simplistic covariance structure, which has been found to be inferior when compared to more complex covariance models in certain applications (Kelly et al. 2007). However, the reliable estimation of the variance–covariance parameters involved in these more complex models is questionable when the number of variables to be modelled exceeds the number of observations informing the parameter estimates. In these situations, the resulting covariance structures are often of reduced rank and thus computationally challenging to estimate. Although the factor analytic variance structure formulated by Thompson et al. (2003), based on that originally proposed by Smith et al. (2001b), can accommodate the estimation of reduced rank variance structures between variables for moderate to large numbers of observations (\(\ge 50\)) (Kelly et al. 2007), evidence suggests that the performance of such structures, especially in terms of estimating covariance parameters, is reduced when the number of observations informing a parameter estimate is small (10–15) (Macdonald 2018; Macdonald et al. 2019). In an attempt to avoid the estimation issues associated with these more complex covariance models and have greater flexibility and heterogeneity in the resulting covariance structure than that possible using a traditional variance component model, a ‘middle-ground’ in complexity and parsimony was reached by implementing the covariance clustering approach.

The definition of covariance clusters in the methods was achieved by grouping estimated effects using a k-means clustering algorithm (Hartigan and Wong 1979). The k-means algorithm was favoured as it resulted in the formation of clusters of more equal size, for smaller numbers of clusters (data not shown). This contrasts with hierarchical clustering methods, which, for small numbers of clusters, often result in one large cluster and multiple clusters consisting of one or two variables (Nazarathy and Klok 2021). When implemented as a covariance structure, the k-means approach results in structures with greater heterogeneity of variance and covariance between a greater number of variables, whereas the hierarchical approach induces homogeneous variance and covariance between a large number of variables, and heterogeneity between a few (data not shown). In the context of the motivating example, it was found that the covariance structure resulting from the k-means clustering approach was better suited for modelling the complex relationships that exist between proteins in the proteome (Agrawal et al. 2013; Robotti et al. 2015) (data not shown).

In addition to providing a means of estimating a parsimonious covariance structure, the covariance clustering method can serve as a dimension reduction technique. This is achieved through a partitioning of variance between the covariance cluster and variable terms included in the LMM. Due to the nested nature of the terms and, with the definition and inclusion of sufficient covariance clusters in the model, it would not be unexpected for a situation to occur where the variance arising between variables (estimated to be nonzero in the baseline model) is fully accounted for by variation between covariance clusters (in the covariance cluster LMM). When applied to the motivating experiment, this was evidenced through the inclusion of an optimal number of spline covariance clusters in the corresponding LMM, whereby the variation that was previously attributable to the Protein:spl(malttime) term in the baseline response curve LMM (Table 3), was subsequently estimated at the boundary of the parameter space once the covariance clusters were introduced (Table 4). This indicated that the smooth, nonlinear variation between the 617 proteins was effectively accounted for, and could be reduced to, 48 nonlinear response profiles, estimated through the spline covariance cluster effects (Fig. 4). The clustering and identification of ‘typical’ response profiles could have been achieved using a range of techniques, such as a post hoc clustering of spline coefficients, general response curve clustering methods (Gladish et al. 2021), or methods established under the Ramsay and Silverman (1997) paradigm of functional data analysis (James and Sugar 2003; Coffey and Hinde 2011; Coffey et al. 2014). However, the choice of the ‘optimal’ number of clusters to be formed using these approaches can rely on subjectively comparing multiple selection criteria (Gladish et al. 2021), or subjectively selecting parameters, in an attempt to avoid computational instabilities (Coffey et al. 2014). Using the LMM representation of the cubic smoothing spline for computationally stable variance parameter estimates, and through the partitioning of variance intrinsic in the covariance clustering method, a model-based and objective choice of the number of clusters, and thus dimension reduction, can be achieved.

The methods outlined in this paper were implemented using a two-stage LMM, in under approximately ten hours. Software limitations involving the commercial R package asreml (Butler et al. 2017) dictated that a single-stage analysis was infeasible due to prohibitive computation times, with the method estimated to take more than 16 days based on initial testing. Although the asreml package is unique in its support for fitting many complex variance structures in an LMM framework, the computation times can be prohibitive and impractical when implementing multiple of these structures to even moderately sized datasets, such as that arising from the motivating experiment. Computational limitations can be reduced by using a two-stage approach (Piepho et al. 2012), and, as such, this was favoured, despite the potential loss of information incurred by using this method as opposed to a single-stage analysis (Gogel et al. 2018). A weighted two-stage approach was used, as this has been shown to be superior to unweighted two-stage approaches, both in terms of loss of information and accuracy of effects (Welham et al. 2010; Piepho et al. 2012).

Application of the covariance clustering method to the MS-based proteomics experiment revealed the importance of approximating, through covariance modelling, the complex relationships that can exist between proteins in the proteome (Robotti et al. 2015). Significant improvement in AIC, and thus model fit, was achieved by including any number of covariance clusters (\(\upsilon _{\text {r}} \ge 2\)) in the residual covariance cluster LMM, when compared to the baseline LMM (Fig. 3a). Modelling complex covariance between proteins is not currently performed as part of routine LMM analysis methods for proteomics data (Oberg et al. 2008; Choi et al. 2014), nor was it modelled in a previous analysis of the data arising from the motivating experiment (Osama et al. 2021). Theoretically, ignoring such relationships will result in less accurate and potentially biased protein abundance predictions than if appropriate covariance between proteins was modelled (De Faveri et al. 2017).

Furthermore, through application of the covariance clustering method, new insights into how the barley grain and malt proteome changes over time in the malting process were discovered. The extent of variation between the 48 ‘typical’ response profiles, each with complexly varying forms (Fig. 4), suggests there is novel and exploitable variability within the proteome that could be further explored to better understand and potentially optimise the changes that occur during the malting process. Additionally, preliminary investigations suggest some alignment between the outcomes of the clustering procedure and the biological function of proteins. An example of this is the proteins HORVU1Hr1G059870.4 and HORVU1Hr1G059900.1, which both cluster together (the only two proteins belonging to spline covariance cluster 45; Figs. 4 and 5), demonstrate similar responses to time in the malting process and are identified as being ‘late embryogenesis proteins’ whose abundance has been previously reported to decrease in the early stages of the malting process (Osama et al. 2021), consistent with their response in this study (Fig. 5). Further investigation of the proteins composing each spline covariance cluster, and the potential alignment of their biological functions in the barley grain and malt proteome, is the topic of ongoing research.

There are multiple possible extensions of the methods proposed in this paper. For instance, the complexity of the covariance structures resulting from covariance clustering could be increased. Currently, as the number of clusters increases, the resulting variance structure is characterised by greater pockets of heterogeneous variance and covariance; however, a greater number of variables are assumed to be related through simple covariance. Alternate implementations of the clustering approach which result in covariance structures with greater heterogeneity, while limiting the extent of simple covariance between variables, are an area open for future investigation. Additionally, further investigation is warranted into the persistence of cluster membership across different initial seeds of the k-means algorithm. Currently, the ‘optimal’ membership of variables to clusters is informed by only one seed \(\times \) number of cluster combination. As such, there is scope to explore the consistency of variables occurring together in the same cluster, across all seeds considered, for a given number of clusters. Such an investigation could influence the reporting of the covariance cluster effects (Fig. 4), or lead to alternate specifications of the ‘optimal’ covariance cluster models to respect these persistent variable groupings.

The covariance clustering method we have proposed provides an LMM-based solution for the analysis of designed experiments that yield datasets characterised by a greater number of variables than experimental units, and for which estimation of complex covariance structures between variables is desired. The act of covariance clustering models heterogeneity of variance–covariance between any random effects in an LMM framework, be it to capture relationships between treatments or experimental units. The method is applicable in situations where alternate complex covariance structures may be computationally difficult to estimate due to being of reduced rank. It is envisaged that covariance clustering could provide an alternative to the use of factor analytic variance structures, when the number of observations informing a variance–covariance parameter are small.