1 Introduction

Many outcome measures are subjective. Two examples in the biomedical field include the interpretation of radiologic scans by multiple experts (Das et al. 2021) and determining which FDA-approved assay is best (Batenchuk et al. 2018). In machine learning, this can occur when assessing predictive models or as a measure of reliability (Thompson et al. 2016; Malafeev et al. 2018). Statistical methods for agreement, such as the general \(\kappa \) structure, can be helpful when assessing subjective outcomes. High levels of agreement should be attained in order to use these methods regularly (Malafeev et al. 2018).

A widely used statistical method for evaluating agreement under the \(\kappa \) structure is Cohen’s \(\kappa \) (Cohen 1960). In the past 23 years, over 9500 peer-reviewed manuscripts citing Cohen’s \(\kappa \) have been published. In 2021 and 2022 alone, at least 2500 of these manuscripts were published, suggesting an increase in popularity of this method. These papers ranged from theoretical discussions to applications in a variety of fields (Blackman and Koval 2000; Shan and Wang 2017; Hoffman et al. 2018; Giglio et al. 2020).

Cohen’s \(\kappa \) agreement studies have been used in the development of biomarkers for Alzheimer’s disease (AD), a progressive neurodegenerative disorder. A major pathophysiologic component to AD is the accumulation of amyloid-\(\beta \) protein in the brain prior to the clinical onset of dementia. Until the recent development of florbetapir positron emission tomography (PET) brain scans, amyloid-\(\beta \) deposition in the brain could only be visualized upon autopsy. The Alzheimer’s Prevention Program (APP) from the Alzheimer’s Disease Research Center (ADRC) at the University of Kansas Medical Center (KUMC) examined the use of florbetapir PET brain scans in identifying cognitively normal individuals with elevated amyloid-\(\beta \) plaques (Harn et al. 2017). They found that visual interpretations supplemented by machine-derived quantifications of amyloid-\(\beta \) plaque burden can identify individuals at risk for AD. Though like many measures such as BMI and blood pressure, machine-derived quantifications of amyloid-\(\beta \) describe only part of the picture of whether an individual has an elevated amyloid-\(\beta \) plaque burden (Schmidt et al. (2015); Schwarz et al. (2017))

Although the results from Harn et al. (2017) are poised to advance our understanding of AD, there are well-known problems with Cohen’s \(\kappa \) cited in the literature (Cicchetti and Feinstein 1990; Feinstein and Cicchetti 1990; Byrt et al. 1993; Guggenmoos-Holzmann, 1996; McHugh 2012). Limitations include dependency on sample disease prevalence, variability of the estimate with respect to the margin totals, and somewhat arbitrary interpretation.

Literature review shows improvement in the estimators of \(\kappa \). Adjustment for covariates can be accomplished through stratification (Barlow et al. 1991), by utilizing complex distributions, such as the bivariate Bernoulli distribution (Shoukri and Mian 1996) and multinomial distribution (Barlow 1996), and using flexible modeling tools, such as generalized estimating equations (Klar et al. 2000; Williamson et al. 2000; Barnhart and Williamson 2001) or generalized linear mixed models (GLMM) (Nelson and Edwards 2008, 2010). Other methods have been developed to account for measures leading to correlated estimates (Kang et al. 2013; Sen et al. 2021). Generally, these more flexible statistical tools model rater variability, include needed factors, and use more practical study designs (Ma et al. 2008).

These methods are not yet widely applied. This could be due to complicated analytical forms and unfamiliar likelihoods. Although advances in computational power have increased the accessibility of these methods, they are still somewhat involved to implement. Importantly, these approaches have restrictive assumptions (e.g., both raters have the same marginal probability of a positive evaluation). None reduce to Cohen’s \(\kappa \), which while not a disadvantage has precluded the expansion of Cohen’s \(\kappa \) to more complex (i.e., realistic, contemporary) settings. The work presented here is advantageous as it directly generalizes Cohen’s \(\kappa \).

Landis and Koch proposed a \(\kappa \)-like measure that (1) defined the expected probability of agreement under baseline constraints; (2) accounted for covariates by calculating \(\kappa \) within each sub-population; and (3) allowed for each sub-population’s \(\kappa \) to be weighted differently (Koch et al. 1977; Landis and Koch 1977b, a). We will also adopt similar language and show that expected agreement is defined under an assumed logistic regression model.

The primary purpose of this paper is to propose an accessible estimator for \(\kappa \) while simultaneously adjusting for covariates. The proposed method utilizes logistic regression to obtain estimates of predicted probabilities conditional on explanatory factors, which are then used to calculate expected agreement. Our method is easily implemented using standard statistical software, can evaluate categorical and continuous explanatory factors, offers an alternative—and perhaps more clinically meaningful—interpretation and has many applications. Our method is algebraically equivalent to Cohen’s \(\kappa \) when covariates are ignored. The main contributions of this work are that unbiased estimates are obtained when the expected probability of agreement accounts for necessary factors, a single estimate of agreement is attained regardless of the number of covariates, and this approach is accessible to our entire scientific community due to utilizing logistic regression.

This paper is organized as follows. In Sect. 2 we describe the \(\kappa \) agreement structure and provide examples of common parameterizations. We also define more general notation. In Sect. 3 we propose a parameterization for \(\kappa \) that accounts for covariates and simplifies to Cohen’s \(\kappa \). We mathematically show our approach is a weighted average of each sub-population’s \(\kappa \) (similar to Landis and Koch’s work). In Sect. 4 we evaluate the impact of model misspecification and mathematically show Cohen’s \(\kappa \) is inflated when necessary factors are ignored. In Sect. 5 we provide simulation results and validate the derived mathematical formulas. In Sect. 6 we apply our proposed method to the APP study. Lastly, in Sect. 7 we provide a brief discussion. Supporting Materials, available at the Journal of Agricultural, Biological and Environmental Statistics website, contain additional mathematical derivations, figures, and details on the simulation framework.

2 \(\kappa \): Agreement Structure

A commonly used structure for assessing agreement is the \(\kappa \) coefficient:

$$\begin{aligned} \kappa =\frac{\pi _{o}-\pi _\textrm{e}}{1-\pi _\textrm{e}} \end{aligned}$$
(1)

where \(\pi _\textrm{o}\) is the observed joint probability two raters agree and \(\pi _\textrm{e}\) is the probability of expected agreement under the assumption of rater independence (\(\pi _\textrm{o}\) is the “observed” agreement and \(\pi _\textrm{e}\) is the “chance-expected” agreement as termed by others (Fleiss et al. 2003)). Several parameterizations and corresponding estimators have been proposed (Scott 1955; Cohen 1960; Fleiss 1975). The difference in each of these special cases of \(\kappa \) lies in the definition of \(\pi _\textrm{e}\). For instance, Scott’s pi defines \(\pi _\textrm{e}\) as the squared average of the marginal probabilities for each outcome (positive or negative), while Cohen’s \(\kappa \) defines \(\pi _{e}\) as the product of the marginal probabilities for each outcome.

When the response is binary, a popular parameterization is Cohen’s \(\kappa \) (Cohen 1960) which is typically defined using a two-way contingency table (Table 1). Here \(\pi _{o}\) or the joint probability two raters agree unconstrained by any hypothesized model is \(\pi _\textrm{o}=\pi _{11}+\pi _{22}\) and \(\pi _\textrm{e}\) or the degree of agreement under the model structure of marginal rater independence is \(\pi _\textrm{e}=\pi _{1+}\pi _{+1}+\pi _{2+}\pi _{+2}\). Therefore, Cohen’s \(\kappa \) is: \(\kappa _{C}=\frac{\pi _{11}+\pi _{22}-\left( \pi _{1+}\pi _{+1}+\pi _{2+}\pi _{+2} \right) }{1-\left( \pi _{1+}\pi _{+1}+\pi _{2+}\pi _{+2} \right) }\).

Table 1 Two-way contingency table of joint and marginal proportions of rater classifications in a given population.
Full size table

Barlow’s stratified \(\kappa \) was developed to accommodate covariates (Barlow et al. 1991). Their approach focuses on calculating \(\kappa _{C}\) within each grouping of covariates (i.e., each stratum) and then estimating \(\kappa \) across all strata as a weighted average of each stratum-specific \(\kappa _{C}\). Barlow, Lai and Azen showed the optimal weights are the relative sample size of each stratum. Suppose there are R stratum each with relative sample size of \(w_{r}\), then Barlow’s’ \(\kappa \) is: \(\kappa _{Brlw}=\sum \nolimits _{r=1}^R {w_{r}\kappa _{C,r}} \) where \(\kappa _{C,r}\) is Cohen’s kappa within stratum r. We include \(\kappa _{Brlw}\) as a comparison of our approach but note that this comparison is not the focus of this work.

\(\kappa \) (Eq. 1) can be re-expressed as:

$$\begin{aligned} {\begin{array}{l} \kappa =\pi _\textrm{o}-\left( 1-\pi _\textrm{o} \right) \frac{\pi _\textrm{e}}{1-\pi _\textrm{e}} \end{array}} \end{aligned}$$
(2)

This reveals that \(\kappa \) is the observed agreement (\(\pi _\textrm{o})\) minus the observed disagreement (\(1-\pi _{o})\) multiplied by the odds of the expected agreement \(\left( \frac{\pi _\textrm{e}}{1-\pi _\textrm{e}} \right) \). Through this form, we see that \(\pi _\textrm{o}\) is penalized by a factor of the odds of expected agreement. Expressing \(\kappa \) in this way is advantageous when evaluating the effect of covariates.

3 Estimator of \(\kappa \) Adjusted For Covariates

Using general notation, we demonstrate that \(\pi _{e}\) is a function of a logistic regression model and \(\kappa _{C}\) is a special case of our proposed estimator. Consider the outcome variable

$$\begin{aligned} Y_{ij}=\left\{ {\begin{array}{*{20}c} 1,\text { rater}\,j\, \text {evaluates subject}\, i\, \text {as positive}\\ 0,\text { rater}\,j\,\text { evaluates}\, \text {subject}\,i\,\text { as negative}\\ \end{array}} \quad i=1,...,N; j=1,...,J \right. \end{aligned}$$

Then \(Y_{ij}\sim \textrm{Bern}(\theta _{ij})\) where \(\theta _{ij}=E\left[ Y_{ij} \right] =P(Y_{ij}=1)\). In words \(\theta _{ij}\) is the probability rater j evaluates subject i as positive. An estimate of rater j’s marginal probability of a positive response in a sample of size n is: \(\frac{1}{n}\sum \nolimits _{i=1}^n y_{ij} \). This form is equivalent to usual notations since \(\frac{1}{n}\sum \nolimits _{i=1}^n y_{ij} \) is the proportion of subjects rater j evaluated as positive (Agresti 2013). While the notation describes the population of J raters and N subjects, this manuscript considers the conventional study design where only two raters are included (i.e., \(j=1,2)\).

The joint probability of agreement between two randomly selected raters (\(j=1,2)\) is defined as the expectation or average:

$$\begin{aligned} \pi _\textrm{o}=\frac{1}{N}\sum \limits _{i=1}^N \left[ P\left( Y_{i1}=Y_{i2} \right) \right] =\frac{1}{N}\sum \limits _{i=1}^N \left[ P\left( Y_{i1}=1\cap Y_{i2}=1 \right) +P\left( Y_{i1}=0\cap Y_{i2}=0 \right) \right] \end{aligned}$$

where N is the number of subjects in a population. Under the assumption of rater independence, we define the probability of expected agreement between the two randomly selected raters as:

$$\begin{aligned} \pi _\textrm{e}=\frac{1}{N}\sum \nolimits _{i=1}^N \left[ P\left( Y_{i1}=1 \right) P\left( Y_{i2}=1 \right) +P\left( Y_{i1}=0 \right) P\left( Y_{i2}=0 \right) \right] \end{aligned}$$

Since the outcome \(Y_{ij}\) is a Bernoulli random variable, logistic regression can be used to model the probability of a positive (or negative) evaluation for each subject i interpreted by rater j. We chose logistic regression as it is flexible, can accommodate categorical and continuous measures, is easily implemented in standard statistical software, and is commonly used in a vast array of research fields.

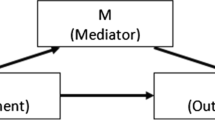
We define the general logistic regression model M as: \(M\equiv logit\left( \theta _{ij} \right) ={\textbf{x}}_{ij}^{T}{\varvec{\beta }}\) where \(i=1,...,N \quad j=1,2\) randomly selected raters \({\varvec{\beta }}\) is a vector of parameters for both subject and rater characteristics and \(\theta _{ij}=E(Y_{ij}\vert {\textbf{x}}_{ij})\). Under model M and the assumption of conditional rater independence, the expected probability of agreement is:

$$\begin{aligned} \pi _\textrm{e}\vert M=\frac{1}{N}\sum \nolimits _{i=1}^N \left[ \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right] \end{aligned}$$

Under this notation, our parameterization of \(\kappa \) under model M is written as:

$$\begin{aligned} \kappa _{M}=\frac{\pi _\textrm{o}-\pi _\textrm{e}\vert M}{1-\pi _\textrm{e}\vert M}=\frac{\frac{1}{N}\sum \nolimits _{i=1}^N \left[ P\left( Y_{i1}=Y_{i2} \right) \right] -\frac{1}{N}\sum \nolimits _{i=1}^N \left[ \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right] }{1-\frac{1}{N}\sum \nolimits _{i=1}^N \left[ \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right] } \end{aligned}$$

The proposed method simply generalizes the definition of the expected probability of agreement by allowing the probability of a positive response to depend on covariates. Defining estimators for \(\kappa \) by altering the definition of \(\pi _{e}\) has been previously discussed (e.g., Scott’s pi).

We use the proportion of subjects in a sample (of size n) of which two raters agreed commonly termed observed agreement (Fleiss et al. 2003) as an estimate for \(\pi _{o}\); that is, \(\hat{\pi }_\textrm{o}=\frac{1}{n}\sum \nolimits _{i=1}^n \left[ y_{i1}y_{i2}+{(1-y}_{i1}{)(1-y}_{i2}) \right] \). This estimate can be shown to be the maximum likelihood estimate (MLE) for \(\pi _\textrm{o}\) (Agresti 2013) and is identical to the usual estimate defined using Table 1. We use an assumed (hypothesized) logistic regression model M to estimate the probability rater j evaluates subject i as positive (\(\theta _{ij})\). These estimated predicted probabilities \(\left( \hat{\theta }_{ij}=\frac{e^{{\textbf{x}}_{ij}^{T}{\varvec{\hat{\beta }}}}}{1+e^{{\textbf{x}}_{ij}^{T}{\varvec{{\hat{\beta }}}}}} \right) \) are used to calculate the expected probability of agreement under the assumption of rater independence: \({\hat{\pi }}_{e}=\frac{1}{n}\sum \nolimits _{i=1}^n \left[ {\hat{\theta }}_{i1}{\hat{\theta }}_{i2}+\left( 1-{\hat{\theta }}_{i1} \right) \left( 1-{\hat{\theta }}_{i2} \right) \right] \).

We utilize empirical bootstrap with subject-level resampling to estimate the variance of \(\kappa _{M}\) (James et al. 2013). Other variance calculations for Cohen’s \(\kappa \) statistic are approximations just like our bootstrap approach (Cohen 1960; Fleiss et al. 1969). According to Cohen’s seminal work (Cohen 1960), the sampling distribution of \(\kappa _{C}\) is approximately normally distributed when the number of subjects is large. In Sect. 6 we provide histograms kernel density curves and the normal distribution pdf overlaid and found that the assumption of normality was consistent upon visual inspection. Thus, confidence intervals were also computed assuming normality.

3.1 \(\varvec{\kappa }_{{{C}}}\) is a Special Case of \(\varvec{\kappa }_{{{M}}}\)

It is worthy to note that \(\pi _\textrm{e}\) for \(\kappa _{C}\) is a special case of \(\kappa _{M}\). Consider the cell means logistic regression model with raters as the fixed effect: \(M_{0}\mathrm {\equiv }logit\left( \theta _{ij} \right) =\beta _{j}\) where \(i=1,...,n,j=1,2\) and \(\theta _{ij}=P\left( Y_{ij}=1 \right) =\frac{\exp \left( \beta _{j} \right) }{1+\exp \left( \beta _{j} \right) }\). Model \(M_{0}\) assumes each subject i has an equal probability of being classified as positive by rater j with probability \(\theta _{ij}=\frac{\exp \left( \beta _{j} \right) }{1+\exp \left( \beta _{j} \right) }\). Under model \(M_{0}\), we can therefore denote \(\theta _{ij}\equiv \theta _{+j}\). The MLE for \(\beta _{j}\) is: \({\hat{\beta }}_{j}=logit\left( \frac{1}{n}\sum \nolimits _{i=1}^n y_{ij} \right) \). Hence, \(\hat{\theta }_{+j}\vert M_{0}=\frac{1}{n}\sum \nolimits _{i=1}^n y_{ij} \) which is the proportion of subjects that rater j evaluated as positive. This is equivalent to the usual estimators from Table 1 (Cohen 1960).

Therefore, \(\kappa _{C}\) is equivalently defined using logistic regression model \(M_{0}\):

$$\begin{aligned} \kappa _{C}=\frac{\pi _{o}-\pi _\textrm{e}\vert M_{0}}{1-\pi _\textrm{e}\vert M_{0}}=\frac{\frac{1}{N}\sum \nolimits _{i=1}^N \left[ P\left( Y_{i1}=Y_{i2} \right) \right] -\left[ \theta _{+1}\theta _{+2}+\left( 1-\theta _{+1} \right) \left( 1-\theta _{+2} \right) \right] }{1-\left[ \theta _{+1}\theta _{+2}+\left( 1-\theta _{+1} \right) \left( 1-\theta _{+2} \right) \right] } \end{aligned}$$

where \(\theta _{+j}=\frac{\exp \left( \beta _{j} \right) }{1+\exp \left( \beta _{j} \right) },j=1,2\). As before \(\hat{\pi }_{o}\) is observed directly from the data as the unconstrained (saturated) proportion where raters agreed, whereas \({\hat{\pi }}_\textrm{e}\) is estimated under model \(M_{0}\) and the assumption of marginal rater independence.

3.2 \(\kappa \) Under Model M as a Weighted Average

Consider the theoretical probability of agreement between raters 1 and 2 on subject i in the population which we denote as \(\pi _{o,i}=P\left( Y_{i1}=1\cap Y_{i2}=1 \right) +P\left( Y_{i1}=0\cap Y_{i2}=0 \right) \). Also consider the corresponding theoretical probability of expected agreement under the assumption of rater independence in the population which we denote as \(\pi _{e,i}=P\left( Y_{i1}=1 \right) P\left( Y_{i2}=1 \right) +P\left( Y_{i1}=0 \right) P\left( Y_{i2}=0 \right) \). We can then write the proposed estimator for \(\kappa \) as:

$$\begin{aligned} {\begin{array}{l} \kappa _{M}=\frac{\pi _\textrm{o}-\pi _\textrm{e}}{1-\pi _\textrm{e}}=\frac{\frac{1}{N}\sum \nolimits _{i=1}^N {\kappa _{i}\left( 1-\pi _{e,i} \right) }}{1-\frac{1}{N}\sum \nolimits _{i=1}^N \pi _{e,i}}=\sum \limits _{i=1}^N {\kappa _{i}\frac{\left( 1-\pi _{e,i} \right) }{c}} \\ \end{array}} \end{aligned}$$
(3)

where \(\kappa _{i}=\frac{\pi _{o,i}-\pi _{e,i}}{1-\pi _{e,i}}\) and \(c=N-\sum \nolimits _{i=1}^N \pi _{e,i} \). Expressing \(\kappa _{M}\) in this way shows that the proposed estimator is a function of the sum of individual observations akin to summing each individual subject’s two-way table. This expression offers a different interpretation than “agreement beyond chance” (Cohen 1960). It is the weighted sum of each subject’s \(\kappa \) in the population where the weight is the fraction of expected disagreement \(\left( 1-\pi _{e,i} \right) \) for that individual. This form is useful for assessing theoretical properties of \(\kappa _{M}\) rather than for actual estimation of \(\kappa _{i}\) in practice. We use this form of \(\kappa _{M}\) in the simulation studies to demonstrate the effect of sample disease prevalence on estimates of \(\kappa \) when the agreement structure among cases and controls may differ (in other words when \(\theta _{ij}\not \equiv \theta _{+j}\) at least generally).

4 Ignoring Necessary Covariates Leads to Inflated Estimates

The impact of excluding needed covariates can be evaluated by comparing the difference in odds of expected agreement between Model \(M_{0}\) (i.e., ignoring covariates as in \(\kappa _{C})\) and Model M (i.e., accounting for covariates as in \(\kappa _{M})\): \(\delta =\left( \left. \frac{\pi _{e}}{1-\pi _{e}} \right| M_{0} \right) -\left( \left. \frac{\pi _{e}}{1-\pi _{e}} \right| M \right) \). We note that this is most useful under simulation scenarios as the true model (i.e., the impact of factors on the probability of a positive evaluation for each subject by each rater) will always be known. This also demonstrates situations where \(\kappa _{C}\) (i.e., \(\kappa \) under model \(M_{0})\) is inflated compared to the true agreement structure.

Under model structure M and the assumption of rater independence, the odds of agreement across all subjects is:

$$\begin{aligned} {\begin{array}{l} \left. \frac{\pi _{e}}{1-\pi _{e}} \right| M=\frac{\sum \nolimits _{i=1}^n \left[ \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right] }{\sum \nolimits _{i=1}^n \left[ 1-\left( \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right) \right] }\\ \end{array}} \end{aligned}$$

This form is similar to the Mantel and Haenszel estimator for the common odds ratio of conditional association (Agresti 2013) in that it is the sum of the numerators (for each conditional table) divided by the sum of the denominators (for each conditional table). Under Cohen’s \(\kappa \)

$$\begin{aligned} {\begin{array}{l} \left. \frac{\pi _{e}}{1-\pi _{e}} \right| M_{0}=\frac{\theta _{+1}\theta _{+2}+\left( 1-\theta _{+1} \right) \left( 1-\theta _{+2} \right) }{1-\left( \theta _{+1}\theta _{+2}+\left( 1-\theta _{+1} \right) \left( 1-\theta _{+2} \right) \right) }\\ \end{array}} \end{aligned}$$

Suppose model \(M_{0}\) truly holds. Then the included explanatory factors in model M do not impact the probability of a positive response for rater j. This indicates that there are no differences in the predicted probabilities between models \(M_{0}\) and M and \(\delta =0\). In an applied setting, a constant probability of a positive evaluation may indicate that the subjects are homogenous or the diagnostic test/criteria (say a neuroimaging brain scan) are not helpful in distinguishing features that discriminate between a positive and negative evaluation.

Now suppose model M truly holds and the probability of a positive evaluation depends on certain measures. Then \(\delta \) will not equal 0. Whether \(\delta \) is positive or negative will determine if \(\kappa _{C}\) is inflated or deflated. The denominator of \(\delta \) is always positive. Therefore, the numerator determines the impact of a model misspecification. After some simplification, the numerator of \(\delta \) (which we now denote as \(\delta ^{*})\) reduces to the difference in \(\pi _{e}\) between models \(M_{0}\) and M:

$$\begin{aligned} {\begin{array}{ll} \delta ^{*}&{}=\textrm{ }\frac{1}{N^{2}}\left( \left[ \sum \nolimits _{i=1}^N \theta _{i1} \right] \left[ \sum \nolimits _{i=1}^N \theta _{i2} \right] +\left[ \sum \nolimits _{i=1}^N \left( 1-\theta _{i1} \right) \right] \left[ \sum \nolimits _{i=1}^N \left( 1-\theta _{i2} \right) \right] \right) \\ &{}\quad -\frac{1}{N}\sum \nolimits _{i=1}^N \left[ \theta _{i1}\theta _{i2}+\left( 1-\theta _{i1} \right) \left( 1-\theta _{i2} \right) \right] \\ \end{array}} \end{aligned}$$

If \(\delta ^{*}<0\), then \(\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M_{0}<\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M\). Therefore, \(\kappa \vert M_{0}>\kappa \vert M\) (i.e., inflated) because there is less of a penalty for the cases where there is disagreement (Eq. 2). Similarly, if \(\delta ^{*}>0\), then \(\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M<\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M_{0}\) and \(\kappa \vert M>\kappa \vert M_{0}\) (i.e., deflated).

We have found no straightforward way to determine in which situations \(\delta \) will be positive or negative We note that \(\left. \pi _{e} \right| M\) is the sum of each subject’s predicted probability of agreement under the assumption of conditional independence. Alternatively, \(\left. \pi _{e} \right| M_{0}\) is based on each rater’s average probability of a positive evaluation. If there is a degree of agreement between two raters, there will be a subset of subjects upon which the raters will provide consistent evaluations (i.e., \(\theta _{ij}\approx \theta _{ij^{'}}\) for some \(i>1)\). Therefore, it is likely \(\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M_{0}<\left. \frac{\pi _{e}}{1-\pi _{e}} \right| M\) and \(\kappa _{C}\) will be inflated.

4.1 Case–control study: \(\varvec{\kappa }_{{{C}}}\) vs \(\varvec{\kappa }_{{{M}}}\)

One simple example where \(\kappa _{C}>\kappa _{M}\) for the same data is when there are two groups of subjects (Group A and Group B) and the probability of a positive evaluation depends on group status. Assume there are two expert raters and that the proportion of subjects in Group A is \(\psi _{A}=N_{A}/N\). In this case model, \(M=\beta _{0}+\beta _{1}\left( \textrm{Rater}=2 \right) +\beta _{2}(\textrm{Group}=B)\) and \(M_{0}=\beta _{0}+\beta _{1}\left( \textrm{Rater}=2 \right) \).

Denote the probability of a positive response for subjects in Group A from Rater 1 as \(\theta _{A1}\) and from Rater 2 as \(\theta _{A2}\). Similarly, denote the probability of a positive response for subjects in Group B from Rater 1 as \(\theta _{B1}\) and from Rater 2 as \(\theta _{B2}\). Then \(\delta ^{*}=2\psi _{A}\left( 1-\psi _{A} \right) (\theta _{A1}-\theta _{B1})(\theta _{B2}-\theta _{A2})\). Note that \(0<\psi _{A}<1\). Assume that Group A has a higher probability of a positive evaluation (Group B could have also been chosen). Assuming raters are experts in their fields \(\theta _{Aj}>\theta _{Bj}\). Hence, the numerator of the difference in odds is negative since \(0<\psi _{A}<1, \quad \theta _{A1}>\theta _{B1}\) and \(\theta _{B2}<\theta _{A2}\).

Under the same situation, \(\kappa _{C}<\kappa _{M}\) if \(\theta _{A1}>\theta _{B1}\) and \(\theta _{B2}>\theta _{A2}\). This is very unlikely unless the two raters are not trained in interpretating the evaluation (e.g., are not experts) or there is great discrepancy among expert interpretations (e.g., the tool used for evaluations is not informative). This could also occur if there was a data entry error (e.g., groups were mislabeled).

In summary, the difference in odds under model \(M_{0}\) and the more general model M could be 0 positive or negative. The direction of this difference depends on the joint probability of agreement. It is likely to be negative which corresponds to \(\kappa _{C}\) being inflated compared to \(\kappa _{M}\).

4.2 Disease Prevalence: \(\varvec{\kappa }_{{{C}}}\) vs \(\varvec{\kappa }_{{{M}}}\)

We define disease prevalence as the proportion of individuals in the population who have the disease (although we note other definitions have been used in the literature such as the average of both rater’s marginal probability of a positive evaluation (Byrt et al. 1993)). We assume the sample disease prevalence is representative of the population. Including disease status as an explanatory factor in model M and allowing the degree of agreement to differ between the diseased and healthy populations will result in Eq. 3 (i.e., \(\kappa \) as a weighted average of each group specific \(\kappa \)) reducing to:

$$\begin{aligned}{} & {} \kappa _{M}=\kappa _{D+}\frac{(1-\pi _{e}^{D+})}{1-\pi _{e}^{D+}\psi _{D+}-\pi _{e}^{D-}(1-\psi _{D+})}\psi _{D+}\\{} & {} \quad +\kappa _{D-}\frac{\left( 1-\pi _{e}^{D-} \right) }{1-\pi _{e}^{D+}\psi _{D+}-\pi _{e}^{D-}(1-\psi _{D+})}\left( 1-\psi _{D+} \right) \end{aligned}$$

where \(D+\) denotes the diseased population and \(D-\) denotes the healthy population.

Table 2 Simulation results from the 5 different situations. The mean estimated value of \(\kappa \), the simulation standard error of \(\kappa \), the estimated bias and MSE are reported.
Full size table

If the degree of agreement remains constant across both groups, \(\kappa _{M}\) will not depend on the sample disease prevalence. However, if the agreement differs, then \(\kappa _{M}\) is the weighted average of each sub-population’s \(\kappa \). The weights and therefore \(\kappa _{M}\) are linearly related to the sample disease prevalence. Similar arguments in the literature have been made (Guggenmoos-Holzmann 1993; Guggenmoos-Holzmann, 1996). See Supplemental Material for further details.

This result is directly related to the appropriateness of model M in estimating the probability of a positive evaluation (\(\theta _{ij})\). When \(\theta _{ij}\) is not constant for all subjects the linear predictor must account for the explanatory factors that contribute to the difference in probabilities. This is true for any factor that confers a higher or lower risk for disease.

5 Simulation Studies

Extensive simulations were completed to confirm mathematical results. One representative simulation study is provided. Data were simulated under the following assumptions: 1) two raters were included in the study (\(j=1,2)\); 2) each subject belonged to one of two mutually exclusive groups (Group A or Group B), and the probability of a positive evaluation depended on group status (\(M:logit\left( \theta _{ij} \right) =\beta _{0}+\beta _{2}\left( \textrm{Rater}=2 \right) +\beta _{3}(\textrm{Group}=\textrm{B}))\); 3) the proportion of subjects in each group was fixed (\(\psi _{A}=\frac{N_{a}}{N}\in [0,1])\).

In this case, group status may refer to a case–control study design (as in Section 4.2). Group A represented the subjects defined as cases, and Group B represented the subjects defined as controls. Let \(\theta _{Aj}=0.6\) and \(\theta _{Bj}=0.1\) be the true probability of a positive evaluation for both raters among the cases and controls, respectively. There were 1000 subjects (\(n=1000)\), and the proportion of cases was 0.44 (\(\psi _{A}=0.44)\). The number of simulations was 2000 for all scenarios.

Fig. 1
figure 1

Simulation results: Density of \(\kappa \) estimates. Density of estimates for all five simulations. \(\kappa \) was estimated ignoring group status (Cohen’s \(\kappa \); yellow) adjusting for group status through Model M (blue), within each group using Cohen’s \(\kappa \) (purple for Group A and orange for Group B) and using Barlow’s stratified \(\kappa \) (green). Nominal \(\kappa \) values for each group are represented by color-coded, vertical reference lines (Color figure online).

Full size image

Data were computed under three hypotheses. The first hypothesis was no agreement beyond conditional independence among the raters (Simulation 1 \(H_{0}:\kappa _{A}=\kappa _{B}=0)\). The second hypothesis was that the agreement for each group was greater than 0 and equal (Simulation 2a \(H_{0}:\kappa _{A}=\kappa _{B}=0.8\) and Simulation 2b \(H_{0}:\kappa _{A}=\kappa _{B}=0.3)\). The last hypothesis was that \(\kappa \) for each group was greater than 0 and not equal (Simulation 3a \(H_{0}:\kappa _{A}=0.8\cap \kappa _{B}=0.3\) and Simulation 3b \(H_{0}:\kappa _{A}=0.3\cap \kappa _{B}=0.8)\). The selected \(\kappa _{A}\) and \(\kappa _{B}\) for each simulation determined the true value of \(\kappa _{C},\kappa _{M}\) and \(\kappa _{Brlw}\).

Under each simulation framework, 2000 Bernoulli samples were drawn. Using the simulated data, \(\kappa _{C}\) was computed within each group (i.e., Landis and Koch’s approach for accommodating covariates) and for the marginal table (incorrectly ignoring group status; \(\kappa _{C})\). Adjustment for group status was completed using \(\kappa _{M}\) (adjusting for group status in the linear predictor) and \(\kappa _{Brlw}\) (Barlow’s stratified \(\kappa \) approach (Barlow et al. 1991)). The average estimated (empirical) bias and the mean-squared error were calculated for each simulation scenario. Mathematical details for sampling when \(\kappa >0\) are provided as Supplemental Material.

Figure 1 plots the densities of the \(\kappa \) estimates from all simulations. We note that the expected probability of agreement for \(\kappa _{C}\) was calculated using the usual approach (i.e., a two-way table such as Table 1) and under model \(M_{0}\). As \(\kappa _{C}\) did not change by estimation method, only estimates under model \(M_{0}\) are reported. Table 2 provides the \(\kappa \) estimates sample standard errors estimated biases and mean-squared errors (MSE).

There are several key findings. First, \(\kappa _{C}>\kappa _{M}\) confirming algebraic findings. Additionally, \(\kappa _{C}>\kappa _{Brlw}\). Simulation results reflected these values (MSE < 0.01 for \(\kappa _{C}, \quad \kappa _{M}\) and \(\kappa _{Brlw})\). When there was conditional independence between raters (Simulation 1), \(\kappa _{C}=0.283\) while \(\kappa _{M}=\kappa _{Brlw}=0\). It is not unreasonable for \(\kappa =0\) as the Bernoulli data were simulated independently between raters. Cohen’s \(\kappa \) was likely inflated because subjects were assumed to have the same probability of a positive response when calculating \({\hat{\pi }}_{e}\). When there was agreement beyond the assumption of conditional independence and this agreement was constant between groups (Simulation 2a and 2b), \(\kappa _{C}\) was also inflated. However, \(\kappa _{M}\) and \(\kappa _{Brlw}\) equaled the \(\kappa \) within each group. This result confirmed the mathematical results shown in Sect. 3.

Lastly, when the degree of agreement differed by group, \(\kappa _{C}\) was larger than \(\kappa _{M}\) and \(\kappa _{Brlw}\). However, \(\kappa _{Brlw}>\kappa _{M}\) when \(\kappa _{B}>\kappa _{A}\) because \(\psi _{A}<0.5\). In other words, \(\kappa _{Brlw}\) depends on the sample size and degree of agreement within each group. As discussed in Sect. 4, \(\kappa _{M}\) depends linearly on sample disease prevalence. In this case \(\kappa _{M}\) depends linearly on \(\psi _{A}\). Therefore, if model M is correctly specified and the subjects are representative of the population, \(\kappa _{M}\) will be the correct mixing of each sub-population’s \(\kappa \).

6 Application to Alzheimer’s Disease

We applied our method to data from the APP study, which studied the value of visual interpretations of florbetapir PET brain scans in identifying cognitively normal individuals with cranial amyloid-\(\beta \) plaques (Harn et al. 2017). This data set may be made available from, and with the approval of, the KUMC ADRC.

Briefly, three experienced raters visually interpreted 54 florbetapir PET scans as either “elevated” or “non-elevated” for amyloid-\(\beta \) plaque deposition. For the purposes of this work, we randomly selected one pair of raters (Rater 2 and Rater 3) to demonstrate our method for ease of presentation. The florbetapir standard uptake value ratio (SUVR) is a software computed measure of the global amyloid burden in the brain. This ratio has been used to try to assist in characterization of PET brain scans by providers. In this study, scans were dichotomized as having a global SUVR value of greater than 1.1 or not. (Others have used a threshold of 1.08 or 1.11 (Sturchio et al. 2021).) Raters did not know the SUVR status. This binary classification was included as a covariate when calculating \(\kappa _{M}\).

Table 3 Estimates, standard errors and 95% confidence intervals (CI) of \(\varvec{\kappa }_{{{C}}}, \quad \varvec{\kappa }_{{{M}}}\), and \(\varvec{\kappa }_{{Brlw}}\)
Full size table

There were 24 scans (44%) classified as having SUVR > 1.1. All 14 scans Rater 2 interpreted as elevated had SUVR > 1.1. Of the 16 scans Rater 3 interpreted as elevated, 2 of those scans had SUVR < 1.1.

The logistic regression model for \(\kappa _{C}\) was \(M_{0}=\beta _{0}+\beta _{1}(\textrm{Rater}=3)\) and for \(\kappa _{M}\) was \(M=\beta _{0}+\beta _{1}\left( \textrm{Rater}=3 \right) +\beta _{2}(\textrm{SUVR}<{1.1})\). The equation for \(\kappa _{Brlw}=0.44\kappa _{SUVR>1.1}+0.56\kappa _{SUVR<1.1}\). Standard errors for \({\hat{\kappa }}_{C}\), \({\hat{\kappa }}_{M}\) and \({\hat{\kappa }}_{Brlw}\) were computed using bootstrap. 95% confidence intervals were computed under the assumption of normality and empirically using the bootstrap sample distribution.

Table 3 provides the estimates, standard errors and 95% confidence intervals for \(\kappa _{C}, \quad \kappa _{M}\) and \(\kappa _{Brlw}\). To summarize, \({\hat{\kappa }}_{C}=0.724\) (empirical 95% CI: 0.483, 0.911), \({\hat{\kappa }}_{M}=0.561\)(empirical 95% CI: 0.222, 0.845) and \({\hat{\kappa }}_{Brlw}=0.292\) (empirical 95% CI: 0.142, 0.407). Consistent with simulations, we found that \(\hat{\kappa }_{C}\) was greater than \({\hat{\kappa }}_{M}\) and \({\hat{\kappa }}_{Brlw}\). However, \({\hat{\kappa }}_{Brlw}\) was much smaller than \({\hat{\kappa }}_{C}\) and \({\hat{\kappa }}_{M}\). This was because among the 30 scans with SUVR < 1.1, one rater gave all negative evaluations while the other rater did not, resulting in an estimate of 0 within this group of scans. Hence, \({\hat{\kappa }}_{Brlw}\) was closer to 0 regardless of the estimate among scans with SUVR > 1.1 because there were more scans with SUVR < 1.1 This relationship can also be seen using estimates from model M (Supplemental Materials Section C). Images with SUVR < 1.1 were less likely to be classified as elevated (odds ratio of 0.024, p< 0.001).

Fig. 2
figure 2

APP study results: Density of \(\kappa \) estimates. Density plots of the empirical distribution of Cohen’s (yellow), model-based (blue) and Barlow’s (green) \(\kappa \). Empirical 95% confidence intervals are represented by the vertical dashed lines. The nonparametric densities (solid lines) and normal probability densities (dotted lines) are also provided (Color figure online)

Full size image

The confidence intervals were larger for \({\hat{\kappa }}_{M}\) than for \({\hat{\kappa }}_{C}\) which is likely a result of including SUVR in the logistic regression model. However, the confidence intervals were smaller for \({\hat{\kappa }}_{Brlw}\) than \({\hat{\kappa }}_{M}\) which is likely due to a \(\kappa \) estimate of 0 among subjects with SUVR < 1.1.

Figure  2 shows the histograms, nonparametric densities and normal densities of \({\hat{\kappa }}_{C}, {\hat{\kappa }}_{M}\) and \({\hat{\kappa }}_{Brlw}\) computed by bootstrap. The bootstrap 95% confidence intervals are overlaid. Both \({\hat{\kappa }}_{C}\) and \({\hat{\kappa }}_{M}\) visually appear approximately normally distributed, while \({\hat{\kappa }}_{Brlw}\) does not. This is likely due to the small sample sizes within each SUVR group.

This analysis suggests there is a sufficient degree of agreement beyond the assumption of rater independence conditional on SUVR. The proposed method accounted for covariates without depending on a stratified analysis, the results of which are dependent on sample size. Moreover, \({\hat{\kappa }}_{M}\) provides an interesting interpretation: there is agreement beyond what is expected under the assumption of conditional rater independence even after accounting for SUVR.

7 Conclusion

We have proposed an estimator of \(\kappa \), \(\kappa _{M}\) that accommodates covariates, encompasses \(\kappa _{C}\) as a special case, can be implemented using standard statistical software and has an interpretation more accurate than “agreement beyond chance”. If factors related to positive/negative status are modeled correctly, \(\kappa _{M}\) will appropriately weight each sub-population’s \(\kappa \) without having to complete a stratified analysis that may be prone to sample size limitations (e.g., \(\kappa _{Brlw})\). If \(\kappa \) is constant across all sub-populations, even though subjects may have unique probabilities of a positive response, \(\kappa _{M}\) will result in that same \(\kappa \) value (whereas \(\kappa _{C}\) will not).

In this paper, we have provided different perspectives on \(\kappa \), such that it is a function of a model-based odds of expected agreement and a weighted sum of each sub-population’s \(\kappa \). By using more explicit language to describe \(\pi _{e}\) (rather than the current convention “chance”), we can suggest a new interpretation for \(\kappa \): the amount of observed agreement beyond the expected agreement under to model M (i.e., the degree of agreement unexplained by the inclusion of explanatory factors). Hence, when \(\kappa =0\), the observed agreement equals the expected agreement and model M truly holds. When \(\kappa \ne 0\), there is a degree of agreement (or disagreement) that is unexplained by model M.

The proposed method addresses several needs. First, it is implemented with logistic regression a commonly available tool. Many proposed methods for assessing agreement are more complex to apply. Second, it includes as a special case \(\kappa _{C}\) in its most reduced form. Other methods (Nelson and Edwards 2008) cannot be similarly simplified. Third continuous and categorical covariates can be assessed for inclusion using available logistic regression theory. This allows for factors that affect the probability of a positive evaluation and therefore potentially agreement to be identified. Additionally subjects can have their own model-based probabilities of being positive. Fourth, we do not constrain the different sample proportions of disagreement to be equal. Other methods (Nelson and Edwards 2008) treat them as interchangeable which implies that the probability of a positive evaluation across raters is constant. Our method allows for variability in the probability of a positive response for each subject-rater combination.

This work has limitations. First study designs often include more than two raters (Harn et al. 2017). Cohen’s \(\kappa \) may not be the optimal statistical method in these situations, although it is commonly used. Second, our method does not account for intra-rater variation. Theoretical developments have proposed including raters as random effects (i.e., using GLMMs as in Nelson and Edwards 2008). However, these methods are more involved to implement and depend on convergence of the GLMM.

Future work will address the described limitations and continue to generalize \(\kappa _{M}\) to be amenable to a variety of research situations. For instance it is possible to generalize our approach to the case where there are multiple classification levels. Additional work will also focus on generalizing \(\kappa _{M}\) to include multiple raters and account for intra-rater variation.

In conclusion, we have proposed an intuitive estimator of \(\kappa \) that is flexible easily implemented adjusts for covariates simplifies to \(\kappa _{C}\) and has a more specific interpretation. This approach can be applied to multiple fields ranging from medicine to machine learning.