A Flexible Generalized Poisson Likelihood for Spatial Counts Constructed by Renewal Theory, Motivated by Groundwater Quality Assessment

Abstract

In recent years, the availability of spatial count data has massively increased. Due to the ubiquity of over- or under-dispersion in count data, we propose a Bayesian hierarchical modeling approach based on the renewal theory that relates nonexponential waiting times between events and the distribution of the counts, relaxing the assumption of equi-dispersion at the cost of an additional parameter. Particularly, we extend the methodology for analyzing spatial count data based on the gamma distribution assumption for waiting times. The model can be formulated as a latent Gaussian model, and therefore, we can carry out fast computation using the integrated nested Laplace approximation method. The analysis of a groundwater quality dataset and a simulation study show a significant improvement over both Poisson and negative binomial models.Supplementary materials accompanying this paper appear on-line.

Appendices

Matérn covariance function

An isotropic Matérn spatial covariance function is given by

$$\begin{aligned} \textrm{cov}(h)=\frac{\sigma ^2}{2^{\nu -1}\Gamma (\nu )}(\kappa \Vert h\Vert )^{\nu }K_{\nu }(\kappa \Vert h\Vert ), \end{aligned}$$

(9)

where $\Vert h\Vert$ denotes the Euclidean distance between any two locations $s,s^\prime \in \Re ^d$, $h=s-s^\prime$, $\Gamma (\cdot )$ is the gamma function, and $K_{\nu }(\cdot )$ is the modified Bessel function of the second kind of order $\nu$. For the Matérn covariance function, $\sigma ^2$ is the marginal variance, and $\nu$ measures the degree of smoothness which is usually fixed. In the INLA-SPDE methodology, for $d=2$, the smoothness is fixed at $\nu =1$. Further, $\kappa > 0$ is the scaling parameter with an empirical range $r=\sqrt{8\nu }/\kappa$ where the spatial correlation is close to 0.1 for all $\nu$ (Lindgren et al. 2011). For a fixed smoothing parameter $\nu$, the larger the value of r, the stronger the spatial correlation.

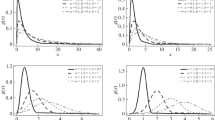
Hazard function of gamma-distributed waiting times

For a gamma distribution, the hazard function is given by

$$\begin{aligned} \frac{1}{h_\tau (t)}=\int _0^{\infty }e^{-\gamma t}(1+\frac{u}{t})^{\alpha -1}du. \end{aligned}$$

It could be proved that $h_{\tau }(t)$ is monotonically increasing for $\alpha >1$, decreasing for $\alpha <1$, and constant for $\alpha =1$. Figure 6 shows the curve of $h_{\tau }(t)$ for different values of parameters.

Fig. 6

Hazard function of gamma distribution