A Modified Neighborhood Hypothesis Test for Population Mean in Functional Data

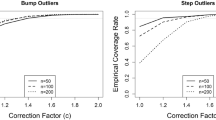
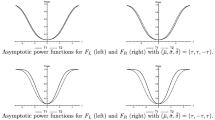
Abstract

When dealing with very high-dimensional and functional data, rank deficiency of sample covariance matrix often complicates the tests for population mean. To alleviate this rank deficiency problem, Munk et al. (J Multivar Anal 99:815–833, 2008) proposed neighborhood hypothesis testing procedure that tests whether the population mean is within a small, pre-specified neighborhood of a known quantity, M. How could we objectively specify a reasonable neighborhood, particularly when the sample space is unbounded? What should be the size of the neighborhood? In this article, we develop the modified neighborhood hypothesis testing framework to answer these two questions. We define the neighborhood as a proportion of the total amount of variation present in the population of functions under study and proceed to derive the asymptotic null distribution of the appropriate test statistic. Power analyses suggest that our approach is appropriate when sample space is unbounded and is robust against error structures with nonzero mean. We then apply this framework to assess whether the near-default sigmoidal specification of dose-response curves is adequate for widely used CCLE database. Results suggest that our methodology could be used as a pre-processing step before using conventional efficacy metrics, obtained from sigmoid models (for example: IC$_{50}$ or AUC), as downstream predictive targets.

A Proofs for Section 3 The Modified Neighborhood Hypothesis Test

Lemma 3.1

If $X_{1}, \ldots , X_{n}$ are independent and identically distributed random elements in a Hilbert space ${\mathbb {H}}$ with population mean $\mu \in {\mathbb {H}}$ and covariance operator $\Sigma :{\mathbb {H}} \rightarrow {\mathbb {H}}$ such that $E \left( ||X||^{4} \right) < \infty ,$ then

$$\begin{aligned} \sigma _1^2= & {} \textrm{Var} \left( \frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}\right) }{{\tau }} \right) =1- \frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}), {\hat{\textrm{v}}_F}\right) \nonumber \\{} & {} + \frac{\gamma ^2}{\tau ^2} \left[ E[\rho ^4(\mu ,X)] - {\textrm{v}_F}^2 \right] . \end{aligned}$$

(8)

Proof

The test statistic $T_1$ can be decomposed as follows:

$$\begin{aligned} T_1 = \frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}+ \gamma {\hat{\textrm{v}}_F}- \gamma {\textrm{v}_F}\right) }{{\tau }} = \frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}\right) }{{\tau }} + \frac{ \gamma \sqrt{n} \left( {\hat{\textrm{v}}_F}- {\textrm{v}_F}\right) }{{\tau }}.\nonumber \\ \end{aligned}$$

(18)

From Patrangenaru and Ellingson (2015, pg. 179), we also know that

$$\begin{aligned} \sqrt{n} ({\hat{\textrm{v}}_F}- {\textrm{v}_F}) \rightarrow _d N \left( 0,E \left[ \rho ^4(\mu ,X) \right] -{\textrm{v}_F}^2 \right) . \end{aligned}$$

As such,

$$\begin{aligned} \sigma _2^2 = \textrm{Var}\left( \frac{\gamma }{\tau } \sqrt{n} ({\hat{\textrm{v}}_F}- {\textrm{v}_F}) \right) = \frac{\gamma ^2}{\tau ^2}\left( E \left[ \rho ^4(\mu ,X) \right] -{\textrm{v}_F}^2 \right) \end{aligned}$$

(19)

From Sect. 2, we know that $Var(T_1)=1$. Combining this with the above results yields

$$\begin{aligned} 1&=\textrm{Var}(T_1) =\sigma _1^2 + \sigma _2^2 +2\textrm{Cov} \left( \frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}\right) }{{\tau }}, \frac{\gamma }{\tau } \sqrt{n} ({\hat{\textrm{v}}_F}- {\textrm{v}_F}) \right) \nonumber \\&\quad =\sigma _1^2 + \sigma _2^2 +\frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}, {\hat{\textrm{v}}_F}-{\textrm{v}_F}\right) \nonumber \\&\quad =\sigma _1^2 + \sigma _2^2 +\frac{2\gamma n}{\tau ^2} \left[ \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\hat{\textrm{v}}_F}\right) - \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\textrm{v}_F}\right) \right. \nonumber \\&\quad \left. -\gamma \textrm{Cov} \left( {\hat{\textrm{v}}_F}, {\hat{\textrm{v}}_F}\right) + \gamma \textrm{Cov} \left( {\hat{\textrm{v}}_F}, {\textrm{v}_F}\right) \right] \nonumber \\&\quad =\sigma _1^2 + \sigma _2^2 +\frac{2\gamma n}{\tau ^2} \left[ \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\hat{\textrm{v}}_F}\right) -\gamma Var \left( {\hat{\textrm{v}}_F}\right) \right] \nonumber \\&\quad =\sigma _1^2 + \sigma _2^2 +\frac{2\gamma n}{\tau ^2} \left[ \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\hat{\textrm{v}}_F}\right) -\gamma \frac{\tau ^2}{\gamma ^2 n} \sigma _2^2 \right] \nonumber \\&\quad =\sigma _1^2 + \sigma _2^2 + \frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\hat{\textrm{v}}_F}\right) - \frac{2\gamma n}{\tau ^2} \frac{\tau ^2}{\gamma n} \sigma _2^2 \nonumber \\&\quad =\sigma _1^2 - \sigma _2^2 + \frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}) , {\hat{\textrm{v}}_F}\right) \end{aligned}$$

(20)

Solving for $\sigma _1^2$ combined with (19) yields

$$\begin{aligned} \sigma _1^2=1- \frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}), {\hat{\textrm{v}}_F}\right) + \frac{\gamma ^2}{\tau ^2} \left[ E[\rho ^4(\mu ,X)] - {\textrm{v}_F}^2 \right] . \end{aligned}$$

(21)

$\square$

Lemma 3.2

Under the conditions of Lemma 3.1, then

$$\begin{aligned}{} & {} \frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}\right) }{\tau } \rightarrow _d N \left( 0, 1 - \frac{2\gamma n}{\tau ^2} \textrm{Cov} \left( \varphi _M({\overline{X}}), {\hat{\textrm{v}}_F}\right) \right. \nonumber \\{} & {} \left. \quad + \frac{\gamma ^2}{\tau ^2} \left[ E[\rho ^4(\mu ,X)] - {\textrm{v}_F}^2 \right] \right) \end{aligned}$$

(9)

Proof

This follows immediately from (18) to (8). $\square$

Theorem 3.1

Under the conditions of Lemma 3.1 and the mild assumption that ${\hat{\sigma }}_1^2 >0$, we arrive at the following asymptotic result:

$$\begin{aligned} T_2=\frac{\sqrt{n} \left( \varphi _M({\overline{X}}) - \gamma {\hat{\textrm{v}}_F}\right) }{{{\hat{\tau }} {\hat{\sigma }}_1}} \rightarrow _d N(0,1). \end{aligned}$$

(11)

Proof

From the proof of Lemma 3.1 and results from nonparametric bootstrap theory, then if ${\hat{\sigma }}_1^2>0$, then it is a consistent estimator of $\sigma _1^2$. We can then apply Slutsky’s Theorem to the result of Lemma 3.2, yielding this result. $\square$