1 Introduction

Agricultural field exp eriments often exhibit treatment interference, that is, the response from a given plot depends on both the treatment applied to that plot and the treatments applied to neighboring plots (Cox 1958,Ch.2). For example, a chemical pesticide applied to one plot can potentially influence the responses on surrounding plots due to spray drift, a taller plant variety in one plot may influence the growth of a shorter variety on a neighboring plot by shading the plants, the lack of control of a foliar disease on one plot may cause there to be a higher disease pressure on neighboring plots, or the control or lack of control of an insect pest on one plot may influence the pest pressure on plants in neighboring plots. Research on reducing or accounting for neighbor effects has mainly concentrated on the construction of either neighbor-balanced designs with crossed and nested blocking structures or designs that are optimal for some interference model (see, e.g., David and Kempton, 1996). The current paper proposes the construction of optimal designs with complex blocking structures, while also accounting for neighbor effects. Although our focus is primarily on agricultural field experiments, the suggested methodology is applicable in a wide variety of medical, marketing and industrial contexts for obtaining efficient designs tailored to the particular experimental requirements and constraints (for experiments on networks, see, e.g., Aral 2016; Bapna and Umyarov 2015; Bond et al. 2012; Centola 2010). For a marketing experiment on a social network, for example, we need to select which users should receive which advertisements of a commercial product in order to assess differences in click-through rates or revenue (see, e.g., Xu et al. 2015).

Blocking involves grouping together experimental units that are expected to have similar responses in the absence of treatments (see, e.g., Mead et al. 2012,Ch.7 and Ch.8). Agricultural field experiments are often designed with simple (e.g., randomized complete block designs) or more complicated (incorporating nested and/or crossed structures) blocking structures to allow for anticipated systematic sources of variability associated with the physical arrangement of plots or with constraints on the management of groups of plots (see, e.g., Verdooren 2020). Systematic sources of variability associated with the physical arrangement of plots might include trends in soil characteristics, such as pH or soil fertility, topography (e.g., locations down a slope), or distance from a field margin or hedge that might be a source for pests or diseases. Constraints imposed by farm management activities could include lines of plots being drilled in a single pass of the farm machinery, or a set of plots being simultaneously sprayed with nutrients or pesticides under a boom sprayer. Where there is only a single source of such variability, or where multiple sources can be confounded, then simple blocked designs can be used, but often these potential systematic sources of variability will affect different subsets of plots, so that more complex blocking structures need to be incorporated into the designs.

With relatively few treatments and the need to block for potential systematic variability in two orthogonal directions, standard row–column designs might be appropriate, such as Latin squares or Youden squares (where rows and/or columns contain a complete replicate of the treatment set). But as the number of treatments increases, particularly where only relatively few complete replicates are possible (as is usually the case with agricultural field experiments), it will often be necessary to consider the impact of rows and columns of plots within each of a number of (replicate) blocks (see, e.g., John and Williams 1995,Ch.6). In some cases, these blocks will be physically separated due to farm management constraints, while in other cases the blocks will be contiguous, additionally allowing for row and column structures to run across multiple blocks. Thus, many agricultural field experiments have to be designed within large two-dimensional (row–column) arrays of plots, allowing for variation between rows and between columns.

A commonly used approach are resolved row–column designs, where each block contains a complete replicate of the set of treatments (John and Williams 1995, Ch.4-6). Several authors have developed resolvable row–column designs for comparing different treatments, for example Bose (1947), Singh and Dey (1979), Ipinyomi and John (1985), Bailey (1993) and Piepho et al. (2015). In general, such designs are preferred when dealing with a large number of treatments (e.g., a large number of varieties) and a small number of replications. Other possibilities include \(\alpha \)-designs (introduced by Patterson and Williams 1976), which are resolvable block designs with respect to a single within-block sub-blocking component (see also John and Eccleston 1986, who developed a class of orthogonal row–column designs based on the \(\alpha \)-designs). The software package CycDesigN (Whitaker et al. 1997) is a practical tool for constructing efficient resolvable nested block and row–column designs. Much recent work on the design of agricultural experiments concerns design for mixed models with complicated correlation structures (see, e.g., Edmondson 2020; Piepho et al. 2021). This literature focuses on the unit structure (including spatial effects). In the current paper, we instead account for treatment interference including spillover (neighbor) effects, additionally to a complicated blocking structure.

Treatment interference is another potential source of experimental error and bias which occurs when the response is affected by treatments applied to neighboring plots. Adjustments to the unit structure or modeling unit effects do not directly address the estimation of such interference effects, which are indirect treatment effects. There are practical methods for reducing the effects of treatment interference, such as using wider spacing between plots, including border plants as guards, or using larger plots and only recording on inner rows Spitters 1979; Besag and Kempton 1986.

Apart from standard experimental practices that aid in decreasing interference through implementation, it may be possible to take account of treatment interference effects by including additional terms in the response model and optimizing the design for such a model. A wide variety of possible models and designs have been suggested for accommodating treatment interference. Examples include the work of David and Kempton (1996), Druilhet (1999), Kunert and Martin (2000), Bailey and Druilhet (2004) and Kunert and Mersmann (2011), who developed models and efficient designs for experiments where units are arranged in a circle or a line allowing for the effects of immediate neighbors. Their suggested designs were primarily neighbor-balanced in the sense that all pairs of treatments occur in adjacent plots equally often in some cases allowing for the direction of any neighbor effects. Important work suggesting ways of accommodating interference in the analysis of field experiments is that of Besag and Kempton (1986), which investigated different causes of association between neighboring plots and provided appropriate models for better capturing each cause (i.e., spatial techniques for the adjustment of field variation, response interference–interplot competition, and treatment interference).

More recently, Parker et al. (2017) suggested a model that relaxed the assumption of neighbor effects being controlled in only one direction and allowed for a network setting. Koutra et al. (2021) constructed efficient block designs using an extended version of that model with the inclusion of blocks in addition to the neighbor effects for accounting for heterogeneity across experimental units. Here, we extend the latter work to consider more complex blocking structures and obtain optimal resolved row–column designs that are suitable for use in agricultural field experiments. Possible treatment interference is governed by a network structure, represented via a graph, and accounts for variation in responses caused by the direct interference or competition effects due to treatments in adjacent plots. The network structure therefore represents sources of variation due to treatments and is quite separate from the systematic sources captured by blocking structures.

Modeling treatment interference in controlled experiments has also been addressed widely in the causal inference literature (see, e.g., Hudgens and Halloran 2008, and Athey et al. 2018), typically for the simpler situation of comparing two treatments in the absence of blocking factors with the aim of estimating both the direct treatment effects and the treatment interference or indirect effects. Our optimal designs are tailored to the estimation of average (direct) treatment effects obtained from a regression modeling approach (see Sect. 3). We adjust the estimators for both blocking factors (Imbens and Rubin 2015,Ch.9) and treatment interference, assuming linear interference (indirect) treatment effects. As is most common in the optimal design of experiments literature, we also assume the linear model is correctly specified; in particular, we assume no heterogeneity in treatment or interference effects as may be caused, for example, by interactions between the treatment factor and unobserved covariates or between the treatment factor and blocking factors. The presence of such effects could result in biased estimators, and we briefly discuss related issues in Sect. 5.

Section 2 considers an agricultural field experiment that was designed and implemented at Rothamsted Research and serves as a motivating example for this paper. The specification of the adjacency matrix for this example experiment is considered in this section. Section 3 provides the model on which the optimal designs will be based capturing the potential treatment interference between neighboring units in the presence of nested and crossed blocking factors. The formulation of \(A_s\)-optimality for estimating differences between the treatment effects in the presence of nuisance network effects is also discussed in this section. Several optimal designs are provided in Sect. 4 for the motivating example field experiment with a detailed comparison made among them. Finally, Sect. 5 discusses relevant practical issues and concludes the paper.

2 Motivating Application

We consider an agricultural field experiment which aimed to assess differences in the natural cereal aphid colonization of eighteen selected lines from the Watkins bread wheat landrace collection (Wingen et al. 2014) compared to three elite wheat varieties. For practical reasons, the experiment was restricted to small plots (1 m by 1 m) for testing insect preference among the different wheat lines, with sufficient seed resources for 4 complete replicates, and space for an array of 84 plots arranged in 14 rows and 6 columns was available. The size of the plots and relatively small distances between neighboring plots (0.75 m between rows, 0.5 m between columns) suggest the potential for direct interference effects because of lines having different levels of susceptibility to aphid infestation.

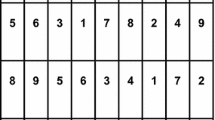
The responses were the total numbers of aphids in each plot, with the square root transformation applied during the analysis to stabilize the response variance (see Appendix for more details). The treatments to be compared are the 21 varieties, which were each replicated four times. The 84 plots were divided into four blocks, with each block containing a full replicate. Farm operations suggest the need for additional blocking structures beyond the relatively compact complete replicate blocks of experimental units. The two farm operations potentially influencing the responses in a systematic way are the drilling of the plots, where a column of 14 plots will be drilled in one pass of the machinery, and the application of any crop protection or nutritional sprays, applied by boom sprayer with rows of 6 plots across the design sprayed simultaneously. These two constraints justify the use of a nested row–column design allowing for variation between rows of 3 plots and columns of 7 plots nested within each complete block, but also suggest a need for blocking structures along long rows of 6 plots and long columns of 14 plots across complete blocks. Since the long rows and long columns are not nested within blocks, we define 2 superrows of 7 rows each and 2 supercolumns of 3 columns each. Formally, these are needed to ensure an orthogonal decomposition of sums of squares into strata—see Theorem 10.9 of Bailey (2008). Then blocks are represented by superrow by supercolumn combinations, long rows are nested within superrows and long columns are nested within supercolumns. The allocation of treatments was restricted so that each block contained a complete replicate of the 21 treatments—see Fig. 1).

Fig. 1
figure 1

Field layout and treatment allocation (numbers) for the motivating agricultural experiment at Rothamsted Research (year 2016). Blue/green shading indicates the superrows and light/dark shading indicates supercolumns considered in the development of alternative models and designs (Color figure online)

Full size image

Figure 1 depicts the physical field layout with the original randomization of the 21 treatments (lines). The different colors denote the four complete blocks of the nested row–column blocking structure. The design was obtained using the CycDesigN package (https://www.vsni.co.uk/software/cycdesign) as a resolvable row–column \(\alpha \)-design with rows of 3 plots and columns of 7 plots, latinized by rows (so that any treatment only occurs once in each long row of 6 plots), partially latinized by long columns (but some treatments appear more than once in some long columns of 14 plots) (Williams and Piepho 2013). Given that for this implementation of the experiment the complete blocks are already defined, we call the design resolved rather than resolvable.

In addition to the direct treatment effects of the 21 varieties, there is also potential for interference among plots due to the neighboring treatments. The definition of neighbors depends on the specific cause of the interference and can be described via a network structure. In our motivating example, the network describes one of two patterns of interference: either capturing the spatial structure to reflect distances between neighboring plots across space, when treatments might affect adjoining plots in addition to those they are applied to; or adjusting for farmer operations which can cause interference in other plots. The aim of the experiment was to compare the selected wheat lines with regards to natural cereal aphid colonization, potentially identifying lines that show some resistance to colonization. The experimental units correspond to plots (areas of land), which form a network structure pre-specified by the physical arrangement and practical management of the field experiment, so as to address the particular characteristics of the field experiment. The plots constitute the vertices of the network, with adjacencies based on the distances between the plot centroids, allowing for both the spatial separation of plots and the plot size and shape. In particular, the horizontal, vertical and diagonal distances between the centroids are 1.5 m, 1.75 m and 2.3 m, respectively (see Fig. 1).

Different causes of interference among neighboring units (vertices) can result in different specifications of the network structure. Issues to be considered include non-directional or directional interference (e.g., impacts of spray drift might be considered as non-directional as wind direction is probably unknown, whereas impacts of shading are probably directional defined by the orientation of the experiment and individual plots), and unweighted or weighted interference effects (e.g., weightings might allow for geographical distances or a different impact of neighboring units at a higher or lower altitude). When dealing with spatial arrangements of experimental units, there are several methods available to specify the neighbor structure. In this case, the experimental units are arranged in a rectangular array, and the physical distances between the units provide a natural basis for calculation of the network structure. We should note, however, that plots are not contiguous but rather they are separated by small distances, with different distances across rows and along columns. We consider the effects due to the network structure separately to the different levels of blocking complexity and additional to the particular treatment allocation.

The specification of the network structure may not be straightforward and this structure will likely be a proxy for the actual dynamics (e.g., farmer operations) and interactions that take place between the plots. We assume that the network structure is pre-specified (non-stochastic) and appropriately captures the observed or potential treatment interference. In common with other features of the design of experiments, such as the blocking structure, subject matter expertise is needed to define an appropriate network structure for a given experiment.

We consider two choices for this network structure, \(\mathcal {G}_1\) and \(\mathcal {G}_2\), as shown in Fig. 2. These networks have been specifically chosen to represent two common forms of interference effects that might occur in agricultural field experiments, accounting for important components of the trial layout that might otherwise introduce a bias to the results and therefore to the conclusions drawn by the experimenter. The network structures can be used to describe interference between plots caused by treatments. Firstly, we consider the network effects of the treatments applied to the immediate neighbors that are vertically, diagonally or horizontally connected. The second choice for the network relates to the farmer operations.

Fig. 2
figure 2

Different connectivity graphs: \(\mathcal {G}_1\) (left) and \(\mathcal {G}_2\) (right). Plots are numbered sequentially following the path of the drilling operations

Full size image

More specifically, for our first specification (\(\mathcal {G}_1\) left panel of Fig. 2) the network is weighted. The weights based on the inverse spatial distance between neighboring plots (centroids) including diagonal neighbors. For the second specification (\(\mathcal {G}_2\) right panel of Fig. 2), the network is unweighted and it is related to the farm operations and specifically the directions of drilling (alternating between columns) and spraying applications (along the rows) implemented by the farmer. In both cases the directions are indicated by arrows in Fig. 2. For brevity we refer to these network specifications as King’s case (as in chess; \(\mathcal {G}_1\)) and Farmer’s case (\(\mathcal {G}_2\)), respectively. Section 4 explores the optimality of the designs for these two scenarios of alternative treatment interference among neighboring plots.

An analysis of the data collected from the motivating agricultural field experiment showed evidence for important network effects even after adjusting for the highly complex blocking structure (for removing spatial variation). In particular, Tables 1 and 2 report the results of two different nested model comparisons for each of the network effect specifications. We delay the complete description of the linear model to Sect. 3; here we fit (sub-models of) model (1), with all blocking factors modeled using random effects and assuming fixed direct and network effects. The network effect corresponds to a specific set of parameters in a linear model specification that dictates how outcomes for a given unit are impacted by treatments applied to connected units (more details can be found in Sect. 3). Satterthwaite’s approximation method (Satterthwaite 1997; Fai and Cornelius 1996) was used for the denominator degrees of freedom. A more detailed discussion of the model fitting can be found in the Appendix.

Comparison 1 in Tables 1 and 2 assumes the network effects are nuisance parameters, with the sums of squares for direct treatment effects adjusted for networks (but not vice versa). This comparison aligns with the design perspective of estimating direct effects in the presence of nuisance network effects. This is the perspective taken in this paper.

Comparison 2 in the tables assumes the network effects are of primary interest, with their sums of squares adjusted for the direct treatment effects. This comparison aligns with the modeling perspective of understanding the added contribution of the network effects over and above that of direct treatments. This perspective might be of particular interest in, e.g., marketing experiments and requires a slight adjustment to the design methods in this paper, see Parker et al. (2017) and Koutra et al. (2021).

For both comparisons and under both network structures, we see substantial variation attributed to the network effects. The network effects appear more important in the King’s case than in the Farmer’s case. This suggests treatment interference is, for this experiment, not strongly driven by farmer operations. However, this experiment was not designed to account for interference effects governed by either network.

Table 1 Analysis with network effects for the King’s case
Full size table
Table 2 Analysis with network effects for the Farmer’s case
Full size table

3 The Design and the Model

We assume a general row–column structure and then we group rows into superrows (as shown by the green and blue shading in Fig. 1) and columns into supercolumns (as shown by the light and dark shadings in Fig. 1). We have (superrows/rows)\(\times \)(supercolumns/columns), where superrows and supercolumns correspond to sets of adjacent rows and sets of adjacent columns, respectively (see, e.g., Bailey 2008; Wingen et al. 2014). Moreover, there is assumed to be an underlying network structure governing the experimental units (plots) which is represented by means of a graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\), with vertex set \(\mathcal {V} = \left\{ 1,\ldots ,n\right\} \) and edge set \(\mathcal {E}\) consisting of the l pairs of vertices connected in the graph. The adjacency matrix of a graph is an \(n\times n\) matrix \(A=\left[ A_{jj'}\right] \) with \(j,j' \in \mathcal {V}\), which is a compact way to represent the connectivity structure. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph where \(A_{jj'}\ne 0\) if and only if the pair \(jj'\in \mathcal {E}\). We aim to improve accuracy as well as the precision of the experiment by controlling for heterogeneity due to multiple sources and by adjusting for the interference between neighboring units due to treatments. Note that we are designing the experiment on the network with respect to fixed effects for each of the blocking model terms. If block labels are properly randomized to blocks, it is reasonable to analyze such experiments with recovery of inter-block information by using random effects for blocks. However, we will develop a design criterion using the model with fixed block effects. Although the model with random block effects may well be better for analysis, the variances of estimated treatment parameters depend on the ratio of between- and within-block variances. Since this ratio is unknown at the design stage, it is safest to design for the worst case, i.e., that which leads to the largest variances of estimated treatment parameters. This occurs when the between-block variance tends to infinity, which is equivalent to the fixed blocks case.

Returning to the motivating agricultural experiment, the entire experiment is broken down into superrows and supercolumns of lengths \(b_1=b_2=2\) (see Fig. 1, the first superrow contains the blue-shaded plots and the second superrow contains the green shaded plots, and the first supercolumn contains the light shaded plots and the second supercolumn contains the dark shaded plots). The superrow by supercolumn combinations are equal to the \(\kappa =4\) blocks, and the complete array can also be broken down to \(\kappa _1=14\) rows each containing 6 plots and \(\kappa _2=6\) columns each containing 14 plots. The Hasse diagram (see, for example, Bailey 2008,Ch.10.4) in Fig. 3 describes the unit structure for this experiment with the corresponding degrees of freedom in each stratum. Each node in this diagram represents either a blocking factor or the interaction of two crossed blocking factors, with the node U at the top of the diagram representing the entire experiment. Recall that for the original design of the trial, the management operations of drilling and spray applications are done column-by-column and row-by-row, respectively, so that it is assumed that the effects of these processes will be confounded with the positional effects (i.e., the row, column, superrow and supercolumn effects and interactions among these terms).

Fig. 3
figure 3

Hasse diagram of the unit structure of the design. Each node has two numbers: the number of levels of the corresponding blocking factor and the corresponding degrees of freedom (in brackets), obtained by subtracting the degrees of freedom for higher factors from the number of levels of the factor under consideration. R, C, r and c represent superrows, supercolumns, rows and columns, respectively

Full size image

Let \(y_{ikgh}\) denote the response from the experimental unit in the gth row and hth column within the ith superrow and kth supercolumn. The quadruple (i, k, g, h), where \(i=1,2,\ldots ,b_1\); \(k= 1,2,\ldots ,b_2\); \(g=1,2,\ldots ,\kappa _1\); and \(h=1,2,\ldots ,\kappa _2\), identifies the experimental unit which corresponds to a vertex from the set \( \left\{ 1,\ldots ,n\right\} \) and t(ikgh) \(\in \left\{ 1,\ldots ,m\right\} \) corresponds to the treatment applied to unit (i, k, g, h). We should also note that the identity of every vertex in the network has been fixed by assigning a unique label to each one (given that a labeling is arbitrary and every choice leads to an equivalent description of the same network space). The most complex model we might consider incorporates blocks (combinations of superrows and supercolumns), rows and columns within superrows and supercolumns, respectively, and network effects. This is the Block Row–Column Network Model (BRCNM), which is an extension of the block network model (Koutra et al. 2021):

$$\begin{aligned} \text{ BRCNM: } \; y_{ikgh}&=\mu +\tau _{t(ikgh)}+\sum _{i'=1}^{b_1}\sum _{k'=1}^{b_2}\sum _{g'=1}^{\kappa _1}\sum _{h'=1}^{\kappa _2} A_{\left\{ ikgh,i'k'g'h'\right\} } \gamma _{t(i'k'g'h')} \nonumber \\&\quad +R_i+C_k+(RC)_{ik}+r_{ig}+c_{kh}+{\left( rC\right) }_{ikg}+{\left( Rc\right) }_{ikh} +\epsilon _{ikgh} , \end{aligned}$$
(1)

where \(\mu \) denotes the overall mean effect, \(\tau _{t(ijkl)}\) is the (direct) treatment effect, \(R_i\) and \(C_k\) denote the ith and kth superrow and supercolumn effects, respectively, while \(r_{ig}\) and \(c_{kh}\) denote the row and column effects nested within the superrows and supercolumns, respectively, \((RC)_{ik}\) denotes the interaction effects of superrows and supercolumns, \({\left( rC\right) }_{ikg}\) denotes the interaction effects of rows and supercolumns, and similarly \({\left( Rc\right) }_{ikh}\) denotes the interaction effects of columns and superrows. The adjacency matrix \(A_{\left\{ ikgh,i'k'g'h'\right\} }\) indicates connections between the units (i, k, g, h) and \((i',k',g',h')\) of the weighted and/or directed graph and \(\gamma _{t(i'k'g'h')}\) is the network effect of the treatment \(t(i'k'g'h')\) applied to the connected unit \((i',k',g',h')\) when there is connection between the two experimental units defined by these indices (neighbor or indirect treatment effect or interference effect). By convention the diagonal elements of the adjacency matrix are all set to zero for avoiding self-loops. Adjacency matrices are also a standard way of representing interference in the causal inference literature (see, e.g., Aronow and Samii 2017). The \(\epsilon _{ikgh}\) are assumed to be independent random variables, each with \(E(\epsilon _{ikgh}) =0\) and \(E({\epsilon _{ikgh}}^2 )=\sigma ^2\). This model assumes that the response of a plot is due to an effect caused by the treatment applied to it directly, a network effect caused by the treatments applied to its neighbors, where neighbors are defined via the adjacency matrix, and effects due to the row, column, superrow, supercolumn, and interactions the plot is in, as well as some random error.

The model in matrix notation can be written as

$$\begin{aligned} {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+A X_\gamma \varvec{\gamma }+X_R \varvec{R}+X_C\varvec{C}\\&\quad +X_{RC}(\varvec{R}\varvec{C})+X_r \varvec{r}+X_c \varvec{c}+X_{r C}(\varvec{r}\varvec{C})+X_{Rc}(\varvec{R}\varvec{c}), \end{aligned}$$

where \(\varvec{\tau }\), \(\varvec{\gamma }\), \(\varvec{R}\), \(\varvec{C}\), \((\varvec{R}\varvec{C})\), \(\varvec{r}\), \(\varvec{c}\), \((\varvec{r}\varvec{C})\) and \((\varvec{R}\varvec{c})\) denote the treatment, network, superrow, supercolumn, superrow\(\times \)supercolumn interaction, row, column, row\(\times \)supercolumn interaction and superrow\(\times \)column interaction effects, respectively. The model matrices \(X_\tau \), \(X_\gamma \), \(X_R\), \(X_C\), \(X_{RC}\), \(X_r\), \(X_c\), \(X_{r C}\) and \(X_{Rc}\) represent the treatments, network effects, superrows, supercolumns, superrow\(\times \)supercolumn interactions, rows, columns, row\(\times \)supercolumn interaction and superrow\(\times \) column interaction, respectively.

Thus, the information matrix for this model is \(M=X^TX\), where

$$\begin{aligned} X=\left( \varvec{1} \; X_\tau \; A X_\gamma \; X_R \; X_C \; X_{RC} \; X_r \; X_c \; X_{r C} \;X_{Rc} \right) . \end{aligned}$$

The information matrix has the form

$$\begin{aligned}M= {\left( \begin{array}{ccccc} n &{} {\textbf {1}}^T {X_\tau } &{} {\textbf {1}}^T A {X_\gamma } &{}\ldots &{}{\textbf {1}}^T X_{Rc} \\ {X_\tau }^T{\textbf {1}} &{} {X_\tau }^T {X_\tau } &{} {X_\tau }^T A {X_\gamma }&{} \ldots &{}{X_\tau }^T X_{Rc} \\ {X_\gamma }^T A^T {\textbf {1}} &{} {X_\gamma }^T A^T {X_\tau } &{} {X_\gamma }^T A^TA {X_\gamma }&{} \ldots &{}{X_\gamma }^T A^T X_{Rc} \\ \vdots &{} \cdots &{}\vdots &{} \ddots &{} \vdots \\ X_{Rc}^T {\textbf {1}} &{} X_{Rc}^T {X_\tau } &{} X_{Rc}^T A {X_\gamma }&{}\ldots &{}X_{Rc}^T X_{Rc} \end{array} \right) . } \end{aligned}$$

We are interested in obtaining the least squares estimators of the pairwise differences of the treatment effects, \(\widehat{\tau _s-\tau _{s'}}\) with \(s,s' \in \left\{ 1,\ldots ,m\right\} \). The design performance will be assessed via the \(A_s\)-optimality criterion, which minimizes the average variance of all pairwise differences of treatment comparisons

$$\begin{aligned} \frac{2}{m(m-1)} \sum _{s=1}^{m-1}\sum _{s'=s+1}^m var(\widehat{\tau _s-\tau _{s'}}). \nonumber \end{aligned}$$

This is proportional to

$$\begin{aligned} \phi =\sum _{v=2}^{m} \sum _{h=v+1}^{m+1} \varvec{s}^T(v,h) M^{-} \varvec{s}(v,h), \end{aligned}$$

where \(\varvec{s}(v,h)\) is a contrast vector formed of zeroes of appropriate dimension, except the v and h elements which are 1 and \(-1\), respectively, corresponding to the particular treatments we wish to compare in a given contrast. The matrix \(M=M(\xi )\) corresponds to the information matrix and \(\xi \) is a design chosen from the set of all possible designs, where a design is a choice of treatment assignments to the experimental units that correspond to the vertices of the network. The matrix \(M^{-}\) is a generalized inverse of the information matrix M (Harville 1997,Ch.9), which is pre- and post-multiplied by this contrast vector in the summation that defines the optimality criterion \(\phi \) across the 210 pairwise comparisons between varieties (treatments) in this experiment. Our interest is in the variance of estimable contrasts, which is invariant with respect to the choice of the generalized inverse. Thus, the minimization of the criterion function leads to an \(A_s\)-optimal design and the minimum value of \(\phi \) is the optimal function value. Koutra et al. (2021) provides a more thorough description of the formulation of the optimality criterion but for a simpler blocking structure.

For each potential model, the optimal design will be obtained following an optimization algorithm that is described in the Appendix, by generating an initial treatment arrangement with some particular properties, e.g., resolved row–column design, and making pairwise interchanges of treatments between plots (restricting these interchanges to maintain the overall properties where appropriate, e.g., only making interchanges within blocks for a resolved design). We have chosen a fairly standard exchange type algorithm because its flexibility can be used for any design structure and it seems to work adequately for the problems of interest. However, other methods can be used such as Tabu search (Glover 1989), or simulated annealing (Kirkpatrick et al. 1983).

For our comparisons, we consider models that are special cases of the BRCNM. In particular:

$$\begin{aligned} \text{ CRM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }\,, \\ \text{ RBM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+X_R \varvec{R}+X_C\varvec{C}+X_{RC}(\varvec{R}\varvec{C})\,, \\ \text{ RCM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+X_r \varvec{r}+X_c \varvec{c}\,, \\ \text{ BRCM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+X_R \varvec{R}+X_C\varvec{C}+X_{RC}(\varvec{R}\varvec{C}) +X_r \varvec{r}+X_c \varvec{c}\\&\quad +X_{r C}(\varvec{r}\varvec{C})+X_{Rc}(\varvec{R}\varvec{c})\,, \\ \text{ LNM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+A X_\gamma \varvec{\gamma }\,, \\ \text{ BNM: } \; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+A X_\gamma \varvec{\gamma }+X_R \varvec{R}+X_C\varvec{C}+X_{RC}(\varvec{R}\varvec{C})\,, \\ \text{ RCNM: }\; \; {E}\left[ \varvec{y} \right]&=\mu \varvec{1}+X_{\tau } \varvec{\tau }+A X_\gamma \varvec{\gamma }+X_r \varvec{r}+X_c \varvec{c}\,. \end{aligned}$$

We consider the standard treatment models derived from the simplest randomization schemes, the Completely Randomized Model (CRM) and the Randomized (complete) Block Model (RBM). The corresponding designs for these models are the simplest forms of designs to compare different treatments by randomly assigning them to experimental units (the Completely Randomized Design (CRD) and the Randomized (complete) Block Design where treatments are additionally arranged in, potentially resolvable, blocks). If instead of a simple blocking structure, we allow for experimental units being in a two-dimensional arrangement of rows and columns then we have the Row–Column Model (RCM) and if, additionally, we consider the row and column effects to be nested within blocks we have the Block Row–Column Model (BRCM). Extending these four models (CRM, RBM, RCM, BRCM) to include a network model term to capture the connections among units lead to the Linear Network effects Model (LNM) (introduced in Parker et al. 2017), the Block Network Model (BNM) (introduced in Koutra et al. 2021), the Row–Column Network Model (RCNM) and the Block Row–Column Network Model (BRCNM). For each model, the responses are functions of the network effects, the treatment (and blocking) factors, plus the error terms. We assume that, in all cases, the errors are independent and random with zero mean and constant variance. Our interest lies in comparing designs under the same model, making \(\sigma ^2\) redundant as it is the same for all proposed designs under the same model.

4 Comparison of Designs

In this section, comparisons are provided of optimal designs for estimating the direct treatment differences under the models specified in Sect. 3 for the two different pre-specified adjacency matrices (King’s and farmer’s). \(A_s\)-optimal, or near-optimal, designs are found using the design search algorithm in the Appendix; we refer to these designs as “unrestricted.” We use an interchange–exchange algorithm running two nested computations sequentially: visiting each unit in order and freely allowing for an exchange of the treatment with any of the listed competitive treatments and then interchanging those treatments until convergence is reached.

In addition, we also find optimal designs under the restrictions of (i) equal replication of treatment and (ii) resolvability with each block, defined by the combination of a superrow and supercolumn, containing a complete replicate of the treatments. These designs are found by adding the necessary restrictions into the design search algorithm.

The designs generated are labeled corresponding to the model assumed for design construction: CRD (for the Completely Randomized Design), RBD (Randomized Block Design), RCD (Row–Column Design), BRCD (nested Block Row–Column Design), LND (network design under the Linear Network effects Model), BND (Block Network Design), RCND (Row–Column Network Design), and BRCND (Block Row–Column Network Design). When different designs have been found either under a different network structure or when a restriction was imposed (equal replication or resolvability), then a number is appended to the design name. For example, design BND1 is the unrestricted optimal design under the BNM assuming the King’s adjacency matrix, BND2 and BND3 are the designs under the King’s adjacency assuming equal replication and resolvability, respectively, BND4 is the unrestricted design under the Farmer’s adjacency (which also has equal replication) with BND5 is the equivalent design under the restricted for resolvability. See Tables 3 and 4. Note that the optimal designs under CRM, RBM, RCM and BRCM always have equal replication, without the need to impose any restriction, and that an arbitrary optimal design, out of the many designs with identical performance, has been chosen for each model. Note also that we always assume that competing block designs have the same block partition. The performance of each design found is then assessed under each of the 8 models. For example, we take the optimal design, labeled BRCND1, found without restriction under the most complex BRCNM, and assess it by calculating the \(A_s\)-optimality objective function \(\phi (\cdot )\) under the BRCNM and also under the other 7 models. Hence, we are assessing the robustness of the designs to misspecification of the model at the stage of design construction. Throughout, the model specified during design assessment is consistent with the data generating process, and hence it is appropriate to assess design performance via precision (as measured by \(\phi (\cdot )\)). The results are given in Tables 3 and 4. When we compare two designs \(\xi _1\) and \(\xi _2\) in the text, we use relative \(A_s\)-efficiency \(\text{ Eff }(\xi _1,\xi _2)=\phi (\xi _1)/\phi (\xi _2) \ge 0\), with the objective function \(\phi (\cdot )\) for the two designs calculated under a common model. Typically, \(\xi _1\) will be the best design found under that particular model with \(\text{ Eff }(\xi _1,\xi _2) \le 1\).

4.1 King’s Case (\({\varvec{\mathcal {G}_1}}\); Table 3)

Here, the adjacency matrix represents the indirect effects of treatments in up to eight neighboring plots (fewer for the edge plots). It has weights corresponding to the reciprocal of the distances between the plot centroids. The optimality function values for each obtained design (labeling the rows of the table) under the different models (labeling the columns of the table) are given in Table 3. The objective function values for the optimal design for each model are highlighted in bold, within each of the three classes of unrestricted, equal-replicated and resolved.

Table 3 King’s Case: values of the objective function \(\phi (\cdot )\) for the \(A_s\)-optimal designs under the different models (\(\phi (\cdot )\) is a smaller the better function). \(^\dagger \) denotes equal treatment replication; \(^\ddagger \) denotes resolvable with respect to blocks
Full size table

When the true model for design assessment is assumed to be the BRCNM (final column of the table), we see that all standard randomized designs found for assuming models without network effects (CRD, RBD, RCD, BRCD, which we will refer to as non-network designs) perform poorly. We obtain approximate \(A_s\)-efficiencies of \(0.4 \; (=254/642)\), \(0.43 \; (=254/589)\), \(0.46 \; (=254/550)\) and \(0.51 \; (=254/499)\) for the optimal CRD, RBD, RCD and BRCD, respectively. Accounting additionally for the network effects, with or without blocks (LND1 and BND1), produces similar efficiencies (efficiencies of \(0.46 \; (=254/549)\) for the LND1 and \(0.50 \; (=254/506)\) for the BND1). A substantial increase in efficiency only occurs when row and column effects are accounting for when designing the experiment (RCND1; efficiency \(0.72 \; (= 254/353\))).

If the experiment is designed for the most complex model (design BRCND1), it maintains high efficiency if a simpler model is eventually used under all models except the RCNM (efficiency \(0.64 \; (=239/373)\)). In general, designing for a more complex model does not lead to a large loss in efficiency under the simpler models; for example LND1, BND1, RCND1 and BRCND1 are \(0.85 \; (=126/149)\), \(0.84\; (=126/150)\), \(0.89 \; (=126/141)\) and \(0.85 \; (=126/148)\) efficient, under the Row–Column Model (RCM). Note also that the BND1 performs almost as well as the LND1 under the LNM (the same holds for BND2 compared to LND2).

Restricting the designs to either be equally replicated or resolvable leads moderate losses in efficiency in this example (the lowest efficiency is \(0.77 \; (=239/311)\) for the RCND2 under the RCNM).

Table 4 Farmer’s Case: values of the objective function \(\phi (\cdot )\) for the \(A_s\)-optimal designs under the different models (\(\phi (\cdot )\) is a smaller the better function). \(^\dagger \) denotes equal treatment replication; \(^\ddagger \) denotes resolvable with respect to blocks
Full size table

4.2 Farmer’s Case (\(\mathcal {G}_2\); Table 4)

The objective function values for the optimal designs under each model are shown in Table 4. We note that, unlike for the King’s case, all designs found were equally replicated.

We see that the results here follow similar patterns to those in the King’s case. One difference, stemming from the different network specification, is that the efficiencies of the non-network designs are slightly higher than before when assessed under a model including the network structures. Assuming, for example, that BRCNM is true, the non-network designs have approximate \(A_s\)-efficiencies of \(0.51 \; (=174/343)\), \(0.64 \; (=174/273)\), \(0.57 \; (=174/306)\) and \(0.68 \; (=174/255)\) for the CRD, RBD, RCD and BRCD, respectively.

Also, under this network structure we no longer see the big differences in efficiency from including the row–column effects. In fact, we have efficiencies of \(0.65 \; (=174/266)\), \(0.78 \; (=174/223)\) and \(0.78 \; (=174/222)\) for the LND4, BND4 and RCND4, respectively, implying that accounting for the block effects produces the same increase in efficiency as accounting for the row and column effects.

When we restrict for resolvability, we lose less than \(10\%\) in efficiency (e.g., \(0.92 =174/189\) for BRCND5 and \(0.97 =132/136\) for BND5 efficient relative to the non-resolved designs). This is an important observation given that in this case imposition of more restrictions reduces the design space leading to faster convergence of the algorithm to an efficient design.

In general, we can infer that when we believe that there may be important spillover (neighbor) effects due to a structure governing the plots under experimentation, it is sensible to incorporate them in the model. For this second network specification (the Farmer’s case) accounting for the network effects even when we question their true existence does not do much harm in the design efficiencies, which means that we are better off accounting for network effects than ignoring them.

4.3 Implemented Design for Motivating Example

We obtained the objective function values under the different models for the resolved \(\alpha \)-RCD design (shown in Fig. 1) actually used for our motivating example. The design efficiency, with respect to the resolved BRCND3, is around \(0.62 \; (=318/513) \) for the King’s case (see Table 3). Likewise with respect to the resolved BRCND5, the design efficiency is around \(0.67 \; (=189/282)\) for the Farmer’s case (see Table 4). This implies that we considerably increase the design efficiency if network effects are both necessary and accounted for when choosing a design.

4.4 Conclusions

In this section we showed that optimal designs that account for network effects outperform conventional non-network designs in terms of efficiency when network effects are actually present in the assumed model. Also, there is no significant loss of efficiency in assuming the more complex model with network effects when designing the experiment; the optimal network design is has efficiency between around 0.02 to 0.15 less than the standard non-networked designs when the network effects are ignored. The loss becomes higher with more complex blocking structure as the randomization of the allocation of treatments to units is more important.

In the resulting optimal network designs, it was noticed that each replicate of every treatment was close to at least one replicate of all the other treatments, a desirable feature previously highlighted by Freeman (1979) for the case of row–column designs. Also, pairs of closely connected units tend to receive the same treatment, also observed by Parker et al. (2017) and Koutra et al. (2021). The optimal designs can be found in the Supplementary Material.

Our study focused on precision, under the assumption that the network structure would be correctly specified and included at the modeling stage if appropriate. Misspecifying or ignoring important network effects may lead to biased estimators of direct treatment effects (see, e.g., Karwa and Airoldi 2018; Forastiere et al. 2021; Sävje et al. 2021; Koutra et al. 2021). Then, a design selection criterion that only accounts for precision would be inappropriate and an alternative, such as mean squared error, should be employed. Some progress in this area has been made using graph cluster randomization, see Eckles et al. (2016).

5 Discussion

In this study, we attempted to control for the potential variation and bias resulting from treatment interference from neighboring plots or from farm operations in agricultural field experiments through incorporating network effects in order to improve the precision of treatment comparisons. We show that optimal designs with network effects outperform conventional designs in terms of efficiency, where there is strong expectation of neighbor or network effects. This approach is especially effective when there is good information about potential effects, for example, associated with the size of effects or the distance of neighbors. Including network effects that might be important is better than ignoring them and still the resulting optimal designs perform well under the conventional models CRM, RBM, RCM, etc. Also, by not taking into account network effects in our design, we produce an experiment which can have higher variance than necessary but also biased treatment effect estimators.

In practice, the adjacency matrix is tailor-made reflecting the suspected underlying treatment interference among plots. The choice of this matrix can also address irregular layouts demanding further potential constraints. According to the specific problem at hand, the experimenter should appropriately choose the adjacency matrix, suggest a suitable model to fit and optimize the design for that model for estimating the important parameters of interest. Various alternative specifications of the adjacency matrix might include detailed measurements between neighboring plots to better reflect the spatial structure, the identification of different field management practices, and the identification of both direct and indirect impacts of treatments on neighboring plots. In practice, the specification of this network might be a result of the scientific knowledge of the experimenter or elicitation of information from farm managers on the suspected sources of spillover effects based on experience which is likely to strongly affect the differences in treatment effects. A conclusion drawn from the comparison of the optimal designs is that randomized designs that ignore network effects are inefficient when network effects are present and may lead to poor results due to additional variability associated with treatment effects.

Increasing constraints on the funding for agricultural research, particularly field experiments, and an interest in being able to detect smaller and smaller treatment differences as being statistically significant, means that there is increasing demand for the development of statistical design approaches that can lead to the implementation of more efficient field experiments. Although the motivating example had a rectangular array of plots, the adjacency matrix can be appropriately specified to accommodate other structures of potential treatment interference. Designs explicitly incorporating neighbor effects overcome these challenges, and the approaches described in this paper, building on the models previously described by Parker et al. (2017) and Koutra et al. (2021), extend the pioneering research of Besag and Kempton (1986). Thus, considering models that combine network and block effects to capture the wide range of “nuisance” and “interference” sources of variability provides an approach to the design of more efficient agricultural field experiments. Such methods can help to address the current challenges of achieving more efficient and sustainable food production with limited resources, through identifying treatments resulting in small incremental improvements.

The advantage of the suggested design approach is that we can control for the neighboring environment according to the shapes, sizes, causes, directions and weights of the neighboring interference. For instance, neighbor effects may depend on the speed and direction of wind or periods in shade, which can result in an appropriate definition of the connectivity matrix imposing suitable weights for the left or right neighbors, etc. This highlights the importance of defining the adjacency matrix based on requirements of the experiment at hand. If the network structure is adequately modeled, this design procedure may be expected to result in an increase in precision of the treatment contrasts.

This study is intended to encourage the future application for agricultural field experiments of designs assuming models including both network effects and complex blocking structures, to account for the anticipated dependence among neighboring experimental units alongside those sources of variation conventionally accounted for using blocking.