Efficient Discretization of Movement Kernels for Spatiotemporal Capture–Recapture

Abstract

Spatially explicit capture–recapture (SECR) models treat detection probability as a function of the distance between each animal and its notional activity centre. Open-population variants of these models (open SECR) are increasingly used to estimate the vital rates (survival and recruitment) of spatial populations subject to turnover between sampling times. If activity centres also move between sampling times then modelling the movement can reduce bias in estimates of vital rates. The usual movement model in open SECR is a random walk with step length governed by a probability kernel. Space is discretized in open SECR for computational convenience, and in some implementations this includes truncation of the probability kernel. Computations for the movement submodel are nevertheless very time-consuming owing to the repeated convolution steps and the need to manage boundary effects. A novel ‘sparse’ discretized kernel is proposed that greatly reduces fitting time. The sparse kernel was tested by simulation and applied to two datasets. Differences between models fitted using the sparse and full kernels were minor and unlikely to matter in practice. The sparse kernel extends the practical limits of the movement modelling in open SECR to greater dispersal distances and greater spatial resolution. Supplementary materials accompanying this paper appear online.

1 Introduction

Open population spatially explicit capture–recapture modelling (open SECR) is used to estimate the vital rates (survival and recruitment) of populations subject to turnover between sampling times. In SECR models, the probability of detecting an individual is a function of the distance from its activity centre to a detector (Borchers and Efford 2008; Royle and Young 2008).

Movement of activity centres between sampling times has been treated as a random walk with step length governed by a probability kernel (Ergon and Gardner 2014; Schaub and Royle 2014). The kernel is assumed to be radially symmetrical, with circular contours of probability, so the probability density is a function of radial distance g(r). Parameters of the kernel may be estimated from the truncated sample of movements observed as recaptures on the study area. Open SECR models that include movement have been found to fit better than static models and to show increased survival (Schaub and Royle 2014; Glennie et al. 2019; Efford and Schofield 2020). The latter has been attributed to the separation of emigration and mortality (Ergon and Gardner 2014; Schaub and Royle 2014).

Space is commonly discretized in open SECR for computational convenience. Activity centres are located at points on a finite square mesh, conceptually the centroids of grid cells. The movement kernel is then a discrete distribution, the probability of moving from a point of origin to each point on the mesh. Probabilities may be approximated by evaluating the centred continuous two-dimensional probability density at each point on the kernel and dividing by their sum. The maximum likelihood implementation of Efford and Schofield (2020) truncates the movement kernel to reduce the number of computations. The radius of truncation is chosen so that the probability of movement approaches zero for points on the edge and increasing the radius has negligible effect on parameter estimates. Computations for the movement submodel are nevertheless very time-consuming owing to the repeated convolution steps and the need to manage boundary effects.

I suggest that a thinned array of kernel points may be sufficient to capture the essence of dispersal in open SECR. A design using only radial ‘spokes’ greatly reduces fitting time and extends the practical limits of the method to greater dispersal distances and greater spatial resolution. Careful weighting of cell probabilities is needed to avoid artefacts. I apply the sparse kernel to two datasets and simulate other scenarios. Differences between the sparse and full kernels were minor and unlikely to matter in practice.

2 Background

2.1 Model for Movement in Open SECR

The state model in open SECR comprises the activity centres of individuals in a spatially distributed population; the population may change over time as animals are born or die, and centres may shift. Population processes (recruitment, mortality, and movement between sampling times) are observed imperfectly and must be estimated by modelling the detections of marked individuals at known locations (detectors). The set of observations of individual i is denoted $\varvec{\omega }_i$, where $\varvec{\omega }_i > 0$ indicates an individual detected at least once. Detection is assumed to be a function of distance between each activity centre $\mathbf {x}_i$ and a detector. Activity centres are not observed directly, and our approach is to marginalize over $\mathbf {x}_i$. If each $\mathbf {x}_i$ is static then the probability of observing $\varvec{\omega }_i$ for an animal hypothetically present from time b to time d is

$$\begin{aligned} \text{ Pr }(\varvec{\omega }_i | b,d, \varvec{\omega }_i>0) = \int \text{ Pr } (\varvec{\omega }_i | b, d, \varvec{\omega }_i> 0, \mathbf {x}_i) \, f(\mathbf {x}_i | b,d, \varvec{\omega }_i > 0) \; {\mathrm {d}} \mathbf {x}_i. \end{aligned}$$

(1)

Efford and Schofield (2020) may be consulted for detail on $\text{ Pr }(\varvec{\omega }_i)$ and $f(\mathbf {x}_i)$. In order to allow for movement in (1), the animal-specific distribution of location at sampling time $j-1$ is projected forwards to time j by convolving the initial distribution with the continuous 2-dimensional kernel $\kappa$:

$$\begin{aligned} f(\mathbf {x}_j | \mathbf {x}_{j-1}) = f(\mathbf {x}_{j-1}) * \kappa = \int \int \kappa (u,v) f(x_{j-1}-u,y_{j-1}-v) \, {\mathrm {d}}u \, {\mathrm {d}} v, \end{aligned}$$

omitting the subscript i on $\mathbf {x}$ for clarity.

A model with movement entails multiple integration over the unknown location of the animal at each sampling occasion. For computational reasons (Efford and Schofield 2020), we replace integration by summation over points on a square mesh S with spacing $\Delta$. Then, for a population of uniform initial density,

$$\begin{aligned} \text{ Pr } (\varvec{\omega }_i | b, d) = \sum _{\mathbf {x}_b \in S} \text{ Pr } (\varvec{\omega }_i | b, d, \mathbf {x}_b) = \sum _{\mathbf {x}_d \in S}\cdots \sum _{\mathbf {x}_b \in S} \text{ Pr } (\varvec{\omega }_{i,b} | \mathbf {x}_b) \prod _{j=b+1}^d \text{ Pr } (\varvec{\omega }_{i,j} | \mathbf {x}_j) \, f(\mathbf {x}_j | \mathbf {x}_{j-1}). \end{aligned}$$

The discretized kernel k(x, y) is defined at an array of points with spacing $\Delta$, centred on the origin and with limits $-w$ and $+w$ on each axis. The limits are chosen so that further increase has negligible effect on the estimates (Efford and Schofield 2020). Then for $\mathbf {x}_j = (x_j, y_j)$,

$$\begin{aligned} f(\mathbf {x}_j | \mathbf {x}_{j-1}) = \sum _{x=-w}^{+w} \sum _{y=-w}^{+w} k(x,y) f(x_{j-1}-x,y_{j-1}-y). \end{aligned}$$

(2)

This note concerns the effect of applying zero weight to some values of k(), while upweighting other values.

2.2 Construction of Full Discretized Kernel

The movement probability for each cell of the full discretized kernel might be obtained by integrating the continuous kernel over the origin and destination cells, but it is sufficient in most respects to use the function of radial distance evaluated at the cell centre and scaled by cell area: $k(x,y) \approx g(r) \Delta ^2$, where $r = \sqrt{x^2+y^2}$. This breaks down at the origin for some movement kernels (Efford and Schofield 2022); then it is suggested to approximate the integral of g(r) over the origin cell by $F(r_0)$, where F is the cumulative distribution function corresponding to g(r) and $r_0 = \Delta /\sqrt{\pi }$ is the radius of a circle with the same area. The approximate probabilities are normalized across the kernel.

Table 1 lists the continuous kernel functions used in this paper (see also Cousens et al. 2008 Table 5.2; Efford and Schofield 2022). The parameter $\alpha$ controls the scale of movement; $\beta$ of the bivariate t distribution (BVT) is a shape parameter (half the degrees of freedom). BVT approaches bivariate normal (BVN) for large $\beta$. The bivariate t and bivariate Laplace (BVE) distributions in Table 1 are not the only bivariate generalizations of these distributions (Kotz et al. 2001; Kotz and Nadarajah, 2004), but they are the ones used widely in ecology (Cousens et al. 2008; Nathan et al. 2012).

Table 1 Circular bivariate movement kernels as a function of radial distance

3 Sparse Kernel

3.1 Construction of Sparse Kernel

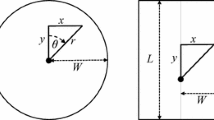
The proposed ‘sparse’ kernel $k_S(x,y)$ comprises points on eight ‘spokes’ at increments of $\theta = \pi /4$ radians (the cardinal and intercardinal directions) (Fig. 1). Other values of $k_S(x,y)$ are set to zero. Each point in the sparse kernel is weighted by the approximate area of the annular sector that it represents in the full kernel (Fig. 1). The width of an annular sector $\Delta _a$ is greater along the intercardinal axes by a factor of $\sqrt{2}$, and accordingly $\Delta _a$ takes value $\Delta$ or $\sqrt{2} \Delta$ depending on the axis type a. Discarding a $\Delta _a^2$ term in the area of each annular sector, the weighted sparse kernel values are:

$$\begin{aligned} k_S(r) = \theta \Delta _a r g(r). \end{aligned}$$

(3)

Fig. 1

Weighting of cells in sparse kernel. Each point represents an annular sector of the full kernel that has greater area away from the centre and in the intercardinal directions (filled circles) than in the cardinal directions (open circles)

The distribution along each radius is related to $f(r) = 2\pi r g(r)$, the univariate probability density of distance moved for the bivariate kernel g(r) (e.g. Cousens et al. 2008; Efford and Schofield 2022). In consequence, the maximum weight lies part way along each radius even if the full kernel has a maximum at the origin (Fig. 2).

Fig. 2

Truncated and discretized bivariate normal kernels. a Full. b Sparse. Relative probability is indicated by shading (black maximum)

3.2 Properties of Sparse Kernel

The number of points in the sparse kernel increases linearly with the truncation radius, rather than with its square, so quite large-diameter kernels become computationally feasible (Table 2).

The kernel describes a single movement step. When movement is compounded over multiple steps, location relative to the starting point becomes increasingly uncertain, blurring initial structure. Each step is a convolution of the kernel with the current distribution, starting at a point. Repeated convolution of the sparse kernel with itself quite soon leads to a distribution that approaches the full kernel (Fig. 3).

Table 2 Number of cells in ‘full’ and ‘sparse’ discretized kernels of various sizes (clipped to radius)

Fig. 3

Convolutions of full and sparse bivariate Laplace movement kernels over 1–4 steps. Line is approximate probability contour of post-dispersal location ($P = 0.0002$ per cell) of an animal initially at the centre

4 Simulations

Simulations were conducted to compare the performance of full and sparse kernels. We focus on the Pradel–Link–Barker (PLB) formulation of the open population capture–recapture model that conditions on the number caught to give estimates of per capita survival $\phi$ and recruitment f, but does not directly estimate population size or density (Efford and Schofield 2020). As the goal was to assess the movement models, the simulated population was not subject to turnover ($\phi = 1.0, f = 0.0$) and turnover parameters were fixed in the fitted model. Movement scenarios were bivariate normal (BVN) and bivariate Laplace (BVE) with median dispersal distance 30 m or 60 m. A notional $8 \times 8$ trapping grid with 30-m spacing was operated for 5 primary sessions, each comprising 5 secondary sessions. Spatial detection was governed by a half-normal hazard function with baseline detection $\lambda _0 = 0.1$ and spatial scale $\sigma = 30$ m. Activity centres ($N = 200$) were initially distributed uniformly within an arena that extended the width of the trapping grid (210 m) beyond the grid in each direction, and the same arena, discretized as 10-m cells, was used as the habitat mask for model fitting. Models were fitted by maximizing the likelihood in the R (R Core Team 2021) package ‘openCR’ 2.1.0 (Efford 2021b) using both full and sparse kernels, each with a radius of 15 or 30 cells (150 m or 300 m) (Supplementary Material, Appendix A). The experiment therefore comprised 16 scenarios, each simulated 100 times.

The performance of sparse kernels closely matched that of the full discretized kernels across all scenarios (Fig. 4). Median CPU time for model fitting with the full kernel was 4.5 to 12.7 times that for the sparse kernel. Sparse kernels showed a faint tendency for negative bias in the estimate of distance moved, and slightly greater sampling variance than the full kernel. The only significant aberration was the failure of the BVE model with both sparse and full kernels of inadequate radius: the same model performed well when the kernel radius was increased (Fig. 4). Coverage of 95% confidence intervals for the movement parameter slightly exceeded the nominal level in scenarios with both full and sparse kernels (coverage 96–98%) except for the two failed BVE scenarios (coverage 81%, 83%).

Fig. 4

Median movement distance estimated from simulated data using full (shaded) and sparse (open) discretized kernels. Scenarios differed in movement model (bivariate normal BVN, bivariate Laplace BVE) and median distance (30 or 60 m; horizontal lines). Kernels were truncated at radius of 15 or 30 cells (10-m side). Box shows upper and lower quartiles

5 Case Studies

5.1 Data

We compared the full and sparse kernels using contrasting publicly available robust-design datasets on a small forest bird and an arboreal marsupial (Efford 2021a).

The ovenbird (Seiurus aurocapilla) is a migratory ground-nesting warbler. The data are from a multi-species banding study over the 2005–2009 breeding seasons on the Patuxent Research Refuge, Maryland, USA. Ovenbirds were mistnetted and banded each year for 9 or 10 days at 44 points spaced 30 m apart on a rectangular loop (Dawson and Efford 2009; Efford 2021a). About 20 ovenbirds were caught each year (details in Supplementary Material, Appendix B). Parameters were constant across years in the fitted model.

The brushtail possum (Trichosurus vulpecula) is invasive in New Zealand forests; adult possums occupy a stable home range year round. We use the 1996 and 1997 data from a long-term trapping study in the Orongorongo Valley near Wellington, New Zealand (Efford and Cowan 2004). Possums were trapped on an array of 167 cage traps at 30-m spacing and individually ear marked for 5 nights in February, June and September of each year. The brushtail possum dataset was an order of magnitude larger than the ovenbird dataset (details in Supplementary Material, Appendix B). Population turnover was strongly seasonal, so separate levels of survival and recruitment were fitted in each ‘season’ (February–June, June–September, September–February); other parameters were constant.

5.2 Models

Activity centres were either static between primary sessions or followed a random walk with step length governed by one of three distributions: BVN, BVE or BVT. We also considered zero-inflated versions of BVN and BVE (suffix ‘zi’) as described in Efford (2021b). Discretized kernels were truncated at a radius of 30 cells; for ovenbirds that exceeded the length of the detector array and for brushtail possums it was more than half its greatest dimension. Models were fitted by maximizing the likelihood in R package ‘openCR’ version 2.1.0 (Supplementary Material, Appendix B).

Spatial PLB models were compared with respect to differences in Akaike’s Information Criterion, $\Delta$AIC. The numerically computed rank of the Hessian was sometimes less than the number of parameters for two-parameter movement models, possibly because parameters were estimated at or near a boundary of the parameter space (Viallefont et al. 1999).

5.3 Results

Sparse kernels fit consistently faster than full kernels, on average by a factor of 9 for the ovenbird data and 14 for the brushtail possum data (Table 3). The maximized log likelihood was nearly identical for sparse and full kernels fitted to the ovenbird dataset and, as a result, so were the relative AIC values within each kernel type (Table 3a). The maximized log likelihood for the sparse kernel movement models fitted to the brushtail possum dataset was consistently lower than the matching full-kernel log likelihood (Table 3b). However, the relative AIC values within each kernel type were similar, and using the sparse kernel consistently would lead to nearly the same AIC model weights.

Modelling movement increased estimates of survival for both datasets and there were no systematic differences between the full and sparse kernels (parameter estimates are tabulated in the Supplementary Material). Rank deficiency was apparent in three ovenbird models and one brushtail possum model. The BVT shape parameter was not estimated well in either case, but BVT was nevertheless the AIC-best model for brushtail possums. The zero-inflated BVN and BVE models with each kernel type produced identical estimates for ovenbirds because the fitted kernels were essentially flat away from the origin.

Table 3 Comparative fit of open SECR movement models using full and sparse discretized kernels. np number of parameters in model (*indicates reduced rank of fitted model). $\Delta$AIC is the difference in AIC from the smallest AIC of each kernel type. $\hat{\phi }$ is the estimated survival rate (${{\hat{\phi }}}_1$ February–June rate scaled to full year for brushtail possums). ‘Time’ is the ratio of CPU time for fitting the full and sparse models

6 Discussion

The efficiency of the sparse discretization makes feasible the fitting by maximum likelihood of open SECR movement models that use large-radius truncated kernels, measured in the number of cells. This enables a greater absolute span, potentially including the whole study area, or smaller cells, for greater spatial resolution. A large span is desirable when the movement kernel has a long tail, as demonstrated in the simulations with the bivariate Laplace distribution. Faster model fitting enables the bivariate normal kernel to be more easily compared with realistic, longer-tailed options, such as the bivariate Laplace and bivariate t distributions used in the case studies.

It is perhaps surprising that the kernel can be reduced to so few points. In open SECR we are concerned with estimating population-level demographic parameters, not tracing the locations and movements of individuals. While movement can be an important factor, the spatial resolution of data from passive detectors is usually poor. The movement model typically has only one or two parameters, and even the large brushtail possum dataset could barely support estimation of a second parameter (Table 3; Supplementary Material, Appendix B). The location of an animal’s activity centre is uncertain even in the primary sessions that it is detected, and the probability distribution after a single step is a convolution that blurs the sharp lines of the sparse kernel. Further, the locations of marked animals missing for one or more sessions are imputed by convolution as in Fig. 3 (Efford and Schofield 2020). The empirical results are therefore not in conflict with intuition.

Explicit truncation of the movement kernel is not required for open SECR in some modes. These include Markov chain Monte Carlo estimation in which the locations of individuals are updated from a continuous movement kernel (e.g. Ergon and Gardner 2014), and the cell-by-cell bivariate normal maximum likelihood method used by Glennie et al. (2019). Maximum likelihood using an explicitly truncated and discretized kernel has some inherent advantages: the kernel may take a shape other than bivariate normal, and model fit may be compared in a straightforward way using the log likelihood and AIC.

The sparse discretization has potential limitations that must be noted. The slight negative bias of estimated movement suggested by the simulation results is unlikely to have practical importance. We did not test the sparse kernel in highly structured habitats. The arbitrary exclusion of some possible destinations from the vicinity of each original location may interact with habitat structure to result in biased parameter estimates. We do not expect this to be a problem in practice because of the large uncertainty in the actual location of each activity centre, and the smoothing effect of convolution over time (Fig. 3). The differences in maximized log likelihood for the brushtail possum dataset appear to reflect the irregularity of the detector array on one edge: the log likelihoods of ‘full’ and ‘sparse’ models fitted to data simulated on a rectangular grid with the estimated parameters were within one unit (unpubl. results). Fitting a model with symmetrical (rectangular) habitat mask did not remove the effect.

Some applications of open SECR have used movement kernels specified in terms of independent marginal distributions on the x- and y-axes, particularly independent Laplace and t distributions. For non-normal marginal distributions the resulting bivariate probability contours are non-circular (Efford and Schofield 2022). These are not strictly compatible with the sparse kernel specified here, which assumes circularity.