A Case-Crossover Study of the Impact of the Modifying Industrial Operations Protocol on the Frequency of Industrial Forestry-Caused Wildland Fires in Ontario, Canada

Abstract

Wildland fire prevention and mitigation is of mutual interest to both government and the forest industry. In 1989, the Ontario Ministry of Natural Resources and Forestry introduced the Woods Modification Guidelines that provided rules on how forestry operations should be modified based on local fire danger conditions. Those guidelines were replaced by the Modifying Industrial Operations Protocol (MIOP) in 2008. One objective of MIOP is to allow forestry operations to be done safely for as long as possible as the fire danger increases. We investigate the impacts of these sets of regulations on the frequency of industrial forestry-caused (IDF) wildland fires in the province of Ontario, Canada. Data from 1976 to 2019 are analyzed. A case-crossover study finds no evidence to suggest that MIOP’s greater flexibility in operating hours has increased the probability of IDF fire occurrences. This result indicates that MIOP’s regulations have had the desired effect of allowing longer working hours on days with heightened fire risk without adding to the seasonal wildland fire load.

1 Introduction

The forested area in the province of Ontario, Canada, constitutes $2\%$ of Earth’s forests. This abundant natural resource supports a sustainable forest industry, which generated $\$18$ billion CAD in revenue in 2018 (Invest Ontario 2021). However, a reality of this industry is that forestry operations can ignite wildland fires (e.g., Woolford et al. 2020). Wildland fires are important for the health of many wildland ecosystems. However, they may also have significant negative socioeconomic impact and threaten public safety, communities, infrastructure, and natural resources. For example, the Fort McMurray wildland fire in Alberta, Canada, is estimated to have resulted in over $\$8.8$ billion in costs (MacEwan University 2017), and the economic cost of the chronic health impacts of smoke in Canada over 2017–2018 ranges between $\$4.3$–$\$19$ billion per year (Matz et al. 2020). Further discussion on the impacts of wildland fire in Canada may be found in Johnston et al. (2020) and the references therein.

Due to the possible negative impacts of fire, it is of mutual benefit to both the government and forest industry to cooperate towards the goal of wildland fire prevention by ensuring that proper precautions are being made to limit risk. In 1989, the Ontario Ministry of Natural Resources (MNR) released their guidelines for modifying forestry operations in response to fire danger, referred to as the Woods Modification Guidelines (Woods Guidelines). The Woods Guidelines were based upon the Fire Weather Index that is used as a general index of wildland fire danger in Canada (Natural Resources Canada 2021). The Fire Weather Index is a component of the Fire Weather Index System (Van Wagner 1987), which is a subsystem of the Canadian Forest Fire Danger Rating System (Stocks et al. 1989).

In 2003, the MNR and the forest industry discussed a possible replacement for Woods Guidelines. The industry desired regulations that were more flexible, possibly extending the window of time during a day that operations could continue safely as fire hazards increase. The Modifying Industrial Operations Protocol (MIOP) (OMNR 2011) was developed and tested from 2004 to 2006, partially implemented in 2007, and following positive feedback was fully implemented across Ontario in time for the 2008 fire season. MIOP has legislative power due to the Crown Forest Sustainability Act (Gov. of Ontario 1994), and adherence is mandatory throughout each fire season (legislatively defined as April 1 through October 31) for all forest industry operations conducted under an approved forest management plan within Ontario’s fire region. The goals of MIOP include, but are not limited to, meeting the following objectives (OMNR 2011):

• 1. Industrial operations are conducted in a manner that prevents wildfires from starting and does not increase the seasonal forest fire load.

• 2. Industrial operators continue to work safely as long as possible as the fire danger increases.

As summarized in Table 1, MIOP’s daily restrictions on hours of operation are flexible. They can vary based on a combination of operational risk, potential fire danger resulting from weather and available fuels, and the level of fire suppression training of the forestry personnel. Personnel that are “Trained and Capable” may be permitted to work longer under riskier conditions than workers who are otherwise considered to be “Limited Operators”.

Table 1 MIOP operation restrictions under limited and trained work modifications. Low-risk operations always use standard levels of prevention (P). The relationship between Fire Intensity Codes and bins of potential Head Fire Intensity (HFI) is included. Adapted from OMNR (2011)

Our objective is to quantitatively assess the effectiveness of MIOP’s prevention efforts, focusing on MIOP’s first goal, which may be interpreted as minimizing the frequency of industrial forestry-caused (IDF) fire ignitions. Rather than modelling counts, we investigate the odds of igniting an IDF fire with the aim of determining MIOP’s impact by contrasting it against Woods Guidelines and the time period preceding the introduction of Woods Guidelines (henceforth referred to as Pre-Woods). This research is in alignment with the goals of the Blueprint for Wildland Fire Science in Canada (Sankey 2018) that identified wildland fire prevention in Canada as an area that is underrepresented in the literature. Some recent literature concerning the impact of government regulations and policies on wildland fire prevention in Canada include Grunstra and Martell (2014) and Labossière and McGee (2017).

In addition to regulations and policies, wildland fire prevention programs and education have proven effective at lowering the frequency of human-caused wildland fires (e.g., Butry et al. 2010a, b; Prestemon et al. 2010; Thomas et al. 2013; Abt et al. 2015; Butry and Prestemon 2019). The impact of wildland fires may also be reduced through preventative measures such as fuel management and treatments including prescribed burning, livestock grazing, or mechanical treatments (e.g., Scott 2006; Price and Bradstock 2012; Ruiz-Mirazo 2012; Marino et al. 2014; Varela et al. 2014; Labossière and McGee 2017). For a recent review of wildland fire prevention research, see Hesseln (2018).

We use a case-crossover framework for our analysis. Brief introductions to case-control studies, including the process involved in finding matched controls, appear in Schulz and Grimes (2002), Grimes and Schulz (2005), and Levin (2006). A detailed overview of case-control methods, including the case-crossover study, appears in Borgan et al. (2018). The case-crossover study was first introduced in Maclure (1991) who used a dataset from a study of myocardial infarction for illustration. Case-crossover studies may be more commonly found in epidemiology (e.g., Janes et al. 2005, who analyze short-term exposure to air pollution), but they also have applications to other types of research problems such identifying a relationship between the use of a cellphone while driving and the risk of motor-vehicle accidents (e.g., Tibshirani and Redelmeier 1997; Redelmeier and Tibshirani 1997; McEvoy et al. 2005).

2 Data

We conducted our analysis using several data sets provided by the Ontario Ministry of Northern Development, Mines, Natural Resources and Forestry (NDMNRF). These data included a fire archive containing historical records on wildland fires, a fire-weather archive, and a fuel grid.

The NDMNRF fire archive consists of historical records on fires. They contain key information for each incident including ignition source and location, final and estimated discovery sizes, important dates (including start, report, attack, and out dates), as well as conditions at the fire’s location such as fuel type and fire-weather codes/indices. We analyzed data for the period 1976–2019, describing a total of 61,862 wildland fires, of which 1175 were industrial forestry-caused (IDF) fires.

The NDMNRF fire weather data consists of daily fire-weather observations recorded 13:00 hr local time at a network of weather stations operated across the province of Ontario. These data include temperature, relative humidity, wind direction, wind speed, and precipitation as well as indices/codes from the Canadian Fire Weather Index System (Van Wagner 1987), namely the Fine Fuel Moisture Code (FFMC), Duff Moisture Code, Drought Code, Initial Spread Index, Buildup Index (BUI), Fire Weather Index, and Daily Severity Rating. For a description of the Canadian Fire Weather Index System and its components, see Wotton (2009).

The NDMNRF fuel data are recorded at a 100 m $\times$ 100 m grid scale resolution that distinguishes between Canadian Forest Fire Behaviour Prediction System fuel types (Natural Resources Canada 2019) or non-fuel (e.g., water). Fuel type can be extracted at a point or as proportional weights over a larger area.

Fig. 1

Visualization of locations of industrial forestry-caused (IDF) fire ignitions within Ontario’s forest management units during 2007. The plotted management unit polygons are from the year 2020

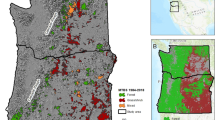
The Crown forest area of Ontario is separated into numerous forest management units (FMUs) to organize the enforcement of approved forest management plans. As we are investigating the impact of MIOP regulations on forest industry operations that are conducted within Ontario’s FMUs, we restrict our study region to the area visualized in Fig. 1 and only consider IDF fires that were ignited on Crown land within this region. A total of 82 fires are removed from the analysis due to not being ignited on Crown land. Exceptions to this exclusion are one fire just outside of the boundary in Lake Superior and two in the southern region of Wabakimi Provincial Park. These were recorded within 5 km of our study region and were included in our study under the assumption that it is likely that there were slight errors in their locations, given that harvesting would not occur within a lake or a provincial park. There was one other IDF fire that was outside of our study area but ignited on Crown land. However, as it was over 200 km from Ontario’s FMUs, it was removed from the analysis.

We note that there was a transition between the enforcement of Woods Guidelines and MIOP. The latter was piloted in two FMUs in 2006, but no IDF fires occurred in those FMUs that year. So, all 2006 IDF fires were classified as occurring under the Woods Guidelines. The phased implementation of MIOP continued in 2007, where it was implemented in six FMUs. Note that one of these FMUs has since been merged with another that was not part of this phased implementation, so we indicate the level of regulations in that FMU as mixed; however, no IDF fires occurred in that FMU in 2007. Figure 1 illustrates the set of FMUs, the regulations they were under, and the locations of IDF fires that occurred in 2007. The shapes of the points at IDF fire locations denote whether they were classified as occurring under the Woods Guidelines or MIOP. From 2008 onward, all IDF fires were classified as occurring under MIOP.

3 Methods

3.1 Case Definition and the Creation of Study Units

We do not have information about when and where industrial forestry operations were being conducted. However, ignition information for industrial forestry-caused (IDF) fires in the historical fire archive confirms the existence of forestry operations at that fire’s specific start date and location. We assume that the same company should have had personnel working nearby that location around that date. This characteristic of our data lends itself to a case-crossover study, a form of matched case-control study in which a researcher begins with information describing cases (i.e., individuals who experienced the negative event that is being studied) and creates controls (i.e., individuals who did not experience the negative event) to match with a given case by reconsidering that individual at different referent times when they did not suffer the event. A case-control or case-crossover study aims to identify a connection between exposure to some factor and the odds of an individual being a case rather than a control.

Fig. 2

Illustrations of how a block is constructed around the fire locations of a set containing (A) one, (B) two, or (C) more than two IDF fires

Full details on the algorithms mentioned in the following paragraphs are available in Appendix A. We define a study unit (i.e., an “individual” to monitor in the case-crossover study) to be a roughly $30 \text { km} \times 30 \text { km}$ block of land in Ontario within which forestry operations are being conducted. IDF fire ignitions are treated as negative events. A study unit is constructed around a set of one or more observed IDF fires ignited during the same year and is considered as a case on the day(s) the fire(s) ignited. Fires were assigned sets using Algorithm 1. A relatively wide area was selected to increase the probability that a block covers not only the operations conducted on the date of the IDF fire ignition(s), but also the operations conducted in nearby locations on the referent days that we will use to create our matched controls in Sect. 3.2.

Initial block locations are determined using Algorithm 2. If a set contains only a single fire, its block is centered on that fire’s ignition location. Otherwise, if a set contains multiple fires, its block is constructed in such a way as to minimize the maximum distance between its center and any of its set’s fire locations while ensuring that all fires are contained within the block. Figure 2 illustrates the positioning of a set’s block relative to its fire locations for examples with (A) one, (B) two, or (C) more than two fires. It is possible that multiple fires within a set were ignited on the same day, and we do not distinguish between days with one or multiple ignitions, so we refine our definition of a case as a day with at least one ignition within its block’s area.

To ensure independence between study units, we require that no two blocks corresponding to sets of fires from the same year spatially overlap. This necessitates shifting the locations of some of the blocks should their initial positions overlap one or more other blocks from the same year. Blocks without intersections do not have their positions shifted. This procedure is outlined in Algorithm 3. Each group of overlapping sets is considered independently, and new non-intersecting locations are determined using the optimizer function “optim()” in the statistical software R (R Core Team 2020) to minimize the maximum distance from the blocks’ centers and their respective fire locations. Constraints ensured that no new intersections may be created and that blocks must still cover all their set’s fire locations. Illustrations of some examples of prohibited and allowed shifts are presented in Fig. 3. In total, 49 blocks (out of 822) had their locations shifted a mean distance of 1.91 km, measured center-to-center.

Fig. 3

Example visualizations of prohibited and allowed shifting of set blocks. Solid black lines denote block boundaries, while dashed grey lines denote original block boundaries if a block has been shifted. (A) Two intersecting blocks that require shifting to remove the intersection. A third block is nearby to the right. (B) A prohibited shift on center block as it creates a new intersection with the nearby right block. (C) A prohibited shift on the left block as it no longer covers its southern-most fire’s location. (D) An allowed shift that results in no intersections while every block covers its set’s fire locations

Note In 2007 (MIOP’s phased implementation), there was a single set created with a pair of IDF fires that are considered to have been ignited under differing regulations. As this was the only such situation of a set having a mix of regulations, it was not included in our analysis.

3.2 Methodological Assumptions and the Creation of Controls

As our study units are cases on days with one or more industrial forestry-caused (IDF) fire ignitions within their areas, the referent times used to create matched controls are days in which an IDF fire did not occur within the same respective areas. Conducting our analysis as a case-crossover study has the advantage of automatically matching on any time-invariant factor that could influence the probability of observing the event, such as local fuels, location, company (including equipment, personnel, and possibly type of operation), and the set of regulations. However, a case-crossover study is only appropriate when a short transient exposure changes the risk of experiencing a negative event that is both rare and has an acute onset. We outline why a case-crossover approach is appropriate for our study in Sect. 5.1.

In order to avoid biases in case-control studies, the conditions that must be met for an individual to be considered a case need to be explicitly defined and individuals who are selected to be controls should not meet these conditions but should be representative of the target population from which the cases belong (e.g., Levin 2006). We have defined our study units to be blocks of land in Ontario on days when forestry operations are being conducted within their boundaries. Judgment must be relied upon when picking our possible referent times so that our controls, like our cases, can be considered as individuals from the same population. We must decide on when we are confident that harvesting likely took place in an area given our existing amount of evidence from the wildland fire archive. We make the following assumptions to enable the selection of possible referent times:

• 1. If we know operations were conducted at a place and time due to an IDF fire ignition, it should be safe to select referent times in that area within 4 weeks before/after that date.

• 2. We refer to an IDF fire as being large if it its final size is greater than 100 ha.

  • 2.1. If an IDF fire is not large, operations may resume immediately after suppression or within a few kilometers very soon after it ignites depending on its size.

  • 2.2. If an IDF fire is large, the forestry company will leave that area for a non-insignificant amount of time. As such, in the absence of evidence of later work in the same area, we do not consider dates after the ignition for possible referent times.

• 3. If two or more IDF fires were ignited on different dates within the same year and general area, then this serves as evidence that forestry operations may have continued in that area throughout the duration between the earliest and latest ignition dates. This can allow for the selection of referent times that are separated from a case date by more than 4 weeks. If an earlier IDF fire is large, the implied assumption is that the company moved elsewhere within the same block following the ignition. However, in the event of a large fire, time is still required to move their equipment, so we do not consider the day following a large ignition as a possible referent time.

• 4. After a large ignition, in the absence of evidence of later work in the same area, the forestry company may have left to work in a different block. If a nearby block (defined to be within 30 km, border-to-border) in the same year experiences its first ignition after the large ignition, it is possible that this block is where the original company moved to. As such, we do not consider referent times for the nearby block corresponding to dates on or before the ignition of the large fire. The day following the ignition is also rejected to parallel the day allocated for moving in Assumption 3.

Selecting referent times before and after a case date is referred to as bidirectional sampling. This sampling method can remove possible biases related to underlying time trends in the exposure variable. This is discussed in more detail in Sect. 5.1. How Assumption 2 interacts with Assumption 1 when determining possible referent times is illustrated in Fig. 4A, while Assumption 3 is illustrated in Fig. 4B. We do not claim the event described in Assumption 4 to be highly likely, but we take this conservative approach and reject some referent times in situations where we are less confident in there having been harvesting operations. Assumption 4 is illustrated in Fig. 4C, where a large fire in “Block j” restricts the possible referent times for “Block i”.

Fig. 4

Illustrations of how our methodological assumptions impact the selection of possible referent times

As MIOP is enforced during the official fire season, we only consider dates from April through October for possible referent times. If a case date is outside of this range, it will not be used in the conditional logistic regression analysis discussed in Sect. 4.2, but it may be used within the context of the above assumptions when determining possible referent times. Note that 1080 of the 1092 IDF fires in the archive were ignited during the operational fire season. Additionally, while a case may occur on any day of the week (since we are sure work was being done there that day), we only consider weekdays for referent times as industrial forestry operations most frequently happen during the workweek.

In the case-control literature, it is known that the marginal benefit to statistical power from increasing the number of controls per case beyond 4 or 5 is small (e.g., Ury 1975; Song and Chung 2010; Borgan et al. 2018). Therefore, when it is costly to obtain matched controls for your cases, there is little incentive to go past this limit. Fortunately, in our study, the only cost incurred from increasing the number of matched controls per case is a small increase in computation time, and so we elected to generate as many matched controls for each set of cases as possible to allow for the maximization our statistical power.

3.3 Calculating Head Fire Intensity, a Measure of Risk Exposure

As summarized in Table 1, MIOP’s daily restrictions vary depending on operational risk, training level of forestry personnel, and the computed Fire Intensity Code (FIC) (OMNR 2011). Unfortunately, we neither have data on what forestry operations happened when, what their deemed level of risk was, nor whether work modifications were treated as limited or trained. The only indication of what level of restrictions may have been enforced on a given day that we do have is related to FIC.

As outlined in Table 1, the FIC can be viewed as an ordinal classification of the Head Fire Intensity (HFI). We calculate the potential HFI from a location’s Buildup Index (BUI), Fine Fuel Moisture Code (FFMC), wind speed, and fuel (i.e., vegetation) type.

These potential HFI calculations were done in R using the cffdrs package (Wang et al. 2017) and the NDMNRF fuel grid and daily weather data. We are interested in the potential HFI within blocks of land, not just at points. Assuming that the spatial distribution of fuels across the province is relatively stable year to year, the fuel data were used to determine the relative proportions of Canadian Forest Fire Behaviour Prediction System fuel types within blocks. For a day’s combination of BUI, FFMC, and wind speed values within a block, potential HFI is calculated for each fuel type within that block and those values are averaged using these relative fuel proportions as weights. Since the fuel grid is static, it does not differentiate between matted or standing dead grass nor between leafless or green mixedwoods, so we approximated the time of year to switch between these respective types based on which fuel in either pair was more commonly recorded in the complete wildland fire archive.

The weather data contain measurements for each variable at weather stations throughout Ontario and these measurements (when/where available) were used to interpolate BUI, FFMC, and wind speed directly. Since spatial interpolation creates a smooth surface of values, the interpolated variables should be comparable throughout our study units (i.e., blocks of land). As such, we simply interpolate BUI, FFMC, and wind speed to the center of a block on a day when we want to calculate the weighted average of potential HFI within it. To ensure a minimum amount of confidence in our interpolated values, we require measurements for each variable to be available from at least 30 weather stations across the province on a considered day. Additionally, a point that we are interpolating to must be within the convex hull of weather stations on a given day to avoid extrapolation. If either of these conditions are not satisfied, we do not include that day and location combination in our analysis. In Table 2, we demonstrate how these restrictions reduce our usable number of cases and controls in each time period.

In order to select what interpolation methods to use, we conducted a leave-one-out cross validation study on the 30 most recent years of weather data and contrasted a range of potential interpolation methods. The details of this study are outside of the scope of this paper, but we ultimately concluded that it was more than reasonable to make use of Ordinary Kriging (OK) (e.g., Cressie 2015) with a Matern semivariogram for each of BUI, FFMC and wind speed. In the event that R failed to fit a valid variogram on a given day to use in OK interpolation, we default back to an inverse distance-weighted (IDW) interpolation method that will never fail mathematically. We used IDW power parameters 3.1, 3.6, and 2.3 for BUI, FFMC, and wind speed, respectively, which were chosen based on their demonstrated optimality versus other considered power parameters. (We investigated all multiples of 0.1 and 0.25 between 1 and 5 for each weather and Fire Weather Index System variable.) How often IDW was used for each variable in each time period for the final sets of cases and controls is noted in Table 2.

Table 2 Breakdown of how the initial counts of cases / sets of cases (determined by fire ignitions in the wildland fire archive as described in Sect. 3.1) and controls (generated using Assumptions 1–4 in Sect. 3.2) were reduced to the final data set used in the conditional logistic regression analysis. A case or control date may be rejected due to it not being within the operational fire season, due to there being insufficient weather data for interpolation on the considered day (i.e., less than 30 active weather stations with measures for each variable), or due to the fire location being outside of the convex hull of active weather stations on the considered day (referred to as extrapolation). If all cases in a set are rejected, the controls for that set can no longer impact the conditional logistic regression model fit, so they may also be rejected. The number of final cases and controls requiring the use of inverse distance weighted (IDW) interpolation for each variable instead of ordinary kriging (OK) is also detailed

4 Results

4.1 Exploratory Analysis of Industrial Forestry-Caused Fire Occurrences and Potential Head Fire Intensity

The nature of the relationship between the probability of observing one or more IDF fires in a given area on a given day and the potential HFI for the different time periods under consideration was explored using plots of the empirical log-odds (empirical logit plots) versus potential HFI, which was classified as either low or high based on the 2000 kW/m threshold where MIOP’s restrictions occur (see Table 1). Cases and controls were unmatched and sorted into groups based on time period and potential HFI classification. These observations were binned using decile bins for low potential HFI, whereas pentile bins were used for high potential HFI due to there being fewer data points. The proportion of cases within each bin were calculated for each time period. The empirical logits were then plotted against each bin midpoint.

Fig. 5

Empirical logits of industrial forestry-caused (IDF) fire ignition probability vs. $\log _{10}(\text {HFI}+1)$ at low potential Head Fire Intensity (HFI) decile bin midpoints and high HFI pentile bin midpoints for MIOP, Woods Guidelines, and Pre-Woods time periods

As illustrated in Fig. 5, the empirical logits for the probability of at least one IDF fire increase roughly linearly over low potential HFI on the log10 scale and then level off after the 2000 kW/m threshold above which operations may be restricted. (Note that we added one to the value of potential HFI bin midpoints to avoid taking the logarithm of a value less than one.) Conversely, for high potential HFI, it appears than an equivalent linear relationship is either non-existent or approximately levels off.

4.2 Conditional Logistic Regression

Given the exploratory results and that $\text {HFI} > 2000$ corresponds to the threshold when MIOP must start deciding on whether to enforce restrictions to hours of operation (Table 1), it is of interest to isolate the impact of MIOP on those days. We incorporate this threshold and these functional relationships into our modelling framework by defining:

$$\begin{aligned} x_\text {Low} = {\left\{ \begin{array}{ll} \log _{10}(\text {HFI} + 1), &{} \text { if HFI} \le 2000, \\ 0, &{} \text { if HFI}> 2000, \end{array}\right. } \quad x_\text {High} = {\left\{ \begin{array}{ll} 0, &{} \text { if HFI} \le 2000, \\ 1, &{}\text { if HFI} > 2000. \end{array}\right. } \end{aligned}$$

Here, $x_\text {Low}$ represents the linear relationship over low HFI on the log10 scale, which turns off and is replaced by a constant indicator $x_\text {High}$ when potential HFI is considered high. We are letting $x_\text {High}$ be a simple indicator function due to identifying no clear increasing relationship over the $\text {HFI} > 2000$ range.

As we wish to contrast MIOP against the other two time periods, we let MIOP be the default and define $x_\text {PreWoods}$ and $x_\text {Woods}$ as indicator variables that equal 1 when the time period for a given case or control is considered as Pre-Woods or Woods Guidelines, respectively (otherwise, they equal 0). We now consider the conditional logistic regression models

$$\begin{aligned} \text {logit}(P_{{\varvec{x}}}^{CC})&= \sum _{i=1}^m \alpha _{M_i} x_{M_i} + \beta _\text {Low}x_\text {Low} \nonumber \\&\quad + \beta _\text {High}x_\text {High} + \beta _\text {High:PreWoods}x_\text {High}x_\text {PreWoods} + \beta _\text {High:Woods}x_\text {High}x_\text {Woods} , \nonumber \\ \end{aligned}$$

(4.1)

and

$$\begin{aligned}&\text {logit}(P_{{\varvec{x}}}^{CC})= \sum _{i=1}^m \alpha _{M_i} x_{M_i} + \beta _\text {Low}x_\text {Low}\nonumber \\&\qquad \qquad \qquad + \beta _\text {Low:PreWoods}x_\text {Low}x_\text {PreWoods} + \beta _\text {Low:Woods}x_\text {Low}x_\text {Woods} \nonumber \\&\qquad \qquad \qquad + \beta _\text {High}x_\text {High} + \beta _\text {High:PreWoods}x_\text {High}x_\text {PreWoods} + \beta _\text {High:Woods}x_\text {High}x_\text {Woods}, \end{aligned}$$

(4.2)

where $x_{M_i} = 1$ iff an individual belongs to the $i^\text {th}$ matched set, $i=1,2,\ldots ,m$, and $m=775$ is the number of matched sets (Table 2). Note that none of the $\alpha _{M_i}$’s are estimated in practice. Equation (4.2) can be considered the full model containing interaction terms for both high and low potential HFI, while Eq. (4.1) only contains the interaction terms for high HFI.

Since the model in Eq. (4.1) is nested within Eq. (4.2), we may make use of the likelihood-ratio test to investigate the significance of the additional interaction terms in Eq. (4.2). This test will confirm whether it is a reasonable assumption to model the odds of IDF fire ignition marginally over the range of low HFI (i.e., grouping time periods together). Once we have identified our model of choice, we may investigate $\beta _\text {High:PreWoods}$ and $\beta _\text {High:Woods}$ to compare how the risk of IDF fire ignition may have changed between MIOP and preceding time periods on days with $\text {HFI} > 2000$.

Section 3.2 outlined how numerous controls can be created from our case data. Whether we elect to use all controls (denoted as the set of Final Controls in Table 2) or a subset of them will have an impact on our conditional logistic regression model fits and the likelihood ratio test. We present results in this paper under the following three scenarios:

• 1. All Data Use all control data to maximize statistical power.

• 2. Week 1 Use only controls whose dates are within 1–7 days of their nearest case. This focuses on the dates when we have the highest confidence that operations were being conducted in their areas.

• 3. Weeks 2–4 Use only controls whose dates are within 8–28 days of their nearest case. By selecting dates further away, their operations should be less impacted by the fire that was ignited on the nearest case date. Considering up through to the end of week 4 results in the inclusion of most data points omitted in the Week 1 scenario.

In these three scenarios, the likelihood-ratio test never provides sufficient evidence to justify using the more complex model in Eq. (4.2). We therefore present the resulting fits of Eq. (4.1) in Table 3 along with their respective likelihood ratio test p-values. In addition to these scenarios, we considered other combinations of weeks (i.e., only dates in week 2, 3, or 4, or only dates in weeks 1–2, 1–3, 1–4, 2–3, or 3–4), although those results are omitted. In every scenario, the coefficients $\beta _\text {High:PreWoods}$ and $\beta _\text {High:Woods}$ are both positive in the fit of Eq. (4.1), with the Pre-Woods interaction term being the largest. While there is never sufficient evidence to conclude that $\beta _\text {High:Woods}$ is significant, the p-value for $\beta _\text {High:PreWoods}$ is lower than 0.1 for all scenarios other than Weeks 1–2 and Weeks 1–3 (and is lower than 0.05 for the presented Weeks 2–4 scenario as well as Weeks 3–4). The scenarios with the smallest likelihood-ratio test p-values are when we only consider the third week or Weeks 3–4, with p-values of 0.0559 and 0.0824, respectively. Otherwise, no likelihood-ratio test p-value is below 0.16.

Table 3 Conditional logistic regression model fits of Eq. (4.1) under three scenarios of control date selection as outlined in Sect. 4.2. Additionally, p-values from the likelihood ratio test (LRT) comparing models from Eqs. (4.2) and (4.1) are presented

5 Discussion

We have investigated the relative impact of MIOP in contrast to Woods Guidelines and Pre-Woods on the frequency of industrial forestry-caused (IDF) fires. The level of restrictions enforced by MIOP can vary on a day-to-day basis depending on Fire Intensity Code (FIC), operational risk, and level of worker training. Consequently, we studied daily occurrences of IDF fires by conducting a case-crossover study that modelled the log-odds of the probability of observing one or more IDF fire ignitions.

Of the factors relevant to MIOP’s regulations, we can approximate potential Head Fire Intensity (HFI) which relates to FIC, but we have no data concerning the training level(s) of workers nor a day’s level of operational risk. An exploratory analysis (Fig. 5) showed that the log-odds of IDF fire ignition probability has an approximately linear relationship with $\log _{10}(\text {HFI}+1)$ for $\text {HFI} \le 2000$, corresponding to the range of conditions where no time restrictions are in place. Conversely, there was no clear increasing relationship in Fig. 5 for $\text {HFI} > 2000$, the threshold after which MIOP’s time restrictions may be enforced. Consequently, we used an indicator variable along with interaction terms which would enable us to test for differences between MIOP and the preceding time periods over the range of high HFI. Various subsets of control dates were considered, and a likelihood ratio test comparing the conditional logistic regression models in Eqs. (4.1) and (4.2) was conducted. It was determined that while including interaction terms for high HFI, there was insufficient evidence to justify the inclusion of interaction terms for low HFI (p-value $> 0.3$, Table 3). That is, it was OK to consider a single term for low HFI to represent this linear relationship for all three considered time periods.

In Table 3, we see that while the point estimates of the coefficients vary depending on what subset of controls we select, it is always the case that ${\hat{\beta }}_\text {High:PreWoods}> {\hat{\beta }}_\text {High:Woods} > 0$, including the omitted scenarios considered in our sensitivity analysis. Therefore, it appears that the probability of igniting an IDF fire while operating during these conditions under MIOP may be lower than under Woods Guidelines, which itself may be lower than under Pre-Woods. However, the standard errors are consistently too large to conclude that $\beta _\text {High:Woods}$ is significantly different from zero, so we have insufficient evidence to conclude that MIOP is indeed safer than Woods Guidelines. It should be pointed out, however, that due to the positive signs of the point estimates ${\hat{\beta }}_\text {High:Woods}$, there is no evidence that MIOP’s increased flexibility in possibly allowing longer working hours under increasing hazards relative to Woods Guidelines has resulted in an increased probability of igniting IDF fires. In contrast, there is some evidence in the form of relatively small p-values (i.e., either less than 0.10 or less than 0.05, depending on the scenario) to the significance of $\beta _\text {High:PreWoods}$. As such, as one would expect, we at least have some confidence in the claim that fewer fires are ignited during these riskier days under MIOP than in the oldest time period that lacked comparable prevention regulations.

5.1 Appropriateness of the Case-Crossover Study and Potential Biases

As outlined by Borgan et al. (2018), several key assumptions must be met for the analysis of a case-crossover study to be trustworthy. We list these assumptions in their decreasing order of importance and consider whether our study meets each assumption.

• 1. Transient exposure We measure exposure in terms of potential Head Fire Intensity (HFI). Depending on weather conditions, particularly rainfall, potential HFI in an area can experience notable variations over the course of a few days. For example, it is possible that an area may experience a high value of HFI one day but return to low or negligible HFI during the following week. Therefore, as the amount of exposure can reduce or go away entirely, exposure is transient by definition.

• 2. Acute outcome The ignition of an industrial forestry-caused (IDF) fire is typically instantaneous, so there is minimal risk of exposure misclassification due to recording incorrect dates. When MIOP restricts the hours of daily operations, dedicated patrols are mandatory after operations conclude for the day. These patrols provide a way to discover and report undetected fires that may have ignited as a result of that day’s operations.

• 3. No underlying time trends Potential HFI can be increasing or decreasing across sequential days depending on extended weather events (e.g., a period of hot and dry weather). However, we make use of bidirectional sampling whenever possible when selecting our referent times. Among our 989 cases, there are 958 without large fires and 31 with one or more large fires. Of the 958 cases with only non-large fires, 6 Pre-Woods cases lack bidirectional sampling due to their dates being too close to the beginning or end of when we have sufficient weather data, while a single Woods Guidelines case lacks bidirectional sampling due to a nearby large fire on the previous day (Assumption 4, Sect. 3.2). Of the 31 large-fire cases, there are two such cases in each time period with bidirectional sampling, while the other 25 only have controls on dates prior to their case dates.

  Cases that have large fires tend to have high HFI more frequently than low. If we consider a likely situation where HFI had been increasing over several days leading up to a large fire, then the resulting bias from a lack of bidirectional sampling should be exaggerating the risk of forestry operations conducted under conditions of high values of potential HFI. However, there is also high HFI on many days with non-large fires, and in fact we have bidirectional sampling for $87.8\%$, $94.2\%$, and $91.8\%$ of high HFI cases during Pre-Woods, Woods Guidelines, and MIOP, respectively. Therefore, the potential bias incurred from the occasional lack of bidirectional sampling should be minimal.

• 4. Constant effect MIOP’s restrictions will be the same on days whose operations pose similar risks if the days’ values of potential HFI are comparable (assuming the personnel have the same training level). It therefore must be a reasonable assumption that the amount of risk related to FIC (and hence, potential HFI) on such days is also comparable. However, note that as we do not have operations data, we must rely on the assumption that the impacts of different operational risks average out, which is not guaranteed.

• 5. Outcome does not influence future exposures This is required when using bidirectional sampling. If an IDF fire was not large enough to prevent bidirectional sampling, then the smoke it generates should not impact the localized weather and potential HFI values over subsequent days.

• 6. No unmeasured time-varying confounders Depending on the subset of control data used in the conditional logistic regression, we may be more or less likely to encounter an unmeasured time-varying confounder depending on how close the control dates are to their case dates. The impacts of varying weather systems are incorporated into our measurement of potential HFI, but one or more possible unmeasured time-varying confounders influencing ignition probability related to operations may exist.

Given the above discussions, outside of the potential for a small amount of bias resulting from how we treat cases with large fires and some uncertainty stemming from the lack of precise daily operations data, there is nothing to suggest that a case-crossover study is an inappropriate way to analyze our dataset. While we are less certain about Assumption 6, it is the least important of these assumptions according to Borgan et al. (2018).

While a case-crossover method is appropriate for our analysis, bias is possible. In what follows we discuss three possible sources of bias and how they relate to our study design.

• 1. Confounding Bias In the discussion of Assumption 6, we have already noted the possibility of short-term unmeasured time-varying confounders related to what operations were being conducted. Additionally, since all referent times for a matched set are within a few weeks of their observed cases, we are incidentally matching based on year. Therefore, a possible long-term confounder is any impacts from improvements in methodology and technology that make operations safer, which would be confounded with the effects of regulations enforced in more recent time periods. This is not necessarily the only source of long-term confounding, but rather the most obvious one.

• 2. Information Bias We measure exposure in terms of potential HFI, which is approximated and hence comes with some inaccuracies (e.g., assuming constant fuel source proportions in an area across multiple decades, interpolating weather variables). These inaccuracies should be largest for higher values of potential HFI where its sensitivities to fuel types are more pronounced. Fortunately, in our conditional logistic regression models, we use a log10 transform on values of HFI below 2000, which compresses them into a smaller range that lessens the impact of a modest discrepancy from the true value due to inaccuracy. Also, we bin together the values of potential HFI exceeding 2000 through the definition of $x_\text {High}$, removing the impact of inaccuracies on days with the highest potential HFI values (i.e., so long as the true and approximated values are both over 2000, $x_\text {High}$ will correctly take on a value of 1). Therefore, the overall impact of inaccuracies when approximating HFI should be limited.

  When selecting our referent times, we are assuming that forestry operations are occurring in a particular area on days when we did not observe any fires. Realistically, there are many referent times used in our analysis corresponding to days when there were not operations which lowers the overall perceived risk of forestry operations. However, since we are not modelling absolute ignition probabilities, but rather, odds, this should not result in a systematic bias in our results. The approximated relationship between the odds of ignition and potential HFI may still have been impacted if, say, a referent time was less likely to have had operations at higher values of potential HFI. However, we would not necessarily count all referent times without operations at high HFI due to MIOP or Woods Guidelines restrictions as inaccuracies, since prohibiting operations is one way that these regulations attempt to prevent ignitions in those extreme weather situations.

• 3. Selection Bias Since we select controls solely based on case data, we are missing information pertaining to companies who operated safely over a time period and location without igniting any IDF fires. The absence of this data in an analysis would increase the perceived risk of forestry operations. However, due to the nature of how conditional logistic regression models are fit to matched sets of data using a conditional likelihood function, the absence of this data has no impact and hence cannot result in bias. For details on why this is true, refer to Appendix B.

5.2 Data Needs for Future Work

The primary limitation of our study is from a lack of fine-scale spatiotemporal harvesting data. Such data would improve the identification of controls, as it would no longer be required to make assumptions to enable the selection of referent times. These data are not feasible to collect for the entire province, but it could make for an interesting case study within a single district. Additionally, the quantity of work done on a day is likely strongly related to the probability of igniting one or more IDF fires (i.e., more operations result in more chances of ignition), so controlling for this currently unmeasured predictor would improve the accuracy of our results.

It would be interesting to investigate the operational risk and/or forestry personnel fire suppression training level for industrial forestry activities, since these represent more precise knowledge of MIOP’s daily restrictions as outlined in Table 1. Such information could be used to extend our analysis. For example, whether a forestry company was operating under compliance of either set of regulations when a given IDF fire was ignited is not incorporated into our analysis. Tracking such information would be necessary for future work to investigate how compliance may impact IDF fire occurrences.

6 Conclusions

While we have found some evidence of IDF fire ignitions on high HFI days being less common under MIOP than during Pre-Woods, we are unable to conclude that the frequency of IDF fire ignitions on these days has been lowered in comparison with Woods Guidelines. However, MIOP represented a modification of the Woods Guidelines to provide increase flexibility in working hours on days with more extreme fire hazards. From our results, we conclude that MIOP has met the desired outcome of increased flexibility without violating its first objective, namely industrial operations being conducted in a manner that prevents wildfires from starting and does not increase the seasonal forest fire load.

Appendices

Appendix A: Algorithms to Convert Observed IDF Fire Data into Study Units

In order to group observed IDF fires into sets and create non-overlapping blocks to act as study units, the following three algorithms were applied for every individual year from 1976 to 2019. We begin with Algorithm 1 which determines how to group fires ignited within a given year into sets.

Algorithm 1
Group IDF fires into sets that can be contained in a $30 \text { km} \times 30 \text { km}$ block of land.
(i) Assign each IDF fire to its own set.
(ii) Calculate the pairwise distances between every combination of IDF fires belonging to differing sets.
(iii) Determine the two sets whose maximum pairwise distance between any two of their points is the smallest.
(iv) If the smallest maximum distance identified in Step 1(iii) is less than 30 km, merge the two corresponding sets and return to Step 1(ii). Otherwise, stop.

If the smallest maximum pairwise distance identified in Algorithm 1’s Step 1(iii) is less than 30 km, then every pairwise distance between points in the new merged set created in Step 1(iv) will be less than 30 km. This guarantees that every point in the merged set can be covered by a single $30 \text { km} \times 30 \text { km}$ block of land. Next, once all sets have been determined, we create preliminary blocks of land for each set according to Algorithm 2.

Algorithm 2
Create $30 \text { km} \times 30 \text { km}$ blocks of land for each set of fires.
(i) For each set i containing $n_i = 1$ IDF fires, construct their blocks by placing their centers on the respective fire ignition locations.
(ii) For each set i containing $n_i > 1$ IDF fires, construct their blocks by placing their centers on the locations that minimize an objective function whose value is determined as described by the following pseudocode. Letting $B_i$ denote block i and $F_{i,j}, j=1,\ldots ,n_i$ denote set i’s fires, the objective function equals
$\quad f(i) = \, \texttt {function}(B_i)\{$
$\quad \texttt {if}(\exists \, j \in \{\texttt {1:}n_i\} \texttt { such}\, \texttt {that } B_i\texttt { fails}\, \texttt {to}\, \texttt {cover }\,F_{i,j})\{$
$\qquad \texttt {return } \infty$
$\quad \} \texttt { else} \{$
$\qquad \texttt {for}(j \texttt { in}\,\texttt { 1:}n_i)\{$
$\qquad Dist _{i,j} = \texttt { distance}\,(\texttt {center}(B_i), F_{i,j})$
$\qquad \}$
$\qquad \texttt {return}\, \texttt {max}( Dist _{i,j}, j \in \{\texttt {1:}n_i\})$
$\quad \}$
$\}$
The halfway points between the smallest and largest longitude and latitude values amongst set i fire locations are used as the initial guess for $B_i$’s center in the optimization.

When creating a block of land for a set having multiple fires, Algorithm 2 ensures that all fires are covered by their set’s block while minimizing the maximum distance from the center of the block to its set’s fire ignition locations. Illustrations of some optimal block constructions for sets having one, two, or more than two IDF fires are presented in Fig. 2. After constructing the initial blocks, we use Algorithm 3 to adjust the positions of blocks that overlap each other to ensure independence of our study units.

Algorithm 3
Adjust some block locations to ensure that none spatially overlap.
(i) Determine which sets’ boxes spatially intersect each other. If there is at least one intersection, advance to Step 3(ii). Otherwise, stop.
(ii) Group together all sets whose blocks spatially intersect at least one other set’s block in that group.
(iii) Sequentially, consider each group k of sets identified in Step 3(ii) on its own and determine new block center positions by minimizing an objective function whose value is determined as described by the following pseudocode. Reusing the notation from Algorithm 2 and letting $G_k$ denote the vector containing as elements the indicies of the sets in group k, the objective function equals
$\quad g(k) = \,\texttt {function}(B_i, i \in G_k)\{$
$\qquad \texttt {if}(\exists \, i \in G_k, j \notin G_k \texttt { such}\, \texttt {that}\,\,\, B_i\,\texttt { intersects }\,B_j)\{$
$\quad \texttt {return } \infty$
$\qquad \} \texttt { else}\, \texttt {if}\,(\exists \, i \in G_k, j \in \{\texttt {1:}n_i\} \texttt { such}\, \texttt {that }\,B_i\texttt { fails}\, \texttt {to}\, \texttt {cover }F_{i,j}) \{$
$\quad \texttt {return } \infty$
$\qquad \} \texttt { else}\{$
$\quad A = 0$
$\quad \texttt {for}(i \in G_k)\{$
$\qquad \, \texttt {for}(j \texttt { in 1:}n_i)\{$
$\quad \quad Dist _{i,j} = \texttt { distance}(\texttt {center}(B_i), F_{i,j})$
$\qquad \, \}$
$\qquad \, MD _i = \texttt { max}( Dist _{i,j}, j \in \{\texttt {1:}n_i\})$
$\qquad \, \texttt {for}(j \in G_k, j \ne i)\{$
$\quad \quad A = A + \texttt {area}(B_i \cap B_j)$
$\qquad \, \}$
$\quad \}$
$\quad P = 10,000,000 \times (A / \texttt {area}(\cup B_i, i \in G_k))$
$\quad \texttt {return}\,\texttt {max}( MD _i, i \in G_k) + \texttt {mean}( MD _i, i \in G_k) + P$
$\qquad \}$
$\}$
The blocks’ original locations are used as initial guesses in the optimization.

The initial locations of the blocks in group k are guaranteed to not result in intersections with blocks from other groups (by the construction of groups in Step 3(ii)), and they are guaranteed to cover their respective fires (by the definition of Step 2(ii)’s objective function). Hence, the first two conditionals in Step 3(iii)’s objective function will not result in returning a value of infinity at our initial guesses, but a potential future violation of either of these constraints will automatically result in a rejection by the optimizer. Figure 3 visualizes a scenario with two overlapping blocks needing a shift in position for one or both of them, in addition to two potential shifts that would be rejected due to violating one of these constraints and a third shift that would be acceptable.

Conversely, our initial guesses will violate the constraint that blocks within the same group should not intersect each other. Note that the definition and inclusion of P are to speed up the optimization with this constraint in mind. We elect to return a function of the continuous value P, which is proportional to the total area of overlap A instead of simply returning infinity if there was any amount of overlap between a group’s blocks. This allows the optimizer to make quick incremental steps that reduce the amount of overlap, without requiring the overlap to be completely removed in one step (which may be difficult for the optimizer to locate without working knowledge of how much overlap there is at a given step, especially since violating either of the other two constraints would also return values of infinity). For our data, the value of 10,000,000 used in the calculation of penalty P was sufficient to completely remove all intersections, with the exception of two blocks in 1999 that maintained a negligible overlapped area of less than 0.1 $\text {m}^2$ (while the individual areas of both blocks are slightly over 900 $\text {km}^2$). This constant could be increased to enforce the constraint of no overlapping blocks more strictly.

If all overlap is removable, then the objective function reduces to the sum of two other components. The use of both $\text {max}( MD _i, i \in G_k)$ and $\text {mean}( MD _i, i \in G_k)$ places higher weighting on minimizing the largest maximum distance between a block and its set’s fire locations out of all blocks in a group, while still encouraging the minimization of this equivalent distance in other blocks. Note that in our implementation of these algorithms, distances were measured in meters. In the absence of the mean term, the optimizer may neglect an obvious improvement in a block’s location if moving it would not result in a change in the largest of these distances.

Appendix B: The Lack of Influence on Conditional Logistic Regression Results by Matched Sets Containing no Cases

A conditional logistic regression involves the maximization of a conditional likelihood function where each set’s contribution to said likelihood is the conditional probability of observing the specific combination of individuals being cases and controls given their risk factors as well as the total number of cases in the set. To define this probability, we first let $J_i$ equal the total number of individuals in the $i^\text {th}$ set, $d_{i,j}$ equal 1 if the $j^\text {th}$ member of the $i^\text {th}$ set is a case or 0 if they are a control, $D_i$ equal the total number of cases in the $i^\text {th}$ set, and $x_{i,j}$ equal the vector of risk factors for the $j^\text {th}$ member of the $i^\text {th}$ set. If we suppose that the individuals are indexed so that $1,2,\ldots ,D_i$ are cases while $D_i+1,D_i+2,...,J_i$ are controls, then the conditional probability of interest (i.e., the $i^\text {th}$’s set’s contribution to the conditional likelihood) is:

$$\begin{aligned} P\left( d_{i,1} = 1, \ldots , d_{i,D_i} = 1, d_{i,D_i+1} = 0, \ldots , d_{i,J_i} = 0 \Bigg | x_{i,1},\ldots ,x_{i,J_i}, \sum _{j=1}^{J_i} d_{i,j} = D_i \right) . \end{aligned}$$

This may in general be evaluated using the Bayes’ theorem.

Note that if a set has no controls (i.e., $D_i = 0$), this conditional probability simplifies to

$$\begin{aligned} P\left( d_{i,1} = 0, \ldots , d_{i,J_i} = 0 \Bigg | x_{i,1},\ldots ,x_{i,J_i}, \sum _{j=1}^{J_i} d_{i,j} = 0 \right) = 1, \end{aligned}$$

which immediately follows from the fact that each $d_{i,j}$ may only take on values of 0 or 1. Therefore, as this conditional probability is trivial, it has no impact on the conditional likelihood maximization. An analogous result also holds true if every member in a matched set is a case (i.e., $D_i = J_i$). In our study, since the presence of data describing matched sets without cases (i.e., sites that experienced no fires from a year’s operations) would have no impact on the conditional likelihood function, the absence of this data cannot result in any biases.