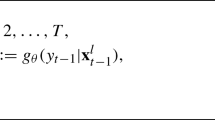Caste-Specific Demography and Phenology in Bumblebees: Modelling BeeWalk Data

Abstract

We present novel dynamic mixture models for the monitoring of bumblebee populations on an unprecedented geographical scale, motivated by the UK citizen science scheme BeeWalk. The models allow us for the first time to estimate bumblebee phenology and within-season productivity, defined as the number of individuals in each caste per colony in the population in that year, from citizen science data. All of these parameters are estimated separately for each caste, giving a means of considerable ecological detail in examining temporal changes in the complex life cycle of a social insect in the wild. Due to the dynamic nature of the models, we are able to produce population trends for a number of UK bumblebee species using the available time-series. Via an additional simulation exercise, we show the extent to which useful information will increase if the survey continues, and expands in scale, as expected. Bumblebees are extraordinarily important components of the ecosystem, providing pollination services of vast economic impact and functioning as indicator species for changes in climate or land use. Our results demonstrate the changes in both phenology and productivity between years and provide an invaluable tool for monitoring bumblebee populations, many of which are in decline, in the UK and around the world. Supplementary materials accompanying this paper appear online.

1 Introduction

Over the past 80 years, two bumblebee species have gone extinct in the UK (Ollerton et al. 2014). Many more have undergone severe contractions in range over the same period, with some species now restricted to tiny fractions of their former distributions (Goulson et al. 2008; Ollerton et al. 2014; Woodcock et al. 2016). Other than these long-term, large-scale distributional changes, little is known about how bumblebee populations have changed over time, even in those species which have remained widespread.

It is likely that both common and localised species have been negatively affected by both pre- and post-war agricultural changes (Ollerton et al. 2014; Rasmont et al. 2015; Woodcock et al. 2016). This is important because bumblebees are major pollinators of many commercial crop species, as well as of the majority of wild and garden plants (Klein et al. 2007; Potts et al. 2010; Garibaldi et al. 2013). Declines, either of distribution or abundance, are thus of serious concern from agricultural and economic viewpoints as well as from a conservation point of view (Garratt et al. 2014; Vanbergen et al. 2014; Hanley et al. 2014; Pywell et al. 2015). Despite this, attempts to discern the precise extent and causes of population trends have been limited by the paucity of data from a wide geographical scale. With this in mind, the Bumblebee Conservation Trust (BBCT) initiated the BeeWalk citizen science scheme in 2009 to gather nationwide data on all bumblebee species from a volunteer-based standardised transect survey (Comont 2017, http://www.beewalk.org.uk).

We introduce in this paper an analytical approach motivated by, and designed for, bumblebee count data, accommodating the ecology of the species and thereby producing invaluable information on demographic parameters, such as indices of caste-specific relative abundance, amongst others. Due to their reliance on sources of nectar and pollen, bumblebees function also as valuable indicators of climatic change through changes in their demography and phenology. The monitoring of changes in these factors too follows directly from the proposed mixture model.

Bumblebees are primitively eusocial insects, with a colony-based annual life cycle. They use a simple caste-based social system, with queens (reproductive females, produced at the end of the colony, that found new colonies in spring after overwintering), workers (sterile female foragers, daughters of the queens), and males (produced at the end of the colony for reproductive purposes only). Each of these castes reaches peak abundance at different stages in the colony life cycle. The relative proportion of each caste is indicative of the stage and health of the colony, and thus is more informative than raw counts of the species alone. Therefore, it is unfortunate that assigning bumblebees to caste in the field is difficult for many species, and so for many detected individuals this remains unknown. Furthermore, the two generations of queens encountered during a season, those emerging from hibernation in the spring, termed here old queens, and their summer offspring, termed new queens, cannot reliably be visually separated. We extend the model developed for successive broods of multivoltine butterflies by Matechou et al. (2014) and its extensions presented in Dennis et al. (2016a, b) in such a way that these uncertainties are explicitly modelled, without the need (for example) to decree a priori that queens are first or second generation using an arbitrary separation date.

Dennis et al. (2016b) model butterfly data using “productivity” parameters to link the successive generations. In bumblebees, successive castes are not necessarily the offspring of the previous caste; rather, each annual caste count obviously comprises the offspring of the old queens in that season. Our model also extends that of Dennis et al. (2016b) in order to estimate these ecologically important rates of within-season productivity, which now index aspects of colony size.

Compared to the butterfly data modelled by Matechou et al. (2014), the more recently introduced BeeWalk contains data which are shorter in duration and more sparsely distributed across the survey season. BeeWalk data are collected monthly (rather than weekly), and accurate modelling of phenology requires use of a finer temporal resolution than this. Hence, we divide the season into 40 weeks beginning on 1 March each year, but with data for each site collected only on a subset of these weeks, usually up to five or six, each year, which results in a very sparse data set with most of the possible entries missing. As a result, we could not estimate site-specific parameters here, such as site-specific relative abundance per caste. We deal with the large number of missing data points implied by this change of resolution by considering the aggregate of counts across all sites. Additionally, the central-place foraging model employed by bumblebees means that they are not distributed haphazardly across each site, but instead are biased towards flight corridors between the nest and favoured foraging sites (Cresswell et al. 2000; Hagen et al. 2011). Our proposed solution of aggregating counts from sites across the UK minimises the effect of this as well as solving issues with fitting such complex models to sparse data, and it also provides country-wide interpretation of bumblebee trends.

An additional advantage of our method is that estimation of the phenology and relative numbers in each caste remains possible from such aggregated data, via the adoption of a mixture model in which the proportions of observations in each caste are additional, estimable parameters. This combination of a rigorous statistical method and ongoing, large-scale data collection greatly increases the capacity to identify changes experienced by wild bumblebee populations and facilitates the adoption, and assessment, of any agri-environment schemes aimed at the recovery of these species and the pollination services they provide.

2 Data

The BeeWalk survey is carried out by a large number of volunteers who each select a local transect on which they carry out a walk on a monthly basis, within times of day and weather conditions designated to be consistent with bumblebee activity. Bumblebees encountered within an imaginary $4\times 4\times 2\,\hbox {m}$ “recording box” are counted and identified (where possible). The recording box extends out to four metres ahead of the observer, from the ground surface to two metres up, and out to two metres either side of the observer (centred on the nominal transect line), following the example of the long-running Butterfly Monitoring Scheme (Brereton et al. 2017).

By the end of the 2016 season, over 6000 visits at nearly 800 sites had taken place as part of the BeeWalk scheme. In this paper, we consider data collected between 2011 and 2016 on the Garden bumblebee Bombus hortorum, the Tree bumblebee Bombus hypnorum, the Red-tailed bumblebee Bombus lapidarius, the Common carder bumblebee Bombus pascuorum, and the Early bumblebee Bombus pratorum. The total counts obtained by BeeWalk volunteers for each of these species are around 7000, 6000, 26,000, 40,000 and 9000, respectively.

There are three biological castes of bumblebees: queens (Q), workers (W) and males (M) fulfilling different ecological roles. Furthermore, within each year there are two generations of Q: old, $Q_{_{\!{o}}}$, and new, $Q_{_{\!{n}}}$, which are visually indistinguishable from one another in the field. In addition, even for W and M, detected individuals may not have their caste identified. Therefore, each bumblebee detected is categorised as belonging to one of four groups: Q, W, M or U (with the latter signifying the individuals that did not have their biological caste identified), but not separately as $Q_{_{\!{o}}}$ or $Q_{_{\!{n}}}$. However, it is important to model changes in demography and phenology of these latter two generations separately. Hence, we build our new model in a way that allows us to perform inference on $Q_{_{\!{o}}}$, W, M and $Q_{_{\!{n}}}$ which for convenience we refer to as the four (rather than three) castes and denote by $c=1,\ldots ,4$ for $Q_{_{\!{o}}}$, W, M and $Q_{_{\!{n}}}$, respectively.

We present here (Table 1) an artificial data set for a single sampling occasion which clarifies the difference between the three biological castes, and the four castes and the four groups as we defined them above. We highlight here that, as mentioned above, only the groups are observed; thus, it is to the counts in these that the model will be fitted. Finally, we note that the total count of group U for the species considered is around 400 for B. hortorum, which corresponds to about 5% of the total count while the corresponding numbers and proportions for the other species are around: B. hypnorum: 700 (11%), B. lapidarius: 800 (3%), B. pascuorum 3600 (9%) and B. pratorum: 400 (4%).

Table 1 Artificial data set for a single sampling occasion.

3 Models

Data are collected at S sites in Y seasons or years, and there are T sampling occasions within each year, assumed to be equally spaced apart. We denote the year by y, $y=1,\ldots ,Y$ and the sampling occasion, which we refer to as time, by t, $t=1,\ldots ,T$ . In practice, visits are not synchronised across sites and many potential samplings will not be carried out, so for the BeeWalk data with sampling occasions corresponding to weeks in the season, even in the latter years less than 10% of the sites are visited on average in any given week.

We consider the aggregate of counts collected at all S sites at each time t, and hence, the data are summarised in $\mathbf {X}$ of dimension $Y\times T \times 4$ with the third dimension, which we denote by $g=1,\ldots ,4$ denoting the group, Q, W, M, U, to which an individual has been assigned. That is, $x_{yt1}$ is the total number of Q, both $Q_{_{\!{o}}}$ and $Q_{_{\!{n}}}$ since they are indistinguishable, detected in year y and at time t and $x_{yt2}$ and $x_{yt3}$ the corresponding counts for W and M, respectively. Finally, $x_{yt4}$ denotes the number of individuals that were detected in year y and at time t that did not have their caste identified.

We model $x_{ytg}$ as the realisation of a Poisson distribution with mean $\lambda _{ytg}$ corresponding to the expected number of individuals detected and assigned to group g in year y and time t at all sites. Since we consider the aggregate count across sites and not every site is visited at each time, i.e. not all S sites contribute to all counts at all times/years, we further decompose $\lambda _{ytg}$ into $\kappa _{ytg}$, which is the average number of individuals per site, i.e. the rate, assigned to group g in year y and time t, and the total number of sites contributing to that count, $n_{yt}$. That is, the expected number of individuals detected and assigned to group g in year y and time t is the product of the rate in group g, year y, time t and the total number of sites visited in year y, time t: $\lambda _{ytg}=n_{yt}\kappa _{ytg}$. This is equivalent to modelling rates using a Poisson regression that includes an offset term, which in our case is the number of sites visited each week. The fact that some (indeed most) individuals have their caste identified requires a modification to the model of Matechou et al. (2014), in which for multivoltine species all butterflies encountered are assumed to have come from one of two or more broods with probabilities estimated under the model. The fact that some bumblebees can be immediately assigned to a recognisable caste is clearly additional information that can improve the performance of the model; the fact that some remain unidentified, however, and especially the fact that $Q_{_{\!{o}}}$ are indistinguishable to $Q_{_{\!{n}}}$, means that a mixture model to account for this uncertainty remains necessary.

We employ the notation established in the capture-recapture stopover literature (Schwarz and Arnason 1996; Pledger et al. 2009; Matechou et al. 2013) and also used by Matechou et al. (2014) and express $\kappa _{ytg}$ as a function of the following model parameters:

• $N_{yc}$: relative abundance (RA) of caste c in year y. This does not correspond to the number of unique individuals detected or to the number of unique individuals available for detection, i.e. super-population (Schwarz and Arnason 1996; Pledger et al. 2009), but under the assumption that initial detection probabilities (per caste) are constant over time, this can be considered proportional to true population abundance (Matechou et al. 2014).

• $\rho _{yc}$: within-season productivity parameter; number of individuals in caste c per $Q_{_{\!{o}}}$, i.e. per (potential) colony, in year y. Hence, $\rho _{y{Q_{_{\!{o}}}}}=1\ \forall y$. Using a deterministic model for the relationship between RA and productivity, we write

  $$\begin{aligned} N_{yc}=N_{y{Q_{_{\!{o}}}}}\rho _{yc}\ \forall y, c. \end{aligned}$$

  (1)

• $\beta _{y(t-1)c}$: entry parameter; the probability an individual from caste c in year y emerges, from the nest or from winter dormancy as appropriate, between times $t-1$ and t, $t\in \{1,\ldots ,T\}$. We model the emergence pattern of each caste using the probability density function of a normal distribution while allowing each caste to have its own mean emergence time in year y, $\mu _{yc}$, and its own variance of arrival times, $\sigma ^2_{yc}$, that is $\beta _{y(t-1)c}=F_{yc}(t)-F_{yc}(t-1)$ where $F_{yc}$ is the cumulative distribution function of $N(\mu _{yc}, \sigma ^2_{yc})$. We treat the first and last intervals as open-ended and set $\beta _{y0c}=F_{yc}(1)$ and $\beta _{y(T-1)c}=1-\sum _{t=1}^{T-1}\beta _{y(t-1)c}$, ensuring that $\sum _{t=1}^T\beta _{y(t-1)c}=1\ \forall y, c$.

• $\xi _{(y-1)}$: winter survival probability; the probability a $Q_{_{\!{n}}}$ survives the winter in year $y-1$ and hence is available for detection, as a $Q_{_{\!{o}}}$, in year y. Once more, using a deterministic model for the relationship between RA and winter survival we write: $N_{y{Q_{_{\!{o}}}}}=N_{(y-1){Q_{_{\!{n}}}}}\xi _{(y-1)}$ which then allows us to express the RA of individuals in all castes in year y as a function of the RA of $Q_{_{\!{n}}}$ in year $y-1$ and hence, as a consequence of Eq. (1), as a function of RA of $Q_{_{\!{o}}}$ in year $y-1$: $N_{y{Q_{_{\!{o}}}}}=N_{(y-1){Q_{_{\!{n}}}}}\xi _{(y-1)}=N_{(y-1){Q_{_{\!{o}}}}}\rho _{(y-1){Q_{_{\!{n}}}}}\xi _{(y-1)}$ and similarly $N_{yc}=N_{(y-1){Q_{_{\!{o}}}}}\rho _{(y-1){Q_{_{\!{n}}}}}\xi _{(y-1)}\rho _{yc}$, for $c\in \{W, M, Q_{_{\!{n}}}\}$. Finally, we obtain the following recursive formula for the RA of caste c in year y

  $$\begin{aligned} N_{yc}=N_{1{Q_{_{\!{o}}}}}\prod _{j=1}^{y-1}\Bigg (\rho _{j{Q_{_{\!{n}}}}}\xi _{j}\Bigg )\rho _{yc}. \end{aligned}$$

  (2)

• $\phi _{ybtc}$: caste-specific within-season apparent weekly survival probability; the probability an individual from caste c that emerged between time $b-1$ and b in year y and is alive at time t survives and hence is available for detection at time $t+1$. Note that an individual can become unavailable for detection either because of death or because of emigration or, in the case of $Q_{_{\!{n}}}$, because of hibernation.

• $\psi _{ytc}$: identification probability; the probability an individual from caste c in year y that is detected at time t has its caste identified.

The rate in cell y, t, g is given by

$\underline{Q, g=1}$ :

$$\begin{aligned} \begin{aligned} \kappa _{yt{Q_{_{\!{o}}}}}+\kappa _{yt{Q_{_{\!{n}}}}}&= N_{y{Q_{_{\!{o}}}}}\sum _{b=1}^t\left[ \beta _{y(b-1){Q_{_{\!{o}}}}}\prod _{k=b}^{t-1}\Bigg \{\phi _{ybk{Q_{_{\!{o}}}}}\Bigg \}\right] \psi _{yt{Q_{_{\!{o}}}}}\\&\quad +\,N_{y{Q_{_{\!{n}}}}}\sum _{b=1}^t\left[ \beta _{y(b-1){Q_{_{\!{n}}}}}\prod _{k=b}^{t-1}\Bigg \{\phi _{ybk{Q_{_{\!{n}}}}}\Bigg \}\right] \psi _{yt{Q_{_{\!{n}}}}}. \end{aligned} \end{aligned}$$

(3)

$\underline{W, g=2}$ :

$$\begin{aligned} \begin{aligned} \kappa _{yt{W}}= N_{y{W}}\sum _{b=1}^t\left[ \beta _{y(b-1){W}}\prod _{k=b}^{t-1}\Bigg \{\phi _{ybk{W}}\Bigg \}\right] \psi _{yt{W}}. \end{aligned} \end{aligned}$$

(4)

$\underline{M, g=3}$ :

$$\begin{aligned} \begin{aligned} \kappa _{yt{M}}= N_{y{M}}\sum _{b=1}^t\left[ \beta _{y(b-1){M}}\prod _{k=b}^{t-1}\Bigg \{\phi _{ybk{M}}\Bigg \}\right] \psi _{yt{M}}. \end{aligned} \end{aligned}$$

(5)

$\underline{U, g=4}$ :

$$\begin{aligned} \begin{aligned} \kappa _{yt{U}}&= \kappa _{yt{Q_{_{\!{o}}}}}\frac{(1-\psi _{yt{Q_{_{\!{o}}}}})}{\psi _{yt{Q_{_{\!{o}}}}}}+\kappa _{yt{Q_{_{\!{n}}}}}\frac{(1-\psi _{yt{Q_{_{\!{n}}}}})}{\psi _{yt{Q_{_{\!{n}}}}}} \\&\quad +\, \kappa _{yt{W}}\frac{(1-\psi _{yt{W}})}{\psi _{yt{W}}} + \kappa _{yt{M}}\frac{(1-\psi _{yt{M}})}{\psi _{yt{M}}}. \end{aligned} \end{aligned}$$

(6)

We denote the vector of parameters by $\pmb \theta$. Assuming independence between all years, groups and between all sampling occasions, the likelihood function is given by

$$\begin{aligned} \begin{aligned} L(\pmb \theta ;\mathbf {X})&= \prod _{y=1}^Y\prod _{t=1}^T\left[ \left\{ \frac{e^{(-\lambda _{yt{Q_{_{\!{o}}}}}-\lambda _{yt{Q_{_{\!{n}}}}})}\left( \lambda _{yt{Q_{_{\!{o}}}}}+\lambda _{yt{Q_{_{\!{n}}}}}\right) ^{x_{yt1}}}{x_{yt1}!}\right\} \right. \\&\quad \times \,\left\{ \frac{e^{-\lambda _{yt{W}}}\left( \lambda _{yt{W}}\right) ^{x_{yt2}}}{x_{yt2}!}\right\} \times \left\{ \frac{e^{-\lambda _{yt{M}}}\left( \lambda _{yt{M}}\right) ^{x_{yt3}}}{x_{yt3}!}\right\} \times \left. \left\{ \frac{e^{-\lambda _{yt{U}}}\left( \lambda _{yt{U}}\right) ^{x_{yt4}}}{x_{yt4}!}\right\} \right] . \end{aligned} \end{aligned}$$

(7)

We fit the model using function optim in R (R Core Team 2016) to maximise the log of the likelihood shown in Eq. (7). We employ constraints, chosen based on biological knowledge of the species, during optimisation for parameters referring to the emergence pattern of the different castes. For example, mean emergence time of $Q_{_{\!{o}}}$ is constrained to be before week eight in the season, while mean emergence times of W and $Q_{_{\!{n}}}$/M are constrained to be after weeks five and eight, respectively. The variance of emergence times for all castes is constrained to be less than 15 weeks. These constraints ensure that the optimisation algorithm does not consume time exploring regions of the parameter space that are infeasible, although their usefulness decreases as sample sizes increase. Finally, we consider at least five different sets of starting values for the parameters and select the fit with the highest resulting log-likelihood value obtained as the final fit in each case; if this maximum value for the log-likelihood is only obtained once in the five runs, then we perform more runs using different starting values for the parameters.

The formatted data for the purposes of this paper and the code to fit the models are given as supplementary material. The original BeeWalk data are available from https://registry.nbnatlas.org/public/show/dp99.

4 Results

To match the species’ ecology, the various parameters are largely required to differ between castes, and for monitoring purposes the model’s appeal lies in the capacity to consider, for example, the extent to which these vary over successive seasons. The number of potential models that might be fitted is therefore very high, and here we consider a single, general model to illustrate the breadth of information that is accessible using the BeeWalk data and our proposed model. We denote the model considered by $\rho (cy)\xi (y)\mu (cy)\sigma (c)\phi (cy)\psi (cy_l)$. Each term is explained below:

• $\rho (cy)$: caste- and year- specific within-season productivity,

• $\xi (y)$: year-specific winter survival of Q,

• $\mu (cy)$: caste- and year- specific mean emergence time,

• $\sigma (c)$: caste-specific standard deviation of emergence times,

• $\phi (cy)$: caste- and year-specific weekly apparent survival probability,

• $\psi (cy_l)$: caste- and year-specific identification probability. The l subscript indicates here that the year effect y is modelled using a logistic regression function, with year as the independent variable, in order to (i) reduce the number of parameters introduced and (ii) represent our expectation regarding changes in the probability of identifying the caste of a detected individual: as the scheme grows and attracts more and more volunteers, we expect the average ability to identify the caste to vary between years.

Here $Y=6$ (2011–2016), $S=798$ and $T=40$. The number of sites visited each week varies greatly between years, as more and more sites are added to the scheme, but also between weeks, as Fig. 1 demonstrates. We also note here that even though in theory each site may be visited monthly, which would suggest that on average about 25% of the sites should be visited each week, due to site turnover, the increasing rate of take-up since the start of the survey, and missed visits, even in 2016 the proportion of sites visited in any 1 week never exceeds 15%. Visitation levels are highest in midsummer, no doubt as a consequence of more dependable availability of suitable weather conditions.

Fig. 1

Proportion of the 798 sites visited each week per year. Week 1 is the week of 1 March each year.

We fitted the model to data on B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum. We used nonparametric bootstrap by resampling with replacement the different sites to obtain summaries of estimates and to quantify the uncertainty around them using 95% confidence intervals (CI). The value of the modelling approach will increase once BeeWalk data have accumulated over a longer time-series. To explore the likely potential, and what might be achieved in the future, we then conducted an additional analysis based upon simulated data where we set $Y=10$.

We consider in turn three main features of the modelling, which either in isolation or in conjunction with one another increase the accuracy with which we can monitor, and explain, fluctuations in the numbers of these important insects, that is, in turn RA (expressed through population trends), productivity and phenology.

4.1 Relative Abundance, RA

Trends in numbers of Q are perhaps of the most interest, providing a more meaningful index of population health, since they are the founding caste for all others. Hence, we plot in Fig. 2 the estimated number of $Q_{_{\!{o}}}$ in each year per $Q_{_{\!{o}}}$ in the baseline year 2011 for all five bumblebee species. Corresponding figures for all other castes are given in Figures 1–5 in section 1.2 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively.

Fig. 2

Median, indicated by the empty circles, and 95% CI, indicated by the vertical bars, obtained using 100 nonparametric bootstrap samples of the number of $Q_{_{\!{o}}}$ in each year per $Q_{_{\!{o}}}$ in 2011. aB. hortorum, bB. hypnorum, cB. lapidarius, dB. pascuorum and eB. pratorum. The dashed horizontal lines indicate the $y=1$ line, while the solid lines connect the median values obtained for each species.

For some of the species the CI obtained for 2016 is widest, which is due to the dynamic nature of the model; information on RA of Q in a given year increases when data in subsequent years become available.

Most CI include one, so no particular trend can be observed in this short time-series. However, point estimates provide a different picture with B. lapidarius and B. pratorum consistently at lower population levels compared to 2011 and B. pascuorum consistently at higher levels compared to 2011.

Due to the sparseness of the data and the shortness of the time-series, some of the 95% CI are comparatively wide. Their width suggests that only major changes in population numbers can be identified at the moment, but we anticipate that with the addition of more sites and years of data to BeeWalk, our methods will enable us to identify even minor variations in population trends, as the results of our simulation study presented in Sect. 5 suggest.

4.2 Productivity

An alternative representation of population health is the within-season productivity, as we termed the number of individuals in each caste per $Q_{_{\!{o}}}$ in the same season. These productivity values, which serve as an index of colony size, are presented in Fig. 3 for all years.

Fig. 3

Median, indicated by the empty circles, and 95% CI, indicated by the vertical bars, obtained using 100 nonparametric bootstrap samples, of within-season productivity in 2011–2016 for all castes. First row: B. hortorum, second row: B. hypnorum, third row: B. lapidarius, fourth row: B. pascuorum, fifth row: B. pratorum. First column: W, second column: M, third column: $Q_{_{\!{n}}}$. The dashed horizontal lines indicate the $y=1$ point, while the solid lines connect the median values obtained for each species.

As expected, the number of W per $Q_{_{\!{o}}}$ is in most cases and for all species significantly greater than 1; once established by a founding $Q_{_{\!{o}}}$, all successful colonies will produce a large number of W and a smaller (but greater than 1) number of each of the subsequent reproductive castes, although, due to differences in ecology and behaviour, relative numbers detected may not accurately reflect variation between castes, and some less-successful nests may not produce one or both reproductive castes. However, it seems likely that any such bias is consistent from year to year, making annual trends for each caste useful indicators of relative productivity. For B. lapidarius, the number of W is estimated in the range of one or two hundred individuals per $Q_{_{\!{o}}}$, especially for years 2013 and 2015. Note that in this case, this high number of W is translated into high numbers of both M and $Q_{_{\!{n}}}$. Seasons 2013 and 2015 were high-productivity years also for B. pascuorum, at least in terms of the number of W, but the effect on the number of M and $Q_{_{\!{n}}}$ is minimal.

Generally, the number of $Q_{_{\!{n}}}$ per $Q_{_{\!{o}}}$ is not significantly different to one, apart from one or two exceptions. Finally, note that although the point estimates would suggest that there are more M produced than $Q_{_{\!{n}}}$, the CI are overlapping and behavioural differences make such a comparison hard to interpret.

4.3 Phenology

Seasonal patterns of emergence for 2016 are shown in Fig. 4 for all species, while for previous years they are given in Figures 6–10 in section 1.3 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively. We also include in Fig. 4 summaries of estimates for the mean emergence time of all castes and species in all 6 years.

Fig. 4

Median, indicated by the empty circles and 95% CI, indicated by the vertical bars, obtained using 100 nonparametric bootstrap samples of the entry parameters in 2016. First row: B. hortorum, second row: B. hypnorum, third row: B. lapidarius, fourth row: B. pascuorum, fifth row: B. pratorum. First column: $Q_{_{\!{o}}}$, second column: W, third column: M, fourth column: $Q_{_{\!{n}}}$. The smaller plots show the median and 95% CI of the mean emergence time for each caste and species with years 1–6 on the x-axis indicating years 2011–2016, respectively.

There is a suggestion that $Q_{_{\!{n}}}$ emerge rather more abruptly than M. $Q_{_{\!{o}}}$ of B. pratorum, also known as the Early bumblebee, are seen to emerge very early in the season, while M and $Q_{_{\!{n}}}$ of the species have mostly emerged by week 20, when most other species are still producing W bumblebees. In keeping with wider field observations, B. pascuorum is the latest species to emerge from hibernation.

Emergence of M and $Q_{_{\!{n}}}$ is estimated as being closely synchronised, again in keeping with ecological expectation, and is worth pointing out here that there was no such constraint placed on the model parameters.

Emergence of W is estimated precisely for all species, regardless of commonality, but that is not the case for the emergence of $Q_{_{\!{n}}}$: this is due to (i) the smaller number of $Q_{_{\!{n}}}$ detected, since there are fewer individuals available for detection compared to W; (ii) the fact that they are estimated to have a lower probability of having their caste identified compared to all other castes (see Figures 11–15 in section 1.4 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively, for estimated probabilities of caste identification); (iii) their shorter flight period, both from ecological expectations and as the model estimates that they become unavailable for detection soon after emergence (see Figures 16–20 in section 1.5 of the supplementary material for estimated within-season apparent weekly survival probability of B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively); and finally (iv) the fact that they are indistinguishable to $Q_{_{\!{o}}}$ and hence verified detections of such individuals do not exist.

Early emergence of $Q_{_{\!{o}}}$ does not yet appear to necessarily correlate with early emergence of the other castes (see estimated emergence curves for all castes in Figures 6–10 in section 1.3 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively); this is possibly due to the fact that there are different factors dictating the emergence of each caste, or at least even if the factors are common, such as temperature, they apply at different parts of the season. The proposed models can easily be extended to account for the effect of covariates in phenology or any of the other parameters of interest. This was not pursued here since with six available data points, the power to detect even the strongest of effects is limited.

As expected, mean emergence time varies between years. This is especially true for $Q_{_{\!{n}}}$ that have a more variable mean emergence, suggesting that they are the caste that is most sensitive to environmental conditions. W, on the other hand, are more stable in their mean emergence time between years, within each species.

As the study expands, we will be able to formally test the correlation between the emergence times of the different castes, but also between the emergence times of $Q_{_{\!{o}}}$ and W and within-season productivity. For example, we can see that years 2013 and 2015, which as mentioned above had high numbers of B. pascuorumW, show for the same species a later peak emergence time of $Q_{_{\!{o}}}$ compared to all other years. However, the same pattern is not observed for B. lapidarius. This may indicate different ecological responses between the species to similar environmental conditions: while B. lapidarius was able to produce an increased number of Q for the next generation, B. pascuorum may have needed an increased number of W to initiate, belatedly, no more than an average level of Q production. It is likely that this is due to inter-specific differences such as dietary and nest site preferences.

4.4 Other Observations

Within-season weekly survival (Figures 16–20 in section 1.5 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively) and winter survival of Q (Figure 21 in section 1.6 of the supplementary material) are the least precisely estimated parameters for all species. The results suggest that, as expected, $Q_{_{\!{n}}}$ do not tend to remain available for detection for long after their summer emergence, as they head to their hibernating spots very soon after first leaving the nest.

Identification probability is estimated as very high and not changing considerably for all castes apart from $Q_{_{\!{n}}}$, which have a lower and decreasing probability of having their caste identified compared to all other castes (Figures 11–16 in section 1.4 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively). It is gratifying that, for example, MB. lapidarius (which are easy to identify) appear to be rarely left unidentified. We fitted a model which assumes a linear trend, on the logit scale, with year as a covariate for identification probability and this was favoured for all species apart from B. hypnorum according to Akaike’s Information Criterion (AIC, Akaike 1976) when compared to the model which assumes a constant identification probability across years. See Table 1 in section 1 of the supplementary material for AIC values of the two models for each species.

4.5 Goodness-of-Fit

The quality of model fit is readily assessed by plotting the counts in each group obtained at each bootstrap iteration alongside counts generated from the fitted model at each of these iterations. These are presented in Figures 22–26 in section 1.7 of the supplementary material for B. hortorum, B. hypnorum, B. lapidarius, B. pascuorum, and B. pratorum, respectively. The model fits well in all cases and naturally the fit improves in the later years when there are more data, a phenomenon which can be anticipated to continue as the survey expands. The results show huge variability in the bootstrapped data which demonstrates the considerable effect of specific sites on the counts; this is because of the sparseness of the data which means that a few sites with high counts, if chosen in the bootstrap samples, will lead to a very high count for that sample. See, for example, B. lapidariusW during week 20 in 2015: the bootstrapped counts range from about 250 to about 1250. This explains the fairly wide, but still reasonable intervals (given the sparseness of the data) that we obtain for parameters in some cases.

We also considered Pearson’s correlation coefficient between the observed counts of each group within each year for all species, and the corresponding fitted counts obtained by our model and the results, shown in Table 7 in section 1.7 of the supplementary material, show high correlation in most cases, and in particular for later years.

5 Simulated Data

We simulated data by setting $Y=10$, to demonstrate the performance of the model in longer time-series than the one currently available in BeeWalk, while $S=500$. We considered the same model as the one fitted to the BeeWalk data, with the only difference being that we set identification probability as constant across years, but still different between castes, for simplicity and also because we expect this to become the case for the BeeWalk study as well, with a core of long-term experienced recorders and turnover mainly amongst newer volunteers.

As was the case for the BeeWalk data, we assumed weekly sampling occasions but realistically set the proportion of sites visited at each time equal to 0.1, so that it is similar to the BeeWalk data, but for simplicity disregarded seasonal variation in this. Expected counts at each visit were then derived from chosen realistic values of the demographic and phenological parameters, and to add noise, we multiplied the expected count in each cell by a randomly generated number in the (0, 1) interval, which represents the differences between different sites or observers and makes the simulation scenarios more realistic. We chose $N_{1{Q_{_{\!{o}}}}}$ for 450 out of the 500 sites randomly from a Uniform{0,...,10} distribution while for the remainder 50 sites we chose it randomly from a Uniform{45,...,55} distribution. This replicates what often happens in reality with some sites producing considerably larger counts than other sites. In all scenarios, we sampled mean emergence of $Q_{_{\!{o}}}$ and W from a Uniform(8, 12) and a Uniform(13, 17) distribution, respectively, while for M and $Q_{_{\!{n}}}$ these were sampled from a Uniform(25, 29) distribution for each year of the simulated study. Standard deviations of arrival times were set equal to 2 for $Q_{_{\!{o}}}$, 3 for W and 1 for M and $Q_{_{\!{n}}}$ for all years. We sampled a year effect from a Uniform($-\,0.1, 0.1$) and then that was added to the weekly apparent survival probability for each caste, which was set equal to 0.8, 0.5, 0.7 and 0.3 for $Q_{_{\!{o}}}$, W, M and $Q_{_{\!{n}}}$, respectively. Finally, identification probability was set equal to 0.9 and 0.8 for $Q_{_{\!{o}}}$ and W, respectively, and 0.7 for M and $Q_{_{\!{n}}}$.

We considered three scenarios: in scenario 1, the population is stable, in scenario 2, within-season productivity decreases proportionally compared to scenario 1 over the years by a randomly generated proportion in the interval (0.04, 0.07), which is the same for all castes in each year. In scenario 3, winter survival for $Q_{_{\!{n}}}$ is lower than in scenario 1, specifically it is generated in the range (0.42, 0.62) instead of the (0.62, 0.82) interval, but within-season productivity remains fairly constant across years and fluctuating proportionally by a proportion randomly chosen in the ($-\,0.1, 0.1$) interval. The parameter values used for within-season productivity and winter survival are given in Tables 8–11 in section 2 of the supplementary material.

In the latter two cases, the population is decreasing and in fact in scenario 2 by the end of the 10 years is has gone extinct. This demonstrates how even such small changes in within-season productivity or winter survival of $Q_{_{\!{n}}}$ can have dramatic effects to population levels.

In Fig. 5 we show the summaries of the estimated population trends for all castes for all scenarios together with the true values. Estimates for all other parameters are summarised in Figures 27–31, 32–36 and 37–41 in section 2 of the supplementary material for, respectively, scenarios 1, 2 and 3.

Fig. 5

Box plots of estimates and true values, indicated by the horizontal lines, for the number of individuals in each caste in each year per individual in the same caste in year 1 of the simulated study. First row: scenario 1 when the population is stable, second row: scenario 2 when the decrease is due to changes in within-season productivity, third row: scenario 3 when the decrease is due to changes in winter survival of $Q_{_{\!{n}}}$. First column: $Q_{_{\!{o}}}$, second column: W, third column: M, fourth column: $Q_{_{\!{n}}}$.

As Fig. 5 demonstrates, the model is able to pick up the decrease in population sizes in both scenarios 2 and 3. As seen in Figures 27–41 in section 2 of the supplementary material, the estimates for all demographic and phenological parameters are unbiased in all three scenarios. Phenology-related parameters are the most precisely estimated while winter survival the least precisely estimated, especially for later years, due to the dynamic nature of the model. Nevertheless, in all cases the results clearly and correctly demonstrate the changes and patterns in the demographic parameters; in scenarios 2 and 3 they identify the reasons behind the decline in numbers and generally demonstrate the potential of the proposed methods in monitoring wildlife populations via citizen science monitoring schemes, such as the BeeWalk.

6 Discussion

The concept of monitoring the health of wild populations via citizen science programmes of the kind described here is now well established. While issues of representativeness (arising from a tendency for sites to be concentrated in areas of generally favourable habitat which are accessible to a large part of the volunteer population) are widely recognised, many such schemes are reported on annually and provide a major component of advice to policy-makers as well as the general public. The more recent establishment of such a scheme for bumblebees is probably largely a consequence of the greater difficulty in identification compared to butterflies, which are the most widely surveyed invertebrate group.

This difficulty of identification extends further when it comes to assigning individuals to caste. This is, however, essential in fully understanding changes in bumblebee populations, as the castes play very different roles in the structure of the colony: only the queens reproduce and found new colonies, and only queens and workers forage for the existing colony. Here, we have introduced a novel approach to modelling bumblebee counts with fully caste-specific parameters even though individual bees are identified only as belonging to a specific “group”, with one group consisting of bees of unknown caste and another combining the queen bees of different generations. This is achieved by a mixture model combining the parameters of interest with probabilities of caste membership.

As yet, the duration of the survey is too short to expect substantial conclusions about trends in demography or phenology in these ecologically and economically important species, though we have shown how differences between years or between species can be identified. Previous surveys of birds and butterflies, for example, have seen rapid increase in uptake after the inaugural years, as resources (and hence data duration, survey infrastructure and public awareness) increase. Public interest in the well-being of pollinator populations is high, and we can expect data to accrue from more sites as the survey continues, increasing the precision of estimators and enabling increasingly accurate monitoring of trends in relative abundance, survival, colony size and phenology. Environmental covariates can be introduced to the model in an attempt not merely to identify, but also to explain, temporal and even spatial variation. This combination of survey and modelling approach solves one of the major knowledge gaps identified in the English National Pollinator Strategy (NPS 2014): our current lack of understanding of fluctuations in abundance of pollinator populations.

We illustrated the methods for five of the seven common British species; the long-tongued B. hortorum, B. lapidarius and B. pascuorum, and the shorter-tongued B. pratorum and B. hypnorum. The last-named species only arrived in the UK within the last 20 years and has rapidly spread (Goulson and Williams 2001; Crowther et al. 2014). We do not here consider B. terrestris and B. lucorum, due to the difficulties in separating workers of these species, though we note that potentially a joint modelling approach with an additional hierarchy taking into account this uncertainty could be developed for these very widespread species.

We note that the developed models can take into account available information on caste but do not rely on this being available as the methods can be applied to cases when no such information exists. At least some fully identified individuals are likely to be necessary for precision, given data on a realistic scale, but it is a great advantage to a survey of potentially difficult taxa that observers without the expert judgement possessed by relatively few people can make a significant contribution. As the models allow for different categories, here castes, of individuals to behave differently in terms of their phenology or survival for example, the models could easily be adapted to cases where the population is categorised according to these latent characteristics and the proportion of individuals in each category can be estimated. This is akin to finite mixture models to account for heterogeneity in uniquely identifiable individuals (Pledger 2000; Pledger et al. 2003, 2009), but developed here for count data.

The proposed models allow for further flexibility than that considered here for the available data. For example, within-season apparent weekly survival probability can be modelled as a function of time-since-emergence, i.e. age. We anticipate that as more data become available, we will be able to explore such models as well.

We have not here, with limited data, attempted to estimate site-specific parameters. This is routinely done in longer and larger surveys and provides the additional means of exploring spatial differences. Should sufficient data become available, we will be able to explore such models also for BeeWalk data. This will increase the capacity to explore differences in population trends or phenology within regions. For example, one might expect the emergence times of bumblebees to be later in the north of the country, as a response to the later spring and availability of food plants. Matechou et al. (2014) found such a delay for the common blue butterfly Polyommatus icarus, although bumblebees are more independent of ambient air temperatures than are butterflies and most other invertebrates, so we expect such differences to be minimal between BeeWalk sites. Introducing site-specific data of sufficient scale also provides the means of separately estimating probabilities of detection (Matechou et al. 2014), which we have not been able to adopt here.

The fairly short time-series of 6 years that is currently available does not allow us at the moment to assess fully the population trends. Through a series of simulation-based analyses, we have shown that in this regard too the BeeWalk and our proposed model show great potential given the anticipated increase in data. Specifically, we showed that the models presented here can be used to assess population trends and, in cases of decline, can be used to identify the underlying reasons, such as changes in within-season productivity or in winter survival of new queens.

Bumblebees play a vital role in pollination of our crops, garden plants and wild flowers, but have suffered some of the largest distributional declines of any of the groups of British insects. To date, an understanding of the population fluctuations of these important pollinator species has been a major missing link, hindering attempts to both conserve rarities and maximise pollination services from more common species (NPS 2014). With the survey organisation and volunteer base now in place, and a method of analysis that properly accounts for visits missed and individuals only partly identified, we believe that monitoring of bumblebees can now become an important cornerstone of future conservation ecology.