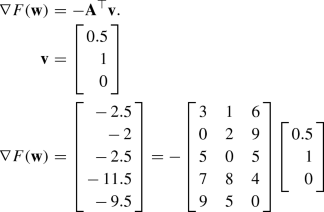Developing Integer Calibration Weights for Census of Agriculture

Abstract

When conducting a national survey or census, administrative data may be available that can provide reliable values for some of the variables. Survey and census estimates should be consistent with reliable administrative data. Calibration can be used to improve the estimates by further adjusting the survey weights so that estimates of targeted variables honor bounds obtained from administrative data. The commonly used methods of calibration produce non-integer weights. For the Census of Agriculture, estimates of farms are provided as integers so as to insure consistent estimates at all aggregation levels; thus, the calibrated weights are rounded to integers. The calibration and rounding procedure used for the 2012 Census of Agricultural produced final weights that were substantially different from the survey weights that had been adjusted for under-coverage, non-response, and misclassification. A new method that calibrates and rounds as a single process is provided. The new method produces integer, calibrated weights that tend to be consistent with more calibration targets and are more correlated with the modeled census weights. In addition, the new method is more computationally efficient. Supplementary materials accompanying this paper appear online.

Appendices

Appendices

A Gradients of the Objective Functions

The gradient of the objective function used for the rounding is

$$\begin{aligned} \nabla F(\mathbf {w})=-\,\mathbf {A}^\top \mathbf {v}, \end{aligned}$$

where the components of $\mathbf {v}$ are given by

$$\begin{aligned} v_i=2 \; \frac{\mathrm {sign}(\varepsilon _i)}{u_{i} - l_{i}}+ {\left\{ \begin{array}{ll} 1 / (u_i - \delta ), &{}\quad \text {if } \mathbf {a}_i^\top \mathbf {w} > u_{i} - \delta ,\\ -1/ (l_i + \delta ), &{}\quad \text {if } \mathbf {a}_i^\top \mathbf {w} < l_{i} + \delta ,\\ 0, &{}\quad \text {otherwise,} \end{array}\right. } \end{aligned}$$

(14)

where $\varepsilon _i = y_i - \mathbf {a}_i^\top \mathbf {w}$, for any $i = 1, \ldots , n$.

The gradient of the objective function used for the calibration is

$$\begin{aligned} \nabla F(\mathbf {w})=-\mathbf {A}^\top \mathbf {v}, \end{aligned}$$

where the components of $\mathbf {v}$ are given by

$$\begin{aligned} v_i= {\left\{ \begin{array}{ll} 1 / (y_i - u_{i} + \delta ), &{}\quad \text {if } \mathbf {a}_i^\top \mathbf {w} > u_{i} - \delta , \\ 1 / (y_i - l_{i} - \delta ), &{}\quad \text {if } \mathbf {a}_i^\top \mathbf {w} < l_{i} + \delta , \\ 0, &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

(15)

B Example

Consider the following illustration of the INCA methodology. To simplify the computation of the objective function and its gradient, let $\phi = 0$.

• The setup Bounds on final calibrated weights

  $$\begin{aligned}{}[1,6] \end{aligned}$$

  The targets

  $$\begin{aligned} \mathbf {y}^\top = \left[ \begin{array}{rrr} 92&\quad 61&\quad 72 \end{array} \right] \end{aligned}$$

  Targets’ lower bound

  $$\begin{aligned} \mathbf {l}_\mathbf {y} = \left[ \begin{array}{rrr} 88&\quad 58&\quad 69 \end{array} \right] \end{aligned}$$

  Targets’ upper bound

  $$\begin{aligned} \mathbf {u}_\mathbf {y} = \left[ \begin{array}{rrr} 96&\quad 64&\quad 75 \end{array} \right] \end{aligned}$$

  The data matrix

  $$\begin{aligned} \mathbf {A} = \left[ \begin{array}{rrrrr} 3 &{} \quad 0 &{} \quad 5 &{} \quad 7 &{} \quad 9 \\ 1 &{} \quad 2 &{} \quad 0 &{} \quad 8 &{} \quad 5 \\ 6 &{} \quad 9 &{} \quad 5 &{} \quad 4 &{} \quad 0 \end{array} \right] \end{aligned}$$

  The DSE weights

  $$\begin{aligned} \mathbf {w}_{\mathrm{DSE}}^\top = \left[ \begin{array}{rrrrr} 15.9&\quad 0.5&\quad 1.3&\quad 3.2&\quad 1.8 \end{array} \right] \end{aligned}$$

  Initial totals

  $$\begin{aligned} \hat{\mathbf {y}}^\top = \left[ \begin{array}{rrr} 63.1&\quad 42.6&\quad 64.3 \end{array} \right] \end{aligned}$$

• Rounding

  • Truncation (Pre-rounding adjustments) First, truncate the weights outside the bounds to either 1 or 6.

    $$\begin{aligned} \mathbf {w}^\top = \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 1.3&\quad 3.2&\quad 1.8 \end{array} \right] \end{aligned}$$

  • Initial errors and objective function calculations Initial errors are given by

    $$\begin{aligned} \varvec{\varepsilon }= & {} \mathbf {y} - \mathbf {A w} \\ \left[ \begin{array}{r} 28.9 \\ 18.4 \\ 7.7 \end{array} \right]= & {} \left[ \begin{array}{r} 92 \\ 61 \\ 72 \end{array} \right] - \left[ \begin{array}{rrrrr} 3 &{} \quad 0 &{} \quad 5 &{} \quad 7 &{} \quad 9 \\ 1 &{} \quad 2 &{} \quad 0 &{} \quad 8 &{} \quad 5 \\ 6 &{} \quad 9 &{} \quad 5 &{} \quad 4 &{}\quad 0 \end{array} \right] \left[ \begin{array}{r} 6 \\ 1 \\ 1.3 \\ 3.2 \\ 1.8 \end{array} \right] \end{aligned}$$

    For example, by setting $\delta = 2$, the initial total loss is given by

    $$\begin{aligned} 17.48=&2*(92-63.1)/(95-89)+(-\,63.1+89+2)/91+\\&2*(61-42.6)/(65-57)+(-\,42.6+57+2)/59+\\&2*(72-64.3)/(75-69)+(-\,64.3+69+2)/71\\ \end{aligned}$$

  • The gradient of the rounding objective function

    $$\begin{aligned} \nabla F(\mathbf {w})= & {} -\mathbf {A}^\top \mathbf {v}.\\ -{\mathbf {A}}^{\top }= & {} - \left[ \begin{array}{rrr} 3 &{} \quad 1 &{} \quad 6 \\ 0 &{} \quad 2 &{} \quad 9 \\ 5 &{} \quad 0 &{} \quad 5 \\ 7 &{} \quad 8 &{} \quad 4 \\ 9 &{} \quad 5 &{} \quad 0 \end{array} \right] \\ \mathbf {v}= & {} \left[ \begin{array}{r} 0.239 \\ 0.317\\ 0.319 \end{array} \right] \\ \nabla F(\mathbf {w})= & {} \left[ \begin{array}{r} -\,2.948 \\ -\,3.505 \\ -\,2.790 \\ -\,5.485 \\ -\,3.736 \end{array}\right] = - \left[ \begin{array}{rrr} 3 &{} \quad 1 &{} \quad 6 \\ 0 &{} \quad 2 &{} \quad 9 \\ 5 &{} \quad 0 &{} \quad 5 \\ 7 &{} \quad 8 &{} \quad 4 \\ 9 &{} \quad 5 &{} \quad 0 \end{array} \right] \left[ \begin{array}{r} 0.239 \\ 0.317\\ 0.319\end{array} \right] \end{aligned}$$

  • Order of processing By taking the absolute value of the gradient

    $$\begin{aligned} |\nabla F(\mathbf {w})|=\left[ \begin{array}{rrrrr} 2.948&\quad 3.505&\quad 2.790&\quad 5.485&\quad 3.736 \end{array}\right] , \end{aligned}$$

    the following processing order of the weights is obtained:

    $$\begin{aligned} w_4, ~ w_5, ~ w_2, ~ w_1, ~ w_3 \end{aligned}$$

  • Processing the weight in position 4

    $$\begin{aligned} \mathbf {w}_{lw_4}= & {} \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 1.3&\quad 3&\quad 1.8 \end{array}\right] \\ \mathbf {w}_{uw_4}= & {} \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 1.3&\quad 4&\quad 1.8 \end{array}\right] \end{aligned}$$

    The total loss using $\mathbf {w}_{lw_4}$ is given by

    $$\begin{aligned} 18.67=\,&2*(92-61.7)/(95-89)+(-\,61.7+89+2)/91\\&+\,2*(61-41)/(65-57)+(-\,41+57+2)/59\\&+\,2*(72-63.5)/(75-69)+(-\,63.5+69+2)/71 \end{aligned}$$

    The total loss using $\mathbf {w}_{uw_4}$ is given by

    $$\begin{aligned} 12.73=\,&2*(92-68.7)/(95-89)+(-\,68.7+89+2)/91\\&+2*(61-49)/(65-57)+(-\,49+57+2)/59\\&+2*(72-67.5)/(75-69)+(-\,67.5+69+2)/71 \end{aligned}$$

    Since the objective function is smaller using $\mathbf {w}_{uw_4}$ than using $\mathbf {w}_{lw_4}$, $w_4$ is rounded to 4. The new total loss is 12.73.

  • Processing the remaining non-integer weights The weight $w_5$ is similarly rounded, and then, $w_3$ is processed in the same way. The following output is the resulting vector of weights after the completion of the rounding sub-algorithm:

    $$\begin{aligned} w^\top = \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 2&\quad 4&\quad 2 \end{array} \right] , \end{aligned}$$

    with a total rounding loss of 9.089.

• Calibration

  • Computing the calibration total loss

    $$\begin{aligned} 20=\,&(92-74)/(92-88-2)\\&+(61-50)/(61-58-2) \end{aligned}$$

  • The gradient of the calibration objective function

    

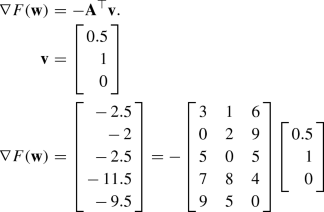
  • Order of processing By taking the absolute value of the gradient

    $$\begin{aligned} |\nabla F(\mathbf {w})|=\left[ \begin{array}{rrrrr} 2.5&\quad 2&\quad 2.5&\quad 11.5&\quad 9.5 \end{array}\right] , \end{aligned}$$

    the following processing order of the weights is obtained:

    $$\begin{aligned} w_4, ~ w_5, ~ w_3, ~ w_1, ~ w_2 \end{aligned}$$

  • Iteration 1: processing$w_4$ Compute $F(\mathbf {w})$ by adjusting $w_4$ in the opposite direction of the gradient. Thus, $w_4 + 1 = 5$, and if $w_4 = 5$, then $F(\mathbf {w}) = 11.5$.

    $$\begin{aligned} 11.5=(92-81)/(92-88-2)+(61-58)/(61-58-2)+(72-75)/(72-75+2) \end{aligned}$$

    When $w_4 = 5$, then $F(\mathbf {w}) < 20$. Therefore, the updated weights are

    $$\begin{aligned} \mathbf {w}^\top = \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 2&\quad 5&\quad 2 \end{array} \right] \end{aligned}$$

  • Iteration 2: set priorities for the second step of calibration

    

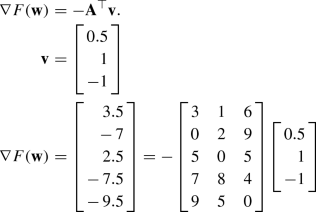
    By taking the absolute value of the gradient

    $$\begin{aligned} |\nabla F(\mathbf {w})| = \left[ \begin{array}{rrrrr} 3.5&\quad 7&\quad 2.5&\quad 7.5&\quad 9.5 \end{array} \right] , \end{aligned}$$

    the following processing order of the weights is obtained:

    $$\begin{aligned} w_5, ~ w_4, ~ w_2, ~ w_1, ~ w_3 \end{aligned}$$

  • Iteration 2: processing the weights Compute $F(\mathbf {w})$ by adjusting $w_5$ in the opposite direction of the gradient. For $w_5 + 1 = 3$, then $F(\mathbf {w}) = 5$.

    $$\begin{aligned} 5=(61-63)/(61-64+2)+(72-75)/(72-75+2) \end{aligned}$$

    When $w_5 = 3$, then $F(\mathbf {w}) < 11.5$. Thus, the updated weights are

    $$\begin{aligned} \mathbf {w}^\top = \left[ \begin{array}{rrrrr} 6&1&2&5&3 \end{array} \right] \end{aligned}$$

  • Iteration 3: set priorities for the second step of calibration

    $$\begin{aligned} \nabla F(\mathbf {w})= & {} -\mathbf {A}^\top \mathbf {v}.\\ \mathbf {v}= & {} \left[ \begin{array}{r} 0 \\ -\,1\\ -\,1\end{array} \right] \\ \nabla F(\mathbf {w})= & {} \left[ \begin{array}{r} 7 \\ 11\\ 5\\ 12\\ 5 \end{array} \right] = - \left[ \begin{array}{rrr} 3 &{} \quad 1 &{} \quad 6 \\ 0 &{} \quad 2 &{} \quad 9 \\ 5 &{} \quad 0 &{} \quad 5 \\ 7 &{} \quad 8 &{} \quad 4 \\ 9 &{} \quad 5 &{} \quad 0 \end{array} \right] \left[ \begin{array}{r} 0 \\ -\,1\\ -\,1\end{array} \right] \end{aligned}$$

    By taking the absolute value of the gradient

    $$\begin{aligned} |\nabla F(\mathbf {w})| = \left[ \begin{array}{rrrrr} 7&\quad 11&\quad 5&\quad 12&\quad 5 \end{array} \right] , \end{aligned}$$

    the following processing order of the weights is obtained:

    $$\begin{aligned} w_4, ~ w_2, ~ w_1, ~ w_5, ~ w_3 \end{aligned}$$

  • Iteration 3: processing the weights

    • Compute $F(\mathbf {w})$ by adjusting $w_4$ in the opposite direction of the gradient. For $w_4 - 1 = 4$: $F(\mathbf {w}) = 10.5$

      $$\begin{aligned} 10.5=(92-83)/(92-88-2)+(61-55)/(61-58-2) \end{aligned}$$

      Since if $w_4 = 4$, then $F(\mathbf {w}) > 5$, $w_4$ is not updated. Therefore, $w_2$ is consider next.

    • Compute $F(\mathbf {w})$ for $w_2 - 1=0$: Since $w_2$ cannot be 0, one cannot decrease $w_2$. Therefore, one moves to $w_1$.

    • Compute $F(\mathbf {w})$ for $w_1 - 1=5$: $F(\mathbf {w}) = 5.5$.

      $$\begin{aligned} 5.5= (92-87)/(92-88-2)+(72-69)/(72-69-2) \end{aligned}$$

      Since if $w_1 = 5$, then $F(\mathbf {w}) > 5$, it is not possible to update $w_1$. Therefore, one moves to $w_3$

    • Compute $F(\mathbf {w})$ for $w_3 - 1=1$: $F(\mathbf {w}) = 7.5$.

      $$\begin{aligned}&(92-85)/(92-88-2)+(61-63)/(61-64+2)\\&+\,(72-70)/(72-69-2)=7.5 \end{aligned}$$

      Since if $w_3 = 1$, then $F(\mathbf {w}) > 5$, there is no need to do update $w_3$. Therefore, one moves to $w_5$

    • Compute $F(\mathbf {w})$ for $w_5 - 1=2$: $F(\mathbf {w}) = 11.5$.

      $$\begin{aligned} 11.5= & {} (92-81)/(92-88-2)+(61-58)/(61-58-2)\\&\quad +\,(72-75)/(72-75+2) \end{aligned}$$

      Since if $w_5 = 2$, then $F(\mathbf {w}) > 5$, it is not necessary to update $w_5$. Therefore, the algorithm stops.

• Final Weights

  The final calibrated weights are

  $$\begin{aligned} \mathbf {w}^\top = \left[ \begin{array}{rrrrr} 6&\quad 1&\quad 2&\quad 5&\quad 3 \end{array} \right] . \end{aligned}$$

  The final calibrated totals are

  $$\begin{aligned} \hat{\mathbf {y}}= \left[ \begin{array}{rrr} 90&\quad 63&\quad 75 \end{array} \right] . \end{aligned}$$

By construction of the matrix $\mathbf {A}$, the summation of the weights is not part of the targets in this example. The purpose of this example is to show how the algorithm works rather than showing what type of results are attainable. At the end, the correlation between the initial vector of DSE weights and the final vector of calibrated weights is about 0.8, which is even higher than those obtained in the real case example provided in Sect. 3 (see Figs. 3 and 4).