Abstract
Closed-loop supply chains involve forward flows of products from production facilities to customer zones as well as reverse flows from customer zones back to remanufacturing facilities. We present an integrated modeling framework for configuring a distribution system with reverse flows so as to minimize the total cost of satisfying customer demand and remanufacturing the returned items that are recoverable. Given a set of existing plants and customer zones, our basic model identifies the optimal number and location of distribution centers and return centers assuming that all plants have remanufacturing capability. We devise a Lagrangian heuristic for this problem. The proposed solution method proved to be computationally efficient for solving large-scale instances of the closed-loop supply chain design problem. The potential benefits of the integrated model are demonstrated by comparing its results with those obtained from an alternative approach that determines optimal forward and reverse network structures sequentially. We also extend the basic model to determine the optimal locations for establishing remanufacturing facilities. Using the extended model, we study the conditions under which the return centers can be co-located with remanufacturing facilities rather than being established at the downstream echelons of the supply chain. Different from the existing works on facility location-allocation models for closed-loop supply chain network design, the main focus in this paper is on the investigation of structural properties of the network such as co-locating return centers with remanufacturing facilities and quantifying the benefit of modeling forward and reverse flows simultaneously rather than sequentially.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The second half of the twentieth century witnessed the global rise of a consumption-based economy. This trend resulted in an ever-increasing threat to environmental sustainability. Environmentally conscious manufacturing, waste reduction and product recovery have emerged as alternative means of coping with this significant societal problem. In this paper, we focus on supply chains with product recovery, which aim at capturing the remaining economical value in used, unsold, or obsolete products. Based on a survey of nine case studies on product recovery processes in different industries, Fleischmann et al. [11] highlight the following common activities: (i) collection of used products, (ii) inspection and separation of the recoverable returns and those that need to be disposed due to economic and/or technological reasons, (iii) reprocessing the returns, which involves reuse, recycling, remanufacturing or repair, and (iv) redistribution of the recovered materials, components or products. From a logistics viewpoint, these activities create a reverse flow of goods from consumers toward upstream layers of the supply chain. The simultaneous presence of forward and reverse flows cause unique challenges for supply chain design, which we tackle in this paper. To this end, we provide an analytical framework for making structural decisions pertaining to distribution systems with reverse flows.
Under pressure from environmental groups and society at large, governments are increasingly involved in regulating product recovery, because it can serve as an effective mechanism for sustaining the environment. The WEEE legislation in the European Union [36] that became effective in February 2014, for example, requires manufacturers to establish environmentally sound recovery processes including remanufacturing for used electrical and electronic equipment. On the other hand, an increasing number of companies have been implementing comprehensive programs in order to reap the potential benefits of remanufacturing. According to the United States International Trade Commission report prepared in October 2012 (USITC Publication 4356, [34]), United States was the world’s largest remanufacturer during the period of 2009-2011 with the total value of remanufactured products exceeding $43 billion. Furthermore, the most remanufacturing intensive industries in the United States comprise aerospace, electrical and electronic equipment, locomotives, machinery, medical devices, motor vehicle parts, office furniture, and retreaded tires. Thanks to HP’s reuse and recycling programs, more than 80% of ink cartridges and 38% of LaserJet toner cartridges are produced with recycled plastic [14]. Moreover, HP Planet Partners have recycled more than 3.3 billion pounds of products since 1987. Xerox reports that their combined returns programs including equipment resale and remanufacturing along with parts and consumable reuse and recycling prevented over 38,000 metric tons of waste in 2003 which otherwise would end up in landfills [37].
Managing the flow of returned products from customer zones to remanufacturing facilities often involves the establishment and operation of return centers. A return center typically offers scale economies in dealing with returned products in much the same way a distribution center plays a role in the distribution networks. It is well understood that the returned products can have considerable variation in their quality level. This implies that the economic value that can be gained from these so-called cores can also vary. To cope with these uncertainty, return centers perform a quality-based classification by means of inspection and screening tests [4]. Those deemed recoverable are shipped to the remanufacturing facilities whereas the rest are either sent to recycling facilities or to landfill and incineration sites for disposal.
A significant majority of the research on the design of reverse logistics (RL) networks has focused on the structural decisions regarding the reverse distribution networks. The location and sizing decisions associated with only the collection, inspection, recycling and remanufacturing facilities are incorporated in the proposed mathematical formulations. A recent and comprehensive review on these papers, which do not incorporate the configurational decisions pertaining to the forward distribution network, can be found in [1, 13]. There are 31 papers that are immediately relevant to our research since they incorporate the flows in both directions in making design decisions. We discuss this stream of research in more detail in the next section.
This paper’s main contribution is a methodology for designing closed-loop supply chains (CLSCs) i.e., making structural decisions pertaining to both the forward and reverse distribution networks simultaneously. To this end, we incorporate the presence of reverse flows, return centers and remanufacturing facilities in the well-known (single-commodity) production-distribution system design model. Using our modeling framework, we address two important strategic questions. “Is there a significant benefit due to designing forward and reverse networks simultaneously rather than sequentially?” and “Under which conditions can the return centers be co-located with remanufacturing facilities rather than being established at the downstream echelons of the supply chain?” Through extensive computational experiments, we find that the general level of capacity utilization in remanufacturing facilities is a key factor determining the potential benefits of the integrated design approach. We also observe that the most appropriate echelon for return centers that perform inspection and separation heavily depends on the overall quality and quantity of the returns collected at the customer zones. On the algorithmic front, we study the effectiveness of Lagrangian relaxation in solving the CLSC design models presented in the paper. Our computational experiments indicate that the Lagrangian relaxation is more efficient than CPLEX for large-scale problem instances.
The remainder of the paper is organized as follows. An overview of the most relevant literature is provided in the next section. “The basic model” presents the integrated model for designing distribution systems with reverse flows and “Solution methodology” outlines the Lagrangian heuristic for this problem. In “Computational experiments”, we implement the heuristic in solving a realistic case study and demonstrate its computational efficiency for large-scale problem instances. “Integrated versus sequential design” is devoted to the comparison of alternative approaches to CLSC design in order to demonstrate the advantages of the proposed integrated approach. “Where to locate the return centers?” extends the basic model to determine whether the firm can benefit from establishing the return centers at the upstream echelon co-located with the remanufacturing facilities. We finish the paper with some concluding remarks.
Detailed overview of the literature
The design of a CLSC is in fact related to the notion of supply chain integration (SCI). SCI represents the level at which a producer works together with its partners in the supply chain to generate an effective and efficient flow of products, information, services and value to the customer. A possible categorization for integration is given in Pishvaee et al. [26] as “horizontal integration” and “vertical integration”. The former one refers to the integration of problems at the same decision level such as strategic level or operational level, while the latter one involves considering the integration of problems at different decision levels. For example, tackling the supplier selection problem together with the network design problem is horizontal integration since both problems occur at the strategic level. Addressing network design problem while taking into account vehicle routing issues for a distribution company can be seen as vertical integration. In our setting, the design of CLSC where configurational decisions concerning both forward and reverse networks are involved is clearly horizontal integration because the corresponding decisions are all pertinent to the strategic level.
In this section, we focus on 31 papers that are immediately relevant to our work due to their focus on the design of distribution systems with reverse flows by incorporating facility location decisions. These papers are given in Table 1 and categorized with regard to the network structure modeled, i.e., whether the designed network includes return centers (RC), remanufacturing facilities (RmF), manufacturing plants (P) and/or distribution centers (DC). We would like to emphasize that facility types called collection centers and inspection centers in some studies are treated under the name “RC”. In Table 1, we also indicate what type of uncertainty is taken into account in the model, the solution approach/algorithm adopted, and whether the proposed methodology is implemented in a real-life case.
In an early effort, Marín and Pelegrin [22] extended the simple plant location problem to define the return plant location problem where each manufacturing plant to be established also serves as a collection center for customer returns. A more realistic extension of this very basic network is considered in Beamon and Fernandes [5] where the manufacturing plants serve the customer demand via warehouses and receive the returns via collection centers and warehouses. Fleischmann et al. [12] compare the sequential and integrated approaches for the design decisions and by analyzing two hypothetical examples inspired by real-life industrial cases the authors conclude that the reverse flows have a significant impact on the overall network structure only when the forward and reverse channels differ in a considerable way with respect to geographical distribution or cost structure. The authors also point out that return volumes constitute a key factor in the design decisions.
Salema et al. [29] offer an alternative formulation where the flow variables are represented at two levels (i.e., plant-warehouse and warehouse-customer) rather than the single level formulation of flow variables in Fleischmann et al. [12] (i.e., plant-warehouse-customer). In solving two cases, based on a document-office company in Spain and copier remanufacturing in Europe, the authors used the CPLEX solver within GAMS Suite. An extended model is also provided for the capacitated and multi-product version of the design problem, which was implemented for only two products during the case analysis. Salema et al. [31] is an effort to incorporate tactical decisions, such as production and inventory levels, in the integrated RL network design. Extending their earlier formulation to represent a set of macro and micro time periods, Salema et al. [31] demonstrate that the arising model can handle fairly large problem instances encountered in practice. Later on, Salema et al. [32] build upon their previous work and propose a generalized model that yields a tactical plan for acquisition, production, storage and distribution in a predefined time horizon in addition to designing the supply chain considering simultaneously the forward and reverse flows.
In perhaps the most detailed case study for integrated RL network design, Krikke et al. [17] focus on the forward and reverse supply chains of refrigerators and evaluate three alternative refrigerator designs from the perspective of their overall costs, energy consumption and waste generated. Ko and Evans [16] address the problem of a third-party logistics (3PL) provider which runs the warehouses and repair centers performing inspection and separation activities. The client company operates a set of existing plants that aim at satisfying the market demand via the warehouses and collect the returns through the repair centers. The authors develop a multi-period model to determine the opening, expansion, and closing decisions of the warehouses and repair centers over time. Lu and Bostel [21] provide an mixed-integer linear (MILP) formulation where the customer zones are directly served from manufacturing or remanufacturing facilities, whereas reverse flows go through intermediate centers (that perform cleaning, disassembly, testing and sorting) on their way to the remanufacturing facilities. The MILP model formulated by Sahyouni et al. [28] extends the model of [25] in the sense that hybrid facilities are established to be utilized in both forward and reverse logistics operations. Lagrangian relaxation is used to solve the developed model. By assuming the existence of a forward flow network, Üster et al. [35] are concerned with the design of the reverse network along with the determination of flows in both forward and reverse channels. Their objective is to determine the locations of the collection centers and remanufacturing facilities along with the forward and reverse flows such that the sum of the processing, transportation, and facility location costs are minimized. Easwaran and Üster [10] incorporate capacitated Hybrid Centers (HCs) and Hybrid Sourcing Facilities (HSFs) into their existing models. HCs can play the role of both DCs and/or RCs and HSFs perform both manufacturing of new products and remanufacturing of used products. The aim of the developed model is to determine the best locations of the HSFs and the HCs as well as the best flow of products in the CLSC network.
Zhou and Wang [40] present a very similar model to that of Fleischmann et al. [12] in which returns can be repaired at centralized return centers and sent back to the warehouses to satisfy the customer demand. Lee and Dong [18] develop a Tabu search based heuristic for integrated RL network design in end-of-lease computers. In their model, there is a single OEM who wants to establish a set of capacitated hybrid processing facilities that serve as both DCs as well as collection centers. The same authors deal with a multi-period location and allocation model where optimal locations for forward processing facilities, collection centers, and hybrid processing are sought under demand and return uncertainty [19]. The solution approach adopted is based on sample average approximation method combined with a simulated annealing heuristic. Pishvaee et al. [25] investigate an integrated forward/reverse logistics network design problem in which the production/recovery centers, distribution/collection centers, and disposal centers are considered while taking into account the uncertainties about the demand, number of returns and variable costs. Pishvaee et al. [26] examine the effect of the capacity levels on logistics network efficiency and responsiveness by formulating a multi-objective, multi-stage forward/reverse logistics network design including production, distribution, collection/inspection, recovery and disposal facilities with multiple capacity levels. Wang and Hsu [38] propose a CLSC network including recovery and landfilling rates to integrate environmental issues into a traditional logistics system.
Zhang et al. [39] address a dynamic capacitated production planning problem in a steel company by means of a multi-echelon, multi-period and multi-product CLSC model. Özkır and Başlıgil [23] incorporate material recovery, component recovery and product recovery processes into design of a CLSC network to increase system profitability. Keyvanshokooh et al. [15] study a multi-echelon, multi-period, multi-commodity and capacitated integrated forward/reverse logistics network concerning the quality levels of the returned products and acquisition price offered according to return type. The paper by Rosa et al. [27] proposes a multi-period CLSC network model by allowing the locations of plants, DCs and RCs to be changed. The capacities of all the facilities can also be modified (i.e., increased or decreased) during the planning horizon. The deterministic model is then extended to a robust optimization model by taking into account the uncertainty in demand and return. Amin and Zhang [3] first formulate a deterministic MILP model where plants and collection centers are opened and then extend it to a stochastic bi-objective model with demand and return uncertainty. As the solution approach, they apply 𝜖-constraint method and weighted sums method.
Demirel et al. [9] examine a multi-period and multi-part MILP model for a capacitated CLSC network under deterministic demand. They contribute to the literature by incorporating second-hand sales, incremental incentives and inventory policies in the return streams of the CLCS network as well as the trade-offs between virgin parts and used parts/products. Chen et al. [6] describe the existing cartridge recycling system in Hong Kong, which includes the classification of used products according to their quality level and the delivery of different materials extracted from them. Chen et al. [7] deviate from other studies on CLSC network design and focus on the following two questions: How do the uncertainties in market size, return quantities and recovery rate affect the profitability of the CLSC and how is product recovery strategy influenced by the consumer perception of remanufactured products and variable cost structure. To this end, the authors develop a stochastic mixed-integer quadratic model use a solution approach based on an integration of the integer L-shaped decomposition with sample average approximation which enables to handle many scenarios.
Shi et al. [33] develop a multi-objective an MILP model for a CLSC network design problem. In addition to the overall costs, the model optimizes overall carbon emissions and the responsiveness of the network. An improved genetic algorithm based on the framework of nondominated sorting genetic algorithm (NSGA II) is developed to obtain Pareto-optimal solutions. In their paper, Pedram et al. [24] examine a CLSC model for tire industry with demand and return uncertainty where both forward and reverse chain consists of three layers. In particular, collection centers, retreading centers and recycling centers constitute the facilities in the reverse channel. Amin and Baki [2] propose a bi-objective CLSC model in which one objective is on-time delivery maximization from the suppliers and the other objective is profit maximization. There exists uncertainty in the demand and factors such as exchange rates and customs duties are also taken into account which differentiates this study from other works. Moreover, a case study is presented involving electrical and electronic equipments.
As can be seen, the first research question we pose is partially examined by Fleischmann et al. [12] where two different real CLSCs are compared and it is shown that integrated design may be beneficial depending on the difference between forward and reverse channels. However, there is no systematic analysis regarding the amount of the resulting benefit based on the relevant parameters. Our paper is an attempt towards filling this gap. The second research question we investigate is somehow covered in Easwaran and Üster [10]. But, in that paper DCs are necessarily co-located with RCs, which means that once an RC is co-located with a remanufacturing facility, there is also a DC established there. We believe that this is rather a restrictive assumption. Therefore, in our paper, we look at the co-location issue only in terms of the facilities handling reverse flows, i.e., remanufacturing facilities and RCs.
The basic model
In this section, we present a basic model that incorporates reverse flows as well as the associated RCs in the distribution network design problem. Based on a set of existing plants (each with given manufacturing and remanufacturing capacities) and a set of customer zones (each with given demand and return quantities for a single product), the model determines the optimal number and location of the DCs and RCs so as to minimize the total cost of establishing and operating this closed-loop network. The model requires that all the demand is met and all the returns are collected at the customer zones. Therefore, the total number of manufactured and remanufactured products must be sufficient to satisfy the demand at the customer zones and the total remanufacturing capacity must be large enough to process all the remanufacturable returns. We assume no capacity limit for the DCs and RCs to be established. In developing the model, our focus has been to understand the nature of the flows and the associated DC/RC configuration in the closed-loop network. To refrain from introducing any plant-based bias into the solution, we assume that both the unit manufacturing cost and the unit remanufacturing cost (which is lower) are the same at all facilities. These costs can be omitted from the model since the total quantities to be manufactured and remanufactured are pre-determined. The basic model is extended in the sequel to also incorporate the location decisions pertaining to the establishment of remanufacturing facilities.
Using the index set i for plants, j for DCs as well as RCs and k for customer zones, we define the following decision variables:
The following is the list of model parameters, which are also depicted in Fig. 1.
The problem can now be formulated as an MILP.
Problem P
The objective function includes the transportation cost of both forward and reverse flows and the fixed cost of opening DCs and RCs. Constraints (1) ensure that the demand of each customer is satisfied, whereas constraints (2) impose that all the returns are collected. Due to the existing manufacturing and remanufacturing capacities, single-sourcing of each customer by a DC and/or an RC cannot be expected. Constraints (3) and (4) are the flow conservation equations at DCs and RCs, respectively. Note that the amount of returns to be shipped from an RC to the plants is only a fraction of the returns arriving at the RC, denoted by α, and the remainder of the returns are to be disposed of. Since this recovery ratio is a proxy for the overall quality of returns, α does not vary with the RC location. Thus, the total amount of disposals is pre-determined and by assuming that the unit disposal costs are the same at all RCs we leave disposal costs out of the model. Constraints (5) ensure that the number of manufactured products is bounded by the manufacturing capacity, whereas constraints (7) guarantee that remanufacturing capacity is not exceeded at each plant. In order to sustain the closed-loop nature of the network, each plant needs to remanufacture all the incoming returns and ship them off to the DCs as part of the forward flows. Since remanufacturing is cheaper than manufacturing on the average, each plant will naturally prioritize processing the returns from RCs. Nonetheless, lower transportation costs between other plant-DC pairs may impede a plant’s ability to ship all the remanufactured goods. To prevent such build-up of remanufactured goods inventories at the plants, we impose constraints (6). Constraints (8) and (9) guarantee that customers can only be assigned to open DCs and open RCs, respectively. Constraints (10) and (11) are the nonnegativity and integrality constraints, respectively.
Note that our model allows the possibility of co-locating a DC and an RC at the same candidate site j. This happens when Y j = T j = 1, and the opening costs of both types of center is added up. In other words, we implicity assume that in case a center serves as both a DC and an RC, no cost benefit can be realized. However, the model can easily be modified to reflect this situation. Another remark is the addition of constraints (12) to the model, which are obtained by adding constraints (5) and (7). Although redundant from the viewpoint of model formulation, constraints (12) tighten the lower bounds (LB) of the subproblems that arise due to Lagrangian relaxation of P.
Solution methodology
In this section, we present a Lagrangian heuristic (LH) to solve the proposed CLSC network design model.
Lagrangian heuristic
LH involves relaxing constraints (1), (2), (3), (4), (5) and (6) with multipliers λ k , 𝜃 k , μ j , π j , γ i , and β i , respectively. Naturally, γ i and β i are required to be nonnegative. After the rearrangement of the terms, we obtain the relaxed problem RP as follows:
Problem RP
Problem RP can be decomposed into the following four subproblems where each subproblem represents the flow between two consecutive echelons in either the forward or the reverse network.
It is important that constraints (12) ensure finite values for variables U i j in subproblem R P 2. In the absence of (12), the U i j values and hence R P 2 will be unbounded.
All the four subproblems can be solved by inspection as shown in Appendix 1, and the objective value of the relaxed problem provides a lower bound on the optimal objective value Z P of the original problem P for any multiplier vectors λ, 𝜃, μ, π, γ, and β. To find the best lower bound, we have to solve the Lagrangian dual:
We use subgradient optimization in updating the multipliers at each iteration of the algorithm, which terminates after t0′ iterations or a pre-specified CPU time. A formal statement of the Lagrangian heuristic is provided in Appendix 2. The solutions to R P 1 and R P 3 prescribe a set of open DCs and a set of open RCs. By fixing the binary variables to represent these open DCs and RCs, a feasible solution for problem P can be found by solving a simple transshipment problem. If the binary location variables for distribution centers and return centers (i.e., variables Y j and T j ) are set to known values as a result of solving subproblems RP1 and RP3, then the MILP problem P reduces to linear programming problem with continuous decision variables representing the amount of flow between plants and DCs as well as DCs and customer zones in the forward network, and between customer zones and RCs as well as RCs and plants in the reverse network. Since it is a linear program, it can be easily solved using commercial solver CPLEX. The objective value of this solution Z P U B provides an upper bound (UB) on the optimal objective value of P.
Computational experiments
In this section, we first apply LH to solve a realistic case study and then assess its performance in solving a set of larger-scale problem instances.
A realistic case study
We study the performance of LH in solving a realistic case study that is based on the copier remanufacturing case in Fleischmann et al. [12]. The original case models 50 European cities with a population of over 500,000 as customer zones. In an effort to use up-to-date population data, we searched wikipedia.org and nationsonline.org and identified 63 European cities with more than 500,000 inhabitants, 27 of which are the national capitals. We assume that there is a plant at each of the 27 capitals, and the 63 major cities constitute the set of alternative sites for the DCs and RCs to be established. Consequently, our case is an I 27,63,63 instance of the network design problem.
The model parameters were set to the values in Fleischmann et al. [12]. The fixed costs of establishing DCs and RCs are f j = 1,500,000 and g j = 500,000 Euros. The unit transport costs per kilometer are c i j = 0.0045, e j k = 0.01, c j i′ = 0.005 and e k j′ = 0.003 Euro. The demand per 1,000 inhabitants is 10 units (i.e., d k = population /100), whereas the return and recovery ratios are τ = 0.6 and α = 0.5, respectively. Since there is no capacity information in the original case, we experimented with three capacity levels for the manufacturing and remanufacturing facilities at each plant. Let n denote the number of plants. We compute the three alternative capacity levels using the formulae below:
where the capacity parameters (a ′,s ′) take the values (1.5,1.2), (3.0,2.4), and (4.5,3.6) for low, medium, and high capacity levels, respectively.
Table 2 compares the performance of LH with that of CPLEX. The percent deviation from the optimal objective value z is denoted by “%” and it is calculated as 100 × (U B − z)/z. We observe that the problem instance becomes more difficult to solve as the manufacturing and remanufacturing capacities are reduced. For the most challenging instance, which has the lowest capacity levels, LH provides a solution that is within 6.1 percent of the optimal solution obtained by CPLEX, albeit it requires about twice the computation time. Perhaps more importantly, CPLEX requires almost triple the time to solve the low capacity instance compared to that of the high capacity instance, whereas the computational requirement increases only 27% for the proposed algorithm.
By studying the optimal sets of DC and RC locations, we conclude that the model is not robust with respect to the manufacturing and remanufacturing capacity levels. It is optimal to establish three DCs and co-locate the RCs with these facilities for all capacity levels. Two out of three sites are common for the low and medium capacities, whereas a set of completely different cities is used for the high capacity levels. We also find that the model is not robust with respect to the solution quality. While LH provides solutions between 2% and 6.1% of the optimal objective value as the capacity levels are varied, none of the sites in the heuristic solution are the same as those in the optimal solution of the same instance. We also solved the case with lower return and recovery ratios i.e., τ = 0.3 and α = 0.2, respectively. The optimal solution in this case is to open a single RC at the same location regardless of the capacity levels (of course, the optimal DC sites do not change). Interestingly, this dominant single RC site is not included in any of the three solutions for the original τ = 0.6 and α = 0.5 instance. This implies that a greedy heuristic may not work well for this closed-loop supply chain design problem.
This I 27,63,63 problem can be considered as a medium-scale instance, and we demonstrate the performance of the proposed Lagrangian relaxation procedure in solving large-scale instances in the next section.
Solving large-scale problem instances
We generate 24 problem instances by fixing the number of plants at 20 and setting the number of customer zones to 100, 200, 400, and 800. Since each customer zone is considered as an alternative DC/RC site, we in fact can group these 24 instances in four sets which we call I 20,100,100, I 20,200,200, and I 20,400,400 in the sequel. The \(\left (x,y\right ) \) coordinates for the plants, potential DC/RC sites and customer zones in each set are generated through uniformly distributed random numbers in \(\left [ 0,1\right ] \). The unit transportation costs are estimated using the Euclidean distance between the facility pairs in consecutive echelons. Therefore, the unit costs of forward and reverse flows are equal for a given pair of sites. For example, the unit cost of shipping goods from plant 1 to a DC at site 2 (c 12) is the same as the unit cost of transporting returned products from an RC at site 2 to plant 1 (c21′). The demand at each customer zone is generated from a uniform distribution between 50 and 100 units. For the ease of exposition we assume that the return ratio τ = r k /d k is the same for all k. For each set, we compute three manufacturing and remanufacturing capacity levels using (13) and use two levels for the fixed costs of establishing DCs and RCs. These are set at $50 and $75, respectively as the low level and $500 and $750, respectively as the high level. The return ratio and the recovery ratio are taken as τ = 0.5 and α = 0.5, respectively. The Lagrangian heuristic has been coded in Matlab 7.4.0 R2007a and the computational experiments were run on a computer with Intel Xeon CPU X5460 at 3.16 GHz processor and 16 GB of RAM. We set a 7,200 seconds time limit for CPLEX.
Table 3 reports on our computational results of the closed-loop supply chain design problem. Four instances could not be solved to optimality within the allowed CPU time. For these more challenging instances, the best solutions identified by CPLEX are reported in the table (each indicated by “ ∗”).
Table 3 confirms our earlier observation that problem complexity increases as the capacity levels are reduced. In addition, we found out that problem instances with higher fixed costs are more difficult than their counterparts with lower fixed costs. Accordingly, CPLEX could not solve two of the three most challenging “high fixed cost-low capacity” instances to optimality within the allowed CPU time. In addition, the other two “high fixed cost” instances of the I 20,400,400 problem could not be solved to optimality by CPLEX. Note that LH performs better than CPLEX for the three “high fixed cost” instances of the largest scale problems we have solved (indicated by the negative % values in Table 3). Notably, the solutions provided by the proposed Lagrangian heuristic for two I 20,400,400 instances are 29–30% better than the best solution identified by CPLEX and these heuristic solutions are obtained by spending much less computational time.
Integrated versus sequential design
In the previous sections we studied an integrated design approach, which involves simultaneous decisions regarding the location of DCs and RCs as well as forward and reverse flows in the closed-loop supply chain. An alternative to our approach is sequential design, which involves first making the DC location and forward flow decisions without incorporating the reverse flows, and then configuring the reverse supply chain by taking the forward chain structure as given [12]. This is particularly relevant for the firms with an existing forward supply chain and considering the launch of product recovery initiatives. In this section, we compare these two approaches in an effort to highlight the potential benefits of integrated design. We address the following question: “Is there a significant difference between integrated and sequential design in terms of cost and solution structure?”
The sequential design approach is represented by the forward problem P F and the reverse problem P R defined below. Note that constraints (5) are revised as (5 ′) in P F since there are no reverse flows in this formulation, i.e., V j i = 0. Also, the optimal forward flows U i j∗ are used in constraints (6 ′) of P R to limit the reverse flows into a plant.
In comparing the integrated and sequential design approaches, we first study the impact of the quantity and quality of the returns. Note that the return ratio τ at the customer zones is a measure of return quantity, whereas the recovery ratio α at the RCs is a proxy for return quality. For the ease of studying the solutions in detail and tracking the changes during the parametric analysis, we use a randomly generated I 5,10,20 instance with fixed costs (f j ,g j ) = (50,50). The total demand \({\sum }_{k} d_{k}=1455\) for this instance, and hence the total amount of reverse flows into the plants is 1455α τ. Although the other 15 I 5,10,20 instances we have solved are not discussed here in the interest of space, we remark that the observed patterns are similar.
We set recovery ratio α = 0.6, manufacturing capacity s i = 300, and remanufacturing capacity a i = 200 for all plants, while varying the return ratio τ in the range \(\left (0,1\right ] \) with increments of 0.1. Table 4 depicts the (optimal) total costs for integrated and sequential design as well as the associated forward and reverse cost components. The last column indicates the percent cost savings that can be achieved by integrated design under each scenario.
In the sequential approach, the optimal objective value of the forward problem does not vary with the return ratio τ because reverse flows are not incorporated in P F . The reverse logistics costs, however, increase with τ in both approaches since more returns need to be shipped back from customer zones. More importantly, the optimal reverse costs in the two approaches are the same in Table 4, whereas the optimal forward cost of the integrated design is always lower than that of the sequential design. That is, the cost disadvantage of the sequential design approach is due to the forward network (i.e., DC locations and forward flows) rather than the reverse network (i.e., RC locations and reverse flows). The open DCs and RCs in both designs are depicted in Table 5. Note that the integrated design has the ability to adapt the forward network configuration according to the return ratio.
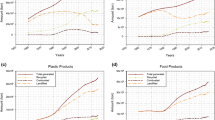
We now focus on the costs related to forward flows. In Table 4, the optimal forward cost first decreases and then increases with respect to the return ratio τ. This can be explained in terms of the overall level of remanufacturing capacity utilization. Clearly, remanufacturing capacity is under-utilized for low values of τ. For example, when τ = 0.2 only 174 units need to be remanufactured which amounts to 17.5 percent utilization of the overall remanufacturing capacity (given that α = 0.6, a i = 200 and there are five plants in this instance). Therefore, as τ increases, the additional returns can be sent to those remanufacturing facilities that are in the plants with smaller forward costs. Thus, the remanufacturing capacity at such plants provides additional capability to serve the customer demand through cheaper forward channels (e.g., plant-DC combinations) and to reduce the forward costs. When these remanufacturing facilities are fully utilized, however, further increases of τ make the use of expensive forward channels inevitable (in Table 4 when τ > 0.7). The forward cost curve behaves similarly for other values of α as shown in Fig. 2. For α = 0.2 and 0.4 the forward cost curves are nonincreasing since the remanufacturing capacity remains significantly under-utilized as the return ratio increases. Also, for α = 0.8 there is no feasible solution to the integrated problem when τ > 0.9. This is because the total remanufacturing capacity is insufficient to process all the recoverable returns (i.e., 1455 × 0.8 × 0.9 = 1048 > 1000 = 5 × 200). In Fig. 3, the forward cost is depicted as a function of the recovery ratio α for fixed values of the return ratio τ. Note that the forward cost curves in Figs. 2 and 3 demonstrate the same patterns. This is expected since it is the product of the return ratio and the recovery ratio that determines the number of items to be remanufactured and consequently the overall utilization of the remanufacturing capacity.
Based on the above observations, we shift our focus on the effect of manufacturing capacity s i and remanufacturing capacity a i on the percent cost difference between the integrated and sequential design approaches. For this set of experiments, we fix τ = 0.5 and α = 0.6 in which case 30 percent of all the demand can be satisfied by remanufacturing returned products. Note that integrated design outperforms sequential design by 9.7 percent for this parameter setting when s i = 300 and a i = 200 (see Table 4).
We vary the remanufacturing capacity a i while manufacturing capacity is fixed at s i = 300. The optimal costs provided by the two design approaches as well as the percent cost differences are depicted in Table 6. At a i = 90, the total remanufacturing capacity of 450 is still sufficient to process all the 437 recoverable returns (i.e., 1455 × 0.5 ×0.6). Consistent with our earlier observations, the increase in remanufacturing capacity has no impact on the total forward cost in sequential design and the total reverse costs are the same for both approaches. The reverse costs decrease as remanufacturing capacity increases since the cheaper reverse channels (e.g., RC-plant combinations) can be used for a larger portion of the recoverable returns. More importantly, Table 6 confirms our earlier findings regarding the impact of remanufacturing capacity utilization on the forward costs of integrated design. Increasing a i reduces the overall utilization level, which enables increased use of the remanufacturing facilities at plants with smaller forward costs.
Our computational experiments on the same problem instance to study the impact of varying the manufacturing capacity s i are summarized in Table 7. We observe that for a given value of the remanufacturing capacity a i the cost savings obtained by integrated design decrease as the manufacturing capacity increases. Although increasing manufacturing capacity enables the use of cheaper plant-DC combinations in both integrated and sequential design, the forward costs decrease faster in the latter case. This can be attributed to the fact that integrated design is constrained to take into account the reverse flows in deciding the forward network structure. Again, the reverse costs are the same for both design approaches.
During the computational experiments, we observed that optimal configuration and cost of the reverse network seem to be robust with respect to the design approach. Note that the same sets of RCs are opened by both integrated and sequential approaches under all τ, α and capacity values in Tables 4–7. Parametric analysis on the other I 5,10,20 instances we studied by varying τ values confirm this observation.
Where to locate the return centers?
The preceding discussion assumes that the firm has a policy of locating RCs in the second echelon. An alternative strategy would be to co-locate the RCs with remanufacturing facilities in the first echelon. This option has the fixed cost advantage due to the possible scale economies associated with co-location. These savings, however, may be offset by the increased transportation costs since the unrecoverable returns are no longer disposed of at the second echelon. In this section, we address the question “Under which conditions would the integration of inspection and remanufacturing operations be beneficial?”
In order to compare the two policies mentioned above, we extend our original model (which assumes remanufacturing capability at all plants) so as to identify the optimal locations for remanufacturing. This can easily be incorporated in Problem P by defining a new binary variable H i which takes the value one if a remanufacturing facility is located at plant i and zero otherwise. We also let h i denote the fixed cost of opening a remanufacturing facility at plant i. The resulting downstream problem P D represents the policy of locating RCs in the second echelon. To capture the decisions pertaining to the establishment of remanufacturing capacity at the existing plants, constraints (7) need to be modified as (7 ′) . Problem P D can be solved via the Lagrangian heuristic presented in “Solution methodology”.
In formulating the upstream problem P U we assume that the returns are sent from customer zones to the RCs at the remanufacturing facilities through the DCs. This is a plausible assumption in many cases since the firms often use the same vehicles to deliver customer orders and collect returns. As a result, the DCs serve as consolidation centers for returns from different customer zones. We define a new variable L i = 1 if an RC and a remanufacturing facility is co-located at plant i and zero otherwise. The fixed cost of this integrated facility is represented by l i . The following formulation of the upstream problem P U also reflects that the unrecoverable returns are disposed of at the first echelon.
In the computational experiments we use the same I 5,10,20 instance with the following parameter values: s i = 300, a i = 200, \(\left (f_{j},g_{j},h_{i}\right ) =(50,75,100)\). We calculate the optimal cost of the upstream and downstream models for return ratio τ and recovery ratio α in the range \(\left (0,1\right ] \) with increments of 0.2 and \(l_{i}\in \left \{ 125,150,175\right \} \). Table 8 shows the results in terms of the percent cost difference with respect to the downstream model. That is, the negative and bold numbers indicate that the optimal cost of the upstream model is less than that of the downstream model. The instances indicated with “–” are infeasible because the total number of recoverable returns is greater than the total remanufacturing capacity.
We observe that when there is no fixed cost advantage (i.e., l i = g j + h i = 175), the downstream location of RCs is always better because P D involves less transportation costs due to the early disposal of unrecoverable returns. Naturally, the upstream model exhibits better performance as the fixed cost advantage increases, particularly when l i = 125. In general, higher values of the recovery ratio α and lower values of the return ratio τ favor the upstream model since the number of unrecoverable returns is smaller in such cases. Note that for fixed α higher values of τ mean more returns that need to be disposed of. This is why the downstream location of RCs is still preferable for α = 0.2 and τ = 0.8 or 1.0 when l i = 125. Based on these observations, we conclude that for any combination of α and τ, the choice between downstream and upstream location policies depends on the fixed cost advantage associated with co-locating an RC and a remanufacturing facility. The impact of increasing return ratio and recovery ratio parameters on the location policy of RCs, however, is complicated by the presence of remanufacturing capacity. The critical issue is whether the reverse system needs additional RCs to accommodate the increase in the number of returns. The discrete nature of these decisions prevents us from observing a clear trend in terms of locating the RCs in the second echelon or together with the remanufacturing facilities in the first echelon. The conclusions drawn from the experiments on this I 5,10,20 remain valid for the other instances we have studied.
Conclusions
In this paper, we provide a general model for the closed-loop supply chain design problem. The proposed model constitutes an integrated approach for designing the forward and reverse networks simultaneously. This enables the firm to take into account the remanufactured items at its plants when planning the shipments to the distribution centers. Our computational experiments show that the proposed Lagrangian relaxation procedure is efficient in solving problems of the size encountered by managers. The quality of the solutions provided by the algorithm is particularly encouraging.
In comparing our integrated approach with the sequential approach for designing distribution networks with reverse flows, we found out that the cost advantages of the former can reach 10 percent. Interestingly, the reverse network structure seems to be robust to the design approach and the cost difference is mainly due to the forward network configuration. This suggests that the ability of the forward network to adapt itself to the presence of reverse flows is the main advantage of the integrated design approach. In the event that the firm already has an established forward network, the integrated solution can serve as a target configuration for the existing distribution centers to converge in the long run.
The level of remanufacturing capacity utilization turns out to be a key determinant of the potential benefits that can be achieved via the integrated approach. This relates to the ability of the firm to ship the recoverable returns to the remanufacturing facilities at the plants with cheaper distribution center connections. During our computational experiments, we consistently observed that the benefits of the integrated model first increase and then decrease as the return ratio increases. For high values of the return ratio, the cost difference between the integrated and sequential approaches is minimal. Note that this confirms the findings of Fleischmann et al. [12] since the forward and reverse network structures become similar as the return ratio approaches to one. While [12] explain the potential benefits of the integrated approach mainly on the basis of cost structures, however, our analysis highlights the difference between the degrees of freedom in designing the forward and reverse networks (the latter being much smaller because the number of facilities is typically less) as another significant factor. The integrated approach is most beneficial for medium values of the return ratio. We also observed that the firm can benefit from the scope economies associated with conducting the inspection and separation operations at the upstream echelon as the overall quality of the returns at the customer zones increases.
References
Agrawal S, Singh RK, Murtaza Q (2015) A literature review and perspectives in reverse logistics. Resour Conserv Recycl 97:76–92
Amin SH, Baki F (2017) A facility location model for global closed-loop supply chain network design. Appl Math Model 41:316–330
Amin SH, Zhang G (2013) A multi-objective facility location model for closed-loop supply chain network under uncertain demand and return. Appl Math Model 37(6):4165–4176
Aras N, Boyacı T, Verter V (2004) The effect of categorizing returned products in re-manufacturing. IIE Trans 36:319–331
Beamon BM, Fernandes C (2004) Supply-chain network configuration for product recovery. Prod Plan Control 15(3):270–281
Chen W, Kucukyazici B, Verter V, Sáenz MJ (2015) Supply chain design for unlocking the value of remanufacturing under uncertainty. Eur J Oper Res 247:804–819
Chen YT, Chan FTS, Chung SH (2015) An integrated closed-loop supply chain model with location allocation problem and product recycling decisions. Int J Prod Res 53(10):3120–3140
Demirel NO ̈, Gökçen H (2008) A Mixed-Integer programming model for remanufacturing in reverse logistics environment. Int J Adv Manuf Tech 39(11–12):1197–1206
Demirel N, Özceylan E, Paksoy T, Gökçen H (2014) A genetic algorithm approach for optimising a closed-loop supply chain network with crisp and fuzzy objectives. Int J Prod Res 52(12):3637–3664
Easwaran G, Üster H (2010) A Closed-Loop supply chain network design problem with integrated forward and reverse channel decisions. IIE Trans 42(11):779–792
Fleischmann M, Krikke HR, Dekker R, Flapper SDP (2000) A characterization of logistics networks for product recovery. Omega 28:653–666
Fleischmann M, Beullens P, Bloemhof-Ruwaard JM, Van Wassenhove LN (2001) The impact of product recovery on logistics network design. Prod Oper Manag 10:156–173
Govindan K, Soleimani H, Kannan D (2015) Reverse logistics and closed-loop supply chain: a comprehensive review to explore the future. Eur J Oper Res 240:603–626
HP (2017) Recycling program overview. http://www8.hp.com/us/en/hp-information/environment/product-recycling.html. (Accessed 29 March 2017)
Keyvanshokooh E, Fattahi M, Syed-Hosseini SM, Tavakkoli-Moghaddam R (2013) A dynamic pricing approach for returned products in integrated Forward/Reverse logistics network design. Appl Math Model 37:10182–10202
Ko HJ, Evans GW (2007) A genetic-based heuristic for the dynamic integrated Forward/Reverse logistics network for 3PLs. Comput Oper Res 34(2):346–366
Krikke HR, Bloemhof-Ruwaard JM, Van Wassenhove LN (2003) Concurrent product and closed-Loop suplly chain design with an application to refrigerators. Int J Prod Res 41(16):3689–3719
Lee D-H, Dong M (2008) A heuristic approach to logistics network design for end-of-lease computer products recovery. Transport Res E-Log 44(3):455–474
Lee D-H, Dong M (2009) Dynamic network design for reverse logistics operations under uncertainty. Transport Res E-Log 45:61–71
Listeş O (2007) A generic stochastic model for supply-and-return network design. Comput Oper Res 34(2):417–442
Lu Z, Bostel N (2007) A facility location model for logistics systems including reverse flows: The case of remanufacturing activities. Comput Oper Res 34(2):299–323
Marín A, Pelegrin B (1998) The return plant location problem: Modelling and resolution. Eur J Oper Res 104(2):375–392
Özkır V, Başlıgil H (2012) Modelling product-recovery processes in closed-loop supply-chain network design. Int J Prod Res 50(18):2218–2233
Pedram A, Bin Yusoff N, Udoncy OE, Mahat AB, Pedram P, Babalola A (2017) Integrated forward and reverse supply chain: a tire case study. Waste Manage 60:460–470
Pishvaee MS, Jolai F, Razmi J (2009) A stochastic optimization model for integrated Forward/Reverse logistics network design. J Manuf Syst 28(4):107–114
Pishvaee MS, Farahani RZ, Dullaert W (2010) A memetic algorithm for bi-objective forward-reverse logistics network design. Comput Oper Res 37(6):1100–1123
Rosa VD, Gebhard M, Hartmann E, Wollenweber J (2013) Robust sustainable bi-directional logistics network design under uncertainty. Int J Prod Econ 145:184–198
Sahyouni K, Savaskan C, Daskin M (2007) facility location model for bidirectional flows. Transport Sci 41(4):484–499
Salema MI, Barbosa-Póvoa AP, Novais AQ (2006) A warehouse-based design model for reverse logistics. J Oper Res Soc 57(6):615–629
Salema MI, Barbosa-Póvoa AP, Novais AQ (2007) An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty. Eur J Oper Res 179(3):1063–1077
Salema MI, Póvoa APB, Novais AQ (2009) A strategic and tactical model for closed-loop supply chains. OR Spectrum 31(3):573–599
Salema MIG, Barbosa-Povoa PB, Novais AQ (2010) Simultaneous design and planning of supply chains with reverse flows simultaneous a generic modelling framework. Eur J Oper Res 203(2):336–349
Shi J, Liu Z, Tang L, Xiong J (2017) Multi-objective optimization for a closed-loop network design problem using an improved genetic algorithm. Appl Math Model 45:14–30
Remanufactured Goods (2012) An Overview of the U.S. and Global Industries, Markets, and Trade. Investigation No. 332-525, U.S. International Trade Commission. https://www.usitc.gov/publications/332/pub4356.pdf (Accessed 29 March 2017)
Üster H, Easwaran G, Akçalı E, Çetinkaya S (2007) Benders decomposition with alternative multiple cuts for a multi-product closed-loop supply chain network design model. Nav Res Log 54:890–907
WEEE Directive 2012/19/EU of directive of the European parliament and council on waste electrical and electrical equipment. http://ec.europa.eu/environment/waste/weee/index_en.htm. (Accessed 29 March 2017)
Xerox (2014) Report on global citizenship https://www.xerox.com/corporate-citizenship/2014/sustainability/sustainable-products/enus.html https://www.xerox.com/corporate-citizenship/2014/sustainability/sustainable-products/enus.html. (Accessed 29 March 2017)
Wang HF, Hsu HW (2010) A closed-loop logistic model with a spanning-tree based genetic algorithm. Comput Oper Res 37(2):376–389
Zhang J, Liu X, Tu YL (2011) A capacitated production planning problem for closed-loop supply chain with remanufacturing. Int J Adv Manuf Technol 54:757–766
Zhou Y, Wang S (2008) Generic model of reverse logistics network design. J Transp Syst Eng Inf Technol 8(3):71–78
Acknowledgments
The second and third authors received financial support from the Scientific and Technological Research Council of Turkey (TÜBİTAK) under the BİDEB 2221 program.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
-
1.
Solution of subproblem R P 1
Subproblem R P 1 is solved separately for each DC j. For a given j we have to solve the problem R P1j with optimal objective value Z R P 1 j= min \(f_{j}Y_{j}+{\sum }_{k}\left (e_{jk}+\lambda _{k}+\right .\) \(\left .\mu _{j}\right ) X_{jk}\) subject to constraints (8), (10) and (11). For fixed λ k and μ j , in the optimal solution to R P1j, Y j is either 0 or 1. If Y j = 0, then X j k = 0 for all k. If Y j = 1, then we assign customers k with \(\left (e_{jk}+\lambda _{k} +\mu _{j}\right ) <0\) to DC j (X j k = d k ), while other customers are not assigned (X j k = 0). If \({\sum }_{k}\min \left \{ \left (e_{jk}+\lambda _{k} +\mu _{j}\right ) d_{k},0\right \} <\) − f j , the optimal solution to R P1j is found by setting Y j = 1 and X j k = d k . If \({\sum }_{k}\min \left \{ \left (e_{jk}+\lambda _{k}+\mu _{j}\right ) d_{k},0\right \} >-f_{j}\), then the optimal solution to R P1j becomes Y j = 0 and X j k = 0 for all k. The solution to R P 1 is then given as \(Z_{RP_{1} }={\sum }_{j}Z_{RP_{1}}^{j}\).
-
2.
Solution of subproblem R P 2
Subproblem R P 2 decomposes by plant, that is we can solve it by considering plants separately. For each plant i the following solution procedure is applied:
-
1.
Sort the values \(\tilde {c}_{j}=c_{ij}+\gamma _{i}-\beta _{i}-\mu _{j}\).
-
2.
Find the smallest value of \(\tilde {c}_{j}\) corresponding to DC j ∗.
-
3.
If \(\tilde {c}_{j^{\ast }}\geq 0,\) then do not ship any product from this plant, i.e., \(U_{ij^{\ast }}=0\) for all j. If \(\tilde {c}_{j^{\ast }}<0,\) then send as many products as possible to DC j ∗ subject to constraint \({\sum }_{j}U_{ij}\leq s_{i}+a_{i}\).
-
1.
-
3.
Solution of subproblem R P 3
Subproblem R P 3 is solved separately for each return center j. For a given j we have to solve problem R P3j with optimal objective value Z R P 3 j as follows. For fixed 𝜃 k and π j , in the optimal solution to R P3j, T j is either 0 or 1. If T j = 0, then W k j = 0 for all k. If T j = 1, then we assign those customers k with \(\left (e_{kj}^{\prime }+\theta _{k}+\alpha \pi _{j}\right ) <0\) to return center j (W k j = r k ) and others not (W k j = 0). If \({\sum }_{k}\min \left \{ \left (e_{kj}^{\prime }+\theta _{k}+\alpha \pi _{j}\right ) r_{k},0\right \} <-g_{j},\) the optimal solution to R P3j is found by setting T j = 1 and W k j = r k . If \({\sum }_{k}\min \left \{ \left (e_{kj}^{\prime } +\theta _{k}+\alpha \pi _{j}\right ) r_{k},0\right \} >-g_{j}\), then the optimal solution to R P3j becomes T j = 0 and W k j = 0 for all k. The solution to R P 3 is then given as \(Z_{RP_{3}}={\sum }_{j}Z_{RP_{3}}^{j}\).
-
4.
Solution of subproblem R P 4
Subproblem R P 4 decomposes by plant, that is we can solve it by considering plants separately. For each plant i the following solution procedure is applied:
-
1.
Sort the values \(\hat {c}_{j}=c_{ji}^{\prime }-\pi _{j}-\gamma _{i} +\beta _{i}.\)
-
2.
Find the smallest value of \(\hat {c}_{j}\) corresponding to RC j ∗.
-
3.
If \(\hat {c}_{j^{\ast }}\geq 0,\) then do not receive any returns from the return centers to this plant, i.e., V j i = 0 for all j. If \(\hat {c}_{j^{\ast }}<0,\) then allow as many returns as possible from RC j ∗ subject to the constraint \({\sum }_{j}V_{ji}\leq a_{i}\).
-
1.
Appendix 2
Let Z P b e s t denote the best (smallest) upper bound identified for P.
- Step 1.:
-
Initialization: Set iteration counter t = 0, ν = 2 multipliers λ k t = 0, 𝜃 k t = 0, μ j t = 0, π j t = 0, γ i t = 0, β i t = 0, \(Z_{P}^{best}=\infty \).
- Step 2.:
-
While t ≤ t0′ or ν < 0.00001, repeat steps 3–6
- Step 3.:
-
Using the current multiplier values λ k t, 𝜃 k t, μ j t, π j t, γ i t, and β i t solve relaxed problems R P 1, R P 2, R P 3, and R P 4. Set \(Z_{P}^{LB}=Z_{RP_{1}}+Z_{RP_{2}}+Z_{RP_{3}}+Z_{RP_{4}}-{\sum } _{k}\lambda _{k}d_{k}-{\sum }_{i}\gamma _{i}s_{i}-{\sum }_{k}\theta _{k}r_{k}\) and obtain Z P U B from the associated feasible solution.
- Step 4.:
-
If Z P U B < Z P b e s t, then Z P b e s t = Z P U B
- Step 5.:
-
Update the multipliers:
\(\lambda _{k}^{t+1}={\lambda _{k}^{t}}+\eta ^{t}\left (\sum \limits _{j}X_{jk} -d_{k}\right ) \)
\(\theta _{k}^{t+1}={\theta _{k}^{t}}+\eta ^{t}\left (\sum \limits _{j}W_{kj} -r_{k}\right ) \)
\(\mu _{j}^{t+1}={\mu _{j}^{t}}+\eta ^{t}\left (\sum \limits _{k}X_{jk} -\sum \limits _{i}U_{ij}\right ) \)
\(\pi _{j}^{t+1}={\pi _{j}^{t}}+\eta ^{t}\left (\alpha \sum \limits _{k}W_{kj} -\sum \limits _{i}V_{ji}\right ) \)
\(\gamma _{i}^{t+1}=\max \left \{ 0,{\gamma _{i}^{t}}+\eta ^{t}\left (\sum \limits _{j}U_{ij}-\sum \limits _{j}V_{ji}-s_{i}\right ) \right \} \) and
\(\beta _{i}^{t+1}=\max \left \{ 0,{\beta _{i}^{t}}+\eta ^{t}\left (\sum \limits _{j}V_{ji}-\sum \limits _{j}U_{ij}\right ) \right \} \).
In the above equations, η t is the step size given as
$$ \eta^{t}=\frac{\nu \left( Z_{P}^{best}-Z_{P}^{LB}\right) }{Denom} $$(14)where
$$\begin{array}{@{}rcl@{}} Denom & =&\sum \limits_{k}\left[ \left( \sum \limits_{j}X_{jk}-d_{k}\right)^{2}+\left( \sum \limits_{j}W_{kj}-r_{k}\right)^{2}\right] \\&&+\sum \limits_{j}\left[ \left( \sum \limits_{k}X_{jk}-\sum \limits_{i}U_{ij}\right)^{2} +\left( \alpha \sum \limits_{k}W_{kj}-\sum \limits_{i}V_{ji}\right)^{2}\right] \\&&+\sum \limits_{i}\left[ \left( \sum \limits_{j}U_{ij} -\sum \limits_{j}V_{ji}-s_{i}\right)^{2}+\left( \sum \limits_{j}V_{ji} -\sum \limits_{j}U_{ij}\right)^{2}\right] \end{array} $$ - Step 6.:
-
Set ν = ν/2 if there is no improvement in the lower bound for the last 30 iterations.
In order to determine the step size for updating the multipliers as in (14), we need an upper bound Z P U B to problem P as well as the associated U i j and V j i values which are feasible to problem R P.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cilacı Tombuş, A., Aras, N. & Verter, V. Designing distribution systems with reverse flows. Jnl Remanufactur 7, 113–137 (2017). https://doi.org/10.1007/s13243-017-0036-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13243-017-0036-4