Abstract
The modern world is experiencing an unprecedented pace of technological change. The introduction of new technological products encourages consumers to trade in old products for new so that they can keep up with the latest in technology. One of the consequences of this rapid change in technology is that product life cycles are very short and there is an abundance of old technology products that need to be disposed of, but this is happening at a time when the earth of running out of natural resources and suitable landfill areas. Remanufactured products are very popular with consumers due to their appeal to offer latest technology with lower prices compared to brand new products. The quality of a remanufactured product induces hesitation for many consumers, in regards to its efficacy and reliability. Therefore, the users are unsure if remanufactured products will have the capacity to render the same expected performance as that of a new device. This uncertainty regarding a remanufactured product could lead the consumer to make a determination against its purchase. With such expansive consumer apprehension, remanufacturers often employ marketing strategies in attempts to provide affirmation about product durability. One stratagem that remanufacturers could employ to encourage customer security are product warranties. The aim of this paper is to study and scrutinize the impact that would be had by offering renewing/non-renewing warranties on remanufactured products. The Advanced Remanufacturing-To-Order (ARTO) system deliberated on in this study is a sort of product recovery system. A discrete-event simulation model was developed from the view of remanufacturer for remanufactured items sold with two-dimensional warranty, in which, an End-Of-Use product (EOUP) is subjected to preventive maintenance action when the remaining life of the product reaches a pre-specified value so that the remanufacturer’s expected profit can be maximized. Experiments were design using Taguchi’s Orthogonal Arrays to represent the full recovery system and observe its behavior under different experimental conditions. In order to assess the impact of warranty and preventive maintenance on remanufacturer total cost, pairwise t tests were carried out along with one-way analyses of variance (ANOVA) and Tukey pairwise comparisons test for each performance measure of the ARTO system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The current rapid technological change has seen facilitation of constant as well as unpredictable change in the desires customers have. This can be justified by how constantly customers abandon their outdated models in order to adopt and cope with new and emerging ones. However, it has been established that advances in technology have been at the center of increased diminished product life cycle. The result of this impact of the life cycle of products has led to an upsurge in their rate of disposal.
With the rise in the disposal rates, effects can be felt through strain expressed by earth’s natural resources as well as landfill areas which have begun to reach their acute peak. It is therefore a significant idea that manufacturing firms should play significant roles in helping to manage the outdated technological products. This can be done by a mechanism where these manufacturing firms are compelled by law to ensure that they recall technological devices which have antiquated. Such initiatives will not only work to enhance their customers’ awareness about pertinent issues of environment but also promote these entities ability to meet the new regulations which have been imposed on them. It is important that these manufacturing entities come up with special facilities that are designed to handle as well as recover their products which have reached their end of lives. Developing such facilities is viewed to be impactful in the initiative set to reduce the amount of mechanical waste that is disposed on the landfills. The initiative can be made possible by encouraging the process of recovering these mechanical materials, parts as well as components from products considered to have reached their end-of-lives. The process of recovery can be conducted in diverse ways; some of these include refurbishing of the products in order to make them useful again, recycling them as well as taking them through a remanufacturing process in order to develop as good as new product from them. Such facilities used for handling end-of-use products (EOUPs) have outstanding commercial benefits. This is because it makes the whole process of making products with diminished life to be recovered to have greater relevance and become more appealing.
In the process of product recovery, most facilities undertaking this work utilize one major operation known as the disassembly operation [40]. This operation is seen to be at the heart of product recovery facility mainly because of its capacity to enhance extraction of desired components from products whose life span has expired. The same process is capable of enhancing a sub assembling process in order to come up with useful materials from EOUPs. In order to enhance the disassembling operation several mechanisms can be utilized in order to make it possible. These involve effectuation of the EOUPs in a singly established workshop, being taken through a disassembling line as well as the desired operations being done in disassembling cells.
Nevertheless the distinction in these mechanisms is based on the amount of yield that each is capable of producing from the EOUPs. It is, therefore established that among the three utilization of a disassembling line emerges to be the most efficient since it is capable to increase the yields obtained from the operation. On the other hand the utilization of single workstation together with disassembly cells are considered to be useful due to their flexibility nature [12]. Disassembly is perceived as an operation that is focused on ensuring that an EOUP is deconstructed down to its core mechanical component. This is achievable because the process makes use of three crucial techniques [19]. These techniques are destructive, semi-destructive as well as non-destructive ones. The main goal why manufacturers carry out disassembling process is to help ensure that recovery process of products is enhanced hence limited dependency on natural resources for their continued operations.
Despite its effectiveness in ensuring that product recovery is enhanced, this process is faced with one uncertainty. That is the possibility of the product quality may have been compromised. This problem is enhanced by the fact that before disassembling most entities do not have informative as well as solid information about the condition of the product that is being disassembled. However this can be countered by promoting individual sample testing prior to disassembling. Despite the capacity to counter this uncertainty through prior testing. It has been established that mechanical disassembly always subjects entities that utilizes it to financial damping particularly of their profits. This consequently has the impact of reducing the profit margin of manufacturers. The profit margin distinction is presumed to be influenced by two major factors and that is, monetary cost of carrying out appropriate as well as required testing on the product as well as magnitude of time demanded to enhance that process. At times it emerges that the product is dysfunctional hence resulting to extra cost due to waste of valuable resources.
Apart from the above challenges encountered, it is evident that the quality of product obtained from the process induces customers’ hesitation. This influenced by question of efficiency as well as reliability of the product. There is always a cloud of uncertainty on capability of the product manufactured to offer services comparable to new one. This level of uncertainty can influence consumers’ decision not to purchase the product. Due to this doubt, manufacturers are always compelled to conduct expensive mechanism to ease consumer apprehension such as devising various marketing strategies that involves warranty provisions [4]. This approach is seen to help in affirming durability of such products as well as taking care of consumer security [33].
On this line it has been established that, to counter uncertainties associated disassembly yields, utilization of sensor-embedded products (SEPs) is an approach with a great future. This approach works in a way that a sensor is implemented into a product when it is manufactured. This sensor therefore will facilitate product monitoring as well as enhancing data collection [47, 51]. This data is critical in establishing potential failure of the product in the future. This is possible because the sensors are capable of providing the necessary information about the current conditions of the components of a given product during its End-of-use (EOU) stage. Further the data that might be collected particularly about dysfunctioning, replacements as well as missing components prior to such products disassembling is crucial as it enhances savings on stages like testing, disposal, holding costs backorder as well as disassembling [16,17,18].
Basing on the advantages postulated in this study on SEP’s, this analysis takes a particularistic approach to review the probable impact that provision of warranties that has information extracted from sensors embedded in products would have on consumers. The study will carry out a quantitative analysis on expansion attained so far in utilizing SEP information on various warranty analyzed models. This will take accounts of information in different manufacturing scenarios. The study will focus on trying to reduce the cost associated with warranty while aiming at increasing the profits that is gained from remanufacturing. This will be done by calculating warranty with an appealing price.
EOU products and required components arrive at remanufacturing facilities in accordance with the Poisson distribution. The disassembly and remanufacturing times exponentially assigned to each station are distributed accordingly [22]. The imposed cost for backorders will be calculated based on the duration of the backorder. Excessive and unessential EOU products and components are disposed of regularly according to a stringent disposal policy. A pull control production mechanism is used in all disassembly line settings considered and reviewed in this research study. Lastly the comparison of warranty costs and temporal periods are made amongst different warranty policies.
The contribution of this paper is basically founded on its capacity to present a quantitative evaluation of the effect that provision of warranty has on manufactured items. This is with focus on a manufacturers` perspective while maintaining their desire to ensure that they offer prices that attract buyers. Despite the fact that studies have been conducted on warranty policies on both brand new products as well as secondhand ones, there is a critical gap on the availability about benefits of warranties on remanufactured products in a comprehensive and quantitative manner. In the existing studies, the profit improvements achieved by offering warranties for different policies determine the range of how much money can be invested in a warranty while still keeping it profitable overall.
Background
This section provides a literature review on the issues considered in this research. First, a brief review on environmentally conscious manufacturing and product recovery is presented. There are two important review papers that are available in the literature and are directly related to the subject area of this paper. The first one is the state of the art survey paper by Gungor and Gupta [11] covering papers in Environmentally Conscious Manufacturing and Product Recovery (ECMPRO) published through 1998. The second one is also the state of the art survey paper in the same area covering papers published between 1998 and 2010 by Ilgin and Gupta [17]. Together, they classified more than 870 papers (330 and 540 respectively) under four main categories, viz. environmentally conscious product design, reverse and closed-loop supply chains, remanufacturing and disassembly. Then, a section on warranty analysis is presented and related literature is highlighted.
Environmentally conscious manufacturing and product recovery
Researchers [11, 14] have recently given more attention to manufacturing practices and product recovery (ECMPRO) issues that take environmental consciousness into account. While factors such as regulatory influences, environmental changes, and public interest have influenced this research, this interest has also arisen because of reverse logistics, product recycling resolutions, and the economic benefits these practices supply. Consumer demand for more environmentally-friendly manufacturing, coupled with stringent environmental legislation, has caused manufacturers to create designated facilities for recycling EOU components and subsequently reducing the waste created by these products. In an attempt to understand the difficulty that product manufacturers face in pursuit of environmentally friendly practices, researchers have reviewed the plethora of challenges that emerge in the sustainable manufacturing and product recovery process (see for example, [13, 23, 32, 34]). Given the key role that disassembly plays in recovery, research has paid particular attention to this step in remanufacturing. (For further detail on the disassembly process, see [28].)
Warranty analysis
Manufacturers (vendors/sellers) create contractual agreements called warranties when selling their products. Warranties exist to hold these manufacturers liable for products that in rare instances do not perform, or prematurely cease in performing, their agreed-upon function. The product’s intended purpose is delineated in the warranty, as well as specifications on promised performance and how customers will be compensated in the event that the product does not meet these specifications [6]. Product warranties can serve one or multiple functions, including: providing insurance and protection so that the manufacturer/seller absorbs the risk of product failure or malfunction [8, 15]; ensure buyers of a product’s reliability [7, 9, 38, 48, 49]; or allow a seller to leverage the protection of a warranty for additional profits at the point of sale [30].
While a variety of literature has discussed the implications of new product warranties, little attention has been given to warranties administered for secondhand items. Furthermore, limited research has been performed on warranty cost analyses on remanufactured products. Saidi-Mehrabad et al. [41] and Shafiee et al. [44] have presented the ideal upgrade strategies for used items using screening test reliability development methods and a stochastic model intended to examine secondhand item sellers’ optimal investments for increasing product reliability using free repair warranty (FRW) policies. Their research suggests a positive correlation between an increased number of investments, declines in virtual age, and increases in reliability levels for the products receiving these investments. Shafiee et al. [45] developed a stochastic reliability improvement model for secondhand products with warranties, as well as a Cobb-Douglas-Type production function to determine optimal upgrade levels. Naini and Shafiee [35] conducted research to pinpoint optimal upgrades, selling prices, and maximum expected profits while applying restrictive assumptions regarding age distribution; this study created a mathematical model that detected and determined the best policies by applying parametric analysis on an item’s chronological age. Yazdian et al. [53] created an additional, integrated mathematical model to determine typical remanufacturing decisions without relying on a received item’s specific age. Liao et al. [29] studied warranty policies from consumer perspectives, as well as their impacts on consumer behavior. According to Alqahtani and Gupta [1], remanufacturers can utilize Free Replacement Warranty (FRW) and Pro-Rata Warranty (PRW) policies to create base and extended one-dimensional warranties for remanufactured products. EOU-derived products, on the other hand, can offer renewable, nonrenewable, one- and two-dimensional warranties. The warranty effect on remanufacturing facilities need further investigation [2].
Maintenance analysis
Product reliability and quality depends heavily on its relationship to maintenance [42]. Literature classifies maintenance into two categories: corrective maintenance (CM) and preventative maintenance (PM). In situations that call for CM, items fail to perform their intended function and maintenance is needed to return them to an operational state. PM occurs before full-fledged product failure occurs as a preventative measure to reduce failure rates and deterioration. If a product only carries a short amount of remaining life, a warranty may cover a shorter time period and only offer CM. Conversely, if products carry a long remaining life, warranties may extend for longer periods and offer PM to reduce warranty servicing costs. Thus, a relationship exists between product life, warranty time frames, CM, and PM.
Extensive literature has commented on maintenance policies, with several published reviews on the topic [10, 46, 52]. Nakagawa [36] provides more detailed information beyond this paper on maintenance theory, and additional publications by Nakagawa [37] supply extensive commentary on modeling maintenance policies.
Comparatively, research has given little interest to warranty-based maintenance policies for secondhand products [43]. Two periodical age reduction PM models have been proposed by Yeh et al. [54] to reduce high failure rates among secondhand products. In the event of expired warranties, Kim et al. [27] research suggested periodic PM policies for secondhand items. To preserve manufacturer profitability, it is recommended that producers only allow PM on secondhand items when savings from the warranty service cost exceeds additional costs incurred by providing PM on the items. Additional research on developing ideal PM policies for remanufactured products is warranted [3].
System description
This study employed discrete-event simulation (DES) to determine the optimal strategy for implementing a two-dimensional renewing warranty policy for secondhand or remanufactured products. Discrete event simulation (DES) is a method of capturing the behavior and performance of a real-life process, facility or system. The increasing speed and memory of modern computers have allowed the technique to be applied to problems of increasing size and complexity. DES models the system as a series of ‘events’ [e.g. a warranty claim arrived, a preventive maintenance performed, a product or component demand met] that occur over time. DES assumes no change in the ARTO system between events. DES allows many ‘what if?’ scenarios to be tested. This allows remanufacturers (decision-makers) to test and better understand alternative ways in which a new policy may be best met. In DES, remanufactured products are modelled as independent entities each of which can be given associated attribute information. This may include parameters such as remaining life of each component, historical maintenance, age, weight, warranty type, warranty validity, previous claims and current condition (functioning or nonfunctioning). DES thus allows complex decision logic to be incorporated that is not as freely possible in other types of modelling. We illustrate this implementation using the Advanced Remanufacturing-To-Order (ARTO) system, a specific type of product recovery system. To understand the system’s reaction to various experimental conditions, the experiments we deployed in this study utilized Taguchi’s Orthogonal Arrays to simulate the entire domain of the recovery system. Pairwise t-tests, one-way analysis of variance (ANOVA), and Tukey pairwise comparison tests were used to analyze warranty and preventative maintenance scenarios to determine a manufacturer’s potential optimum strategies.
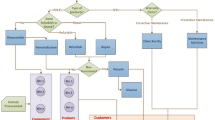
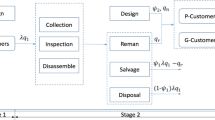
The ARTO system referenced in this study can be considered a type of product recovery system. We use a sensor-embedded washing machine (WM) as a product example for implementing ARTO. Judging by the WM’s EOU, the machine will progress through steps in a recovery process as shown in Fig. 1. To meet quality and manufacturing demands for the WM and satisfy internal and external component demands, the refurbishing and repair process may call for using recycled parts. The ARTO system classifies item arrivals into three different categories: EOU products designated for the recovery process, failed SEP with the need to rectify, or SEP due for maintenance.
To continue with the WM example, EOU WMs would first pass through the ARTO system where a radio frequency data reader in the facility’s database would scan products and retrieve key information. Following this scan, WMs enter a disassembly line that separates components in a six-step process of total disassembly. WMs are made of nine key components: the metal cover, control panel, agitator, spin tub, motor, pump, water and train hoses, pulley, and transmission, as Fig. 2 illustrates. Station disassembly times, interarrival times of each component’s demand, and interarrival times of EOU WM are all generated using exponential distributions. After retrieving this information, all EOUPs ship to station 1 for disassembly; alternatively, if EOUP only requires a singular repair on a component, it is transported to the station corresponding with the repair. The condition of components will dictate the type of disassembly operation, of which there are two: destructive or nondestructive. Destructive disassembly is used for components that have lost all functionality (e.g., parts are broken or have 0 % remaining life) while ensuring that the remaining working components are not damaged. The effort needed to preserve working components means that unit disassembly costs for functional components tend to exceed costs for nonfunctional components. Given the availability of comprehensive, sensor-detected component information after disassembly, no further component testing is required at this stage. It is assumed that the cost of retrieving information is lower than inspections and testing, and that EOUPs have known demands and life cycle information.
An SEP’s overall condition and estimated remaining life will determine its unique recovery operations. Different components meet different needs; recovered components may be used for spare parts demand, while consumer product demands can absorb recovered and refurbished products. Depending on inventory, recycled products and components may also meet materials demands. As salvaged products wait to be recovered by customers, they are placed in varied life-bins (e.g., one year, two years, etc.) after being categorized on their remaining lifespan. In events where the higher-life bins are full, product components with longer life spans are placed in lower-life bins and thus subject to underutilization. If products, components, or other material inventory ever exceed the maximum inventory levels allowed, or are simply assumed as excess, they are disposed of or used for material demands.
Repair and refurbish options, presented in Fig. 3, may also be chosen to fulfill product demands. If an EOUP contains missing or nonfunctional (broken, zero remaining life) components, the repair or refurbishing process must replace or replenish these parts to ensure that remaining life requirements are still fulfilled. Alternatively, components in EOUP may have lower remaining lives than requirements specify, and would thus also need to be replaced.
In the event of SEP failure within a warranty period, failed WMs undergo information retrieval in the ARTO system with the help of radio frequency data readers stored in the facility’s database. After this stage, the WMs undergo the same recovery process as an EOUP.
Finally, to increase longevity and mitigate any risk for failure, WMs receive PM actions within the warranty period. The remanufactured SEPs undergo information retrieval after traveling through the ARTO system with the help of radio frequency data readers stored in the facility’s database, so long as the remanufactured WM receives a pre-specified value on its remaining life. The sensors supply information about product condition, then SEPs experience a four-step maintenance process with this information in mind. Steps in this process include measurement, adjustment, parts replacement, and cleaning. As illustrated in Fig. 4, PM actions performed on remanufactured WMs with degree δ receive δ units of added remaining life compared to their condition upon entering the ARTO system. In addition, the manufacturer will rectify any in-warranty failures between two successive PM actions at no additional cost to customers.
According to Ilgin and Gupta’s [20] comprehensive study that quantitatively evaluated SEP impact on disassembly line performance, results indicated that remanufacturing customer uncertainty is reduced with the use of smart SEPs and that these are favorable in improving performance. To translate and test this claim on an ARTO system, we developed a simulation model mimicking a full recovery system and logged its behaviors under various environmental conditions. We built our discrete-event simulation models using ARENA program, Version 14.5, and incorporated 90 factors into a three-level factorial design for additional consideration, viz., low, intermediate, or high. We proposed these three-level designs with the intention to model any possible curvatures in the response function, as well as to handle any nominal factors occurring at these three levels. Tables 1, 2 and 3 detail the specific parameters, factors, and factor levels [21]. To implement a full-factoral design with 90 factors at three levels, an extensive number of experiments were required (viz., 8.728E + 42). However, we opted to choose only a segment of all possible combinations to shrink the required number of experiments to a researchable level. We used a selection method called a partial fraction experiment to determine an experiment’s number, which produces the most comprehensive information on factors that impact performance parameters while still utilizing the smallest number of experiments possible. Taguchi [50] provides key recommendations for implementing these experiments, and built a special set of arrays called orthogonal arrays (OAs) to incorporate into this method and experimental design. The design of orthogonal arrays allows researchers to conduct a minimal number of experiments with statistical accuracy, and in most cases OAs allow for more efficient analysis compared to other statistical designs. Using the degrees of freedom approach, we can use the minimum number of experiments possible to implement the Taguchi method.
For accuracy, the number of experiments selected must exceed or equal degrees-of-freedom in a system. We chose the Precisely, L181(390) (i.e., 181 = [(Number of levels −1) x Number of Factors] +1) Orthogonal Arrays given that there are 181 degrees of freedom in the ARTO system; in other words, 181 experiments are required to address 90 factors in the three-level design. Orthogonal Arrays also assume that no two factors interact with one another.
To further validate and verify our findings, we built multiple dynamic and counters plots and animations for each simulation model. The time frame to run each experiment spanned 2000 replications with six months, assuming eight hours per shift, one shift per day, and five days per week. The following equation is used for arena models to calculate profit:
in which SR represents total product revenue generated; component and material sales during run time in the simulation; CR represents the total revenue that the collection of EOU WMs produces during the simulated run time; SCR represents scrap component sale revenue during the simulated run time; HC represents total holding cost for products, components, materials and EOU WMs during the simulated run time; BC represents all backorder costs for products, components, and materials during the simulated run time; DC represents all disassembly costs incurred during the simulated run time; DPC includes all disposal costs for components, materials, and EOU WMs during the simulated run time. TC is defined as total testing costs for the simulated run time; RMC includes total product remanufacturing costs for the simulated run time; TPC represents all transportation costs incurred during the simulated run time; WC represents total warranty cost; PMC outlines total preventative maintenance costs during the simulated run time.
Three categories of scraps are recovered and sold for each EOU WM processed. First, metal covers and pumps turn a profit as copper scrap. Second, remanufacturers sell chassis and metal covers to become steel scraps and agitators. Third, water and drain hoses and spin tubs are repurposed and sold as fiberglass. Any additional components are not sold and considered waste. Revenue generated from scrap steel, copper and fiberglass component sales is calculated by multiplying scrap weight in pounds by units of scrap revenue produced for each of the three categories. Additionally, one may calculate disposal costs by multiplying the weight of waste by the unit disposal cost. We assume that it takes 20 s per WM to retrieve the information that smart sensors detect, and that each truck trip requires $50 in transportation costs. The secondary market for recovery products renders different price points depending on quality levels.
Two-dimensional warranty
During the product buying process, customers will often engage in comparison shopping to assess a potential product’s features with its competing brands. This comparison shopping can uncover a range of products with similar, if not seemingly alike, features. Customers compare costs, special product qualities, product and brand credibility, and even insurance from the provider. In cases of close similarity between competing products, customers may also consider after-sale factors to aid in their decision, such as discounts, warranties, parts availability, and other post-sales service. These post-sale factors can become extremely important to the buyer in difficult product buying decisions; thus, the warranty is a key factor that can assure product reliability for the customer and may serve as a focal point for purchase decisions.
Warranties are contractual agreements that manufacturers initiate as a promise to customers to correct product failures or compensate buyers for product issues that arise during the warranty period in relation to the product sale. Warranties exist as a supplementary feature that can enhance the customer’s perception of the product’s quality and performance, as well as an assurance that the product will perform as intended for a specified period of time. Statistically speaking, warranty costs for new items are equal in cases where the manufacturer practices good quality control. On the other hand, EOU products undergo differing warranty costs depending on factors such as age, usage, and maintenance history; thus, warranty costs from EOU items will statistically differ from those for new items.
Remanufactured products are receiving increased stress on the importance of warranties as consumer demands trend toward higher product quality and more attention toward environmental sustainability; these trends will increase demand for remanufactured products, and subsequently the costs of replacements and repairs for failing products. Remanufacturers for refurbished products are thus placing higher priority on warranty management, and now must spend time accurately estimating warranty costs to incorporate into product pricing structures. Such analysis ensures that remanufacturers can still maintain profitability when selling these items to quality and environmentally-conscious consumers. New product manufacturers struggle less with analyzing warranty costs because factors such as usage and maintenance history do not need to be accounted for; remanufacturers, however, must engage in a more complex warranty cost analysis because warranties akin to new or secondhand products may not be economically sustainable for them. To ensure profits, remanufacturers must test and compare warranties for these products and accurately estimate how much it will cost to implement them. They must also take into account other key issues that can impact costs, such as how remanufactured spare parts will be serviced, and how to replace or repair in-warranty failures [33].
In the two-dimensional warranty, a policy is defined by a region in a two-dimensional plane, typically with one axis representing time or age and the other axis representing the usage. For renewing policies, the warranty period begins anew with each replacement or repair. Therefore, the warranty period is uncertain as the warranty expires only when an item does not fail for a period W. in this paper we consider four different shapes of warranty region viz., Rectangular, Infinite Strips, Four Parameters and Triangular shaped as shown in Fig. 5.
There are many different available two-dimensional consumer warranty policies which most products are sold with. The most famous two-dimensional consumer warranties are the Free Replacement Warranty (FRW), Pro-Rata Warranty (PRW), Renewable Free Replacement Warranty (RFRW), Renewable Pro-Rata Warranty (RPRW) and a combination of the both FRW/PRW or RFRW/RPRW.
Notations
- W :
-
Warranty period;
- W i :
-
Limits of warranty period;
- U :
-
Warranty usage;
- U i :
-
Limits of warranty usage;
- Ω :
-
Warranty region;
- Ω i :
-
Warranty sub-region i;
- C o :
-
Operating cost of item;
- C S :
-
Sale price of item;
- C p :
-
Cost of remanufacturing a remanufactured item;
- n :
-
Number of components in a remanufactured item;
- RL :
-
Remaining life of remanufactured item at sale;
- RL i :
-
Remaining life of component i (1 ≤ i ≤ n);
- j :
-
Number of preventive maintenance;
- v :
-
Virtual remaining life;
- v j :
-
Virtual remaining life after performing the jth PM activity;
- m :
-
Level of PM effort;
- δ(m):
-
Remaining life increment factor of PM with effort m;
- t :
-
Remaining life of remanufactured item at failure;
- x :
-
Usage of remanufactured item at failure;
- Ʌ(RL):
-
Intensity function for system failure;
- F i (.):
-
Marginal distribution function of F(.,.);
- F (.,.):
-
Bivariate distribution function;
- F (. |.):
-
Conditional distribution function;
- R (.,.):
-
Refund function for two-dimensional warranty;
- N (.):
-
Number of replacements under warranty;
- N(.,.):
-
Tow-Dimensional renewal function associated with F (.,.);
- N (W; RL):
-
Number of failures over the warranty period with remaining life, RL;
- τ ri :
-
Time at which warranty expires;
- G(.):
-
Distribution function of usage rate;
- E [.]:
-
Expected value of expression within [.];
- C d (W; RL):
-
Total warranty cost to remanufacturer;
Maintenance and warranty formulation
Modelling preventive maintenance effect
Usually, PM activities involve a set of maintenance tasks, such as, cleaning, systematic inspection, lubricating, adjusting and calibrating, replacing different components, etc. [5]. The right PM activities may be able to reduce the number of failures efficiently, as a result reduce the warranty cost and increase the customer satisfaction. This study, adopts the modelling framework proposed by [26] to model the effect of PM activities.
A series of PM activities of a remanufactured item are performed at remaining life RL 1, RL 2,… RL j ,…, with RL 0 = 0. Here, the effect of PM results in a restoration of the item so that the item’s virtual remaining life is effectively increased. The concept of virtual age is introduced in [25]; and then extended in Kijima [24]. In this study, the jth PM only reimburses the damage accrued during the time between the (j − 1)th and the jth PM activities, as a result an arithmetic reduction of virtual remaining life can be obtain [31].
Modelling failures
Most products are complex and multipart so that an item can be viewed as a system consisting of several components. The failure of an item occurs due to the failure of one or more components. A remanufactured products or component is categorized in terms of two states viz., working or failed. The time intervals between consecutive failures are random variables and modelled by proper distribution functions. Interchangeably, the number of failures over time can be modeled by a suitable counting process.
Time to first failure of a remanufactured component depends on the remaining life of the component at the time of sale of the remanufactured product. If the sensor information about EOU component (the component when the item was new) indicates that it has never failed, or was always minimally repaired, then the remaining life of the component at sale is the same as that of the item. Usually, the remaining life of remanufactured component at sale differs due to the replacement or repair actions being different from minimal repair. Therefore, the time to first failure under warranty needs to be defined. Let RL i denote the remaining life of remanufactured component, i.
The sensor embedded in the item provides the remanufacturer with the remaining life of the item at sale RL. The item failure is modelled by a point process with intensity function Ʌ (t) where t represents the remaining life of the item. Ʌ (t) is an increasing function of t indicating that the number of failures increases with age. The failures over the warranty period [RL, RL + W) occur according to a non-stationary Poisson process with intensity function Ʌ (t). This implies that N (W; RL), the number of failures over the warranty period W for an item of remaining life RL at the time of sale, is a random variable with
The expected number of failures over the warranty period is given by
Modelling warranty policies
All warranty formulations for different policies are shown in Table 4.
Non-renewing 2D free replacement warranty policy
Under this policy whenever a remanufactured item fails in the warranty region, Ω, the remanufacturer replaces all failures with a remanufactured item at no cost to the buyer. The replacement comes with the remaining warranty coverage. If the replacement remanufactured item fails during the remaining coverage, the process is repeated till the end of warranty coverage. There are four different warranty regions under FRW policy as shown in Fig. 5.
Non-renewing FRW with rectangle region
The warranty region is characterized by a rectangular shape as shown in Fig. 5a. The warranty expires the first time a failure occurs outside the warranty region. The policy assures the buyer a maximum coverage for W unit of time and/or U unit of usage. As a result the number of replacements under warranty, N(RL), is a random variable distributed with E [N(RL)] as shown in Table 4 along with the expected warranty cost per remanufactured item.
Non-renewing FRW with infinite strips region
The warranty region is characterized by two infinite dimensional strips as shown in Fig. 5b. Under this warranty region, the policy assures the buyer a guaranteed minimum coverage for W units of time after sale and for U units of usage. The warranty expires the first time instant both time and usage exceed the limits W and U respectively. As a result the number of replacements under warranty and the expected warranty cost per remanufactured item are given in Table 4 where M1 (.) and M2 (.) are the one-dimensional renewal function associated with the two marginal distribution function.
Non-renewing FRW with four parameters region
The warranty region is characterized by four parameters (W1, W2, U1 and U2) as shown in Fig. 5c. Under this policy, a buyer is assured of warranty coverage for a minimum time period W1 and for a minimum usage U1 and for a maximum cover for W2 unit of time and U2 unit of usage. As a result the number of replacements under warranty and the expected warranty cost per remanufactured item are shown in Table 4.
Non-renewing FRW with triangle region
The warranty region is characterized by a triangle shape as shown in Fig. Fig. 5d. The number of replacements under warranty and the expected warranty cost per remanufactured item are given in Table 4.
Non-renewing 2D pro-Rata warranty policy
Under this policy, if the remanufactured item fails in the warranty region, Ω, the buyer is refunded a fraction of the original sale price. The amount of refund is a fraction of the remaining life of the remanufactured item at failure. The refund is unconditional as the buyer has no obligation to buy a replacement item. Similar to FRW policy, two different forms for warranty region and refund function, R(t, x) are considered for PRW.
Non-renewing PRW with rectangle region
The warranty region is characterized by a rectangle shape as shown in Fig. 5a and the refund function and the expected warranty cost per remanufactured are shown in Table 4.
Non-renewing PRW with infinite strips region
The warranty region is characterized by two infinite dimensional strips as shown in Fig. 5b and the refund function and the expected warranty cost per remanufactured are shown in Table 4.
Non-renewing FRW-PRW combination policy
In combination warranty, the warranty region, Ω, consists of .two disjoint sub-regions Ω1 and Ω2 where the warranty terms are different for each region. If a failure occurs in Ω1, the buyer is entitle to non-renewable FRW policy. While, if a failure occurs in Ω2, the buyer is entitle to non-renewable PRW policy. In other words, the refund is full and conditional when item failure occurs in Ω1 and partial and unconditional if failure occurs in Ω2. Similar to PRW policy, two different forms for warranty region and refund function, R(t, x) are considered for FRW-PRW combination policy as shown in Fig. 5.
Non-renewing FRW-PRW combination with rectangle regions
The warranty region is characterized by two rectangle shape sub-region as shown in Fig. 5a. The warranty expires the first time a failure occurs outside the rectangle. The refund function and the expected warranty cost per remanufactured item are shown in Table 4.
Non-renewing FRW-PRW combination with infinite strips regions
The warranty region is characterized by two infinite dimensional strips regions as shown in Fig. 5b. As a result the refund function and the expected warranty cost per remanufactured item are given in Table 4.
Renewing 2D free replacement warranty policy
Under this policy whenever a remanufactured item fails in the warranty region; Ω, the remanufacturer replaced all failures with a remanufactured one at no cost to the buyer. The replacement comes with a new warranty identical to the original one. There are four different warranty regions under FRW policy as shown in Fig. 6.
Renewing FRW with rectangle region
The warranty region is characterized by a rectangle shape as shown in Fig. 6a. The warranty expires the first time a failure occurs outside the rectangle. The policy assures the buyer a maximum cover for W unit of time and/or U unit of usage. As a result the number of replacements under warranty, N(RL), is a random variable distributed according to a geometric distribution function with E [N(RL)] and the expected warranty cost per remanufactured item are given in Table 4.
Renewing FRW with infinite strips region
The warranty region is characterized by two infinite dimensional strips as shown in Fig. 6b. Under this warranty region, the policy assures the buyer is guaranteed a minimum coverage for W units of time after sale and for U units of usage. The warranty expires the first time instant both time and usage exceeds the limits W and U respectively. As a result the number of replacements under warranty and the expected warranty cost per remanufactured item are given in Table 4.
Renewing FRW with four parameters region
The warranty region is characterized by four parameters (W1, W2, U1 and U2) as shown in Fig. 6c. Under this policy, a buyer is assured of warranty coverage for a minimum time period W1 and for a minimum usage U1 and for a maximum cover for W2 unit of time and U2 unit of usage. As a result the number of replacements under warranty and the expected warranty cost per remanufactured item are given in Table 4.
Renewing FRW with triangle region
The warranty region is characterized by a triangle shape as shown in Fig. 6d. The number of replacements under warranty and the expected warranty cost per remanufactured item are given in Table 4.
Renewing 2D pro-Rata warranty policy
Under this policy, if the remanufactured item fails in the warranty region, Ω, a remanufactured replacement is supplied at reduced price. This can be viewed as a conditional refund since the refund is tied to a remanufactured replacement purchase. Similar to FRW policy, two different forms for warranty region and refund function, R(t, x) are been consider for PRW.
Renewing PRW with rectangle region
The warranty region is characterized by a rectangle shape as shown in Fig. 6a and the refund function and the expected warranty cost per remanufactured item are given in Table 4.
Renewing PRW with infinite strips region
The warranty region is characterized by two infinite dimensional strips as shown in Fig. 6b and the refund function and the expected warranty cost per remanufactured item are given in Table 4.
Renewing FRW-PRW combination policy
In combination warranty, the warranty region, Ω, consists of .two disjoint sub-regions Ω1 and Ω2 where the warranty terms are different for each region. If a failure occurs in Ω1, the buyer is entitle to FRW policy. While, if a failure occurs in Ω2, the buyer is entitle to PRW policy. The replacement is covered with a new warranty identical to that of the original item. Similar to PRW policy, two different forms for warranty region and refund function, R(t, x) are been consider for FRW-PRW combination policy as shown in Fig. 6.
Renewing FRW-PRW combination with rectangle region
The warranty region is characterized by two rectangle shape sub-region as shown in Fig. 6a. The warranty expires the first time a failure occurs outside the rectangle. The refund function and the expected warranty cost per remanufactured item are given in Table 4.
Renewing FRW-PRW combination with infinite strips regions
The warranty region is characterized by two infinite dimensional strips regions as shown in Fig. 6b. As a result the refund function and the expected warranty cost per remanufactured item are given in Table 4.
Modelling warranty policies
Assuming that the cost of each PM action is C pm (δ). Each PM cost is a non-negative and non-decreasing function of remaining life increment factor of PM (δ) with effort m. Therefore, the cost of each PM is a linear function of PM degree and is given by:
Results
The results are divided into three sections. Section 7.1 deals with the evaluation of the effect of offering different warranty policies to help the decision maker choose the best warranty policy to offer. Section 7.2, shows a quantitative assessment of offering PM on warranty policies. Finally, section 7.3 presents a quantitative assessment of the impact of SEPs on the warranty and maintenance costs and policies to the remanufacturer. Section 7.4 discusses pricing of a remanufactured item with consideration of warranty and maintenance actions.
Remanufacturing warranty policies evaluation
In this section, the results to compute the expected number of failures and expected cost to the remanufacturer were obtained using the ARENA 14.5 program. We evaluate different warranty period with offering a preventive maintenance policy during each period. For illustration we will discuss only the results of FRW in details where the rest are in similar fashion.
Table 5 presents the expected cost for remanufactured WM and components for two-dimensional warranty policies. In Table 5, the expected cost to the remanufacturer includes the cost of supplying the original item, C s . Thus, the expected cost of warranty is calculated by subtracting C s from the expected cost to remanufacturer. For example, from Table 5, for W = 0.5 and RL = 1, the warranty cost for WM is |$102.88 – Cs| = |$102.88 - $120.00| = $17.12 which is ([$17.12 / $120.00] × 100) = 14.27% saving of the cost of supplying the item, C s , which is significantly less than that $120.00, C s . This saving might be acceptable, but the corresponding values for longer warranties costs are much higher. For example, for W = 2 years and RL = 1, the corresponding percentage is ([|$145.90 - $120.00| / $120.00] × 100) = 21.58% of the total cost extra for offering FRW on remanufactured WM with 1 year remaining life.
Preventive maintenance evaluation
In order to assess the impact of PM on warranty cost, pairwise t tests were carried out for each performance measure. Table 6 presents all models costs for warranty models with PM respectively. According to these tables, PM achieves significant savings in holding, backorder, disassembly, disposal, remanufacturing, transportation, warranty, PM costs and number of warranty claims. In addition, SEPs provide significant improvements in total revenue and profit. According to Table 6, offering PM helps remanufacturer achieve saving 18%, 21%, 19% and 18% in total cost for Conventional, SEM with FRW, SEM with FRW, and SEM with FRW respectively.
The lowest average value of warranty and the number of warranty claims during the warranty period for remanufactured WMs across all policies are $16,473.42 and 19,934 claims respectively for the Sensor Embedded Model with FRW policy and $3159.75 PM cost for the SEPs with RPRW policy. Whereas the RPRW has the worst values for the warranty and the number of warranty claims while PRW policy has the worst PM cost during the warranty period.
Sensor embedded evaluation
In order to assess the impact of SEPs on warranty cost, pairwise t tests were carried out for each performance measure. Tables 7, 8 and 9 present 95 % confidence interval, t value and p value for each test. According to these tables, SEPs achieve statistically significant savings in holding, backorder, disassembly, disposal, testing, remanufacturing and transportation costs. In addition, SEPs provide statistically significant improvements in total revenue and profit.
MINITAB-17 program was used to carry out one-way analyses of variance (ANOVA) and Tukey pairwise comparisons for all the results in this section. ANOVA was used in order to determine whether there are any significant differences between the warranty costs, number of claims and PM costs for the four different models viz., SEPs with FRW, SEPs with PRW, SEPs with FRW/PRW, SEPs with RFRW, SEPs with RPRW and SEPs with RFRW/RPRW, while the Tukey pairwise comparisons was conducted to identify which models are similar and which models are not. Table 7 shows that there is a significant difference in warranty costs between different warranty policies. Tukey test shows that all the models are different and the SEP model with FRW policy has the lowest warranty cost. In addition, there is a significant difference in the number of warranty claims between different warranty policies (see Table 8). The FRW policy has the lowest number of claims. Finally, Table 9 shows that there is a significant difference in PM costs between different warranty policies. Tukey test shows that all models are different except for RPRW and FRW/PRW there are no significant difference between them and between RFRW/RPRW and FRW in term of PM cost. The SEP model with CSW policy has the lowest costs. These results can be useful in the determining the economical warranty policy associated with embedding sensors in WMs.
Pricing of a remanufactured item
A remanufactured item with small remaining life indicates a higher expected warranty cost where a younger item with large remaining life implies a smaller expected warranty cost. Remanufacturer sell remanufactured items of different remaining life. If a remanufacturer were to price each item so as to recover the warranty and preventive maintenance costs associated with the item, then the sale price, CS (v), of a remanufactured item of virtual remaining life v needs to satisfy the inequality given below and failure to do so would imply a loss (rather than profit) in an expected sense.
If the remanufacturer were to price an item based on a fixed expected warranty cost, then the warranty duration (W) must decrease as the virtual remaining life (v) decrease. This indicates a shorter warranty period for a remanufactured item with low remaining life. An alternative strategy for overcoming this problem is to determine the sale price based on a warranty cost averaged over the different remaining lives. That will make higher warranty costs for less remaining life. Remanufactured items are balanced by lower warranty costs for higher remaining life items. This lowers the sale price of lower remaining life items at the expense of higher sale price for higher remaining life items. From a marketing point of view, this is a more attractive and better strategy for the remanufacturer.
Conclusions
Sensor embedded products utilize sensors implanted into products during their production process. Sensors are useful in predicting the best warranty policy and warranty period to offer a customer for the remanufactured components and products. The conditions and remaining lives of components and products can be estimated prior to offering a warranty based on the data provided by the sensors. This helps reduce the number of claims during warranty periods and eliminates unnecessary costs inflicted on the remanufacturer. The two-dimensional Free Replacement Warranty (FRW), Pro-Rata Warranty (PRW) Renewable FRW, Renewable PRW and combination FRW/PRW or RFRW/RPRW policies’ costs for remanufactured products and components were evaluated for different periods in this paper. To that end, the effect of offering two-dimensional warranty policies to each disassembled component and sensor embedded remanufactured product was examined and the impact of sensor embedded products on warranty costs was assessed. A case study and varying simulation scenarios were examined and presented to illustrate the model’s applicability.
References
Alqahtani AY, Gupta SM (2017a) Warranty cost analysis within sustainable supply Chain. In: Akkucuk U (ed) Ethics and sustainability in global supply Chain management. IGI Global, Hershey, pp 1–25
Alqahtani AY, Gupta SM (2017b) Optimizing two-dimensional renewable warranty policies for sensor embedded remanufacturing products. J Ind Eng Manag 10(2):73–89
Alqahtani AY, Gupta SM (2017c) One-Dimensional Renewable Warranty Management within Sustainable Supply Chain. Resources 6:16
Balachander S (2001) Warranty signalling and reputation. Manag Sci 47(9):1282–1289
Ben Mabrouk A, Chelbi A, Radhoui M (2016) Optimal imperfect preventive maintenance policy for equipment leased during successive periods. Int J Prod Res 54(17):1–16
Blischke W (ed) (1994) Warranty cost analysis. Marcel Dekker Inc., New York, United States
Blischke W (1996) Product warranty handbook. Marcel Dekker Inc., New York, United States
Blischke WR, Murthy DP (2000) Reliability: modeling, prediction, and optimization, Wiley Series in Probability and Statistics. John Wiley & Sons Inc., Danvers, Massachusetts, United States
Gal-Or E (1989) Warranties as a signal of quality. Can J Econ 22(1):50–61
Garg A, Deshmukh SG (2006) Maintenance management: literature review and directions. J Qual Maint Eng 12(3):205–238
Gungor A, Gupta SM (1999) Issues in environmentally conscious manufacturing and product recovery: a survey. Comput Ind Eng 36(4):811–853
Gungor A, Gupta SM (2002) Disassembly line in product recovery. Int J Prod Res 40(11):2569–2589
Gupta SM (2013) Reverse supply chains: issues and analysis. CRC Press, Boca Raton, Florida, United States
Gupta SM, Lambert AJD (eds) (2007) Environment conscious manufacturing. CRC Press, Boca Raton
Heal G (1977) Guarantees and risk-sharing. Rev Econ Stud 44(3):549–560
Ilgin MA, Gupta SM (2010a) Comparison of economic benefits of sensor embedded products and conventional products in a multi-product disassembly line. Comput Ind Eng 59(4):748–763
Ilgin MA, Gupta SM (2010b) Environmentally conscious manufacturing and product recovery (ECMPRO): a review of the state of the art. J Environ Manag 91(3):563–591
Ilgin MA, Gupta SM (2010c) Evaluating the impact of sensor-embedded products on the performance of an air conditioner disassembly line. Int J Adv Manuf Technol 53(9–12):1199–1216
Ilgin MA, Gupta SM (2011a) Performance improvement potential of sensor embedded products in environmental supply chains. Resour Conserv Recycl 55(6):580–592
Ilgin MA, Gupta SM (2011b) Recovery of sensor embedded washing machines using a multi-kanban controlled disassembly line. Robot Comput Integr Manuf 27(2):318–334
Ilgin MA, Gupta SM (2012) Remanufacturing modeling and analysis. CRC Press, Boca Raton, Florida, United States
Ilgin MA, Gupta SM, Nakashima K (2014) Coping with disassembly yield uncertainty in remanufacturing using sensor embedded products. J Remanuf 1(7):1–14
Ilgin MA, Gupta SM, Battaïa O (2015) Use of MCDM techniques in environmentally conscious manufacturing and product recovery: state of the art. J Manuf Syst 37:746–758
Kijima M (1989) Some results for repairable systems with general repair. J Appl Probab 26(1):89–102
Kijima M, Morimura H, Suzuki Y (1988) Periodical replacement problem without assuming minimal repair. Eur J Oper Res 37(2):194–203
Kim CS, Djamaludin I, Murthy DNP (2004) Warranty and discrete preventive maintenance. Reliab Eng Syst Saf 84(3):301–309
Kim DK, Lim JH, Park DH (2011) Optimal maintenance policies during the post-warranty period for second-hand item. The 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, pp 446–450
Lambert AF, Gupta SM (2005) Disassembly modeling for assembly, maintenance, reuse and recycling. CRC press, London, England, United Kingdom
Liao BF, Li BY, Cheng JS (2015) A warranty model for remanufactured products. J Ind Prod Eng 32(8):551–558
Lutz NA, Padmanabhan V (1995) Why do we observe minimal warranties? Mark Sci 14(4):417–441
Martorell S, Sanchez A, Serradell V (1999) Age-dependent reliability model considering effects of maintenance and working conditions. Reliab Eng Syst Saf 64(1):19–31
Moyer LK, Gupta SM (1997) Environmental concerns and recycling/disassembly efforts in the electronics industry. J Electron Manuf 7(01):1–22
Murthy, D. P., & Blischke, W. R. (2006). Warranty management and product manufacture. Springer Science & Business Media
Mutingi M, Mapfaira H, Monageng R (2014) Developing performance Management Systems for the Green Supply Chain. J Remanuf 4(6):1–20
Naini SGJ, Shafiee M (2011) Joint determination of price and upgrade level for a warranted remanufactured product. Int J Adv Manuf Technol 54:1187–1198
Nakagawa, T. (2006). Maintenance theory of reliability. Springer Science & Business Media
Nakagawa, T. (2008). Advanced reliability models and maintenance policies. Springer Science & Business Media
Pecht, M. (2008). Prognostics and health management of electronics, John Wiley & Sons, Ltd, Hoboken, New Jersey, United States
Petriu EM, Georganas ND, Petriu DC, Makrakis D, Groza VZ (2000) Sensor-based information appliances. IEEE Instrum Meas Mag 3(4):31–35
Priyono A, Ijomah WL, Bititci US (2015) Strategic operations framework for disassembly in remanufacturing. J Remanuf 5(11):1–16
Saidi-Mehrabad M, Noorossana R, Shafiee M (2010) Modeling and analysis of effective ways for improving the reliability of remanufactured products sold with warranty. Int J Adv Manuf Technol 46(1–4):253–265
Scheidt L, Shuqiang Z (1994) An approach to achieve reusability of electronic modules. In Proceedings of the IEEE international symposium on electronics and the environment, San Francisco, pp 331–336
Shafiee M, Chukova S (2013) Maintenance models in warranty: a literature review. Eur J Oper Res 229(3):561–572
Shafiee M, Chukova S, Yun WY, Akhavan Niaki ST (2011a) On the investment in a reliability improvement program for warranted remanufactured items. IIE Trans 43(7):525–534
Shafiee M, Finkelstein M, Chukova S (2011b) On optimal upgrade level for used products under given cost structures. Reliab Eng Syst Saf 96(2):286–291
Sharma A, Yadava GS, Deshmukh SG (2011) A literature review and future perspectives on maintenance optimization. J Qual Maint Eng 17(1):5–25
Simon M, Bee G, Moore P, Pu J-S, Xie C (2001) Modelling of the life cycle of products with data acquisition features. Comput Ind 45(2):111–122
Soberman DA (2003) Simultaneous signaling and screening with warranties. J Mark Res 40(2):176–192
Spence M (1977) Consumer misperceptions, product failure and producer liability. Rev Econ Stud 44(3):561–572
Taguchi G (1986) Orthogonal arrays and linear graphs. American Supplier Institute, Inc., Dearborn, Ml.
Vadde S, Kamarthi SV, Gupta SM, Zeid I (2008) Product life cycle monitoring via embedded sensors. In: Gupta SM, AJD L (eds) Environment conscious manufacturing. CRC, Boca Raton, pp 91–103
Wang H (2002) A survey of maintenance policies of deteriorating systems. Eur J Oper Res 139(3):469–489
Yazdian, S. A., Shahanaghi, K., & Makui, A. (2014). Joint optimisation of price, warranty and recovery planning in remanufacturing of used products under linear and non-linear demand, return and cost functions. Int J Syst Sci, 47(5):1155-1175
Yeh RH, Lo HC, Yu RY (2011) A study of maintenance policies for second-hand products. Comput Ind Eng 60(3):438–444
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alqahtani, A.Y., Gupta, S.M. Evaluating two-dimensional warranty policies for remanufactured products. Jnl Remanufactur 7, 19–47 (2017). https://doi.org/10.1007/s13243-017-0032-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13243-017-0032-8