Abstract
Purpose
Recent studies have noted a degree of variance between the geometries segmented by different groups from 3D medical images that are used in computational fluid dynamics (CFD) simulations of patient-specific cardiovascular systems. The aim of this study was to determine if the applied sequence of magnetic resonance imaging (MRI) also introduced observable variance in CFD results.
Methods
Using a series of phantoms MR images of vessels of known diameter were assessed for the time-of-flight and multi-echo data image combination sequences. Following this, patient images of arterio-venous fistulas were acquired using the same sequences. Comparisons of geometry were made using the phantom and patient images, and of wall shear stress quantities using the CFD results from the patient images.
Results
Phantom images showed deviations in diameter between 0 and 15% between the sequences, depending on vessel diameter. Patient images showed different geometrical features such as narrowings that were not present on both sequences. Distributions of wall shear stress (WSS) quantities differed from simulations between the geometries obtained from the sequences.
Conclusion
In conclusion, choosing different MRI sequences resulted in slightly different geometries of the same anatomy, which led to compounded errors in WSS quantities from CFD simulation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Computational Fluid Dynamics (CFD) is a well-known tool in engineering, used to assess the flow of fluids in silico. This computational method is applied in cardiovascular engineering to predict and analyze blood flow patterns in complex situations, such as cerebral aneurysms, valve prosthesis, stented vessels, and arteriovenous fistulae (AVFs).16 Commonly, these studies are performed using 3D geometries segmented from medical images, such as computed tomography (CT) and magnetic resonance imaging (MRI), with or without contrast agent. Certain patient groups cannot receive Gd-based contrast agents commonly used for MRI,1 so non-contrast (NCE) MRI sequences are used to image blood vessels in these cases. Multiple NCE sequences exist, including the well-known time of flight (ToF), TrueFISP, and the multi echo data image combination (MEDIC) sequence which has been shown to depict vessel diameters in agreement with ultrasound when used in the upper extremity.13
The accuracy of CFD in predicting flow dynamics depends on a series of factors including the boundary conditions, turbulence modeling, meshing techniques, researcher experience, and geometrical accuracy. Recently, the American Food and Drug Administration (FDA) has begun to consider a good practice to use computational models in the design process of medical devices. The FDA conducted a multi-center study to compare CFD results to an experimental model, and observed a large degree of variability between research groups.21 Another large study conducted by The International Aneurysm Challenged observed wide variability in CFD results between researchers.26 Similarly, variations in results have been observed when segmentations from MRI images and CT images are compared, and when imaging of the same participant is undertaken at different time points23 suggesting that deviations in geometry are an important factor in CFD variation. It is possible different MRI sequences can introduce similar variability into blood vessel segmentation, and, consequently, the CFD analysis.
Used as a vascular access for hemodialysis,6 the autologous AVF is a non-physiological anatomy formed by creating an anastomosis between an artery and vein, which produces a blood-flow in the vein which would never occur naturally. However, AVFs suffer from failure rates of around 30–40% at one year,2 typically due to stenosis secondary to occlusion. AVF failure has associated cost and morbidity, and can significantly disrupt a patient’s life. The AVF presents an interesting case for CFD studies due to intertwined morphological and hemodynamic changes, which occur after its creation, which ultimately affect its clinical usability. Wall shear stress (WSS) patterns have been identified as having a significant effect on the development of stenoses in AVFs, and has been studied extensively using CFD. In these studies a number of different MRI sequences have been used in geometry acquisition.7,10,11,20
The aim of this study was to assess whether ToF and MEDIC MRI produce similar depiction of geometry, and similar results from corresponding CFD simulations. Specifically, we hypothesized that since MEDIC has been shown to agree with US measurements of peripheral vessels, and ToF to underestimate their size, WSS quantities from ToF would be overestimated in CFD simulation. In order to assess the differences introduced by changing MRI sequence, a series of phantoms simulating morphological features of the AVF were scanned. Using these phantoms, the objectives were to explore the effect of vessel diameter, flow velocity in the vessel, and flow direction relative to the imaging plane on the geometry of segmented models used for CFD analysis. To follow up, WSS quantities were obtained from patient-specific CFD simulations using geometries obtained from the two MRI sequences.
Methods
Briefly, this study examined differences in geometric and simulated WSS quantities between ToF and MEDIC MRI, and was achieved in the following steps. A series of phantoms were used to obtain MR images of vessels of known diameter, allowing observation of the effect of changing pulse sequence parameters, vessel size, vessel flow, and vessel orientation on geometry measurements. WSS quantities were determined in order to give a baseline error value. Next, patient images were acquired from the two sequences and segmented to generate WSS quantities from CFD. WSS quantities from the two sequences were compared to determine whether changing the MRI sequence had measurable effects on CFD simulations.
Phantom Preparation
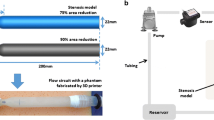
Two phantom setups were manufactured, a straight tube aligned with the MRI scanner z-axis, and a loop swing. The first setup consisted of an open acrylic box, with a couple of supporting structures glued to a plastic tube with its inlet and outlet points on the opposite walls of the box. Three phantoms of this type were manufactured, with internal tube diameters (D) 2, 3 and 5 mm and 1-1.6 mm wall thickness. The inlet of the tubing on one side wall of the box was connected to a water source and a pulsatile flow pump (Cole Parmer, Masterflex Digital Pump System, Germany). Each phantom was imaged with water flowing at flow rates (Q) which maintained a flow velocity of 0.5 or 1.0 m s−1 in the phantom. With water density ρ = 1 × 103 kg m−3 and dynamic viscosity µ = 1 × 10−3 Pa s, the Reynolds number \(Re = \frac{4}{\pi }\frac{\rho Q}{\mu D}\) of the flow in the phantoms ranged from 2100–10,600, indicating that the flow conditions were either transitional or turbulent.
The second phantom setup consisted of an open acrylic box with both inlet and outlet points positioned on the same wall. In this case, three plastic cylinders were glued into the phantom body, two of which acted as supporting structures, and the most distal one as a wrapping post (curve-H). This setup was then repeated with the tubing wrapped around the center cylinders (curve-L). The effect of this was to decrease the curvature of the phantom vessel. In other words, phantom curve-H had a higher curvature than phantom curve-L. All phantoms were filled with a small amount of water in order to prime the scanner. All phantoms were placed into the scanner bore with the center of the phantom aligned with the scanner isocenter. Images of the phantoms can be seen in the supplementary material (sup. Figs. 1 and 2).
Patient Population
Four patients with end-stage renal failure who had been referred for AVF creation surgery at our institution were recruited into this study as part of the ReDVA project (www.redva.eu), a multicenter study aiming to assess longitudinal changes in AVFs using CFD . All patients provided informed written consent, and ethical approval was obtained. Two of the patients were indicated for brachio-cephalic AVF creation (AV1, AV3) and two were indicated for radio-cephalic AVF creation (AV2, AV4). Post AVF surgery, all patients underwent an MRI surveillance session, 17–26 days after surgery.
All patients were placed head first and supine into the bore with their arms relaxed by their side. An 8-channel phased array RF coil was placed around the arm of interest. The patient was positioned slightly off-axis in relation to the scanner bore, in order to ensure that the arm (anatomical area of interest) was as near as possible to the isocenter of the magnet. The site of the anastomosis was identified by palpable thrill and was marked by positioning a cod liver oil capsule on the skin adjacent to the site, which can be seen in the supplementary material (sup. Fig. 3).
MR Imaging
All images were acquired on a 3.0 T PrismaFIT scanner (SIEMENS, Erlangen, Germany) with an 8-channel small flexible array coil. A 2D gradient echo localizer sequence was used for initial visualization of the area of interest. Following this, a 2D ToF MR sequence was applied in an axial oblique orientation and region coverage was maintained at approximately 10 cm to 15 cm. Imaging parameters used were TR/TE: 14/5.8 ms, FA 18°, slice thickness: 1.5 mm, FOV: 140 mm, matrix: 512 × 512 px (no interpolation), and receiver bandwidth: 165 Hz px−1. This was followed by a 3D T2* MEDIC sequence (TR/TE: 29/16 ms, FA: 30°, slice thickness: 1.06 mm (176 slices in the imaging block), FoV: 136 mm, matrix: 512 × 512 px (no interpolation), and receiver bandwidth: 160 Hz px−1) over the same area. The MRI sequences had similar voxel sizes, with voxToF = 0.273 mm and voxMEDIC = 0.266 mm.
Patients had one additional sequence added to their protocol in order to obtain flow velocity measurements. A retrospectively ECG gated 2D phase-contrast (PC) MRI was performed, both proximally and distally (approx. 5 cm) to the anastomosis, in order to measure the through plane flow rates at each branch of the AVF. Imaging parameters used were TR/TE: 99.7/7.62 ms, FA: 20°, FOV 100 mm, matrix 192 × 115, receiver bandwidth: 440 Hz/pixel, VENC: 10–250 cm s−1 (depending on whether artery or vein) and 16–64 temporal phases over the cardiac cycle. Velocity wave-forms for the blood flow were produced by semi-automated segmentation using Segment (Medviso, Switzerland).
Vessel Segmentation
All MEDIC and ToF images were segmented using the sweeping method available on SimVascular (Stanford University, CA, USA).25 Nodes of 3D splines were manually positioned near the center of the vessel for working as sweeping pathlines. Next, the 3D scans were interpolated onto a sequence of planes perpendicular to the pathlines, where 2D closed-loop splines segmenting the vessel lumen were obtained. Finally, the closed-loop spline segmentations were lofted together to form the 3D tubular models with smooth transition between the segmented planes. These models were exported as finely-spaced stereolithography (STL) files for geometry analysis and CFD meshing.
Geometry Analysis
To compare geometric features (primarily vessel diameter and area) between the MRI sequences it was necessary to define an origin point shared between the images. For the phantom models the origin point was defined as the first segment of vessel to enter the phantom box area. For the patient models the origin point was defined as the point at the anastomosis where the vein centerline intersects with the artery centerline.
Vessel centrelines in the form of splines were extracted using the maximum inscribed sphere radius method.3 The distance along the centerlines to the defined origin point s was defined as a topological 1D coordinate system to locate and compare the geometrical features of the vessel. Thus the Cartesian position of any point of the centerline splines was found from the distance along the centerline as γ(s) = (x(s), y(s), z(s)), where the distance coordinate s was obtained from a line integral of γ using any arbitrary parametric coordinate. The vessel cross-sectional area A = A(s) was obtained by integrating slices of the geometrical models perpendicular to the centerline.
Computational Fluid Dynamics
The CFD meshing and processing were both performed with HELYX v.2.5 using the STL files obtained from the patient images. A hexahedra-dominant octree algorithm was used for meshing, which is the native mesh method in the OpenFOAM package. This method generates a surface mesh with defined cell spacing, totally independent of the quality of the STL surface obtained from the segmentation. Furthermore, this method minimises the formation of non-orthogonal cell surfaces, which introduce integration errors in the finite volume method (FVM). For the patient models, the mesh surface was divided by four patches: wall, proximal artery, distal artery, and proximal vein; at which the boundary conditions were applied. Most cells had sides of 250 µm, and an inflation prism layer of five cells from 50 to 125 µm covered the wall patch. The walls were considered rigid, and the boundary conditions of all exits of the fistula were specified according to the patient-specific flow rate pulses obtained from the PC-MRI scans. The flow rate time series of the proximal artery and vein were obtained by integrating the same 2D PCMRI cross-sectional plane. These flow rates were used to apply velocity values in a paraboloid distribution to both the proximal artery and proximal vein caps, whilst the distal artery velocity boundary condition was set to fluctuate freely.
Blood was considered a Newtonian fluid with dynamic viscosity µ = 3.5 × 10−3 Pa s and density ρ = 1.06 × 103 kg m−3.
Since it is believed that WSS has significant influence in the patency of AVFs by its role in the genesis of intimal hyperplasia [15], both time-averaged WSS
and oscillatory shear index
were used in the analysis. In Eqs. (1) and (2), τw is the WSS tensor, T is the pulse period, and t0 is a point in time. The OSI shows whether the τw\(\hat{\varvec{n}}\) vector oscillates on a single pulse orientation (OSI = 0.0) or oscillating between positive and negative orientations (OSI = 0.5) during the pulse period, where \(\hat{\varvec{n}}\) is the surface normal vector. Time averaged quantities were measured in the third pulse (i.e., t0 ≡ 2T) of the simulation in order to remove flow-dependent effects.
Phantom Signal Analysis
In order to profile each imaging sequence, signal intensity measurements were taken using FIJI.19 Circular regions of interest (RoI) were used to measure signal from the flowing water, background and stationary water sources in the image. This was done manually for each slice in the series. Signal intensity values were normalized using a min-max normalization algorithm available in scikit- learn17about:blank. Signal distributions were visualized graphically using the Seaborn and matplotlib libraries in Python 2.7.
The STL model for the curved phantom was used to assess correlations between the signal intensity to the flow angle relative to the magnetic field direction in the curved phantom. Tangent unit vectors \(\hat{\varvec{t}}\) = dγ/ds were sampled at intervals ∆s = 1 mm along the centerline. The metric
defined by the dot product between \(\hat{\varvec{t}}\) and the B0 (z-axis) unit vector was calculated for each instance in order to assess the effect of flow-direction. Γ takes values of 0 for flow parallel to B0, and values of 1 for flow perpendicular to B0. Correlations between Γ and the signal intensity were assessed graphically, and with Spearman’s correlation statistic. Similarly, correlations between signal intensity and the first spatial derivative of Γ (i.e. the instantaneous curvature) were assessed
Data Analysis and Comparison Methods
Agreement between diameter measurements from MEDIC and ToF phantom images was assessed using Bland-Altman methodology.5 For each area measurement, the mean and difference between the MEDIC and ToF model areas were calculated. This was done for the full length of the straight phantoms, and for a length of 5 cm centered on the curve center for the curved phantoms.
Results from CFD simulations were interpolated onto the same space as area measurements, allowing observation of the effect of area on WSS quantities. The mean value for all measured quantities was calculated at 1mm intervals from the origin as previously described, and plotted as a function of distance from the origin. Differences in the segmented models area and WSS quantities from CFD simulation for the patient data were interpreted graphically throughout the length of the vessels for the patient cases.
Differences in measurements were also interpreted numerically through the use of an error metric which was defined as the summed difference divided by the average:
where n is the number of sampled data, and fT and fM are any quantity f obtained from the ToF and MEDIC images, respectively. Ef takes a value of zero for identical measurements, and increases as the difference between the measurements increases.
Results
Phantom Analysis
A number of observations were common to all phantom cases:
-
The signal intensity from flowing water was similar for both sequences.
-
Signal intensity from the water used to prime the scanner was higher on the MEDIC than the ToF.
-
Background noise was higher for the ToF image series.
Example MRI images of the phantoms can be seen in the supplementary material (sup. Fig. 4). Flow direction data were generated as described, and are visualized in Fig. 1. Signal intensity was plotted alongside Γ, and no clear trend was observed (data not shown). When the signal intensity was plotted alongside the first derivative, Γ′, a correlation was observed with the MEDIC sequence. This is visualised in Fig. 2. The signal intensity of the MEDIC exhibited a strong negative correlation with Γ′, for both phantom geometries, as assessed with Spearman’s correlation coefficient (curve-L, r = −0.89, p < 0.05; curve-H, r = −0.85, p < 0.05). Phantom curve-H lost all visible signal near the curve centre. No such observation was observed consistently on the ToF images.
Values for EA, along with mean differences in diameters for the phantom cases are reported in Table 1. Values of EWSS were higher than EA, with error largest in the 3 mm phantom, which was possibly caused by a misalignment or kink in the tubing. From Table 1, mean differences in diameter for the phantoms can be seen to be around 0–15% for all cases. Differences between the imaging sequences increased as the vessel radius decreased, however no other clear trend was observed. Bland-Altman plots for these phantom geometries can be seen in Fig. 3. A larger degree of variability was observed when the flow-velocity was altered as can be visualised in Fig. 3(b). For the curved phantoms, the largest deviation was seen at the center of the curve. Bland-Altman plots for these phantom geometries can be seen in Fig. 3(c).
Bland–Altman plots for all phantom cases, showing differences in the diameter measurement on the y-axis, and mean value on the x-axis. (a) Agreement between MEDIC and ToF sequences for different flow and diameter rates; (b) agreement between high and low flow for different diameter and MRI sequence; (c) agreement between high and low-curve, with diameter = 5 mm and flow velocity = 1 m s−1.
Patient Analysis
Segmentation using both MEDIC and ToF sequences was possible for all MRI series. Examples of the patient MRI images can be seen in the supplementary material (supp. Fig. 5). Nevertheless, the 3D segmentations of the same patients were not completely identical when comparing the MEDIC and ToF sequences. The segmentation end points were at different positions, because the FoV of the two sequences were not over a precisely shared volume (see Fig. 4). For example, the depiction of vessel area was generally larger for the MEDIC, although the lumen area, shape and curvature were variable throughout the length of all vessels studied. For instance, the venous section of the MEDIC sequence of patient AVF1 revealed a larger anastomosis, a narrowing around 1 cm, as well as a dilation around 4 cm from the anastomosis (see Fig. 5(a)). Signal drop-out was observed in the area near the anastomosis, meaning that segmentation was reliant on interpretation at this point. All these variations impact the flow dynamics in the CFD study.
Area variability directly interferes with the hydrodynamics of internal flows, but the order of this influence depends on other flow features too. By looking at Figs. 5 and 6, one can see that area and TAWSS have a negative correlation at many points, but not in the whole extent of the vessels. The negative correlation between area and WSS is observed in the arterial segment of the MEDIC sequence, where flow was mostly unidirectional. However, this negative correlation is less apparent in the venous segment nearer the anastomosis, due to the presence of more complex flow patterns, such as flow separation and jet oscillations. These flow features redistribute the velocity gradients away from the vessel wall, minimizing the sensitivity of TAWSS to cross-sectional area variations.
The OSI shows how strongly the direction of WSS changes during the pulse cycle due to flow reversal or varying flow direction. In general, the regions of high OSI do not correlate with regions of high TAWSS. In Fig. 7, it is possible to compare the spatial distribution of OSI for both MEDIC and ToF sequences of patient AVF1. Ef values for all patient cases, including area, WSS and OSI can be seen in Table 2 and Fig. 8.
Discussion
This study has demonstrated that the choice of MRI sequence can lead to subtle differences in segmented model geometry and corresponding CFD results. The differences are of varying magnitude throughout the length of the vessel, suggesting that local effects are causing the observed differences. The effect of this area variation caused disagreement between the CFD results from the two MRI sequences.
We analyzed the signal distributions of the MEDIC and ToF sequences using a series of phantoms in an attempt to determine the cause of area variations, and observed no differences in the signal intensity profiles from the vessels. Plots of signal intensity revealed the ToF sequence was noisier, and the MEDIC produced a higher signal from stationary water used to prime the scanner, as expected. We then created an analogous geometry to the curved swing-site segment of the AVF using two curved phantoms and analyzed the effect of an off-axis flow on signal intensity measurements for two different curvatures. This led to the observation that for the MEDIC sequence, the signal intensity was inversely correlated with the instantaneous curvature (as assessed by Γ′), which may be a contributing factor in the observed signal dropout in the patient images. Signal loss in the curved phantom was not apparent on the ToF images, but both sequences exhibited signal loss on the patient images at the swing-site, suggesting that local flow effects at the anastomosis may have more effect than flow-direction effects as represented by Γ (Eq. 4).
CFD has been widely used in the study of AVFs. Multiple studies have assessed flow distributions in AVFs, using patient specific models, with imaging modalities such as 3D ultrasound, MRI, and CT having been used to obtain patient specific data. Considering MRI, multiple sequences such as T2 weighting, black-blood, and ToF have been used. As our results indicate, the distributions of flow parameters utilizing spatial data from different modalities may not be comparable. For example, McGah et al.14 used 3D US to create patient specific models, and observed increased WSS around the anastomosis, and also in the proximal vein of an AVF. Using BB-MRI, He et al.11 observed increased WSS at only the anastomosis. Sigovan et al.20 used a 2D ToF sequence and identified increased WSS again at the anastomosis, but also in the proximal vein and the distal artery. Similarly, Ende-lordache et al.10 identified increased WSS at the anastomosis, and also increased OSI in the venous and arterial segments of the AVF. As demonstrated in our work, we cannot yet be sure which model could be considered the most accurate of these cases. One reassuring aspect is that the distributions are generally similar, and the anastomosis is consistently cited as an area of increased WSS. We can be relatively confident that the anastomosis undergoes high WSS, despite being unsure of the magnitude, or other specific locations.
The MEDIC sequence has been observed to give vessel diameter measurements in agreement with US in the upper periphery, before and after AVF creation.13 The area disagreement EA between the straight phantoms increased as the tube diameter was decreased, which would be expected as the size of the phantom reduces and approaches the resolution of the scanner. However, the mean difference was consistently maximised at around 15% in the straight phantoms, similar to the error reported in diameter in other studies of vessels used for AVF creation.18 The differences in error between the flow velocities assessed demonstrate how one a sequence which may be working well for a flow of 0.5 m s −1 may perform poorly with higher or lower velocities, and vice-versa. The error was also increased in the curved phantoms as compared with the straight phantoms of the same diameter. Error in WSS was typically lower in the phantoms than in the patient cases, which is reassuring given that the vessels used were lower in diameter than we would expect from matured AVF vessels.
The distributions of WSS and OSI in the patient models were observed to differ between the sequences. As the only difference in the simulations was the vessel geometry, it is evident how sensitive WSS/OSI are to variations in geometry. Intermittent flow separations occurred at different positions, such as on the posterior and anterior vessel walls of the MEDIC and ToF sequences respectively. In general, MEDIC showed more regions of high OSI than ToF, because the geometry from MEDIC had more variability in cross-sectional area than ToF due to its lower slice thickness. In light of these results, further study should be undertaken to determine which sequence produces geometries which agree with experimental results.
The anastomosis of the AVF introduces challenges for MR imaging, and signal drop-out was observed in all the anastomoses studied. Flow recirculation at the anastomosis is reported in simulations of AVFs,9 and it is likely that this effect could be a major cause of spin dephasing24 resulting in signal loss at the anastomosis. Due to the orientation of the swing site, flow is no longer confined along the z-axis of the B0 field, effectively reducing the velocity of any incoming spins relative to the B0 field, which can be another cause of signal loss. AVF flow is known to be turbulent, and this is the cause of the signature ‘thrill’ of the AVF. Turbulent flow can undergo spin dephasing causing MR signal heterogeneities, however, turbulent flow was observed in the phantoms, and did not seem to decrease the MR signal. Further, due to the nature of the anatomy, the region of interest (the arm) is typically placed in a region of heterogeneous magnetic field. These problems may act together to lower signal at the swing site and anastomosis, making this region particularly difficult to segment and heavily reliant on operator interpretation, an under-reported aspect in most CFD based studies of AVFs.
These geometric errors propagate into larger errors for parameters derived from CFD. The error metric EWSS was larger than EA for every phantom and patient vessel studied (tables 1, 2 and Fig. 8). Wall shear stress and cross-sectional area are inversely related through a straight vessel, as given by the Darcy-Weisbach equation
where fD is an empirical friction factor, ρ is fluid density, Q is flow rate, and A is area. In the laminar regime, the relation of WSS and area is weaker (τw ~ A−1.5), because the friction factor is inversely proportional to the Reynolds number (Re), fD = 64/Re. However, in the turbulent regime, the friction factor does not scale with Re, but it rather depends more on the roughness of the vessel, which leads to a second-order inverse relationship between WSS and area (τw ~ A−2). Hence, it is important that accurate measurements of vessel area are obtained for accurate estimation of WSS. As OSI is derived from WSS, and depends on more non-linear effects, such as flow separations, EOSI was larger than EA and EWSS for all cases studied.
This study has a number of limitations. The Reynolds number of the phantoms was typically higher than we would expect from AVFs, and despite the flow-rates being in the optimal region for haemodialysis, real vessels would ideally be at least 5mm. The slice thicknesses of the sequences were not identical, however the voxel sizes were similar. Reducing the slice thickness on ToF resulted in unacceptable SNR losses. A major advantage of the MEDIC is the ability to acquire thinner slices with superior SNR to even the thicker ToF. Despite both sequences suffering from signal loss around the anastomosis, the MEDIC sequence does provide good vessel edge detail at the locations in and around the anastomosis13 facilitating segmentation, and it is possible that this may prove useful as a surveillance tool to characterise the development of stationary structures such as possible stenosis sites. One user segmented the geometries from all MR image sets, so it was not possible to assess variability between operators. This is well covered in the literature and was not the purpose of our study. We did not compare our results to an experimental model, such as in the FDA-sponsored study.21
Importantly, we did not use specifically optimized sequences for imaging of the different flow velocities studied. Optimization of the sequences could have been performed to find the parameters giving the truest geometric depiction for each flow velocity, or to identify the parameters which reduce the error between the velocities. However, as we were imaging both arteries and veins with different flow velocities in one sitting, optimization would have resulted in a trade-off between venous or arterial depiction, thus we opted to use vendor default parameters. If researchers could optimize sequence parameters prior to imaging, this would be one method to increase geometric accuracy before progressing to CFD. Similarly, the boundary conditions used for CFD modeling could be further optimized. Whilst we made the assumption that the outflow would be of a parabolic distribution at a distance of 5 cm from the anastomosis, this could be considered a simplified case. It is possible that more complex flow patterns may be present distal from the anastomosis. Different boundary conditions could be considered in advances in this line of research.
No comparison was made with any black-blood sequences or other modalities such as CT, which are also used to create 3D models for CFD studies of AVFs. Black-blood MRI has been shown to yield good results when measuring vessel parameters for intracranial vessels.4 Similarly to this work, other authors signify that sequence parameters affect wall measurements and sharpness of the vessel wall borders, which require optimization prior to commencing the study. Black blood MRA could in theory help with measurements of rapidly flowing or turbulent blood, which may yield low signal due to loss of spins phase-coherence and in-flow effects. Use of black-blood techniques in lumen measurements of AVFs and CFD modeling of wall shear stress has been demonstrated.11 However, 3D black-blood scans take longer to perform,12 resulting in scan times that can be uncomfortable for some patients.
Another emerging method not considered in this study is 4D flow MRI. In addition to morphological information, this technique has been shown to non-invasively characterize physiological properties, such as velocity, flow volume, wall shear stress, pressure gradients, streamlines and flow path lines in cerebral arterio-venous malformations.8 4D flow MRI has been shown to currently underestimate WSS values in intracranial arteries, but with good estimate of WSS distribution when compared to CFD methods.22 As 4D flow methods would remove the need for segmentation, any error associated with this stage could be eliminated. However, one limitation of this technique is the long scan time required, which may be a difficulty for certain patients. A number of studies have also reported underestimation of 4D flow derived velocities when compared to Doppler US, which would need to be considered when assessing flow properties.15, 27
In conclusion, we have demonstrated that different MRI sequences do not give reproducible results when considering CFD studies of AVFs. Small geometric differences encountered during imaging propagated into larger differences during CFD modeling, meaning results were not fully comparable between MRI sequences. Vessel diameter, flow velocity, and patient specific flows were all sources of error that could have caused these differences. The results from this study should be taken into consideration when planning patient specific CFD studies and researchers should justify their choice of MRI sequence a-priori. Comparisons with known results from experiment should be performed to fully understand the impact of changing MRI sequence, and to determine which sequences provide geometries closest to the ground-truth.
References
ACR Committee on MR Safety, T. D. Greenberg, M. N. Hoff, T. B. Gilk, E. F. Jackson, E. Kanal, et al. ACR guidance document on MR safe practices: updates and critical information 2019. J. Magn. Reson. Imaging. 51(2):331–338, 2019.
Almasri, J., M. Alsawas, M. Mainou, R. A. Mustafa, Z. Wang, K. Woo, et al. Outcomes of vascular access for hemodialysis: a systematic review and meta-analysis. J. Vasc. Surg. 64(1):236–243, 2016.
Antiga, L., B. Ene-Iordache, and A. Remuzzi. Computational geometry for patient-specific reconstruction and meshing of blood vessels from MR and CT angiography. IEEE Trans. Med. Imaging. 22(5):674–684, 2003.
Antiga, L., B. A. Wasserman, and D. A. Steinman. On the overestimation of early wall thickening at the carotid bulb by black blood MRI, with implications for coronary and vulnerable plaque imaging. Magn. Reson. Med. 60(5):1020–1028, 2008.
Bland, J. M., and D. G. Altman. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1(8476):307–310, 1986.
Brescia, M. J., J. E. Cimino, K. Appel, and B. J. Hurwich. Chronic hemodialysis using venipuncture and a surgically created arteriovenous fistula. N. Engl. J. Med. 275(20):1089–1092, 1966.
Carroll, G. T., T. M. McGloughlin, P. E. Burke, M. Egan, F. Wallis, and M. T. Walsh. Wall shear stresses remain elevated in mature arteriovenous fistulas: a case study. J. Biomech. Eng. 133(2):021003, 2011.
Chang, W., M. W. Loecher, Y. Wu, D. B. Niemann, B. Ciske, B. Aagaard-Kienitz, et al. Hemodynamic changes in patients with arteriovenous malformations assessed using high-resolution 3D radial phase-contrast MR angiography. AJNR Am. J. Neuroradiol. 33(8):1565–1572, 2012.
Ene-Iordache, B., L. Cattaneo, G. Dubini, and A. Remuzzi. Effect of anastomosis angle on the localization of disturbed flow in ‘side-to-end’ fistulae for haemodialysis access. Nephrol. Dial. Transplant. 28(4):997–1005, 2013.
Ene-Iordache, B., and A. Remuzzi. Disturbed flow in radial-cephalic arteriovenous fistulae for haemodialysis: low and oscillating shear stress locates the sites of stenosis. Nephrol. Dial. Transplant. 27(1):358–368, 2012.
He, Y., C. M. Terry, C. Nguyen, S. A. Berceli, Y.-T. E. Shiu, and A. K. Cheung. Serial analysis of lumen geometry and hemodynamics in human arteriovenous fistula for hemodialysis using magnetic resonance imaging and computational fluid dynamics. J. Biomech. 46(1):165–169, 2013.
Jin, W. T., G. F. Zhang, H. C. Liu, H. Zhang, B. Li, and X. Q. Zhu. Non-contrast-enhanced MR angiography for detecting arteriovenous fistula dysfunction in haemodialysis patients. Clin. Radiol. 70(8):852–857, 2015.
MacDonald, C. J., S. Gandy, E. C. M. Avison, S. Matthew, R. Ross, and J. G. Houston. Non-contrast MRI methods as a tool for the pre-operative assessment and surveillance of the arterio-venous fistula for haemodialysis. MAGMA. 31(6):735–745, 2018.
McGah, P. M., D. F. Leotta, K. W. Beach, R. Eugene Zierler, and A. Aliseda. Incomplete restoration of homeostatic shear stress within arteriovenous fistulae. J. Biomech. Eng. 135(1):011005, 2013.
Meckel, S., L. Leitner, L. H. Bonati, F. Santini, T. Schubert, A. F. Stalder, et al. Intracranial artery velocity measurement using 4D PC MRI at 3 T: comparison with transcranial ultrasound techniques and 2D PC MRI. Neuroradiology. 55(4):389–398, 2013.
Morris, P. D., A. Narracott, H. von Tengg-Kobligk, D. A. Silva Soto, S. Hsiao, A. Lungu, et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart. 102(1):18–28, 2016.
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in python. arXiv:12010490 [cs] [Internet]. 2018 Jun 5 [cited 2019 Oct 22]; Available from: http://arxiv.org/abs/1201.0490
Planken, N. R., J. H. Tordoir, L. E. Duijm, H. C. van den Bosch, F. M. van der Sande, J. P. Kooman, et al. Magnetic resonance angiographic assessment of upper extremity vessels prior to vascular access surgery: feasibility and accuracy. Eur. Radiol. 18(1):158–167, 2008.
Schindelin, J., I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, et al. Fiji: an open-source platform for biological-image analysis. Nat Methods. 9(7):676–682, 2012.
Sigovan, M., V. Rayz, W. Gasper, H. F. Alley, C. D. Owens, and D. Saloner. Vascular remodeling in autogenous arterio-venous fistulas by MRI and CFD. Ann. Biomed. Eng. 41(4):657–668, 2013.
Stewart, S. F. C., E. G. Paterson, G. W. Burgreen, P. Hariharan, M. Giarra, V. Reddy, et al. Assessment of CFD performance in simulations of an idealized medical device: results of FDA’s First Computational Interlaboratory Study. Cardiovasc. Eng. Tech. 3(2):139–160, 2012.
Szajer, J., and K. Ho-Shon. A comparison of 4D flow MRI-derived wall shear stress with computational fluid dynamics methods for intracranial aneurysms and carotid bifurcations—a review. Magn. Reson. Imaging. 48:62–69, 2018.
Thomas, J. B., J. S. Milner, B. K. Rutt, and D. A. Steinman. Reproducibility of image-based computational fluid dynamics models of the human carotid bifurcation. Ann. Biomed. Eng. 31(2):132–141, 2003.
Tsuruda, J., D. Saloner, and D. Norman. Artifacts associated with MR neuroangiography. AJNR Am. J. Neuroradiol. 13(5):1411–1422, 1992.
Updegrove, A., N. M. Wilson, J. Merkow, H. Lan, A. L. Marsden, and S. C. Shadden. SimVascular: an open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 45(3):525–541, 2017.
Valen-Sendstad, K., A. W. Bergersen, Y. Shimogonya, L. Goubergrits, J. Bruening, J. Pallares, et al. Real-world variability in the prediction of intracranial aneurysm wall shear stress: the 2015 International Aneurysm CFD Challenge. Cardiovasc. Eng. Technol. 9(4):544–564, 2018.
Wentland, A. L., T. M. Grist, and O. Wieben. Repeatability and internal consistency of abdominal 2D and 4D phase contrast MR flow measurements. Acad. Radiol. 20(6):699–704, 2013.
Acknowledgments
We would like to thank Dr. S. Henderson for internal review of this manuscript. Funding was provided by FP7 Ideas: European Research Council (Grant Agreement No. 324487 (ReDVA)).
Author information
Authors and Affiliations
Corresponding author
Additional information
Associate Editor Kevin K. Whitehead oversaw the review of this article.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
MacDonald, C.J., Hellmuth, R., Priba, L. et al. Experimental Assessment of Two Non-Contrast MRI Sequences Used for Computational Fluid Dynamics: Investigation of Consistency Between Techniques. Cardiovasc Eng Tech 11, 416–430 (2020). https://doi.org/10.1007/s13239-020-00473-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13239-020-00473-z