Multi-Agent Natural Actor-Critic Reinforcement Learning Algorithms

Abstract

Multi-agent actor-critic algorithms are an important part of the Reinforcement Learning (RL) paradigm. We propose three fully decentralized multi-agent natural actor-critic (MAN) algorithms in this work. The objective is to collectively find a joint policy that maximizes the average long-term return of these agents. In the absence of a central controller and to preserve privacy, agents communicate some information to their neighbors via a time-varying communication network. We prove convergence of all the three MAN algorithms to a globally asymptotically stable set of the ODE corresponding to actor update; these use linear function approximations. We show that the Kullback–Leibler divergence between policies of successive iterates is proportional to the objective function’s gradient. We observe that the minimum singular value of the Fisher information matrix is well within the reciprocal of the policy parameter dimension. Using this, we theoretically show that the optimal value of the deterministic variant of the MAN algorithm at each iterate dominates that of the standard gradient-based multi-agent actor-critic (MAAC) algorithm. To our knowledge, it is the first such result in multi-agent reinforcement learning (MARL). To illustrate the usefulness of our proposed algorithms, we implement them on a bi-lane traffic network to reduce the average network congestion. We observe an almost 25% reduction in the average congestion in 2 MAN algorithms; the average congestion in another MAN algorithm is on par with the MAAC algorithm. We also consider a generic 15 agent MARL; the performance of the MAN algorithms is again as good as the MAAC algorithm.

1 Introduction

Reinforcement learning (RL) has been explored in recent years and is of great interest to researchers because of its broad applicability in many real-life scenarios. In RL, agents interact with the environment and take decisions sequentially. It is applied successfully to various problems, including elevator scheduling, robot control, etc. There are many instances where RL agents surpass human performance, such as openAI beating the world champion DOTA player, DeepMind beating the world champion of Alpha Star.¹

The sequential decision-making problems are generally modeled via Markov decision process (MDP). It requires the knowledge of system transitions and rewards. In contrast, RL is a data-driven MDP framework for sequential decision-making tasks; the transition probability matrices and the reward functions are not assumed, but their realizations are available as observed data.

In RL, the purpose of an agent is to learn an optimal or nearly-optimal policy that maximizes the “reward function" or functions of other user-provided “reinforcement signals" from the observed data. However, in many realistic scenarios, there is more than one agent. To this end, researchers explore the multi-agent reinforcement learning (MARL) methods, but most are centralized and relatively slow. Furthermore, these MARL algorithms use the standard/vanilla gradient, which has limitations. For example, the standard gradients cannot capture the angles in the state space and may not be effective in many scenarios. The natural gradients are more suitable choices because they capture the intrinsic curvature in the state space. In this work, we are incorporating natural gradients in the MARL framework.

In the multi-agent setup that we consider, the agents have some private information and a common goal. This goal could be achieved by deploying a central controller and converting the MARL problem into a single-agent RL problem. However, deploying a central controller often leads to scalability issues. On the other hand, if there is no central controller and the agents do not share any information, then there is almost no hope of achieving the common goal. An intermediate model is to share some parameters via (possibly) a time-varying, and sparse communication matrix [53]. The algorithms based on such intermediate methods are often attributed as consensus-based algorithms.

The consensus-based algorithm models can also be considered as intermediate between dynamic non-cooperative and cooperative game models. Non-cooperative games, as multi-agent systems, model situations where the agents do not have a common goal and do not communicate. On the contrary, cooperative games model situations where a central controller achieves a common goal using complete information.

Algorithm 2 of [53] is a consensus-based actor-critic algorithm. We call it MAAC (multi-agent actor-critic) algorithm. The MAAC algorithm uses the standard gradient and hence lacks in capturing the intrinsic curvature present in the state space. We propose three multi-agent natural actor-critic (MAN) algorithms and incorporate the curvatures via natural gradients. These algorithms use the linear function approximations for the state value and reward functions. We prove the convergence of all the three MAN algorithms to a globally asymptotically stable equilibrium set of ordinary differential equations (ODEs) obtained from the actor updates.

Here is a brief overview of our two time-scale approach. Let $J(\theta )$ be the global MARL objective function of n agents, where $\theta = (\theta ^1, \dots , \theta ^n)$ is the actor (or policy) parameter. For a given policy parameter $\theta$ of each MAN algorithm, we first show in Theorem 4 the convergence of critic parameters (to be defined later) on a faster time scale. Note that these critic parameters are updated via the communication matrix. We then show the convergence of each agent’s actor parameters to an asymptotically stable attractor set of its ODE. These actor updates use the natural gradients in the form of Fisher information matrix and advantage parameters (Theorem 6, 8 and 10). The actor parameter $\theta$ is shown to converge on the slower time scale.

Our MAN algorithms use a log-likelihood function via the Fisher information matrix and incorporate the curvatures. We show that this log-likelihood function is indeed the KL divergence between the consecutive policies, and it is the gradient of the objective function up to scaling (Lemma 1). Unlike standard gradient methods, where the updates are restricted to the parameter space only, the natural gradient-based methods allow the updates to factor in the curvature of the policy distribution prediction space via the KL divergence between them. Thus, two of our MAN algorithms, FI-MAN and FIAP-MAN, use a certain representation of the objective function gradient in terms of the gradient of this KL divergence (Lemma 1). It turns out these two algorithms have much better empirical performance (Sect. 5.1).

We now point out a couple of important consequences of the representation learning aspect of our MAN algorithms for reinforcement learning. First, we show that under some conditions, our deterministic version of the FI-MAN algorithm converges to local minima with a better objective function value than the deterministic counterpart of the MAAC algorithm, Theorem 3. To the best of our knowledge, this is a new result in non-convex optimization; we are not aware of any algorithm that is proven to converge to a better local maxima [13, 37]. This relies on the important observation, which can be of independent interest, that 1/m is uniform upper bound on the smallest singular value of Fisher information matrix $G(\theta )$, Lemma 2; here, m is the common dimension of the compatible policy parameter $\theta$ and the Fisher information matrix $G(\theta )$.

The natural gradient-based methods can be viewed as quasi-second order methods, as the Fisher information matrix $G(\cdot )$ is an invertible linear transformation of basis that is used in first-order optimization methods [1]. However, they are not regarded as second-order methods because the Fisher information matrix is not the Hessian of the objective function.

To validate the usefulness of our proposed algorithms, we perform a comprehensive set of computational experiments in two settings: a bi-lane traffic network and an abstract MARL model. On a bi-lane traffic network model, the objective is to find the traffic signaling plan that reduces the overall network congestion. We consider two different arrival patterns between various origin-destination (OD) pairs. With the suitable linear function approximations to incorporate the humongous state space $(50^{16})$ and action space $(3^4)$, we observe a significant reduction ($\approx 25\%$) in the average network congestion in two of our MAN algorithms. One of our MAN algorithms that are only based on the advantage parameters and never estimate the Fisher information matrix inverse is on-par with the MAAC algorithm. In the abstract MARL model, we consider 15 agents with 15 states and two actions in each state and generic reward functions [18, 53]. Each agent’s reward is private information and hence not known to other agents. Our MAN algorithms either outperform or are on-par with the MAAC algorithm with high confidence.

2 MARL Framework and Natural Gradients

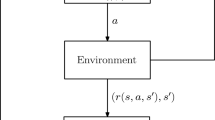
Let $N = \{1,2,\dots , n\}$ denote the set of agents. Each agent independently interacts with a stochastic environment and takes a local action. We consider a fully decentralized setup in which a communication network connect the agents.

This network is used to exchange information among agents in the absence of a central controller so that agents’ privacy remains intact. The communication network is possibly time-varying and sparse. We assume the communication among agents is synchronized, and hence there are no information delays. Moreover, only some parameters (that we define later) are shared among the neighbors of each agent. It also addresses an important aspect of the privacy protection of such agents. Formally, the communication network is characterized by an undirected graph ${\mathcal {G}}_t = (N, {\mathcal {E}}_t)$, where N is the set of all nodes (or agents) and ${\mathcal {E}}_t$ is the set of communication links available at time $t\in {\mathbb {N}}$. We say, agents $i,j \in N$ communicate at time t if $(i,j)\in {\mathcal {E}}_t$.

Let ${\mathcal {S}}$ denote the common state space available to all the agents. At any time t, each agent observes a common state $s_t\in {\mathcal {S}}$, and takes a local action $a^i_t$ from the set of available actions ${\mathcal {A}}^i$. We assume that for any agent $i\in N$, the entire action set ${\mathcal {A}}^i$ is feasible in every state $s\in {\mathcal {S}}$. The action $a^i_t$ is taken as per a local policy $\pi ^i: {\mathcal {S}} \times {\mathcal {A}}^i \rightarrow [0,1]$, where $\pi ^i(s_t,a^i_t)$ is the probability of taking action $a^i_t$ in state $s_t$ by agent $i\in N$. Let ${\mathcal {A}} {:=}\prod _{i=1}^n {\mathcal {A}}^i$ be the joint action space of all the agents. To each state and action pair, every agent receives a finite reward from the local reward function ${R}^i: {\mathcal {S}} \times {\mathcal {A}} \rightarrow {\mathbb {R}}$. Note that the reward is private information of the agent, and it is not known to other agents. The state transition probability of MDP is given by $P: {\mathcal {S}} \times {\mathcal {A}} \times {\mathcal {S}} \rightarrow [0,1]$. Using only local rewards and actions, it is hard for any classical reinforcement learning algorithm to maximize the averaged reward determined by the joint action of all the agents. To this end, we consider the multi-agent networked MDP given in [53]. The multi-agent networked MDP is defined as $({\mathcal {S}}, \{{\mathcal {A}}^i\}_{i\in N}, P, \{R^i\}_{i\in N}, \{{\mathcal {G}}_t\}_{t\ge 0})$, with each component described as above. Let joint policy of all agents be denoted by $\pi :{\mathcal {S}} \times {\mathcal {A}} \rightarrow [0,1]$ satisfying $\pi (s,a) = \prod _{i\in N} \pi ^i(s,a^i)$. Let $a_t = (a^1_t,\dots , a^n_t)$ be the action taken by all the agents at time t. Depending on the action $a^i_t$ the agent i receives a random reward $r^i_{t+1}$ with the expected value $R^i(s_t,a_t)$. Moreover, with probability $P(s_{t+1}| s_t,a_t)$ the multi-agent MDP shifts to next state $s_{t+1} \in {\mathcal {S}}$.

Due to the large state and action space, it is often helpful to consider the parameterized policies [23, 45]. We parameterize the local policy, $\pi ^i(\cdot , \cdot )$ by $\theta ^i\in \varTheta ^i \subseteq {\mathbb {R}}^{m_i}$, where $\varTheta ^i$ is the compact set. To find the global policy parameters, we can pack all the local policy parameters as $\theta = [(\theta ^1)^{\top }, \dots , (\theta ^n)^{\top }]^{\top }\in \varTheta \subseteq {\mathbb {R}}^m$, where $\varTheta {:=}\prod _{i\in N}\varTheta ^i$, and $m=\sum _{i=1}^n m_i$. The parameterized joint policy is then given by $\pi _{\theta }(s,a) = \prod _{i\in N}\pi ^i_{\theta ^i}(s,a^i)$. The objective of the agents is to collectively find a joint policy $\pi _{\theta }$ that maximizes the averaged long-term return $J(\theta )$, provided each agent has local information only, i.e.,

$$\begin{aligned} max_{\theta } ~ J(\theta ) = \underset{T\rightarrow \infty }{lim} \frac{1}{T} {\mathbb {E}} \left( \sum _{t=0}^{T-1} \frac{1}{n} \sum _{i\in {N}} r^i_{t+1} \right) = \sum _{s\in {\mathcal {S}}} d_{\theta }(s) \sum _{a\in {\mathcal {A}}} \pi _{\theta }(s,a) {\bar{R}}(s,a), \end{aligned}$$

(1)

where ${\bar{R}}(s,a) = \frac{1}{n} \sum _{i\in {N}} R^i(s,a)$ is the globally averaged reward function. Let ${\bar{r}}_t = \frac{1}{n}\sum _{i\in {N}}r^i_t$. Thus, ${\bar{R}}(s,a) = {\mathbb {E}}[{\bar{r}}_{t+1}|s_t=s,a_t=a]$.

Like single-agent RL [7], we also require following regularity assumption on networked multi-agent MDP and parameterized policies.

X 1

For each agent $i\in N$, the local policy function $\pi ^i_{\theta ^i}(s,a^i)>0$ for any $s \in {\mathcal {S}}, a^i\in {\mathcal {A}}^i$ and $\theta ^i \in \varTheta ^i$. Also $\pi ^i_{\theta ^i}(s,a^i)$ is continuously differentiable with respect to parameters $\theta ^i$ over $\varTheta ^i$. Moreover, for any $\theta \in \varTheta$, let $P^{\theta }$ be the transition matrix for the Markov chain $\{s_t\}_{t\ge 0}$ induced by policy $\pi _{\theta }$, that is, $P^{\theta }(s^{\prime }|s) = \sum _{a\in {\mathcal {A}}} \pi _{\theta }(s,a) P(s^{\prime }|s,a)$ for any $s,s^{\prime } \in {\mathcal {S}}$. Further, the Markov chain $\{s_t\}_{t\ge 0}$ is ergodic under $\pi _{\theta }$ with stationary distribution $d_{\theta }(s)$ over ${\mathcal {S}}$.

The regularity assumption X. 1 on a multi-agent networked MDP is standard in the work of single agent actor-critic algorithms with function approximations [7, 27]. The continuous differentiability of policy $\pi _{\theta }(\cdot , \cdot )$ with respect to $\theta$ is required in policy gradient theorem [45], and it is commonly satisfied by well-known class of functions such as neural networks or deep neural networks. Moreover, assumption X. 1 also implies that the Markov chain $\{(s_t,a_t)\}_{t\ge 0}$ has stationary distribution ${\tilde{d}}_{\theta }(s,a) = d_{\theta }(s) \cdot \pi _{\theta }(s,a)$ for any $s \in {\mathcal {S}}, a\in {\mathcal {A}}$.

Based on the objective function given in Eq. (1), the global state-action value function associated with state-action pair (s, a) for a given policy $\pi _{\theta }$ is defined as $Q_{\theta }(s,a) = \sum _{t\ge 0} {\mathbb {E}}[{\bar{r}}_{t+1}-J(\theta ) | s_0 =s, a_0=a, \pi _{\theta }]$. Note that $Q_{\theta }(s,a)$ is motivated from the gain and bias relation for average reward criteria of the single-agent MDP as given in say, Sect. 8.2.1 in [41]. It captures the expected sum of fluctuations of the global rewards about the globally averaged objective function (“average adjusted sum of rewards” [30]) when action a is taken in state $s\in {\mathcal {S}}$ at time $t=0$, and thereafter the policy $\pi _{\theta }$ is followed. The global state value function is defined as $V_{\theta }(s) = \sum _{a\in {\mathcal {A}}} \pi _{\theta }(s,a) \cdot Q_{\theta }(s,a)$.

Let $A_{\theta }(s,a) {:=}Q_{\theta }(s,a) - V_{\theta }(s)$ be the global advantage function. Note that the advantage function captures the benefit of taking action a in state s and thereafter following the policy $\pi _{\theta }$ over the case when policy $\pi _{\theta }$ is followed from state s itself. For the multi-agent setup, we define the local advantage function for each agent $i\in N$ as $A^i_{\theta }(s,a) {:=}Q_{\theta }(s,a) - {\widetilde{V}}^i_{\theta }(s,a^{-i})$, where ${\widetilde{V}}^i_{\theta }(s,a^{-i}) {:=}\sum _{a^i\in A^i} \pi ^i_{\theta ^i} (s,a^i) Q_{\theta }(s,a^i,a^{-i})$. Note that ${\widetilde{V}}^i_{\theta }(s,a^{-i})$ represents the value of state s to an agent $i\in N$ when policy $\pi (\cdot ,\cdot )$ is parameterized by $\theta$, and all other agents are taking action $a^{-i} = (a^1, \dots , a^{i-1}, a^{i+1}, \dots , a^n)$.

Theorem 1

(Policy gradient theorem for MARL [53]) Under assumption X. 1, for any $\theta \in \varTheta$, and each agent $i\in N$, the gradient of $J(\theta )$ with respect to $\theta ^i$ is given by

$$\begin{aligned} \nabla _{\theta ^i}J(\theta ) = {\mathbb {E}}[\nabla _{\theta ^i} \log \pi ^{i}_{\theta ^i}(s,a^i) \cdot A_{\theta }(s,a)]={\mathbb {E}}[\nabla _{\theta ^i} \log \pi ^{i}_{\theta ^i}(s,a^i) \cdot A^i_{\theta }(s,a)]. \end{aligned}$$

We refer to Appendix A. 1 of [49] for complete proof. The idea of the proof is as follows: we first recall the policy gradient theorem for single agent. Now using the fact that for multi-agent case, the global policy is product of local policies, i.e., $\pi _{\theta }(s,a) = \prod _{i=1}^n \pi ^i_{\theta ^i}(s,a^i)$, and $\sum _{a^i\in {\mathcal {A}}^i} \pi ^i_{\theta ^i} (s,a^i) = 1$, hence $\nabla _{\theta ^i} \left[ \sum _{a^i\in {\mathcal {A}}^i} \pi ^i_{\theta ^i} (s,a^i)\right] = 0$, we show $\nabla _{\theta ^i} J(\theta ) = {\mathbb {E}}_{s\sim d_{\theta },a \sim \pi _{\theta }}[\nabla _{\theta ^i} \log \pi ^i_{\theta ^i}(s,a^i) \cdot Q_{\theta }(s,a)]$. Now, observe that adding/subtracting any function $\varLambda$ that is independent of the action $a^i$ taken by agent $i\in N$ to $Q_{\theta }(s,a)$ does not make any difference in the above expected value. In particular, considering two such $\varLambda$ functions $V_{\theta }(s)$ and ${\tilde{V}}_{\theta }^i(s,a^{-i})$, we have desired results.

We call $\psi ^i(s,a^i) := \nabla _{\theta ^i} \log \pi ^{i}_{\theta ^i} (s,a^i)$, the score function. We will see in Sect. 3.2 that the same score function is called the compatible features. This is because the above policy gradient theorem with linear function approximations require the compatibility condition (Theorem 2 [46]). The policy gradient theorem for MARL relates the gradient of the global objective function w.r.t. $\theta ^i$ and the local advantage function $A^i_{\theta }(\cdot , \cdot )$. It also suggests that the global objective function’s gradients can be obtained solely using the local score function $\psi ^i(s,a^i)$, if agent $i\in N$ has an unbiased estimate of the advantage functions $A^i_{\theta }$ or $A_{\theta }$. However, estimating the advantage function requires the rewards $r^i_t$ of all the agents $i\in N$; therefore, these functions cannot be well-estimated by any agent $i\in N$ alone. To this end, [53] have proposed two fully decentralized actor-critic algorithms based on the consensus network. These algorithms work in a fully decentralized fashion and empirically achieve the same performance as a centralized algorithm in the long run. We use algorithm 2 of [53] which we are calling as multi-agent actor-critic (MAAC) algorithm.

In the fully decentralized setup, we consider the weight matrix $C_t = [c_t(i,j)]$, depending on the network topology of communication network ${\mathcal {G}}_t$. Here, $c_t(i,j)$ represents the weight of the message transmitted from agent i to agent j at time t. For generality, we take the weight matrix $C_t$ to be random. This is either because ${\mathcal {G}}_t$ is a time-varying graph or the randomness in the consensus algorithm [14]. Following are the assumptions on the matrix $C_t$.

X 2

The sequence of nonnegative random matrices $\{C_t\}_{t \ge 0} \subseteq {\mathbb {R}}^{n\times n}$ satisfy

• 1. $C_t$ is row stochastic, i.e., $C_t \mathbbm {1} = \mathbbm {1}$. Moreover, ${\mathbb {E}}(C_t)$ is column stochastic, i.e., $\mathbbm {1}^{\top }{\mathbb {E}}(C_t)=\mathbbm {1}^{\top }$. Furthermore, there exists a constant $\gamma \in (0,1)$ such that for any $c_t(i,j)>0$, we have $c_t(i,j)\ge \gamma$.

• 2. Weight matrix $C_t$ respects ${\mathcal {G}}_t$, i.e., $c_t(i,j) = 0$, if $(i,j)\notin {\mathcal {E}}_t$.

• 3. The spectral norm of ${\mathbb {E}}[C_t^{\top } (I - \mathbbm {1}\mathbbm {1}^{\top }/n)C_t]$ is smaller than one.

• 4. Given the $\sigma$-algebra generated by the random variables before time t, $C_t$ is conditionally independent of $r^i_{t+1}$ for each agent $i\in {N}$.

Assumption X. 2(1) of considering a doubly stochastic matrix is standard in the work of consensus-based algorithms [10, 32]. To prove the stability of the consensus update (see Appendix A of [53] for detailed proof), we require the lower bound on the weights of the matrix [35]. Assumption X. 2(2) is required for the connectivity of ${\mathcal {G}}_t$. For geometric convergence in distributed optimization, authors in [34] provide the connection between the time-varying network and the spectral norm property. The same is required for convergence in our work also (assumption X. 2(3)). Assumption X. 2(4) on the conditional independence of $C_t$ and $r_{t+1}$ is common in many practical multi-agent systems.

Next, we outline the actor-critic algorithm using linear function approximations in a fully decentralized setting. The actor-critic algorithm consists of two steps—critic step and actor step. At each time t, the actor suggests a policy parameter $\theta _t$. The critic evaluates its value using the policy parameters and criticizes or gives the feedback to the actor. Using this feedback, actor then update the policy parameters, and this continues until convergence. Let the global state value temporal difference (TD) error be defined as ${\bar{\delta }}_t = {\bar{r}}_{t+1} - J(\theta ) + V_{\theta }(s_{t+1}) - V_{\theta }(s_t)$. It is known that the state value temporal difference error is an unbiased estimate of the advantage function $A_{\theta }$ [45], i.e., ${\mathbb {E}}[{\bar{\delta }}_t~|~ s_t=s, a_t =a, \pi _{\theta }] = A_{\theta }(s,a),~ \forall ~ s\in {\mathcal {S}},~a\in {\mathcal {A}}$. The TD error specifies how different the new value is from the old prediction. In many applications [16, 17], the state space is either large or infinite. To this end, we use the linear function approximations for state value function. Later in Sect. 3.2, we use linear function approximation for advantage function also.

Let the state value function $V_{\theta }(s)$ be approximated using the linear function as $V_{\theta }(s; v) := v^{\top }\varphi (s)$, where $\varphi (s) = [\varphi _1(s), \dots , \varphi _L(s)]^{\top } \in {\mathbb {R}}^L$ is the feature associated with state s, and $v\in {\mathbb {R}}^L$. Note that $L<< |{\mathcal {S}}|$; hence, the value function is approximated using very small number of features. Moreover, let $\mu ^i_t$ be the estimate of the global objective function $J(\theta )$ by agent $i\in N$ at time t. Note that $\mu ^i_t$ tracks the long-term return to each agent $i \in N$. The MAAC algorithm (Appendix C. 4 of [49]) uses consensus network and consists of the following updates for objective function estimate and the critic parameters

$$\begin{aligned} {\tilde{\mu }}^i_t= & {} (1-\beta _{v,t}) \cdot \mu ^i_t + \beta _{v,t} \cdot r^i_{t+1}; ~~\mu ^i_{t+1} = \sum _{j\in {N}} c_t(i,j) {\tilde{\mu }}^j_t \end{aligned}$$

(2)

$$\begin{aligned} {\tilde{v}}^i_t= & {} v^i_t + \beta _{v,t} \cdot \delta ^i_t \cdot \nabla _v V_t(v^i_t); ~~ v^i_{t+1} = \sum _{j\in {N}}c_t(i,j){\tilde{v}}^j_t, \end{aligned}$$

(3)

where $\beta _{v,t}> 0$ is the critic step-size and $\delta ^i_t = r^i_{t+1} - \mu ^i_t + V_{t+1}(v^i_t) - V_{t}(v^i_t)$ is the local TD error. Here, $V_{t+1}(v^i_t) := v_t^{i^{\top }} \varphi (s_{t+1})$, and hence, $V_{t+1}(v^i_t) = V_{\theta }(s_{t+1}; v^i_t)$. It is a linear function approximation of the state value function, $V_{\theta }(s_{t+1})$ by agent $i\in N$. Note that the estimate of the advantage function $A_{\theta }(s,a)$ require ${\bar{r}}_{t+1}$ which is not available to each agent $i\in N$. Therefore, we parameterize the reward function ${\bar{R}}(s,a)$ used in the critic update as well.

Let ${\bar{R}}(s,a)$ be approximated using a linear function as ${\bar{R}}(s,a;\lambda ) = \lambda ^{\top }f(s,a)$, where $f(s,a) = [f_1(s,a), \dots , f_M(s,a)]^{\top } \in {\mathbb {R}}^M, ~M<< |{\mathcal {S}}||{\mathcal {A}}|$ are the features associated with state action pair (s, a). To obtain the estimate of ${\bar{R}}(s,a)$, we use the following least square minimization:

$$\begin{aligned} min_{\lambda } ~ \sum _{s\in {\mathcal {S}}, a\in {\mathcal {A}}} {\tilde{d}}_{\theta }(s,a) [ {\bar{R}}(s,a) - {\bar{R}}(s,a; \lambda )]^2, \end{aligned}$$

where ${\bar{R}}(s,a) := \frac{1}{n}\sum _{i\in {N}} R^i(s,a)$, and ${\tilde{d}}_{\theta }(s,a) = d_{\theta }(s) \cdot \pi _{\theta }(s,a)$. This optimization problem can be equivalently characterized as follows:

$$\begin{aligned} min_{\lambda } ~ \sum _{i\in {N}} \sum _{s\in {\mathcal {S}}, a\in {\mathcal {A}}} {\tilde{d}}_{\theta }(s,a) [ {R}^i(s,a) - {\bar{R}}(s,a; \lambda ) ]^2, \end{aligned}$$

i.e., both the optimization problems have the same stationary points.

For more details on stationary points, see Appendix A.2 of [49]. Taking first-order derivative with respect to $\lambda$ implies that we should also do the following in critic update:

$$\begin{aligned} {\tilde{\lambda }}^i_t = \lambda ^i_t + \beta _{v,t} \cdot [r^i_{t+1} - {\bar{R}}_t(\lambda ^i_t)] \cdot \nabla _{\lambda }{\bar{R}}_t(\lambda ^i_t); ~~ \lambda ^i_{t+1} = \sum _{j\in {N}} c_t(i,j) {\tilde{\lambda }}^j_t, \end{aligned}$$

(4)

where ${\bar{R}}_t(\lambda ^i_t)$ is the linear function approximation of the global reward ${\bar{R}}_t(s_t,a_t)$ by agent $i\in N$ at time t, i.e., ${\bar{R}}_t(\lambda ^i_t) = \lambda _t^{i^{\top }} f(s_t,a_t)$. The TD error with parameterized reward ${\bar{R}}_t(\cdot )$ is given by ${\tilde{\delta }}^i_t {:=}{\bar{R}}_{t}(\lambda ^i_t) - \mu ^i_t + V_{t+1}(v^i_t) - V_{t}(v^i_t)$.

Note that each agent $i\in N$ know its local reward function $r^i_{t+1}(s_t, a_t)$, but at the same time also seeks to get some information about the global reward, ${\bar{r}}_{t+1}(s_t, a_t)$ because the objective is to maximize the globally averaged reward function. Therefore, in Eq. (4), each agent $i\in N$ uses ${\bar{R}}_t(\lambda ^i_t)$ as an estimate of the global reward function. Let $\beta _{\theta ,t}>0$ be the actor step-size, then each agent $i\in N$ updates the policy/actor parameters as

$$\begin{aligned} \theta ^i_{t+1} = \theta ^i_t + \beta _{\theta ,t} \cdot {\tilde{\delta }}^i_t \cdot \psi ^i_t. \end{aligned}$$

Note that we have used ${\tilde{\delta }}^i_t \cdot \psi ^i_t$ instead of gradient of the objective function $\nabla _{\theta ^i} J(\theta )$ in the actor update. However, ${\tilde{\delta }}^i_t \cdot \psi ^i_t$ may not be an unbiased estimate of $\nabla _{\theta ^i} J(\theta )$. That is,

${\mathbb {E}}_{s_t\sim d_{\theta }, a_t \sim \pi _{\theta }}[{\tilde{\delta }}^i_t \cdot \psi ^i_t ] = \nabla _{\theta ^i} J(\theta ) + b,$ where $b = {\mathbb {E}}_{s_t\sim d_{\theta }, a_t \sim \pi _{\theta }}[({\bar{R}}_{t}(\lambda ^i_t) - {\bar{R}}(s_t,a_t)) \cdot \psi ^i_{t} ] + {\mathbb {E}}_{s_t \sim d_{\theta }}[(V_{\theta }(s_t) - V_{t}(v^i_t)) \cdot \psi ^i_{t} ]$ is the bias term. (For more details, please refer to page 6 of [49].)

The bias term captures the sum of the expected linear approximation errors in the reward and value functions. If these approximation errors are small, the convergence point of the ODE corresponding to the actor update (as given in Sect. 4) is close to the local optima of $J(\theta )$. In fact, in Sect. 4, we show that the actor parameters converge to asymptotically stable equilibrium set of the ODEs corresponding to actor updates, hence possibly nullifying the bias.

To prove the convergence of actor-critic algorithm, we require $\beta _{\theta ,t} = o(\beta _{v,t})$, and $lim_{t} \frac{\beta _{v,t+1}}{\beta _{v,t}} = 1$. Moreover, we also require $(a)~ \sum _{t} \beta _{v,t} = \sum _{t} \beta _{\theta ,t} = \infty ; ~(b)\sum _t \left( \beta _{v,t}^2 + \beta _{\theta ,t}^2 \right) <\infty$, i.e., critic update is made at the faster time scale than the actor update. Condition in (a) ensures that the discrete time steps $\beta _{v,t}, \beta _{\theta ,t}$ used in the critic and actor steps do cover the entire time axis while retaining $\beta _{v,t}, \beta _{\theta ,t} \rightarrow 0$. We also require the error due to the estimates used in the critic and actor updates are asymptotically negligible almost surely. So, condition in (b) asymptotically suppresses the variance in the estimates [11]; see [47] for some recent developments that do away with this requirement.

The MAAC algorithm uses standard gradients. However, they are most useful for the reward functions that have single optima and whose gradients are isotropic in magnitude for any direction away from its optimum [3]. None of these properties are valid in typical reinforcement learning environments. Apart from this, the performance of standard gradient-based RL algorithms depends on the coordinate system used to define the objective function. It is one of the most significant drawbacks of the standard gradient [26].

Moreover, in many applications such as robotics, the state space contains angles, so the state space has manifolds (curvatures). The objective function will then be defined in that curved space, making the policy gradients methods inefficient. Thus, we require a method that incorporates the knowledge about curvature of the space into the gradient. The natural gradients are the most “natural" choices in such cases.

2.1 Natural Gradients and the Fisher Information Matrix

For single agent actor-critic methods, the natural gradients of the objective function $J(\theta )$ are defined in [7, 39] as ${\widetilde{\nabla }}_{\theta } J(\theta ) = G(\theta )^{-1} \nabla _{\theta } J(\theta )$, where $G(\theta ) := {\mathbb {E}} [\nabla _{\theta } \log \pi _{\theta }(s,a)\nabla _{\theta } \log \pi _{\theta }(s,a)^{\top }]$ is the Fisher information matrix, and $\nabla J(\theta )$ is the standard gradient. The Fisher information matrix is the covariance of score function. It can also be interpreted via KL divergence between the policy $\pi (\cdot ,\cdot )$ parameterize at $\theta$ and $\theta + \varDelta \theta$ as [31, 42]

$$\begin{aligned} KL(\pi _{\theta }(\cdot ,\cdot )|| \pi _{\theta + \varDelta \theta }(\cdot ,\cdot )) \approx \frac{1}{2} \varDelta \theta ^{\top } \cdot G(\theta ) \cdot \varDelta \theta . \end{aligned}$$

(5)

The above expression is obtained from the second-order Taylor expansion of $\log \pi _{\theta + \varDelta \theta }(s, a)$, and using the fact that the sum of the probabilities is one. In above, the right-hand term is a quadratic involving positive definite matrix $G(\theta )$, and hence $G(\theta )$ approximately captures the curvature of the KL divergence between policy distributions at $\theta$ and $\theta + \varDelta \theta$.

Lemma 1

The gradient of the KL divergence between two consecutive policies is approximately proportional to the gradient of the objective function, i.e., $\nabla KL(\pi _{\theta _t}(\cdot , \cdot ) || \pi _{\theta _t + \varDelta \theta _t}(\cdot , \cdot )) \propto \nabla J(\theta _t)$.

Proof

From Eq. (5), the KL divergence is a function of the Fisher information matrix and delta change in the policy parameters.

We find the optimal step-size $\varDelta \theta _t^{\star }$ via the following optimization problem:

$$\begin{aligned} \varDelta \theta _t^{\star } = argmax_{\varDelta \theta _t}~ J(\theta _t + \varDelta \theta _t) ~~~s.t. ~~~KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) = c. \end{aligned}$$

Writing the Lagrange function ${\mathcal {L}}(\theta _t + \varDelta \theta _t; \rho _t)$ (where $\rho _t$ is the Lagrangian multiplier) of the above optimization problem and using the first-order Taylor approximation along with the KL divergence approximation as given in Eq. (5), we have

$$\begin{aligned} \varDelta \theta _t^{\star }= & {} argmax_{\varDelta \theta _t}~ J(\theta _t + \varDelta \theta _t) + \rho _t (KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) - c) \\\approx & {} argmax_{\varDelta \theta _t}~ J(\theta _t) + \varDelta \theta _t^{\top } \nabla _{\theta } J(\theta _t) + \frac{1}{2} \cdot \rho _t \cdot \varDelta \theta _t^{\top } \cdot G(\theta _t) \cdot \varDelta \theta _t - \rho _t c. \end{aligned}$$

Setting the derivative (w.r.t. $\varDelta \theta _t$) of Lagrangian to zero, we have $\nabla _{\theta } J(\theta _t) + \rho _t \cdot \varDelta \theta _t^{\star {^\top }} \cdot G(\theta _t) = 0~\implies ~ \varDelta \theta _t^{\star } = -\frac{1}{\rho _t} G(\theta _t)^{-1} \nabla J(\theta _t)$, i.e., upto the factor of $-\frac{1}{\rho _t}$, we get an optimal step-size in terms of the standard gradients and the Fisher information matrix at point $\theta _t$. Moreover, from Eq. (5), we have $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) \approx G(\theta _t) \varDelta \theta _t^{\star }$ and $G(\theta _t) \varDelta \theta _t^{\star } = -\frac{1}{\rho _t} \nabla J(\theta _t)$. Hence, $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) \approx - \frac{1}{\rho _t} \nabla J(\theta _t)$. This ends the proof. $\square$

The above lemma relates the gradient of the objective function to the gradient of the KL divergence between the policies separated by $\varDelta \theta _t$. It provides a valuable observation because we can adjust the updates (of actor parameter $\theta _t$) just by moving in the prediction space of the parameterized policy distributions. Thus, those MAN algorithms discussed later that rely on Fisher information matrix $G(\cdot )$ implicitly use the above representation for $\nabla J(\cdot )$. We recall these aspects in Sect. 3.6 for the Boltzmann policies.

2.2 Multi-Agent Natural Policy Gradient Theorem and Rank-One Update of $G_{t+1}^{i^{-1}}$

In this section, we provide some details of natural policy gradient methods and the Fisher information matrix in the multi-agent setup. Similar to single agent setup, in a multi-agent model the natural gradient of the objective function is ${\widetilde{\nabla }}_{\theta ^i} J(\theta ) = G(\theta ^i)^{-1} \nabla _{\theta ^i} J(\theta ),~ \forall ~ i\in N$, where the Fisher information matrix $G(\theta ^i) {:=}{\mathbb {E}}_{s \sim d_{\theta }, a \sim \pi _{\theta }} [\nabla _{\theta ^i} \log \pi ^i_{\theta ^i}(s,a^i)\nabla _{\theta ^i} \log \pi ^i_{\theta ^i}(s,a^i)^{\top }]$ is a positive definite matrix for each agent $i\in N$. We now present the policy gradient theorem for multi-agent setup involving the natural gradients.

Theorem 2

(Policy gradient theorem for MARL with natural gradients) Under assumption X. 1, the natural gradient of $J(\theta )$ with respect to $\theta ^i$ for each $i\in N$ is

$$\begin{aligned} {\widetilde{\nabla }}_{\theta ^i}J(\theta )= & {} G(\theta ^i)^{-1}{\mathbb {E}}_{s\sim d_{\theta }, a\sim \pi _{\theta }}[\nabla _{\theta ^i} \log \pi ^{i}_{\theta ^i}(s,a^i) \cdot A_{\theta }(s,a)] \\= & {} G(\theta ^i)^{-1} {\mathbb {E}}_{s\sim d_{\theta }, a\sim \pi _{\theta }}[\nabla _{\theta ^i} \log \pi ^{i}_{\theta ^i}(s,a^i) \cdot A^i_{\theta }(s,a)]. \end{aligned}$$

The proof follows from the multi-agent policy gradient Theorem 1 and definition of natural gradients, i.e., ${\widetilde{\nabla }}_{\theta ^i} J(\theta ) = G(\theta ^i)^{-1} \nabla _{\theta ^i} J(\theta ),~\forall ~ i\in N$.

It is known that inverting a Fisher information matrix is computationally heavy [26, 40], whereas in our natural gradient-based multi-agent actor-critic methods, we require $G(\theta ^i)^{-1},~ \forall ~ i\in N$. To this end, for every $t>0$, let $G^i_{t+1} = \frac{1}{t+1} \sum _{l=0}^t \psi _l \psi _l^{\top }$ be the sample average of the Fisher information matrix $G(\theta ^i)$ by agent $i\in N$. Using the Sherman–Morrison–Woodbury matrix inversion [43] (see also [7, 37]), we recursively estimate the $G(\theta ^i)^{-1}$ for each agent $i\in N$ at the faster time scale (more details are available in Sect. 2.2 in [49]).

$$\begin{aligned} G_{t+1}^{i^{-1}} = \frac{1}{1-\beta _{v,t}}\left[ G_{t}^{i^{-1}} - \beta _{v,t} \frac{(G_{t}^{i^{-1}}\psi ^i_t)(G_{t}^{i^{-1}}\psi _t^{i})^{\top }}{1-\beta _{v,t} + \beta _{v,t}\psi _t^{i^{\top }}G_{t}^{i^{-1}}\psi _t^i} \right] . \end{aligned}$$

(6)

The following section provides three multi-agent natural actor-critic (MAN) RL algorithms involving consensus matrices. Moreover, we will also investigate the relations among these algorithms and their effect on the quality of the local optima they attain.

3 Multi-Agent Natural Actor-Critic (MAN) Algorithms

This section provides three multi-agent natural actor-critic (MAN) reinforcement learning algorithms. Two of the three MAN algorithms explicitly use the Fisher information matrix inverse, whereas one uses the linear function approximation of the advantage parameters.

3.1 FI-MAN: Fisher Information Based Multi-Agent Natural Actor-Critic Algorithm

Our first multi-agent natural actor-critic algorithm uses the fact that natural gradients can be obtained via the Fisher information matrix and the standard gradients. The updates of the objective function estimate, critic, and the rewards parameters in FI-MAN algorithm are the same as given in Eqs. (2), (3), and (4), respectively. The major difference between the MAAC and the FI-MAN algorithm is in the actor update. FI-MAN algorithm uses the following actor update:

$$\begin{aligned} \theta ^i_{t+1} \leftarrow \theta ^i_t + \beta _{\theta ,t} \cdot G_t^{i^{-1}} \cdot {\tilde{\delta }}^i_t \cdot \psi ^i_t,~\forall ~ i\in N. \end{aligned}$$

FI-MAN algorithm explicitly uses $G^{i^{-1}}_t$ in the actor update. Though the Fisher information inverse matrix is updated according to the Sherman–Morrison inverse at a faster time scale, it may be better to avoid explicit use of the Fisher inverse in the actor update. To this end, we use the linear function approximation of the advantage function. This leads to the AP-MAN algorithm, i.e., advantage parameters based multi-agent natural actor-critic algorithm.

3.2 AP-MAN: Advantage Parameters-Based Multi-Agent Natural Actor Critic Algorithm

Consider the local advantage function $A^i(s,a^{i}): {\mathcal {S}}\times {\mathcal {A}} \rightarrow {\mathbb {R}}$ for each agent $i\in N$. Let the local advantage function $A^i(s,a^i)$ be linearly approximated as $A^i(s,a^i; w^i) := w^{i^{\top }} \psi ^{i}(s,a^i)$, where $\psi ^i(s,a^i) = \nabla _{\theta ^i} \log \pi ^i_{\theta ^i}(s,a^i)$ are the compatible features, and $w^i \in {\mathbb {R}}^{m_i}$ are the advantage function parameters. Recall, the same $\psi ^i(s,a^i)$ was used to represent the score function in the policy gradient theorem, Theorem 1. However, it also serves as the compatible feature while approximating the advantage function as it satisfies the compatibility condition in the policy gradient theorem with linear function approximations (Theorem 2 [46]). The compatibility condition as given in [46] is for single agent; however, we are using it explicitly for each agent $i\in N$. Whenever there is no confusion, we write $\psi ^{i}$ instead of $\psi ^i(s,a^i)$, to save space.

We can tune $w^i$ in such a way that the estimate of least squared error in linear function approximation of advantage function is minimized, i.e., ${\mathcal {E}}^{\pi _{\theta }}(w^i) = \frac{1}{2} \sum _{s\in {\mathcal {S}}, a^i\in {\mathcal {A}}^i} {\tilde{d}}_{\theta }(s,a^i)[w^{i^{\top }}\psi ^i(s,a^i) - A^i(s,a^i)]^2$ is minimized. Here, ${\tilde{d}}_{\theta }(s,a^i) = d_{\theta }(s)\cdot \pi ^i_{\theta ^i}(s,a^i)$ as defined earlier. Taking the derivative of above equation w.r.t $w^i$, we have $\nabla _{w^i} {\mathcal {E}}^{\pi _{\theta }}(w^i) = \sum _{s\in {\mathcal {S}}, a^i\in {\mathcal {A}}^i} {\tilde{d}}_{\theta }(s,a^i)[w^{i^{\top }}\psi ^i - A^i(s,a^i)] \psi ^i$. Noting that parameterized TD error ${\tilde{\delta }}^i_t$ is an unbiased estimate of the local advantage function $A^i(s,a^i)$, we will use $\widehat{\nabla _{w^i}} {\mathcal {E}}^{\pi _{\theta }}(w^i_t) = \psi ^i_t \psi ^{i^{\top }}_t w^i_t - {\tilde{\delta }}^i_t \psi ^i_t$ as an estimate of $\nabla _{w^i} {\mathcal {E}}^{\pi _{\theta }}(w^i)$. Hence, the update of advantage parameter $w^i$ in the AP-MAN algorithm is $w^i_{t+1} = w^i_t - \beta _{v,t} \widehat{\nabla _{w^i}} {\mathcal {E}}^{\pi _{\theta }}(w^i_t) =(I - \beta _{v,t} \psi ^i_t \psi ^{i^{\top }}_t)w^i_t + \beta _{v,t} {\tilde{\delta }}^i_t \psi ^i_t.$ The updates of the objective function estimate, critic, and reward parameters in the AP-MAN algorithm are the same as given in Eqs. (2), (3), and (4), respectively. Additionally, in the critic step, we update the advantage parameters as given above. For single-agent RL with natural gradients [39, 40], show that ${\widetilde{\nabla }}_{\theta } J(\theta ) = w$. In MARL with natural gradient, we separately verified and hence use ${\widetilde{\nabla }}_{\theta ^i} J(\theta ) = w^i$ for each agent $i\in N$ in the actor update of AP-MAN algorithm. The AP-MAN actor-critic algorithm thus uses $\theta ^i_{t+1} \leftarrow \theta ^i_t + \beta _{\theta ,t} \cdot w^i_{t+1}$ in the actor update. The algorithm’s pseudo-code involving advantage parameters is given in the AP-MAN algorithm.

Remark 1

We want to emphasize that the AP-MAN algorithm does not explicitly use $G(\theta ^i)^{-1}$ in the actor update (as also in [7]); hence, it requires fewer computations. However, it involves the linear function approximation of the advantage function that itself requires $\psi ^i_t \psi ^{i^{\top }}_t$ which is an unbiased estimate of the Fisher information matrix. We will see later in Sect. 3.4 that the performance of the AP-MAN algorithm is almost the same as the MAAC algorithm. We empirically verify this observation in Sect. 5.

Remark 2

The advantage function is a linear combination of $Q_{\theta }(s, a)$ and $V_{\theta }(s)$; therefore, the linear function approximation of the advantage function alone enjoys the benefit of approximating the $Q_{\theta }(s, a)$ or $V_{\theta }(s)$. Moreover, MAAC uses the linear function approximation of $V_{\theta }(s)$; hence, we expect the behavior of AP-MAN to be similar to that of MAAC; this comes out in our computational experiments in Sect. 5.

The FI-MAN algorithm is based solely on the Fisher information matrix and the AP-MAN algorithm on the advantage function approximation. Our next algorithm, FIAP-MAN algorithm, i.e., Fisher information and advantage parameter-based multi-agent natural actor-critic algorithm combines them in a certain way. We see the benefits of this combination in Sects. 3.4 and 5.1.

3.3 FIAP-MAN: Fisher Information and Advantage Parameter Based Multi-Agent Natural Actor-Critic Algorithm

Recall in Sect. 3.2, for each agent $i\in N$, the local advantage function has linear function approximation $A^i(s,a^i; w^i) = w^{i^{\top }} \psi ^{i}(s,a^i)$, where $\psi ^i(s,a^i)$ are the compatible features as before, and $w^i \in {\mathbb {R}}^{m_i}$ are the advantage function parameters. In AP-MAN algorithm the Fisher inverse $G(\theta ^i)^{-1}$ is not estimated explicitly; however, in FIAP-MAN algorithm, we explicitly estimate $G(\theta ^i)^{-1}$, and hence use $\widehat{\nabla _{w^i}} {\mathcal {E}}^{\pi _{\theta }}(w^i_t) = G^{i^{-1}}_{t}(\psi ^i_t \psi ^{i^{\top }}_t w^i_t - {\tilde{\delta }}^i_t \psi ^i_t),~~ \forall ~ i\in N$ as an estimate of $\nabla _{w^i} {\mathcal {E}}^{\pi _{\theta }}(w^i)$. The update of advantage parameters $w^i$ along with the critic update in the FIAP-MAN algorithm is $w^i_{t+1} = w^i_t - \beta _{v,t} \widehat{\nabla _{w^i}} {\mathcal {E}}^{\pi _{\theta }}(w^i_t) = w^i_t - \beta _{v,t} G^{i^{-1}}_t(\psi ^i_t \psi ^{i^{\top }}_t w^i_t - {\tilde{\delta }}^i_t \psi ^i_t) = (1 - \beta _{v,t})w^i_t + \beta _{v,t} G^{i^{-1}}_t {\tilde{\delta }}^i_t \psi ^i_t$.

Remark 3

Note that we take $G^{i^{-1}}_t \psi ^i_t \psi ^{i^{\top }}_t = I,~ \forall ~i \in N$, though $G_{t+1} = \frac{1}{t+1} \sum _{l=0}^{t} \psi _l {\psi _l}^{\top }$. A similar approximation is also implicitly made in natural gradient algorithms in [7, 8] for single-agent RL. Convergence of FIAP-MAN algorithm with above approximate update in MARL is given in Sect. 4. Later, we use these updates in our computations to demonstrate their superior performance in multiple instances of traffic network (Sect. 5).

The updates of the objective function estimate, critic, and reward parameters in the FIAP-MAN algorithm are the same as given in Eqs. (2), (3), and (4), respectively. Similar to the AP-MAN algorithm, the actor update in FIAP-MAN algorithm is $\theta ^i_{t+1} \leftarrow \theta ^i_t + \beta _{\theta ,t} \cdot w^i_{t+1},~\forall ~i\in N$. Again for the same reason as in the AP-MAN algorithm, we take ${\widetilde{\nabla }}_{\theta ^i}J(\theta ) = w^i$.

3.4 Relationship Between Actor Updates in Algorithms

Recall, the actor update for each agent $i\in N$ in FIAP-MAN algorithm is $\theta ^i_{t+1} = \theta ^i_t + \beta _{\theta ,t} w^i_{t+1}$, where $w^i_{t+1} = (1 - \beta _{v,t})w^i_t + \beta _{v,t} G^{i^{-1}}_t {\tilde{\delta }}^i_t \psi ^i_t$. Therefore, the actor update of FIAP-MAN algorithm is $\theta ^i_{t+1} = \theta ^i_t + \beta _{\theta ,t}(1 - \beta _{v,t})w^i_t + \beta _{v,t} \left( \beta _{\theta ,t} G^{i^{-1}}_t {\tilde{\delta }}^i_t \psi ^i_t \right)$. The above update is almost the same as the actor update of the FI-MAN algorithm with an additional term involving advantage parameter $w^i_t$. However, the contribution of the second term is negligible after some time t. Moreover, the third term is a positive fraction of the second term in the actor update of FI-MAN algorithm. Therefore, the actor parameters in FIAP-MAN and FI-MAN algorithms are almost the same after time t. Hence, both the algorithms are expected to converge almost to the same local optima.

Similarly, consider the actor update of the AP-MAN algorithm, i.e., $\theta ^i_{t+1} = \theta ^i_t + \beta _{\theta ,t} w^i_{t+1}$, where $w^i_{t+1} = (I - \beta _{v,t} \psi ^i_t \psi ^{i^{\top }}_t)w^i_t + \beta _{v,t} {\tilde{\delta }}^i_t \psi ^i_t$. Therefore, the actor update of AP-MAN algorithm is $\theta ^i_{t+1} = \theta ^i_t + \beta _{\theta ,t} (I - \beta _{v,t} \psi ^i_t \psi ^{i^{\top }}_t)w^i_t + \beta _{v,t} \left( \beta _{\theta ,t} {\tilde{\delta }}^i_t \psi ^i_t \right)$. Again, the second term in the above equation is negligible after some time t, and the third term is a positive fraction of the second term in the actor update of the MAAC algorithm. Hence, the actor update in AP-MAN algorithm is almost the same as the MAAC algorithm; therefore, AP-MAN and MAAC are expected to converge to the same local optima.

3.5 Comparison of Variants of MAN and MAAC Algorithms

In this section, we show that under some conditions the objective function of a variant of the FI-MAN algorithm dominates that of the corresponding variant of the MAAC algorithm for all $t\ge t_0$, for some $t_0 <\infty$. For this purpose, we propose a model to evaluate the “efficiency” of MAAC and FI-MAN algorithms in terms of their goal; maximization of MARL objective function, $J(\theta )$. This comparison exploits the intrinsic property of the Fisher information matrix $G(\theta )$ (Lemma 2, an uniform upper bound on its minimum eigenvalue).

Let $\theta ^M_t$ and $\theta ^N_t$ be the actor parameters in MAAC and FI-MAN algorithms, respectively. Recall the actor updates in MAAC and FI-MAN algorithms were $\theta ^M_{t+1} = \theta ^M_t + \beta _{\theta ,t} {\tilde{\delta }}_t \cdot \psi _t$, and ${\theta }^N_{t+1} = \theta ^N_t + \beta _{\theta ,t} G^{-1}_{t}{\tilde{\delta }}_t \cdot \psi _t$, respectively. However, these updates use the biased estimate of $\nabla J(\cdot )$. Moreover, the Fisher information matrix inverse is updated via the Sherman–Morrison iterative method. In this section, we work with the deterministic variants of these algorithms where we use $\nabla J(\cdot )$ instead of ${\tilde{\delta }}_t \cdot \psi _t$, and $G(\theta ^N_t)^{-1}$ instead of using $G_t^{{-1}}$ in the actor updates. This avoids the approximation errors; however, the same is not possible in the computations since the gradient of the objective function is not known. For ease of notation, we denote the actor parameters in the deterministic variants of MAAC and FI-MAN algorithms by ${\tilde{\theta }}^{M}$, and ${\tilde{\theta }}^{N}$, respectively. In particular, we consider the following actor updates.

$$\begin{aligned} \begin{aligned} \mathbf{Deterministic} \,\, \mathbf{MAAC} ~~ {\tilde{\theta }}^M_{t+1}&= {\tilde{\theta }}^M_t + \beta _{{\tilde{\theta }},t} \nabla J({\tilde{\theta }}^M_t); \\ \mathbf{Deterministic} \,\, \mathbf{FI}-MAN ~~ {\tilde{\theta }}^N_{t+1}&= {\tilde{\theta }}^N_t + \beta _{{\tilde{\theta }},t} G({\tilde{\theta }}^N_t)^{-1} {\nabla } J({\tilde{\theta }}^N_t). \end{aligned} \end{aligned}$$

(7)

We give sufficient conditions when the objective function value of the limit point of the deterministic FI-MAN algorithm is not worse off than the value by deterministic MAAC algorithm while using the above actor updates. We want to emphasize that with these updates, the actor parameters in Eq. (7) will converge to a local maxima under some conditions (for example, the strong Wolfe’s conditions) on the step-size [37]. Let ${\tilde{\theta }}^{M^{\star }}$ and ${\tilde{\theta }}^{N^{\star }}$ be the corresponding local maxima. The existence of the local maxima for the deterministic MAN algorithms is also guaranteed via the Wolfe’s conditions in the natural gradients space. Note that these local maxima need not be the same as the one obtained from actor updates of MAAC and FI-MAN algorithms. However, the result given below may be valid for the MAAC and FI-MAN algorithms because both ${\tilde{\delta }} \cdot \psi$ and $\nabla J(\cdot )$ go to zero asymptotically.

We also assume that both algorithms use the same sequence of step-sizes, $\{\beta _{{\tilde{\theta }},t}\}$. The results in this section uses Taylor’s series expansion and comparison of the objective function, $J(\cdot )$, rather than its estimate $\mu$. Similar ideas are used in [4, 38] where the certainty equivalence principle holds, i.e., the random variables are replaced by their expected values. However, we work with the estimates in convergence theory/proofs and computations since the value of global objective is unknown to the agents. We first bound the minimum singular value of the Fisher information matrix in the following Lemma.

Lemma 2

For $G(\theta ) = {\mathbb {E}}[\psi \psi ^{\top }]$, such that $|| \psi ||\le 1$, the minimum singular value $\sigma _{\min }(G(\theta ))$ is upper bounded by $\frac{1}{m}$, i.e., $\sigma _{\min }(G(\theta )) \le \frac{1}{m}$.

The proof of this Lemma is based on the observation that the trace of matrix $\psi \psi ^{\top }$ is $|| \psi ||^2$. Though this is a new result, we defer its detailed proof to Appendix A. 3 of [49] due to space considerations.

Remark 4

In the literature, the compatible features are assumed to be uniformly bounded, Assumption X. 3. For the linear architecture of features that we are using, assuming this bound to be 1 is not restrictive. The features $\psi$ that we use in our computational experiments in Sect. 5 automatically meet the condition of being normalized by 1, i.e., $||\psi || \le 1$.

Lemma 3

Let $J(\cdot )$ be twice continuously differentiable function on a compact set $\varTheta$, so that $|\{\nabla ^2 J({\tilde{\theta }}^M_t)\}_{(i,j)}| \le H, ~ \forall ~i,j\in [m]$ for some $H< \infty$. Moreover, let $J({\tilde{\theta }}^M_t) \le J({\tilde{\theta }}^N_t)$, $|| \nabla J({\tilde{\theta }}^M_t)|| \le || \nabla J({\tilde{\theta }}^N_t)||$, and $\beta _{{\tilde{\theta }},{t}} \frac{mH}{2} + {1} - m^2 \le 0$. Then, $J({\tilde{\theta }}^M_{t+1}) \le J({\tilde{\theta }}^N_{t+1})$.

Proof

The Taylor series expansion of a twice differentiable function $J({\tilde{\theta }}^M_{t+1})$ with Lagrange form of remainder [22] is $J({\tilde{\theta }}^M_{t+1}) = J({\tilde{\theta }}^M_t + \varDelta {\tilde{\theta }}^M_t) = J({\tilde{\theta }}^M_t) + \varDelta {\tilde{\theta }}_t^{M^{\top }} \nabla J({\tilde{\theta }}^M_t) + R_M(\varDelta {\tilde{\theta }}^M_t)$, where $R_M(\varDelta {\tilde{\theta }}^M_t) = \frac{1}{2!} \varDelta {\tilde{\theta }}_t^{M^{\top }} \nabla ^2 J({\tilde{\theta }}^M_t + c_M \cdot \varDelta {\tilde{\theta }}^M_t) \varDelta {\tilde{\theta }}^M_t$ for some $c_M\in (0,1)$.

Similarly, the Taylor series expansion of $J({\tilde{\theta }}^N_{t+1})$ with Lagrange remainder form is $J({\tilde{\theta }}^N_{t+1}) = J({\tilde{\theta }}^N_t + \varDelta {\tilde{\theta }}^N_t) = J({\tilde{\theta }}^N_t) + \varDelta {\tilde{\theta }}_t^{N^{\top }} {\widetilde{\nabla }} J({\tilde{\theta }}^N_t) + R_N(\varDelta {\tilde{\theta }}^N_t)$, where $R_N(\varDelta {\tilde{\theta }}^N_t) = \frac{1}{2!} \varDelta {\tilde{\theta }}_t^{N^{\top }} {\widetilde{\nabla }}^2 J({\tilde{\theta }}^N_t + c_N \cdot \varDelta {\tilde{\theta }}^N_t) \varDelta {\tilde{\theta }}^N_t$ for some $c_N \in (0,1)$.

Now, consider the difference

$$\begin{aligned}&J({\tilde{\theta }}^M_{t+1}) - J({\tilde{\theta }}^N_{t+1}) \nonumber \\&\quad = J({\tilde{\theta }}^M_t) - J({\tilde{\theta }}^N_t) + \varDelta {\tilde{\theta }}^{M^{\top }}_{t} \nabla J({\tilde{\theta }}^M_t) \nonumber \\&\qquad - \varDelta {\tilde{\theta }}^{N^{\top }}_{t} {\widetilde{\nabla }} J({\tilde{\theta }}^N_t) + R_M(\varDelta {\tilde{\theta }}^M_t) - R_N(\varDelta {\tilde{\theta }}^N_t) \nonumber \\&\quad \overset{(i)}{\le } \varDelta {\tilde{\theta }}^{M^{\top }}_{t} \nabla J({\tilde{\theta }}^M_t) - \varDelta {\tilde{\theta }}^{N^{\top }}_{t} G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t)+ R_M(\varDelta {\tilde{\theta }}^M_t) \nonumber \\&\quad \overset{(ii)}{=} ({\tilde{\theta }}^M_{t+1} - {\tilde{\theta }}^M_t)^{\top } J({\tilde{\theta }}^M_t) - ({\tilde{\theta }}^N_{t+1} - {\tilde{\theta }}^N_t)^{\top } G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t) + R_M(\varDelta {\tilde{\theta }}^M_t) \nonumber \\&\quad \overset{(iii)}{=} \beta _{{\tilde{\theta }},{t}} \left( || \nabla J({\tilde{\theta }}^M_t) ||^2 - || G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t))||^2 \right) + R_M(\varDelta {\tilde{\theta }}^M_t) \nonumber \\&\quad \overset{(iv)}{\le } \beta _{{\tilde{\theta }},{t}} \left( || \nabla J({\tilde{\theta }}^N_t) ||^2 - || G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t))||^2 \right) + R_M(\varDelta {\tilde{\theta }}^M_t), \end{aligned}$$

(8)

where (i) follows because $J({\tilde{\theta }}^M_t) \le J({\tilde{\theta }}^N_t)$, $R_N(\varDelta {\tilde{\theta }}^N_t) \ge 0$ and ${\widetilde{\nabla }} J({\tilde{\theta }}^N_t) = G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t)$. (ii) uses the fact that $\varDelta {\tilde{\theta }}^M_t = {\tilde{\theta }}^M_{t+1} - {\tilde{\theta }}^M_t;~ \varDelta {\tilde{\theta }}^N_t = {\tilde{\theta }}^N_{t+1} - {\tilde{\theta }}^N_t$. (iii) is consequence of the updates in Eq. (7). Finally, (iv) follows from the fact that $||\nabla J({\tilde{\theta }}^M_t)|| \le ||\nabla J({\tilde{\theta }}^N_t)||$.

Now, from Eq. (8) and using the fact that for any positive definite matrix ${\mathbf {A}}$ and a vector ${\mathbf {v}}$, $||{\mathbf {A}} {\mathbf {v}}|| \ge \sigma _{\min }({\mathbf {A}}) ||{\mathbf {v}}||$, we have $|| G({\tilde{\theta }}^N_t)^{-1} \nabla J({\tilde{\theta }}^N_t))||^2 \ge \sigma _{\min }^2( G({\tilde{\theta }}^N_t)^{-1}) || \nabla J({\tilde{\theta }}^N_t))||^2$. Therefore, from Eq. (8), we have

$$\begin{aligned} J({\tilde{\theta }}^M_{t+1}) - J({\tilde{\theta }}^N_{t+1})&\le \beta _{{\tilde{\theta }},t} \left( 1 - \frac{1}{\sigma _{\min }^2(G({\tilde{\theta }}^N_t))} \right) || \nabla J({\tilde{\theta }}^N_t))||^2 + R_M(\varDelta {\tilde{\theta }}^M_t)\nonumber \\&\overset{(v)}{\le } \beta _{{\tilde{\theta }},{t}} \left( 1 - m^2 \right) || \nabla J({\tilde{\theta }}^N_t))||^2 + R_M(\varDelta {\tilde{\theta }}^M_t), \end{aligned}$$

(9)

(v) follows from Lemma 2 as $\sigma _{\min }(G({\tilde{\theta }}^N_t)) \le \frac{1}{m}$, implies $-\frac{1}{\sigma _{\min }^2(G({\tilde{\theta }}^N_t)) } \le -m^2$.

Since $J(\cdot )$ is twice continuously differentiable function on the compact set $\varTheta$, we have for all $i, j\in [m]$, $|\{\nabla ^2 J({\tilde{\theta }}^M_t\}_{(i,j)}| \le H < \infty$. Therefore, we have $| R_M(\varDelta {\tilde{\theta }}^M_t)| \le \frac{H}{2!} || \varDelta {\tilde{\theta }}^M_t ||^2_1 \overset{(vii)}{=} \beta _{{\tilde{\theta }},{t}}^2 \frac{H}{2} || \nabla J({\tilde{\theta }}^M_t) ||^2_1 \overset{(viii)}{\le } \beta _{{\tilde{\theta }},{t}}^2 \frac{mH}{2} || \nabla J({\tilde{\theta }}^M_t) ||^2 \overset{(ix)}{\le } \beta _{{\tilde{\theta }},{t}}^2 \frac{mH}{2} || \nabla J({\tilde{\theta }}^N_t) ||^2$, where (vii) follows from actor update of the FI-MAN algorithm. (viii) holds because for any ${\mathbf {x}} \in {\mathbb {R}}^l$, the following is true:

$||{\mathbf {x}}||_2 \le ||{\mathbf {x}}||_1 \le \sqrt{l}~ ||{\mathbf {x}}||_2$ [25]. (ix) comes from the assumption that $|| \nabla J({\tilde{\theta }}^M_t) ||^2 \le || \nabla J({\tilde{\theta }}^N_t) ||^2$. From Eq. (9) and upper bound on $|R_M(\varDelta {\tilde{\theta }}^M_t)|$, we have

$$\begin{aligned} J({\tilde{\theta }}^M_{t+1}) - J({\tilde{\theta }}^N_{t+1})\le & {} \beta _{{\tilde{\theta }},{t}} \left( 1 - m^2 \right) || \nabla J({\tilde{\theta }}^N_t))||^2 + \beta _{{\tilde{\theta }},{t}}^2 \frac{mH}{2} || \nabla J({\tilde{\theta }}^N_t) ||^2\\= & {} \beta _{{\tilde{\theta }},{t}} \left\{ \beta _{{\tilde{\theta }},{t}} \frac{mH}{2} + {1} - m^2 \right\} || \nabla J({\tilde{\theta }}^N_t) ||^2 \le 0, \end{aligned}$$

where the last inequality follows from the assumption $\beta _{{\tilde{\theta }},{t}} \frac{mH}{2} +{1} - m^2 \le 0$. Therefore, $J({\tilde{\theta }}^M_{t+1}) \le J({\tilde{\theta }}^N_{t+1})$. $\square$

Theorem 3

Let $J(\cdot )$ be twice continuously differentiable function on a compact set $\varTheta$, so that $|\{\nabla ^2 J({\tilde{\theta }}^M_t)\}_{(i,j)}| \le H, ~ \forall ~i,j\in [m]$ for some $H< \infty$. Moreover, let $J({\tilde{\theta }}^M_{t_0}) \le J({\tilde{\theta }}^N_{t_0})$ for some $t_0 > 0$, and for every $t\ge t_0$, let $|| \nabla J({\tilde{\theta }}^M_t)|| \le || \nabla J({\tilde{\theta }}^N_t)||$, and $\beta _{{\tilde{\theta }},t} \frac{mH}{2} + 1 - m^2 \le 0$. Then, $J({\tilde{\theta }}^M_t) \le J({\tilde{\theta }}^N_t)$, for all $t\ge t_0$. Further, for the local maxima ${\tilde{\theta }}^{M^{\star }}$, and ${\tilde{\theta }}^{N^{\star }}$ of the updates in Eq. (7), we have $J({\tilde{\theta }}^{M^{\star }}) \le J({\tilde{\theta }}^{N^{\star }})$.

Proof

We prove this theorem via principle of mathematical induction (PMI). From assumption, we have $J({\tilde{\theta }}^M_{t_0}) \le J({\tilde{\theta }}^N_{t_0})$. Now, using $t=t_0$ in Lemma 3, we have $J({\tilde{\theta }}^M_{t_0+1}) \le J({\tilde{\theta }}^N_{t_0+1})$. Thus, the base case of PMI is true.

Next, we assume that $J({\tilde{\theta }}^M_t) \le J({\tilde{\theta }}^N_t)$ for any $t=t_0+k$, where $k\in {\mathbb {Z}}^{+}$. Also from assumption, for every $t\ge t_0+k$, we have $|| \nabla J({\tilde{\theta }}^M_t)|| \le || \nabla J({\tilde{\theta }}^N_t)||$, and $\beta _{{\tilde{\theta }},t} \frac{mH}{2} + 1 - m^2 \le 0$. Therefore, again from Lemma 3, we have $J({\tilde{\theta }}^M_{t_0+k+1}) \le J({\tilde{\theta }}^N_{t_0+k+1})$. From PMI, we have $J({\tilde{\theta }}^M_t) \le J({\tilde{\theta }}^N_t),~~ \forall ~~t \ge t_0$.

Finally, consider the limiting case. Taking the limit $t \rightarrow \infty$ in the above equation and using the fact that $J(\cdot )$ is continuous on the compact set $\varTheta$, we have $lim_{t\rightarrow \infty } J({\tilde{\theta }}^M_t) = J({\tilde{\theta }}^{M^{\star }}), ~ and~ lim_{t\rightarrow \infty } J({\tilde{\theta }}^N_t) = J({\tilde{\theta }}^{N^{\star }})$, so that $J({\tilde{\theta }}^{M^{\star }}) \le J({\tilde{\theta }}^{N^{\star }})$. This ends the proof. $\square$

3.6 KL Divergence-Based Natural Gradients for Boltzmann Policy

One specific policy that is often used in RL literature is the Boltzmann policy [20]. Recall, the parameterized Boltzmann policy is $\pi _{\theta _t}(s,a) = \frac{\exp (q^{\top }_{s,a} \theta _t)}{\sum _{b\in {\mathcal {A}}} \exp (q^{\top }_{s,b} \theta _t)}$, where $q^{\top }_{s,a}$ is the feature for any state-action pair (s, a). Here, the features $q_{s,a}$ are assumed to be uniformly bounded by 1.

Lemma 4

For the Boltzmann policy, we have $KL(\pi _{\theta _t}(s,a)|| \pi _{\theta _t + \varDelta \theta _t} (s,a)) = {\mathbb {E}} \left[ \log \left( \sum _{b\in {\mathcal {A}}} \pi _{\theta _t}(s,b) \exp (\varDelta q^{\top }_{s,ba} \varDelta \theta _t)\right) \right]$, where $\varDelta q^{\top }_{s,ba} = q^{\top }_{s,b} - q^{\top }_{s,a}$.

The proof of this Lemma just uses the definition of KL divergence and the Boltzmann policy. So, we defer it to Appendix A.4 of [49]. The above KL divergence suggests that we have a nonzero curvature if the action taken is better than the averaged action. Moreover, $\exp (\varDelta q_{s, ba}\varDelta \theta _t) \ne 1$ if and only if ${\varDelta q_{s,ba}}$ is orthogonal to $\varDelta \theta _t$. So, except when they are orthogonal, $\log (\sum _{b \in {\mathcal {A}}}\pi _{\theta _t}(s,b) \cdot \exp {(\varDelta q_{s, ba} \varDelta \theta _t})) \ne 0$ as $\sum _{b \in {\mathcal {A}}} \pi _{\theta _t}(s,b) = 1$. Thus, the curvature is nonzero, larger or smaller depends on the direction $\varDelta \theta _t$ makes with the feature difference $q_{s, b}^{\top } - q^{\top }_{s,a}$; if the angle is zero, it is better.

Lemma 5

For the Boltzmann policy, we have $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) = -{\mathbb {E}}[\nabla \log \pi _{\theta _t + \varDelta \theta _t} (s,a)]$.

So, $\psi _{\theta _{t+1}} = \nabla \log \pi _{\theta _t + \varDelta \theta _t}$ is an unbiased estimate of $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot ))$. The proof uses the fact that the action set is finite and hence expectation and gradients can be interchanged. Moreover, for Boltzmann policies, the compatible features are same as the features associated to policy, except normalized to be mean zero for each state. Proof follows from the definition of KL divergence and the Boltzmann policy. For details, we refer to Appendix A.5 of [49].

Recall from Eq. (5), we have $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) \approx G(\theta _t) \varDelta \theta _t$. Also, in Lemma 1, we obtain that $G(\theta _t) \varDelta \theta _t = -\frac{1}{\rho _t} \nabla _{\theta } J(\theta _t)$. Moreover, we obtain $\nabla KL(\pi _{\theta _t}(\cdot ,\cdot )|| \pi _{\theta _t + \varDelta \theta _t}(\cdot ,\cdot )) \approx -\frac{1}{\rho _t} \nabla J(\theta _t)$. Thus, from Lemma 5, and above equations, we have ${\mathbb {E}}[\nabla \log \pi _{\theta _t + \varDelta \theta _t} (s,a)] \approx \frac{1}{\rho _t} \nabla J(\theta _t)$. So, $\nabla \log \pi _{\theta _t + \varDelta \theta _t} = \psi _{\theta _{t+1}}$ is approximately an unbiased estimate of $\nabla J(\theta _t)$ upto scaling of $\frac{1}{\rho _t}$ for the Boltzmann policies. It is a valuable observation because to move along the gradient of objective function $J(\cdot )$, we can adjust the updates (of actor parameter) just by moving in the $\pi _{\theta _t}$ prediction space via the compatible features.

We now prove the convergence of FI-MAN, AP-MAN, and FIAP-MAN algorithms. The proofs majorly use the idea of two-time scale stochastic approximations from [11].

4 Convergence Analysis

We now provide the convergence proof of all the three MAN algorithms. To this end, we need following assumptions on the features $\varphi (s)$, and f(s, a) for the value and rewards function, respectively, for any $s\in {\mathcal {S}}, a\in {\mathcal {A}}$. This assumption is similar to [53], and also used in single-agent natural actor-critic methods [7].

X 3

The feature vectors $\varphi (s)$, and f(s, a) are uniformly bounded for any $s\in {\mathcal {S}}, a\in {\mathcal {A}}$. Moreover, let the feature matrix $\varPhi \in {\mathbb {R}}^{|{\mathcal {S}}|\times L}$ have $[\varphi _l(s), s\in {\mathcal {S}}]^{\top }$ as its l-th column for any $l\in [L]$, and feature matrix $F \in {\mathbb {R}}^{|{\mathcal {S}}||{\mathcal {A}}|\times M}$ have $[f_m(s,a), s\in {\mathcal {S}},a\in {\mathcal {A}}]^{\top }$ as its m-th column for any $m\in [M]$, then $\varPhi$ and F have full column rank, and for any $\omega \in {\mathbb {R}}^L$, we have $\varPhi \omega \ne \mathbbm {1}$.

Apart from assumption X. 3, let $D^s_{\theta } = [d_{\theta }(s), s\in {\mathcal {S}}]$, and ${\bar{R}}_{\theta } = [{\bar{R}}_{\theta }(s), s\in {\mathcal {S}}]^{\top } \in {\mathbb {R}}^{|{\mathcal {S}}|}$ with ${\bar{R}}_{\theta }(s) = \sum _a \pi _{\theta }(s,a)\cdot {\bar{R}}(s,a)$. Define the operator $T^V_{\theta }: {\mathbb {R}}^{|{\mathcal {S}}|}\rightarrow {\mathbb {R}}^{|{\mathcal {S}}|}$ for any state value vector $X\in {\mathbb {R}}^{|{\mathcal {S}}|}$ as $T^V_{\theta } (X) = {\bar{R}}_{\theta } - J(\theta )\mathbbm {1} + P^{\theta }X$. The proof of all the three MAN algorithms are done in two steps: (a) convergence of the objective function estimate, critic update, and rewad parameters keeping the actor parameters $\theta ^i$ fixed for all agents $i\in N$, and (b) convergence of the actor parameters to an asymptotically stable equilibrium set of the ODE corresponding to the actor update. So, we require the following assumption on $G^i_t$ and its inverse $G^{i^{-1}}_t$. This assumption is used for single-agent natural actor-critic algorithms in [7]; here, we have modified it for multi-agent setup.

X 4

The recursion of Fisher information matrix $G^i_t$ and its inverse $G^{i^{-1}}_t$ satisfy $sup_{t,\theta ^i,s,a^i} || G_t^i || < \infty$; $sup_{t,\theta ^i,s,a^i} || G_t^{i^{-1}} || < \infty$ for each agent $i\in N$.

Assumption X. 4 ensures that the FI-MAN and FIAP-MAN actor-critic algorithms does not get stuck in a non-stationary point. To ensure the existence of local optima of $J(\theta )$, we make the following assumptions on policy parameters $\theta ^i_t$, for each agent $i\in N$.

X 5

The policy parameters $\{\theta ^i_t\}_{t\ge 0}$ of the actor update include a projection operator $\varGamma ^i: {\mathbb {R}}^{m_i} \rightarrow \varTheta ^i \subset {\mathbb {R}}^{m_i}$ that projects $\theta ^i_t$ onto a compact set $\varTheta ^i$. Moreover, $\varTheta = \prod _{i=1}^n \varTheta ^i$ is large enough to include a local optima of $J(\theta )$.

For each agent $i\in N$, let ${\hat{\varGamma }}^i$ be the transformed projection operator defined for any $\theta \in \varTheta$ with $h: \varTheta \rightarrow {\mathbb {R}}^{\sum _{i\in N} m_i}$ being a continuous function as ${\hat{\varGamma }}^{i}(h(\theta )) = lim_{0<\eta \rightarrow 0}\frac{\varGamma ^i(\theta ^i + \eta h(\theta )) - \theta ^i}{\eta }$. If the above limit is not unique, ${\hat{\varGamma }}^i(h(\theta ))$ denotes the set of all possible limit points. This projection operator is useful in convergence proof of the policy parameters. It is an often-used technique to ensure boundedness of iterates in stochastic approximation algorithms. However, we do not require a projection operator in computations because the iterates remain bounded.

We begin by proving the convergence of the critic updates given in Eqs. (2), (3), and (4), respectively. The following theorem will be common in the proof of all the three MAN algorithms. For proof see Appendix A. 6 of [49].

Theorem 4

[53] Under assumptions X. 1, X. 2, and X. 3, for any policy $\pi _{\theta }$, with sequences $\{\lambda ^i_t\}, \{\mu ^i_t\}, \{v^i_t\}$, we have $lim_t~ \mu ^i_t = J(\theta ),~ lim_t~ \lambda ^i_t = \lambda _{\theta }$, and $lim_t~v^i_t = v_{\theta }$ a.s. for each agent $i\in N$, where $J(\theta ),~ \lambda _{\theta }$, and $v_{\theta }$ are unique solutions to $F^{\top }D_{\theta }^{s,a}({\bar{R}} - F\lambda _{\theta })=0; ~~ \varPhi ^{\top } D_{\theta }^s[T_{\theta }^V(\varPhi v_{\theta }) - \varPhi v_{\theta }] = 0.$

4.1 Convergence of FI-MAN Actor-Critic Algorithm

To prove the convergence of FI-MAN algorithm, we first show the convergence of recursion for the Fisher information matrix inverse as in Eq. (6).

Theorem 5

For each agent $i \in N$, and given parameter $\theta ^i$, we have $G_t^{i^{-1}} \rightarrow G(\theta ^i)^{-1}$ as $t\rightarrow \infty$ with probability one.

Please refer to Theorem 5 of [49] for detailed proof. Next, we prove the convergence of actor update. To this end, we can view $-r^i_{t+1}$ as the cost incurred at time t. Hence, transform the actor recursion in the FI-MAN algorithm as $\theta ^i_{t+1} \leftarrow \theta ^i_t - \beta _{\theta ,t} \cdot G_t^{i^{-1}} \cdot {\tilde{\delta }}^i_t \cdot \psi ^i_t$. The convergence of the FI-MAN actor-critic algorithm with linear function approximation is given in the following theorem.

Theorem 6

Under the assumptions X. 1 - X. 5, the sequence $\{\theta ^i_t\}_{t\ge 0}$ obtained from the actor step of the FI-MAN algorithm converges almost surely to asymptotically stable equilibrium set of the ODE

$$\begin{aligned} {\dot{\theta }}^i = {\hat{\varGamma }}^i[-G(\theta ^{i})^{-1}{\mathbb {E}}_{s_t\sim d_{\theta }, a_t\sim \pi _{\theta }} ( {\tilde{\delta }}^i_{t,\theta } \psi ^i_{t,\theta })],~~~ \forall ~i\in N. \end{aligned}$$

(10)

Proof

Let ${\mathcal {F}}_{t,1} = \sigma (\theta _{\tau }, \tau \le t)$ be the $\sigma$-field generated by $\{\theta _{\tau }\}_{\tau \le t}$. Moreover, let $\xi _{t+1,1}^i = -G(\theta ^i_t)^{-1} \left\{ {\tilde{\delta }}^i_t \psi ^i_t - {\mathbb {E}}_{s_t\sim d_{\theta _t}, a_t\sim \pi _{\theta _t}}({\tilde{\delta }}^i_t \psi ^i_t | {\mathcal {F}}_{t,1}) \right\}$, and $\xi _{t+1,2}^i = -G(\theta ^i_t)^{-1} {\mathbb {E}}_{s_t\sim d_{\theta _t}, a_t\sim \pi _{\theta _t}}( ( {\tilde{\delta }}^i_t -{\tilde{\delta }}^i_{t, \theta _t}) \psi ^i_t | {\mathcal {F}}_{t,1})$, where ${\tilde{\delta }}^i_{t,\theta _t} = f_t^{\top }\lambda _{\theta _t} - J(\theta _t) + \varphi _{t+1}^{\top }v_{\theta _t} - \varphi _t^{\top }v_{\theta _t}$. The actor update in the FI-MAN algorithm with local projection then become $\theta ^i_{t+1} = \varGamma ^i [\theta ^i_t - \beta _{\theta ,t} G(\theta ^{i}_t)^{-1}{\mathbb {E}}_{s_t\sim d_{\theta _t}, a_t\sim \pi _{\theta _t}} ( {\tilde{\delta }}^i_{t} \psi ^i_{t} | {\mathcal {F}}_{t,1}) + \beta _{\theta ,t} \xi ^i_{t+1,1} + \beta _{\theta ,t} \xi ^i_{t+1,2}]$. For a.s. convergence to the asymptotically stable equilibria set of the ODE Eq. (10) for each $i \in N$, we appeal to Kushner–Clark lemma (see appendix C. 3 of [49] and references therein), and we verify its three main conditions below.

First, note that $\xi _{t+1,2} = o(1)$ since critic converges at the faster time scale, i.e., ${\tilde{\delta }}^i_t \rightarrow {\tilde{\delta }}^i_{t,\theta _t}$ a.s. Next, let $M^{1,i}_t = \sum _{\tau = 0}^t \beta _{\theta ,\tau } \xi ^i_{\tau +1,1}$; then $\{M^{1,i}_t\}$ is a martingale sequence. The sequences $\{z^i_t\}, \{\psi ^i_t\}, \{G^{i^{-1}}_t\}$, and $\{\varphi ^i_t\}$ are all bounded (by assumptions), and so is the sequence $\{\xi _{t,1}^i\}$ (Here $z^i_t = [\mu ^i_t, (\lambda ^i_t)^{\top },(v^i_t)^{\top }]^{\top }$ is the same vector used in the proof of Theorem 4). Hence, $\sum _t {\mathbb {E}}[|| M^{1,i}_{t+1} - M^{1,i}_t||^2 ~|~ {\mathcal {F}}_{t,1}] < \infty$ a.s., so the martingale sequence $\{M^{1,i}_t\}$ converges a.s. [36]. So, for any $\epsilon >0$, we have $\underset{t\rightarrow \infty }{lim}~ {\mathbb {P}}[sup_{p\ge t} || \sum _{\tau =t}^p \beta _{\theta ,\tau }\xi ^i_{\tau ,1}|| \ge \epsilon ] = 0$, as needed.

Regarding continuity of $g^{1,i}(\theta _t) = -G(\theta ^{i}_t)^{-1} {\mathbb {E}}_{s_t\sim d_{\theta _t}, a_t\sim \pi _{\theta _t}} ( {\tilde{\delta }}^i_{t} \psi ^i_{t} | {\mathcal {F}}_{t,1})$, we note that $g^{1,i}(\theta _t) = -G(\theta ^{i}_t)^{-1} \sum _{s_t\in {\mathcal {S}}, a_t\in {\mathcal {A}}} d_{\theta _t}(s_t)\cdot \pi _{\theta _t}(s_t,a_t)\cdot {\tilde{\delta }}^i_{t,\theta _t} \cdot \psi ^i_{t,\theta _t}$. Firstly, $\psi ^i_{t,\theta _t}$ is continuous by assumption X. 1. The term $d_{\theta _t}(s_t)\cdot \pi _{\theta _t}(s_t,a_t)$ is continuous in $\theta ^i_t$ since it is the stationary distribution and solution to $d_{\theta _t}(s)\cdot \pi _{\theta _t}(s,a) = \sum _{s^{\prime }\in {\mathcal {S}}, a^{\prime } \in {\mathcal {A}}} P^{\theta _t}(s^{\prime }, a^{\prime } | s,a) \cdot d_{\theta _t}(s^{\prime })\cdot \pi _{\theta _t}(s^{\prime },a^{\prime })$ and $\sum _{s\in {\mathcal {S}}, a\in {\mathcal {A}}}d_{\theta _t}(s)\cdot \pi _{\theta _t}(s,a) = 1$, where $P^{\theta _t}(s^{\prime }, a^{\prime } | s,a) = P(s^{\prime }| s,a) \cdot \pi _{\theta _t}(s^{\prime },a^{\prime })$. From assumption X. 1, $\pi _{\theta _t}(s,a)>0$ and hence the above set of linear equations has a unique continuous solution in $\theta _t$ by assumption X. 1. Moreover, ${\tilde{\delta }}^i_{t,\theta _t}$ is continuous in $\theta ^i_t$ since $v_{\theta _t}$ as the unique solution to the linear equation $\varPhi ^{\top } D_{\theta }^s[T_{\theta }^V(\varPhi v_{\theta }) - \varPhi v_{\theta }] = 0$ is continuous in $\theta _t$. Thus, $g^{1,i}(\theta _t)$ is continuous in $\theta ^i_t$, as needed in Kushner–Clark lemma. $\square$

4.2 Convergence of AP-MAN Actor-Critic Algorithm

The convergence of critic step, the reward parameters and the objective function estimate are the same as in Theorem 4. So, we show the convergence of advantage parameters and actor updates as given in the AP-MAN algorithm. Similar to the FI-MAN algorithm we again consider the transformed problem; rewards replaced with costs. Thus, the transformed recursion is ${w}^i_{t+1} \leftarrow (I-\beta _{v,t} \psi ^i_t \psi ^{i^{\top }}_t)w^i_t - \beta _{v,t} {\tilde{\delta }}^i_t \psi ^i_t$. Section 4.2 of [49] has proof details.

Theorem 7

Under the assumptions X. 3 and X. 4, for each agent $i\in N$, with actor parameters $\theta ^i$, we have $w_t^i \rightarrow -G(\theta ^i)^{-1} {\mathbb {E}}[{\tilde{\delta }}^i_{t,\theta } \psi ^i_t]$ as $t\rightarrow \infty$ with probability one.

We now consider the convergence of actor update of the AP-MAN algorithm.

Theorem 8

Under the assumptions X. 1 - X. 5, the sequence $\{\theta ^i_t\}$ obtained from the actor step of AP-MAN algorithm converges a.s. to asymptotically stable equilibrium set of ${\dot{\theta }}^i = {\hat{\varGamma }}^i[-G(\theta ^{i})^{-1} {\mathbb {E}}_{s_t\sim d_{\theta }, a_t\sim \pi _{\theta }} ( {\tilde{\delta }}^i_{t,\theta } \psi ^i_{t,\theta })], ~\forall ~i\in N$.

4.3 Convergence of FIAP-MAN Actor-Critic Algorithm

The critic convergence, the convergence of reward parameters, and objective function estimate are the same as in Theorem 4. Like FI-MAN and AP-MAN algorithms, we again consider the transformed problem; rewards are replaced with costs. Therefore, we consider the following recursion: $w^i_{t+1} = (1 - \beta _{v,t})w^i_t - \beta _{v,t} G^{i^{-1}}_t {\tilde{\delta }}^i_t \psi ^i_t$. Again, we refer to Sect. 4.3 of [49] for detailed proofs.

Theorem 9

Under the assumptions X. 3 and X. 4, for each agent $i\in N$, with actor parameters $\theta ^i$, we have $w_t^i \rightarrow -G(\theta ^i)^{-1} {\mathbb {E}}[{\tilde{\delta }}^i_{t,\theta } \psi ^i_t]$ as $t\rightarrow \infty$ with probability one.

Theorem 10

Under assumptions X. 1 - X. 5, the sequence $\{\theta ^i_t\}$ obtained from the actor step of FIAP-MAN algorithm converges a.s. to asymptotically stable equilibrium set of the ODE ${\dot{\theta }}^i = {\hat{\varGamma }}^i[-G(\theta ^{i})^{-1} {\mathbb {E}}_{s_t\sim d_{\theta }, a_t\sim \pi _{\theta }} ( {\tilde{\delta }}^i_{t,\theta } \psi ^i_{t,\theta })],~\forall ~i\in N$.

Remark 5

Though the ODEs corresponding to actor update in all MAN algorithms seem similar, we emphasize that they come from three different algorithms, each with a different critic update implicitly. Moreover, all the three MAN algorithms have their ways of updating the advantage parameters. Also, the objective function $J(\theta )$ can have multiple stationary points and local optima. Thus, all the three algorithms can potentially attain different optima, and this was clearly illustrated in our comprehensive computational experiments in Sect. 5.1. See also the discussion in Sects. 3.4 and 3.5.

To validate the usefulness of our proposed MAN algorithms, we implement them on a bi-lane traffic network and an abstract multi-agent RL model. The detailed computational experiments follow in the next section.

5 Performance of Algorithms in Traffic Network and Abstract MARL Models

This section provides comparative and comprehensive experiments in two different setups. Firstly, we model traffic network control as a multi-agent reinforcement learning problem. A similar model is available in [9] in a related but different context. Another setup is an abstract multi-agent RL model with 15 agents, 15 states, and 2 actions in each state. The model, parameters, rewards, and the linear function approximation features are as given in [18, 53].

All the computations are done in python 3.8 on a machine equipped with 8 GB RAM and an Intel i5 processor. For the traffic network control, we use TraCI, i.e., “Traffic Control Interface.” TraCI uses a TCP-based client/server architecture to provide access to sumo-gui, thereby sumo act as a server [28].

5.1 Performance of Algorithms for Traffic Network Controls

Consider the bi-lane traffic network as shown in Fig. 1. The network consists of $N_1, N_2, S_1,S_2, E_1, E_2, W_1$, and $W_2$ that act as the source and the destination nodes. $T_1, T_2, T_3$, and $T_4$ represents the traffic lights and act as agents. All the edges in the network are assumed to be of equal length. The agent’s objective is to find a traffic signaling plan to minimize the overall network congestion. Note that the congestion to each traffic light is private information and hence not available to other traffic lights.

Fig. 1

A bi-lane traffic network with four traffic lights $T_1,T_2,T_3,T_4$. All the other nodes $N_1, N_2, S_1, S_2, E_1, E_2, W_1$, and $W_2$ act as the source and destination nodes

The sumo-gui requires the user to provide T, the total number of time steps the simulation needs to be performed, and $N_v$, the number of vehicles used in each simulation. As per the architecture of sumo-gui, vehicles arrive uniformly from the interval $\{1,2, \dots , T\}$. Once a vehicle arrives, it has to be assigned a source and a destination node. We assign the source node to each incoming vehicle according to various distributions. Different arrival patterns (ap) can be incorporated by considering different source-destination node assignment distributions. We first describe the assignment of the source node. Two different arrival patterns to capture high or low number of vehicles assigned to the source nodes in the network are taken. Let $p_{s,ap}$ be the probability that a vehicle is assigned a source node s if arrival pattern is ap. Table 1 gives probabilities, $p_{s,ap}$ for two arrival patterns ($ap \in \{1, 2\}$) that we consider. The destination node is sampled uniformly from the nodes except the source node. We assume that vehicles follow the shortest path from the source node to the destination node. However, if there are multiple paths with the same path length, then any one of them can be chosen with uniform probability.

Table 1 Probability $p_{s,ap}$ for source node s and arrival pattern ap. $ap=1$ assigns high probability to $N_2,S_2$ and $E_1,W_1$, whereas $ap=2$ assigns high probability to all north and south nodes $N_1,S_1,N_2,S_2$ in Fig. 1

For $ap=1$, we have higher $p_{s,ap}$ for north–south nodes $N_2, S_2$, and east–west nodes $E_1,W_1$. Thus, we expect to see heavy congestion for traffic light $T_2$; almost same congestion for traffic lights $T_1$ and $T_4$; and the least congestion for traffic light $T_3$. For $ap=2$, more vehicles are assigned to all the north–south nodes. So we expect that all the traffic lights will be equally congested. We now provide the distribution of the number of vehicles assigned to a source node s at time t for a given arrival pattern ap.

Let $N_t$ be the number of vehicles arrived at time t, and $N^s_t$ be the number of vehicles assigned to source node s at time t. Thus, $N_t = \sum _{s} N^s_t$. Note that the arrivals are uniform in $\{0,1,\dots , T\}$, so $N_t$ is a binomial random variable with parameters $\left( N_v,\frac{1}{T} \right)$. Therefore, we have ${\mathbb {P}}(N_t = r) = \left( {\begin{array}{c}N_v\\ r\end{array}}\right) \left( \frac{1}{T}\right) ^r \left( 1-\frac{1}{T}\right) ^{N_v-r},\quad \forall ~r=0,1,\cdots , N_v$. Moreover, using the law of total probability, for all $ap~\in \{1,2\}$, we obtain

$$\begin{aligned} {\mathbb {P}}(N^s_t = k ~|~ ap) = \left( {\begin{array}{c}N_v\\ k\end{array}}\right) \left( \frac{p_{s,ap}}{T}\right) ^k \left( 1-\frac{p_{s,ap}}{T}\right) ^{N_v-k}, ~ \forall ~k=0,1,\cdots , N_v, \end{aligned}$$

(11)

i.e., the distribution of $N_t^s$ for a given arrival pattern ap is also binomial with parameters $\left( N_v, \frac{p_{s,ap}}{T}\right)$. More details on above probability are available in Appendix B.2.3 of [49].

In our experiments, we take $T= 180000$ seconds which is divided into simulation cycle (called decision epoch) of $T_c = 120$ seconds each. Thus, there are 1500 decision epochs. The number of vehicles are taken as $N_v = 50000$.

5.1.1 Decentralized Framework for Traffic Network Control

In this section, we model the above traffic network control as a fully decentralized MARL problem with traffic lights as agents, $N = \{T_1,T_2, T_3, T_4\}$. Let $E_{in} = \{e_1, e_2, e_{12}, e_{16}, e_3, e_4, e_9, e_{15}, e_8, e_7, e_{11}, e_{13}, e_5, e_6, e_{10}, e_{14}\}$ be the set of edges directed toward the traffic lights. Let the maximum capacity of each lane in the network be $C = 50$. The state-space of the system consists of the number of vehicles in the lanes belonging to $E_{in}$. Hence, the size of the state space is $50^{16}$. At every decision epoch, each traffic light follows one of the following traffic signal plans for the next $T_c = 120$ simulation steps.

• 1. Equal green time of $\frac{T_c}{2}$ for both north–south and east–west lanes

• 2. $\frac{3T_c}{4}$ green time for north–south and $\frac{T_c}{4}$ green time for east–west lanes

• 3. $\frac{T_c}{4}$ green time for north–south and $\frac{3T_c}{4}$ green time for east–west lanes.

Thus, the total number of actions available at each traffic light is $3^4 = 81$. The rewards given to each agent is equal to the negative of the average number of vehicles stopped at its corresponding traffic light. Note that the rewards are privately available to each traffic light only. We aim to maximize the expected time average of the globally averaged rewards, which is equivalent to minimize the (time average of) number of stopped vehicles in the system. Since the state space is huge $(50^{16})$, we use the linear function approximation for the state value function and the reward function. The approximate state value for state s is $V(s;v) = v^{\top } \varphi (s)$, where $\varphi (s) \in {\mathbb {R}}^{L},~ L<< |{\mathcal {S}}|$, is the feature vector for the state s. Moreover, the reward function is approximated as ${R}(s,a;\lambda ) = \lambda ^{\top } f(s,a)$ where $f(s,a)\in {\mathbb {R}}^M,~ M<< |{\mathcal {S}}||{\mathcal {A}}|$ are the features associated with each state-action pair (s, a). Next, we describe these features [9].

Let $x_t^i$ denote the number of vehicles in lane $e_i \in E_{in}$ at time t. We normalize $x_t^i$ via maximum capacity of a lane C to obtain $z_t^i = x_t^i / C$. We define $\xi (s) = \left( \begin{matrix}z_t^1,&z_t^2,&\cdots ,&z_t^{16},&z_t^1 z_t^2,&\cdots ,&z_t^6 z_t^5,&z_t^1 z_t^2 z_t^{12},&\cdots ,&z_t^5 z_t^6 z_t^{10} \end{matrix} \right)$ as a vector having components containing $z_t^i$, as well as components with products of two or three $z_t^i$’s. The product terms are of the form $z_t^i z_t^j$ and $z_t^i z_t^j z_t^l$, where all terms in the product correspond to the same traffic light. The feature vector $\varphi (s)$ is defined as having all the components of $\xi (s)$ along with an additional bias component, 1. Thus, $\varphi (s) = \left( \begin{matrix} 1,&\xi (s)\end{matrix} \right) ^{\top }$. The length of the feature vector $\varphi (s)$ is $L = 1 + (16+4\times (4^2 + 4^3)) = 337$.

For each agent $i\in N$, we parameterize the local policy $\pi ^i(s,a^i)$ using the Boltzmann distribution as $\pi ^i_{\theta ^i}(s,a^i) = \frac{\exp (q^{\top }_{s,a^i} \cdot \theta ^i)}{\sum _{b^i\in {\mathcal {A}}^i} \exp (q^{\top }_{s,b^i}\cdot \theta ^i)}$, where $q_{s,b^i}\in {\mathbb {R}}^{m_i}$ is the feature vector of dimension same as $\theta ^i$, for any $s \in {\mathcal {S}}$ and $b^i\in {\mathcal {A}}^i$, for all $i\in N$. The feature vector is $q_{s,a^i} = \left( 1, ~a^{i,1} \xi (s),~ a^{i,2} \xi (s), ~ a^{i,3} \xi (s) \right) ^{\top }, ~\forall ~ i\in N$, where $\xi (s)$ is defined as earlier, and $a^{i,j}$ is 1 if signal plan j is selected in action $a^i$ by agent $i\in N$, and 0 otherwise. The length of $q_{s,a^i}$, i.e., $m_i = 3\times 336+1 = 1009$. For the Boltzmann policy function $\pi ^i_{\theta ^i}(s,a^i)$, we have $\nabla _{\theta ^i} \log \pi ^i_{\theta ^i} (s, a^i) = q_{s,a^i} - \sum _{b^i\in {\mathcal {A}}^i} \pi ^i_{\theta ^i} (s, b^i) q_{s,b^i}$, where $\nabla _{\theta _i} \log \pi ^i_{\theta _i}(s, a^i)$ are the compatible features as in the policy gradient Theorem [46]. Note that the compatible features are same as the features associated to policy, except normalized to be mean zero for each state. The features f(s, a) for the rewards function are similar to $q_{s,a^i}$ for each $i\in N$, thus $M = 4\times 3\times 336 + 1 = 4033$.

We implement all the three MAN algorithms and compared the average network congestion with the MAAC algorithm. For all $i\in {N}$, the initial value of parameters $\mu ^i_0$, ${\tilde{\mu }}^i_0$, $v^i_0$, ${\tilde{v}}^i_0$, $\lambda ^i_0$, ${\tilde{\lambda }}^i_0$, $\theta ^i_0$, $w^i_0$ are taken as zero vectors of appropriate dimensions. The Fisher information matrix inverse, $G_0^{i^{-1}}$, is initialized to $I, ~ \forall ~ i\in N$. The critic and actor step-sizes are taken as $\beta _{v,t} = \frac{1}{(t+1)^{0.65}}$, and $\beta _{\theta ,t} = \frac{1}{(t+1)^{0.85}}$, respectively. These step-sizes satisfy the Robbins–Monro conditions. We assume that the communication graph ${\mathcal {G}}_t$ is a complete graph at all time instances t and $c_t(i,j)=\frac{1}{4}$ for all pairs i, j of agents. Although we do not use the eligibility traces in the convergence analysis, we use them ($\lambda = 0.25$ for TD($\lambda$) [45]) to provide better performance in case of function approximations. We believe that the convergence of MAN algorithms while incorporating eligibility traces is easy to follow, so we avoid them here.

5.1.2 Performance of Traffic Network for Arrival Pattern 1

Recall, for arrival pattern 1 we assign high probability $p_{s,ap}$ to the source nodes $N_2,S_2$ and $E_1,E_2$ and low probability to other source nodes. Table 2 provides the average network congestion (averaged over 10 runs, and round off to 5 decimal places), standard deviation and 95% confidence interval.

Table 2 Average network congestion, standard deviation and 95% confidence interval for arrival pattern 1. FIAP-MAN has $\approx$ 18%, and FI-MAN has $\approx$ 14% less congestion than MAAC algorithm. The congestion for the AP-MAN algorithm is almost the same as the MAAC algorithm with high confidence

We observe an $\approx$ 18% reduction in average congestion for FIAP-MAN and $\approx$ 14% reduction for FI-MAN algorithms compared to the MAAC algorithm. These observations are theoretically justified in Sect. 3.4.

To show that these algorithms have attained the steady state, we provide average congestion, and the correction factor (CF), i.e., the 95% confidence value which is defined as $CF = 1.96 \times \frac{std~dvn}{\sqrt{10}}$ for last 200 decision epochs in Table 8 of Appendix B.2.1 of [49]. The average network congestion for the MAN algorithms are almost (up to 1st decimal) on decreasing trend w.r.t. network congestion; however, this decay is prolonged (0.1 fall in congestion in 200 epochs), suggesting the convergence of these algorithms to local minimum. Thus, we see that algorithms involving the natural gradients dominate those involving standard gradients. Figure 2 shows the (time) average network congestion for single run (thus lower the better).

Fig. 2

(Time) average network congestion of all the algorithms with ap 1. The congestion is least for FIAP-MAN and FI-MAN algorithms. However, MAAC and AP-MAN algorithms have almost the same congestion. For a few initial decision epochs $\approx$ 180, all the algorithms have almost the same performance, but afterward, they find different directions and ends in different optima

For almost 180 decision epochs, all the algorithms have the same (time) average network congestion. However, after 180 decision epochs, FI-MAN and FIAP-MAN follow different paths and hence find different local minima as shown in Theorem 3. We want to emphasize that the Theorem 3 is for maximization framework. As given in Sect. 5.1.1, we are also maximizing the globally average rewards, which is equivalent to minimizing the (time average of) number of stopped vehicles.

5.1.3 Actor Parameter Comparison for Arrival Pattern 1

Recall, in Theorem 3, we show that under some conditions $J({\tilde{\theta }}^N_{t+1}) \ge J({\tilde{\theta }}^M_{t+1})$, for all $t\ge t_0$, and hence at each iterate the average network congestion in FI-MAN, and FIAP-MAN algorithms are better than MAAC algorithm. To investigate this further, we plot the norm of difference of the actor parameter of all the three MAN algorithms with MAAC algorithm for each agent. For traffic light $T_1$ (or agent 1), these differences are shown in Fig. 3 (for other agents see Fig. 8 in Appendix B.2.1 of [49]).

Fig. 3

Norm of difference in the actor parameter of agent 1 for all the 3 MAN algorithms with MAAC algorithm for arrival pattern 1. Figure (a) is shown for 350 decision epochs; to show that the differences in the actor parameter are from decision epoch 2 itself, we zoom it in figure (b) in the left panel. However, the significant differences are observed only after $\approx$ 180 epochs. This illustrates Theorem 3 and related discussions in Sect. 3.4

We observe that all the three MAN algorithms pick up $\theta _2$ (i.e., the actor parameter at decision epoch 2) that is different from that of the MAAC scheme at varying degrees, with FI-MAN being a bit more “farther.” However, a significant difference is observed around decision epoch $\approx 180$. For better understanding, the same graphs are also shown in the logarithmic scale for agent 1 and agent 2 with arrival pattern 1 in Fig. 4.

Fig. 4

Norm of differences of the actor parameters for agents 1 and 2 with traffic arrival pattern 1 in logarithmic scale illustrating Theorem 3 and related discussions in Sect. 3.4

We see that the norm difference is linearly increasing in FI-MAN and FIAP-MAN algorithms, whereas it is almost flat for the AP-MAN algorithm. So, the iterates of these 2 algorithms are exponentially separating from those of the MAAC algorithm. This again substantiates our analysis in Sect. 3.4.

Though we aim to minimize the network congestion, in Table 3, we also provide the average congestion and the correction factor (CF) to each traffic light for last decision epoch (Table 8 in Appendix B.2.1 shows these values for last 200 decision epochs). Expectedly, the average congestion for traffic light $T_2$ is highest; it is almost same for traffic lights $T_1,T_4$; and least for $T_3$.

Table 3 Average congestion and correction factor (CF) for each traffic light for arrival pattern 1 (described in Sect. 5.1.2). CF is defined as $1.96 \times \frac{std~dvn}{\sqrt{10}}$

5.1.4 Performance of Traffic Network for Arrival Pattern 2

In arrival pattern 2, the traffic origins $N_1, N_2, S_1$ and $S_2$ have higher probabilities of being assigned a vehicle. We take $p_{s,ap}$ for these nodes as $\frac{3}{14}$, and for all other nodes, it is $\frac{1}{28}$. So, we expect almost the same average congestion to all the traffic lights. This observation is reported in Appendix B.2.2 of [49]. Table 4 provides the average network congestion (averaged over 10 runs, and round off to 5 decimal places), standard deviation and 95% confidence interval for arrival pattern 2.

Table 4 Average network congestion, standard deviation and 95% confidence interval at last decision epoch for arrival pattern 2 (described in Sect. 5.1.3). FI-MAN and FIAP-MAN algorithms has $\approx$ 25% less average network congestion than MAAC algorithm. The performance of AP-MAN algorithm is almost similar to MAAC algorithm as shown in Theorem 3 and in Sect. 3.4

We observe an $\approx$ 25% reduction in the average congestion with FI-MAN and FIAP-MAN algorithms as compared to the MAAC algorithm. AP-MAN is on par with the MAAC algorithm. This again shows the usefulness of the natural gradient-based algorithms. As opposed to ap 1 where FIAP-MAN algorithm has slightly better performance than FI-MAN algorithm, in ap 2, both algorithms have almost similar average network congestion. Moreover, the standard deviation in ap 1 is much higher than in ap 2. Figure 5 shows the (time) average congestion for single simulation run of all the algorithms.

Fig. 5

(Time) average network congestion for arrival pattern 2. For few initial decision epochs $\approx$ 180 all the algorithms have almost same performance, but afterward they find different directions, and hence ends in different optima

5.1.5 Actor Parameter Comparison for Arrival Pattern 2

Similar to arrival pattern 1, in Fig. 6, we plot the norm of the difference for traffic light $T_1$ (for other traffic lights (agents) see Fig. 9 of [49]). For better understanding, the same graphs are also shown for agent 1 and 2 in the logarithmic scale in Fig. 7 of [49]. Again, we see that the norm difference is linearly increasing in FI-MAN and FIAP-MAN algorithms, whereas it is almost flat for the AP-MAN algorithm. So, the iterates of these 2 algorithms are exponentially separating from the MAAC algorithm. This again substantiates our analysis in Sect. 3.4. Moreover, we also compute the average congestion and (simulation) correction factor for each traffic light. Table 5 of [49] shows these values for last decision epoch (See Table 9 for last 200 decision epochs). As expected, the average congestion to each traffic light is almost the same.

Fig. 6

Norm of difference in the actor parameter of agent 1 for all the 3 MAN algorithms with MAAC algorithm. Figure (a) is shown for 350 decision epochs; to show that the differences in the actor parameter are from decision epoch 2 itself, we zoom it in Figure (b). However, the significant differences are observed only after $\approx$ 180 epochs

We now present another computational experiment where we consider an abstract MARL with $n=15$ agents. The model, algorithm parameters, including transition probabilities, rewards, and features for state value function, and rewards are the same as given in [18, 53]

5.2 Performance of Algorithms in Abstract MARL Model

The abstract MARL model that we consider consists of $n=15$ agents and $|{\mathcal {S}}| = 15$ states. Each agent $i\in N$ is endowed with the binary valued actions ${\mathcal {A}}^i \in \{0,1\}$. Therefore, the total number of actions are $2^{15}$. Each element of the transition probability is a random number uniformly generated from the interval [0, 1]. These values are normalized to incorporate the stochasticity. To ensure the ergodicity, we add a small constant $10^{-5}$ to each entry of the transition matrix. The mean reward $R^i(s,a)$ are sampled uniformly from the interval [0, 4] for each agent $i\in N$, and for each state-action pair (s, a). The instantaneous rewards $r^i_t$ are sampled uniformly from the interval $[R^i(s,a)-0.5, R^i(s,a) + 0.5]$. We parameterize the policy using the Boltzmann distribution with $m_i = 5, ~ \forall ~i\in N$. All the feature vectors (for the state value and the reward functions) are sampled uniformly from the set [0, 1] of suitable dimensions. The following table compares the globally averaged return from all the three MAN actor-critic algorithms with the MAAC algorithm. The globally averaged rewards are almost close to each other. To provide more details we also compute the relative V values for each agent $i\in N$ that is defined as $V_{\theta }(s;v^i) = v^{i^\top } \varphi (s)$; this way of comparison of MARL algorithms was earlier used by [53]. Thus, the higher the value, the better is the algorithm. More details of model and computations are available in Appendix B.1 of [49].

Table 5 Globally averaged rewards, standard deviation and 95% confidence for all the algorithms for the abstract multi-agent RL problem. We observe that globally averaged rewards and standard deviation are almost same for all the algorithms with high confidence. All the values are averaged over 25 runs

6 Related Work

Reinforcement learning has been extensively studied and explored by researchers because of its varied applications and usefulness in many real-world applications [16, 17, 21]. Single-agent reinforcement learning models are well-explained in many works including [5, 6, 45]. The average reward reinforcement learning algorithms are available in [19, 30].

Various algorithms to compute the optimal policy for single-agent RL are available; these are mainly classified as off-policy and on-policy algorithms in the literature [45]. Moreover, because of the large state and action space, it is often helpful to consider the function approximations of the state value functions [46]. To this end, actor-critic algorithms with function approximations are presented in [27]. In actor-critic algorithms, the actor updates the policy parameters, and the critic evaluates the policy’s value for the actor parameters until convergence. The convergence of linear architecture in actor-critic methods is known. The algorithm in [27] uses the standard gradient while estimating the objective function. However, as mentioned in Sect. 2, we outlined some drawbacks of using standard gradients [31, 42].

To the best of our knowledge, the idea of natural gradients stems from the work of [3]. Afterward, it has been expanded to learning setup in [2]. For recent developments and work on natural gradients we refer to [31]. Some recent overviews of natural gradients are available in [13] and lecture slides by Roger Grosse.² The policy gradient theorem involving the natural gradients is explored in [26]. For the discounted reward [1, 33] recently showed that despite the non-concavity in the objective function, the policy gradient methods under tabular setting with softmax policy characterization find the global optima. However, such a result is not available for average reward criteria with actor-critic methods and the general class of policy. Moreover, we also see in our computations in Sect. 5.1 that MAN algorithms are stabilizing at different local optima. Actor-critic methods involving the natural gradients for single-agent are available in [7, 40]. On the contrary, we deal with the multi-agent setup where all agents have private rewards but have a common objective. For a comparative survey of the MARL algorithms, we refer to [15, 50, 52].

The MARL algorithms given in [52] are majorly centralized, and hence relatively slow. However, in many situations [16, 17] deploying a centralized agent is inefficient and costly. Recently, [53] gave two different actor-critic algorithms in a fully decentralized setup; one based on approximating the state-action value function and the other approximating the state value function. Another work in the same direction is available in [24, 32, 44, 51]. In particular, for distributed stochastic approximations, authors in [32] introduced and analyzed a non-linear gossip-based distributed stochastic approximation scheme. We use some proof techniques as part of consensus updates from it. We build on algorithm 2 of the [53] and incorporate the natural gradients into it. The algorithms that we propose use the natural gradients as in [7]. We propose three algorithms incorporating natural gradients into multi-agent RL based on Fisher’s information matrix inverse, approximation of advantage parameters, or both. Using the ideas of stochastic approximation available in [11, 12, 29], we prove the convergence of all the proposed algorithms.

7 Discussion

This paper proposes three multi-agent natural actor-critic (MAN) reinforcement learning algorithms. Instead of using a central controller for taking action, our algorithms use the consensus matrix and are fully decentralized. These MAN algorithms majorly use the Fisher information matrix and the advantage function approximations. We show the convergence of all the three MAN algorithms, possibly to different local optima.

We prove that a deterministic equivalent of the natural gradient-based algorithm dominates that of the MAAC algorithm under some conditions. It follows by leveraging a fundamental property of the Fisher information matrix that we show: the minimum singular value is within the reciprocal of the dimension of the policy parameterization space.

The Fisher information matrix in the natural gradient-based algorithms captures the KL divergence curvature between the policies at consecutive iterates. Indeed, we show that the KL divergence is proportional to the objective function’s gradient. The use of natural gradients offered a new representation to the objective function’s gradient in the prediction space of policy distributions which improved the search for better policies.

To demonstrate the usefulness of our algorithm, we empirically evaluate them on a bi-lane traffic network model. The goal is to minimize the overall congestion in the network in a fully decentralized fashion. Sometimes the MAN algorithms can reduce the network congestion by almost $\approx 25\%$ compared to the MAAC algorithm. One of our natural gradient-based algorithms, AP-MAN, is on par with the MAAC algorithm. Moreover, we also consider an abstract MARL with $n=15$ agents; again, the MAN algorithms are at least as good as the MAAC algorithm with high confidence.

We now mention some of the further possibilities. Firstly, some assumptions on the communication network can be relaxed [48]. A careful study of the trade-off between extra per iterate computation versus the gain in the objective function value of the learned MARL policy obtained by these MAN algorithms would be useful. It is in the context of a similar phenomenon in optimization algorithms [13, 37] and other computational sciences.

Moreover, further understanding of the natural gradients and its key ingredient, the Fisher information matrix $G(\theta )$, is needed in their role as learning representations. Our uniform bound on the smallest singular value of $G(\theta )$ and its role in the dominance of deterministic MAN algorithms are initial results in these directions. More broadly, various learning representations for RL like natural gradients and others are further possibilities.