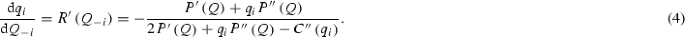Abstract
We consider a model of evolutionary competition between adjustment processes in the Cournot oligopoly model and investigate the effect of increasing the number of firms. Our focus is on Nash play versus a general short-memory adaptive adjustment process. We find that, although Nash play has a stabilizing influence, a sufficient increase in the number of firms in the market tends to make the Cournot-Nash equilibrium unstable. This shows that the famous result by Theocharis (Rev Econ Stud 1960), that Cournot oligopoly markets are unstable for more than three firms, is robust, although the instability threshold increases in the presence of Nash firms. We establish that both the existence and the level of this threshold depend on the information costs associated with Nash play. Moreover, the interaction between adjustment processes naturally leads to the emergence of complicated endogenous fluctuations as the number of firms increases, even when demand and costs are linear.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The seminal work by Palander [36] and Theocharis [45] shows that, in a quantity-setting game with firms using the Cournot [14] adjustment process,Footnote 1 the Cournot-Nash equilibrium becomes unstable as the number of firms increases.Footnote 2 In fact, with linear demand and constant marginal costs, the Cournot-Nash equilibrium looses stability and bounded but perpetual oscillations arise already for triopoly (\(n=3\)). For more than three firms, oscillations grow until the nonnegativity price and demand constraints become effective. Other short-term learning processes, such as gradient learning (see, e.g., Arrow and Hurwicz [6]) also tend to be less stable if the number of firms on a market increases. However, the assumption underlying these conventional adjustment processes, that rivals will not revise their output from the last period, is continuously invalidated outside equilibrium and has been criticized as a consequence (see, e.g., Seade [42], Al-Nowaihi and Levine [3]). An alternative to these intuitive, but simple, adaptive processes is the more sophisticated model where firms have full knowledge of the demand function and of their own and their opponents’ cost functions and coordinate on the Cournot-Nash equilibrium instantaneously.Footnote 3 The price for the resulting stability is that these more sophisticated models put much higher demands on the cognitive capacities of the players. It seems reasonable that in a market where all firms use the same adjustment process a tendency exists for some firms to change to another type of behavior—either to avoid structural decision making errors in an unstable environment or to save on cognitive efforts in a stable environment. In this paper, we therefore introduce a model that presents a middle ground between these alternatives by allowing firms to use different adjustment processes and switch between those on the basis of past performance, as in, e.g., Brock and Hommes [10] and Droste et al. [20]. Our aim is to study whether the classic instability result by Palander [36] and Theocharis [45] will survive in an environment where firms can switch to more sophisticated adjustment processes when market dynamics are volatile and simple adjustment processes do not perform well.
We focus in particular on the interaction between a single short-memory adjustment process and Nash behavior, where the latter refers to firms that have correct expectations about the choices of the other firms, and are able to coordinate on the corresponding equilibrium.Footnote 4 That is, we consider a large population of firms of which a fraction \(\rho _{t}\) are Nash firms in period t, and the remaining firms use the short-memory adjustment process. Every period firms are randomly matched in groups of n firms to play the Cournot oligopoly game. By averaging over all groups, where groups typically differ in their composition of adjustment processes, we can express the dynamics of the population-wide average individual supply of non-Nash players, \(q_{t}\), as a function of the fraction of Nash players in the previous period, \(\rho _{t-1}\), and the average individual supply of non-Nash players in the previous period, \(q_{t-1}\). Similarly, by letting the fraction of Nash players, \(\rho _{t}\), evolve according to their performance relative to the non-Nash players in the previous period, it can be expressed as a function of \(q_{t-1}\) and \(\rho _{t-1}\) as well. The model therefore gives rise to a system of two first-order nonlinear difference equations, of which the fixed point corresponds to the Cournot-Nash equilibrium.
We find that the classic instability result of Theocharis [45] is quite robust: it persists under endogenous switching between adjustment processes. However, the presence of Nash firms increases the threshold number of firms that triggers instability. This threshold number of firms furthermore varies with the information costs for Nash firms and with the level of evolutionary pressure between the different adjustment processes. As the number of firms increases, a period-doubling route to chaos typically arises, and the model might exhibit complicated but bounded dynamics, a feature not present in the original model of Theocharis [45]. These fluctuations have a smaller amplitude than the fluctuations that would emerge when all firms use the short-memory adjustment process, but they are more erratic and less predictable and arise naturally from the interaction of two opposing forces. If the fraction of Nash firms is sufficiently high, the Cournot-Nash equilibrium will be stable. This induces firms to switch to a short-memory adjustment process that gives similar market profits, but does not require as much cognitive effort. As a sufficiently large fraction of the population of firms uses this short-memory adjustment process, the Cournot-Nash equilibrium becomes unstable and quantities start fluctuating. When these fluctuations are sufficiently large, firms are attracted to Nash play, which stabilizes the dynamics again, and so on.
To some extent, our approach is supported by findings from laboratory experiments with human subjects. In particular, neither the Cournot-Nash equilibrium nor the predictions of less sophisticated short-memory adjustment processes describe the data from these experiments convincingly. Rassenti et al. [40], for example, present an experiment on a Cournot oligopoly with linear demand, constant (but asymmetric) marginal costs and five firms, implying that the Cournot-Nash equilibrium is unstable under best-reply dynamics. Indeed, they find that aggregate output persistently oscillates around the equilibrium and does not converge. Individual behavior, however, is not explained very well by best-reply dynamics. Huck et al. [28] discuss a linear (and symmetric) Cournot oligopoly experiment with four firms. Instead of diverging quantities, as predicted by best-reply dynamics, they find that the time average of quantities converges to the Cournot-Nash equilibrium quantity, although there is substantial volatility around this equilibrium throughout the experiment. Interestingly, Huck et al. [28] find that a process where participants mix between best-replying and imitating the previous period’s average quantity describes participants’ behavior best. This supports our model of heterogeneous adjustment processes.
Our paper extends the literature on the stability of the Cournot-Nash equilibrium that emerged in response to Theocharis [45] by considering switching between adjustment processes. It also contributes to a separate but related literature on complicated dynamics and endogenous fluctuations in Cournot oligopoly. This literature typically considers Cournot duopolies with non-monotonic reaction functions that are postulated ad hoc (Rand [39]), derived from iso-elastic demand functions together with substantial asymmetries in marginal costs (Puu [37]) or derived from cost externalities (Kopel [30]) and shows that best-reply dynamics might result in periodic cycles and chaotic behavior. For these models with non-monotonic reaction curves, complicated behavior might also arise for other adjustment processes (see, e.g., [1, 9]). Although non-monotonic reaction curves cannot be excluded on economic groundsFootnote 5 complicated behavior in our model emerges in a much more natural fashion and perpetual but bounded fluctuations occur even for linear demand and cost curves.
Finally, our work is closely related to Droste et al. [20] who investigate evolutionary competition between best-reply dynamics and Nash play in a Cournot duopoly with linear demand and quadratic costs, but there are several important differences with respect to that earlier work.Footnote 6 First, whereas in Droste et al. [20], as in the vast majority of other contributions in this field, the number of firms in the market is given and fixed, we analyze the effect on the dynamics—for fixed values of the other (demand, cost and behavioral) parameters—of an increase in the number of firms. This is particularly relevant in light of the original results from Palander [36] and Theocharis [45] that show that under homogeneous best-reply an increase in the number of firms is destabilizing. It is therefore very natural to study the robustness of that result under the presence of more sophisticated behavior and evolutionary competition. To the best of our knowledge, this has not been done before. Second, and related to the first point, Droste et al. [20] find that complicated dynamics are only possible in their Cournot duopoly model when the production function satisfies strong increasing returns to scale. That is, firm’s cost functions should be sufficiently concave, or marginal costs should be decreasing sufficiently fast. Although there might be markets for specific products that satisfy this condition, it nevertheless corresponds to a rather special case. In particular, this condition implies the existence of multiple Cournot-Nash equilibria (a symmetric interior equilibrium and two asymmetric boundary equilibria where one of the firms has a monopoly and the other firm is inactive). Moreover, it gives rise to a perverse and counterintuitive comparative statics effect: instead of increasing the Cournot-Nash equilibrium price, as one would expect, an exogenous increase in demand reduces the equilibrium price. The model studied in the current paper does not require such a special and non-typical feature and works both for increasing and decreasing marginal costs, as well as for the textbook case of linear demand and constant marginal costs. It therefore generalizes the results from Droste et al. [20] to a much wider range of market structures.Footnote 7 The third difference with Droste et al. [20] is that the latter uses the (noisy) replicator dynamics as a model of evolutionary competition, whereas the current paper employs a different class of evolutionary models, which includes (but is not restricted to) the discrete choice model. Both approaches model evolutionary selection between adjustment processes, but the mechanisms are different. In particular, the replicator dynamics—which can be derived from a process of pairwise imitation—inhibits adjustment processes to spread quickly through the population of firms. With the class of evolutionary processes studied here this is much easier, because the adoption of an adjustment process only depends upon its relative performance and not on the fraction of firms currently using that process. As a consequence, the two types of evolutionary processes give rise to similar local stability results, but (at least for the economic model studied here) the global dynamics of the models is quite different. Under the noisy replicator dynamics, typically the dynamics, when the equilibrium is unstable, are attracted to a period two cycle or are explosive, whereas the discrete choice model exhibits a much wider range of possible complicated behaviors, including cycles with a high period and strange attractors that give rise to complicated and erratic endogenous fluctuations.
The rest of the paper is organized as follows. Section 2 briefly reviews short-memory adjustment processes in the general symmetric n-player Cournot model. Section 3 introduces a Cournot population game where firms can choose between Nash play and a general short-memory adjustment process and Sect. 4 illustrates the global dynamics of this model for the Cournot oligopoly game with Nash play versus best-reply dynamics for linear demand and constant marginal costs. Section 5 provides a short discussion. The Appendix contains the proofs of our two main results.
2 Short-Memory Adjustment Processes in Cournot Oligopoly
Consider a Cournot oligopoly with n firms supplying a homogeneous commodity.Footnote 8 The inverse demand function \(P\left( Q\right) \) is nonnegative, nonincreasing and, whenever it is strictly positive, twice continuously differentiable. Here \(Q=\sum _{i=1}^{n}q_{i}\) is aggregate output,where \(q_i\) denotes production of firm i. The cost function \(C\left( q_{i}\right) \) is twice continuously differentiable and the same for every firm. Moreover, \(C\left( q_{i}\right) \ge 0\) and \(C^{\prime }\left( q_{i}\right) \ge 0\) for every \(q_{i}\).
Each firm wants to maximize instantaneous profits \(P\left( Q_{-i} +q_{i}\right) q_{i}-C\left( q_{i}\right) \), where \(Q_{-i}=\sum _{j\ne i}q_{j}=Q-q_{i}\). This gives the following first-order condition for an interior solution
with second-order condition for a local maximum given by \(2P^{\prime }\left( Q_{-i}+q_{i}\right) +q_{i}P^{\prime \prime }\left( Q_{-i}+q_{i}\right) -C^{\prime \prime }\left( q_{i}\right) \le 0\).
The first-order condition (1) implicitly defines the best-reply correspondence or reaction curve:
We assume that a symmetric Cournot-Nash equilibrium \(q^{*}\), that is, the solution to \(q^{*}=R\left( \left( n-1\right) q^{*}\right) \), exists and is strictly positive and unique.Footnote 9 Aggregate equilibrium production is then given by \(Q^{*}=nq^{*}\).
The key question is: how do firms learn to play \(q^{*}\)? One approach is to assume that firms have complete information about their environment and are able to coordinate on the Nash equilibrium instantaneously. As an alternative, we consider short-memory adaptive adjustment processes with the following general structure
That is, the firm’s current production decision depends upon its own choice and the aggregate choices of the other firms from the previous period. We make the following assumption on the adjustment process (3), where \(F_{q}^{*}=\left. \frac{\partial F\left( q,Q_{-i}\right) }{\partial q}\right| _{\left( q^{*},\left( n-1\right) q^{*}\right) }\) and \(F_{Q}^{*}=\left. \frac{\partial F\left( q,Q_{-i}\right) }{\partial Q_{-i}}\right| _{\left( q^{*},\left( n-1\right) q^{*}\right) }\) denote the partial derivatives of F, evaluated at the Cournot-Nash equilibrium.
Assumption A
For all n, the adjustment process (3) satisfies (i) \(F\left( q^{*},\left( n-1\right) q^{*}\right) =q^{*}\), (ii) \(\left| F_{q}^{*}\right| <1\), \(F_{Q}^{*}\in \left( -1,-\delta \right) \), where \(0<\delta <1\) is a strictly positive constant, and \(F_{q}^{*}-F_{Q}^{*}<1\).
Part (i) of Assumption A ensures that the Cournot-Nash equilibrium quantity corresponds to a steady state of the adjustment process. Part (ii) puts some natural restrictions on the partial derivatives of F which facilitate stability of adjustment process (3). In particular, note that either \(\left| F_{q}^{*}\right| >1\) or \(F_{Q}^{*}<-1\) would make the adjustment process inherently unstable: a small change in q or \(Q_{-i}\) in the previous time period, respectively, would then bring about a larger change in q in the current period. Similarly, \(F_{q}^{*}-F_{Q}^{*}>1\) would imply that a redistribution of production from \(Q_{-i}\) to q in the current period additionally increases next period’s output q by more than that redistribution. The assumption that \(F_{Q}^{*}\) is negative and bounded away from zero makes sense because quantities are strategic substitutes.
A number of well-known adjustment processes can be represented by (3).Footnote 10 Probably best known is the best-reply dynamics (see, e.g., Theocharis [45]) which assumes that firms best-reply to the aggregate quantity of the other firms from the previous period, that is
Note that we have \(F_{q}^{*}=0\) and \(F_{Q}^{*}=R^{\prime }\left( Q_{-i}^{*}\right) \), which is indeed typically negative.Footnote 11 The closely related adaptive best-reply dynamics (see, e.g., Fisher [21] ), where firms move in the direction of their best reply, can be written as \(F\left( q,Q_{-i}\right) =\alpha R\left( Q_{-i}\right) +\left( 1-\alpha \right) q_{i}\), with \(\alpha \in \left( 0,1\right] \) and where \(F_{q}^{*}=1-\alpha \) and \(F_{Q}^{*}=\alpha R^{\prime }\left( Q_{-i}^{*}\right) \). Another variation is suggested in Huck et al. [28], where it is found that participants to a laboratory experiment use a weighted average of best-reply and imitation.
Another famous adjustment process is gradient learning (see, e.g., Arrow and Hurwicz [6] and Bischi et al. [7]) where firms adapt their decision in the direction of increasing profits, that is
with \(\lambda >0\) the speed of adjustment parameter.Footnote 12 Here \(F_{Q}^{*} =\lambda \left[ P^{\prime }\left( Q^{*}\right) +q^{*}P^{\prime \prime }\left( Q^{*}\right) \right] \) and \(F_{q}^{*}=1+\lambda \left[ 2P\left( Q^{*}\right) +q^{*}P^{\prime \prime }\left( Q^{*}\right) -C^{\prime \prime }\left( q^{*}\right) \right] \), where \(F_{q}^{*}<1\) follows from the second-order condition for a local maximum and \(F_{Q}^{*}<0\) holds under the familiar condition that the inverse demand function is “not too convex” (see footnote 11).
Besides these benchmark adjustment processes, many other processes obey the general form (3), such as local monopolistic approximationFootnote 13 or imitating the average (although the latter does not satisfy part (i) of Assumption A). Some other adjustment processes, such as fictitious play and least squares learning (see, e.g., Anufriev et al. [5]), cannot be represented by (3).
The next proposition characterizes when the Cournot-Nash equilibrium is stable, given that all firms use the same adjustment process (3).Footnote 14
Proposition 1
Let all firms use adjustment process (3). The symmetric Cournot-Nash equilibrium \(\left( q^{*},\ldots ,q^{*}\right) \) is locally stable if
Proposition 1 suggests that the Cournot-Nash equilibrium becomes unstable, under adjustment process (3), if the number of firms increases sufficiently. In particular, a sufficient condition for instability is \(\left| F_{q}^{*}+\left( n-1\right) F_{Q}^{*}\right| >1\), which gives the following instability threshold
The intuition is that individual firms, who choose their production level partly on the basis of last period’s aggregate production of the other firms, do not take into account that those other firms also adjust their production level. Obviously, disregarding other firms’ adjustments will have a larger effect when there are more firms in the market (or when \(\left| F_{Q}^{*}\right| \) is higher) and eventually destabilizes the Cournot-Nash equilibrium. For example, with linear demand and costs, the slope of the resulting linear reaction curve equals \(-\frac{1}{2}\). This means that if one firm deviates from the equilibrium by producing one additional unit, under best-reply dynamics every other firm responds by decreasing its own production by half a unit. Consequently, for \(n>3\) the aggregate reduction in production is larger than the earlier increase in production, which renders the dynamics unstable. Similarly, for gradient learning with a speed of adjustment \(\lambda \) low enough to induce convergence to the Cournot-Nash equilibrium when the number of firms is small, a sufficient increase in the number of firms will destabilize the dynamics.
Since \(F_{Q}^{*}\) typically depends upon n through \(q^{*}\), in principle a market structure could exist with the property that \(F_{Q}^{*}\) decreases in n faster than \(\frac{1}{n}\), meaning that (3) may converge to the Cournot-Nash equilibrium for any number of firms. However, such a market structure seems unlikely and, to the best of our knowledge, has not been considered in the literature.Footnote 15 The assumption that \(F_{Q}^{*}\) is bounded away from zero therefore seems innocuous.
3 Evolutionary Competition Between Adjustment Processes
Proposition 1 establishes that dynamic behavior under adjustment processes of the form (3) is quite different from more sophisticated adjustment processes, such as Nash play or fictitious play, particularly when the number of firms in the market is large. However, the latter typically require more cognitive effort. In this section, we introduce an evolutionary competition between the different adjustment processes. For this, we model our Cournot oligopoly as a population game. That is, we consider a large population of firms from which in each period groups of n firms are sampled randomly to play the one-shot n-firm Cournot oligopoly. Firms may use different adjustment processes, and they switch between these processes according to a general, monotone selection dynamic, capturing the idea that an adjustment process that performs better is more likely to spread through the population of firms. In this paper, we focus on the interaction between Nash play and a single short-memory adjustment process of the form (3). Denote by \(\rho _{t}\in \left[ 0,1\right] \) the fraction of Nash firms in the population in period t, with a fraction \(1-\rho _{t}\) using the short-memory adjustment process—from here on we will refer to the latter as F-firms. After each period, the fraction \(\rho _{t}\) is updated and the random matching procedure is repeated.
First consider the decision of a Nash firm that knows the fraction of Nash firms in the population and the production decision of the F-firms, but does not know the exact composition of firms in its market (or it has to make a production decision before observing this). This firm forms expectations over all possible mixtures resulting from independently drawing \(n-1\) other players from a large population, each of which is either a Nash firm or a F-firm. Nash firm i therefore chooses quantity \(q_{i}\) such that the objective function
is maximized. Here \(q^{N}\) is the (symmetric) output level of each of the other Nash firms, and \(q_{t}\) is the output level of each F-firm, which is given by (3). Assuming that F-firms respond to the industry-wide average quantity from the previous period, the quantities they set will be symmetric (provided all of them start out with the same quantity \(q_{0}\)), see Eq. (8) below. The first-order condition for an optimum is characterized by equality between marginal cost and expected marginal revenue. We assume that, given the value of \(q_{t}\), all Nash firms coordinate on the same output level \(q^{N}\). The first-order condition, with \(q_{i}=q^{N}\), reads
Let the solution to (7) be given by \(q^{N}=H\left( q_{t},\rho _{t}\right) \).Footnote 16 Note that if the F-firms play the Cournot-Nash equilibrium quantity \(q^{*}\), or if all firms are Nash firms, then Nash firms will produce \(q^{*}\) as well, that is \(H\left( q^{*},\rho _{t}\right) =q^{*}\), for all \(\rho _{t}\) and \(H\left( q_{t},1\right) =q^{*}\) for all \(q_{t}\). Moreover, a Nash firm that is certain it will only meet F-firms plays a best-reply to current aggregate output of these F-firms, that is \(H\left( q_{t},0\right) =R\left( \left( n-1\right) q_{t}\right) \), for all \(q_{t}\).
We assume that F-firms know the average quantity \({\overline{q}}_{t-1}\) played across the population of firms in period \(t-1\). We therefore obtain
with the output of a Nash firm in period t given by \(q_{t}^{N}=H\left( q_{t},\rho _{t}\right) \).
The evolutionary competition between adjustment processes is driven by the profits they generate. Taking into account that a Nash firm meets between 0 and \(n-1\) other Nash firms, expected profits for a Nash firm are given by
where \(q^{N}\) and q are the (symmetric) quantities set by Nash firms and F-firms, respectively. Expected profits \(\Pi _{F}\left( q^{N},q,\rho \right) \) for an F-firm can be determined in a similar manner. If the population of firms and the number of groups of n firms drawn from that population are large enough, average profits will be approximated quite well by these expected profits, which we will use as a proxy for average profits from now on. In addition, because the information requirements for Nash play are substantially higher than those for short-memory adjustment processes, we allow for differences in information or deliberation costs \(\kappa _{N},\kappa _{F}\ge 0\) required to implement these types of behavior. Performance of Nash and F-firms is then evaluated according to \(V_{i} =\Pi _{i}-\kappa _{i}\) where \(i=N,F\).
The fraction \(\rho _{t}\) of Nash firms evolves endogenously according to a dynamic which is an increasing function of the performance differential between the two adjustment processes, that is
where \(\kappa \equiv \kappa _{N}-\kappa _{F}\) is the difference in deliberation costs, which we—given the information requirements for Nash play in a heterogeneous environment—assume to be nonnegative.Footnote 17 The map \(G: {\mathbb {R}} \rightarrow \left[ 0,1\right] \) is a continuously differentiable, monotonically increasing function with \(G\left( 0\right) =\frac{1}{2}\), \(\lim _{x\rightarrow -\infty }G\left( x\right) =0\) and \(\lim _{x\rightarrow \infty }G\left( x\right) =1\). One possible choice for \(G\left( \cdot \right) \) that satisfies these properties is the discrete choice model, \(G\left( x\right) =\left[ 1+\exp \left( -\beta x\right) \right] ^{-1}\), see Anderson et al. [4]. This model is based on stochastic choice of firms, who observe performance of the different adjustment processes and tend to choose the better performing process with a higher probability. This model is very popular in heterogeneous agent models (see, e.g., Brock and Hommes [10]) and in the literature on quantal response equilibria (see, e.g., McKelvey and Palfrey [33]), and we will use this specification in Sect. 4. It is straightforward to generalize this approach to allow for other (and more than two) adjustment processes, or to let it depend upon performance of these processes from earlier periods.
The dynamics of the quantities and fractions are governed by Eqs. (8) and (10). The steady state of this dynamic system is \(\left( q^{*},\rho _{\kappa }\right) \), where \(q^{*}\) is the Cournot-Nash equilibrium quantity, and \(\rho _{\kappa }=G\left( -\kappa \right) \) is the fraction of Nash firms at the steady state. Because market profits are the same in equilibrium, this fraction depends only on the difference in deliberation costs. We have the following stability result:
Proposition 2
Let \(P^{\prime }\left( Q^{*}\right) +q^{*}P^{\prime \prime }\left( Q^{*}\right) <0\). Then the equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) of the model with evolutionary competition between Nash play and the short-memory adjustment process (3) is locally stable if:
and unstable if
Note that it follows from condition (11) that for a sufficiently large fraction of Nash firms the Cournot-Nash equilibrium will be stable. On the other hand, from rearranging condition (12), we find that a sufficient condition for instability is
Note that the right-hand sides of conditions (6) and (13) are the same, but that the left-hand side of (13) is smaller than n [the left-hand side of (6)], provided \(-1\le R^{\prime }\left( Q_{-i}^{*}\right) \le 0\). Introducing Nash firms in an environment with F-firms therefore has a stabilizing effect.
In the next section, we will see that instability is still possible and that the model with interaction between Nash play and a short-memory adjustment process may actually give rise to complicated and unpredictable dynamics. Before we go into that, however, a remark on the evolutionary process (10) is in order, since it does not include the well-known replicator dynamics. These replicator dynamics—developed by evolutionary biologists (see [26] and [44]), but also applied to many evolutionary economic models—can be derived from a model of imitation, see, e.g., Gale et al. [24] or Schlag [41]. For our case, the standard replicator dynamics is given as:
For \(\kappa >0\) the model consisting of (8) and (14) has two equilibria, \(\left( q^{*},0\right) \) and \(\left( q^{*},1\right) \), both of which are unstable if the market with only F-firms is unstable. Because in equilibrium Nash firms and F-firms do not coexist, the standard replicator dynamics does not seem to be a suitable model to study the stabilizing effect of an increase in the fraction of Nash firms. This issue can be addressed by introducing noisy decision making in the replicator dynamics (see, e.g., [20] and [22, 24]), which gives rise to
Here each period a fraction \(2\delta \) of the population chooses between the adjustment processes randomly (with equal probability) and independent of past performance. For this specification of the replicator dynamics, there will be a unique equilibrium \(\left( q^{*},\rho _{\delta }\right) \), with \(\rho _{\delta }\in \left( 0,1\right) \). As \(\delta \) decreases (or as \(\kappa \) increases), \(\rho _{\delta }\) decreases and for \(\rho _{\delta }\) small enough (and n high enough) the equilibrium will be unstable. The local stability properties for the model with the noisy replicator dynamics will therefore be similar to that of the model we study here, although the global dynamics is typically different, see the discussion in the next section. Note that the economic interpretation of the replicator dynamics is also different from that of models of the form (10), such as the discrete choice model. The former relies upon (pairwise) imitation which implies that if one adjustment process performs better than the other, but is initially used by only a small fraction of the population (that is, \(\rho _{t}\) is close to 0 or 1), it may take quite some periods for that adjustment process to be used by almost all firms. In contrast, for models of the form (10) almost the full population may switch to the better performing adjustment process in only one period. Since in oligopolistic markets firms may arguably perform some kind of (possibly restricted) optimization, instead of simply imitating another firm, we have a slight preference for models of the form (10) as a description of how firms choose adjustment processes.
4 Nash Play Versus Best-Reply: Global Dynamics and Perpetual Bounded Fluctuations
In this section, we study the global dynamical behavior of the model discussed in Sect. 3 where for the short-memory adjustment process we take the best-reply dynamics, \(F\left( q_{i},Q_{-i}\right) =R\left( Q_{-i}\right) \). This choice is supported by evidence from laboratory experiments that suggests that best-reply dynamics is relevant in human decision making. Cox and Walker [15], for example, present an experiment on Cournot duopoly with linear demand and quadratic costs where participants’ quantity choices fail to converge to the (interior) Cournot-Nash equilibrium when that equilibrium is unstable under best-reply dynamics. Also Rassenti et al. [40] and Huck et al. [28] find that a Cournot-Nash equilibrium that is unstable under best-reply dynamics will not be reached by human subjects.
Applying Proposition 2 to best-reply dynamics (that is, \(F_{q}^{*}=0\) and \(F_{Q}^{*}=R^{\prime }\left( Q_{-i}^{*}\right) <0\)) and using \(\rho _{0}=\frac{1}{2}\), we find that the Cournot-Nash equilibrium is locally stable for any number of firms if there are no information costs for Nash play:
Corollary 3
Let \(P^{\prime }\left( Q^{*}\right) +q^{*} P^{\prime \prime }\left( Q^{*}\right) <0\). Then the equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) of the model of endogenous switching between Nash play and best-reply dynamics is locally stable if
Moreover, in the absence of a difference in information costs, \(\kappa =0\), the equilibrium \(\left( q^{*},\rho _{0}\right) \) is locally stable for all \(n\ge 2\).
To investigate global dynamics, we need to specify the demand and cost structure, as well as the switching mechanism. We will use linear demand \(P\left( Q\right) =a-bQ\), and costs, \(C_{i}\left( q_{i}\right) =cq\), with \(a>c\ge 0\) and \(b>0\). The reaction curve then becomes
with \(q^{*}=\frac{a-c}{b\left( n+1\right) }\) the unique Cournot-Nash equilibrium. Furthermore, given \(q_{t}\) and \(\rho _{t}\), Nash firms in period t coordinate on the solution to Eq. (7) which is
It can be easily checked that \(q_{t}=R\left( \left( n-1\right) \left( \rho _{t-1}H\left( q_{t-1},\rho _{t-1}\right) \right) +\left( 1-\rho _{t-1}\right) q_{t-1}\right) =H\left( q_{t-1},\rho _{t-1}\right) =q_{t-1}^{N}\), that is, in each period best-reply firms produce the quantity that Nash firms produced in the period before, illustrating the information advantage of the latter. From Eq. (18), we see that Nash firms respond to best-reply firms by choosing a high (low) production level when production of best-reply firms is low (high) in that period.Footnote 18 Nash firms therefore partially neutralize the instability created by best-reply firms. However, if the equilibrium fraction \(\rho _{\kappa }\) of Nash firms in the population is too small, or the number of firms n in a market sufficiently large, the Cournot-Nash equilibrium will still be unstable, as can be seen by condition (16) which, for the current specification, reduces to
We model evolutionary competition by the discrete choice dynamics (see, e.g., Brock and Hommes [10]):
The parameter \(\beta \ge 0\) measures the intensity of choice: for a higher value of \(\beta \), firms are more likely to switch to the more successful adjustment process from the previous period. A straightforward computation shows that the profit difference is given by
Note that, abstracting from information costs \(\kappa \), average profits of Nash firms are always higher than those of the best-reply firms. The difference increases with the deviation of \(q_{t}\) from its equilibrium value and decreases with the fraction of Nash firms. The full model with endogenous switching between Nash and best-reply behavior is
with the equilibrium given by \(\left( q^{*},\rho _{\kappa }\right) =\left( \frac{a-c}{b\left( n+1\right) },\left[ 1+\exp \left[ \beta \kappa \right] \right] ^{-1}\right) \). This equilibrium is locally stable when condition (19) holds.
This condition is always satisfied for \(n\le 3\), but for \(n>3\) the Cournot-Nash equilibrium becomes unstable if the fraction of Nash firms in equilibrium is too low, with the critical value for \(\rho \) given by
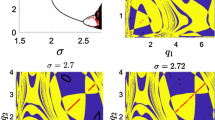
Upper panel: stability curve for Nash versus best-reply firms in (\(\beta \kappa \), n) space. When the stability curve is crossed from below the interior Cournot-Nash equilibrium loses stability and a two-cycle is born. Lower panel: stability curves for Nash play versus gradient learning, for different values of \(\rho _{\kappa }\). (This case is briefly discussed in Sect. 5)
As is already clear from Corollary 3, the equilibrium is always locally stable in the absence of information costs, \(\kappa =0\) (note that \({\overline{\rho }}<\rho _{0}=\frac{1}{2}\) for all n). However, for any \(n>3\) there exists an intensity of choice \(\beta \) and information costs \(\kappa \) such that the equilibrium becomes unstable, because the fraction of Nash firms in equilibrium is too small. In fact, the equilibrium is unstable for all \(n\ge 4\) when \(\rho _{\kappa }<\frac{1}{6}\), that is, whenever \(\beta \times \kappa >\ln 5\approx 1.609\).
The trade-off between evolutionary pressure and the number of firms n in the market for which the equilibrium is stable is illustrated in the upper panel of Fig. 1. This figure plots the period-doubling bifurcation curve, where, for convenience, we interpret n as a continuous variable.Footnote 19 For combinations of \(\beta \kappa \) and n to the northeast of the curve the equilibrium is unstable.
The dynamics can become quite complicated when the equilibrium is unstable. Figure 2 shows the results of some representative numerical simulations of the model with \(a=17\), \(b=1\), \(c=10\), \(\beta =5\) and \(\kappa =\frac{1}{2}\). Note that in this case \(\rho _{\kappa }=\left[ 1+\exp \left[ \frac{5}{2}\right] \right] ^{-1}\approx 0.076\) and the equilibrium will be unstable for any \(n>3\). Panel (a) shows a bifurcation diagram for \(n=2\) to \(n=20\), with the composite variable \(q_{t}+\rho _{t}\) on the vertical axis.Footnote 20 The main dynamic scenario as n increases is a so-called period-doubling bifurcation route to chaos. The equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) becomes unstable through a period-doubling bifurcation at \(n\approx 3.36\). At this primary bifurcation, an attracting period two cycle is created. This period two cycle undergoes a period-doubling bifurcation itself at \(n\approx 6.04\). Two coexisting and stable period four cycles emerge from that secondary bifurcation. In \(\left( q,\rho \right) \)-space, these cycles are symmetric to each other with respect to the vertical line at \(q=q^{*}\).Footnote 21 Because for some values of n the initial condition \(\left( q_{0},\rho _{0}\right) \) lies in the so-called basin of attraction of one period four cycle, whereas for slightly different values of n it lies in the basin of attraction of the other period four cycle, the bifurcation diagram in panel (a) of Fig. 2 gives the impression that for many values of n (roughly between 9 and 15) the dynamics converges to a period eight cycle, although this in fact illustrates the coexistence of two period four cycles. At \(n\approx 15.70\) each of these period four cycles undergoes another period-doubling bifurcation leading to the emergence of two coexisting attracting period eight cycles. This sequence of period-doubling bifurcations continues, creating coexisting period 16 cycles (emerging at \(n\approx 17.19\)) and coexisting period 32 cycles (emerging at \(n\approx 17.51\)) and eventually leading to two coexisting four piece attractors, characterized by complicated aperiodic dynamics. At approximately \(n\approx 18.55\), these two attractors merge into one large attractor which is symmetric with respect to \(q=q^{*}\) and has a complicated geometric structure. The dynamics of the model exhibits other features as well. For example, for values of n approximately between 6.64 and 8.76 a two-piece complicated attractor exists, which does not emerge from the two period four cycles (see panel (e) of Fig. 2 for \(n=8\)).
The obvious caveat to the discussion above is that the dynamics are only meaningful if the parameter n, representing the number of firms in the market, takes on an integer value. Therefore, not necessarily all types of behavior presented in Panel (a) of Fig. 2 and discussed above can be observed. For example, period 16 or period 32 cycles do not appear for integer values of n. However, by varying another parameter of the model, such as \(\beta \) or \(\kappa \), we can also observe dynamic behavior that arises for non-integer values of n in panel (a) of Fig. 2. To illustrate consider the left panel of Fig. 3, which considers a bifurcation diagram for \(\kappa \) running from 0.47 to 0.53, with \(n=17\) and all other parameters the same as in Fig. 2. The left panel of Fig. 3 shows that at \(\kappa =0.47\) the dynamics is attracted to a period four cycle and as \(\kappa \) increases to the dynamics undergoes a number of period-doubling bifurcations leading to a complicated attractor when \(\kappa =0.53\). To illustrate this bifurcation scenario in a bit more detail, the right panel of Fig. 3 zooms in on one point of the period four cycle from the left panel. From this panel, it follows that the period four cycle undergoes a standard period-doubling bifurcation scenario as \(\kappa \) increases, including cycles of period 16, 32 and so on. Figure 3 suggests that we can obtain the behavior that arises for non-integer values of n also from choosing an integer value of n, combined with varying one or more other parameters (that can take on real values).
Linear n-player Cournot game with Nash versus best-reply firms. Panel a depicts a sequence of period-doubling bifurcations as the number of players n increases. Instability sets in already for the triopoly game. Panels b–d display oscillating time series of the quantity chosen by the best-reply firm, the profit differential (net of information costs \(\kappa =0.5\)) and the fraction of Nash firms, respectively. The threshold fraction of Nash firms \(\rho =5/14\) for which the dynamics become stable is also marked in Panel (d). A typical phase portrait is shown in Panel e while Panel f plots the largest Lyapunov exponent for increasing \(\beta \). Game and behavioral parameters: \(n=8, a=17,b=1,c=10, \kappa =0.5, \beta =5\)
Panels (b–d) in Fig. 2 show the dynamics of quantities, profit differences and fractions for \(n=8\), respectively.Footnote 22 Note that close to the equilibrium (in fact, when \(\left| q_{t}-q^{*}\right| <\frac{1}{9}\sqrt{2}\left( 1+\frac{7}{2}\rho _{t}\right) \)) best-reply firms do better than Nash firms because they do not have to pay information costs and the difference in average market profits is relatively small. This decreases the fraction of Nash firms, which destabilizes the quantity dynamics. As the dynamics moves away from the equilibrium, eventually Nash firms outperform best-reply firms and more firms become Nash firms again, increasing \(\rho _{t}\). Now, when \(\rho _{t}>{\overline{\rho }}=\frac{5}{14}\) (the horizontal dashed line in panel (d)) the quantity dynamics stabilizes again and quantities converge to their Cournot-Nash equilibrium level, and the whole story repeats. Panel (f) shows that, for \(n=8,\) the largest Lyapunov exponent tends to be strictly positive if the intensity of choice \(\beta \) is high enough, indicating chaotic behavior.
Linear n-player Cournot game with Nash versus best-reply firms. For a fixed number of players \(n=17\), panel a depicts a 4-cycle of the composite variable \(q+\rho \) and its subsequent period-doubling bifurcation with respect to the information costs \(\kappa \). Panel b zooms in the bifurcation scenario for one particular point of the 4-cycle. Game and behavioral parameters: \(n=17, a=17,b=1,c=10, \beta =5\)
We conclude this section with a brief discussion of the dynamics when evolutionary competition is modeled by the replicator dynamics, instead of the discrete choice model. For the standard replicator dynamics (14), there will be two equilibria for \(\kappa >0\), one with only Nash firms and one with only best-reply firms.Footnote 23 Both equilibria will be unstable for \(n>3\). The noisy replicator dynamics (15) has a unique equilibrium, which is interior, and which becomes unstable if the noise parameter \(\delta \) becomes small enough. As the equilibrium becomes unstable, the dynamics is either attracted to a stable period two cycle or it is explosive. More complicated dynamics only appear to occur in a very small region of the parameter space. This is an important difference with respect to the model in Droste et al. [20], which also uses (15) but typically gives rise to different types of complicated behavior for \(\delta \) small enough.Footnote 24
5 Discussion
In this paper, we introduced a model of evolutionary competition between different adjustment processes in Cournot oligopoly. We focused on the interaction between Nash play and a single adaptive adjustment process. The availability of Nash play stabilizes the dynamics: although the Cournot-Nash equilibrium will typically still be unstable if the number of firms is sufficiently high, the stability threshold increases. For the special case of Nash play versus best-reply dynamics, we find that the Cournot-Nash equilibrium is locally stable for any number of firms if, in the equilibrium of the evolutionary model, at least half of the population of firms uses Nash play.Footnote 25 However, this does not generalize to other adjustment processes. The lower panel of Fig. 1 shows stability curves for Nash play versus gradient learning (for the case of linear demand and costs) where the horizontal axis shows the normalized speed of adjustment parameter \(b\lambda \) and the vertical axis shows the number of firms n.Footnote 26 The lowest curve demarcates the stability region when all firms use gradient learning (for combinations of \(b\lambda \) and n to the northeast of this curve the Cournot-Nash equilibrium is unstable) and the highest curve characterizes stability in the case where, in equilibrium, half of the population consists of Nash firms. It follows immediately that the stability region increases with \(\rho _{\kappa }\), although, even for \(\rho _{\kappa }=\rho _{0}=\frac{1}{2}\) (and \(b\lambda >\frac{1}{2}\)), one can always find a number of firms n such that the Cournot-Nash equilibrium is unstable.
For the case of Nash play versus best-reply dynamics, the dynamics of the evolutionary model can give highly irregular, perpetual but bounded fluctuations, even if demand and costs are linear. Complicated dynamics have been established in Cournot models before, but typically require non-monotonic reaction curves, which are not standard, or very specific cost structures, as in Droste et al. [20]. In our model, the bounded fluctuations are created naturally, in a wide range of market structures, by the interaction of different adjustment processes and the increase in the number of firms.
The analysis provided in this paper can be extended by considering other adjustment processes, although this will lead to qualitatively similar results.Footnote 27 In addition, our local stability results are robust against changing the switching mechanism to the noisy replicator dynamics, and simulations suggest that the global dynamics are similar to those of the noisy exponential replicator dynamics. Finally, continuous-time processes typically generate stable equilibria for a wide array of adjustment processes,Footnote 28 at least for Cournot oligopoly with linear demand and costs and an arbitrary number of firms. It remains an open question whether continuous-time processes with evolutionary competition between adjustment processes can generate complicated dynamics in such an environment.
Notes
Firms employ a Cournot adjustment process, also referred to as best-reply dynamics, whenever they take the last period’s aggregate output of their rivals as a predictor for the current period choices of those rivals and best-respond to it.
The Cournot-Nash equilibrium is also supported by relatively sophisticated long-memory adjustment processes. For example, fictitious play (see Brown [11]), which asserts that each player best-replies to the empirical distribution of the opponents’ past record of play, converges to the Cournot-Nash equilibrium for a large set of demand-cost structures (see, e.g., Deschamp [18] and Thorlund-Petersen [46]).
Note that the equilibrium the Nash firms coordinate on typically only coincides with the Cournot-Nash equilibrium if firms using the short-memory adjustment process also choose the Cournot-Nash equilibrium quantity—see the discussion of Nash play in a heterogeneous environment in Sect. 3.
Corchon and Mas-Colell [13] show that any type of behavior can emerge for continuous-time gradient (or best-reply) dynamics in heterogeneous oligopoly, although Furth [23] argues that for homogeneous Cournot oligopoly there are certain restrictions as to what behavior can arise. Relatedly, Dana and Montrucchio [16] show that in a duopoly model where firms maximize their discounted stream of future profits and play Markov perfect equilibria—and therefore are rational—any behavior is possible for small discount factors.
See Ochea [35] for an analysis of the model from Droste et al. [20] with a larger selection of adjustment processes. Other recent contributions employing this framework are Bischi et al. [8] and Cerboni Baiardi et al. [12] who study evolutionary competition between local monopolistic approximation on the one hand and best-reply dynamics and gradient dynamics on the other hand, respectively, and Kopel et al. [31] and De Giovanni and Lamantia [17], who study evolutionary competition between different types of objective functions for firms (profit maximizing firms versus socially concerned firms and profit maximizing firms versus firms that take revenues into account as well, respectively).
Moreover, the present paper is also more general than Droste et al. [20] in two other directions. Where the main focus of Droste et al. [20] is on evolutionary competition, modelled by the noisy replicator dynamics, between Nash firms and best-reply firms, in this paper we focus on competition between Nash firms and a more general short-run adjustment process under a general set of evolutionary processes.
For a thorough treatment of the Cournot oligopoly game under general demand and cost structures, we refer the reader to Bischi et al. [7].
Sufficient conditions for the existence and uniqueness of the Cournot-Nash equilibrium are that \(P\left( \cdot \right) \) is twice continuously differentiable, nonincreasing and concave on the interval where it is positive and that \(C\left( \cdot \right) \) is twice continuously differentiable, nondecreasing and convex, see Szidarovszky and Yakowitz [43]. For more general conditions on existence and uniqueness, see, e.g., Novshek [34] and Kolstad and Mathiesen [29], respectively.
Bischi et al. [7] provide a systematic analysis of a variety of adjustment processes in Cournot oligopoly games.
From the first-order condition (1), we find that
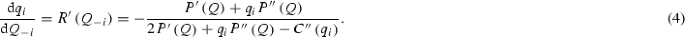
Note that the second-order condition for a local maximum implies that the denominator, evaluated at the Cournot-Nash equilibrium, is negative. Typically the numerator is also negative (although this is not necessarily the case if the inverse demand function is sufficiently convex), and therefore, we generally have \(R^{\prime }\left( Q_{-i}^{*}\right) <0\).
In a more general version of the gradient dynamics, the speed of adjustment is a function of the quantity, \(\lambda \left( q_{i}\right) \).
The idea behind local monopolistic approximation is that every firm estimates a linear demand curve on the basis of his last observed price-quantity combination and the slope of the inverse demand function at that quantity in the last period. It then uses this estimated demand function to determine its perceived profit maximizing quantity. For constant marginal costs c, this gives rise to adjustment process
$$\begin{aligned} F\left( q,Q_{-i}\right) =\frac{1}{2}q-\frac{1}{2}\frac{P\left( q+Q_{-i}\right) -c}{P^{\prime }\left( q+Q_{-i}\right) }. \end{aligned}$$Recall that the local stability properties of the fixed point of a nonlinear dynamical system are qualitatively the same as those of the linearized system, provided that the fixed point is hyperbolic (that is, the Jacobian matrix has no eigenvalues on the unit circle), see, e.g., Kuznetsov [32]. Such a fixed point is locally stable (a sink) if all eigenvalues of the Jacobian matrix (evaluated at that fixed point) lie within the unit circle, and the fixed point is unstable either when all eigenvalues lie outside the unit circle (the fixed point is then called a source) or when at least one eigenvalue lies outside the unit circle, and at least one eigenvalue lies inside the unit circle (the fixed point is then called a saddle).
For the specification of Theocharis [45], with linear inverse demand function and constant marginal costs the reaction curve is linear with a constant slope that is independent of n. For an iso-elastic inverse demand function and constant marginal costs, the slope of the reaction curve, evaluated at the Cournot-Nash equilibrium, does depend upon n. In this case, the Cournot-Nash equilibrium is unstable under best-reply dynamics for \(n\ge 5\) (see [2] and [38]). Puu [38] provides an example for which the best-reply dynamics do remain stable when n increases, but he assumes that the cost function of each firm depends directly upon the number of firms n: as the number of firms increases the capacity of each individual firm is reduced, increasing its marginal costs.
Note that in general the solution to (7) does not necessarily have to be unique, although it will be unique under the standard assumptions of nondecreasing marginal costs and concave inverse demand. If, for some \(q_{t}\) and \(\rho _{t}\), there are multiple solutions to (7) we assume that the Nash firms are able to identify which of these solutions corresponds to the global maximum of their profit function and coordinate on this solution, which we then refer to as \(H\left( q_{t},\rho _{t}\right) \).
Note that \(\kappa \) does not necessarily only represent the difference in information costs; it could also capture a predisposition towards (or away from) Nash play.
In fact, the production level of Nash firms will lie between \(q^{*}\) and \(R\left( \left( n-1\right) q_{t}\right) \). To be specific, for \(\rho \in \left( 0,1\right) \) and \(q_{t}\ne q^{*}\) we either have \(R\left( \left( n-1\right) q_{t}\right)<H\left( q_{t},\rho \right)<q^{*}<q_{t}\) or \(R\left( \left( n-1\right) q_{t}\right)>H\left( q_{t},\rho \right)>q^{*}>q_{t}\).
For a discussion on these period-doubling thresholds for more general adjustment processes, i.e., adaptive expectations and fictitious play, see Chapter IV in Ochea [35].
We choose to plot \(q_{t}+\rho _{t}\) on the vertical axis for the following reason. For a large range of values of n, the dynamics of the model converges to a period four cycle of the type \(\left\{ \left( q_{1},\rho _{1}\right) ,\left( q_{2},\rho _{2}\right) ,\left( q_{3},\rho _{3}\right) ,\left( q_{4},\rho _{4}\right) \right\} =\ \{ \left( a,x\right) ,\left( b,x\right) ,\left( c,y\right) ,\left( b,y\right) \}\). That is, although the period four cycle consists of four different points in \(\left( q,\rho \right) \)-space, it is characterised by only three distinct q-values and two distinct \(\rho \)-values. Plotting q (or \(\rho \)) on the vertical axis of panel (a) of Fig. 2 would therefore suggest the existence of a period three (period two) cycle. The composite variable \(q+\rho \) does take on four distinct values along the period four cycle, and we therefore prefer that variable as a presentation of the dynamics.
Denoting by \(x_{t}=q_{t}-q^{*}\) the deviation of the quantity from its Nash equilibrium level, we can write (21) as \(\left( x_{t},\rho _{t}\right) =\left( {\tilde{H}}\left( x_{t-1},\rho _{t-1}\right) ,{\tilde{G}}\left( x_{t-1},\rho _{t-1}\right) \right) \), with \({\tilde{H}}\left( x,\rho \right) =-\frac{\left( 1-\rho \right) \left( n-1\right) }{2+\left( n-1\right) \rho }x\) and \({\tilde{G}}\left( x,\rho \right) =G\left( x+q^{*},\rho \right) \). It is easily checked that this map has a so-called reflection symmetry with respect to \(x=0\). That is, \(\left( {\tilde{H}}\left( -x,\rho \right) ,{\tilde{G}}\left( -x,\rho \right) \right) =\left( -{\tilde{H}}\left( x,\rho \right) ,\tilde{G}\left( x,\rho \right) \right) \) for all x and \(\rho \). This implies that if an attractor of this dynamical system is not symmetric with respect to \(x=0\) (or \(q=q^{*}\)), that is, if it includes the point \(\left( x_{0},\rho _{0}\right) \) but not the point \(\left( -x_{0},\rho _{0}\right) \), then another attractor must exist (which does include the latter point). For more on the properties of dynamical systems with symmetries, see Golubitsky et al. [25] for an overview and Tuinstra [47] for an application to economics.
Observe that the dynamics of quantities have a smaller amplitude and are much less regular than they would be under pure best-reply dynamics. In that case (under symmetric initial conditions), individual quantities would fluctuate in a period-two cycle between 0 and \(\frac{1}{2}\left( n+1\right) q^{*}\).
For \(\kappa =0\) the combination \(\left( q^{*},\rho \right) \) is an equilibrium of the model for any \(\rho \in \left[ 0,1\right] \). The dynamics will then always end up in an equilibrium with \(\rho >{\overline{\rho }}\).
The exponential replicator dynamics (see, e.g., [8, 12, 19, 27, 31]) is a popular variation of the replicator dynamics. Applying the noisy version of the exponential replicator dynamics, given by
$$\begin{aligned} \rho _{t}=\delta +\left( 1-2\delta \right) \rho _{t-1}\left[ \rho _{t-1}+\left( 1-\rho _{t-1}\right) \exp \left( -\beta \left[ V_{N,t-1}-V_{F,t-1}\right] \right) \right] ^{-1}, \end{aligned}$$to our model gives a complicated period-doubling route to chaos, comparable to the dynamics under the discrete choice model, when \(\delta \) decreases (or when n, \(\beta \) or \(\kappa \) increase).
One would expect the number of Nash firms to be lower in equilibrium however, since in equilibrium best-reply firms can free ride on the Nash firms: they produce the same quantity, but do not incur the high information costs.
Gradient learning, for \(P\left( Q\right) =a-bQ\) and \(C\left( q\right) =cq\), is given by
$$\begin{aligned} q_{i,t+1}=\left( 1-2b\lambda \right) q_{i,t}+\lambda \left[ a-c-bQ_{-i,t} \right] . \end{aligned}$$Note that \(\left| F_{q}^{*}\right| <1\), from Assumption A, requires \(b\lambda <1\). The critical value for n implied by stability condition (11) then becomes
$$\begin{aligned} n^{GD}=\frac{2-b\lambda -\rho _{\kappa }}{b\lambda -\rho _{\kappa }}. \end{aligned}$$The equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) is locally stable as long as \(b\lambda \le \rho _{\kappa }\). For any \(\rho _{\kappa }<1\) and \(b\lambda \in \left( \rho _{\kappa },1\right) \) we can always find n large enough such that the equilibrium is unstable. In particular, in the absence of information costs for Nash play, the equilibrium will be unstable for \(n>\left( 3-2b\lambda \right) /\left( 2b\lambda -1\right) \) and \(b\lambda >1/2\).
For example, we could use our framework to study evolutionary competition between imitation and best-reply dynamics (which is the combination of adjustment processes found in the laboratory experiment presented in Huck et al. [28]). When a fraction \(\rho _{t}\) of the population imitates last period’s average and a fraction of \(1-\rho _{t}\) uses best-reply, the average quantity produced evolves as \({\overline{q}} _{t}=\rho _{t}{\overline{q}}_{t-1}+\left( 1-\rho _{t}\right) R\left( \left( n-1\right) {\overline{q}}_{t-1}\right) \). The equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) is stable if and only if \(\left| \rho _{\kappa }+\left( 1-\rho _{\kappa }\right) \left( n-1\right) R^{\prime }\left( \left( n-1\right) q^{*}\right) \right| <1\). In absence of information costs (\(\kappa =0\) and \(\rho _{0}=\frac{1}{2}\)) and with linear demand and costs we obtain that the Cournot-Nash equilibrium is locally stable in this setting for \(n\le 7\).
See Bischi et al. [7, p. 90] for the stability analysis of two continuous-time adjustment processes: best-reply with adaptive expectations and partial adjustment towards the best-reply with naive expectations.
References
Agiza H, Bischi G, Kopel M (1999) Multistability in a dynamic Cournot game with three oligopolists. Math Comput Simul 51:63–90
Ahmed E, Agiza H (1998) Dynamics of a Cournot game with n-competitors. Chaos Solitons Fract 9:1513–1517
Al-Nowaihi A, Levine P (1985) The stability of Cournot oligopoly model: a reassessment. J Econ Theory 35(2):307–321
Anderson S, de Palma A, Thisse J (1992) Discrete choice theory of product differentiation. MIT Press, Cambridge
Anufriev M, Kopányi D, Tuinstra J (2013) Learning cycles in Bertrand competition with differentiated commodities and competing learning rules. J Econ Dyn Control 37(12):2562–2581
Arrow KJ, Hurwicz L (1960) Stability of the gradient process in n-person games. J Soc Ind Appl Math 8(2):280–294
Bischi G, Chiarella C, Kopel M, Szidarovszky F (2010) Nonlinear oligopolies: stability and bifurcations. Springer, Heidelberg
Bischi G, Lamantia F, Radi D (2015) An evolutionary Cournot model with limited market knowledge. J Econ Behav Organ 116:219–238
Bischi G, Naimzada A, Sbragia L (2007) Oligopoly games with local monopolistic approximation. J Econ Behav Organ 62:371–388
Brock W, Hommes CH (1997) A rational route to randomness. Econometrica 65:1059–1095
Brown GW (1951) Iterative solution of games by fictitious play. In: Koopmans C (ed) Act Anal Prod Alloc. Wiley, New York, pp 374–376
Cerboni Baiardi L, Lamantia F, Radi D (2015) Evolutionary competition between boundedly rational behavioral rules in oligopoly games. Chaos Solitons Fractals 79:204–225
Corchon L, Mas-Colell A (1996) On the stability of best reply and gradient systems with applications to imperfectly competitive models. Econ Lett 51:59–65
Cournot A (1838) Researches into the mathematical principles of the theory of wealth. Macmillan Co., New York Transl. by Nathaniel T. Bacon (1897)
Cox JC, Walker M (1998) Learning to play Cournot duopoly strategies. J Econ Behav Organ 36:141–161
Dana R-A, Montrucchio L (1986) Dynamic complexity in duopoly games. J Econ Theory 40(40):40–56
De Giovanni D, Lamantia F (2016) Control delegation, information and beliefs in evolutionary oligopolies. J Evolut Econ 26:1089–1116
Deschamp R (1975) An algorithm of game theory applied to the duopoly problem. Eur Econ Rev 6:187–194
Dindo P, Tuinstra J (2011) A class of evolutionary models for participation games with negative payoff. Comput Econ 37:267–300
Droste E, Hommes C, Tuinstra J (2002) Endogenous fluctuations under evolutionary pressure in Cournot competition. Games Econ Behav 40:232–269
Fisher F (1961) The stability of the Cournot solution: the effects of speeds of adjustment and increasing marginal costs. Rev Econ Stud 28(2):125–135
Foster D, Young HP (1990) Stochastic evolutionary game dynamics. Theor Popul Biol 38:219–232
Furth D (2009) Anything goes with heterogeneous, but not always with homogeneous oligopoly. J Econ Dyn Control 33:183–203
Gale J, Binmore K, Samuelson L (1995) Learning to be imperfect: the ultimatum game. Games Econ Behav 8:56–90
Golubitsky M, Stewart I, Schaeffer D (1988) Singularities and groups in bifurcation theory II, vol II of applied mathematical sciences, vol 69. Springer, New York
Hofbauer J, Sigmund K (1988) The Theory of Evolution and Dynamical Systems. Cambridge University Press, Cambridge
Hofbauer J, Weibull J (1996) Evolutionary selection against dominated strategies. J Econ Theory 71:558–573
Huck S, Normann HT, Oechssler J (2002) Stability of the Cournot process-experimental evidence. Int J Game Theory 31:123–136
Kolstad C, Mathiesen L (1987) Necessary and sufficient conditions for uniqueness of Cournot equilibrium. Rev Econ Stud 54(4):681–690
Kopel M (1996) Simple and complex adjustment dynamics in Cournot duopoly models. Chaos Solitons Fractals 7(12):2031–2048
Kopel M, Lamantia F, Szidarovszky F (2014) Evolutionary competition in a mixed market with socially concerned firms. J Econ Dyn Control 48:394–409
Kuznetsov YA (1995) Elements of applied bifurcation theory. Springer, Berlin
McKelvey R, Palfrey T (1995) Quantal response equilibria for normal form games. Games Econ Behav 10:1–14
Novshek W (1985) On the existence of Cournot equilibrium. Rev Econ Stud 52(1):85–98
Ochea M (2010) Essays on nonlinear evolutionary game dynamics. Ph.D. thesis, University of Amsterdam
Palander T (1939) Konkurrens och marknadsjmvikt vid duopol och oligopol. Ekon Tidskr 41:124–145
Puu T (1991) Chaos in duopoly pricing. Chaos Solitons Fractals 1:573–581
Puu T (2008) On the stability of Cournot equilibrium when the number of competitors increases. J Econ Behav Organ 66:445–456
Rand D (1978) Exotic phenomena in games and duopoly models. J Math Econ 5:173–184
Rassenti S, Reynolds S, Smith V, Szidarovszky F (2000) Adaptation and convergence of behaviour in repeated experimental Cournot games. J Econ Behav Organ 41:117–146
Schlag K (1998) Why imitate, and if so, how?: A boundedly rational approach to multi-armed bandits. J Econ Theory 78(1):130–156
Seade J (1980) The stability of Cournot revisited. J Econ Theory 23:15–27
Szidarovszky F, Yakowitz S (1977) A new proof of the existence and uniqueness of the Cournot equilibrium. Int Econ Rev 18(3):783–789
Taylor PD, Jonker L (1978) Evolutionarily stable strategies and game dynamics. Math Biosci 40:145–156
Theocharis RD (1960) On the stability of the Cournot solution on the oligopoly problem. Rev Econ Stud 27:133–134
Thorlund-Petersen L (1990) Iterative computation of Cournot equilibrium. Games Econ Behav 2:61–75
Tuinstra J (2000) A discrete and symmetric price adjustment process on the simplex. J Econ Dyn Control 24:881–907
Tuinstra J (2004) A price adjustment process in a model of monopolistic competition. Int Game Theory Rev 6(3):417–442
Author information
Authors and Affiliations
Corresponding author
Additional information
An earlier version of this paper circulated under the title “On the stability of the Cournot equilibrium: An evolutionary approach”.
Appendix
Appendix
Proof of Proposition 1
The dynamics of quantities is governed by a system of n first-order difference equations, given by (3) for \(i=1,\ldots ,n\). All of the diagonal elements of the corresponding \(n\times n\) Jacobian matrix \({\mathbf {J}}^{*}\), evaluated at the Cournot-Nash equilibrium, are equal to \(F_{q}^{*}\) and all of its off-diagonal elements are equal to \(F_{Q}^{*}\). It follows that \({\mathbf {J}}^{*}\) has eigenvalues \(\lambda _{1}=F_{q}^{*}-F_{Q}^{*}\), with multiplicity \(n-1\), and \(\lambda _{2}=F_{q}^{*}+\left( n-1\right) F_{Q}^{*}\). Because the Cournot-Nash equilibrium is locally stable if all eigenvalues of \({\mathbf {J}}^{*}\) lie within the unit circle, and since by Assumption A we have \(\left| \lambda _{1}\right| <1\), a sufficient condition for local stability is \(\left| \lambda _{2}\right| =\left| F_{q}^{*}+\left( n-1\right) F_{Q}^{*}\right| <1\). Similarly, a sufficient condition for instability is \(\left| \lambda _{2}\right| >1\). Because \(F_{Q}^{*}\le -\delta <0\) and \(F_{q}^{*} \in \left( -1,1\right) \), we will have \(\left| \lambda _{2}\right| >1\) for n sufficiently large. \(\square \)
Proof of Proposition 2
The variables \(q_{t}\) and \(\rho _{t}\) evolve according to
Local stability of \(\left( q^{*},\rho _{\kappa }\right) \) is determined by the Jacobian matrix of (23), evaluated at \(\left( q^{*},\rho _{\kappa }\right) \).
First, we determine the partial derivatives of \(\Phi ^{2}\) with respect to \(q_{t-1}\) and \(\rho _{t-1}\), respectively. To that end, note that we can write the profit differential as
with \(A_{k}\left( \rho _{t-1}\right) =\left( {\begin{array}{c}n-1\\ k\end{array}}\right) \rho _{t-1}^{k}\left( 1-\rho _{t-1}\right) ^{n-1-k}\), which does not depend upon \(q_{t-1}\), and
which only depends upon \(\rho _{t-1}\) through \(q_{t-1}^{N}=H\left( q_{t-1},\rho _{t-1}\right) \). Note that \(D_{k}\left( q^{*},\rho _{\kappa }\right) =0\). Moreover, the partial derivatives of \(D_{k}\left( q_{t-1},\rho _{t-1}\right) \), evaluated at the equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) are given by
where we use the fact that at the Cournot-Nash equilibrium the individual firm’s first-order condition (1) is satisfied. We now have
and
The Jacobian matrix of (23), evaluated at \(\left( q^{*},\rho _{\kappa }\right) \), therefore has the following structure
with eigenvalues \(\lambda _{1}=\left. \frac{\partial \Phi ^{1}}{\partial q_{t-1}}\right| _{\left( q^{*},\rho _{\kappa }\right) }\) and \(\lambda _{2}=0\). Hence, a sufficient condition for \(\left( q^{*},\rho _{\kappa }\right) \) to be locally stable (unstable) is \(\left| \lambda _{1}\right| <1\) (\(\left| \lambda _{1}\right| >1\)).
We have
where \(H_{q}^{*}=\left. \frac{\partial H\left( q_{t-1},\rho _{t-1}\right) }{\partial q_{t-1}}\right| _{\left( q^{*},\rho _{\kappa }\right) }\). To determine \(H_{q}^{*}\) we totally differentiate first-order condition (7):
Using \(\sum _{k=0}^{n-1}\left( {\begin{array}{c}n-1\\ k\end{array}}\right) \rho ^{k}\left( 1-\rho \right) ^{n-1-k}=1\) and \(\sum _{k=0}^{n-1}\left( {\begin{array}{c}n-1\\ k\end{array}}\right) \rho ^{k}\left( 1-\rho \right) ^{n-1-k}k=\rho \left( n-1\right) \) and rearranging we find that
The last equality follows from the fact that from (1) the slope of the best-reply function equals
where the inequality follows from the second-order condition of a profit maximum and the assumption that \(P^{\prime }\left( Q^{*}\right) +q^{*}P^{\prime \prime }\left( Q^{*}\right) <0 \). Substituting (25) into (24), we get
Note that, by Assumption A and given that \(R^{\prime }\left( Q_{-i}^{*}\right) <0\), we know that \(\lambda _{1}<F_{q}^{*}<1\). The equilibrium \(\left( q^{*},\rho _{\kappa }\right) \) is therefore locally stable (unstable) when \(\lambda _{1}>-1\) (\(\lambda _{1}<-1\)). Rearranging these inequalities gives conditions (11) and (12). \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hommes, C.H., Ochea, M.I. & Tuinstra, J. Evolutionary Competition Between Adjustment Processes in Cournot Oligopoly: Instability and Complex Dynamics. Dyn Games Appl 8, 822–843 (2018). https://doi.org/10.1007/s13235-018-0238-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-018-0238-x
Keywords
- Stability of Cournot-Nash equilibrium
- n-Player Cournot games
- Evolutionary competition
- Endogenous fluctuations