Abstract
Guava (Psidium guajava) seeds were used for the preparation of activated carbon (AC) activated using zinc chloride (GCZ36), phosphoric acid (GCH36), potassium hydroxide (GCK36), and one other sample was prepared without activation (GC36), carbonized for 3 h at 600 °C. They were added to cellulose acetate to form hybrid membranes (Ms) using the phase inversion technique. The prepared AC was characterized by % ash content, % weight loss on drying, nitrogen adsorption isotherm, TEM, and XRD. FTIR and SEM were used for the ACs and Ms. GCK36 sample exhibited a higher surface area (905.27 m2/g) and total pore volume (0.5360 mL/g). The hybrid membranes were used to remove malachite green dye (MG) from wastewater. The effect of initial dye concentration, adsorbent dosage, pH, and contact time were studied. Pseudo-first-, pseudo-second-order, and intraparticle diffusion rate equations were proposed and the kinetic data were analyzed. Maximum adsorption capacity (31.82 mg/g) was achieved after 100 min, at pH 6 and 0.25% AC. The adsorption capacity of the cellulose acetate membrane was increased by 111.7% using the prepared activated carbon. The results indicated the chemisorption process and the adsorption was fitted to Langmuir > Freundlich > Tempkin due to R2 values.
Graphical abstract

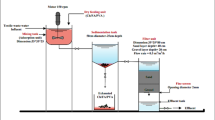
Schematic diagram of preparation of a composite membrane of cellulose acetate and guava seeds activated carbon
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Water pollution is defined as the change in the physical or chemical properties of water which makes it inappropriate for various uses. The increase in water pollution has been drawing more attention to the treatment of wastewater. The plastic, metal, pharmaceutical, and food industries effluents are important causes of water pollution which are very harmful to living beings [1].
Many industries are using dyes in large quantities including leather, textile, cosmetics, printing, paper, plastic, pharmaceuticals, food, etc. to color their products which produce highly-colored wastewater containing organic contents. The colored waste interferes with the transmission of sunlight and reduces photosynthetic action. Also, the colored wastes may have toxic effects on microbial populations and can be toxic and carcinogenic to mammals. Dye removal using conventional biological treatment processes is not very effective [2]. Malachite green dye (MG) (Fig. 1) is a synthetic basic dye that has been widely used for leather, acrylic, silk, wood, wool, and paper dyeing [3]. It is also used as an antifungal and antimicrobial in the aquaculture industry for controlling fish disease and parasites [4]. MG is environmentally persistent that it is difficult to be removed from aqueous solution and very toxic to terrestrial and aquatic animals [5]. Photo-degradation [6], photocatalytic degradation [7], and adsorption using natural sources of adsorbent [8,9,10,11] have been utilized for the removal of MG from wastewater.
Adsorption is a highly effective and an easy method to perform among all the treatment processes. Adsorption included the extraction of chemicals from one phase and bonding onto the surface of another phase. Adsorption increased by increasing the specific surface area which is the total surface area that is available for adsorption [12].
Activated carbon (AC) is the most widely used adsorbent for pollutants removal. Activated carbons have high adsorption capacities due to its high micro-pore structure, large surface areas, and its adjustable nature according to the different chemical or physical treatments. Because the activated carbon application for the treatment of wastewater is picking up the production of activated carbon is always increasing. Activated carbons preparation is based on two procedures—one is the thermal pyrolysis process and the other is the activation step which may be physical activation or chemical activation.
Due to the significantly lower ash content of activated carbon produced by the chemical activation method and the high surface area, it is preferable. In addition, the yields of carbon are usually very high in the presence of the chemicals. When compared to physical activation, chemical activation consumes less energy. In chemical activation, there is no need to heat the activating agent, and pyrolysis and activation are combined into a single stage [13]. Different compounds were used for the chemical activation of the activated carbon such as CaCl2, FeCl2, ZnCl2 [14], and potassium tartrate (C4H6K2O7) [15]. The activated carbon was studied in terms of activation time, temperature, and activating agent concentration [16, 17]. Several studies on the production of activated carbon from various sources have been conducted [18,19,20,21,22,23]. In our work, we deal with the use of guava seeds as a source of carbon for the production of activated carbon. Membrane water treatment is a low-cost technology for expanding water resources and treating contaminated water. Treating water using membrane has a superior performance in the removal of particles, microorganisms, and turbidity in natural and wastewater [24]. Using adsorption phenomena associated with membranes is fast and effective water purification; it can be applied to the removal of organic, inorganic, and biological pollutants [25, 26].
Thermally induced phase inversion, immersion precipitation, vapor-induced phase inversion, and dry casting of polymer solution are the most commonly used precipitation methods for membrane formation [27]. The phase inversion process occurred as a result of the reduced solubility of the membrane-forming polymer in the solvent. Among polysaccharides, cellulose acetate (CA) has some advantages, including nontoxicity, ease of manufacture, hardness, good impact resistance, optical transparency, resistance to hydrocarbons, and lack of static electricity [28]. A lot of research based on the use of CA membrane incorporated with nanoparticles such as silver, ZnO and TiO2 were done and utilized in different applications [29,30,31].
These composite membranes improved the properties of the polymeric membrane [32,33,34,35]. Through the study of the lifecycle of CA polymer, it was found that the biodegradation rate decreases as the degree of acetyl substitution increases [36]. In our study, we will illustrate the effect of adding the prepared activated carbons derived from guava seeds on the adsorption capacity of the cellulose acetate membrane.
2 Materials and methods
2.1 Materials
Cellulose acetate powders, acetone (99%), calcium carbonate, hydrochloric acid HCl (37%), malachite green dye, sodium hydroxide, phosphoric acid, potassium hydroxide, and zinc chloride were all purchased from EL-Naser for chemical and pharmaceutical (Egypt). Guava (Psidium guajava) seeds were purchased from a local market. Distilled water was utilized throughout the experiments for solution preparation and glassware cleaning. All chemicals were used as received, without further purification.
2.2 Preparation adsorbent
A sample of guava (Psidium guajava) seeds powder was used without activation and carbonized at the same temperature and time. To prepare AC, guava (Psidium guajava) seeds (biomass) were first washed several times using deionized water to remove adhered impurities from their surface. The seeds were dried at 105 °C for 24 h. Then, it was milled and sieved. The guava seeds powder was well mixed with an impregnation ratio of 1:3 (wt.) (guava seeds: activating agent (KOH, ZnCl2, and H3PO4)) and then the solution was stirred for 1h. The solutions were placed for 48 h to complete the activation process. Then, it was filtered and dried at 105 °C for 24 h. After that, the carbonization was done in a muffle furnace in the absence of air using a closed crucible at a rate of 10 °C/min up to 600 °C for 3 h. After cooling to room temperature, the activated samples were ground, sieved, and washed several times with distilled water until a neutral filtrate was obtained. The washed samples were dried at 110 °C and stored in clean and dry glass bottles for characterization and adsorption studies.
For the preparation of CA membrane (M1), 1 g of the CA powder was dissolved in 19 ml acetone (5% wt/v) and stirred for 1 h. The pore-forming reagent of calcium carbonate CaCO3 (1.5 g) was added to the solution and stirred for 3 0min. The casting solution was left for 30 min. The prepared casting solution was poured onto a clean glass plate and distributed with the help of a glass rod. The nascent membrane was dried in the air for 15 s and immersed in a bath of HCl (0.02 M) for 15 min. Then, it was immersed in a deionized water bath. The CA membranes hybrids by the prepared activated carbon shown in Table 1 were fabricated in the same way but with adding certain amounts of activated carbon with stirring for 1/2 h before pouring them onto a clean glass plate. A stock solution of malachite green dye MG with concentration of (1000 ppm) was prepared by dissolving 1 g of MG dye in distilled water to form 1 L solution. This solution will be used to prepare the different concentration of dye used in our research. The schematic diagram of the prepared composite membrane of cellulose acetate and guava seeds activated carbon is illustrated in (Fig. 2).
2.3 Adsorbent characterization
The following equation was used to calculate the yield percentage of the prepared activated carbon.
The percentage of ash content was determined by placing the AC samples in crucible and then transferred into muffle furnace at 650 °C for 6 h till reaching a constant weight. The burned samples were cooled in desiccator and weighted again [37]. The ash content was determined from Eq. (2).
The percentage of weight loss on drying was determined where 0.5g of each AC samples was placed in an oven for 24 h at 110 °C until the weight of the samples became constant. The weight loss can be calculated from Eq. (3).
Specific surface area (SBET, m2/g), total pore volume (VT, mL/g), and pore radius (ṝ, nm) were determined through nitrogen adsorption at – 196 °C using BelsorbminiII, BET inc., Japan. Scanning electron micrographs (SEM) were performed (JEOL JSM 6360LA, Japan) at Egypt-Japan University of Science and Technology, New Borg El-Arab City, Alexandria, Egypt. Fourier transform infrared spectra (FTIR) were recorded in the range between 4000 and 400 cm−1 on Spectrum BX 11 spectrometer FTIR LX 18-5255 Perkin Elmer. Transmission Electron Microscopy and TEM (JEOL JEM-100CX, Japan with an accelerating voltage of 80 kV). The graphitizing level of adsorbent was analyzed using Raman spectroscopy (Renishaw-RM2000). Powder diffractometry (XRD) was detected via (Shimadzu 7000) diffractometer with Cu-Kα radiation beam (λ = 1.5406Ao) to define the crystalline structure of the prepared activated carbon. The grinded powdered materials were placed onto smooth aluminum holder and subjected to the rotating anode as X-ray source which operate at 30 kV and 30 mA, then rotated over 2θ of 10 and 80.
2.4 Adsorption studies
0.05g of M1, M2, M3, M4, and M5 membranes was added to 20ml of MG solution and shaken at 60 rpm in a thermostatic shaker (model RUMO 4050; shaking rate 300 rpm) at room temperature for 1.5 h. The membranes were removed after the adsorption process take place and the concentrations of the dye solution were determined using a double UV–Vis spectrophotometer (UV-1800 Shimadzu, Japan) at λ = 617 nm. The effect of adsorption parameters of initial MG concentration (10, 20, 30, 40 and 50 mg/ L), adsorbent dosage (M5, M6 and M7 membranes) using 40 mg/L MG solution, pH (2–10), and contact time (10–120min) was studied at 25 °C. The pH of the solution was adjusted using 1M HCl and 1M NaOH. The concentration retained in the adsorbent phase (qe, mg/ g) and the percentage removed % R were calculated using the following Eqs. (4) and (5):
where Co is the initial concentration of MG dye, Ce is the concentration of MG dye at equilibrium (mg/L); V is the volume of the solution in liter, and W is the weight of adsorbent added.
2.5 Adsorption kinetics models
Pseudo-first order Eq. (6) and pseudo-second order Eq. (7) were used to fit the kinetics process of malachite green adsorption on M6 membrane.
where qe and qt are the amounts of MG dye adsorbed (mg/g) at equilibrium after all the sites occupied by the adsorbate and at time t (h), respectively, K1 the PFO rate constant for adsorption (h−1) and K2 (g /mg h) is the rate constant of PSO adsorption. In our studies, pseudo-first and pseudo-second order were applied for the adsorption of MG dye on M6 membrane.
The linear form of the pseudo-second-order (PSO) model [38] can be expressed as:
where, K2 is the reaction rate constant (g/ mg min). The plot of t/qt against t gives a linear relationship, and the slope and intercept can be used to derive qe and K2. The intraparticle diffusion model [39] considers the case where solute molecule diffusion into the interior of adsorbent pores is rate limiting. The equation is as follows:
where Kid is the reaction rate constant (mg/ m t0.5) and Ci refers to the boundary layer thickness. It can be derived from the slop of the plot of qt versus t0.5. This model assumes that:
The external resistance to mass transfer occurred very early in the diffusion process.
-
(1)
The diffusion direction is radial, and the concentration is.
-
(2)
The pore diffusivity is constant and unchanging over time.
2.6 Adsorption isotherm models
Some well-established isotherms such as Langmuir, Freundlich, and Tempkin equations were utilized to study the adsorption of MG on the surface of M5 membrane [40]. Langmuir isotherm suggests that adsorption is reversible and occurs only in a single layer of the adsorbate. The Langmuir isotherm is given by the Eq. (10) [41, 42].
where b (L/mg) is the Langmuir constant, Ce (mg/L) is the equilibrium concentration, qe (mg/g) is the amount adsorbed at equilibrium, and qm (mg/g) represents the monolayer capacity. The Ce/qe versus Ce plot gives a straight line of a slope equal 1/qm and intercept 1/bqm. The essential characteristics of Langmuir isotherm can be configured by a dimensionless constant known as equilibrium parameter (RL), which is written as:
where Co is the highest initial dye concentration introduced to the solution (mg/L). RL is a degree of favorability of adsorption. 0 < RL < 1 indicates favorable adsorption and RL > l or irreversible RL = 0 means unfavorable adsorption [43]. Freundlich isotherm describes the heterogeneous systems with non-identical adsorption sites. Freundlich isotherm model considers a heterogeneous adsorption due to the non-uniform heat distribution on the absorbent surface.
where Ce is the solute concentration in the liquid at equilibrium (mg/L), qe is the amount of dye sorbed at equilibrium (mg/g), KF (mg/g) and n are the Freundlich constants related to adsorption capacity and adsorption intensity. The linearized form of Freundlich isotherm can be written as follows:
where Kf measures the adsorption capacity of adsorbents and l/n is an empirical parameter relating the adsorption intensity, which varies with adsorbent heterogeneity. From the intercept and slope of the linear plot between log qe and log Ce, the Freundlich constants KF and n were calculated. The extent of correlation between solution concentration and adsorption depends on the adsorption intensity, n. The adsorption can be linear (n = l), chemical (n < l), and favorable physical process (n > 1) [44, 45]. A normal Freundlich isotherm is indicated if 1/n < 1 and heterogeneous nature of surface was identified by a value of 1/n the range 0–1. The adsorbent–adsorbate interaction of surfaces and the heat of adsorption have been studied by Tempkin and Pyzhev (1940). The Tempkin isotherm is based on the assumption that the adsorbent–adsorbate interactions lead to linear decrease in the heat of adsorption [46, 47]. Furthermore, the adsorption is characterized by a uniform distribution of binding energies, up to some maximum binding energy. The isotherm is given as in Eqs. (14) and (14) is linearized to Eq. (15):
where qe in Eq. (14) is the amount of adsorbate adsorbed at equilibrium (mg/g), R is the universal gas constant (8.314 J/mol k) and KT is the equilibrium binding constant (L/mg). In Eq. (15) BT is the heat of adsorption, and it is given by BT = RT/b and T is the temperature in Kelvin.
3 Results and discussion
3.1 Characterization of the prepared activated carbon
The yield, the ash content, and the moisture percentage of GC36, GCH36, GCZ36 and GCK36 are shown in Table 2. Ash contents in case of ZnCl2 activated samples are lower than that for KOH and H3PO4 activated samples because of the ability of ZnCl2 to dissolve some ash atoms of the solid samples as volatile chlorides during activation. The weight loss on drying for activated carbon samples is proportional to the surface area and surface function groups.
Figure 3a shows nitrogen adsorption–desorption isotherms of the GC36, GCH36, GCK36, and GCZ36. The four samples exhibited adsorption isotherm of type IV, showing a hysteresis loop at relative pressures above 0.3. The adsorption isotherms showed the similar shape, i.e., with a steep curve at the low-pressure range, then parallel to the relative pressure axis at the high-pressure range. The adsorption and desorption branches followed nearly the same path with a relatively narrow hysteresis loop. The observation of a hysteresis loop indicates the presence of wider pores, which may be related to the corrosive effect of KOH, H3PO4, and ZnCl2 on the microporous carbon walls. This type of hysteresis loop is attributed to cylindrical pores and or the 'ink bottle' pores [48]. All the samples GC36, GCH36, GCK36, and GCZ36 gave isotherm with type H4 According to the IUPAC classification in which parallel and almost horizontal branches and this is often associated with narrow slit pores (mesoporous). The surface area of GC36 (174.5 m2/g) and total pore volume (0.07846 mL/g) are low due to the absence of activating agent. In case of GCZ36 activated carbon sample which was activated using ZnCl2, the surface area was increased to 667.58 m2/g with 283% increases in relative to the GC36 sample and total pore volume of 0.3463 mL/g. This increase may be related to the ability of ZnCl2 to create new pores by dissolving more ash atoms. For the GCH36 activated carbon sample which was activated using H3PO4, the surface area was (618.79 m2/g) and total pore volume also was (0.3223 mL/g). This means that ZnCl2 is better than H3PO4 as activating agent. This fact is related to its ability to form more pores due to the formation of more gases which volatilized during the decomposition process to form more pores. Activation with KOH in case of GCK36 increases the surface area to 905.27 m2/g with 420% increases in relative to the GC36 sample and total pore volume to 0.5360 mL/g which indicates the creation of new pores, where the mechanism of activation with KOH may be related to some reactions that may take place due to thermal decomposition of KOH as listed below:
Meanwhile, the reaction current that occurred between CO2 gas and char is as follows:
The pore structure of GC36 (1.7980 nm) and GCZ36 (2.0751 nm) consists mainly of micropores, which are defined by IUPAC as pores smaller than 2 nm in diameter. In case of GCH36 and GCK36, it was found that their pores radius increased to 2.0835 and 2.3684 nm, respectively, which related to the mesopores formed according to the IUPAC classification (mesopore has a radius ranging from 2 to 50 nm). The results show that the different activating agents were efficient in generating an activated carbon having a high specific surface area using guava seeds as the precursor. The textural properties of the prepared activated carbon produced are listed in Table 3.
Scanning electron microscopy (SEM) analysis, which shows the pore morphology, was performed on all samples and is shown in (Fig. 3b–e). From the micrographs, the GC36 sample has a smooth surface of carbon with fewer amounts of micropores. The GCH36 sample has developed porous structure as a result from the decomposition of the guava seeds matrix using phosphoric acid and evaporation of tars through activation process in the absence of air at 600 °C [49]. The GCZ36 sample has a smooth surface of carbon with large amounts of micropores. It is clearly shown that GCK36 sample has the highly porous surface which agreed with the nitrogen adsorption / desorption isotherms results shown before. The SEM images of the GCK36 sample reveal an irregular structure with crevices and cracks on the surface, as well as some grains of varying sizes in large holes as a result of activation. Moreover, the GCK36 sample shows the pores in a tunnel shape and the overall surface appears in honey-comb structure. This is confirmed that the GCK36 sample has the amorphous and heterogeneous structures. The images showed that high porosity of activated carbon samples compared by the sample of guava seeds carbons without activation due to the effect of activating agents (H3PO4, KOH, and ZnCl2).
The presence of spherical carbon particles are highly observed from the TEM micrographs (Fig. 4a–d) of the activated carbon prepared GC36, GCZ36, GCH36 and GCK36 with varying sizes between 15 and 360 nm. For GCK36 sample most pores appeared mesoporous and a web-like arrangement of amorphous carbon particles around the carbon spheres were observed, which confirmed its higher specific surface area and porosity. It is known that spherical carbon particles have better packing density than non-spherical structures [50]. The morphological view of activated carbon from the guava seeds for GC36 and GCZ36 reveals irregular shape with ununiformed structure of carbon. Nano-rod structure was observed in case of GCH36. Fig. 4e illustrates the FTIR analysis which is used to identify some characteristic functional groups of the guava seeds carbon without activation GC36 and the prepared activated carbon GCZ36, GCH36, and GCK36. The broad absorption peak at 3425.73 cm−1 for GC36 was shifted to 3422.84, 3421.62, and 3446.11 cm−1 for GCZ36, GCH36, and GCK36, respectively, due to the effect of using the activating agent. This peak corresponds to the N–H stretching vibration of aryl or alkyl amine which related to the amino acid of guava seed protein [23]. The peaks at 1587.88, 1593.51, 1572.49, and 1589.67 cm−1 for GC36, GCZ36, GCH36, and GCK36, respectively, are due to –NH2 stretching for the amino acid L-tyrosine cycle and considering the glutelins amino acids content in guava seeds with an observed chemical shift related to the used activating agent. The broad band obtained in the region between 1300 and 1000 cm−1 for GCK36 activated carbon may be attributed to C–O stretching present in ether and alcohol. From the latter, it is observed that the activated carbon activated using KOH is rich in C–O surface functional groups compared with the others. Also the C–O–C stretching vibration occurs at 1166.42, 1159.75, and 1177.33 cm−1 for GC36, GCZ36, and GCH36, respectively. In addition, the bands at 575.01, 570, 590, and 550 cm−1 are attributed to out-of-plane angular deformation of aromatic rings [51]. A spike at 505.27 cm−1 represents the vibration of PO4−3 in case of GCH36 [52]. The bands in the region 850–440 cm−1 referred to the alkene vibrations. The broadband around with maxima at 1100 cm−1 have been assigned to C–O stretching in alcohols, acids, ethers, phenols and/or esters groups [53]. The entire different activating agent didn't give an obvious influence on the surface functional groups of the samples but there effect appeared in the chemical shifts occurred for the functional groups. (Fig. 4f) shows the XRD diffractogram of GC36, GCZ36, GCH36, and GCK36 without and with activation. The diffractograms exhibited two weak and broad peaks at 22.5° ≤ 2θ ≤ 25° and around 43.5° that correspond to Bragg’s reflection planes of (002) and (101) obtained the amorphous carbon skeleton [54]. The low-intensity and not well-defined peaks indicated a low degree of graphitization of the obtained carbon irrespective of the activation process. Finally, the XRD investigation supported the amorphous structure of the obtained activated carbons. The Raman spectrum of the prepared activated carbons had shown two sharp peaks (Fig. 5). The first peak at about 1580.1, 1584.34, 1585.79, and 1588.54 cm−1 (G peak), for GC36, GCH36, GCZ36, and GCK36, respectively, which is the characteristic scattering peak of graphite. The second peak at about 1345.31, 1348.25, 1350.2, and 1345.14 cm−1 (D peak) for GC36, GCH36, GCZ36, and GCK36, respectively, which is caused by lattice defects indicating the low symmetry carbon structure of the prepared activated carbon. The degree of graphitization can be evaluated by dividing the intensity of the D peak on the intensity of the G peak. The degree of graphitization increased as the R value decreased. The values of GC36, GCH36, GCZ36, and GCK36, respectively, activated carbon were 1.35, 1.48, 1.58, and 1.72, respectively.
3.2 Characterization of the cellulose acetate membrane and cellulose acetate membrane combined with guava seeds activated carbon.
Figure 6a, c shows the morphology of CA membrane M1 and the corresponding morphology for M6 membrane with 0.25% activated carbon loading. SEM was used to prove the pores formation in the CA polymer membrane M1. A comparison of the surface morphology of the CA polymer matrix membrane (M1) and that of M6 the mixed matrix membrane of cellulose acetate combined with guava seeds activated carbon (GCK36) revealed more pores. As indicated, the M6 membrane has a more porous surface than M1 membrane. According to the micrographs, it is clearly observed that M1 and M6 membranes have asymmetric structure consisting of a porous top layer. The surface morphology of M1 and M6 membranes after adsorption of malachite green dye indicates the occupation of the pores by the dye molecules (Fig. 6b, d). The solid content (additive) has an effect on the permeability of the membranes and contributed to form porous structure observed in the cross section [55]. The cross-section images of cellulose acetate membranes hybrid using (Fe3O4 and ZnO nanoparticles) were also explained by Sivasankari, Kalaivizhi, and Gowriboy [56] where the membrane clarifies the increase of pores (finger-like morphology). (Fig. 6e) shows the FTIR spectra of neat CA membrane (M1) and cellulose acetate membrane combined with guava seeds activated carbon (M6). The peaks of the cellulose acetate membrane combined with guava seeds activated carbon (M6) were similar to those of neat CA membrane. Thus, it was confirmed that the addition of guava seeds activated carbon did not collapse CA structure. The absence of new peaks in case of the hybrid membranes indicates there is no chemical bond between guava seeds activated carbon and CA chains. For CA membrane (M1), the obtained spectra showed peak at 3480 cm−1 representing –OH stretching. The band at 2935 cm−1 represents the aliphatic of C–H group. The band at 1750 cm−1 is attributed to the stretching vibration of C=O bond, the band at 1616 cm−1 related to c=c aromatic, and a band at 1373 cm−1 showed O–H group. The characteristic bands around 1475 cm−1 represent the bending vibration of CH2, 1230 cm−1 assigned stretching vibration of the C–O group, and the band at 900 cm−1 corresponding to the out-of-plane C–H bend [57]. The peaks around 1050 cm−1 correspond to the stretching of the C–O bond. When guava seeds activated carbon was added to the CA, the IR peak intensity were increased implied intermolecular interaction between functional groups in guava seeds activated carbon and CA. In addition, the main characteristic bands of CA at 3480, 2935, 1750, 1373, 1230, and 1050 cm−1 are slightly shifted to 3473, 2931, 1742, 1370, 1215, and 1037 cm−1, respectively, may be related to the overlapping characteristic bands of CA and guava seeds activated carbon or weak interaction. The effect of malachite green dye adsorption on the spectrum produced by M1 and M6 membranes is shown in Fig. 6e. The IR peaks intensity was decreased which implied intermolecular interaction between functional groups in membranes and malachite green dye. In addition, the main characteristic bands of CA are slightly shifted due to the overlapping characteristic bands of membrane and malachite green dye or weak interaction.
3.3 Adsorption of malachite green onto the prepared cellulose acetate membranes.
3.3.1 Effect of initial dye concentration
MG adsorption capacities of M1, M2, M3, M4, M5, M6, and M7 membranes were determined (Fig. 7a). The cellulose acetate membrane M1 showed the lower amount of dye adsorbed of 15.03 mg/g due to the use of cellulose acetate only without any additive. On using the adsorbent produced from guava seeds without activation in case of M2 membrane, the amount of MG dye adsorbed was increased to 16.12 mg/g. In case of M4 membrane by the addition of activated carbon derived from guava seeds activated using ZnCl2 activating agent, the amount of MG dye adsorbed was increased to 18.24 mg/g. This increase is due to the effect of the addition of ZnCl2 on the creation of new pores and the increase of the active sites on the surface of the prepared carbon. The use of H2SO4 as activating agent in case of M3 membrane was found to be better than the use of ZnCl2. The amount of MG dye adsorbed by M3 membrane was increased to be 19.11 mg/g. M5 membrane was found to have the highest amount of MG dye adsorbed qe = 24.55 mg/g. On increasing the amount of activated carbon (GCK36) in case of M6 and M7 membranes, the amount of dye adsorbed was found to be 31.82 and 28.7 mg/g, respectively. Finally on using different activating agent for the activation of the carbon, KOH was found to be the best one due to its effect on the creation of more pores which increase the surface area of the carbon and increase its adsorption capacity. (Fig. 7b) shows the adsorption capacity versus the different initial dye concentrations of M1, M2, M3, M4, and M5 membranes. From the results, the concentration of the amount of the dye adsorbed on the surface of the membranes increased when the initial concentration of the dye increased. On using dye concentration more than 40 mg/L, the amount of MG adsorbed nearly has constant values because of the establishment of adsorption equilibrium. The maximum amount of dye adsorbed was reached on using initial dye concentration of 40 mg/L. The adsorption mechanism of MG dye on the surface of the prepared cellulose acetate membrane immobilized by different types of prepared activated carbon can be discussed by two different processes. The first is the monolayer adsorption on the first layer and the second is the multilayer adsorption on the subsequent layers. The monolayer adsorption involves the interaction of MG and adsorbent surface (membrane). The possible interactions include the electrostatic interactions of the carboxylic groups on the cellulose acetate surface itself and the activated carbon with the positive charge on MG cations. Also, H-bonding is between the carboxyl groups or hydroxyl groups (H-bond donors) or amine groups of the adsorbent (cellulose acetate surface itself and the activated carbon used) and H-bond acceptor in MG. The π–π interaction is between the aromatic groups in the membranes surface and MG molecules. The multilayer adsorption results from the H-bonding between H-bond donor and H-bond acceptor in hydroxyl groups of dye molecules and the π–π interaction is between the aromatic rings of the dye. The comparison between the adsorption capacity of MG on different adsorbents and this work is illustrated in Table 4.
3.3.2 Effect of adsorbent dosage
The capacity and removal efficiency of the adsorbent for a given initial concentration of MG dye have been determined by the adsorbent dose. (Fig. 7c) shows the effect of adsorbent dosage (0.1% (M5), 0.25% (M6) and 0.5% (M7)) on the MG dye adsorption. The trend of MG dye removal efficiency increases with increasing the adsorbent dosage. The percentage removal of MG dye increased from 67.5 to 95.6% along the increase of adsorbent dose from 0.1% (M5) to 0.25% (M6). As the dose of adsorbent is increased, the free surface area and adsorption sites also increase and then more MG dye molecules can be adsorbed on the membranes surface. Increasing the amount of adsorbent above 0.25% in case of M7 membrane is considered to have no effect on the percent removed of the MG dye (slightly decreased). High concentration of activated carbon in the membrane may be caused by interparticle interaction such as aggregation; this leads to increasing the length of the diffusion path as well as decreasing the available surface area. The percent removed of the MG dye increased from 67.5% for M5 membrane to 95.6% in case of M6 and then slightly decreased using M7 to 91.25%.
3.3.3 Effect of PH
The initial pH effect on the dye solution has an important role in the whole adsorption process. Fig. 7d shows the effect of the initial pH (ranged from 2 to 10) on the percentage removed of MG dye adsorbed using M6 membrane (0.25%) at initial concentration of MG dye of 40 mg/L and at room temperature. Results showed that the equilibrium uptake of MG on M6 significantly increased from 37% at pH = 2 to 95% at pH = 6 and after that, it is slightly decreased by increasing the pH of the solution. The declined in MG uptake below pH 6 was attributed to electrostatic repulsion force. The MG dye is a basic dye carrying positive charge when dissolved in water. In acidic medium the positively charged surface of sorbent opposed the adsorption of the cationic adsorbate. At pH 6, the adsorption was favorable due to the electrostatic attraction between positively charged MG and negatively charged ACs surface. The maximum MG removal was observed at pH = 6 of 95%.
3.3.4 Effect of contact time
The effect of contact time on the removal of MG dye is shown in (Fig. 7e). From 10 to 100 min, the amount of dye adsorbed increased sharply due to the availability of free active sites on the adsorbent surface and high concentration of MG dye. 95.6% dye removal takes place in 100 min for M6 membrane where the equilibrium occupied. At the beginning of the adsorption process, all the adsorbent sites are vacant and solute concentration gradient is very high so the adsorption increased. Later, the lack of available active sites required for further uptake after attaining the equilibrium lowered the adsorption rate [58]. The maximum removal percentage was found at 100 min of 95.6%; this is greater than the bionanocomposite synthesized by Mohamed E., El-Sharkawy and Ibrahim (87.07%) [59]. When the maximum adsorption reached, a very few free active sites on the adsorbent surface are available so the slow increase in the MG dye removal was observed.
3.4 Adsorption kinetics
To characterize the kinetics of the adsorption process, pseudo-first-order, pseudo-second-order, and intraparticle diffusion rate equations were proposed, and kinetic data were analyzed.
3.4.1 Pseudo-first- and pseudo-second-order kinetic models.
Figure 8a, b shows the Lagrangian’s pseudo-first-order and pseudo-second-order plots, respectively. The experimental kinetic parameters were calculated using the figures of the pseudo-first and -second orders from the slope and intercept. It can be seen from the data summarized in Table 5 that the Lagrangian's first-order plot does not fit with the experimental kinetic data very well with correlation coefficient (R2 = 0.9739). However, there was a large difference in qe value between the experimental and calculated values, suggesting a poor fit for the pseudo-first- order kinetic model to the experiment data. The higher value of the correlation coefficient of pseudo-second-order plot (R2 = 0.9858) indicates that the applicability of the pseudo-second-order equation is better than Lagrangian's first-order plots. Furthermore, the pseudo-second-order model provides the best agreement between calculated and experimental qe values. The results show that chemisorption occurs between the adsorbent and adsorbate, so the rate of adsorption is determined by the number of adsorption sites on the adsorbent surface rather than the concentration of adsorbate in bulk solution. The chemisorption involves valence forces through sharing (covalent force) or exchange of electron between sorbent and sorbate [71, 72]. Based on an examination of the data in Table 5, we can observe that the qe values are 35.87 and 31.25 mg/g for PFO and PSO, respectively. The rate constant values are 1.903 and 2.8 × 10–4 g/mg min for K1 and K2, respectively. Table 5 shows correlation coefficient (R2) values that approached unity, indicating the applicability of the PSO kinetic model for MG adsorption on M6 membrane.
3.4.2 The intraparticle diffusion model.
The intraparticle diffusion model was used to determine the rate limiting step and the involved mechanism to understand the mechanism of MG dye adsorption onto the M5 membrane. Multilinearity can be obtained using the Weber and Morris model when qt is plotted versus t0.5 for MG dye adsorption on the prepared membrane, as shown in (Fig. 8c). This indicates that the current investigation involves two steps (phases 1 and 2). The external surface adsorption is indicated by the first sharper line (phase 1). The second part (phase 2) refers to gradual adsorption, which is controlled by intraparticle diffusion. If the lines do not pass through the origin, intraparticle diffusion is not the rate limiting step, indicating that film diffusion has an effect on MG dye adsorption [73]. Table 5 summarizes the calculated parameters of breakthrough adsorption curves such as the correlation coefficient R2, Kid, and C. in general, the R2 of Weber and Morris model for all the prepared membranes ranged 0.9438–0.9844. Furthermore, it does not pass through the origin point. This means that this model cannot adequately describe dye adsorption on prepared membranes, and intraparticle diffusion is more than just an adsorption rate controlling step. Because the plot revealed a multi-linear nature, the adsorption process must involve more than one mechanism [74]. Before 90 min of MG adsorption on the M6 membrane, surface adsorption was the dominant adsorption step; after that, the surface active sites were completely occupied. The MG adsorption process progresses to the second stage (pore diffusion adsorption). The three rate constants K of the kinetic models revealed that the rate constant Kid of intraparticle diffusion was significantly higher than K1 and K2 for all prepared membranes. This means that the dyes are chemically adsorbed at the inner active sites in the appropriate manner, chemisorption is the adsorption rate controlling step, external mass transfer is important in the adsorption process, and intraparticle diffusion has a minor effect.
3.5 Equilibrium adsorption isotherms
When the adsorption process reaches an equilibrium state, the adsorption isotherm shows how the adsorbed molecules are distributed between the solid surface phase and the liquid phase.
3.5.1 The Langmuir model
From the linear form of the Langmuir equation (Fig. 8d) and Table 5, the Langmuir's adsorption constant b (L/mg) is the affinity between the adsorbent and adsorbate. The b value was calculated for M5 membrane and it was 3.62 L/mg; this small value of b indicates the low heat of adsorption. The correlation coefficient R2 was 0.9938 for M5 membrane which indicates the applicability of the Langmuir equation for MG dye adsorption. The maximum adsorption capacity was calculated qm = 24.55 mg/g which was near the experimental values of the adsorption capacity. The adsorption capacity of M5 membrane was increased with about 31.4% more than M1 membrane due to the effect of the prepared activated carbon derived from guava seeds GCK36. The RL value of the adsorption of MG on M5 membrane was found to be 0.0068. This indicates that the adsorption process is favorable for MG by the prepared membrane M5 loaded with the prepared activated carbon GCK36.
3.5.2 Freundlich model.
Figure 8e shows the linear plot of Freundlich equation for the adsorption of MG dye on M5 membrane. From the linear plot of Freundlich equation, R2 is equal to 0.9816 indicating the good applicability of Freundlich equation. The slope (1/n) value was 0.2521 which indicated their favorable adsorption at the experimental conditions studied and correlation coefficient. The KF value was calculated from the intersect of the linear plot of Freundlich equation and it was 12.95. The Langmuir isotherm model fits the adsorption isotherm data of MG dye onto M5 membrane better than the Freundlich isotherm model. Because, the correlation coefficients of the Langmuir model R2 = 0.9938 were greater than those of the Freundlich model R2 = 0.9816. From Table 5, the n value for M5 membrane indicated a high adsorption capacity in M5 membrane isotherms and regression coefficient. These findings suggest that the Langmuir equation is more applicable than the Freundlich equation. The Langmuir equation's validity indicates monolayer adsorption of MG dye on specific homogeneous sites of the M5 membrane.
3.5.3 Tempkin model
The Tempkin isotherm constants BT and KT were calculated from the slope and the intercept of the plot of qe versus lnCe as shown in (Fig. 8f), Table 5. The heat of adsorption (b) is corresponding to coverage of malachite green dye on M5 membrane because of the adsorbent–adsorbate interaction. The Tempkin isotherm constant b was less than 8000J/mol which represents physical adsorption of MG on the prepared membrane. The equilibrium binding constant (KT) was 38.47 L/g high (2.245) which indicates the strong binding force between MG dye and M5 membrane. The good linearity of Tempkin plot and the value of the correlation coefficients (R2 = 0.9717) indicated the applicability of Tempkin model to MG dye adsorption on M5 membrane. The three adsorption isotherms are fitted to MG dye adsorption on M5 membrane surface by the order Langmuir > Freundlich > Tempkin due to R2 values in the same order.
4 Conclusion
The effect of using different activating agents on the preparation of activated carbon using guava seeds as a biomass source was studied. It was found that the activated carbon prepared using KOH as activating agent had the highest surface area SBET (905.27 m2/g) and total pore volume (0.5360 ml/g). Easily formed composite membranes of cellulose acetate and the activated carbon were prepared using the phase inversion technique. The adsorption capacity obtained was 31.82 mg/g, which occurred in an MG initial concentration of 40 mg/L at PH = 6 over a contact time of 100 min and concentration of activated carbon of 0.25%. Finally, it was concluded that the adsorption capacity of the cellulose acetate membrane was increased by 111.7% using 0.25% (wt. %) of the prepared activated carbon, 4.75% (wt. %) of cellulose acetate and 95% (vol. %). The adsorption process was best described by the pseudo-second-order and the Langmuir models. The results demonstrated that the cellulose acetate hybrid guava seeds activated carbon is a good adsorbent that is suitable for cationic dye removal from waste water.
References
T. Viraraghavan, F. de Maria Alfaro, J. Hazard. Mater. 57(1–3), 59–70 (1998)
O. Abdelwahab, N.K. Amin, E.Z. El-Ashtoukhy, J. Hazard. Mater. 163(2–3), 711–716 (2009)
R. Kant, Text. Res. J. 4, 22–26 (2011)
D.J. Alderman, J. Fish Dis. 8(3), 289–298 (1985)
S. Srivastava, R. Sinha, D. Roy, Aquat. Toxicol. 66(3), 319–329 (2004)
L. Yong, G. Zhanqi, J. Yuefei, H. Xiaobin, S. Cheng, Y. Shaogui, F. Die, J. Hazard. Mater. 285, 127–136 (2015)
A.M. Saad, M.R. Abukhadra, S.A.K. Ahmed, A.M. Elzanaty, A.H. Mady, M.A. Betiha, A.M. Rabie, J. Environ. Manag. 258, 110043 (2020)
T.K. Murthy, B.S. Gowrishankar, M.C. Prabha, M. Kruthi, R.H. Krishna, Microchem. J. 146, 192–201 (2019)
E.O. Oyelude, J.A. Awudza, S.K. Twumasi, Chem. Cent. J. 12(1), 1–10 (2018)
A.S. Sartape, A.M. Mandhare, V.V. Jadhav, P.D. Raut, M.A. Anuse, S.S. Kolekar, Arab. J. Chem. 10, S3229–S3238 (2017)
B.H. Hameed, M.I. El-Khaiary, J. Hazard. Mater. 154(1–3), 237–244 (2008)
A.H. El-Sheikh, A.P. Newman, H. Al-Daffaee, S. Phull, N. Cresswell, S. York, Surf. Coat. Technol. 187, 284–292 (2004)
H.J. Huang, S. Ramaswamy, Sep. Purif. Technol. 1, 1–36 (2013)
O.P. Junior, A.L. Cazetta, R.C. Gomes, É.O. Barizão, I.P. Souza, A.C. Martins, V.C. Almeida, J Anal Appl Pyrolysis. 105, 166–176 (2014)
X. Zhu, Y. Gao, Q. Yue, Y. Kan, W. Kong, B. Gao, Ecotoxicol. Environ. Saf. 145, 289–294 (2017)
T.E. Oladimeji, B.O. Odunoye, F.B. Elehinafe, R.O. Oyinlola, A.O. Olayemi, Heliyon. 7(1), e05960 (2021)
A. Ahmadpour, D.D. Do, Carbon 35(12), 1723–1732 (1997)
N.A. Bakar, N. Othman, Z.M. Yunus, W.A.H. Altowayti, A. Al-Gheethi, S.M. Asharuddin, S.N.A. Mohd-Salleh, Biomass Convers. Biorefinery. 11, 1–14 (2021)
D.F. Hernández-Barreto, L. Giraldo, J.C. Moreno-Piraján, Data Br. 32, 106312 (2020)
E. Taer, A. Apriwandi, R. Taslim, A. Agutino, D.A. Yusra, J. Mater. Res. Technol. 9(6), 13332–13340 (2020)
Z. Ranjkesh, K. Nasouri, Macromol. Res. 31, 1–14 (2023)
F. Mikšík, T. Miyazaki, K. Thu, J. Miyawaki, K. Nakabayashi, A.T. Wijayanta, F. Rahmawati, Energy Rep. 6, 255–263 (2020)
S.M. Anisuzzaman, C.G. Joseph, D. Krishnaiah, A. Bono, E. Suali, S. Abang, L.M. Fai, Water Resour. Ind. 16, 29–36 (2016)
M.A. Aroon, A.F. Ismail, T. Matsuura, M.M. Montazer-Rahmati, Sep. Purif. Technol. 75(3), 229–242 (2010)
M.E. El-Naggar, E.K. Radwan, S.T. El-Wakeel, H. Kafafy, T.A. Gad-Allah, A.S. ElKalliny, T.I. Shaheen, Int. J. Biol. Macromol. 113, 248–258 (2018)
W.G. Lee, D.Y. Kim, S.W. Kang, Macromol. Res. 26(7), 630–633 (2018)
T.A. Saleh, V.K. Gupta, Sep. Purif. Technol. 89, 245–251 (2012)
A. Ach, J. Macromol. Sci. Pure Appl. Chem. 30(910), 733–740 (1993)
S. Beisl, S. Monteiro, R. Santos, A.S. Figueiredo, M.G. Sánchez-Loredo, M.A. Lemos, M.N. De Pinho, Water Res. 149, 225–231 (2019)
S.A. Khan, S.B. Khan, A. Farooq, A.M. Asiri, Int. J. Biol. Macromol. 130, 288–299 (2019)
R. Abedini, S.M. Mousavi, R. Aminzadeh, Desalination 277(1–3), 40–45 (2011)
B.K. Nandi, R. Uppaluri, M.K. Purkait, J. Membr. Sci. 330(1–2), 246–258 (2009)
M. Ayaz, A. Muhammad, M. Younas, A.L. Khan, M. Rezakazemi, Macromol. Res. 27, 565–571 (2019)
L. Wu, M. Shamsuzzoha, S.M.C. Ritchie, J. Nanoparticle Res. 7(4), 469–476 (2005)
A.M. Pandele, F.E. Comanici, C.A. Carp, F. Miculescu, S.I. Voicu, V.K. Thakur, B.C. Serban, Vacuum 146, 599–605 (2017)
N. Yadav, M. Hakkarainen, Chemosphere 265, 128731 (2020)
F.A. Adecola, H.I. Adekoge, IJS. 7(1), 151–157 (2005)
Y.S. Ho, G. McKay, Process Biochem. 34(5), 451–465 (1999)
T.A. Khan, S. Dahiya, I. Ali, Appl. Clay Sci. 69, 58–66 (2012)
L. Xu, M. Zhang, Y. Wang, F. Wei, Environ. Pollut. 274, 116591 (2021)
I. Langmuir, J. Am. Chem. Soc. 40, 1361 (1918)
T. Sumathi, G. Alagumuthu, Int. J. Chem. Eng. 7, 430417 (2014)
M. Hiemant, S.R. Suprakas, Int. J. Biol. Macromol. 88, 66–80 (2016)
A.O. Dada, A.P. Olalekan, A.M. Olatunya, O.J.I.J.C. Dada, IOSR j. appl. chem. 3(1), 38–45 (2012)
H. Freundlich, W. Heller, J. Am. Chem. Soc. 61, 2228–2230 (1939)
T.E. Oladimeji, B.O. Odunoye, F.B. Elehinafe, R.O. Oyinlola, A.O.O. layemi, Heliyon. 7(1), e05960 (2021)
L.N. Yossa, S.K. Ouiminga, S.S. Sidibe, I.W.K. Ouedraogo, Sci. Afr. 9, e00476 (2020)
R. Frost, O. Carmody, Y. Xi, S. Kokot, Surf. Sci. 601(9), 2066–2076 (2007)
S. Yorgun, D. Yıldız, J Taiwan Inst Chem Eng. 53, 122–131 (2015)
M. Abdar, F. Pourpanah, S. Hussain, D. Rezazadegan, L. Liu, M. Ghavamzadeh, S. Nahavandi, Inf. Fusion. 76, 243–297 (2021)
H. Deng, L. Yang, G. Tao, J. Dai, J. Hazard. Mater. 166(2–3), 1514–1521 (2009)
N. Tangboriboon, R. Kunanuruksapong, A. Sirivat, J. Ceram. Process. Res. 13(4), 413–419 (2012)
J. Zawadzki, CHEM PHYS CARBON 21, 147–380 (1989)
X. Sun, H. Hao, F. Zhao, Z. Liu, RCR. 124, 50–61 (2017)
J. Wang, H. Song, L. Ren, M.E. Talukder, S. Chen, J. Shao, Membrane 12(1), 9 (2021)
S. Sivasankari, R. Kalaivizhi, N. Gowriboy, Chem. Sel. 6(9), 2350–2359 (2021)
A. Zafar, F. Bertocco, J. Schjødt-Thomsen, J.C. Rauhe, Compos. Sci. Technol. 72(6), 656–666 (2012)
H. Wang, L.F. Cui, Y. Yang, H. Sanchez Casalongue, J.T. Robinson, Y. Liang, H. Dai, J. Am. Chem. Soc. 132(40), 13978–13980 (2010)
M.E. Mahmoud, R.M. El-Sharkawy, G.A. Ibrahim, J. Mol. Liq. 368, 120676 (2022)
G.Y. Abate, A.N. Alene, A.T. Habte, D.M. Getahun, Environ. Syst. Res. 9(1), 1–13 (2020)
A.K. Kushwaha, N. Gupta, M.C. Chattopadhyaya, J. Saudi Chem. Soc. 18, 200–207 (2014)
H. Zhang, F. Zhang, Q. Huang, RSC Adv. 7(10), 5790–5799 (2017)
A.A. Ahmad, M.A. Ahmad, N.K.E. Yahaya, J. Karim, Arab. J. Chem. 14(4), 103104 (2021)
M.N. Idris, Z.A. Ahmad, M.A. Ahmad, Int. J. Basic Appl. Sci. 11(3), 38–43 (2011)
R. Gong, Y. Jin, F. Chen, J. Chen, Z. Liu, J. Hazard. Mater. 137(2), 865–870 (2006)
K.N. Awokoya, V.O. Oninla, G.C. Adeyinka, M.O. Ajadi, O.T. Chidimma, E.G. Fakola, O.F. Akinyele, Sci. Afr. 16, e01194 (2022)
M. Mohammad, S. Maitra, B.K. Dutta, Water Air Soil Pollut. 229, 1–14 (2018)
T. Santhi, S. Manonmani, V.S. Vasantha, Y.T. Chang, Arab. J. Chem. 9, S466–S474 (2016)
N. Gupta, A.K. Kushwaha, M.C. Chattopadhyaya, Arab. J. Chem. 9, S707–S716 (2016)
F. Ali, S. Bibi, N. Ali, Z. Ali, A. Said, Z.U. Wahab, H.M. Iqbal, CSCEE. 2, 100025 (2020)
I. El-Sharkawy, A. Pal, T. Miyazaki, B.B. Saha, S. Koyama, Appl. Therm. Eng. 98, 1214–1220 (2016)
S.M. Lamine, C. Ridha, H.M. Mahfoud, C. Mouad, B. Lotfi, A.H. Al-Dujaili, Energy Proc. 50, 393–400 (2014)
A.M. Youssef, A.I. Ahmed, U.A. El-Bana, Carbon Lett. 13, 61 (2012)
H. R. Lotfy, H. Roubík, Biomass Convers. Biorefinery, p. 1–1 (2022)
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). No funding was received.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elwardany, R.E., Shokry, H., Mustafa, A.A. et al. Influence of the prepared activated carbon on cellulose acetate for malachite green dye removal from aqueous solution. Macromol. Res. 31, 1043–1060 (2023). https://doi.org/10.1007/s13233-023-00187-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13233-023-00187-w