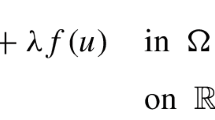Abstract
This paper deals with a class of singular problems involving the fractional \(p(x,\cdot )\)-Laplace operator of the form
where \(\Omega \) is a smooth bounded domain in \({\mathbb {R}}^N\) (\(N\ge 3\)), \(0<s<1\), \(\lambda \) is a positive parameter and \(\gamma : {\mathbb {R}}^N \longrightarrow (0,1)\) is a continuous function, \(p:\; {\mathbb {R}}^{2N} \longrightarrow \;(1,\infty )\) is a bounded, continuous and symmetric function, \(q: {\mathbb {R}}^N \longrightarrow (1,\infty )\) is a continuous function. Using the direct method of minimization combined with the theory of fractional Sobolev spaces with variable exponents, we prove that the problem has one positive solution for \(\lambda >0\) small enough. To our best knowledge, this paper is one of the first attempts in the study of singular problems involving fractional \(p(x,\cdot )\)-Laplace operators.
Similar content being viewed by others
References
K. B. Ali, M. Hsini, K. Kefi and N. T. Chung, On a nonlocal fractional p(.,.)-Laplacian problem with competing nonlinearities, Complex Analysis and Operator Theory, 13(3) (2019), 1377-1399.
A. Ambrosetti and A. Malchiodi, Nonlinear analysis and semilinear elliptic problems, Cambridge University Press, 2007.
E. Azroul, A. Benkirane, M. Shimi, M. Srati, On a class of fractional p(x)-Kirchhoff type problems, Appl. Anal. (2019), 1-20. https://doi.org/10.1080/00036811.2019.1603372.
A. Baalal and M. Berghout, Traces and fractional Sobolev extension domains with variable exponent, Int. J. Math. Anal., 12(2) 2018, 85-98.
A. Bahrouni, Comparison and sub-supersolution principles for the fractional p(x)-Laplacian, J. Math. Anal. Appl., 458 (2018), 1363-1372.
A. Bahrouni and V. D. Radulescu, On a new fractional Sobolev space and applications to nonlocal variational probems with variable exponent, Discrete Contin. Dyn. Syst. S, 11(3) (2018), 379-389.
G.M. Bisci, V.D. Radulescu and R. Servadei, Variational methods for nonlocal fractional problems, Encyclopedia Math. Appl. 162, Cambridge University Press, Cambridge, 2016.
L. Brasco and E. Parini, The second eigenvalue of the fractional p-Laplacian, Adv. Calc. Var., 9(4) (2016), 323-355.
N.T. Chung, Eigenvalue problems for fractional p(x,y)-Laplacian equations with indefinite weight, Taiwanese Journal of Mathematics, 23(5) (2019), 1153-1173.
N.T. Chung and H.Q. Toan, On a class of fractional Laplacian problems with variable exponents and indefinite weights, Collectanea Mathematica, 71(2) (2020), 223-237.
M. M. Coclite, G. Palmieri, On a singular nonlinear Dirichlet problem, Comm. Partial Differential Equations 14 (1989) 1315–1327.
M.G. Crandall, P.H. Rabinowitz and L. Tartar, On a Dirichlet problem with a singular nonlinearity, Comm. Partial Differential Equations. 2 (1977), 193-222.
L. Diening, P. Harjulehto, P. Hastö and M. Ružička, Lebesgue and Sobolev Spaces with Variable Exponents, Lectures Notes in Mathematics, Vol. 2017, Springer-Verlag, Berlin, 2011.
X.L. Fan, Solutions for p(x)-Laplacian Dirichlet problems with singular coefficients, J. Math. Appl. 312 (2005), 464-477.
X. Fan and D. Zhao, On the spaces\(L^{p(x)}\) (Omega) and \(W^{m,p(x)}\) (Omega), J. Math. Anal. Appl., 263 (2001), 424-446.
A. Fiscella, A fractional Kirchhoff problem involving a singular term and a critical nonlinearity, Adv. Nonlinear Anal., 8 (2019), 645-660.
M. Ghergu, V. Radulescu, Singular elliptic problems: bifurcation and asymptotic analysis, Oxford Lecture Series in Mathematics and its Applications, 37. The Clarendon Press, Oxford University Press, Oxford, 2008.
J. Giacomoni and K. Saoudi, Multiplicity of positive solutions for a singular and critical problem, Nonlinear Anal. 71 (2009), no. 9, 4060–4077.
K. Ho, K. Perera, I. Sim and M. Squassina, A note on fractional p-Laplacian problems with singular weights, J. Fixed Point Theory Appl., 19 (2017), 157-173.
A. Iannizzotto, S. Mosconi and M. Squassina, Global Hölder regularity for the fractional p-Laplacian, Rev. Mat. Iberoam., 32(4) (2016), 1353-1392.
U. Kaufmann, J.D. Rossi and R. Vidal, Fractional Sobolev spaces with variable exponents and fractional p(x)-Laplacians, Electronic J. Qual. Theory Differ. Equ., 2017(76) (2017), 1-10.
O. Kavian, Introduction à la théorie des points critiques et applications aux problèmes elliptiques, Springer-Verlag, (1993).
J.J. Liu, Positive solutions of the p(x)-Laplace equation with singular nonlinearity, Nonlinear Anal.,72 (2010), 4428-4437.
J. Liu, Q. Zhang and C. Zhao, Existence of positive solutions for p(x)-Laplacian equations with a singular nonlinear term, Electron. J. Differ. Equ. Conf., 2014(155) (2014), 1-21.
J. J. Liu, Positive solutions of the p(x)-Laplace equation with singular nonlinearity, Nonlinear Anal., 72 (2010), 4428–4437.
A. Mohammed, Positive solutions of the p-Laplace equation with singular nonlinearity, J.Math. Anal. Appl. 352 (2009), 234–245.
T. Mukherjee and K. Sreenadh, On Dirichlet problem for fractional p-Laplacian with singular non-linearity , Adv. Nonlinear Anal., 8 (2019), 52-72.
E. Di Nezza, G. Palatucci and E. Valdinoci, Hitchhike guide to the fractional Sobolev spaces, Bull. Sci. Math., 136(5) (2012), 521-573.
V. D. Rădulescu, D. D. Repovš, Partial differential equations with variable exponents: variational methods and qualitative analysis, CRC Press, Boca Raton, 2015.
K. Saoudi and A. Ghanmi, A multiplicity results for a singular equation involving the p(x)-Laplace operator, Complex Var. Elliptic Equ., 62 (2017), 695-725.
K. Saoudi and M. Kratou, Existence of multiple solutions for a singular and quasilinear equation, Complex Var. Elliptic Equ. 60 (2015), no.7, 893–925.
K. Saoudi, Existence and non-existence for a singular problem with variables potentials, Electronic Journal of Differential Equations 2017,291.
K. Saoudi, Existence and non-existence of solution for a singular nonlinear Dirichlet problem involving the p(x)-Laplace operator, J. Adv. Math. Stud. Vol. 9(2016), No. 2, 292-303.
L. Silvestre, Regularity of the obstacle problem for a fractional power of the Laplace operator, Comm. Pure Appl. Math., 60(1) (2007), 67-112.
Q. Zhang, Existence and asymptotic behavior of positive solutions to p(x)-Laplacian equations with singular nonlinearities, J. Inequal. Appl. 2007, Art. ID 19349, 9 pp.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by G.D. Veerappa Gowda.
Rights and permissions
About this article
Cite this article
Mokhtari, A., Saoudi, K. & Chung, N.T. A fractional \(p(x,\cdot )\)-Laplacian problem involving a singular term. Indian J Pure Appl Math 53, 100–111 (2022). https://doi.org/10.1007/s13226-021-00037-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13226-021-00037-4
Keywords
- Fractional \(p(x, \cdot )\)-Laplace operators
- Singular equations
- Minimization methods
- Fractional Sobolev spaces