1 Introduction

The ability to change their beliefs is a central characteristic of intelligent agents. In Knowledge Representation and Reasoning, the subarea of belief change [8] investigates fundamental principles, characterizations, and interrelations of principles for belief changes. The following two kinds of belief changes are of central interest:

  • Revision. The process of incorporating new beliefs, while maintaining consistency, whenever possible.

  • Contraction. The process of revoking beliefs without introducing new beliefs.

In this paper, we will consider several contributions to the theories of revision and contraction given in the authors’ dissertation thesis [18]. Due to space reasons, we will focus on the high-level ideas and descriptions and refer for the full details to the corresponding references [7, 18, 19].

2 Brief Introduction to the Theory of Belief Change

We start with visiting several aspects that are considered in the theory of belief change:

Agents’ Capability to Deduce and Minimal Change. A goal of belief change is to take the agent’s ability to make deductions into account. If an agent is convinced that A implies B (\({A\!\rightarrow \! B}\)) and that A holds, then she also believes in B (and other implications). Because of that, to successfully achieve that the agent believes in the contrary of B (\(\lnot B\)) without believing in inconsistencies, the agent also has to give up at least one of the beliefs A and \({A\!\rightarrow \! B}\). These changes should be made minimally, in the sense that as much as possible of the initial beliefs are preserved.

Agents’ Preferences. When giving up beliefs, there are often multiple possible beliefs the agent could give up (to achieve success). One can understand how these choices are made as an expression of the agent’s preferences (in the space of all possible choices). We consider the preceding example. Giving up the belief in B involves the choice of giving up the belief in A or giving up the belief in \({A\!\rightarrow \! B}\). If the agent chooses to give up A and not \(A\!\rightarrow \! B\), then we can say that the agent prefers \(A\!\rightarrow \! B\) over A. However, other agents might have different preferences, e.g., another agent could choose A and \(A\!\rightarrow \! B\), then we could say that for this agent A and \(A\!\rightarrow \! B\) are equally preferable.

Conditionals. Conditionals and belief changes are interrelated via Ramsey-test-like connections [18, 21]: B is believed after revision by A if and only if the conditional \((B \mid A)\) is accepted by the agent. Hence, sets of conditionals provide a semantics for belief changes.

Iterated Belief Change. The way an agent adjusts her beliefs may be influenced by prior changes. We consider the previous example again for further elucidation. Assume that the agent has chosen to give up A for beliving in \(\lnot B\), but to keep \({A\!\rightarrow \! B}\). The agent then might believe neither in A nor in B (\(\lnot A \wedge \lnot B\)). What would happen if the agent becomes aware after some time that A or B (\(A \vee B\)) has to be true? The agent has to choose how to establish belief in \(A \vee B\) by starting to believe in, e.g., in A, in B or fully in \(A\vee B\). However, in light of the prior change, the agent might consider some choices as more reasonable. For example, because the belief in B was just revoked, she might not consider B as a good choice.

The area of belief change employs mathematical logic. Given a logic \(\mathbb {L}=({\mathscr {L}},\varOmega ,\models )\), the formulas \(\alpha \in {\mathscr {L}}\) of the logic are employed to describe beliefs, the interpretations \(\omega \in \varOmega\) stand for possible worlds (that the agent can imagine), and logical entailment represents the agent’s reasoning capabilities. Belief change is the process of changing a set of formulas K by new information \(\alpha\) to a new set \(\textrm{K}\circ \alpha\), whereby \(\circ\) stands for any belief change operator. A prominent and widely accepted logic-based approach to revision and contraction is by Alchourrón, Gärdenfors and Makinson (AGM) [1] that captures the principle of minimal change when K and \(K\circ \alpha\) are deductively closed, especially when \(\mathbb {L}\) is a propositional logic. In this paper, each of “AGM revision” and “AGM contraction” contraction refer to the respective full set of postulates, including the supplementary ones [1], or an adaption of these for the respective framework.

3 Characterization of Revision in Tarskian Logics

Agents are confronted with choosing which beliefs they want to give up when doing revisions. A very prominent approach to represent such choices is by “preferences” over possible worlds. Roughly, the connection is as follows [9]:

$$\begin{aligned} \text { When revising } K \text { by } \alpha , \text { obtain } K \star \alpha \text { by selecting all }\nonumber \\ \text { those beliefs whose model set is a} \text { superset of the most} \nonumber \\ \text {``preferred'' worlds where } \alpha \text { holds}. \quad \quad \quad \quad \quad \quad \quad \quad \quad (\dagger ) \end{aligned}$$

Specifically for propositional logic, for every K, the changes on K by \(\star\) are AGM revisions if and only if there is a total preorder such that one obtains \(K\star \alpha\) as in \((\dagger )\) [9, 14]. This gives rationale to say that for propositional logic, every AGM revision operator is total-preorder-representable, which we express informally as follows:

$$\begin{aligned} \text {AGM revision } \simeq \text { total preorders.} \end{aligned}$$
(1)

Because preorders are considered as basic structure for representing preferences in knowledge representation [20] and beyond [15], there is theoretical interest in (1). However, for many logics it is unclear whether (1) holds.

The author’s dissertation focuses on Tarskian logics, i.e., logics where the logical consequence is a closure operator. This includes many classical monotonic logics with a model theory, e.g., first-order predicate logic, propositional logic, many modal logics, description logics, etc. Surprisingly, it turns out that (1) does not hold in some Tarskian logics; but, for Tarskian logics a correspondence similar to (1) holds [7]:

$$\begin{aligned} \text {AGM revision } \simeq \text { total min-retractive relations,} \end{aligned}$$
(2)

where min-retractivity is the following weakening of transitivity [7], demanding closure under certain refinements in \(\le\):

$$\begin{aligned}&\text {For all } \varGamma \text { and all } \omega ,\omega'\in \llbracket \alpha \rrbracket \text { holds}\\&\quad \ \omega \in \min (\llbracket \varGamma \rrbracket ,\le ) \text { and } \omega '\le \omega \text { imply } \omega '\in \min (\llbracket \varGamma \rrbracket ,\le ) . \end{aligned}$$

When going back to, e.g., propositional logic, the property of being total and min-retractive coincides with being a total preorder. This gives rise to the quest to identify those logics, where (1) still holds.

A main contribution given in the author’s dissertation thesis is a characterization of those Tarskian logics where every AGM revision operator is total-preorder-representable, i.e., (1) holds for every AGM revision operator. For this result, the notion of a critical loop is central, which we present in a simplified version for the sake of comprehensibility.

Definition 1

Let \(\mathbb {L}\) be a Tarskian logic. \(\varGamma _{0,1},\varGamma _{1,2},\varGamma _{2,0}\) form a critical loop (of length 3) for \(\mathbb {L}\) if there exists \(\textrm{K}\) and consistent \(\varGamma _0,\varGamma _1,\varGamma _2\) such that

  1. (I)

     \(\llbracket \textrm{K}\cup \varGamma _{0,1}\rrbracket = \llbracket \textrm{K}\cup \varGamma _{1,2}\rrbracket = \llbracket \textrm{K}\cup \varGamma _{2,0}\rrbracket = \emptyset\),

  2. (II)

     \(\llbracket \varGamma _{0}\rrbracket \cup \llbracket \varGamma _{1}\rrbracket \subseteq \llbracket \varGamma _{0,1}\rrbracket\),

    \(\llbracket \varGamma _{1}\rrbracket \cup \llbracket \varGamma _{2}\rrbracket \subseteq \llbracket \varGamma _{1,2}\rrbracket\),

    \(\llbracket \varGamma _{2}\rrbracket \cup \llbracket \varGamma _{0}\rrbracket \subseteq \llbracket \varGamma _{2,0}\rrbracket\), and

    \(\llbracket \varGamma _{j} \cup \varGamma _{i}\rrbracket = \emptyset\) for each \(i,j\in \{0,1,2\}\) with \(i \ne j\), and

  3. (III)

     for each \(\varGamma _{\!\triangledown }\) that is consistent with \(\varGamma _{0}\), \(\varGamma _{1}\), and \(\varGamma _{2}\), there exists some consistent \(\varGamma _{\!\triangledown }'\) such that:

    1. (a)

       \(\llbracket \varGamma _{\!\triangledown }'\rrbracket \subseteq \llbracket \varGamma _{\!\triangledown }\rrbracket\)

    2. (b)

       \(\llbracket \varGamma _{\!\triangledown }'\rrbracket \cap ( \llbracket \varGamma _{0,1}\rrbracket \cup \llbracket \varGamma _{1,2}\rrbracket \cup \llbracket \varGamma _{2,0}\rrbracket ) {=}\, \emptyset\).

Note that for a general characterization, the notion of critical loops has to be extended to arbitrary lengths [7, 18]. Given such a notion, a Tarskian logic \(\mathbb {L}\) is called loop-free if there is no critical loop (of any length) for \(\mathbb {L}\). The general result can be then summarized as follows.

Theorem 2

([7, 18]) Let \(\mathbb {L}\) be a Tarskian logic. Every AGM revision operator for \(\mathbb {L}\) is total-preorder representable if and only if \(\mathbb {L}\) is loop-free.

We illustrate the notion of critical loop and Theorem 2 by an example that is based on Delgrande and Peppas [6].

Fig. 1
figure 1

Graphical illustration of a critical loop from Example 3. The areas within borders represent sets of models. The arrows depict a non-transitive relation between the interpretations; each arrow indicates that the interpretation at the start of the arrow is strictly preferred over the interpretation(s) at the arrow tip

Full size image

Example 3

We consider Horn-logic over \(\varSigma =\{p_1,p_2,p_3\}\), which is a Tarskian logic. Let \(\varGamma _{0,1}\), \(\varGamma _{1,0}\) and \(\varGamma _{2,0}\) given by

$$\begin{aligned} \varGamma _{0,1}&= \{(p_1), (p_2\wedge p_3 \rightarrow \bot )\}\ , \\ \varGamma _{1,2}&= \{(p_3), (p_1\wedge p_2\rightarrow \bot )\}\ , \text { and } \\ \varGamma _{2,0}&= \{(p_2), (p_1\wedge p_3\rightarrow \bot )\}\ . \end{aligned}$$

We show \(\varGamma _{0,1},\varGamma _{1,2},\varGamma _{2,0}\) is a critical loop, by showing that the following K, and \(\varGamma _0,\varGamma _1,\varGamma _2\) are as described in Definition 1:

$$\begin{aligned} \textrm{K}&= \{(p_1\wedge p_2\wedge p_3)\}&\varGamma _0&= \{(p_1 \wedge p_2), (p_3\rightarrow \bot )\} \\ \varGamma _1&= \{(p_1 \wedge p_3), (p_2\rightarrow \bot )\}&\varGamma _2&= \{(p_2\wedge p_3), (p_1\rightarrow \bot )\} \end{aligned}$$

In the following, we list the models of these sets:

$$\begin{aligned} \llbracket \textrm{K}\rrbracket&\begin{aligned}&= \{p_{1}p_{2}{p_3}\}&\llbracket \varGamma _0\rrbracket&= \{p_{1}p_{2}\bar{p_3}\} \end{aligned}\\ \llbracket \varGamma _1\rrbracket&\begin{aligned}&= \{p_1\bar{p_2}{p_3}\}&\llbracket \varGamma _2\rrbracket&= \{\bar{p_1}p_2{p_3}\} \end{aligned}\\ \llbracket \varGamma _{0,1}\rrbracket&= \{p_{1}p_2\bar{p_3},\ p_1\bar{p_2}{p_3},\ p_1\bar{p_2}\bar{p_3}\}\\ \llbracket \varGamma _{1,2}\rrbracket&= \{p_1\bar{p_2}{p_3},\ \bar{p_1}p_{2}p_3,\ \bar{p_1}\bar{p_2}p_3\}\\ \llbracket \varGamma _{2,0}\rrbracket&= \{p_{1}p_2\bar{p_3},\ \bar{p_1}p_{2}p_3,\ \bar{p_1}p_2\bar{p_3}\} \end{aligned}$$

One can check quickly that Condition (I) and Condition (II) are satisfied by considering the intersections of the corresponding sets of models. For Condition (III), one has to check all \({\varGamma _{\!\triangledown }}\) that are consistent with each of \(\varGamma _{0,1},\varGamma _{1,0}\), and \(\varGamma _{2,0}\). In this logic, only \(\varGamma _{\!\triangledown }=\emptyset\) satisfies this condition. Because \(\varGamma _{\!\triangledown }'=\textrm{K}\) is consistent, and (a) and (b) from Definition 1 hold, Condition (III) is also satisfied.

Because \(\varGamma _{0,1},\varGamma _{1,2},\varGamma _{2,0}\) is a critical loop, Theorem 2 yields that there is an AGM revision operator \(\star\) that is not total-preorder-representable. The operator \(\star\) behaves as follows:

$$\begin{aligned} \llbracket \textrm{K}\star (p_3\wedge p_2\rightarrow \bot )\rrbracket&=\{ {p_1}{p_2}\bar{p_3} \}\\ \llbracket \textrm{K}\star (p_2\wedge p_1\rightarrow \bot )\rrbracket&=\{ {p_1}\bar{p_2}{p_3} \}\\ \llbracket \textrm{K}\star (p_1\wedge p_3\rightarrow \bot )\rrbracket&=\{ \bar{p_1}{p_2}{p_3} \} \end{aligned}$$

Fig. 1 illustrates the critical loop and illustrates the connection of a non-transitive part of a min-retractive relation that encodes the behaviour of \(\star\) shown above (via \((\dagger )\)).

Because Tarskian logics with a disjunction connective are always loop-free, we obtain the following corollary, showing that for most well-known logics, like first-order predicate logic, the connection (1) still holds.

Corollary 4

If \(\mathbb {L}\) is a Tarskian logic that supports disjunction, then every AGM revision operator for \(\mathbb {L}\) is total-preorder representable.

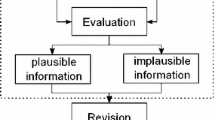
4 Revision with Limited Scope

Not every agent accepts all beliefs for revision, as, e.g., agents make distinctions based on the quality and credibility of beliefs and thus ignore certain new information. Because of this, it has been stated [10] that AGM revision operators are not an adequate model of how agents treat beliefs for revision, in the sense that agents do not accept all beliefs for revision, whereas AGM revision assumes that every belief is accepted for revision.

A prominent approach is credibility-limited revision [2, 11], which develops the idea that an agent accepts only credible new information for revision. The concept of credibility includes that an agent’s beliefs are inherently credible. Consequently, when performing credibility-limited revision, the agents want to keep as much of their current beliefs as possible during revision (as they are credible). This leads to a kind of belief revision which is guarded by a set of credibles \({\mathscr {C}}\) invoking the following dynamics:

$$\begin{aligned} \llbracket K\star \alpha \rrbracket = {\left\{ \begin{array}{ll} \llbracket K\rrbracket \cap \llbracket \alpha \rrbracket &{} \text {if } \llbracket K\rrbracket \cap \llbracket \alpha \rrbracket \ne \emptyset \\ \llbracket \alpha \rrbracket \cap {\mathscr {C}} &{} \text {if } \llbracket \alpha \rrbracket \cap {\mathscr {C}}\ne \emptyset \text { and } \llbracket K\rrbracket \cap \llbracket \alpha \rrbracket =\emptyset \\ \llbracket K\rrbracket &{} \text {otherwise} \end{array}\right. } \end{aligned}$$
Fig. 2
figure 2

Exemplary semantic description of the dynamics of dynamic-limited revision. \(\textrm{K}\) denotes the initial beliefs, \({\mathscr {S}}\) is the set of acceptables, and \(\alpha\) is the newly arriving information. The red area is the area containing the revision result \(K\star \alpha\)

Full size image

The dissertation thesis develops a novel theory of revision for propositional logic where the outcome of revisions is limited to certain predetermined beliefs. Developing this idea formally leads to dynamic-limited revision, an approach formalized in the same style as credibility-limited revision. Dynamic-limited revision involves a set of acceptables \({\mathscr {S}}\) (also called the scope), and dynamic-limited revision behaves as follows:

$$\begin{aligned} \llbracket K\star \alpha \rrbracket = {\left\{ \begin{array}{ll} \llbracket \alpha \rrbracket \cap {\mathscr {S}}\ne \emptyset &{} \text {if } \llbracket \alpha \rrbracket \cap {\mathscr {S}}\ne \emptyset \\ \llbracket K\rrbracket &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Fig. 2 provides examples of the induced belief dynamics. The long-term motivation to study dynamic-limited revision is to find good formal approaches with inherent expressiveness and explainability to describe real-world processes, e.g., transitions in psychological systems and engineering systems. Because of its different philosophical approaches, the difference to credibility-limited revision is that \({\mathscr {S}}\) is not necessarily interrelated with the current beliefs of the agent. For example, K might contain outdated beliefs, yet the agent does not realise this, but as soon she revises K according to new information, she becomes aware.

5 Iteration Principles for Contraction

Iterated belief change is about how prior changes influence subsequent changes, e.g., if \({K\!\circ \!\alpha \!\circ \!\beta }\) is different from \({K\!\circ \!\gamma \!\circ \!\beta }\). A different perspective on iterated change can be obtained by employing the characterization of belief changes by preference relations: the problem of iterated belief change can be understood as the question of how to obtain a relation \(\le '\) that characterizes \(K\circ \alpha \circ \beta\) from the relation \(\le\) that characterizes \(K\circ \alpha\). Principles and approaches for the iteration of AGM revision are a well-studied topic in belief change [8, 17]. The situation is different for AGM contraction, as there is a much smaller body of literature specially devoted to the topic of principles for iterated contraction, e.g., [4, 12, 16, 17].

The author’s thesis discovers several principles for iterated contraction in propositional logic. The main source of inspiration are principles for iterated revision, e.g., by Darwiche and Pearl [5]. The following types of principles are considered for iterated contraction:

  • Natural contraction. This is the kind of change where the contraction strategy does not evolve.

  • Substantiation of changes. When \(\beta _1\) and \(\beta _2\) are both consistent with \(\alpha\), or both are inconsistent with \(\alpha\), then the relative credibility of \(\beta _1\) and \(\beta _2\) does not change when contracting \(\alpha\).

  • Non-improvement of negation. When contracting \(\alpha\) the credibility of \(\alpha\) shall not be improved.

  • Independence. In analogy to the independence principle for revision [3, 13], this means that contraction of \(\alpha\) enforces improvement of the credibility of \(\lnot \alpha\).

Furthermore, gentle versions of the above-mentioned principles are considered. Besides investigating principles of change, the thesis also provides a coherent picture and a landscape of novel and known principles of iterated contraction. In particular, for all considered contraction principles, the thesis provides corresponding postulates from three different viewpoints (and proof of the equivalence of these postulates):

  • the viewpoint of changing beliefs,

  • the viewpoint of changing conditional beliefs, and

  • the viewpoint of changing “preferences”.

Note that for some of these operations, the description of how conditional beliefs are affected is an additional novelty.

6 Summary

We considered several contributions to the theory of belief change from [18]: novel characterizations of belief revision in arbitrary Tarskain logics; dynamic-limited belief revision operators, an approach for revision where agents are limited in what are the outcomes of a revision; advancements in the theory of iterated belief contraction by an investigation of several principles and their interrelation. Whereas all these results employ a semantic perspective on belief change.