Spanish GDP short-term point and density forecasting using a mixed-frequency dynamic factor model

Abstract

We have assessed the effect of data releases when constructing short-term point and density forecasts of the Spanish gross domestic product growth. For this purpose, we considered a real-forecasting exercise in which we defined several pseudo-data vintages that had a mixture of monthly and quarterly frequencies and were unbalanced towards the end of the sample. We implemented a mixed-frequency dynamic factor model to deal with data features and to produce gross domestic product forecasts. We evaluated the predictive content of data releases from point and density forecast perspectives, the latter aspect of the analysis being previously unexplored in the literature producing Spanish gross domestic product short-term forecasts. We observed significant improvements in point forecasts as information is released throughout the quarter, confirming existing results. Additionally, our findings indicated substantial enhancements in the accuracy of density forecasts as new data releases materialized.

1 Introduction

One of the well-known facts about gross domestic product (GDP) is that its values are released with a delay that exceeds 3 weeks for the first advance estimate of the previous quarter. For this reason, many economic agents, central banks, government statistical offices, and other financial institutions spend much of their time and resources constructing GDP short-term forecasts. For this purpose, they use a variety of monthly indicators, more frequently and more timely available than the target quarterly GDP. The combination of the quarterly GDP and monthly indicators used as predictors generates a mixed-frequency nature of data. Furthermore, as variables are asynchronous, with their latest data made available at different points in time and with different delays, a mix of available and missing observations comes up towards the end of the sample, a pattern known as unbalancedness or ragged edge data structure. Hence, constructing GDP short-term forecasts involves coping with missing observations as an essential part of data processing.

In Spain’s case, monitoring and tracking the short-term evolution of GDP is often supported by the dynamic factor model (DFM) and its state-space representation. These are, for instance, the Spain-STING (short-term indicator of growth) and MIDPred (integrated model of prediction), which are used by institutions like the Bank of Spain and the Independent Authority for Fiscal Responsibility, respectively, or the FASE model (factor analysis of the Spanish economy) which is originally designed to oversee and forecast GDP within the Ministry of Economy; see Camacho and Quiros (2011), Cuevas and Quilis (2012), Cuevas et al. (2017), and Pareja et al. (2020). Moreover, the MICA-BBVA (Model of economic and financial Indicators used to monitor the Current Activity by Banco Bilbao Vizcaya Argentaria) model has also been proposed to obtain GDP projections through real and several financial indicators; see Camacho and Doménech (2012). An essential part of the task of all these real-time forecasting applications is the construction of Spanish GDP short-term point estimates and evaluating their accuracy. A common finding is the existence of accuracy gains as new data become available during the quarter. Nevertheless, in an environment of increasing economic uncertainty, users of GDP forecasts demand point projections for its short-term evolution and, more assiduously, the complete future characterization provided by its short-term density forecasts; see, for instance, Mazzi et al. (2014), Aastveit et al. (2014, 2018), Bäurle et al. (2021), Mitchell et al. (2022), and Çakmakl i and Demircan (2022). Consequently, it is crucial to assess the information content of data at each point in time from the perspective of the GDP short-term density forecasts.

In the present paper, we have aimed to address the information when constructing Spanish GDP short-term forecasts, using the standard evaluation approach through point forecasts and, more relevantly and innovatively, density forecasts. For this purpose, we have combined thirty-two monthly indicators from the Spanish economy, including real-activity, financial and survey variables, and the quarterly employment and GDP growth rates within a mixed-frequency model-based forecasting methodology. The data-rich framework has enabled us to cover most of the indicators previously considered in the referenced models for Spain. As we did not have access to published historical records of the variables, we have assumed that the publication calendar on a recent date, i.e. beginning of October 2023, has been stable over the entire period and used this to define patterns of the missing observations towards the end of the sample.¹ Based on the data release timings, we first considered three temporal blocks, the early, the middle, and the late, which we further disaggregated into sub-blocks according to their economic content. Finally, the unbalancedness patterns of the temporal blocks and economic sub-blocks have been replicated in all quarters of the 1995–2023 period, producing pseudo-real-time data vintages that we have used to address the information inflow; see, for instance, Giannone et al. (2008) for USA, Kuzin et al. (2011) for the Euro area, and Cuevas et al. (2017) for Spain.

Apart from some specific nuances, the essence of the model we have used is the same as those referenced for Spain. We have constructed GDP forecasts using factors that summarize the overall state of the business cycle. The factor extraction is based on principal components (PC) and DFM; see Bańbura and Modugno (2014). The advantage of implementing a DFM approach is that it enables a large panel of variables to be modelled in a parsimonious way. Even more importantly, the DFM and its state-space representation deal with the mixed-frequency and unbalanced nature of the data. For this purpose, we ran the Kalman filter to fill any missing observations throughout, and at the end of the sample, and to produce a point forecast and conditional variance. We have used the latter with a normal assumption to provide a conditional distribution of the future GDP given the data availability, or density forecast.

We have performed a recursive estimation scheme incorporating the information flow and obtained point forecasts, as most papers on short-term Spanish GDP evolution have. Furthermore, we have investigated the performance of short-term density forecasts obtained by mixed-frequency DFM, an aspect almost always overlooked by the literature. Our findings confirmed the existence of valuable information released during the quarter from point forecasts perspective. Moreover, we observed substantial enhancements in the accuracy of Spanish GDP short-term density forecasts obtained through mixed-frequency DFM as the quarter progresses, and new information is incorporated into the data.

It is worth stressing that the literature concerning Spanish GDP short-term forecasting has focused solely on constructing and evaluating short-term point forecasts. The present paper adds the perspective of an evaluation through the GDP short-term density forecasts that can be generated through DFM and its state-space representation. By doing this, we have not sought an analysis of the relative merits of the different models to the phenomenon of Spanish GDP short-term forecasting. The real-time forecasting exercise and the evaluation of point and density forecasts for different data vintages may as well be employed in the methodological frameworks of the referenced papers.

We have organized the remainder of the paper as follows. The second section describes the data. The third explains how we artificially generated the pseudo-data vintages and describes the notation related to them. The fourth section presents the mixed-frequency DFM, its state-space representation, and how the Kalman filter produces point and density forecasts under data irregularities. Then, it discusses the forecast design and how we evaluated point and density forecasts. The fifth section presents and discusses the main findings. We have concluded in the sixth section.

2 Data description

Table 1 shows the basic set of indicators, consisting of thirty-two monthly variables and the quarterly employment and GDP growth rates. The target variable is the quarterly GDP for which we have considered its real (chained volume index) version. The indicators used as predictors of GDP represent a broad spectrum of the business cycle activities. Accordingly, we have included hard indicators related to real economic activity. These represent the labour market (such as registered unemployment and social security contributors), domestic economic activity (the manufacture industrial production index, electric power consumption, apparent consumption of cement, etc.), and the foreign sector (real export and import). In addition, we have considered the financial sector through the interest rate spread and the credit to companies and households; see Camacho and Doménech (2012) who found that financial indicators are specially relevant in producing a GDP forecast during periods of recession. Finally, we have also considered some of the soft indicators that potentially capture agents’ sentiment and confidence about the short-term future of the economy. These indicators cover opinion polls, i.e. survey-based indicators such as the purchasing managers’ index, economic sentiment and industry production perspective indicators.

In selecting indicators, we have been guided by the following criteria. Firstly, although it was not a requirement, we attempted, as much as possible, to have a balanced pattern of observations at the beginning of the sample period.² Thus, all monthly indicators have observations spanning from 1995, except for the registered unemployment, large companies’ sales variables, whose figures began in January 1996, the purchasing managers’ index, overnights, turnover index service, and turnover index industry, whose first observations were made in August 1998, January 1999, 2000 and 2002, respectively. Secondly, as far as possible, we wanted to have a rich data framework covering most of the indicators previously considered in the literature that has dealt with Spanish GDP short-term forecasting. Consequently, we have considered indicators previously used in the large-scale approach by Cuevas and Quilis (2012), or the small-scale DFMs of the Spanish economy by Camacho and Quiros (2011), Cuevas et al. (2017) and Pareja et al. (2020).³

We considered the seasonally adjusted variables to identify a systematic measure underlying the pure economic fluctuations of the GDP growth rate.⁴ Moreover, the type of DFM implemented in this paper requires stationarity in order to identify and estimate factors, which materialize through appropriate transformations that remove secular trends. We have obtained stationary fluctuations for most indicators by taking the first differences of their level or logarithm. The exceptions are the spread rate, and two soft indicators obtained from surveys, the purchasing managers’ index and the industrial production perspective indicator, for which we have considered their levels, as well as the registered unemployment and the credit to companies and households, for which we have induced stationarity by taking a second difference of its logarithm. Finally, the quarterly employment and GDP exhibit trend behaviours that led us to consider their first difference of their log transformations as an approximation of their quarterly growth rate.⁵

In the present paper, we have analysed two data frameworks in a real-time GDP forecasting exercise in the following sections. We have considered a data-rich environment, including all variables in Table 1. This comprehensive dataset has enabled us to analyse the information content over the quarter of a broad set of indicators encompassing those previously used in the literature constructing Spanish GDP nowcasts. It is the primary data framework for which we have conducted most of the short-term forecast evaluation analysis. On the other hand, for comparison, we have also considered a small-scale data framework, reproducing the indicators and data transformation of the MIDPred; see Cuevas et al. (2017).⁶ The variables with an ‘X’ in Table 1 correspond to those in the MIDPred data framework.

Table 1 List and information of monthly indicators and GDP: n, variable name, label, source code, unit of measurement, publication calendar (approximate number of days after the beginning of a month), composition of temporal blocks (i.e. early, middle, and late), composition of economic sub-blocks, (i.e. PMI, TRAIN, FUEL, etc.), and publication delay, in months, to which the last data release refers

3 Pseudo-real-time data vintages

Ideally, we would like to work with data vintages constructed with records of variables at the points in time when they were released, also including any revisions to previously published values that may have been made. Nevertheless, we cannot work with pure real-time vintages since we cannot access historical records of monthly indicators, employment and GDP. Instead, we have relied on pseudo-real-time vintages that were generated artificially to resemble the publication pattern of variables. The data were collected at the beginning of October 2023, just after the first advance of the third quarter of 2023, together with the publication dates of all indicators. The sixth column in Table 1 provides the publication calendar obtained in October 2023, i.e. the approximate number of days after the beginning of a month.

The critical assumption behind the pseudo-real-time vintages is that the publication calendar has always been the same for all months of the sample period 1995–2023, or, if it has changed, the timing basically remained unaltered. This assumption has served as the purpose of investigating the consequences that a rather new publication schedule has for GDP short-term forecasting, assuming that such a calendar will not undergo further alterations. We have not sought a historical assessment of the information content of past data vintages, but rather an analysis of what is implied by a recent publication schedule, keeping in mind forecasts that may be made with a similar schedule in the time to come. Of course, using pseudo-real-time data vintages did not enable us to tackle the effect of data revisions on forecast performance. We will leave this aspect for future research.

Using the assumed publication calendar, we grouped the variables according to the time of the month in which their new figures were published, which led us to distinguish three temporal blocks of publication that included indicators whose values are published early (E) in the month, i.e. approximately in the first third of it, in the middle (M), i.e. in the second third, and late (L) in the month, i.e. in the last third. The seventh column in Table 1 shows the variables that have made up each temporal block. Finally, the last column of Table 1 shows the delay in months, to which the last data release refers. We observed that the indicators’ published values refer to different periods. In blocks ‘E’ and ‘M’, data releases refer either to 1-lag or 2-lag months for registered unemployment and industrial production index, for example. On the other hand, in block ‘L’, the values released also refer to the current month, as is the case of soft survey-based economic sentiment and industrial production perspective indicators. As a result, each block is characterized by a certain pattern of available and missing observations.

The publication delay of the temporal blocks are replicated in the first month (0q/1m), second (0q/2m) and third (0q/3m) of the current quarter, generating a certain pattern of available and missing observations. In addition, we considered the last month of the preceding quarter ($-1q/3m)$, which illustrates the evolution of the information before the current quarter began, i.e. it gives a time perspective, and helps to seize the value of the information released in subsequent months, and the blocks ‘E’ and ‘M’ of the following quarter’s first month ($+1q/1m)$ that illustrate the data availability just before the release of the GDP first advance.

Note that each month has three temporal blocks of data releases, with the exception of the last month, which has only two. As a result, we had $\upsilon =1,2,...,14$ vintages, i.e. three for the first four months, and two for the last month.

The main issue of the temporal blocks is that they end up including variables with very diverse definitions. To overcome this issue, we have further divided them according to the economic content and temporarily ordered them, respecting their publication dates as much as possible.⁷ Therefore, we split the vintage ‘E’ into six sub-blocks: purchasing managers’ index (PMI), consumption of electric power (ENERGY), labour market (LABOUR), entry of tourist (TOUR), train traffic (TRAIN), consumption of gasoline and diesel (FUEL), spread and credit (FIN), industrial production (IPI), and sea traffic (SEA); ‘M’ in cement consumption (CEMENT), air traffic (AEREO), car and truck registration (VEHICLE R), large companies sales and compensation (SALES), construction production (CONSTRUCT), turnover service and industry indexes (TURNOVER), and the foreign sector (FOREIGN); finally, ‘L’ includes nights stays (OVERNIGHTS), employment, GDP, the survey-based indicator as economic sentiment and industrial perspective (SURVEY), activity related to the retail trade (RETAIL), and building permits and mortgage (BUILDING). In any case, the results were robust to changes in the order chosen for the sub-blocks. The eight column in Table 1 shows the resulting economic sub-blocks within each temporal block.

Grouping the indicators according to their economic content enabled us to investigate within the temporal blocks. We used economic sub-blocks in months within quarters, following the same reasoning explained above for the temporal blocks. There were $\upsilon =1,2,...,100$ data vintages when we took into consideration the economic sub-groups: twenty for first, second and fourth months, twenty-two for the third month (i.e. we have two additional vintages due to releases of quarterly employment and GDP), and eighteen for the last (i.e. only sub-groups before the release of the first advanced of GDP).

3.1 Notation

Let $t=1,2,...$ be a monthly time index. We denote the stationary monthly indicators by ${\tilde{X}}_{j,\,t}$, for $j=1,2,...,N_{X}$. On the other hand, we represent the quarterly stationary variables with ${\tilde{Y}}_{i,\,t}$, for $i=1$,..., $N_{Y}$, and assume that they only can be observed at months $t=3,6,9,...$ , and have missing observations for the rest of the months. The total number of indicators is $N=N_{X}+N_{Y};$ in the present paper, $N=34$ with $N_{X}=32$ and $N_{Y}=2$.

Let ${\tilde{X}}_{t}=({\tilde{X}}_{1,\,t},...,{\tilde{X}}_{N_{X},t})^{\prime }$ and ${\tilde{Y}}_{t}=({\tilde{Y}}_{1,\,t},...,{\tilde{Y}}_{N_{Y},\,t})^{\prime }$ be the $N_{X}\times 1$ and $N_{Y}\times 1$ vectors of monthly and quarterly indicators, respectively, and let ${\tilde{Z}}_{t}=({\tilde{X}}_{t}^{\prime },\,{\tilde{Y}}_{t}^{\prime })^{\prime }$ be the $N\times 1$ vector of mix-frequency variables. We denote the information set contained in a vintage $\upsilon$ by

$$\begin{aligned} \Omega _{\upsilon }=\left\{ {\tilde{Z}}_{n,\,t}\,|\,n=1,...,N,\,t=1,...,T_{n}\right\} , \end{aligned}$$

(1)

where $T_{n}$ is the last month for which there is an available observation for the nth variable. It emerges from (1) that associated with each $\Omega _{\upsilon }$, there is a total ($T_{1},T_{2},...,T_{34}$) that reflects the flow of information over time. For instance, consider the first month of the current quarter (0q/1m) and assume that it corresponds to time period $t=t_{0}$. The ‘E’ block delivers information of, among others, 1-lag months of purchasing managers’ index ($T_{1}=t_{0}-1$), 2-lag months of tourist entry ($T_{2}=t_{0}-2$), and so forth for the monthly indicators in Table 1. Regarding the quarterly series, the ‘E’ vintage has information of 2-lag quarters of employment and GDP (i.e. $T_{27}=t_{0}-6$ and $T_{28}=t_{0}-6$ ). When we move to vintage ‘M’, new data of, for instance, cement consumption is published, so that $T_{15}$ goes from $t_{0}-2$ in block ‘E’ to $t_{0}-1$ in ‘M’. Finally, the temporal block ‘L’ adds new data of, among others, the GDP of the previous quarter, $T_{28}$ changes to $t_{0}-3$. As a result, by late the first month of the current quarter (i.e. block L in 0q/1m), the GDP short-term projection changes from a two-period to a one-period-ahead forecast from the perspective of its last observation

Finally, let T $=\underset{j}{\textrm{max}}(T_{j})$, for $j=1,...,N_{X}$, be the last month for which we have information on at least one monthly variable, and $T^{*}=\underset{i}{\textrm{max}}(T_{i})/3$, for $i=1,...,N_{Y}$, be last quarter for which we have available information of employment and GDP.

4 Econometric methodology

Our aim is to forecast the short-term Spanish GDP growth based on the flow of monthly information during the quarter. Therefore, our econometric methodology must cope with missing observations and temporal aggregation from a monthly to quarterly frequency. In this study, we have combined the monthly variables and the quarterly employment and GDP in a mixed-frequency DFM (MFDFM).

All the models that produced Spanish GDP short-term forecasts using DFM are based on the same premise, which was to summarize the co-movement of a set of monthly and quarterly indicators through a common factor. They differed in the specific indicators and data transformations they used. Additionally, the choice of data framework influenced their modelling strategies. In the present paper, the basic model have tackled all variables using a MFDFM without modelling the serial correlation of the idiosyncratic errors. However, for comparison, we have also considered a different version of the MFDFM, reproducing the data framework and model specification (i.e. MFDFM with autoregressive -AR- idiosyncratic errors) of the MIDPred approach; see Cuevas et al. (2017).

Next, we summarize the most notable features of the MFDFM. Also, we present its state-space representation and briefly discuss how the Kalman filter handles missing observations and produces GDP short-term point and density forecasts. Details of state-space representation can be found in Appendix C.

4.1 Mixed-frequency dynamic factor model

Here, we consider the standardized versions of ${\tilde{X}}_{j,\,t}$ and ${\tilde{Y}}_{i,t^{*}}$,

$$\begin{aligned} X_{j,\,t}=({\tilde{X}}_{j,\,t}-\bar{\tilde{X_{j}}})/\sigma _{X_{j}},\quad j=1,...,N_{X},\,t=1,...,T_{j}, \end{aligned}$$

and

$$\begin{aligned} Y_{i,\,t}=({\tilde{Y}}_{i,\,t}-\bar{{\tilde{Y}}}_{i})/\sigma _{Y_{i}},\quad i=N_{X}+1,...,N_{Y},\,t=3,6...,T_{i}, \end{aligned}$$

where $\bar{\tilde{X_{j}}}$ and $\sigma _{{\tilde{X}}_{j}}$, and $\bar{{\tilde{Y}}}_{i}$ and $\sigma _{{\tilde{Y}}_{i}}$ are the sample mean and standard deviation of the jth monthly indicator and the ith quarterly variable growth rate, respectively.⁸⁹

Let $(X_{t}^{\prime },\,Y_{t}^{*\prime })^{\prime }$ be a $N\times 1$ zero mean and stationary vector containing the monthly variables at time $t=1,2,...,T$. This includes the observed monthly indicators $X_{j,t}$ and the unobserved quarterly employment $Y_{1,\,t}^{*}$ and GDP $Y_{2,\,t}^{*}$ growth rates. The DFM relies on the assumption that $(X_{t}^{\prime },\,Y_{t}^{*\prime })^{\prime }$ contains common components that represent, for example, the evolution of the business cycle. The model states that

$$\begin{aligned} \left( \begin{array}{c} X_{t}\\ Y_{t}^{*} \end{array}\right) =\left( \begin{array}{c} \Lambda _{X}\\ \Lambda _{Y} \end{array}\right) F_{t}+\left( \begin{array}{c} \varepsilon _{X,t}\\ \varepsilon _{Y,t} \end{array}\right) , \end{aligned}$$

(2)

where $\Lambda _{X}$ and $\Lambda _{Y}$ are $N_{X}\times r$ and $N_{Y}\times r$ matrices of loading coefficients of monthly and quarterly series, $F_{t}$ is a $r\times 1$ vector of common factors, and $\varepsilon _{X,t}$ and $\varepsilon _{Y,t}$ are $N_{X}\times 1$ and $N_{Y}\times 1$ vectors of idiosyncratic errors. Let $\Lambda =(\Lambda _{X}^{\prime }\,\Lambda _{Y}^{\prime })^{\prime }$ be the $N\times r$ matrix of loadings and $\varepsilon _{t}=(\varepsilon _{X,t}^{\prime },\varepsilon _{Y,t}^{\prime })^{\prime }$ be the $N\times 1$ vector of idiosyncratics with variance–covariance matrix $\Sigma _{\varepsilon }$. For the purpose of identification of the factors, we assume that $\left( \Lambda ^{\prime }\Lambda \right) /N=I_{r}$. The dynamics of the common factors are represented by a VAR(p) model,

$$\begin{aligned} F_{t}=\Phi _{1}F_{t-1}+\cdots +\Phi _{p}F_{t-p}+u_{t}, \end{aligned}$$

(3)

where $\Phi _{j}$, for $j=1,...,p$, are $r\times r$ autoregressive matrices satisfying the stationarity condition and $u_{t}$ is a $r\times 1$ zero mean error term with covariance matrix $\Sigma _{u}$. Furthermore, we assume that $\varepsilon _{t}$ and $u_{s}$ are uncorrelated for all $(t,\,s).$

It is worth noting that the factor model of Eqs. (2) and (3) is expressed in the monthly frequency. We need a connection between the quarterly GDP and its underlying and unobserved monthly value to turn it into the mixed-frequency setting of the present paper. For this purpose, we have assumed that the observed quarterly GDP growth rate is related to its unobserved monthly counterpart by the following equation:

$$\begin{aligned} Y_{t}=Y_{t}^{*}+2Y_{t-1}^{*}+3Y_{t-2}^{*}+2Y_{t-3}^{*}+Y_{t-4}^{*}; \end{aligned}$$

(4)

see, for instance, Mariano and Murasawa (2003) and Bańbura et al. (2013). Then, we readily obtain an expression for the observables $(X_{t}^{\prime },\,Y_{t}^{\prime })^{\prime }$

$$\begin{aligned} \left( \begin{array}{c} X_{t}\\ Y_{t} \end{array}\right)= & {} \left( \begin{array}{c} \Lambda _{X}F_{t}\\ \Lambda _{Y}(F_{t}+2F_{t-1}+3F_{t-2}+2F_{t-3}+F_{t-4}) \end{array}\right) \nonumber \\ \nonumber \\{} & {} +\left( \begin{array}{c} \varepsilon _{X,t}\\ \varepsilon _{Y,t}+2\varepsilon _{Y,t-1}+3\varepsilon _{Y,t-2}+2\varepsilon _{Y,t-3}+\varepsilon _{Y,t-4} \end{array}\right) . \end{aligned}$$

(5)

Equations (5) and (3) define the MFDFM. Note that within it, the expression for $Y_{t}$ (2nd equation) shows a dependency on the current and lag values of the common factors $F_{t}$ and errors $\varepsilon _{Y,t}$, a feature that has implications when representing the model in state-space form.

4.1.1 State-space representation of the MFDFM

For the sake of exposition, we have assumed that the lag order of the (V)AR dynamics is less than 5, i.e. $p\le 4,$ and no dynamics for the idiosyncratic error. The generalization to a larger lag order and dynamics of the idiosyncratic is straightforward. The state-space (SS) representation can be approximated by

$$\begin{aligned} \left( \begin{array}{c} X_{t}\\ Y_{t} \end{array}\right) =Cs_{t}+\left( \begin{array}{c} \varepsilon _{X,t}\\ \nu _{Y,t} \end{array}\right) , \end{aligned}$$

(6)

$$\begin{aligned} s_{t}=As_{t-1}+\eta _{t}, \end{aligned}$$

(7)

where the state variable is a $\left[ 5\times (r+N_{Y})\right] \times 1$ vector

$$\begin{aligned} s_{t}=(F_{t}^{\prime },F_{t-1}^{\prime },F_{t-2}^{\prime },F_{t-3}^{\prime },F_{t-4}^{\prime },\varepsilon _{Y,t}^{\prime },\varepsilon _{Y,t-1}^{\prime },\varepsilon _{Y,t-2}^{\prime },\varepsilon _{Y,t-3}^{\prime },\varepsilon _{Y,t-4}^{\prime })^{\prime }, \end{aligned}$$

and $\nu _{Y,t}$ is a $N_{Y}\times 1$ zero mean error with diagonal variance–covariance matrix, the elements of the latter, i.e. $\sigma _{\nu _{Y_{i}}}^{2}$, being very small numbers, and $\eta _{t}=(u_{t}^{\prime },0^{\prime })^{\prime }$ is a $\left[ 5\times (r+N_{Y})\right] \times 1$ vector.¹⁰ Let $(\varepsilon _{X,t}^{\prime },\nu _{Y,t}^{\prime })^{\prime }\,\overset{i.i.d.}{\sim }{\mathscr {N}}(0,R)$ and $u_{t}\,\overset{i.i.d.}{\sim }{\mathscr {N}}(0,\Sigma _{u})$.

The SS matrices are the $N\times \left[ 5\times (r+N_{Y})\right]$ measurement coefficient matrix C that includes the loadings $\Lambda$, the $N\times N$ diagonal variance matrix R that has as its diagonal elements $\sigma _{\varepsilon _{X_{j}}}^{2}$, for $j=1,...,N_{X}$, and $\sigma _{\nu _{Y_{i}}}^{2}$, for $i=N_{X}+1,...,N,$ the $\left[ 5\times (r\times N_{Y})\right] \times \left[ 5\times (r\times N_{Y})\right]$ state matrices A that includes the dynamics of the factors $[\Phi _{1},...,\Phi _{p}]$, and Q that includes $\Sigma _{u}$ and ${\Sigma _{\varepsilon _{Y}}}$(i.e. $N_{Y}\times N_{Y}$ diagonal variance matrix of the error $\varepsilon _{Y,t})$.

The Kalman filter is able to handle efficiently missing observations by making adjustments to the observation vector and relevant matrices, and treating missing values as zeros with error variances set to one. This modification allows the Kalman filter to work even when data are missing. We estimated the parameters C, R,  A and Q using the KF with the EM algorithm, obtaining ${\hat{C}}$, ${\hat{R}}$ ${\hat{A}}$ and ${\hat{Q}}$; see Doz et al. (2012) and Bańbura and Modugno (2014).¹¹ Once we had the parameters estimates, we ran the KF recursions to obtain in-sample predictions $({\hat{X}}_{t|\,t-1}^{\prime },\,{\hat{Y}}_{t|\,t-1}^{\prime })^{\prime }$ and smoothed $({\hat{X}}_{t|\,T}^{\prime },\,{\hat{Y}}_{t|\,T}^{\prime })^{\prime }$ observations, for $t=1,2,...,T$.

The aim is to forecast GDP growth rate $h^{*}$ quarters out-of-sample given the information in $\Omega _{\upsilon },$ i.e. $Y_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }}$; or, equivalently, using data up to T, the last month with available observations in vintage $\Omega _{\upsilon }$, i.e. $Y_{2,\,3(T^{*}+h^{*})|\,T}$ . Let $h=3(T^{*}+h^{*})-T$. The $h^{*}-$quarter-ahead forecast of GDP is

$$\begin{aligned} {\hat{Y}}_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }}=J{\hat{C}}{\hat{A}}^{h}{\hat{s}}_{T|\,T-1}, \end{aligned}$$

(8)

where J is a $N\times 1$ selection vector $(0,0,...,1)^{\prime }$, when $h\ge 0$, and the smoothed observation, when $h<0$. The MSPE is

$$\begin{aligned} {\hat{F}}_{Y_{2},\,3(T^{*}+h^{*})}={\left\{ \begin{array}{ll} J^{\prime }\left[ {\hat{C}}{\hat{A}}^{h}{\hat{P}}_{T}{\hat{C}}^{\prime }{\hat{A}}^{h\prime }+{\hat{C}}\left( \sum _{j=0}^{h-1}{\hat{A}}^{j}{\hat{Q}}{\hat{A}}^{j\,\prime }\right) {\hat{C}}^{\prime }\right] J, &{} \quad h\ge 0\\ \\ V_{Y_{2},\,3(T^{*}+h^{*})|\,T,} &{} \quad h<0 \end{array}\right. }. \end{aligned}$$

(9)

where $V_{Y,\,3(T^{*}+h^{*})|\,T}$ is the smoothed variance. Under the assumption of normality of the errors, the forecast density of $Y_{2,\,3(T^{*}+h^{*})}$ is also Normal

$$\begin{aligned} Y_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }}\sim \mathrm {{\mathscr {N}}}\left( {\hat{Y}}_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }},\,{\hat{F}}_{Y_{2},\,3(T^{*}+h^{*})}\right) . \end{aligned}$$

(10)

Finally, to return to the original units of measurement of GDP, we transform (8) by

$$\begin{aligned} \hat{{\tilde{Y}}}_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }}=\bar{{\tilde{Y}}}_{2}+\sigma _{{\tilde{Y}}_{2}}\times {\hat{Y}}_{2,\,3(T^{*}+h^{*})|\,\Omega _{\upsilon }}. \end{aligned}$$

Accordingly, the conditional variance of ${\tilde{Y}}_{2,\,3(T^{*}+h^{*})}$ is

$$\begin{aligned} \textrm{V}({\tilde{Y}}_{2,\,3(T^{*}+h^{*})}|\,\Omega _{\upsilon })=\sigma _{{\tilde{Y}}_{2}}^{2}\times {\hat{F}}_{Y_{2},\,3(T^{*}+h^{*})}. \end{aligned}$$

4.2 Forecast design

We carried out a recursive estimation scheme that started with the period 1995Q2–2004Q4. We estimated model parameters, for given r and p,  using the first vintage early of the second month of the third quarter 2004, and constructed the fourth quarter point forecast of GDP $\hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\,\Omega _{\upsilon }}$, and the conditional variance $\textrm{V}({\tilde{Y}}_{2,\,T^{*}+h^{*}}|\,\Omega _{\upsilon })$. Then, we obtained the forecast error $e_{T^{*}+h^{*}|\,\Omega _{1}}^{(1)}={\tilde{Y}}_{2,\,T^{*}+h^{*}}^{(1)}-\hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\Omega _{1}}^{(1)}$, and density forecast ${\mathscr {N}}\left( \hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\,\Omega _{1}}^{(1)},\textrm{V}({\tilde{Y}}_{2,\,T^{*}+h^{*}}|\,\Omega _{\upsilon })\right)$. We continued successively, replicating the pattern of missing observations and the ragged edge structure at the end of the sample for each vintage $\Omega _{\upsilon }$, estimating the parameters and obtaining the 2004Q4 GDP forecast, conditional variance, forecast error and density forecast, for data vintages $\upsilon =2,...,\Upsilon$. Then, we roll the end of the sample period one quarter to the first quarter 2005, and repeated the process of replicating vintages, estimating parameters, forecasting the first quarter GDP growth, constructing its conditional variance, and obtaining the corresponding forecast error and density forecast, for $\upsilon =1,...,\Upsilon$. We did this until we exhausted the pre-COVID period, and obtained as the last estimation window 1995Q2–2019Q4.

The year 2020 is unprecedented in recent history, marked by the outbreak of COVID-19 and the consequent lockout to fight against the virus’s spread and to control the pandemic. As a result, in 2020, atypical observations in the system variables were introduced. These observations posed challenges for the econometric time series models because of their adverse effect on estimation and forecasting, and the discussion of possible solutions is still at an early stage, ranging from modelling outliers or estimating models with observations prior to the pandemic; see Carriero et al. (2021), Schorfheide and Song (2021) and Ng (2021), among others. To exemplify the magnitudes, we refer to when discussing exceptional values in economic variables during the COVID-19 pandemic, consider the Great Recession in which the Spanish GDP fell by 2.6% in the first quarter of 2009, the bottom of economic slowdown. By comparison, in the first quarter of 2020, when mobility restrictions began in mid-March, GDP experienced a 5.5% drop, followed by the lowest point in the second quarter, when the GDP growth rate registered − 19.4%. These unusual declines were followed by a rebound of 15.5% in the third quarter.

To deal with the atypical observations that appeared in 2020 with the onset of the pandemic, we worked with parameter estimates obtained using the pre-COVID period 1995Q1–2019Q4 and the post-Covid period 2021Q2 onward. For this purpose, we replaced the values of the variables in the data vintages that corresponded to the months between March and December 2020 with missing observations; see, for instance, Schorfheide and Song (2021) who estimated a Bayesian mixed-frequency VAR with pre-COVID and found that this strategy compared favourably to treating atypicals with the inclusion of a stochastic volatility process. Then, we estimated the mixed-frequency DFM and fed the estimated model with the original observations to construct the GDP forecasts. As the GDP 2020Q1–2021Q1 forecasts were far from the observed GDP values, the resulting forecast errors were very large and log-scores extremely low. We left out the extreme 2020–2021 months, thereby avoiding performance measures that varied considerably and were far from the more usual values obtained when considering the rest of the quarters.

In the end, we have $\hat{{\tilde{Y}}}_{2,T^{*}+h^{*}|\,\Omega _{\upsilon }}^{(w)}$, $\textrm{V}({\tilde{Y}}_{2,\,T^{*}+h^{*}}|\,\Omega _{\upsilon }),$ $e_{T^{*}+h^{*}|\,\Omega _{\upsilon }}^{(w)}$ and ${\mathscr {N}}\left( \hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\,\Omega _{\upsilon }}^{(w)},\textrm{V}({\tilde{Y}}_{2,\,T^{*}+h^{*}}|\,\Omega _{\upsilon })\right)$, for data vintages $\upsilon =1,...,\Upsilon ,$ and for quarters $w=1,...,W=70$ covering the period 2004Q4–2019Q4 and 2021Q2–2023Q2, to compute out-of-sample measures of forecast performance.¹²

4.3 Assessing the effects of vintages

Our goal was to evaluate the impact of the flow of information on GDP nowcasts. For this purpose, we used two types of measures that focused either on points or density forecasts.

Firstly, we considered, as most of the papers analysing the performance of short-term GDP point forecasts do, the average squared deviation of the observed GDP growth rates from their point forecasts, or MSPE, given by

$$\begin{aligned} \textrm{MSPE}=\frac{1}{W}\sum _{w=1}^{W}({\tilde{Y}}_{2,\,T^{*}+h^{*}}^{(w)}-\hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\,\Omega _{\upsilon }}^{(w)})^{2}, \end{aligned}$$

(11)

where W is the total number of quarters for which we computed out-of-sample forecasts. The MSPE is low for forecasts close to the observed GDPs. When we discussed the results, instead of presenting MSPE directly, we consider its square root, or the Root MSPE. The latter has the advantage of returning to the original unit of measurement of the series. On the other hand, we considered the average log score (ALS) to measure the accuracy of density forecasts that are based on different data vintages. The ALS is the average of the natural logarithm of density forecasts evaluated at the realized GDPs, as follows:

$$\begin{aligned} \textrm{ALS}=\frac{1}{W}\sum _{w=1}^{W}\textrm{log}\left( \hat{\phi }_{\Omega _{\upsilon }}\left( {\tilde{Y}}_{2,\,T^{*}+h^{*}}^{(w)}\right) \right) , \end{aligned}$$

(12)

where $\hat{\phi }_{\Omega _{\upsilon }}(\cdot )$ denotes the normal density forecast of $Y_{2,\,T^{*}+h^{*}}^{(w)}$. Indeed, it is large when the density forecasts assign a high probability to the observed GDP growth rates and, consequently, can be used to rank them; see Bao et al. (2007). Note that in Eqs. (11) and 12, the point and density forecast depend on the estimated model and the information set. As a result, MSFE and ALS reflect the uncertainty associated with parameter estimation and model instability, and the information flow.

Furthermore, we have provided statistical tests to assess the predictive content of new data releases. The crucial point is whether the information inflow improves the forecast performance. Relevant new information, when included in an expanding information set, should lead to a forecast with lower MSPE. On the contrary, information lacking a predictive value should alter neither the point forecast nor the resulting MSPE. We implemented a Mincer–Zarnowitz type of regression to test the predictive content of new information, as follows:

$$\begin{aligned} e_{T^{*}+h^{*}|\Omega _{\upsilon }}^{(w)}=\beta _{0}+\beta _{1}\Delta \hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\Omega _{\upsilon +1}}^{(w)}+u_{T^{*}+h^{*}},\quad w=1,...,W, \end{aligned}$$

(13)

where $\Delta \hat{{\tilde{Y}}}_{2\,T^{*}+h^{*}|\Omega _{\upsilon +1}}^{(w)}=\hat{{\tilde{Y}}}_{2\,T^{*}+h^{*}|\Omega _{\upsilon +1}}^{(w)}-\hat{{\tilde{Y}}}_{2,\,T^{*}+h^{*}|\Omega _{{\upsilon }}}^{(w)}$, is the forecast revision; see Mincer and Zarnowitz (1969), and Elliott and Timmermann (2016), pp. 355–358. The no relevant new information hypothesis can be expressed in terms of the slope coefficient $\beta _{1}$, which must be zero. Rejecting the null hypothesis means that the forecast error obtained using the information in $\Omega _{\upsilon }$ is correlated with the new information in $\Omega _{\upsilon +1}$ that is comprised in the forecast revision. Therefore, we would conclude that the inflow of information is relevant to the GDP forecast, and including it in the information set can lead to a MSPE reduction. We implemented a similar argument to test whether new information significantly changes ALS. The regression used is of the same type as (13) but it has as dependent variable the scaled forecast error $e_{T^{*}+h^{*}|\Omega _{\upsilon }}^{(w)}/\textrm{V}({\tilde{Y}}_{2,\,T^{*}+h^{*}}|\,\Omega _{\upsilon })$. Once more, rejecting the null of a slope coefficient equal to zero implies that the new information improves the expected log-scored.¹³

Finally, we assessed the density forecast in terms of its calibration. A well-calibrated density forecast reasonably estimates the unknown conditional distribution of the future variable (Gneiting et al. (2007) and Mitchell and Wallis (2011)). We used the probability integral transform numbers (PITs), the inverse forecast cumulative distribution evaluated at the realized observations, and the inverse PITs (INTs). If the density forecast shows conformity with the true and unknown one, i.e. it is well-calibrated, the PITs are i.i.d. uniform over the interval (0,1) and, thus, the INTs are i.i.d. standard normal; see Diebold et al. (1998) and Berkowitz (2001). We considered the likelihood ratio test devised by Berkowitz (2001), which is based on the INTs and exploits their three characteristics under the null hypothesis of correct calibration: zero mean, unit variance, and absence of serial correlation. Berkowitz’s test statistics is

$$\begin{aligned} B=-2\left[ \mathfrak {{\mathscr {L}}}(0,1,0)-{\mathscr {L}}({\hat{c}},\hat{\sigma }^{2},\hat{{\rho }})\right] \sim \chi _{3}^{2}, \end{aligned}$$

where ${\mathscr {L}}(c,\sigma ^{2},\rho )$ is the exact log-likelihood when we assume that $INT_{t}=c+{\rho }INT_{t-1}+e_{t},\quad e_{t}\overset{i.i.d.}{\sim }{\mathscr {N}}(0,\sigma ^{2})$, and hats denote estimated parameters. Accordingly, $\mathfrak {{\mathscr {L}}}(0,1,0)$ is the log-likelihood function obtained under the assumption that INTs are i.i.d. normal zero mean and unit variance; see Berkowitz (2001). An inspection of the constant, variance and autoregressive coefficient estimates can reveal the reasons behind the quality of calibration, i.e. causes that lead away from the null hypothesis of conformity between the estimated density forecast and the true and unknown one.

The asymptotic chi-squared distribution of Berkowitz’s statistics is obtained assuming that the sample size is large enough so that the estimation errors of the constant, variance, and autoregressive coefficient vanish. Nevertheless, in our case, the sample size (i.e. number of the INTs) was small, so this assumption was difficult to maintain. Also, estimation errors underlies the INTs as they are based on a MFDFM with parameters fixed at some estimates. Thus, parameter uncertainty makes the asymptotic distribution of the Berkowitz’s statistic very conservative. For this reason, we also constructed its bootstrap distribution to tackle parameter and estimation errors and obtained its critical values of interest; see Hall and Wilson (1991) and Kreiss and Franke (1992).

5 Empirical results

To implement the MFDFM, we first need to set the number of common factors (r) and the lag order of their dynamics (p). Here, we have followed the referenced literature producing Spanish GDP short-term forecasts and chosen $r=1$ and $p=2$ to present the results of the real-time forecasting exercise; see Camacho and Quiros (2011), Cuevas and Quilis (2012), Cuevas et al. (2017), and Pareja et al. (2020).¹⁴

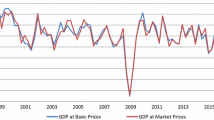
To characterize the factor, i.e. to give it an economic interpretation, we considered as an illustration the estimation results when we used the complete data set covering the period 1995Q2–2023Q2. The first factor explained 57% of the total variability and described the business cycle, as suggested by Fig. 1, with large positive weights for social security affiliates (SSAFI), industrial production perspective (S INDUPP), and purchasing managers’ index (PMI), and large negative weight for the spread rate (INT), and medium-size positive weights for large companies’ sales (SALES), turnover index service (TURNOVER S), industrial production indexes (IPI and IPIM), retail trade index (RETAIL), and consumption of cement (CEMENT). Furthermore, Fig. 2 shows the estimated re-centred and scaled common component

$$\begin{aligned} \bar{{\tilde{Y}}}_{2}+\sigma _{{\tilde{Y}}_{2}}\times \left[ \hat{\Lambda }_{Y_{2}}\times ({\hat{F}}_{t}+2{\hat{F}}_{t-1}+3{\hat{F}}_{t-2}+2{\hat{F}}_{t-3}+{\hat{F}}_{t-4})\right] \end{aligned}$$

tracks quite well the GDP growth rate and it is effective in capturing in advance the movement of the latter. Both are highly correlated contemporaneously, with an estimated correlation coefficient of 0.95. They are also dynamically correlated, with estimated cross-correlation coefficients between GDP and the common component’s one- and two-quarter lags of 0.92 and 0.86, respectively.

Fig. 1

Estimated loadings obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset. The estimation period is 1995Q2–2023Q2

Fig. 2

Quarterly Spanish GDP growth rate and estimated common component obtained using a obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset. The estimation period 1995Q2–2023Q2

5.1 Point and density forecast performance

Figure 3 plots the root MSPE (RMSPE) over the temporal blocks and their economic disaggregation obtained for the large data framework with the MFDFM without modelling the dynamics of the idiosyncratic errors. For comparison, we have also included the point accuracy when we estimated and forecasted the GDP growth rate using MIDPred approach. Furthermore, we also reported the AR(1) forecast as a benchmark. The first panel of Fig. 3 shows that publication releases throughout the quarter are essential as they reduce the RMSPE. However, the rates at which RMSPE decreases are not constant for all releases. We observe that the steepest declines in point forecast accuracy attained by the MFDFM occur at vintages $-1q/3m$, and 0q/1m, then dampen before disappearing towards mid $+0q/3m$. The first panel of Fig. 3 also suggests that when the purpose is to produce Spanish GDP short-term estimates, the rich data environment and the MIDPred approaches provide somewhat similar performance for all data vintages. Nevertheless, these approaches systematically outperform the AR(1), attaining better accuracy than the benchmark for all publication releases. Interesting to note is that MDDFM are comparatively more attractive than the AR(1) for data vintages before the release of the first advance of GDP than for the subsequent releases.

The first panel of Fig. 3 also reports the observed test statistics for the null hypothesis of no informational gain between consecutive vintages. We have reported these test statistics for the large data frame approach. In the first panel in Fig. 3, we observed that those vintages with steep drops in MSPE are associated with positive and significant observed statistics, meaning a rejection of the null of no informational gain. In contrast, contained drops in MSPE between consecutive vintages show statistics that are small in magnitude and non-significant, i.e. with no strong evidence against the null. Therefore, we corroborated that referring to the pronounced reductions in MSPE and the presence of significant informational gains are equivalent.

We can analyse which type of series contributes the most to the improvement of forecast performance using the second panel in Fig. 3, which reports the RMSPE, and the observed test statistic for the economic sub-blocks. The first aspect to highlight is that the overall behaviour of the point forecast accuracy. Moreover, we observed that MFDFM approaches are better than AR(1) for all vintages, although much more attractive before the release of the latest GDP data in the current quarter’s first month. Remarkably, the closest approach between the performances of the MFDFM methods and the AR(1) models is produced when the advanced of the previous quarter’s GDP is released.

The labour market (LABOUR) data has a pronounced impact on MSPE. The LABOUR sub-block includes the registered unemployment, social security affiliates, and registered contracts, indicators that are published as soon as the month begins, with the latest values referring mainly to the previous month. Also important in terms of RMSPE reduction is SURVEY, composed of survey-based indicators, which are released at the end of the month and are the most timely since they are the first to have information about it. The purchasing managers’ index service (PMI S) also provides pronounced drops in RMSPE. Beyond LABOUR, SURVEY, and PMI S, we observed a substantial reduction in the RMSPE when the latest GDP data is released towards the end of the quarter’s first month. Another sub-group that provides additional point forecast accuracy, although less pronounced, is IPI, which gives positive and statistically significant MSPE reductions in the first two months.

It is worth noting that the existing literature on Spanish GDP short-term forecasts has consistently observed improvements in the accuracy of point forecasts as new data related to GDP and its predictors becomes available throughout the quarter. Furthermore, our findings have emphasized the significance of LABOUR, SURVEY, IPI, and PMI indicators, which have already been recognized as relevant for producing Spanish GDP short-term forecasts, while also prompting questions about the contributions of retail sales, overnight stays, energy consumption, and large companies’ sales.

Fig. 3

RMSPE over temporal blocks (first) and economic sub-groups (second) between $-1q/3m$ and $+1q/1m$ for quarterly GDP growth rate obtained using a: (i) MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset (continuous-dotted blue line), (ii) a MFDFM with $r=1$ and $p=2$ and AR(1) idiosyncratic errors applied to the small-data set, i.e. MIDPred model (continuous blue line), and, (iii) univariate AR(1) model (dashed blue line). The vertical bars show the observed test statistics obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset for the null hypothesis of no information gain between the data vintage on the x-axis and the one immediately preceding it, and the vertical area outside the dash horizontal lines represent a 5% Rejection Region (color figure online)

We have further evaluated the predictive content of the information flow for GDP short-term destiny forecasts. The panels in Fig. 4 report the ALS for the Spanish GDP growth rate density forecasts for the MFDFM approaches and the AR(1) model over the temporal blocks and their economic disaggregation. They also include the observed test statistics for the null hypothesis of no relevant information for the density forecasts, obtained for large data frame. Once more, a rejection of the null hypothesis points to a potential improvement in the density forecast that we could achieve by recomputing the point forecast and, consequently, the density, leading to an improvement in log score.

The first panel in Fig. 4 shows that the ALS increases as the new data becomes available, i.e. Spanish GDP short-term density forecasts improve with the information inflow. More specifically, the ALS varies only slightly in $-1q/3m$ , then changes most sharply during the 0q/1m and 0q/2m , stabilizing its growth from 0q/3m onward. Remarkably, most of the significant temporal blocks in the first panel in Fig. 4 are also relevant in the first one in Fig. 3 when we focus on point forecast accuracy. The second panel of Fig. 4 shows positive changes in density forecast accuracy during 0q/1m that moderate after it, confirming the results of the first panel. The most relevant economic vintages in terms of log score improvement are the LABOUR, SURVEY, GDP, and IPI, which sometimes produce positive moderate, and significant changes in the log score, in that order.

Furthermore, Fig. 4 suggests that the large dataset and the MIDPred approaches provide similar ALS, perhaps slightly better for the former than the latter from mid 0q/1m onwards. The comparison of the ALS of MFDFM methods and the AR(1) model also revealed, on one side, that the former provides, on average, much better density forecasts and, on the other, that the difference between the two is more pronounced until the release of the first GDP advance of the previous quarter. Moreover, this point in the current quarter produces the closest approximation between the ALS of both models.

An explanation is that before the release of the latest GDP data, the more timely monthly indicators signal the evolution of the business cycle, replacing the most recent and unavailable GDP information. Accordingly, monthly predictors produce substantial relative gains with respect to an AR model in which only GDP information is exploited. The latest GDP figure brings information on business cycle conditions that were summarized, until that time in the monthly indicators and produces an approximation of the performances of the MFDFM and the AR model.

Fig. 4

ALS over temporal blocks (first) and economic sub-groups (second) between $-1q/3m$ and $+1q/1m$ for quarterly GDP growth rate obtained using a: (i) MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset (continuous-dotted blue line), (ii) a MFDFM with $r=1$ and $p=2$ and AR(1) idiosyncratic errors applied to the small-data set, i.e. MIDPred model (continuous blue line), and (iii) univariate AR(1) model (dashed blue line). The vertical bars show the observed test statistics obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset for the null hypothesis of no information gain between the data vintage on the x-axis and the one immediately preceding it, and the vertical area outside the dash horizontal lines represent a 5% Rejection Region (color figure online)

In summary, there are point forecast performance measures revealed the importance of the information flow Spanish GDP growth rate nowcasts. Likewise, with some nuances, they point out that the most pronounced improvement are attained towards the end of the current quarter’s first month. This moment in the quarter emerges as the period of separation between data vintages that produces, firstly, the greatest improvement in forecast performances and, secondly, the largest difference between the MFDFM approaches and the AR(1) model. An explanation is that before the release of the latest GDP data, the timely monthly indicators signal the evolution of the business cycle, providing a summary of the unavailable previous quarter’s GDP information. Accordingly, relevant monthly predictors produce a substantial improvement in forecast accuracy measures and generate the most evident relative gain with respect to an AR model in which only the GDP information has been exploited. Finally, those indicators with a high information content are those in the LABOUR, SURVEY, PMI S, and IPI.

5.2 Density forecast calibration

We now turn to the calibration of density forecasts. Figure 5 shows Berkowitz’s observed test statistics obtained for density forecasts over economic data vintages and its 5% asymptotic and bootstrap critical values. An observed test statistic larger than the critical value at a given significance level implies that we cannot reject the null hypothesis of good calibration of the density forecast. But beyond this rigid interpretation, we implement the critical values as a reference to globally differentiate data vintages that generate an inadequate density forecast calibration from those in which there is no evidence against a good one. In Fig. 5, we observe less and less evidence against good calibration as more and more data becomes available in the first three months. In other words, the GDP short-term density forecasts steadily improve and approach the region of no evidence against good calibration with the flow of information. It is also remarkable that the steepest changes in the observed B occur throughout 0q/1m, generating an apparent clustering between the vintages for which we clearly reject the null of good calibration hypothesis and those for which there is no strong evidence against it.

Fig. 5

First, Berkowitz’s observed test statistics for the null of good density forecast calibration over data vintages between $-1q/3m$ and $+1q/1m$ obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset applied. The vertical areas above the horizontal continuous lines and the dash line represent the 5% asymptotic and bootstrap rejection regions. Second, estimates of constant (${\hat{c}})$, variance $\hat{\sigma }^{2}$ and autoregressive coefficient $(\hat{\rho })$ for each economic sub-block

Berkowitz’s test signals a violation of the hypothesis of good calibration, but it does not provide reasons for it. The latter need to be found in the characteristics that INTs should have and may lack. Thereby, we included the second panel in Fig. 5 which plots the estimated values ${\hat{c}}$, $\hat{\sigma }^{2}$, and $\hat{\rho }$ underlying the test. Firstly, the estimated constant is always negative, showing little approximation towards its null value of zero with data releases. A negative constant indicates a density forecast giving high probabilities to large values of the future outcome, i.e. it has a large mean, signalling a positive bias of point forecasts. Secondly, the estimated variance decreases with data releases, especially since the beginning of the current quarter, indicating that the reason for the closer proximity between the density forecasts and the unknown ones archived with data releases is a better estimation of the conditional variance. Furthermore, the fact that the estimated auto-correlation of INTs diminishes over data vintages indicates that the mixed-frequency DFM used to construct GDP forecasts better captures the GDP dynamics, as more information becomes available.¹⁵

Overall, the estimated values of ${\hat{c}}$, $\hat{\sigma }^{2}$ and $\hat{\rho }$ indicate that the less evidence against the null of conformity between the density forecast and the unknown achieved with data releases is mainly due to a reduction in the dispersion and the auto-correlation of the INTs. In other words, calibration improves with data releases because the density forecasts better capture the conditional variance of the unknown ones.

As an illustration, Figs. 6 and 7 show the GDP growth rates density forecasts and its realized value for several quarters. The first notable impression from these figures is that GDP short-term density forecasts evolve with the data releases throughout the quarter, as the information flow affect the conditional mean and variance estimates underlying the conditional normal densities. The centre of the latter, i.e. the point forecast, moves as if trying to catch the realized GDP growth rate, and the dispersion narrows with new data releases. For example, Fig. 6 displays the situation during the great economic recession of 2008/2009. The fourth quarter of 2008 and the first quarter of 2009 show a continuous adjustment towards the left in short-term density forecasts as the information flow proceeds, but not enough because the realized GDP growth rates are well located on the left tail of the densities. In the second and third quarters of 2009, the situation reverses, and the flow of information pushes densities from the left to GDP. Moreover, the reduction in dispersion with data releases is apparent.

Changes in GDP density forecasts with the information flow are also evident in panels of Fig. 7, which describe the quarters in 2019, although comparatively less pronounced than those seen in Fig. 6. A sharp contrast in these figures shows us that the responses of the conditional means and variances are much more pronounced in periods of economic turbulence than in periods of relative calm when the releases of the latest data reveal more abrupt changes in the evolution of the economic indicators.

Finally, it is noteworthy that realized GDP growth rates are generally below the centre of its short-term density forecasts in all but the second and third quarters of 2009. Hence, the probability of observing a value less than the observed GDP for most densities is smaller than 0.5, i.e. PITs are smaller than 0.5, implying negative INTs. This exemplifies what happens on average for data vintages of all quarters and is the reason behind the negative estimates of constants in models for INTs.

Fig. 6

Quarterly GDP growth rate density forecasts over data vintages between $-1q/3m$ and $+1q/1m$ obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset applied. The quarters are 2008Q4, 2009Q1, 2009Q2, 2009Q3. The black vertical line represents the observed GDP growth rate in the reference quarter

Fig. 7

Quarterly GDP growth rate density forecasts over data vintages between $-1q/3m$ and $+1q/1m$ obtained using a MFDFM with $r=1$ and $p=2$ and no modelling of the idiosyncratic errors applied to the large dataset applied for the quarters. The quarters are 2019Q1, 2012Q2, 2012Q3, 2012Q4. The black vertical line represents the observed GDP growth rate in the reference quarter

6 Conclusion

We have investigated the predictive content of data releases for short-term Spanish GDP forecasting. We used information from a wide group of monthly variables that were then implemented as predictors of the Spanish GDP growth rate within a MFDFM. We based our analysis on a recursive estimation scheme, using pseudo real-time data vintages that replicated the publication calendar of the monthly indicator and the GDP. Then, we evaluated from the more common perspective of point forecasts and the more novel one of density forecasts.

As time passes and monthly indicators and GDP are released there are notable improvements in short-term GDP forecasts. However, a significant portion of the improvements in point forecasts and density forecasts occur before the end of the current quarter’s first month. Also, the calibration of density forecasts improves with data releases, with the end of the current quarter’s first month also being a hinge point in time, serving to separate densities for which there is evidence against the hypothesis of good calibration from those for which there is not. It is worth noting that the last GDP data is released towards the end of the first month of the quarter, corresponding to its estimate for the previous quarter. The analysis further suggests that the better density forecast calibration achieved with data releases is mainly due to the reduction in the conditional variance.

Finally, the real-time GDP forecasting exercises are based on the artificial creation of real-time data vintages, using a relatively recent publication calendar, and imposing them on the data collected by the end of 2021. While helpful in determining the impact of pseudo-real-time data vintages on short-term GDP forecasting, this approach does not allow to dealing with data revisions that occur over time. For that, we need to carefully investigate historical records of the series that may be predictors of GDP and formulate and develop a set of real-time data vintages using, for example, the Euro Area Real-Time Database.

Appendices

Data sources

The data have been collected from the Ministry of Economic Affairs and Digital Transformation http://serviciosede.mineco.gob.es/Indeco/BDSICE/Busquedas/busquedas_new.aspx, the Bank of Spain in the case of the interest rates https://www.bde.es/webbde/en/estadis/infoest/temas/sb_tiimerval.html ( B Secondary Market, Table 1.3 of the IR), and EUROSTAT https://ec.europa.eu/eurostat. The original data sources can be found in the referenced web pages.

Augmented Dickey–Fuller tests

We have analysed the trend behaviour using the ADF. To avoid the adverse effect of outlier observations due to the COVID pandemic explosion, we considered the sub-period 1995m1–2020m2 when performing the ADF tests. The latter seemed to confirm that most of the series in levels (or their logarithms) are non-stationary due to the presence of a unit root. On the other hand, ADF tests provided evidence against the non-stationarity of the first differences. Consequently, we have induced stationarity through the first differences of the level or logarithm of the series. The exceptions are spread rate and the industrial production perspective indicator for which the presence of a unit root is rejected, in which case we considered directly with the series in levels. Finally, the ADF could not reject that the logarithm of registered unemployment and credit to companies and household and their first differences contain a unit root. Accordingly, we have considered a second difference of their logarithms as the proper stationary transformation. Table 2 provides information on the auxiliary regression of the ADF test and the transformation used to achieve stationarity fluctuations. It is worth noting that the results are robust to other test specifications.

Table 2 ADF observed test statistics and asymptotic p-value for the null of the presence of a unit root (i.e. non-stationarity) for the level (or its logarithms) of an indicator and its first differences of an indicator

State-space representation of the MFDFM

We continue with the DFM model without dynamics in the idiosyncratic error (Sect. 4) in order to make explicit the form of the matrices of its SS representation. Then, we briefly describe how we estimate the MFDFMs. The extension to the DFM model with AR dynamics is straightforward; see, for instance, Bańbura and Modugno (2014).

1.1 Matrices of the State-Space representation

The measurement coefficient matrix C and variance–covariance matrix R have the following structure:

$$\begin{aligned} \underset{\left( N\times \left[ 5\times (r+N_{Y})\right] \right) }{C}=\left( \begin{array}{cccccccccc} \Lambda _{X} &{} \quad &{} \quad \underset{N_{X}\times 4r}{0} &{} \quad &{} \quad &{} \quad &{} \quad &{} \quad \underset{N_{X}\times (5\times N_{Y})}{0}\\ \Lambda _{Y} &{} \quad 2\Lambda _{Y} &{} \quad {3\Lambda _{Y}} &{} \quad 2\Lambda _{Y} &{} \quad \Lambda _{Y} &{} \quad I_{N_{Y}} &{} \quad 2I_{N_{Y}} &{} \quad {3I_{N_{Y}}} &{} \quad 2I_{N_{Y}} &{} \quad 1I_{N_{Y}} \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \underset{\left( N\times N\right) }{R}=\left( \begin{array}{ccccc} \sigma _{\varepsilon _{X_{1}}}^{2} &{} \quad 0 &{} \quad \cdots &{} \quad 0 &{} \quad 0\\ 0 &{} \quad \ddots &{} \quad 0 &{} \quad \cdots &{} \quad 0\\ \vdots &{} \quad \cdots &{} \quad \sigma _{\varepsilon _{X_{N_{X}}}}^{2} &{} \quad \cdots &{} \quad \vdots \\ 0 &{} \quad \cdots &{} \quad 0 &{} \quad \sigma _{\nu _{Y_{1}}}^{2} &{} \quad 0\\ 0 &{} \quad 0 &{} \quad \cdots &{} \quad 0 &{} \quad \sigma _{\nu _{Y_{2}}}^{2} \end{array}\right) , \end{aligned}$$

where $\sigma _{\nu _{Y_{1}}}^{2}$ are very small number (10$^{-10}).$ On the other hand, the state matrix A and the variance–covariance matrix Q have the following form:

$$\begin{aligned} \underset{\left( \left[ 5\times (r\times N_{Y})\right] \times \left[ 5\times (r\times N_{Y})\right] \right) }{A}=\left( \begin{array}{cccc} \underset{r\times (r\times p)}{\Phi }\ &{} \quad \underset{r\times \left[ (5-p)\times r\right] }{0}\ &{} \quad &{} \quad \underset{(5\times r)\times (5\times N_{Y})}{0}\\ \underset{4\times r}{I}\ &{} \quad \underset{(4\times r)\times r}{0}\\ &{} \quad &{} \quad \underset{N_{Y}\times N_{Y}}{0} &{} \quad \underset{N_{Y}\times (4\times N_{Y})}{0}\\ \underset{(5\times N_{Y})\times (5\times r)}{0} &{} \quad &{} \quad \underset{4\times N_{Y}}{I} &{} \quad \underset{(4\times N_{Y})\times N_{Y}}{0} \end{array}\right) \end{aligned}$$

with $\Phi =[\Phi _{1},...,\Phi _{p}]$, and

$$\begin{aligned} \underset{\left( \left[ 5\times (r\times N_{Y})\right] \times \left[ 5\times (r\times N_{Y})\right] \right) }{Q}=\left( \begin{array}{cccc} \underset{r\times r}{{\Sigma _{u}}} &{} \quad \underset{r\times (4\times r)}{0}\ &{} \quad &{} \quad \underset{(5\times r)\times (5\times N_{Y})}{0}\\ \underset{(4\times r)\times r}{0}\ &{} \quad \underset{(4\times r)\times (4\times r)}{0}\\ &{} \quad &{} \quad \underset{N_{Y}\times N_{Y}}{{\Sigma _{\varepsilon _{Y}}}} &{} \quad \underset{N_{Y}\times (4\times N_{Y})}{0}\\ \underset{(5\times N_{Y})\times (5\times r)}{0} &{} \quad &{} \quad \underset{(4\times N_{Y})\times N_{Y}}{0} &{} \quad \underset{(4\times N_{Y})\times (4\times N_{Y})}{0} \end{array}\right) . \end{aligned}$$

To handle the missing observations with the KF the equation for $Y_{t}$ is replaced by

$$\begin{aligned} \left( \begin{array}{c} X_{t}\\ Y_{t} \end{array}\right) =W_{t}Cs_{t}+W_{t}\nu _{t}+(I_{N}-W_{t})\epsilon _{t}, \end{aligned}$$

where $W_{t}$ is a $N\times N$ diagonal matrix that identifies the observed data. If all variables are observed at time t,  then $W_{t}=I_{N}$. However, when some data are unavailable at time t, $W_{t}$ has zero entries in the position of the diagonal of $W_{t}$ corresponding to those variables with missing values and ones otherwise. The error $\epsilon _{t}$ is of dimension $N\times 1$, i.i.d. Gaussian with zero mean and identity variance–covariance matrix, that is further independent of $\nu _{s}$ for all $(t,\,s)$. The Kalman recursions are still valid if we consider this slightly modification to deal with missing observation, i.e. C and Q are replaced by $W_{t}C$ and $W_{t}QW_{t}^{\prime }+(I-W_{t})(I-W_{t})^{\prime }$, respectively. This means that missing observations are generated by a standard Normal and replaced by zeros in the observation vector. Furthermore, variances of errors that correspond to missing observations are replaced by ones. In terms of the Kalman equations, this implies that missing observations have zero prediction errors and zero Kalman gains.

1.2 Estimation

We estimated the initial loadings and factors applying PC and restricted Least Squares (LS) to a balanced data set, obtaining $C_{0}$, $F_{0,\,t}$ and the residuals $\varepsilon _{0,\,t}=Z_{t}-C_{0}F_{0,\,t},$ for $t=1,...,T$. Note that the residuals $\varepsilon _{0,\,t}$ have missing observation at the same t as $Z_{t}$. Then, we used the monthly residuals to compute an initial estimate $\sigma _{0,\,\varepsilon _{X_{j}}}^{2},$for $j=1,...,N_{X}$ in $R_{0}$, and $\sigma _{0,\,\varepsilon _{Y_{i}}}^{2}$, for $i=1,...,N_{Y}$, in $Q_{0}.$ We also considered the initial factor $F_{0,\,t}$ to estimate the (V)AR coefficients in $A_{0}$ and the upper sub-matrix of the initial $Q_{0}$.

Having obtained the initial SS representation, the estimation procedure uses the KF recursions to re-estimate the factors as the projection of $F_{t}$ onto the space spanned by the observations $(X_{t},\,Y_{t})^{\prime },$ for $t=1,...,T$. This leads to an iterative procedure implemented using the EM algorithm that we stop when the log-likelihood does not change much, i.e. its increment is smaller than $10^{-4}$.

Testing the hypothesis of no informational gain between consecutive data vintages

Let ${\mathscr {F}}(\cdot )$ be a differentiable loss function that can be a quadratic loss function when we use the MSFE to assess point forecast or the log score when considering the forecast density. Let $\Omega _{\upsilon }$, the information set vintage $\upsilon$ , be an increasing sigma-algebra. New information is subsequently released and incorporated to the information set, giving rise to $\Omega _{\upsilon +1}$. Thus, information expands between two consecutive vintages $\Omega _{\upsilon }$ and $\Omega _{\upsilon +1}$. We assume that there is no forecast revision. Let $Y_{T^{*}+h^{*}}(\omega _{\upsilon })$ be the point forecast of $Y_{T^{*}+h^{*}}$ given $\Omega _{\upsilon }$, where $\omega _{\upsilon +1}$ $\in$ $\Omega _{\upsilon +1}$.

Consider the first order (Taylor) expansion of ${\mathscr {F}}(\cdot )$ around the point forecast $Y_{T^{*}+h^{*}}(\omega _{\upsilon })$

$$\begin{aligned} {\mathscr {F}}\left( Y_{T^{*}+h^{*}}(\omega _{j+1}),\,Y_{3(T^{*}+h^{*})}\right)= & {} {\mathscr {F}}\left( Y_{T^{*}+h^{*}}(\omega _{\upsilon }),\,Y_{T^{*}+h^{*}}\right) \nonumber \\{} & {} \quad + {\mathscr {F}}^{\prime }\left( Y_{T^{*}+h^{*}}(\omega _{\upsilon }),\,Y_{T^{*}+h^{*}}\right) \left( Y_{T^{*}+h^{*}}(\omega _{\upsilon +1})\right. \nonumber \\{} & {} \quad \left. -Y_{T^{*}+h^{*}}(\omega _{\upsilon })\right) . \end{aligned}$$

(14)

The hypothesis of no additional relevant information can be expressed as no change in expected loss, i.e.

$$\begin{aligned} H_{0}&:&\mathrm {no\,\,relevant\,\,new\,\,information}\nonumber \\&:&\textrm{E}\left[ {\mathscr {F}}\left( Y_{T^{*}+h^{*}}(\omega _{\upsilon +1}),\,Y_{T^{*}+h^{*}}\right) \right] -\textrm{E}\left[ {\mathscr {F}}\left( Y_{T^{*}+h^{*}}(\omega _{\upsilon }),\,Y_{T^{*}+h^{*}}\right) \right] =0. \end{aligned}$$

(15)

Taking expectations on both sides of equation (14), we obtain that (15) implies that

$$\begin{aligned} \textrm{E}\left[ {\mathscr {F}}^{\prime }\left( Y_{T^{*}+h^{*}}(\omega _{\upsilon }),\,Y_{T^{*}+h^{*}}\right) \left( Y_{T^{*}+h^{*}}(\omega _{\upsilon +1})-Y_{T^{*}+h^{*}}(\omega _{\upsilon })\right) \right] =0. \end{aligned}$$

(16)

The last can be viewed as an orthogonality condition. Under the hypothesis of no change in the expected loss, ${\mathscr {F}}^{\prime }$ $(\cdot )$ (i.e. in words of Granger, “the generalized forecast error”) is uncorrelated to the change in point forecasts.

The orthogonality condition (16) put forward Mincer-Zarnowitz type of regression of the following form:

$$\begin{aligned} {\mathscr {F}}^{\prime }\left( Y_{T^{*}+h^{*}|\Omega _{\upsilon }},\,Y_{T^{*}+h^{*}}\right) =\beta _{0}+\beta _{1}\left( Y_{T^{*}+h^{*}|\Omega _{v+1}}-Y_{T^{*}+h^{*}|\Omega _{\upsilon }}\right) +u_{T^{*}+h^{*}}, \end{aligned}$$

and testing whether the slope coefficient $\beta _{1}$ is equal to zero. The rejection of null hypothesis means that the additional relevant information in $\Omega _{\upsilon +1}$ improves the point forecast and, consequently, helps achieve a lower expected loss.

An intuitive explanation is as follows. The forecast error $e_{T^{*}+h^{*}|\Omega _{\upsilon }}$ is the unexpected component $Y_{T^{*}+h^{*}}$ with respect to the information set $\Omega _{\upsilon },$comprised in the point forecast. On the other hand, $\Delta Y_{T^{*}+h^{*}|\Omega _{\upsilon +1}}$ is the part of the new forecast orthogonal to the previous one, thus corresponding to the change in point forecasts that can be attributed to the new information in $\Omega _{v+1}$. If the forecast error $e_{T^{*}+h^{*}|\Omega _{\upsilon }}$ relates to $\Delta Y_{T^{*}+h^{*}|\Omega _{\upsilon +1}}$, then it means that $\Omega _{\upsilon +1}$ contains new relevant information that can lead to a MSPE improvement.

The final form of the Mincer-Zarnowitz regression, i.e. its dependent variable, depends on the loss function. Consider first the quadratic loss function

$$\begin{aligned} Q(Y_{T^{*}+h^{*}|\Omega _{\upsilon +1}},Y_{T^{*}+h^{*}|\Omega _{j+1}})=(Y_{T^{*}+h^{*}}-Y_{T^{*}+h^{*}|\Omega _{j}})^{2}, \end{aligned}$$

in which case we have that

$$\begin{aligned} Q^{\prime }(Y_{T^{*}+h^{*}|\Omega _{\upsilon +1}},Y_{T^{*}+h^{*}|\Omega _{\upsilon +1}})=-2(Y_{T^{*}+h^{*}}-Y_{T^{*}+h^{*}|\Omega _{\upsilon }}). \end{aligned}$$

On the other hand, in the case the loss is the logarithmic score, $S\left( \phi _{\Omega _{\upsilon }}(Y_{T^{*}+h^{*}}),Y_{T^{*}+h^{*}}\right)$, where $\phi _{\Omega _{\upsilon }}(\cdot )$ is forecast density under $\Omega _{\upsilon }$. As before, we assume that new information arrives and the density forecast is recomputed, giving rise to $\phi _{\Omega _{\upsilon +1}}(\cdot )$. It is straightforward to obtain

$$\begin{aligned} S^{\prime }\left( \phi _{\Omega _{\upsilon }}(Y_{T^{*}+h^{*}}),Y_{T^{*}+h^{*}}\right) =\frac{1}{\phi _{\Omega _{\upsilon }}}\frac{\delta \phi _{\Omega _{\upsilon }}}{\delta Y_{T^{*}+h^{*}|\Omega _{\upsilon }}}, \end{aligned}$$

which reduces, in the case of a Normal forecast density, to

$$\begin{aligned} \frac{Y_{T^{*}+h^{*}}-Y_{T^{*}+h^{*}|\Omega _{\upsilon }}}{\textrm{V}(Y_{T^{*}+h^{*}}|\,\Omega _{\upsilon })}. \end{aligned}$$