New results on asymptotic properties of likelihood estimators with persistent data for small and large T

Abstract

This paper revisits the panel autoregressive model, with a primary emphasis on the unit-root case. We study a class of misspecified Random effects Maximum Likelihood (mRML) estimators when T is either fixed or large, and N tends to infinity. We show that in the unit-root case, for any fixed value of T, the log-likelihood function of the mRML estimator has a single mode at unity as $N\rightarrow \infty$. Furthermore, the Hessian matrix of the corresponding log-likelihood function is non-singular, unless the scaled variance of the initial condition is exactly zero. As a result, mRML is consistent and asymptotically normally distributed as N tends to infinity. In the large-T setup, it is shown that mRML is asymptotically equivalent to the bias-corrected FE estimator of Hahn and Kuersteiner (Econometrica 70(4):1639–1657, 2002). Moreover, under certain conditions, its Hessian matrix remains non-singular.

1 Introduction

Dynamic panel data analysis is highly popular in econometrics for its ability to capture the dynamics of microeconomic agents (such as households and firms) using a limited number of time series observations. The prevalent approach in the literature has been the autoregressive (AR) panel model with individual-specific intercepts.

Early research on the estimation of the panel AR model utilized unconditional maximum likelihood estimators, treating individual-specific intercepts as random variables. See e.g., Balestra and Nerlove (1966) and Maddala (1971).

During the 1980s, however, a growing awareness of the significance of accounting for heterogeneity across entities led to the emergence of the fixed effects approach. This approach treats individual-specific intercepts as parameters, requiring fewer distributional assumptions compared to the random effects approach. Notwithstanding, a major challenge arises in that the number of parameters increases with the total cross-sectional observations (N).

An early popular way to address the “incidental parameters problem” involved transforming the data by subtracting individual-specific means and then running least-squares. The resulting Within Group (WG) estimator is a Maximum Likelihood (ML) estimator conditional on individual fixed effects. Unfortunately, in dynamic panels the within transformation induces a correlation between lagged dependent variables and idiosyncratic errors, which is non-negligible when T is fixed (Nickell 1981). Thus, the WG estimator is inconsistent as $N \rightarrow \infty$.

More recently, several alternative ML approaches have been proposed in the literature to deal with the incidental parameters problem. Many of these methods treat individual-specific effects as fixed but either rely on modifications of the profile likelihood, as in Lancaster (2002) and Dhaene and Jochmans (2016), or they start from the likelihood function of the model transformed in first differences, as in Hsiao et al. (2002) and Hayakawa and Pesaran (2015). Alternative likelihood-based estimators treat individual-specific effects as random variables but make use of Chamberlain-type projections to explicitly model the dependence between these effects and initial conditions (Anderson and Hsiao 1982; Alvarez and Arellano 2003; and Moral-Benito (2013)).

The present paper revisits the transformed maximum likelihood approach (TML) as in Hsiao et al. (2002), and the random effects maximum likelihood estimator (RML) as in Alvarez and Arellano (2003). In addition, we study a class of RML-type estimators that arises by misspecifying (i.e., imposing an incorrect value for) the correlation strength between the initial conditions and the individual-specific intercepts. Thus, the class of misspecified RML (mRML) estimators considered in this paper generalizes (Hahn et al. 2004), whose setting corresponds to the misspecified likelihood that imposes (potentially incorrectly) such correlation to be zero.

We mainly focus on the case where the data are highly persistent, that is, the autoregressive parameter equals unity. This case is important from an empirical point of view because many economic variables exhibit time series properties very close to random walks. Examples arise in the estimation of production functions, household income and consumer spending, to mention a few.¹

The contributions of the paper are as follows:

• (i) Firstly, we show that in the unit root setting for any fixed value of T, the log-likelihood function of the mRML estimator has a single mode at unity as $N \rightarrow \infty$. It is also shown that the Hessian matrix of the corresponding log-likelihood function is non-singular, unless the scaled variance of the initial condition is exactly zero. As a result, the misspecified RML estimator for the autoregressive parameter is consistent and asymptotically normally distributed, as $N \rightarrow \infty$ for T fixed. This implies that standard inference procedures are valid. To the best of our knowledge, this is the first result in the literature that shows that a class of mRML estimators has desirable asymptotic properties in the unit-root case for fixed-T.

• (ii) Secondly, the paper also provides new insights on the properties of mRML and TML in large N, T samples. In specific, in a stable autoregressive setting, we show that the mRML estimator is asymptotically equivalent to the bias-corrected FE estimator of Hahn and Kuersteiner (2002). This result complements that in Alvarez and Arellano (2003) and Hahn et al. (2004), who show asymptotic equivalence between the RML estimator and the bias-corrected FE estimator.

In a Monte Carlo study, we investigate how informative our asymptotic results are for the finite sample properties of all estimators considered. We find that this asymptotic characterization is only informative about the finite sample behavior of the estimators that have non-singular limiting Hessian matrices. This excludes the TML and RML estimators, which have singular Hessian matrices in the limit.

The remainder of this paper is structured as follows. The next section sets out the panel AR(1) model and specifies the underlying assumptions. Section 3 introduces the misspecified RML approach and links it to the TML and RML approaches. Section 4 provides the asymptotic results of the paper. Section 5 reports finite-sample results from a Monte Carlo study, and a final section concludes. Proofs of all propositions are provided in the Appendix.

2 The linear panel AR(1) model

We consider the following simple AR(1) specification without exogenous regressors²:

$$\begin{aligned} y_{i,t}=\alpha y_{i,t-1}+\eta _{i}+\varepsilon _{i,t}, \quad {\text {E}}[\varepsilon _{i,t}|y_{i,0},\eta _{i}]=0, \end{aligned}$$

(1)

for $i=1, \ldots , N, t=1, \ldots , T$ where the true parameter is $\alpha =\alpha _{0}$. For example, simple linear models of this form played a prominent role in the early econometric literature on the propagation of income shocks to consumption, by decomposing the income shocks into a permanent component (a function of $\eta _{i}$), and a transitory component (a function of $y_{i,t-1}$). Some recent contributions to this literature include the papers of Botosaru and Sasaki (2018) and Botosaru (2022), while the paper of Arellano et al. (2017) provides the most recent advances in the literature on nonlinear models for incomes shocks.

In this paper, we limit our attention to the stylized setting in Eq. (1), where the parameters of interest $\alpha _{0}$ and $\sigma _{0}^{2}={\text {E}}[\varepsilon _{i,t}^{2}]$ can be estimated using the Maximum Likelihood principle. Our prime focus is the behavior of Maximum Likelihood estimators when $\alpha _{0}\rightarrow 1$.

In this paper, we operate under the conditions of the following Random Effects ML (RML) assumption.

Assumption:

RML: For $\eta _{i}=(1-\alpha _{0})\mu _{i}$, the vector $(y_{i,0},\mu _{i})$ is i.i.d. across i, with finite fourth moments. $\varepsilon _{i,t}$ is i.i.d. $(0,\sigma ^{2})$ across all i, t and ${\text {E}}[\varepsilon _{i,t}^{4}]$ is finite.

Here we implicitly assume that initial conditions $y_{i,0}$ are observed by the econometrician and can be used in the formulation of the likelihood function. In particular, this assumption imposes restrictions on the joint distribution of $y_{i,0}$ and $\mu _{i}$. Note that we do not impose any form of stationarity restrictions (mean and/or covariance) on the initial condition. This fact is essential in the derivations of the asymptotic results of the two estimators for $\alpha _{0}=1$ in the remainder of this paper.

Next, consider the Mundlak (1978)-Chamberlain (1982) type of projection for $\eta _{i}$³:

$$\begin{aligned} \eta _{i}=\pi y_{i,0}+v_{i},\quad {\text {E}}[v_{i}y_{i,0}]=0,\quad v_{i}\sim i.i.d.(0,\sigma _{v}^{2}). \end{aligned}$$

(2)

Different likelihood-based estimators discussed in this paper will primarily differ in the way they treat the $\pi$ parameter or an associated function of $\pi$. For example, when we set $\pi =1-\alpha$ the projection corresponds exactly to the TML (Transformed Maximum Likelihood) framework of Hsiao et al. (2002). On the other hand, for the RML approach as in Alvarez and Arellano (2003), the $\pi$ is treated as an unrestricted parameter to be estimated.

The conditional AR(1) model in Eq. (1) can be rewritten in the following stacked form:

$$\begin{aligned} \varvec{y}_{i}=\alpha \varvec{y}_{i-}+\varvec{\imath }_{T}\eta _{i}+\varvec{\varepsilon }_{i},\quad \varvec{\varepsilon }_{i}=(\varepsilon _{i,1},\ldots ,\varepsilon _{i,T})'. \end{aligned}$$

(3)

Alternatively, using the projection device, the model can also be described as follows⁴:

$$\begin{aligned} \varvec{R}\varvec{y}_{i}=(\varvec{e}_{1}\alpha +\varvec{\imath }_{T}\pi ) y_{i,0}+\varvec{u}_{i}, \end{aligned}$$

(4)

where $\varvec{R}=\varvec{I}_{T}-\varvec{L}_{T}\alpha$, $\varvec{e}_{1}$ is the first column of the $\varvec{I}_{T}$ matrix, and $\varvec{u}_{i}\equiv \varvec{\imath }_{T}v_{i}+\varvec{\varepsilon }_{i}$.⁵ This correlated random effects decomposition can then be directly used to formulate the (quasi-) log-likelihood in the next section.

3 Maximum likelihood estimation approaches

3.1 The log-likelihood function

The derivations hereby mostly follow those in Bun et al. (2017) and have been adapted appropriately for the purpose of this paper. Note that

$$\begin{aligned} {\text {E}}[\varvec{u}_{i}]=\varvec{0}_{T},\quad {\text {var}}[\varvec{u}_{i}]=\varvec{\varSigma }=\sigma _{v}^{2}\varvec{\imath }_{T}\varvec{\imath }_{T}'+\sigma ^{2}\varvec{I}_{T}, \end{aligned}$$

(5)

where the variance–covariance structure of $\varvec{\varSigma }$ is of the usual random effects (or Generalized Least Squares) form. The quasi-log-likelihood function for some individual i is defined as:

$$\begin{aligned} \ell _{i}(\varvec{\kappa })= & {} -\frac{1}{2}\left( (T-1)\log (\sigma ^{2})+\log (\theta ^{2})+\left[ (\varvec{y}_{i}-\alpha \varvec{y}_{i-}\right. \right. \nonumber \\{} & {} \left. \left. -\varvec{\imath }_{T}\pi y_{i,0})'\varvec{\varSigma }^{-1}(\varvec{y}_{i}-\alpha \varvec{y}_{i-}-\varvec{\imath }_{T}\pi y_{i,0})\right] \right) , \end{aligned}$$

(6)

where $\varvec{\kappa }=(\alpha ,\pi ,\sigma ^{2},\sigma _{v}^{2})'$. This function is the true likelihood function if $\varvec{u}_{i}$ is a multivariate Gaussian vector.

Given the specific structure of the $\varvec{\varSigma }$ matrix, the above expression can be substantially simplified. For example, using the notation in Bun et al. (2017) (e.g., ${\widetilde{y}}_{i,t}=y_{i,t}-{\bar{y}}_{i}$ and $\ddot{y}_{i}={\bar{y}}_{i}-y_{i,0}$, $\ddot{y}_{i-}={\bar{y}}_{i-}-y_{i,0}$) and defining $\rho =\pi -(1-\alpha )$, we obtain the following final expression for the log-likelihood function (after summing over all individual log-likelihood functions):

$$\begin{aligned} \ell (\varvec{\kappa })&=-\frac{N}{2}\left( (T-1)\log (\sigma ^{2})+\log (\theta ^{2}) +\frac{1}{N\sigma ^{2}}\sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t} -\alpha {\widetilde{y}}_{i,t-1})^{2}\right. \nonumber \\&\quad \left. +\frac{T}{N\theta ^{2}}\sum _{i=1}^{N}(\ddot{y}_{i}-\alpha \ddot{y}_{i-}-\rho y_{i,0})^{2}\right) , \end{aligned}$$

(7)

where $\varvec{\kappa }=(\alpha ,\pi ,\sigma ^{2},\theta ^{2})'$ with $\theta ^{2}=\sigma ^{2}+T\sigma _{v}^{2}$. As it is extensively discussed in Bun et al. (2017), the parameters ($\sigma ^{2},\theta ^{2},\rho$) can be concentrated out as:

$$\begin{aligned} \ell ^{c}(\alpha )= & {} -\frac{N}{2}\left( (T-1)\log \left( \frac{1}{N(T-1)}\sum _{i=1}^{N} \sum _{t=1}^{T}({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})^{2}\right) \right. \nonumber \\{} & {} \left. +\log \left( \frac{T}{N}\sum _{i=1}^{N}({\dot{y}}_{i}-\alpha {\dot{y}}_{i-})^{2}\right) \right) . \end{aligned}$$

(8)

Here we define ${\dot{y}}_{i}$ and ${\dot{y}}_{i-}$ as follows:

$$\begin{aligned} {\dot{y}}_{i}=\ddot{y}_{i}-y_{i,0}\frac{\sum _{i=1}^{N}\ddot{y}_{i}y_{i,0}}{\sum _{i=1}^{N}y_{i,0}^{2}},\quad {\dot{y}}_{i-}=\ddot{y}_{i-}-y_{i,0}\frac{\sum _{i=1}^{N}\ddot{y}_{i-}y_{i,0}}{\sum _{i=1}^{N}y_{i,0}^{2}}, \end{aligned}$$

(9)

The above characterization of the log-likelihood function is highly appealing to empirical researchers, as the numerical/computational burden decreases dramatically. Moreover, a simple grid search-based procedures can be used to investigate the curvature of the likelihood, see Sect. 3.3.

Remark 1

Note that the TML log-likelihood function of Hsiao et al. (2002) and Bun et al. (2017) is obtained by setting $\rho =0$ in Eq. (7), such that ${\dot{y}}_{i}=\ddot{y}_{i}$ and ${\dot{y}}_{-i}=\ddot{y}_{i-}$.

3.2 The misspecified RML approach

The TML and the RML approaches can be viewed as two special cases in the way the $\rho$ parameter is being handled in estimation. In particular, TML sets $\rho =0$, whereas RML estimates $\rho$ (or $\pi$ for that mater) freely, without imposing any restrictions. An alternative approach, that we label as the misspecified RML (mRML) approach, uses a more general formulation for the $\pi$ parameter. In particular, we consider $\pi (\phi )$ such that

$$\begin{aligned} \pi (\phi )=\pi =(1-\alpha )\phi , \end{aligned}$$

(10)

where $\phi \in {\mathbb {R}}$ denotes some arbitrary a priori chosen scalar. Note that since the population value of the correlation between $y_{i,0}$ and $\eta _{i}$ corresponds to a specific “true” value of $\phi$, (say) $\phi _{0}$, setting $\phi \ne \phi _{0}$ implies a misspecification of the correlation between the initial condition and the individual-specific effect. The term “misspecified ML estimator” was first used by Hahn et al. (2004), who studied the properties of this estimator for the special case where $\phi =0$.

The only exception for the appropriateness of this terminology is setting $\phi =1$ (corresponding to the TML approach), as in that case the TML estimator is known to be fixed-T consistent for all $|\alpha _{0}|\le 1$. For all other values of $\phi$, the mRML estimator is not generally fixed-T consistent for $\alpha _{0}<1$, as we formally show in Sect. 4.

The concentrated log-likelihood function of the mRML estimator (for any $\phi$) is given by:

$$\begin{aligned} \ell _{mRML}^{c}(\alpha )&=-\frac{N}{2}\left( (T-1)\log \left( \frac{1}{N(T-1)} \sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})^{2}\right) \right) \nonumber \\&\quad -\frac{N}{2}\left( \log \left( \frac{T}{N}\sum _{i=1}^{N}({\dot{y}}_{i}(\phi )-\alpha {\dot{y}}_{i-}(\phi ))^{2}\right) \right) , \end{aligned}$$

(11)

where we now set ${\dot{y}}_{i}(\phi )={\overline{y}}_{i}-\phi y_{i,0}$ and ${\dot{y}}_{i-}(\phi )={\overline{y}}_{i-}-\phi y_{i,0}$. From this formulation, the mRML approach with $\phi =0$ can be alternatively motivated as a special case of the approach studied by Bai (2013a) if one erroneously assumes that $y_{i,0}=0 \hspace{5.0pt}\forall i$, while in reality the initial conditions are non-zero.

3.3 The problem of multiple solutions

Consider the first derivative of the concentrated log-likelihood function for all estimators considered above. Let

$$\begin{aligned} {\widehat{\sigma }}^{2}\left( \phi \right)&= \frac{1}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T} \left( {\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1}\right) ^{2}, \end{aligned}$$

(12)

$$\begin{aligned} {\widehat{\theta }}^{2}\left( \phi \right)&= \frac{T}{N}\sum _{i=1}^{N}\left( {\dot{y}}_{i}(\phi )-\alpha {\dot{y}}_{i-}(\phi )\right) ^{2}, \end{aligned}$$

(13)

then the first derivative of the concentrated log-likelihood function is given by:

$$\begin{aligned} \frac{\textrm{d}\ell ^{c}(\alpha )}{\textrm{d}\alpha }= & {} \frac{1}{{\widehat{\sigma }}^{2}(\alpha )}\sum _{i=1}^{N}\sum _{t=1}^{T}{\widetilde{y}}_{i,t-1} ({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})\nonumber \\{} & {} +\frac{T}{{\widehat{\theta }}^{2} (\alpha )}\sum _{i=1}^{N}{\dot{y}}_{i-}(\phi )({\dot{y}}_{i}(\phi )-\alpha {\dot{y}}_{i-}(\phi )). \end{aligned}$$

(14)

In particular, any solution of the corresponding first-order conditions (FOC) should satisfy:

$$\begin{aligned} {\widehat{\theta }}^{2}(\alpha )\sum _{i=1}^{N}\sum _{t=1}^{T}{\widetilde{y}}_{i,t-1} ({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})+{\widehat{\sigma }}^{2} (\alpha )T\sum _{i=1}^{N}{\dot{y}}_{i-}({\dot{y}}_{i}(\phi )-\alpha {\dot{y}}_{i-}(\phi ))=0.\nonumber \\ \end{aligned}$$

(15)

Given that ${\widehat{\sigma }}^{2}(\alpha )$ and ${\widehat{\theta }}^{2}(\alpha )$ are quadratic in $\alpha$, it is not difficult to see that the FOC are cubic in $\alpha$. Thus, for any value of T and any realization of $\{\varvec{y}_{i}\}_{i=1}^{N}$ there will be at least one and at most three solutions to Eq. (15).

As noted by Alvarez and Arellano (2004, 2022), the TML estimator might suffer from issues related to non-identification for $T=2$. Bun et al. (2017) and Juodis (2018a) built upon those results and obtained further insights on the properties of the distribution of the TML and RML estimators for stationary data. Among other things, they note that the TML approach is more susceptible to generating bimodal finite sample distributions of the corresponding estimator.⁶

As the mRML estimator shares the same structure of the concentrated log-likelihood function Eq. (15), the finite sample distribution of the estimator might be bimodal. However, the choice of $\phi$ might play a non-trivial effect in determining the shape of the corresponding log-likelihood function.

4 Asymptotic results

Section 4.1 analyzes asymptotic properties of the mRML estimator when T is fixed. We shall focus on the unit-root case, $\alpha _{0}=1$. Before we embark on the asymptotic analysis for this case, we present the following general (although negative) result for $|\alpha _{0}|<1$:

Proposition 1

Let $\nabla _{\alpha }\ell$ denote the score of the mRML log-likelihood function with respect to $\alpha$ evaluated at true $\varvec{\kappa }_{0}$. Then, for any T and $|\alpha _{0}|<1$:

$$\begin{aligned} {\text {E}}[\nabla _{\alpha }\ell ]={{\,\mathrm{\mathcal {O}}\,}}(N). \end{aligned}$$

(16)

Moreover, ${\text {E}}[\nabla _{\alpha }\ell ]=0$ if and only if ${\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})](\phi -1)=0$.

Proposition 1 shows that for $|\alpha _{0}|<1$, there exist only two values of $\phi$ that can guarantee fixed-T consistency of the mRML estimator; either $\phi =1$, which corresponds to the TML approach, or the value of $\phi$ corresponding to the infeasible (unknown) correlation coefficient between the initial conditions and the individual-specific effects.

4.1 Fixed-T results for the unit-root case

Our main result of this section is formulated in Proposition 2.

Proposition 2

For any fixed-T as $N\rightarrow \infty$, the log-likelihood function corresponding to the mRML estimator is unimodal at the point $\alpha _{0}=1$, for any fixed value of $\phi$.

This proposition extends the analytical and numerical results obtained by Bun et al. (2017), which apply only to $|\alpha _{0}|<1$ for the TML approach. Note that since the log-likelihood function corresponding to TML can be deduced from mRML by setting $\phi =1$, the result of Proposition 2 also applies to TML.

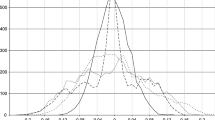
In order to grasp the intuition of the above proposition, Fig. 1 revisits some of the results in Juodis (2018a), which correspond to TML. One can observe from this figure that while for $|\alpha _{0}|<1$ the asymptotic concentrated log-likelihood function is bimodal, the second mode is always at $\alpha =1$, and the first mode naturally approaches the second one as $\alpha _{0}\rightarrow 1$.⁷ Thus, for the true value of $\alpha _{0}=1$ the two modes collapse into one and the log-likelihood function of mRML is unimodal.

Fig. 1

Concentrated asymptotic log-likelihood function for TML. In all figures, the first mode is at the corresponding true value $\alpha _{0}$, while the second mode is located at $\alpha =1$. The initial observation is from the covariance stationary distribution. The dashed line represents the Within Group part of the log-likelihood function, while the dotted line the Between Group part. The solid line, which stands for the log-likelihood function, is a sum of dashed and dotted lines

When it comes to the actual shape of the log-likelihood function of mRML in the unit-root case, it turns out that this is of standard form, unless $\phi =1$. To see this, let ${\widetilde{\sigma }}_{y_0}^{2}(\phi )\equiv T(1-\phi )^{2}{\text {E}}[y_{i,0}^{2}]$ be the scaled second moment of the initial condition. Moreover, let the true value of $\theta ^{2}$ be defined as $\theta ^{2}_{0}=\sigma _{0}^{2}+(1-\alpha _{0})(\mu _{i}-\phi y_{i,0})$, with $\phi =1$ as the special case of the TML estimator. Obviously, for $\alpha _{0}=1$ the value of $\theta ^{2}_{0}$ is the same irrespective of $\phi$.

Using this notation, the following result is obtained for the Hessian of the mRML estimator.

Proposition 3

(Singularity mRML) The $\varvec{\mathcal {H}}_{\ell }(\phi )$ matrix is equal to:

$$\begin{aligned} \varvec{\mathcal {H}}_{\ell }(\phi )=\frac{T-1}{2\sigma _{0}^{2}}\left( \begin{array}{ccc} T\sigma _{0}^{2}+\frac{2}{T-1}{\widetilde{\sigma }}_{y_0}^{2}(\phi ) &{}\,\,\,-1 &{}\,\,\, 1\\ -1&{}\,\,\, \frac{1}{\sigma _{0}^{2}} &{}\,\,\, 0 \\ 1&{}\,\,\, 0 &{}\,\,\, \frac{1/(T-1)}{\sigma _{0}^{2}}\\ \end{array} \right) . \end{aligned}$$

(17)

Moreover, this matrix is singular for fixed-T if and only if ${\widetilde{\sigma }}_{y_0}^{2}(\phi )=0$.

The proof of this proposition largely follows the proof strategy of Theorem 1 in Juodis (2018b), once appropriately modified for the setting at hand.⁸ To the best of our knowledge, Proposition 3 is the first result in the literature that proves that the mRML estimator has desirable asymptotic properties for fixed-T in the unit-root case $\alpha _{0}=1$. In particular, as a corollary of the two results presented above, the mRML estimator is consistent and asymptotically normal (subject to the usual other regularity conditions, e.g., compactness of the parameter space).

Since setting $\phi =1$ implies ${\widetilde{\sigma }}_{y_0}^{2}(\phi )=0$, it is straightforward to see that the Hessian matrix for the TML estimator is singular. This result is well known in the literature, see e.g., Ahn and Thomas (2006); Kruiniger (2013) or Juodis (2018b).⁹ Hence, the corresponding asymptotic distribution of the TML estimator is non-standard and non-normal. In particular, following the results in Roznitzky et al. (2000) and Dovonon and Hall (2018), one can show that

$$\begin{aligned} \root 4 \of {N}({\widehat{\alpha }}-1)={{\,\mathrm{\mathcal {O}}\,}}_{P}(1), \end{aligned}$$

(18)

where the asymptotic distribution is determined by the higher-order expansion of the likelihood function. As such, the limiting distribution of TML is asymmetric. Due to such non-standard properties of TML, it appears to us that there are no approaches suggested in the literature that can be used to construct uniformly valid confidence intervals for $\alpha _{0}\in (-1;1]$.

Remark 2

We note that the TML approach is not the only fixed-T consistent “bias-corrected” FE-type approach that suffers from the singularity of the limiting Hessian matrix for $\alpha _{0}=1$. It is well known in the literature that the standard bias-corrected FE estimator, as studied by Lancaster (2002); Bun and Carree (2005); Dhaene and Jochmans (2016), and Kruiniger (2018), shares this property at $\alpha _{0}=1$. For more details, we refer to Kruiniger (2018). Thus, we are not aware of any estimator that would satisfy all three requirements below: (i) it is consistent for all $\alpha _{0}\in (-1;1]$; (ii) consistency does not depend on the stationarity of the initial condition; and (iii) it has asymptotic normal distribution.

Remark 3

The result in Proposition 3 might seem at odds with the unit-root results in Norkutė and Westerlund (2021), who use the factor analytic approach of Bai (2013a) to construct their estimator. The main difference between their approach and the approach in this paper is that their explicit model is of the error-components structure:

$$\begin{aligned} y_{i,t}=\nu _{i}+u_{i,t},\quad u_{i,t}=\alpha _{0} u_{i,t-1}+\varepsilon _{i,t}. \end{aligned}$$

(19)

While the two coincide asymptotically when $|\alpha _{0}|<1$, this is not the case when $\alpha _{0}=1$. In particular, their results build upon the assumption that ${\text {E}}[\nu _{i}^{2}]>0$. As such, their results are not uniformly valid when the true individual heterogeneity is degenerate. Hence, the desirable finite sample properties of the proposed procedure (as compared to the standard FE-type methods, e.g., Moon et al. (2007) and Juodis and Westerlund (2019)) are achieved at the expense of non-uniformity with respect to this nuisance parameter.

4.2 Large-T results

4.2.1 Asymptotic equivalence in the stationary case

As shown by Alvarez and Arellano (2003), when $N,T\rightarrow \infty$ and $|\alpha _{0}|<1$, the RML estimator is asymptotically equivalent to the bias-corrected FE estimator of Hahn and Kuersteiner (2002) (provided that $N^{3}/T\rightarrow 0$ is satisfied for the latter).

In what follows, we show that the same conclusion can be reached for the mRML estimator for any $\phi$ (thus also the TML estimator). The intuition for this result is fairly simple. Consider the likelihood function in Eq. (8). It is fairly easy to see that as $N,T\rightarrow \infty$ (irrespective of the relative magnitude):

$$\begin{aligned} \ell ^{c}(\alpha )=-\frac{(T-1)N}{2}\log \left( \frac{1}{N(T-1)}\sum _{i=1}^{N} \sum _{t=1}^{T}({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})^{2}\right) +{{\,\mathrm{\mathcal {O}}\,}}_{P}(N\log (T)),\nonumber \\ \end{aligned}$$

(20)

uniformly for all $\alpha$ and $\phi$. Hence, the large-T consistency of all estimators follows from large-T consistency of the corresponding FE estimator. That is, both the RML and the mRML estimators provide an in-built bias-correction term for the standard fixed effects log-likelihood function. As both approaches handle bias-correction rather differently for T fixed, the underlying asymptotic properties depend on the way $\rho$ (or $\pi$) is handled, i.e., whether it is estimated or it is fixed. On the other hand, for large-T this choice is mostly inconsequential, as it can be expected from the expansion in Eq. (20). Our next result formalizes this conjecture.

Proposition 4

Under assumption RML, as $N,T\rightarrow \infty$ such that $N/T^{3}\rightarrow 0$:

$$\begin{aligned} \sqrt{NT}({\widehat{\alpha }}(\phi )-\alpha _{0})\rightarrow N(0,1-\alpha _{0}^{2}), \end{aligned}$$

(21)

for all $|\alpha _{0}|<1$ and any constant value of $\phi$ such that $\pi =(1-\alpha )\phi$.

Hence, the class of RML estimators indexed by $\phi$ is asymptotically equivalent to the bias-corrected FE estimator of Hahn and Kuersteiner (2002). This result is not unexpected, as the mRML specification can be seen as a “bias reducing prior” for $\eta _{i}$ using the terminology of Arellano and Bonhomme (2009).

Proposition 4 extends the analogous result in Hahn et al. (2004), which was proven for the special case $\phi =0$. In particular, their setting corresponds to the misspecified likelihood where one incorrectly assumes that ${\text {E}}[\eta _{i}y_{i,0}]=0$,¹⁰ when in fact this is not the case. Here we have shown that the specific choice of $\phi$ is inconsequential for the asymptotic distribution of the estimator as long as $N/T^{3}\rightarrow 0$.

4.2.2 Singularity of the Hessian matrix of mRML in the unit-root case when T is large

The results in Proposition 3 have been derived for any fixed value of T. It is then natural to wonder what happens when $T\rightarrow \infty$. For the Hessian matrix to be non-singular also as $T\rightarrow \infty$, it is necessary that ${\widetilde{\sigma }}_{0}^{2}={{\,\mathrm{\mathcal {O}}\,}}(T^{1+\beta })$ or alternatively ${\text {E}}[y_{i,0}^{2}]={{\,\mathrm{\mathcal {O}}\,}}(T^{\beta })$, where $\beta \ge 1$. Observe that elements of $\varvec{\mathcal {H}}_{\ell }$ are not of the same order of magnitude. Thus, heuristically, it can be expected that the corresponding coefficients in $\varvec{\kappa }$ will exhibit different rates of convergence if we let $T\rightarrow \infty$. This heuristic is formalized in our next proposition based on sequential limit theory where $N\rightarrow \infty$ first followed by $T\rightarrow \infty$.

Proposition 5

(Singularity mRML large-T) Let $(N,T)_{seq}\rightarrow \infty$, then the scaled mRML Hessian matrix is non-singular if and only if $\beta \ge 1$.

We conjecture that equivalent result can be also proven rigorously using the joint limit theory with $N,T\rightarrow \infty$, but we leave this question for future research. Furthermore, we will not attempt to properly characterize the asymptotic distribution of the misspecified RML estimator in this case, as it would involve a complete characterization of all components in the Taylor’s expansion of the log-likelihood function.

We expect that our previous result in Proposition 3 is useful to characterize the asymptotic distribution of mRML, provided that ${\widetilde{\sigma }}_{0}^{2}$ is not too small.

Remark 4

The non-vanishing effect of the initial condition $y_{i,0}$ in this setting can be compared with the similar result obtained by Juodis and Poldermans (2021) in the unit-root non-stationary setting for the Backwards Orthogonal Deviations (BOD) estimator of Everaert (2013). In that setting, the initial condition is not asymptotically dominant, but it has a variance reduction effect. Note that the rate ${\text {E}}[y_{i,0}^{2}]={{\,\mathrm{\mathcal {O}}\,}}(T^{\beta })$ can be achieved if the process $y_{i,t}$ has a distant or infinite past, see e.g., Westerlund (2016).

5 Monte Carlo study

5.1 The setup

In this section, we investigate the finite sample performance of the various estimators and corresponding test statistics using simulated data. In particular, we consider the following panel AR(1) model:

$$\begin{aligned} y_{i,t}&=\alpha y_{i,t-1}+(1-\alpha )\mu _{i}+\varepsilon _{i,t}; \quad \varepsilon _{i,t}\sim {\mathcal {N}}\left( 0,1\right) ;\quad t=1,\ldots ,T. \end{aligned}$$

(22)

$$\begin{aligned} y_{i,0}&=\gamma \mu _{i}+\varepsilon _{i,0};\quad \varepsilon _{i,0}\sim {\mathcal {N}}\left( 0,\zeta ^{2} \right) ;\quad \mu _{i}\sim {\mathcal {N}}\left( 0,\sigma _{\mu }^{2}\right) . \end{aligned}$$

(23)

Mean-stationarity of $y_{i,t}$ is achieved for designs with $\gamma =1$, while the process $y_{i,t}$ is covariance stationary if and only if $\gamma =1$ and $\zeta ^{2}=1-\alpha ^{2}$. The actual value of $\sigma _{\mu }^{2}$ is irrelevant for the TML estimator as long as $\gamma =1$, but for the RML estimator this parameter is always important.

As we are interested in setups with $\alpha _{0}\approx 1$, we will set $\zeta ^{2}=1$, so that the process is never covariance stationary. Moreover, we restrict our attention to mean stationary settings with $\gamma =1$. Even for the simple AR(1) model, the parameter space is already very large. We have tried to cover its most relevant part by considering the following parameter settings:

$$\begin{aligned} N=\{50,200,500\},\quad T=\{5,10,20\}, \quad \alpha _{0}=\{0.5,0.9,1.0\}. \end{aligned}$$

We consider three estimation approaches, namely TML, RML and mRML with $\phi =0$. For all three approaches, we report two types of estimators: (i) based on global maximum of the objective function; (ii) based on local-maximum of the WG mode. The second option is the suggest “left” rule-of-thumb by Bun et al. (2017). We report the mean bias, the median bias and the RMSE for all estimators. Moreover, for all estimators we report the fraction of replications the objective function is found to be unimodal. For all estimators, we use root finder algorithms based on the eigenvalues of the companion matrix to obtain the maximum likelihood estimates in all three cases.¹¹ The number of Monte Carlo replications is set to 4000.

5.2 Results

The estimation results are summarized in Tables 1, 2, 3, while in Table 4 we summarize the unimodality properties of the three approaches considered.

To begin with, consider the results in Table 1. Initially we focus on $\alpha _{0}=0.5$. One observes that the mRML estimator is the one with the largest bias. This is not surprising given that the correlation between the initial condition and the individual-specific effect is misspecified.¹² However, this bias quickly disappears as T increases to at least $T=10$. This observation is consistent with the results of Sect. 4.2. The two fixed-T consistent estimators for $|\alpha _{0}|<1$, RML and TML, exhibit much smaller bias than mRML, with most of the bias being present due to the bimodality of their finite sample distributions. Such bias can be effectively mitigated using the “left” option.

Table 1 Monte Carlo results for $\alpha _{0}=0.5$

Table 2 Monte Carlo results for $\alpha _{0}=0.9$

Table 3 Monte Carlo results for $\alpha _{0}=1.0$

Regarding $\alpha _{0}=0.9$ and $\alpha _{0}=1.0$, we note that the bias of the mRML estimator becomes comparable to that of the RML/TML approaches and becomes nearly negligible in the unit-root setting. Moreover, for $\alpha _{0}=1.0$ the mRML estimator has smaller RMSE, as predicted by the potentially faster convergence rate of the estimator in this case (provided that ${\text {E}}[y_{i,0}^{2}]$ is sizeable).

Next, we consider the bimodality properties of the three estimators. From Table 4, it is clear that the behavior of the RML and TML estimators differs dramatically between the stable setting of $|\alpha _{0}|<1$ and the unit-root setup $\alpha _{0}=1$. In the latter case, even for large N, T, in almost $40\%$ of the replications the likelihood functions are bimodal. This is in sharp contrast with the theoretical predictions from Proposition 2. The misspecified likelihood function, on the other hand, is mostly unaffected by the exact value of the $\alpha _{0}$ parameter.

Table 4 Unimodality analysis

Finally, one may wonder whether our results support the theoretical prediction in Proposition 3 or not. In Fig. 2, we summarize the finite sample distributions of RML and mRML estimators for a given choice of design parameters. The results are fairly revealing on the differences between the finite sample distributions of the two estimators. In particular, while the mRML estimator has a distinct unimodal distribution (even if asymmetric), the finite sample distribution of the RML estimator is distinctively non-standard and asymmetric. While not presented here, the results in Table 4 also indicate that in this setting the results of the mRML estimator are unchanged when one considers the “left” option of the estimator. The same is not true, however, for the RML estimator that is bimodal in $40\%$ of the Monte Carlo replications.

Fig. 2

The finite sample distributions of the mRML and RML estimators for $N=200$, $T=20$, $\alpha _{0}=1$

6 Conclusions

The present paper studied a class of misspecified Random effect Maximum Likelihood estimators. The misspecification arises by imposing the wrong value for the correlation strength between the initial condition and the individual-specific intercepts. As a special case, we have analyzed the asymptotic behavior of the transformed maximum likelihood approach as in Hsiao et al. (2002).

We have shown that for any fixed value of T, the log-likelihood function of the mRML estimator has a single mode at the true value as $N \rightarrow \infty$. In addition, the Hessian matrix of the corresponding log-likelihood function is non-singular, unless the scaled variance of the initial condition is exactly zero. As a result, mRML is consistent and asymptotically normally distributed, as $N \rightarrow \infty$ for T fixed. Thus, standard inference procedures are valid. To the best of our knowledge, this is the first result in the literature that shows that a class of mRML estimators has desirable asymptotic properties in the unit-root case for fixed-T.

Secondly, the paper also provided new insights on the properties of TML and mRML in large-T samples in a stable autoregressive setting. When N, T are both large, the TML estimator is asymptotically equivalent to the bias-corrected FE estimator of Hahn and Kuersteiner (2002). Moreover, for $\alpha _{0}=1$, the Hessian matrix corresponding to the likelihood function of mRML remains non-singular, so long as the scaled variance of the initial conditions is of order ${{\,\mathrm{\mathcal {O}}\,}}(T^{1+\beta })$, $\beta \ge 1$.

In a Monte Carlo study, we have explored how informative our asymptotic results are for the finite sample properties of all estimators considered. We found that this asymptotic characterization is informative about finite sample behavior only for those estimators that have non-singular limiting Hessian matrices. This excludes the TML and RML estimators, which have singular Hessian matrices in the limit.

In this paper, we have limited our attention to the stylized panel AR(1) model. This may be too restrictive for many real-life applications. In our future research, we are planning to extend the present analysis to panel vector autoregressive models, similarly to Binder et al. (2005); Arellano (2016), and Juodis (2018a, 2018b), in order to account for feedback effects from other variables, as it is commonly the case in micro- and macro-economic panels.

Appendix A: Proofs

1.1 Notation

In what follows we introduce a few terms used in the next derivations.

$$\begin{aligned} \theta _{0}^{2}&=\sigma _{0}^{2}+T(1-\alpha _{0})^{2}{\text {E}}[(\mu _{i}-\phi y_{i,0})^{2}], \end{aligned}$$

(A.1)

$$\begin{aligned} \xi&=\sum _{l=0}^{T-2}(T-1-l)\alpha _{0}^{l}, \end{aligned}$$

(A.2)

$$\begin{aligned} {\widetilde{\sigma }}_{y_{0}}^{2}(\phi )&=T(1-\phi )^{2}{\text {E}}[y_{i,0}^{2}], \end{aligned}$$

(A.3)

$$\begin{aligned} \Delta _{\alpha }&=\alpha -\alpha _{0}, \end{aligned}$$

(A.4)

$$\begin{aligned} \theta _{1}&=\frac{(T-1)(2T-1)}{6}\sigma _{0}^{2}, \end{aligned}$$

(A.5)

$$\begin{aligned} \sigma _{1}&=\frac{T+1}{6}\sigma _{0}^{2}, \end{aligned}$$

(A.6)

$$\begin{aligned} \theta _{1}(\phi )&={\widetilde{\sigma }}_{y_{0}}^{2}(\phi )+\theta _{1}. \end{aligned}$$

(A.7)

Here (unless specified otherwise) all terms are defined for all values of $\sigma _{0}^{2},\alpha ,\alpha _{0},\phi$.

1.2 Appendix A.1: Fixed T results

Proof Proposition 1

Let $\nabla _{\alpha } \ell$ denote the partial derivative of $\ell (\varvec{\kappa })$ with respect to $\alpha$ once evaluated at $\varvec{\kappa }_{0}$. Consider the element of the score that corresponds to $\alpha$:

$$\begin{aligned} \nabla _{\alpha } \ell =\frac{1}{\sigma _{0}^{2}}\sum _{i=1}^{N}\sum _{t=1}^{T}{\widetilde{y}}_{i,t-1}({\widetilde{\varepsilon }}_{i,t}) +\frac{T}{\theta _{0}^{2}}\sum _{i=1}^{N}{\dot{y}}_{i-}({\dot{y}}_{i}(\phi )-\alpha _{0}{\dot{y}}_{i-}(\phi )), \end{aligned}$$

(A.8)

where $\theta _{0}^{2}$ is defined as above.

Consider the “between group” part in isolation. Using analogous steps to those in Appendix Lemma A.2 of Juodis (2018a), we expand:

$$\begin{aligned} {\dot{y}}_{i}(\phi )-\alpha _{0}{\dot{y}}_{i-}(\phi )&={\overline{\varepsilon }}_{i}+(1-\alpha _{0})(\mu _{i}-\phi y_{i,0}). \end{aligned}$$

(A.9)

Note that from ${\text {E}}[T{\overline{y}}_{i-}{\overline{\varepsilon }}_{i}]=\xi /T$, we have

$$\begin{aligned} T{\dot{y}}_{i-}(\phi )&=\xi (1-\alpha _{0})(\mu _{i}-y_{i,0})-T(\phi -1) y_{i,0} +\sum _{t=1}^{T-1}\sum _{s=0}^{t-1}\alpha _{0}^{s}\varepsilon _{i,t-s}\nonumber \\&=\xi (1-\alpha _{0})(\mu _{i}-\phi y_{i,0})+(\phi -1) y_{i,0}(\xi (1-\alpha _{0})-T)\nonumber \\&\quad +\sum _{t=1}^{T-1}\left( \sum _{s=0}^{T-1-t}\alpha _{0}^{s}\right) \varepsilon _{i,t}\nonumber \\&=\xi (1-\alpha _{0})(\mu _{i}-\phi y_{i,0})-(\phi -1) y_{i,0}\left( \sum _{s=0}^{T-1}\alpha _{0}^{s}\right) \nonumber \\&\quad +\sum _{t=1}^{T-1}\left( \sum _{s=0}^{T-1-t}\alpha _{0}^{s}\right) \varepsilon _{i,t}. \end{aligned}$$

(A.10)

Thus,

$$\begin{aligned} {\text {E}}[T{\dot{y}}_{i-}(\phi )({\dot{y}}(\phi )_{i}-\alpha _{0}{\dot{y}}_{i-}(\phi ))]&=\frac{\theta _{0}^{2}}{T}\xi -{\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})]\nonumber \\&\quad \left( \sum _{s=0}^{T-1}\alpha _{0}^{s}\right) (1-\alpha _{0})(\phi -1)\nonumber \\&=\frac{\theta _{0}^{2}}{T}\xi -{\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})]\nonumber \\&\quad \left( 1-\alpha _{0}^{T}\right) (\phi -1), \end{aligned}$$

(A.11)

where, as before, $\theta _{0}^{2}=\sigma _{0}^{2}+T(1-\alpha _{0})^{2}{\text {E}}[(\mu _{i}-\phi y_{i,0})^{2}]$. Using this insight, we can expand the score as follows:

$$\begin{aligned} \nabla _{\alpha } \ell&=\frac{1}{\sigma _{0}^{2}}\sum _{i=1}^{N}\left( \sum _{t=1}^{T}{\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t} -{\text {E}}[{\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t}]\right) \nonumber \\&\quad +\frac{T}{\theta _{0}^{2}}\sum _{i=1}^{N}\left( {\dot{y}}_{i-}(\phi )({\dot{y}}_{i}(\phi ) -\alpha _{0}{\dot{y}}_{i-}(\phi ))-{\text {E}}[{\dot{y}}_{i-}({\dot{y}}_{i}(\phi )-\alpha _{0}{\dot{y}}_{i-}(\phi ))]\right) \nonumber \\&\quad -\frac{N}{\theta _{0}^{2}}{\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})]\left( 1-\alpha _{0}^{T}\right) (\phi -1). \end{aligned}$$

(A.12)

From here, it follows immediately that:

$$\begin{aligned} {\text {E}}[\nabla _{\alpha } \ell ]=-\frac{N}{\theta _{0}^{2}}{\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})]\left( 1-\alpha _{0}^{T}\right) (\phi -1). \end{aligned}$$

(A.13)

The conclusion of this proposition follows immediately. $\square$

Proof Proposition 2

In what follows, we consider the probability limit of Eq. (15). Without loss of generality, we set $\sigma ^{2}=1$.

The most critical component of this expression (that varies over $\phi$) is ${\widehat{\theta }}^{2}(\alpha )$, and the corresponding derivative with respect to $\alpha$. In particular,

$$\begin{aligned} {\widehat{\theta }}^{2}(\alpha )&=\frac{T}{N}\sum _{i=1}^{N}({\dot{y}}_{i}(\phi )-\alpha {\dot{y}}_{i-}(\phi ))^{2}\nonumber \\&=(1-\alpha )^{2}\frac{T}{N}\sum _{i=1}^{N}({\dot{y}}_{i-}(\phi ))^{2}+2(1-\alpha ) \frac{T}{N}\sum _{i=1}^{N}({\dot{y}}_{i-}(\phi )){\overline{\varepsilon }}_{i}+\frac{T}{N}\sum _{i=1}^{N}({\overline{\varepsilon }}_{i})^{2}. \end{aligned}$$

(A.14)

Upon inspection of the proof of Theorem 1 in Juodis (2018b), it is clear that the only term affected by $\phi$ is

$$\begin{aligned} {\text {E}}\left[ \frac{T}{N}\sum _{i=1}^{N}({{\overline{y}}}_{i-}-\phi y_{i,0})^{2}\right]&={\text {E}}\left[ \frac{T}{N}\sum _{i=1}^{N}(\ddot{y}_{i-}-(\phi -1) y_{i,0})^{2}\right] \nonumber \\&=T(1-\phi )^{2}{\text {E}}[y_{i,0}^{2}]+\frac{(T-1)(2T-1)}{6}\sigma _{0}^{2}\nonumber \\&={\widetilde{\sigma }}_{y_{0}}^{2}+\theta _{1}. \end{aligned}$$

(A.15)

The final line follows from the fact that, under our assumptions, in the unit-root setting ${\dot{y}}_{i-}$ and $y_{i,0}$ are actually independent. This result can then be used to show that ${\text {E}}[{\widehat{\theta }}^{2}(\alpha )]$ equals

$$\begin{aligned} {\text {E}}[{\widehat{\theta }}^{2}(\alpha )]&=(1-\alpha )^{2}\left( \frac{(T-1)(2T-1)}{6}\right) +(1-\alpha )(T-1)+1\nonumber \\&=\Delta _{\alpha }^{2} \theta _{1}(\phi )+\Delta _{\alpha }(T-1)+1, \end{aligned}$$

(A.16)

where $\theta _{1}(\phi )$ is defined as above. Next, we consider the Within-Group transformed components of the log-likelihood function. In particular, note that

$$\begin{aligned} {\widehat{\sigma }}^{2}(\alpha )&=\frac{1}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t} -\alpha {\widetilde{y}}_{i,t-1})^{2}\nonumber \\&=(1-\alpha )^{2}\frac{1}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t-1})^{2}\nonumber \\&\quad +(1-\alpha )\frac{2}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t-1}){\widetilde{\varepsilon }}_{i,t}\nonumber \\&\quad +\frac{1}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{\varepsilon }}_{i,t})^{2}. \end{aligned}$$

(A.17)

By Theorem 1 in Juodis (2018b), it follows immediately that

$$\begin{aligned} {\text {E}}[{\widehat{\sigma }}^{2}(\alpha )]&=(1-\alpha )^{2}\left( \frac{T+1}{6}\right) -(1-\alpha )+1\nonumber \\&=\Delta _{\alpha }^{2} \sigma _{1}-\Delta _{\alpha }+1. \end{aligned}$$

(A.18)

Next, we plug in these expressions into the corresponding limiting FOC. From here, it is clear that all solutions $\Delta _{\alpha }$ satisfy

$$\begin{aligned}&(T-1)(2\Delta _{\alpha }\sigma _{1}-1)(\Delta _{\alpha }^{2} \theta _{1}(\phi )+\Delta _{\alpha }(T-1)+1)+(2\Delta _{\alpha }\theta _{1}(\phi )\nonumber \\&\quad +(T-1))(\Delta _{\alpha }^{2} \sigma _{1}-\Delta _{\alpha }+1)=0. \end{aligned}$$

(A.19)

After a bit of re-arrangement, we obtain

$$\begin{aligned}&\Delta _{\alpha }^{3}(2T\sigma _{1}\theta _{1}(\phi ))+\Delta _{\alpha }^{2}((T-1)(2\sigma _{1}(T-1) -\theta _{1}(\phi )+\sigma _{1})-2\theta _{1})\nonumber \\&\quad +2\Delta _{\alpha }((T-1)(\sigma _{1}-1)+\theta _{1}(\phi ))=0. \end{aligned}$$

(A.20)

After removing the root $\Delta _{\alpha }=0$, we are left with the following polynomial:

$$\begin{aligned} f(\Delta _{\alpha })&=\Delta _{\alpha }^{2}(2T\sigma _{1}\theta _{1}(\phi )) +\Delta _{\alpha }((T-1)(2\sigma _{1}(T-1)-\theta _{1}(\phi )+\sigma _{1})-2\theta _{1})\nonumber \\&\quad +2((T-1)(\sigma _{1}-1)+\theta _{1}(\phi )). \end{aligned}$$

(A.21)

As the coefficient in front of $\Delta _{\alpha }^{2}$ is clearly positive, we shall first consider the coefficient in front of $\Delta _{\alpha }$. Noting that

$$\begin{aligned} (T-1)(2\sigma _{1}(T-1)-\theta _{1}+\sigma _{1})-2\theta _{1}&=\sigma _{1}(2T-1)(T-1)-\theta _{1}(T+1)\nonumber \\&=\frac{(2T-1)(T+1)}{6}(T-1-(T-1))=0, \end{aligned}$$

(A.22)

the quadratic equation simplifies to

$$\begin{aligned} f(\Delta _{\alpha })&=\Delta _{\alpha }^{2}(2T\sigma _{1}\theta _{1}(\phi )) +2((T-1)(\sigma _{1}-1)+\theta _{1}(\phi ))-\Delta _{\alpha }(T+1)(\theta _{1}(\phi )-\theta _{1})\nonumber \\&=\Delta _{\alpha }^{2}(2T\sigma _{1}\theta _{1})+2((T-1)(\sigma _{1}-1)+\theta _{1})\nonumber \\&\quad +{\widetilde{\sigma }}_{y_{0}}^{2}(\Delta _{\alpha }^{2}(2T\sigma _{1})-\Delta _{\alpha }(T+1)+2). \end{aligned}$$

(A.23)

It is not difficult to see that

$$\begin{aligned} (T-1)(\sigma _{1}-1)+\theta _{1}=(T-1)\left( \frac{T+1}{6}-1+\frac{2T-1}{6}\right) =\frac{T-1}{6}(3T-6)\ge 0,\nonumber \\ \end{aligned}$$

(A.24)

for all $T\ge 2$. From here, we conclude that

$$\begin{aligned} \Delta _{\alpha }^{2}(2T\sigma _{1}\theta _{1})+2((T-1)(\sigma _{1}-1)+\theta _{1})> 0, \end{aligned}$$

(A.25)

for all $\Delta _{\alpha }$. Similarly, it is easy to see that for all $\Delta _{\alpha }$:

$$\begin{aligned} \Delta _{\alpha }^{2}2T\sigma _{1}-\Delta _{\alpha }(T+1)+2>0. \end{aligned}$$

(A.26)

Hence, we conclude that

$$\begin{aligned} f(\Delta _{\alpha })>0, \end{aligned}$$

(A.27)

for all $\Delta _{\alpha }$. As a result, the only real root of the initial cubic equation is $\Delta _{\alpha }=0$, or $\alpha =1$. $\square$

Proof Proposition 3

The proof of this proposition (with minor changes) is largely based on Theorem 1 in Juodis (2018b). The only element of the Hessian matrix that depends on the actual value of $\phi$ is the one in the top left corner, i.e., the (1, 1) element, all other elements are the same as $\theta _{0}^{2}=\sigma _{0}^{2}$ is invariant to $\phi$ in the unit-root case.

In particular, this element can be expressed as:

$$\begin{aligned} \varvec{\mathcal {H}}_{\ell }^{(1,1)}(\phi )=-\left( \frac{\sigma _{1}(T-1)}{\sigma _{0}^{2}}+\frac{\theta _{1}(\phi )}{\theta _{0}^{2}}\right) . \end{aligned}$$

(A.28)

Note that $\sigma _{1}(T-1)=\sigma _{0}^{2}(T+1)(T-1)/6$ where we use the $\sigma _{1}$ notation as in the proof of Proposition 2. Similarly,

$$\begin{aligned} \theta _{1}(\phi )=T(1-\phi )^{2}{\text {E}}[y_{i,0}^{2}]+\frac{(T-1)(2T-1)}{6}\sigma _{0}^{2}. \end{aligned}$$

(A.29)

Combining the two expressions, the first result of this proposition follows immediately.

As for the second part of this proposition, this follows directly from the fact that it is only the (1, 1) element that is affected by ${\widetilde{\sigma }}_{y_{0}}^{2}(\phi )$. Thus, using direct calculations, we conclude that

$$\begin{aligned} |\varvec{\mathcal {H}}_{\ell }(\phi )|=|\varvec{\mathcal {H}}_{\ell }(1)|+\frac{{\widetilde{\sigma }}_ {y_{0}}^{2}(\phi )}{(T-1)\sigma _{0}^{4}}. \end{aligned}$$

(A.30)

The desired result follows by noticing that $|\varvec{\mathcal {H}}_{\ell }(1)|=|\varvec{\mathcal {H}}_{\ell }^{TML}|=0$. $\square$

1.3 Appendix A.2: Large T results

Proof Proposition 4

In what follows, we sketch the main arguments behind the claim of this proposition. First of all, we note that consistency of ${\widehat{\alpha }}$ can be directly established from Eq. (20). A similar result holds for ${\widehat{\sigma }}^{2}$, as a direct implication. Next, in order to avoid any triangular array arguments, it is easier to analyze the log-likelihood function after concentrating out $\theta ^{2}$ and keeping the parameter vector at $\varvec{\psi }=(\alpha ,\sigma ^{2})'$. From here:

$$\begin{aligned} \ell (\varvec{\psi })&=-\frac{N}{2}\left( (T-1)\log (\sigma ^{2})+\log \left( \frac{T}{N\theta ^{2}} \sum _{i=1}^{N}({\dot{y}}_{i}-\alpha {\dot{y}}_{i-})^{2}\right) \right. \nonumber \\&\quad \left. +\frac{1}{N\sigma ^{2}} \sum _{i=1}^{N}\sum _{t=1}^{T}({\widetilde{y}}_{i,t}-\alpha {\widetilde{y}}_{i,t-1})^{2}\right) , \end{aligned}$$

(A.31)

where, for simplicity, we drop the dependence on $\phi$ in the definition of ${\dot{y}}_{i}$ and ${\dot{y}}_{i-}$, as this dependence is inconsequential for the final result of this proposition. Using analogous steps to those used in the proof of Proposition 1, we can show that

$$\begin{aligned} \nabla _{\alpha } \ell&=\frac{1}{\sigma _{0}^{2}}\sum _{i=1}^{N}\left( \sum _{t=1}^{T} {\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t}-{\text {E}}[{\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t}]\right) \nonumber \\&\quad +\frac{T}{{\widehat{\theta }}^{2}(\alpha _{0})}\sum _{i=1}^{N} \left( {\dot{y}}_{i-}({\dot{y}}_{i}-\alpha _{0}{\dot{y}}_{i-}) -{\text {E}}[{\dot{y}}_{i-}({\dot{y}}_{i}-\alpha _{0}{\dot{y}}_{i-})]\right) \nonumber \\&\quad -\xi \frac{N}{T}\left( \frac{{\widehat{\theta }}^{2}(\alpha _{0}) -{\text {E}}[{\widehat{\theta }}^{2}(\alpha _{0})]}{{\widehat{\theta }}^{2}(\alpha _{0})}\right) \nonumber \\&\quad -\frac{N}{{\widehat{\theta }}^{2}(\alpha _{0})}{\text {E}}[y_{i,0}(\mu _{i}-\phi y_{i,0})]\left( 1-\alpha _{0}^{T}\right) (\phi -1). \end{aligned}$$

(A.32)

Next, we show that

$$\begin{aligned} \frac{1}{\sqrt{NT}}\nabla _{\alpha } \ell&=\frac{1}{\sigma _{0}^{2}}\frac{1}{\sqrt{NT}} \sum _{i=1}^{N}\left( \sum _{t=1}^{T}{\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t} -{\text {E}}[{\widetilde{y}}_{i,t-1}{\widetilde{\varepsilon }}_{i,t}]\right) \nonumber \\&\quad +{{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{T})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{T})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(\sqrt{N/T^{3}}). \end{aligned}$$

(A.33)

As ${\text {E}}[{\widehat{\theta }}^{2}(\alpha _{0})]=\sigma _{0}^{2}+T(1-\alpha _{0})^{2}{\text {E}}[(\mu _{i}-\phi y_{i,0})^{2}]={{\,\mathrm{\mathcal {O}}\,}}(T)$, the above result holds provided that

$$\begin{aligned}&{\widehat{\theta }}^{2}(\alpha _{0})-{\text {E}}[{\widehat{\theta }}^{2}(\alpha _{0})]={{\,\mathrm{\mathcal {O}}\,}}_{P}(T/\sqrt{N}), \end{aligned}$$

(A.34)

$$\begin{aligned}&\frac{1}{N}\sum _{i=1}^{N}\left( {\dot{y}}_{i-}({\dot{y}}_{i} -\alpha _{0}{\dot{y}}_{i-})-{\text {E}}[{\dot{y}}_{i-}({\dot{y}}_{i}-\alpha _{0}{\dot{y}}_{i-})]\right) ={{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{N}). \end{aligned}$$

(A.35)

In particular, let

$$\begin{aligned} {\widehat{\theta }}^{2}(\alpha _{0})-{\text {E}}[{\widehat{\theta }}^{2}(\alpha _{0})]&=\frac{1}{N} \sum _{i}(T({\overline{\varepsilon }}_{i})^{2}-\sigma _{0}^{2})+\frac{T}{N} \sum _{i}(1-\alpha _{0})^{2}((\mu _{i}-\phi y_{i,0})^{2}\nonumber \\&\quad -{\text {E}}[(\mu _{i}-\phi y_{i,0})^{2}])\nonumber \\&\quad +2\frac{(1-\alpha _{0})^{2}}{N}\sum _{i}\sum _{t}(\mu _{i}-\phi y_{i,0})\varepsilon _{i,t}\nonumber \\&=\frac{1}{NT}\sum _{i}\sum _{t}(\varepsilon _{i,t}^{2}-\sigma _{0}^{2})+\frac{1}{NT}\sum _{i} \sum _{t}\sum _{s\ne t}\varepsilon _{i,t}\varepsilon _{i,s}\nonumber \\&\quad +{{\,\mathrm{\mathcal {O}}\,}}_{P}(T/\sqrt{N})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(\sqrt{T/N})\nonumber \\&={{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{NT})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{N})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(T/\sqrt{N})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(\sqrt{T/N}). \end{aligned}$$

(A.36)

Here the corresponding orders can be obtained by continuous application of Chebyshev’s inequality and the fact that all stochastic elements have a finite fourth moment, while $\{\varepsilon _{i,t}\}$ are independent over all (i, t). Finally, the following conclusion:

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^{N}\left( {\dot{y}}_{i-}({\dot{y}}_{i}-\alpha _{0}{\dot{y}}_{i-}) -{\text {E}}[{\dot{y}}_{i-}({\dot{y}}_{i}-\alpha _{0}{\dot{y}}_{i-})]\right)&={{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{N}), \end{aligned}$$

can be established analogously upon noticing that $\xi /T=O(1)$, and using the fact that

$$\begin{aligned}&\frac{1}{T^{2}N}\sum _{i}\sum _{l=1}^{T-1}\sum _{t=1}^{T-1}\left( \sum _{s=0}^{T-1-t}\alpha _{0}^{s}\right) \varepsilon _{i,t}\varepsilon _{i,l}-\frac{\xi \sigma _{0}^{2}}{T}\nonumber \\ {}&\quad =\frac{1}{T^{2}N}\sum _{i}\sum _{l=1}^{T-1}\sum _{t=1}^{T-1} \left( \sum _{s=0}^{T-1-t}\alpha _{0}^{s}\right) (\varepsilon _{i,t}\varepsilon _{i,l} -{\text {E}}[\varepsilon _{i,t}\varepsilon _{i,l}]) \nonumber \\&\quad ={{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{NT^{3}})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{NT^{2}}), \end{aligned}$$

(A.37)

since this rate is the same as with $\frac{1}{NT}\sum _{i}(T({\overline{\varepsilon }}_{i})^{2}-\sigma _{0}^{2})$. For this result, it is critical that $\left( \sum _{s=0}^{T-1-t}\alpha _{0}^{s}\right) =O(1)$ for $|\alpha _{0}|<1$. Furthermore, using similar derivations we can further simplify

$$\begin{aligned} \frac{1}{\sqrt{NT}}\nabla _{\alpha } \ell&=\frac{1}{\sigma _{0}^{2}}\frac{1}{\sqrt{NT}}\sum _{i=1}^{N}\sum _{t=1}^{T}y_{i,t-1}\varepsilon _{i,t} +{{\,\mathrm{\mathcal {O}}\,}}_{P}(1/\sqrt{T})+{{\,\mathrm{\mathcal {O}}\,}}_{P}(\sqrt{N/T^{3}}). \end{aligned}$$

(A.38)

From here, the main result follows directly using the results in Hahn and Kuersteiner (2002). $\square$

Proof Proposition 5

Define the following normalization matrix:

$$\begin{aligned} \varvec{S}=\left( \begin{array}{ccc} T^{(1\vee \beta )} &{}\,\,\, 0 &{}\,\,\, 0 \\ 0 &{}\,\,\, \sqrt{T} &{}\,\,\, 0 \\ 0 &{}\,\,\, 0 &{}\,\,\, 1 \\ \end{array} \right) . \end{aligned}$$

(A.39)

Then, it follows that

$$\begin{aligned} \varvec{S}^{-1}\varvec{\mathcal {H}}_{\ell }\varvec{S}^{-1}\rightarrow \varvec{\mathcal {H}}_{\ell }^{\infty }=\left( \begin{array}{ccc} h_{11}&{}\,\,\, 0 &{}\,\,\, h_{13}\\ 0&{}\,\,\, \frac{1}{2\sigma ^{4}} &{}\,\,\, 0 \\ h_{13}&{}\,\,\, 0 &{}\,\,\, \frac{1}{2\sigma ^{4}}\\ \end{array} \right) , \end{aligned}$$

(A.40)

where several cases are available:

$$\begin{aligned} h_{11}&=\left\{ \begin{array}{ll} 1/2, &{} \beta <1; \\ 1/2+\lim _{T\rightarrow \infty }{\widetilde{\sigma }}_{0}^{2}/T^{2}, &{} \beta =1; \\ \lim _{T\rightarrow \infty }{\widetilde{\sigma }}_{0}^{2}/T^{1+\beta }, &{} \beta >1. \end{array} \right. \end{aligned}$$

(A.41)

$$\begin{aligned} h_{13}&=\left\{ \begin{array}{ll} 1/(2\sigma _{0}^{2}), &{} \beta \le 1; \\ 0, &{} \beta >1. \end{array} \right. \end{aligned}$$

(A.42)

$\square$