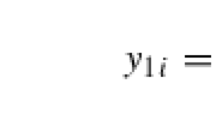Identification in dynamic binary choice models

Abstract

This paper studies identification in a binary choice panel data model with choice probabilities depending on a lagged outcome, additional observed regressors and an unobserved unit-specific effect. It is shown that with two consecutive periods of data identification is not possible (in a neighborhood of zero), even in the logistic case.

1 Foreword from the editors

In 1993, Gary Chamberlain released Harvard Institute of Economic Research (HIER) discussion paper no. 1656, titled “Feedback in Panel Data.” The material in this paper appears to be a revision and extension of ideas that circulated at least as early as 1991, in a draft paper titled “Sequential Moment Conditions in Panel Data.” Some of the material in the earlier, 1991, paper appeared as a, now well-known, comment in the Journal of Business and Economic Statistics (Chamberlain 1992). The “Feedback in Panel Data” paper, however, remained unpublished for many years.

Prior to his passing in 2020, Gary submitted a version of the feedback paper to the Journal of Econometrics in connection with a conference that was held in his honor at Harvard University (Chamberlain 2022) (Manuel Arellano was among the participants at this conference). Before its eventual publication in 2022, the “Feedback in Panel Data” paper was not widely circulated and, to our knowledge, unavailable in any form online.

One version of the 1993 paper included a fifth and final section titled “Binary Response.” This material was not published as part of Chamberlain (2022). The “Binary Response” section contained two sets of results. The first, dealing with the identification of static binary choice models, can be found in Chamberlain (2010). The second part, which is reproduced below, deals with the identification of dynamic binary choice models.

Gary establishes that with two consecutive observations of a binary dependent variable, identification is not possible (in a neighborhood of zero), even in the logistic case. This result is not widely known, although it has been cited by, for example, Honoré and Kyriazidou (2000). Publishing this material makes it easily available to researchers worldwide for the first time.

Gary was a great admirer of Manuel Arellano’s research, and they engaged in many intellectual exchanges over the years. Gary would no doubt have wanted to celebrate and honor Manuel’s considerable achievements and scholarship. Including this short note in this special issue provides a way to do so.

Stéphane Bonhomme, Bryan Graham and Laura Hospido.

2 Identification in dynamic binary response

The outcome variable is binary. There are two periods of observation on each unit ($T=2$). The random vector $(y_{i1},y_{i2},x_{i1}',x_{i2}',c_{i})$ is independently and identically distributed for $i=1,...,n$. We observe $z_{i}'=(y_{i1},y_{i2},x_{i1}',x_{i2}')$; the (scalar) latent variable $c_{i}\in \mathcal {R}$ is not observed. The binary variable $y_{\textrm{it}}=0$ or 1, and $x_{i}'=(x_{i1}',x_{i2}')$ has support $X\subset \mathcal{{R}}^{J}\times \mathcal{{R}}^{J}$.

We assume that

$$\begin{aligned}&\Pr (\left. y_{i1}=1\right| x_{i},c_{i})&=F(\beta _{0}'x_{i1}+c_{i})\nonumber \\&\Pr (\left. y_{i2}=1\right| x_{i},y_{i1},c_{i})&=F(\alpha _{0}+\beta _{0}'x_{i2}+\gamma _{0}y_{i1}+c_{i}). \end{aligned}$$

(1)

The distribution function F is given as part of the prior specification; it is strictly increasing on the whole real line with a bounded, continuous derivative, and with $\text{ lim}_{s\rightarrow \infty }\,F(s)=1$ and $\text{ lim}_{s\rightarrow -\infty }\,F(s)=0$. The parameter space is $\Theta =\Theta _{1}\times \Theta _{2}\times \Theta _{3}$, where $\Theta _{1}$ is an open subset of $\mathcal{{R}}$, $\Theta _{2}$ is an open subset of $\mathcal{{R}}^{J}$, and $\Theta _{3}$ is an open subset of $\mathcal{{R}}$, and $\theta _{0}'\equiv (\alpha _{0},\beta _{0}',\gamma _{0})\in \Theta$. We assume that $\Theta$ contains a neighborhood of 0. Define

$$\begin{aligned} p(x,c,\theta )=\left( \begin{array}{c} \left[ 1-F(\beta 'x_{1}+c)\right] \left[ 1-F(\alpha +\beta 'x_{2}+c)\right] \\ \left[ 1-F(\beta 'x_{1}+c)\right] F(\alpha +\beta 'x_{2}+c)\\ F(\beta 'x_{1}+c)\left[ 1-F(\alpha +\beta 'x_{2}+\gamma +c)\right] \\ F(\beta 'x_{1}+c)F(\alpha +\beta 'x_{2}+\gamma +c) \end{array}\right) . \end{aligned}$$

Theorem 1

If X is bounded, then there is a point $(\alpha ,\gamma )\in \Theta _{1}\times \Theta _{3}$ such that identification fails in (1) for all $\theta _{0}$ in a neighborhood of $(\alpha ,0,\gamma )$.

Proof

Define

$$\begin{aligned} H(x,c_{1},...,c_{4},\theta )=\left[ p(x,c_{1},\theta ),...,p(x,c_{4},\theta )\right] . \end{aligned}$$

Suppose that for some $(\alpha ,\gamma )\in \Theta _{1}\times \Theta _{3}$ and points $c_{1},...,c_{4}\in \mathcal{{R}}$, we have $H(x,c_{1},...,c_{4},\theta ^{*})$ nonsingular, where $\theta ^{*}=(\alpha ,0,\gamma )$. Consider a convex combination

$$\begin{aligned} a=\sum _{j=1}^{4}p(x,c_{j},\theta ^{*})\pi _{j}^{*}=H(x,c_{1},...,c_{4},\theta ^{*})\pi ^{*}, \end{aligned}$$

where $\pi ^{*\prime }=(\pi _{1}^{*},...,\pi _{4}^{*})$, $\pi _{j}^{*}>0$, and $\sum _{j=1}^{4}\pi _{j}^{*}=1$. Let

$$\begin{aligned} \pi _{0}(x)=H(x,c_{1},...,c_{4},\theta _{0})^{-1}a, \end{aligned}$$

where $\theta _{0}\ne \theta ^{*}$ is any point in $\Theta$ sufficiently close to $\theta ^{*}$ that the inverse exists and $\pi _{0j}(x)>0$ for all $x\in X$; there is such a neighborhood of $\theta ^{*}$ because X is bounded. Note that $l'H=l'$, where l is a $4\times 1$ vector of ones; hence $l'H^{-1}=l'$ and $l'\pi _{0}(x)=1$. Hence

$$\begin{aligned} \sum _{j=1}^{4}p(x,c_{j},\theta _{0})\pi _{0j}(x)=\sum _{j=1}^{4}p(x,c_{j},\theta ^{*})\pi _{j}^{*}, \end{aligned}$$

and we cannot distinguish $\theta _{0}$ from $\theta ^{*}$.

We conclude that for every $(\alpha ,\gamma )\in \Theta _{1}\times \Theta _{3}$ we must have $H(x,c_{1},...,c_{4},(\alpha ,0,\gamma ))$ singular for every choice of $c_{1},...,c_{4}\in \mathcal{{R}}$. Otherwise identification fails for all $\theta _{0}$ in some neighborhood of $(\alpha ,0,\gamma )$. So there must exist scalars $\psi _{1},...,\psi _{4}$ (not all zero) such that

$$\begin{aligned} \psi 'p(x,c,(\alpha ,0,\gamma ))&=\psi _{1}\left[ 1-F(c)\right] \left[ 1-F(\alpha +c)\right] +\psi _{2}\left[ 1-F(c)\right] F(\alpha +c)\\&\quad +\psi _{3}F(c)\left[ 1-F(\alpha +\gamma +c)\right] +\psi _{4}F(c)F(\alpha +\gamma +c)=0 \end{aligned}$$

for all $c\in \mathcal{{R}}$. Letting $c\rightarrow \infty$ gives $\psi _{4}=0$. Letting $c\rightarrow -\infty$ gives $\psi _{1}=0$. Hence we have

$$\begin{aligned} \psi _{2}\left[ 1-F(c)\right] F(\alpha +c)+\psi _{3}F(c)\left[ 1-F(\alpha +\gamma +c)\right] =0 \end{aligned}$$

for all $(\alpha ,\gamma )\in \Theta _{1}\times \Theta _{3}$ and all $c\in \mathcal{{R}}$.

Set $\gamma =0$. Letting $Q\equiv F/(1-F)$, we must have

$$\begin{aligned} \psi _{2}Q(\alpha +c)+\psi _{3}Q(c)=0; \end{aligned}$$

setting $c=0$ gives $\psi _{3}/\psi _{2}=-Q(\alpha )/Q(0)$, and so

$$\begin{aligned} Q(\alpha +c)=Q(\alpha )Q(c)/Q(0) \end{aligned}$$

for all $\alpha \in \Theta _{1}$ and all $c\in \mathcal{{R}}$. The only positive, continuously differentiable solution to this form of Cauchy’s equation is

$$\begin{aligned} Q(s)=\exp (\phi _{1}+\phi _{2}s); \end{aligned}$$

then, from $F=Q/(1+Q)$ it follows

$$\begin{aligned} F(s)=\exp (\phi _{1}+\phi _{2}s)/\left[ 1+\exp (\phi _{1}+\phi _{2}s)\right] . \end{aligned}$$

Now set $\alpha =0$. Then, with $G=1-F$, we have

$$\begin{aligned} \psi _{2}G(c)+\psi _{3}G(\gamma +c)=0; \end{aligned}$$

setting $c=0$ gives $\psi _{2}/\psi _{3}=-G(\gamma )/G(0)$, and so

$$\begin{aligned} G(\gamma +c)=G(\gamma )G(c)/G(0) \end{aligned}$$

for all $\gamma \in \Theta _{3}$ and all $c\in \mathcal{{R}}$. The only positive, continuously differentiable solution to this form of Cauchy’s equation is

$$\begin{aligned} G(s)=\exp (\tau _{1}+\tau _{2}s), \end{aligned}$$

which implies that

$$\begin{aligned} F(s)=1-\exp (\tau _{1}+\tau _{2}s). \end{aligned}$$

So we have

$$\begin{aligned} \exp (\tau _{1}+\tau _{2}s)&=1-F(s)=\left[ 1+\exp (\phi _{1}+\phi _{2}s)\right] ^{-1},\\ \tau _{1}+\tau _{2}s&=-\log \left[ 1+\exp (\phi _{1}+\phi _{2}s)\right] , \end{aligned}$$

and taking the derivative with respect to s gives

$$\begin{aligned} \tau _{2}=-\phi _{2}F(s). \end{aligned}$$

But this is a contradiction, since F is strictly increasing. So it is not possible to maintain the singularity condition on H, and identification fails for all $\theta _{0}$ in some neighborhood of $(\alpha ,0,\gamma )$.    Q.E.D. $\square$