On the identification of the effect of education on health: a comment on Fonseca et al. (2020)

Abstract

In this note we revisit the paper by Fonseca et al. (Series 11: 83-103, 2020) who find that education has a positive effect on health. They use several compulsory schooling reforms as instruments for education. Our objective is to replicate this causal finding, so we start by thoroughly discussing their identification strategy. In particular, we emphasize the importance of carefully defining birth cohort groups and using country-specific time trends. Once we take these issues into account, we show that the instrument they use is too weak.

1 Introduction

There are many works in the literature that find a strong correlation between education and health outcomes. However, there is still no consensus on whether education improves health. Several recent studies as Clark and Royer (2013), Meghir et al. (2018), Albarrán et al. (2020) and Avendano et al. (2020) do not find any causal effect of education on health. Xue et al. (2021) perform a meta-analysis including 99 published papers on this topic. They find a slight publication bias that favors papers that report a positive effect of education on health. Once they correct for this bias, they find that education no longer has a causal effect on health.

In a recent paper in this journal, Fonseca et al. (2020, in the sequel FMZ20) combine data on education and health from three sources, SHARE (continental Europe), ELSA (England) and HRS (USA). They find that education has a positive effect on health, both with self-reported measures and with various objective measures. The technique they use to prove causality is instrumental variables, exploiting the exogenous variation in education generated by compulsory schooling laws (CSLs) that increase the minimum school leaving age (SLA) as an instrument for education. The intuition is that individuals in year-of-birth cohorts affected by CSLs are forced to stay in school longer than earlier cohorts. Comparing cohorts that are a few years apart, CSLs induce an exogenous change that only affects people’s health through increased education.

Given this apparent contradiction between what FMZ20 obtain and what seems to be a growing consensus in this literature—the absence of a causal effect—we have tried to replicate their work.

The main conclusion we reach, using the same data sets and the same countries, is that we cannot prove a causal effect of education on any of the different health outcomes. The reason for this result is not that education has no effect on health, but rather that the instrument (CSL) is too weak to generate an exogenous variation in people’s education for these datasets. We want to stress that we cannot exclude the possibility of a causal effect, but simply that this methodology does not work in this specific case. In particular, we do not claim that CSLs are an invalid instrument. There are several papers in this literature that also rely on CSLs and have a convincing identification strategy. Some recent examples are Brunello et al. (2013), Crespo et al. (2014), Brunello at el. (2016), Albarrán et al. (2020), and Hofmarcher (2021). As much as an instrument has proven to be valid before, this does not mean that it will work in all situations. The validity of an instrument (or more generally of an identification strategy) is, to some extent, an empirical matter determined by the specific context, institutional setting and sample. Then, in each new application one must carefully show that it is plausible that it works.

This note is structured as follows. First, we discuss data problems and model specification issues often found when using CSLs as an instrument in a multi-country setting. Next, we present our replication results, without accounting for concerns previously discussed and once we account for them. Finally, we conclude with a simulation exercise focused on the importance of using country-specific trends to avoid getting misleading conclusions about the validity of the instrument.

2 Data and model specification

We construct a database with the same fourteen countries as FMZ20. Since credible causal results rely on the validity of the identification strategy, we focus on potential problems in the first stage. We claim that the problems in FMZ20 lie on this part. However, we have managed to reproduce closely their Summary Statistics and the results of the effect of years of education on health outcomes (OLS), that is, Tables 1 and 5 in FMZ20 (see the Appendix).

Table 1 Impact of education reforms on years of education

To account for the potential endogeneity of education, we use the exogenous variation in education provided by the CSLs and therefore we estimate the following first-stage model (like Eq. 3 in FMZ20):

$$ Ed_{icb} = \beta_{0} + \beta_{1} YC_{cb} + \beta_{2} W_{i} + T_{cb} + C_{c} + u_{icb} $$

(1)

Here, Ed_icb denotes years of education of an individual i from a country c born in the cohort year b¹; YC_cb is the number of years she was required to attend school; W_i is a dummy equal to 1 for women; T_cb denotes the “year of birth time trends” (below we discuss in detail how to define them), and C_c is a country fixed effect, captured using country dummies for each country:

$$ C_{c} = \mathop \sum \limits_{m = 1}^{M} \mu_{m} D_{cm} $$

(2)

where D_cm is a dummy that takes value 1 if observation c comes from country m, and 0 otherwise.²

It is worth noting that a person’s years of compulsory schooling only varies, in principle, with their country and year of birth (that is, it depends on whether they are affected by a CSL in their country). Table 4 in FMZ20 shows that only eight of the fourteen countries implement a CSL reform.³ For the remaining six countries there is no variation in the instrument across year-of-birth cohorts: YC_cb is YC_c, so its effect on education is already captured by the country dummies. In other words, including these six countries does not contribute anything to the identification of the parameter ${\beta }_{1}$. However, since we want to focus on the role of time trends for proper identification, we include the fourteen countries of FMZ20 to keep our analysis as close as possible to the original one.

In these types of models, by construction, treated individuals are younger than controls, so we must include time trends to account for secular tendencies. This is particularly relevant when we talk about education or health. Younger cohorts typically have a higher educational level and also better health. Adding time trends to the specification allows us to identify the effect of the reform on those people who, even with the positive trend, would not have acquired more education without the reform. When we do not include these trends, we may end up incorrectly attributing improvements in education to school reforms, when in fact those improvements are simply the result of secular trends.

FMZ20 include forty cohorts of individuals in their analysis, including those born between 1917 and 1956. The age of their sample ranges from 50 to 89. The inclusion of a temporal trend, as the authors do, can partially control for the positive trend in education and health in the countries considered. However, there are several potential issues to be aware when specifying time trends.

First, it is very unusual to impose a common time trend for all countries. This has shown too restrictive to capture the great heterogeneity in the temporal evolution of health and education. From Stephens and Yang (2014) we know that it is crucial that these time trends are country-specific, T_cb, rather than a single time trend for all countries, T_b. Suppose that different countries exhibit different time trends in education, but we impose a common time trend (as FMZ20 do). This model would have an omitted variable, the country-specific time evolution, which is correlated with the instrument, YC_cb, since this has also country-specific time variation. The differential country-specific trend would be attributed to the (country-specific) reform, YC_cb. As a result, its estimated coefficient would be biased and could lead us to wrongly conclude that the instrument is valid. To avoid any potential bias, we use a more general and flexible specification, T_cb. Moreover, this allows us to test whether the restrictions implied by the common trend are true, thus giving an empirical answer to the question of which is the correct specification.⁴

Second, a specific formula must be used for time trends. A relatively flexible approach is to group multiple birth cohorts into one group and use a dummy variable for each of these groups:

$$ T_{b} = \mathop \sum \limits_{j = 1}^{J} \delta_{j} D_{bj} $$

(3)

where D_bj is a dummy that takes value 1 when the birth cohort b belongs to the cohort group j (and 0 otherwise). In the case of country-specific trends if we have M countries and J groups of cohorts:

$$ T_{cb} = \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{m = 1}^{M} \delta_{jm} D_{bj} D_{cm} $$

(4)

where D_cm is a dummy variable that takes value 1 for country m, and 0 otherwise. As discussed above, testing that ${\delta }_{jm}={\delta }_{j}$ for all m and for each j implies testing whether a common trend specification is preferred over one with country-specific trends.

This approach requires choosing the number of groups, J, and which cohorts are included in each of them. In the most extreme case, the groups could include a single cohort. In this case, this would involve defining a dummy variable for each of the 40 years of birth. In any case, it is very important to do a robustness analysis considering various alternatives. We guess that FMZ20 use eight groups in their main specification (see Table 1 in FMZ20, Summary Statistics). Each of them corresponds to a set of five birth cohorts. This is very unfortunate, due to the timing of the reforms shown in Table 4. To illustrate this problem, we represent in the figure below all the years of birth included in this analysis, the eight time dummies and the control and treatment groups in each country.

The problem with this specification of time trends is that there are two countries (Italy and Greece) in which the treated cohorts correspond exactly to the years included in the last time dummy. For these two countries, the effect of being a treated cohort cannot be identified separately from the country-specific time effect in these last five years. This is another potential source of bias that can lead to the erroneous conclusion that the instrument is valid. One way to verify this problem is to slightly change the way we define the birth cohort dummies to avoid that the treated cohorts correspond to a single time dummy. For example, suppose we group birth years into ten blocks of four cohorts each instead of eight blocks of five cohorts each.⁵ Intuitively, things should not change much.

An alternative way to define time trends is by using age trends. FMZ20 replicate their analysis with polynomial specifications for age (in particular, age and age squared), rather than birth cohort dummies. For the same reason discussed above, these age trends should be country-specific:

$$ T_{bc} = \mathop \sum \limits_{m = 1}^{M} \gamma_{0m} D_{cm} + a_{b} \mathop \sum \limits_{m = 1}^{M} \gamma_{1m} D_{cm} + a_{b}^{2} \mathop \sum \limits_{m = 1}^{M} \gamma_{2m} D_{cm} $$

(5)

where a_b is the age of the individuals of cohort b at the time t of the survey. Again, we can test whether a common trend specification is preferred over one with country-specific trends by using a joint test for all the country-specific coefficients being the same across countries, that is, $\gamma_{0m} = \gamma_{0} ,\gamma_{1m} = \gamma_{1} ,\gamma_{2m} = \gamma_{2}$ for all m.

Third, using the forty cohorts of individuals in the sample is an unusual choice in the literature. In the ideal experiment, one would like to use only individuals born on 1st January in the year of the first cohort affected by the reform as the treatment group and those born on 31st December of the previous year as the control group to ensure that they are as similar as possible and that the only source of (exogenous) variation comes from being affected or not by the reform. Of course, this is typically impractical because the sample would be too small. In practice, the literature uses a small number of cohorts around the first affected cohort. Typical window sizes are five or seven cohorts, so no more than a total of fourteen cohorts are included in the analysis. It is a very unrealistic assumption to consider that cohorts born more than 30 years apart are good counterfactuals for each other, even if extremely flexible time trends were used. It is very likely that at least part of the effect captured by the instrument is due to uncontrolled differences between the treatment and control groups.

Another reason for limiting the number of cohorts in the control and treatment groups is that several countries changed the length of compulsory schooling several times during the period considered (Horfmarcher 2021). However, as we said above, since we want to focus on the issue of temporal trends, we are going to include all 40 cohorts in our analysis.

3 Results and discussion

We present our main results in Table 1. We use the fourteen countries and the forty cohorts in FMZ20 to estimate the first stage of ten alternative models. We consider a number of different first-stage specifications to cover all the relevant dimensions discussed in the literature that uses CSLs as an instrument. In Model 1 we replicate the specification in FMZ20 (Table 6) that has a common time trend and no control for age. To estimate the common time trend, we group birth cohorts into eight blocks of five cohorts each. The model estimates the corresponding dummies for each block. Model 2 is similar to Model 1, with the only change that we group the cohort dummies into ten blocks of four cohorts each. Models 3 and 4 add a country-specific trend to the specifications of models 1 and 2, respectively. To do this, we interact the cohort dummies with the country dummies.

In the rest of the models, we consider polynomial specifications for age to account for time trends. Model 5, instead of including cohort dummies, adds individual age as a linear regressor. The effect of age is assumed to be common across all countries. Model 6 is like model 5, but adding age squared as a regressor. Models 7 to 10 all include interactions of age with the country dummies. In model 7, age enters only linearly. Model 8 is like 7, also adding forty cohort dummies. Models 9 and 10 are like models 7 and 8, respectively, but adding a quadratic term in age. That is, both of them use a quadratic specification for the time trend (interactions of age and its square with the country dummies) rather than a linear one. The only difference is that Model 10 additionally includes the forty cohort dummies. Our preferred specifications are those in models 9 and 10. They correspond to those used by Crespo et al. (2014), Brunello et al. (2016), and Hofmarcher (2021).

Notice that FMZ20 do not provide results on standard errors, nor on the F-statistic or the number of observations (see Table 6 in FMZ20). We can only compare our results in Model 1 with their reported first-stage estimated coefficient, and its magnitude is different (0.5623 vs. 0.2736). This is surprising since we closely reproduce their Tables 1 and 5 (see the Appendix). In any case, the main finding is qualitatively the same: the estimated effect is positive and significant, so the instrument is valid.⁶ This conclusion is maintained in models 2, 3 (although the F-statistic is now clearly lower), 5, and 6. Except for Model 3, every time we include country-specific trends, the effect of the instrument completely disappears. The instrument is too weak and/or its effect cannot be separately identified from the country-specific secular trend. In all these cases the F-statistics here are always below the “safe” value of 10 (see Staiger and Stock, 1997). Furthermore, we find strong evidence against a common time trend in all cases. In summary, a proper specification of time trends, combining both a flexible and careful definition of the birth cohorts blocks and country-specific trends, implies a first stage that does not validate the identification of the causal effect of education on health.

Following the work by Stephens and Yang (2014), which shows that it is crucial to account for country-specific time trends, most (if not all) recent papers in the related literature include country-specific trends. In this case, we have empirically rejected that the time trend is common to all countries. So, they are relevant variables that must be included in the model. Moreover, the country-specific time trends are obviously correlated with the secular trends in education: younger cohorts are often more educated, but with different patterns across countries. If omitted, the “instrument” exploits a source of variation that is not exogenous, since it does not come from the reform alone but also from the country-specific trend.

We find extremely important the differences between models 3 and 4. As we have said above, both models include country-specific time trends, and the only difference between them is that in model 3 we group the cohorts into eight groups of five, while in model 4 we group them into ten groups of four. A priori, the results should be very similar. The fact that they are not indicates that there is a problem with this specification. As we discuss above, we argue that the reason for this discrepancy is that in Model 3, all the time effect of the last five years in Italy and Greece is erroneously attributed to the instrument.

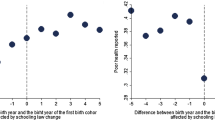
The fact that the instrument has no bite is also apparent in Fig. 1 of FMZ20, in which there is no clear jump in education around the cut-off. To further illustrate this, we have built a similar graph for each one of the eight reform countries:

Fig. 1

Time dummies, control, and treatment groups in each country

In Fig. 2 we see three countries where there is a clear jump up around the threshold (England, the Netherlands, Sweden). However, in Austria, France, Greece, and Italy there is a downward leap around the threshold. Finally, in the Czech Republic, there is no noticeable change.⁷

Fig. 2

Control and treatment, by country

As an additional check, we present estimates corresponding to the reduced form of the ten models in Table 1. The reduced form estimates the direct effect of the instrument on the outcome variables. We report in Table 2 the results corresponding to the case in which the dependent variable is a dummy variable that takes value 1 when the subject reports to have poor health. Again, we highlight in bold type models with country-specific time trends (Fig. 3).

Table 2 Reduced form (poor health)

Fig. 3

Histograms and kernel density functions for the estimated coefficient of the instrument in the first stage across replications

Again, we see that, except for Model 3, every time we include country-specific trends, the effect of years of compulsory education on the endogenous variable vanishes. This confirms our evidence from the first-stage analysis. In words of Angrist and Pischke, “If you can’t see it in the reduced form, it ain’t there” (Angrist and Pischke, 2015).

4 Simulations

To further illustrate the problem of time trends, we are going to construct an artificial example in which, by definition, the instrument has no effect on education. We simulate 60,000 observations for five countries. Each observation represents an individual. To keep things simple, there is no gender. We number the years from 0 to 39, and we define age as 89 minus the year, so the age of individuals ranges from 50 to 89 years. In each of the five countries, there is a reform that increases the number of years of compulsory schooling. However, these reforms have no effect on education. The years of schooling of the population follow a linear time trend for the entire period, and we assume that the error term u follows a normal distribution with mean 0 and standard deviation of 2. We summarize the example in Table 3.

Table 3 Data used in the simulations

As can be seen, the first simulated cohort affected in each of the five countries reproduces the real ones for AT, NL, IT, FR and GR, respectively (see Table 4 in FMZ20). Moreover, the simulated trends in years of schooling are such that the average years of schooling for these same countries and provided in Table 4 coincide with those obtained in the simulation exercise for countries 1 to 5.

Table 4 Summary Statistics (Table 1 in FMZ20)

The model we estimate is an OLS regression in which the dependent variable is education and the main regressor is the number of years of compulsory education. We also include country fixed effects and a time trend. We propose the same ten alternative ways to model time trends as in Tables 1 and 2. We simulate 100 repetitions of our model. We estimate each regression and plot the estimated coefficient of years of compulsory education in each replication.

The only models that correctly detect that the coefficient of years of compulsory education is zero are models 7–10 (see Fig. 3). Not surprisingly, these are the specifications used by Crespo et al. (2014), Brunello et al. (2016), and Albarrán et al. (2020), among other.

Appendix

See Tables 4 and 5.

Table 5 OLS models years of education on health outcomes (Table 5 in FMZ20)