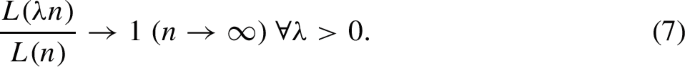Abstract
Professor Dolado has developed much of his professional career in three cities: Zaragoza, Oxford and Madrid. This fact, together with the recent appearance of literature relating climate with human behavior, has inspired us to analyze a set of relevant climate change issues linked to these areas, particularly any possible heterogeneity. The novel methodology proposed in (Gadea Rivas and Gonzalo in J Econom 214:153–174, 2020a for analyzing a wide range of characteristics of the temperature distribution (converting them into time series objects), instead of focusing solely on the mean, allows us to carry out this analysis . Using this methodology, we can identify local warming patterns within the global warming phenomenon of different types and intensities. The results show that there is a clear warming process in the three areas. The two Spanish cities (Zaragoza and Madrid) have many similarities, but Oxford fits into a different type of warming category. The former are characterized by higher trends in the upper quantiles than in the lower, an increase in dispersion, acceleration and an “upper amplification” with respect to the mean. In Oxford, the type of climate change is different, displaying higher trends in the lower quantiles, a weak negative trend in dispersion, “lower amplification” and a more attenuated acceleration in recent decades. There is no doubt that a better knowledge of local warming heterogeneity is recommendable for the design of more effective mitigation policies. The influence of the climate on human behavior and, specifically, on Professor Dolado’s personality, takes us into lesser-known regions which are left for the reader to discern.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There is a rapidly growing body of research analyzing the influence of climate change on economic outcomes. The extensive survey by Dell et al. (2014) reviews the impact on agricultural output, industrial output, labor productivity, energy demand, health, conflict and economic growth, among other outcomes.
At the micro-level, the evidence of the impact of climate change on human behavior (personality) is not so extensive. It is known that high temperatures have strong impacts affecting not only physical labor capacity but also mood, behavior and mental health through heat exhaustion and effects on cognitive and psychological performance (see Taylor et al. 2015)). A recent study by Wenqui Wei and 25 co-authors (2017) tests the relationship between ambient temperature and personality. The authors conducted two large-scale studies in China and the US revealing that compared with individuals who grew up in regions with less clement temperatures, individuals who grew up in regions with more clement temperature (closer to 22C) score higher on personality factors related to socialization and stability (agreeableness, conscientiousness and emotional stability) and personal growth and plasticity (extraversion and openness to new experiences).
In this paper, we analyze the climate of the three geographical places that have marked Prof. Dolado’s life: Zaragoza (place of birth), Oxford (Phd studies) and Madrid (place of residence). The existence of a clear local warming heterogeneity process is shown, while the task of inferring how this climate heterogeneity has influenced Dolado’s personality is left to the reader.
The study of local warming is carried out using the novel methodology introduced in Gadea and Gonzalo (JoE 2020a, GG) where all the distributional characteristics of the local temperature distribution are transformed into time series objects. These distributional characteristics, not only the standard mean, are fully analyzed. In this paper, the analysis is focused on the following three issues that are used to describe the existence of climate-warming heterogeneity:
-
Existence of Local Warming (LW) and determination of the type of LW in each region
-
LW acceleration over time.
-
LW amplification with respect to the mean temperature.
This climate-warming heterogeneity is crucial in order to design more efficient mitigation policies to fight against global warming.
The rest of the paper is organized as follows. Section 2 summarizes the novel econometric methodology introduced in GG. Section 3 describes the temperature data of Zaragoza, Madrid and Oxford. Section 4 presents the results that show the existence of local warming in all the three cities and its heterogeneity. In this section, we introduce a warming typology and definitions of warming acceleration and warming amplification. Finally, Sect. 5 concludes.
2 Climate econometrics methodology
In this section, we briefly summarize the novel econometric methodology introduced in GG to analyze Global and Local Warming processes. Following GG, Warming is defined as an increasing trend in certain characteristics of the temperature distribution. More precisely:
Definition 1
(Warming) Warming is defined as the existence of an increasing trend in some of the characteristics measuring the central tendency or position (quantiles) of the temperature distribution.
An example is a deterministic trend with a polynomial function for certain values of the \(\beta \) parameters \(C_{t}=\beta _{0}+\beta _{1}t+\beta _{2}t^{2}+...+\beta _{k}t^{k}\).
In GG, temperature is viewed as a functional stochastic process \(X=(X_{t}(\omega ), t \in {\mathbf {T}})\), where \({\mathbf {T}})\) is an interval in \({\mathbb {R}}\), defined in a probability space \((\Omega , \mathfrak {I}, P)\). A convenient example of an infinite-dimensional discrete-time process consists of associating \(\xi =(\xi _n, n \in {\mathbb {R}}_{+})\) with a sequence of random variables whose values are in an appropriate function space. This may be obtained by setting
so \(X=(X_{t}, t=0,1,2,...,T)\). If the sample paths of \(\xi \) are continuous, then we have a sequence \(X_{0}, X_{1}, ....\) of random variables in the space C[0, N]. The choice of the period or segment t will depend on the situation in hand. In our case, t will be the period of a year, and N represents cross-sectional observations.
We may be interested in modeling the whole sequence of \({\mathbf {G}}\) functions, for instance the sequence of state densities (\(f_{1}(\omega ), f_{2}(\omega ), ..., f_{T}(\omega ) \) ) as in Chang et al. (2015, 2016) or only certain characteristics (\(C_{t}(w)\)) of these \({\mathbf {G}}\) functions, for instance, the state mean, the state variance, the state quantile, etc. These characteristics can be considered time series objects, and, therefore, all the econometric tools already developed in the time series literature can be applied to \(C_{t}(w)\). With this characteristic approach, we go from \(\Omega \) to \({\mathbb {R}}^{T}\), as in a standard stochastic process, passing through a \({\mathbf {G}}\) functional space:
Going back to the convenient example and abusing notation, the stochastic structure can be summarized in the following array:

As in GG, we assume that the stochastic functional process \(X=(X_{}t(\omega ),t \in {\mathbf {T}})\) satisfies certain regularity conditions, such that the state densities, distribution and, therefore, quantiles and any distributional characteristics are estimated consistently.
The objective of this section is to provide a simple test to detect the existence of a general unknown trend component in a given characteristic \(C_t\) of the temperature process \(X_t\). To do this, we need to convert Definition 1 into a more practical definition.
Definition 2
(Trend test) Let h(t) be an increasing function of t. A characteristic \(C_{t}\) of a functional stochastic process \(X_{t}\) contains a trend if \(\beta \ne 0\) in the regression
The main problem of this definition is that the trend component in \(C_t\) as well as the function h(t) are unknown. Therefore, this definition cannot be easily implemented. If we assume that \(C_t\) does not have a trend component (it is I(0)) and h(t) is linear, then we have the following well-known result.
Proposition 1
Let \(C_{t}=I(0)\). In the regression
the OLS estimator
satisfies
The t-test of the null hypothesis \(\beta =0\) (vs. \(\beta \ne 0\)) asymptotically (\(T \rightarrow \infty \)) behaves as a N(0,1)
In order to analyze the behavior of the t-statistic \(t_{\beta =0 },\) for a general trend component in \(C_t\), it is very convenient to use the concept of Summability (Berenguer and Gonzalo, 2014)
Definition 3
(Order of summability) A trend h(t) is said to be summable of order “\(\delta \)” \((S(\delta ))\) if there exists a slowly varying function L(T),Footnote 1 such that
is O(1), but not o(1).
Proposition 2
Let \(C_{t}=h(t)+I(0)\) such that h(t) is \( S(\delta )\) with \(\delta \ge 0\), and such that the function \(g(t)=h(t)t \) is \( S(\delta +1)\). In the regression
the OLS \({\widehat{\beta }}\) estimator satisfies
Assuming that the function \(h(t)^{2}\) is \( S(1+2 \delta -\gamma )\) with \(0\le \gamma \le 1+\delta \), then the t-test of the null hypothesis \(\beta =0\) (vs. \(\beta \ne 0\))
Examples of how this proposition applies for different particular Data Generating Processes (DGP) can be found in GG.
A question of great empirical importance is how our trend test (TT) of Proposition 2 behave when \(C_t=I(1)\). Following Durlauf and Phillips (1988), \(T^{1/2}{\widehat{\beta }}=O_{p}(1)\); however, \(t_{\beta =0}\) diverges as \( T {\rightarrow } \infty \). Therefore, our TT can detect the stochastic trend generated by an I(1) process. In fact, our test will detect trends generated by any of the three standard persistent processes considered in the literature (see Müeller and Watson 2008): (i) fractional or long-memory models; (ii) near-unit-root AR models; and (iii) local-level models. Let
In the first model, \(z_{t}\) is a fractional process with \(1/2<d<3/2\). In the second model, \(z_{t}\) follows an AR, with its largest root close to unity, \(\rho _{T}=1-c/T\). In the third model, \(z_{t}\) is decomposed into an I(1) and an I(0) component. Its simplest format is \(z_{t}\) = \(\upsilon _{t}\) + \(\epsilon _{t}\) with \(\upsilon _{t}\) = \(\upsilon _{t-1}\) +\(\eta _{t}\), where \(\epsilon _{t}\) is \(ID(0,q*\sigma ^{2}\)), \(\eta _{t}\) is \(ID(0,\sigma ^{2})\), \(\sigma ^{2} >0\) and both disturbances are serially and mutually independent. Note that the pure unit-root process is nested in all three models: \(d=1\), \(c=0\), and \(q=0\).
The long-run properties implied by each of these models can be characterized using the stochastic properties of the partial sum process for \(z_{t}\). The standard assumptions considered in the macroeconomics or finance literature assume the existence of a “\(\delta \),” such that \(T^{-1/2+\delta }\sum _{t=1}^{T}z_{t}\longrightarrow \sigma \) H(.), where “\(\delta \)” is a model-specific constant and H is a model-specific zero-mean Gaussian process with a given covariance kernel k(r, s). Then, it is clear that the process \(C_{t}=\mu +z_{t}\) is summable (see Berenguer-Rico and Gonzalo 2014). This is the main reason why Proposition 3 holds for these three persistent processes.
Proposition 3
Let \(C_{t}=\mu +z_{t},t=1,...,T\), with \(z_{t}\) any of the following three processes: (i) a fractional or long-memory model, with \(1/2<d<3/2\); (ii) a near-unit-root AR model; or (iii) a local-level model. Furthermore, \(T^{-1/2+\delta }\sum _{t=1}^{T}z_{t}\longrightarrow \sigma \) H(.), where “\(\delta \)” is a model-specific constant and H is a model-specific zero-mean Gaussian process with a given covariance kernel k(r, s). Then, in the LS regression
the t-test of the null hypothesis \(\beta =0\) (vs. \(\beta \ne 0\)) asymptotically diverges,
In summary, Propositions 2 and 3 imply that Definition 3 can be simplified to the following practical definition.
Definition 4
(Practical definition 2) A characteristic \(C_{t}\) of a functional stochastic process \(X_{t}\) contains a trend if in the LS regression,
\(\beta \ne 0\) is rejected.
Several remarks are relevant with respect to this definition: (i) regression (13) has to be understood as the linear LS approximation of an unknown trend function h(t) (see White 1980); (ii) the parameter \(\beta \) is the plim of \({\widehat{\beta }}_{ols}\); (iii) if the regression (13) is the true data-generating process, with \(u_t\sim I(0)\), then the OLS \({\widehat{\beta }}\) estimator is asymptotically equivalent to the GLS estimator (see Grenander and Rosenblatt 1957; iv) in practice, in order to test \(\beta =0\), it is recommended to use a robust HAC version of \(t_{\beta =0}\) (see Busetti and Harvey 2008)Footnote 2 and (v) this test only detects the existence of a trend but not the type of trend.
For all these reasons, in the empirical applications we implement Definition 4 by estimating regression (13) using OLS and constructing a HAC version of \(t_{\beta =0}\) (Newey and West 1987).
These linear trends can be common indicating similar patters in the time evolution of several characteristics.
Definition 5
(Co-trending) A set of m distributional characteristics (\(C_{1t}\),\(C_{2t}\),...,\(C_{mt}\)) do linearly co-trend if in the multivariate regression
all the slopes are equal, \(\beta _{1}=\beta _{2}=...=\beta _{m}.\)Footnote 3
This co-trending hypothesis can be tested by a standard Wald test.
When \(m=2\), an alternative linear co-trending test can be obtained from the regression
\(i\ne j\) \(i,j=1,...,m\) by testing the null hypothesis of \(\beta =0\) vs \(\beta \ne 0\) using a simple \(t_{\beta }\) = 0 test.
3 The data of the temperature in the three cities
The data sources for the two Spanish cities and the Central England area are different, but both are available at daily frequency for the same period of time.
In Spain, AEMET (Agencia Estatal de Meterología) is the agency responsible for storing, managing and providing meteorological data to the public. In 2015, AEMET developed AEMET OpenData, an Application Programming Interface (API REST) that allows the dissemination and reuse of Spanish meteorological and climatological information.Footnote 4 In this paper, we are concerned with Spanish daily station data, specifically temperature data. In particular, each station records the minimum, maximum and average temperature and in some cases the time the temperature is recorded. The data period ranges from 1920 to the present although not all stations cover the same time periods. Specifically, the two stations selected, Zaragoza-Aeropuerto and Madrid-Retiro start in 1951 and 1920, respectively.
As regards the Central England region, we have the longest temperature record series (thermometer measured) which runs from 1659 to the present. These data are measured monthly and annually for England. There are also daily temperature data that have been measured since 1772. However, there are no instrumental data prior to 1659 because the thermometer was only invented a few decades earlier. These data were originally published by Gordon Manley in 1953 in a database called The Central England Temperature (CET), which is available from http://www.metoffice.gov.uk/hadobs/hadcet/. These daily and monthly temperatures are representative of a roughly triangular area of the United Kingdom enclosed by Lancashire, London and Bristol, in which the city of Oxford is located (Figs. 1,2,3,4,5).
In order to homogenize the results and make them comparable, the entire analysis has been carried out from 1950 to 2019, following the shortest temperature data available (Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16). Specifically, 1951-2019 for Zaragoza, 1950-2019 for Madrid and 1950-2020 for Central England. This period also coincides with the life cycle of Prof. Dolado. Figures 1,2, 6 and 10 represent the temporal density of the temperature data at daily frequency for the three geographical areas.
The three cities have different geographical characteristics. Focusing on those that most affect the climate, latitude and height, Oxford is located at a latitude of 51.72, the highest of the three, and at an altitude of 76m, almost at sea level. Zaragoza and Madrid have similar latitudes, 41.66 and 40.42, respectively, but differ in altitude: 208m for Zaragoza and 667m for Madrid, the latter being one of the highest European capitals. The longitudes are -0.88, -3.70 and -1.26 for Zaragoza, Madrid and Oxford, respectively, although this coordinate has less influence on the climate since the three cities receive the warming effect of the Gulf Stream. The type of climate is oceanic in the case of Oxford and continental in the case of the two Spanish cities (see map in Fig. 1).
Following the convenient example (see scheme 2 in Sect. 2), X is the local temperature, T (number of periods) is measured in years, N has a temporal structure (days), and \(C_t= (C_{1t}, C_{2t}, ..., C_{pt})\) is a vector of p distributional characteristics (mean (mean), maximum (max), minimum (min), standard deviation (std), interquartile range (iqr), total range (range), kurtosis (kur), skewness (skw), and the following quantiles: q05, q10, q20, q30, q40, q50, q60, q70, q80, q90, and q95 estimated from N observations. The evolution of these characteristics throughout the available sample is displayed in Figs. 3, 7 and 11 for Zaragoza, Madrid and Central England, respectively. These characteristics are obtained from the corresponding estimated temperature densities (see Figs. 2, 6 and 10).
4 Local climate in the three cities
In this section, we apply our methodology to each one of the three main regions where Prof. Dolado has spent part of his life. We compare the results focusing particularly on the main differences, in the local warming heterogeneity. With our methodology (Gadea and Gonzalo 2020b), we are able to construct a typology of the different types of warming processes. This typology is based on the evolution of the different distributional characteristics, especially the lower and upper quantiles.
Definition 6
(Warming typology) We define four types of Warming processes:
-
W0: Only the median has a positive trend.
-
W1: All the quantiles share the same positive trend (iqr does not contain a trend)
-
W2: The Lower quantiles have a larger positive trend than the Upper quantiles (iqr has a negative trend)
-
W3: The Upper quantiles have a larger positive trend than the Lower quantiles (iqr has a positive trend).
W0 is an unrealistic case that is introduced only for comparison-explanatory purposes. Most of the literature on Global or Local Warming only considers the trend behavior of the central part of the distribution (mean or median). By doing this, we are losing very useful information that can be used to describe the whole warming process. This information is considered in the other elements of the typology W1, W2 and W3. This typology does not say anything about the intensity of the warming process. Part of this intensity is considered in the following definitions of warming acceleration and warming amplification.
Definition 7
(Warming acceleration) We say that there is warming acceleration in a distributional temperature characteristic \(C_{t}\) between the time periods \(t_1\) and \(t_2\) if in the following two regressions:
the second trend slope is larger than the first: \(\beta _{2} > \beta _{1}\).
Definition 8
(Warming amplification with respect the mean) We say that there is a warming amplification in distributional characteristic \(C_{t}\) with respect the mean if in the following regression:
the mean slope is greater than one: \(\beta _{1} >1\).
The results are presented according to the following steps: first, we apply our TT to determine the existence of local warming; second, we test different co-trending hypotheses to determine the type of local warming of each region; third, we analyze heuristically the particular warming acceleration process of each region, and finally we test the warming amplification hypothesis for different quantiles with respect to the mean: \(H_{0}: \beta _{1}=1\) versus \(H_{a}: \beta _{1}>1\) in (17).Footnote 5
4.1 Zaragoza
Zaragoza shows positive and significant trends in all the characteristics measuring the central tendency or position (quantiles) of its temperature distribution. These trends are stronger in the upper part of the distribution (see Table 1), implying that dispersion measures like std and iqr have a positive trend coefficient. The mean has a trend slope of 0.0352, which means an increase of 3.52 degrees Celsius in 100 years. The highest positive trend occurs in the upper quantiles represented by q95 with a coefficient value of 0.053, which implies an increase of 5.3 degrees in 100 years. The lower quantile which is represented by q05 registers a value of 0.0303.
Table 2 shows the trend homogeneity behavior of all the quantiles. Full homogeneity is rejected, but partial homogeneity cannot be rejected. There is a certain degree of homogeneity in the lower-middle part and in the upper part of the temperature distribution. A positive and very significant trend between q95 and q50 and between q95 and q05 is identified.
This pattern of the temperature distribution accelerates as time passes (Table 3 and Fig. 4). The heatmap (Fig. 5) that represents the year-by-year recursive trend slope estimation since 1950 also confirms the greater increase in the highest quantiles compared to the low ones and highlights the strong increase in the trend in extreme values (maximum and minimum) at the end of the period.
Finally, we cannot reject the amplification hypothesis with respect to the mean for medium and higher quantiles (from q60 to q95), which can be interpreted as a greater increase in high temperatures with respect to the average. We call this phenomenon “upper amplification.”
Summing up, the existence of local warming, acceleration and “upper amplification” is confirmed. In this case, warming is not homogeneous throughout the whole temperature distribution; it is more intense in the right tail of the distribution. Putting all the pieces together, we classify the warming process in Zaragoza as type W3.
4.2 Madrid
Madrid shows positive and significant trends in all the characteristics measuring the central tendency or position (quantiles) of its temperature distribution. These trends are stronger in the upper part of the distribution (see Table 5), implying that dispersion measures like std and iqr have a positive trend coefficient. The mean has a trend slope of 0.0326, which means an increase of 3.26 degrees Celsius in 100 years. The highest positive trend occurs in the upper quantiles represented by q95 with a coefficient value of 0.0527, which implies an increase of 5.3 degrees in 100 years. The lower quantile which is represented by q05 registers a value of 0.0248. These estimates are very similar to those found for Zaragoza.
Table 6 shows the trend homogeneity behavior of all the quantiles. Full homogeneity is rejected, but, again, partial homogeneity cannot be rejected. There is a certain degree of homogeneity in the lower-middle part and in the upper part of the temperature distribution. A positive and very significant trend between q95 and q50 and between q95 and q05 is identified.
This pattern of the temperature distribution accelerates as time passes (Table 7 and Fig. 8). The recursive estimate in the heatmap shows, as in the case of Zaragoza, that the highest acceleration is produced in the high quantiles.
Finally, we cannot reject the amplification hypothesis (see Table 8) with respect the mean for medium and higher quantiles (from q60 to q95), which can be interpreted as a greater increase in high temperatures with respect to the average. As in Zaragoza, Madrid’s warming experiences an “upper amplification.”
Summing up, the existence of local warming, acceleration and “upper amplification” is confirmed. In this case, warming is not homogeneous throughout the whole temperature distribution but is more intense in the right tail of the distribution. Putting all the pieces together, we classify the warming process in Madrid as type W3.
4.3 Central England
The trend-test indicates a significant trend in all the characteristics of the temperature distribution of Central England (CET). All the trends are positive, except those corresponding to the dispersion measures (std, iqr), which are negative but non significant at \(10\%\) (See Table 9). The dispersion results differ from those in GG for the period 1772-2018 for which clearer reduction in dispersion is found (similar results for the USA are reported in Diebold and Rudebusch 2019 and for the whole Globe in Gadea et al. 2020). Obviously, the decrease in the dispersion measures has a lower bound and it seems that recently this dispersion decrease has been reduced. The mean has a trend coefficient of 0.0178, which implies an increase of 1.78 degrees Celsius in 100 years (Table 9). The highest positive trends occur in the lower quantiles. The trend coefficient of the quantiles ranges from 0.0246 in the quantile (q05) to 0.0184 in quantile (q95).
According to the co-trending Wald test for CET data (see Table 10), trend homogeneity for the whole temperature distribution cannot be rejected. All the quantiles share a trend co-feature.
Contrary to the full trend acceleration experienced by the Zaragoza and Madrid temperatures, CET only presents partial acceleration (middle part of the distribution from q20 to q80)(see Table 12 and Fig. 12). The recursive estimation shown in the heatmap reinforces this finding (Fig. 13).
In contrast to the findings for the Spanish cities, in Central England the amplification phenomenon with respect to the mean is found in the lower quantiles, from q05 to q20. We call this phenomenon “lower amplification.”
Summing up, the existence of local warming with no trend in the dispersion measures, acceleration in the middle part of the distribution and “lower amplification” is confirmed. In this case, we classify the warming process in CET as a mild W1 type.Footnote 6
4.4 Comparing: a tale of three cities
We have already classified the warming process of three cities according to definition 5. In this subsection, we compare the numerical intensity of this warming process.
A descriptive look at the evolution of the temperature distribution of the three cities is presented in Fig. 14 for three of the relevant characteristics, the mean, and the quantiles q05 and q95. In relation to the mean, higher values are observed on average in the Spanish cities throughout the comparable period, specifically, 15.15 in Zaragoza, 14.73 in Madrid and 9.82 in Central England. The difference is very marked in the case of the upper quantile with figures of 26.71, 26.77 and 17.73, respectively. In relative terms, the differences in the lower quantiles, 3.94, 4.32 and 1.37, are also large. In all three cases, a stronger upward trend seems to be observed for recent decades in the two Spanish cities than in Central England.
From the detailed analysis of the characteristics of the temperature distribution of the three cities, we have concluded that there are two types of climate change at the local level. However, size matters because it shows the intensity of each of these patterns. What Fig. 15 illustrates is the different trend slopes of each of the characteristics in two different periods. It is found that the trend is greater in almost all the characteristics in the Spanish cities than in Oxford, especially in the mean and in the highest quantiles, a feature that is accentuated in the second period. Also, noteworthy is the uneven behavior of the characteristics associated with dispersion (std and iqr) which, as has already been pointed out, have a different sign, positive in the case of Zaragoza and Madrid and negative (non significant) in Oxford.
Finally, Fig. 16 represents the recursive estimate used in the heat maps jointly for the three cities and three relevant characteristics. These figures clearly show the differences in terms of the climate typology of the three regions. There are two elements to highlight. The first is the existence of positive trends in the three selected characteristics. The second is the difference in magnitude that clearly points to a more intense warming in the Spanish cities compared to the English one. Other results are more subtle. For example, the trend increase in q05 in Central England, which is attenuated as we approach the end of the sample, or the small differences between the behavior of Zaragoza and Madrid that are manifested only at the end of the period.
5 Conclusions
Professor Dolado has developed much of his professional career in three cities: Zaragoza, Oxford and Madrid. This fact, together with the recent research linking climate with personal behavior (personality), has inspired us to analyze a set of relevant climate change issues linked to these places, particularly any possible heterogeneity. The findings of this paper, achieved using the novel methodology introduced in GG, are very clear: There exists Local Warming in the three regions. This LW is not homogeneous. The warming in Zaragoza and Madrid is not only stronger than in Oxford, it also follows different warming typologies according to definition 5. Zaragoza and Madrid are of type W3 and Oxford is W1. There are also other differences summarized as follows:
-
Zaragoza shows a warming acceleration over its whole temperature distribution although it is stronger from q30 upwards. Madrid also suffers a strong acceleration from q30 upwards, while Oxford has a very mild acceleration in the middle part of its distribution (between q20 and q80).
-
Zaragoza and Madrid show an upper warming amplification (above q60), while Oxford has a lower amplification (below q20) with respect their corresponding means.
Properly identifying the type of local warming is crucial in order to know its causes as well as its influence on the economy so as to implement the appropriate efficient mitigation policies. Regions with different warming processes may require different economic mitigation policies. These are issues under current investigation by the authors. Much less is known about the influence of climate on human behavior, although we believe that having shown the existence of a clear climate heterogeneity can help shed light on this issue. Prof. Dolado’s life has alternated between Zaragoza and Madrid with average temperatures slightly above 20 degrees and an intermediate period in Oxford whose average temperature is around 10 degrees and with very different distributional characteristics. We leave it up to the reader to assess the extent to which some of Dolado’s personality traits, such as his sociability, extraversion, and capacity for diverse and hard work have been influenced by the climates of the main cities in his life.
Notes
A positive Lebesgue measurable function, L, on \((0,\infty )\) is slowly varying (in Karamata’s sense) at \(\infty \) if
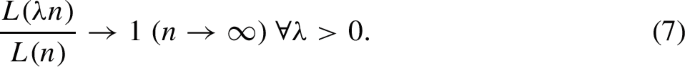
(See Embrechts et al. 1999, p. 564).
Note that all the characteristics (mean, median, etc.) contain an estimation error. This estimation error would be accommodated into the regression error in (13) and assuming it is stationary it will not represent any problem for the robust \(t-statistic\).
This definition is slightly different from the one in Carrion-i-Sivestre and Kim (2019).
A detailed description of the historical publications on climate in Spain and the way to access AEMET data can be found in Gadea and Gonzalo (2020b).
Before testing for the presence of trends in the distributional characteristics of the data, we test for the existence of unit roots. To do so, we use the well-known Augmented Dickey–Fuller test (ADF; Dickey and Fuller 1979), where the number of lags is selected in accordance with the SBIC criterion. The results, available form the authors on request, show that the null hypothesis of a unit root is rejected for all the considered characteristics.
In GG, the CET warming for the period 1772–2018 shows a more significant negative trend in the dispersion measures. For this reason, the CET warming for 1772–2018 is considered a W2 type. Nevertheless, it seems that over time the trend behavior of CET temperature distribution has become more homogenous (W1 type).
References
Berenguer-Rico V, Gonzalo J (2014) Summability of stochastic processes–a generalization of integration and co-integration valid for non-linear processes. J Econom 178:331–341
Busetti F, Harvey A (2008) Testing for trend. Econometric 24:72–87
Carrion-i-Sivestre JL, Kim D (2019) Quasi-likelihood ratio tests for cointegration, cobreaking, and cotrending. Economet Rev 38(8):881–898
Chang Y, Kim Ch.S, Miller JI, Park JY, Park S (2015) Time series analysis of global temperature distributions: identifying and estimating persistent features in temperature anomalies. Working Paper 15-13, University of Missouri
Chang Y, Kim CS, Park JY (2016) Nonstationarity in time series of state densities. J Econom 192:152–167
Dell M, Jones BF, Olken BA (2014) What do we learn from the weather? The new climate-economy lieterature. J Econ Literat 52(3):740–798
Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74:427–431
Diebold FX, Rudebusch GD (2019) On the evolution of US temperature dynamics. PIER Working Paper 09-12
Durlauf SN, Phillips PCB (1988) Trends versus random walks in time series analysis. Econometrica 56:1333–1354
Embrechts P, Klüppelberg C, Mikosh T (1999) Modelling extremal events for insurance and finance. Springer, Berlin
Gadea MD, Gonzalo J (2020a) Trends in distributional characteristics: existence of global warming. J Econom 214:153–174
Gadea MD, Gonzalo J (2020b) Local and global warming heterogeneity: Spain and the Globe. Mimeo
Gadea MD, Gonzalo J (2021) Polar Warming. Mimeo
Gadea MD, Gonzalo J, Montañes A (2020) Global warming: does it exhibit a homogeneous pattern of behavior? Mimeo
Grenander U, Rosenblatt M (1957) Statistical analysis of stationary time series. Wiley, New York
Manley G (1953) The mean temperature of Central England, 1698 to 1952. Q J R Meteorol Soc 79:242–261
Müeller UK, Watson M (2008) Testing models of low-frequency variability. Econometrica 76:979–1016
Newey WK, West KD (1987) A Simple positive semi-definite, heterekodasticity and autocorrelation consistent covariance matrix. Econometrica 55:703–708
Taylor L, Watking SL, Marshall H, Dascome BJ, Foster J (2015) The impact of different environmental conditions on cognitive function: a focused review. Front Physiol 6:372
Wei W, Lu JG, Galinsky AD et al (2017) Regional ambient temperature is associated with human personality. Nat Hum Behav 1:890–895
White H (1980) Using least square to approximate unknown regression function. Int Econ Rev 21:149–170
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Special issue of SERIES in homage to Juan J. Dolado.
The authors gratefully acknowledge the financial support from the Gobierno de Aragon and FEDER funds (Grant, LMP71-18), the Spanish Ministerio de Ciencia y Tecnología, Agencia Española de Investigación (AEI) and European Regional Development Fund (ERDF, EU) under Grants PID2019-104960GB-IOO, ECO2017-83255-C3-1-P (AEI/ERDF, EU), ECO2016-81901-REDT, and PID2020-114646RB-C44, and Bank of Spain (ER grant program). We thank Rodrigo Gonzalez Laiz for excellent research assistance.
Appendix: typology of warming processes
Appendix: typology of warming processes
To illustrate graphically the four different types of Warming processes described in the text, the following simulation exercise has been carried out. We have generated 100 replications of series \(y_{it}\) \((i=1, ..., N\) and \(t=1, ..., T)\) with T=150 and N=200 as a mixture of 3 normal distributions with weights \(\eta _{1}\), \(\eta _{2}\), \(\eta _{3}\), that take values of 0.05, 0.95 and 0.05, respectively. We define a discrete indicator variable S taking values in the set 1, 2, 3 . The marginal density p(y) is obviously given by the following mixture density,
In each replication, the random variable y follows the distribution \(p(y|\theta _{S})\) with \(\theta _{S}\) being the parameter in group S. In this case, \(p(y|\theta _{S})\) \(\sim N(\mu _{St},1)\), where \(\mu _{St}=\alpha _{S}+\beta _{S}*t+\epsilon _{t}\) with \(\epsilon _{t}\) \(\sim N(0,1)\). The value of \(\alpha _{S}\ \)and \(\beta _{S}\) are different for each group labeled with S and for each type of Warming process (Figs. 17, 18, 19, 20).
The following figures show the distributional characteristics q05, q50, q95 and iqr=q95-q05 corresponding to the 100 replications. The linear trend for a given characteristic is estimated from its average across replications.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gadea Rivas, M.D., Gonzalo, J. A tale of three cities: climate heterogeneity. SERIEs 13, 475–511 (2022). https://doi.org/10.1007/s13209-021-00254-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-021-00254-4
Keywords
- Climate change
- Global Warming
- Local Warming
- Functional stochastic processes
- Distributional characteristics
- Trends
- Quantiles
- Temperature distributions