Abstract
We propose simple specification tests for independent component analysis and structural vector autoregressions with non-Gaussian shocks that check the normality of a single shock and the potential cross-sectional dependence among several of them. Our tests compare the integer (product) moments of the shocks in the sample with their population counterparts. Importantly, we explicitly consider the sampling variability resulting from using shocks computed with consistent parameter estimators. We study the finite sample size of our tests in several simulation exercises and discuss some bootstrap procedures. We also show that our tests have non-negligible power against a variety of empirically plausible alternatives.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The literature on structural vector autoregressions (Svar) is vast. Popular identification schemes include short- and long-run homogenous restrictions [see, e.g. Sims (1980), Blanchard and Quah (1989)], sign restrictions [see, e.g. Faust (1998), Uhlig (2005)], time-varying heteroskedasticity (Sentana and Fiorentini 2001) or external instruments [see, e.g. Mertens and Ravn (2012), Stock and Watson (2018) or Dolado et al. (2020)]. Recently, identification through independent non-Gaussian shocks has become increasingly popular after Lanne et al. (2017) and Gouriéroux et al. (2017). The signal processing literature on Independent Component Analysis (Ica) popularised by Comon (1994) shares the same identification scheme. Specifically, if in a static model the \(N\times 1\) observed random vector \( \varvec{y}\)—the so-called signals or sensors—is the result of an affine combination of N unobserved shocks \(\varvec{\varepsilon }^{*}\)—the so-called components or sources—whose mean and variance we can set to \( \varvec{0}\) and \(\varvec{I}_{N}\) without loss of generality, namely
then the matrix \(\varvec{C}\) of loadings of the observed variables on the latent ones can be identified (up to column permutations and sign changes) from an i.i.d. sample of observations on \(\varvec{y}\) provided the following assumption holds:Footnote 1
Assumption 1
: Identification
-
(1)
the N shocks in (1) are cross-sectionally independent,
-
(2)
at least \(N-1\) of them follow a non-Gaussian distribution, and
-
(3)
\(\varvec{C}\) is invertible.
Failure of any of the three conditions in Assumption 1 results in an underidentified model. The best known counterexample is a multivariate Gaussian model for \(\varvec{\varepsilon } ^{*}\), in which we can identify \(V(\varvec{y)=CC}^{\prime }\) but not \( \varvec{C}\) without additional structural restrictions despite the fact that the elements of \(\varvec{\varepsilon }^{*}\) are cross-sectionally independent. Intuitively, the problem is that any rotation of the structural shocks \(\varvec{\varepsilon }^{**}=\varvec{Q\varepsilon }^{*}\), where \(\varvec{Q}\) is an orthogonal matrix, generates another set of N observationally equivalent, cross-sectionally independent shocks with standard normal marginal distributions. A less well-known counterexample would be a non-Gaussian spherical distribution for \(\varvec{\varepsilon } ^{*}\), such as the standardised multivariate Student t. In this case, the lack of identifiability of \(\varvec{C}\) is due to the fact that \(\varvec{ \varepsilon }^{*}\) and \(\varvec{\varepsilon }^{**}\) share not only their mean vector (\(\varvec{0}\)) and covariance matrix (\(\varvec{I}\)), but also the same nonlinear dependence structure.
The purpose of our paper is to propose simple to implement and interpret specification tests that check the normality of a single element of \(\varvec{ \varepsilon }^{*}\) and the potential cross-sectional dependence among several of them. In very simple terms, our tests compare the integer (product) moments of the shocks in the sample with their population counterparts. Specifically, in the Gaussian tests we compare the marginal third and fourth moments of a single shock to 0 and 3, respectively. In turn, in the case of two or more shocks, we assess the statistical significance of their second, third and fourth cross-moments, which should be equal to the product of the corresponding marginal moments under independence. Many of these moments tests can be formally justified as Lagrange multiplier tests against specific parametric alternatives [see, e.g. Mencía and Sentana (2012)], but in this paper we do not pursue this interpretation. Like Almuzara et al. (2019), though, we focus on the latent shocks rather than the observed variables in view of the fact that identifying Assumption 1 is written in terms of \(\varvec{\varepsilon }^{*}\) rather than \(\mathbf{y}\).
If we knew the true values of \(\varvec{\mu }\) and \(\varvec{C}\), \(\varvec{\mu }_{0}\) and \(\varvec{C}_{0}\) say, with \(rank(\varvec{C}_{0})=N\), our tests would be straightforward, as we could trivially recover the latent shocks from the observed signals without error. In practice, though, both \(\varvec{ \mu }\) and \(\varvec{C}\) are unknown, so we need to estimate them before computing our tests.
Although many estimation procedures for those parameters have been proposed in the literature [see, e.g. Moneta and Pallante (2020) and the references therein], in this paper we consider the discrete mixtures of normals-based pseudo-maximum likelihood estimators (PMLEs) in Fiorentini and Sentana (2020) for three main reasons. First, they are consistent for the model parameters under standard regularity conditions provided that Assumption 1 holds regardless of the true marginal distributions of the shocks. Second, they seem to be rather efficient, the rationale being that finite normal mixtures can provide good approximations to many univariate distributions. And third, the influence functions on which they are based are the scores of the pseudo-log-likelihood, which we can easily compute in closed form. As we shall see, these influence functions play a very important role in adjusting the asymptotic variances of the different tests we propose so that they reflect the sampling variability resulting from computing the shocks with consistent but noisy parameter estimators.
In this respect, we derive computationally simple closed-form expressions for the asymptotic covariance matrices of the sample moments underlying our tests under the relevant null adjusted for parameter uncertainty. Importantly, we do so not only for static Ica model (1) but also for a Svar, which is far more relevant in economics.
In many empirical finance applications of Svars, the number of observations is sufficiently large for asymptotic approximations to be reliable. In contrast, the limiting distributions of our tests may be a poor guide for the smaller samples typically used in macroeconomic applications. For that reason, we thoroughly study the finite sample size of our tests in several Monte Carlo exercises. We also discuss some bootstrap procedures that seem to improve their reliability. Finally, we show that our tests have non-negligible power against a variety of empirically plausible alternatives in which the cross-sectional independence of the shocks no longer holds.
The rest of the paper is organised as follows. Section 2 discusses the model and the estimation procedure. Then, we present our general moment tests in Sect. 3 and particularise them to assess normality and independence in Sect. 4. Next, Sect. 5 contains the results of our Monte Carlo experiments. We present our conclusions and suggestions for further research in Sect. 6 and relegate some technical material and additional simulations to several appendices.
2 Structural vector autoregressions
2.1 Model specification
Consider the following N-variate Svar process of order p:
where \(I_{t-1}\) is the information set, \(\varvec{C}\) the matrix of impact multipliers and \(\varvec{\varepsilon }_{t}^{*}\) the “structural” shocks, which are normalised to have zero means, unit variances and zero covariances.
Let \(\varvec{\varepsilon }_{t}=\varvec{C}\varvec{\varepsilon }_{t}^{*}\) denote the reduced form innovations, so that \(\varvec{\varepsilon } _{t}|I_{t-1}\sim i.i.d.\) \((\varvec{0},\varvec{\Sigma })\) with \(\varvec{ \Sigma }=\varvec{CC}^{\prime }\). As we mentioned in introduction, a Gaussian (pseudo) log-likelihood is only able to identify \(\varvec{\Sigma }\), which means the structural shocks \(\varvec{\varepsilon }_{t}^{*}\) and their loadings in \(\varvec{C}\) are only identified up to an orthogonal transformation. Specifically, we can use the so-called LQ matrix decompositionFootnote 2 to relate the matrix \(\varvec{C}\) to the Cholesky decomposition of \(\varvec{\Sigma }=\varvec{\Sigma }_{L}\varvec{\Sigma }_{L}^{\prime }\) as
where \(\varvec{Q}\) is an \(N\times N\) orthogonal matrix, which we can model as a function of \(N(N-1)/2\) parameters \(\varvec{\omega }\) by assuming that \(| \varvec{Q}|=1\).Footnote 3 Notice that if \(|\varvec{Q} |\!=\!-1\) instead, we can change the sign of the \(i^{th}\) structural shock and its impact multipliers in the \(i^{th}\) column of the matrix \(\varvec{C}\) without loss of generality as long as we also modify the shape parameters of the distribution of \(\varepsilon _{it}^{*}\) to alter the sign of all its nonzero odd moments.
In this context, Lanne et al. (2017) show that statistical identification of both the structural shocks and \(\varvec{C}\) (up to column permutations and sign changes) is possible under Ica identification Assumption 1, which we maintain in what follows. Popular examples of univariate non-normal distributions are the Student t and the generalised error (or Gaussian) distribution, which includes normal, Laplace and uniform as special cases, as well as symmetric and asymmetric finite normal mixtures.
2.2 Pseudo-maximum likelihood estimators
2.2.1 The criterion function
Let \(\varvec{\theta \!}=\varvec{\!}[\varvec{\tau }^{\prime },vec^{\prime }(\varvec{A}_{1}),\ldots ,vec^{\prime }(\varvec{A} _{p}),vec^{\prime }(\varvec{C})\varvec{]}^{\prime }\varvec{\!}=\varvec{\!}( \varvec{\tau }^{\prime },\varvec{a}_{1}^{\prime },\ldots ,\varvec{a} _{p}^{\prime },\varvec{c}^{\prime })\varvec{\!}=\varvec{\!}(\varvec{\tau } ^{\prime },\varvec{a}^{\prime },\varvec{c}^{\prime })\), denote the structural parameters characterising the first two conditional moments of \(\varvec{y} _{t}\). In addition, we assume \(\varepsilon _{it}^{*}|I_{t-1}\sim i.i.d.\) \(D(0,1,\varvec{\varrho }_{i})\), where \(\varvec{\varrho }_{i}\) is a \( q_{i}\times 1\) vector of variation-free shape parameters, so that in principle different shocks could follow different distributions. For simplicity of notation, though, we maintain that the univariate distributions of the shocks belong to the same family. We can then collect all the shape parameters in the \(q\times 1\) vector \(\varvec{\varrho }=( \varvec{\varrho }_{1}^{\prime },\ldots ,\varvec{\varrho }_{N}^{\prime })^{\prime }\), with \(q=\mathop {\textstyle \sum }\nolimits _{i=1}^{N}q_{i}\), so that \(\varvec{\phi }=(\varvec{\theta }^{\prime },\varvec{\varrho }^{\prime })^{\prime }\) is the \([N+(p+1)N^{2}+q]\times 1\) vector containing all the model parameters.
Given the linear mapping between structural shocks and reduced form innovations, the contribution to the conditional log-likelihood function from observation \(\varvec{y}_{t}\) \((t=1,\ldots ,T)\) for those parameter configurations for which \(\varvec{C}\) has full rank will be given by
where \(f[\varepsilon _{it}^{*}(\varvec{\theta });\varvec{\varrho }_{i}]\) is the univariate log-likelihood function for the \(i^{th}\) structural shock, \(\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })=\varvec{C}^{-1}\varvec{ \varepsilon }_{t}(\varvec{\theta })\), and \(\varvec{\varepsilon }_{t}(\varvec{ \theta })=\varvec{y}_{t}-\varvec{\tau -A}_{1}\varvec{y}_{t-1}-\cdots - \varvec{A}_{p}\varvec{y}_{t-p}\) are the reduced-form innovations.
2.2.2 The score vector
Let \(\varvec{s}_{t}(\varvec{\phi })\) denote the score function \( \partial l_{t}(\varvec{\phi })\varvec{/\partial \phi }\) and partition it into two blocks, \(\varvec{s}_{\varvec{\theta }t}(\varvec{\phi })\) and \( \varvec{s}_{\varvec{\varrho }t}(\varvec{\phi })\), whose dimensions conform to those of \(\varvec{\theta }\) and \(\varvec{\varrho }\), respectively. Fiorentini and Sentana (2021) show that the scores can be written as
where
and
by virtue of the cross-sectional independence of the shocks, so that the derivatives involved correspond to the underlying univariate densities.
2.2.3 The asymptotic distribution
For simplicity, we assume henceforth that Svar model (2) generates a covariance stationary process.Footnote 4 Consider the reparametrisation \(\varvec{C}=\varvec{J\Psi }\), where \(\varvec{\Psi }\) is a diagonal matrix whose elements contain the scale of the structural shocks, while the columns of \(\varvec{J}\), whose diagonal elements are normalised to 1, measure the relative impact of each of the structural shocks on all the remaining variables. Proposition 3 in Fiorentini and Sentana (2020) shows that the parameters \(\varvec{a}_{i}=vec(\varvec{A}_{i}{)}\) and \( \varvec{j}=veco(\varvec{J})\) are consistently estimated regardless of the true distribution.Footnote 5 As a result, the pseudo-true values of those parameters will coincide with the true ones, i.e. \(\varvec{a}_{i\infty }= \varvec{a}_{i0}\) and \(\varvec{j}_{\infty }=\varvec{j}_{0}\). In contrast, \( \varvec{\tau }\) and \(\varvec{\psi }=vecd(\varvec{\Psi })\) will generally be inconsistently estimated, so \(\varvec{\tau }_{\infty }\ne \varvec{\tau } _{0} \) and \(\varvec{\psi }_{\infty }\ne \varvec{\psi }_{0}\).
Nevertheless, Fiorentini and Sentana (2020) prove that the unrestricted PMLEs of \(\varvec{\tau }\) and \(\varvec{\psi }\) which simultaneously estimate \(\varvec{\varrho }\) will be consistent too when the univariate distributions used for estimation purposes are discrete mixtures of normals, in which case \(\varvec{\theta }_{\infty }=\varvec{\theta }_{0}\) and \(\varvec{\varepsilon } _{t}^{*}(\varvec{\theta }_{0})=\varvec{\varepsilon }_{t}^{*}\). For that reason, in what follows we focus on the finite normal mixtures-based PMLEs of the original parameters \(\varvec{\theta }=(\varvec{\tau }^{\prime }, \varvec{a}^{\prime },\varvec{c}^{\prime })^{\prime }\).
Still, the potential misspecification of this distributional assumption implies that the asymptotic covariance matrix of the corresponding PMLEs must be based on the usual sandwich formula. Let
and
denote the (−) expected value of the log-likelihood Hessian and the variance of the score, respectively, where \(\varvec{\varrho }_{\infty }\) are the pseudo-true values of the shape parameters of the distributions of the shocks assumed for estimation purposes, \(\varvec{\upsilon }\) contains the potentially infinite-dimensional shape parameters of the true distributions of the shocks, and \(\varvec{\varphi }=(\varvec{\theta }^{\prime },\varvec{\upsilon }^{\prime })^{\prime }\) . The asymptotic distribution of the pseudo-ML estimators of \(\varvec{\phi }\) , \(\varvec{{\hat{\phi }}}_{T}\), under standard regularity conditions will be given by
In what follows, we shall make extensive use of the detailed expressions for the conditional expected value of the Hessian and covariance matrix of the score for finite normal mixtures-based PMLEs in Amengual et al. (2021b).
3 Specification tests based on integer product moments
3.1 The influence functions
As we have stressed earlier, the parametric identification of the structural shocks \(\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })\) and their impact coefficients \(\varvec{C}\) that appear in the Svar model (2) critically hinges on the validity of identifying Assumption 1. As a consequence, it would be desirable that empirical researchers estimating those models reported specification tests that would check those assumptions. Given that rank failures in \(\varvec{C}\) will be inextricably linked to singular dynamic systems,Footnote 6 we focus on testing that at most one of the structural shocks is Gaussian and that all the structural shocks are indeed independent of each other.
As is well known, stochastic independence between the elements of a random vector is equivalent to the joint distribution being the product of the marginal ones. In turn, this factorisation implies lack of correlation between not only the levels but also any set of single-variable measurable transformations of those elements. Thus, a rather intuitive way of testing for independence without considering any specific parametric alternative can be based on individual moment conditions of the form
where \(\varvec{h}=\{h_{1},...,h_{N}\}\), with \(h_{i}\in \mathbb {Z}_{0+}\), denotes the index vector characterising a specific product moment. While the influence function in (14) will generally require the estimation of \(E[\varepsilon _{it}^{*h_{i}}(\varvec{\theta }_{0}{) }]\) for some of the shocks, the constant term \(\mathop {\textstyle \prod }_{i=1}^{N}E[\varepsilon _{it}^{*h_{i}}(\varvec{\theta }_{0}{)}]\) is either 0 or 1 for the second, third and fourth cross-moments we study in this paper in view of the standardised nature of the shocks, so we do not need to worry about it. Amengual et al. (2021b) discuss in detail how to deal with the estimation of the required \(E[\varepsilon _{it}^{*h_{i}}(\varvec{ \theta }_{0}{)}]\) in the general case.
Although we have motivated (14) as the basis for our tests of independence, by setting all the elements of \(\varvec{h}\) but one to 0, we can also use this expression to look at the marginal moments of a single shock. In this paper, we focus on \(h_{i}=3\) and 4 because most common departures from normality of the shocks will be reflected in coefficients of skewness or kurtosis different from 0 and 3, respectively.
3.2 The moment tests
Let \(\varvec{m}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\) denote a \(K\times 1\) vector containing a collection of influence functions \( m_{\varvec{h}^{k}}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\) of form (14) for different index vectors \(\varvec{h} ^{1},\ldots ,\varvec{h}^{k},,\ldots ,\varvec{h}^{K}\). The following result, which specialises the general expressions in Newey (1985) and Tauchen (1985) to our context, derives the asymptotic distribution of the scaled sample average of \(\varvec{m}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\) when we evaluate the structural shocks at the PMLEs \(\varvec{{\hat{\theta }}} _{T}\) rather than at \(\varvec{\theta }_{0}\):
Proposition 1
Under Assumption 1 and standard regularity conditions
where
and \(\mathcal {A}(\varvec{\phi }_{\infty };\varvec{\varphi }_{0})\) and \( \mathcal {B}(\varvec{\phi }_{\infty };\varvec{\varphi }_{0})\) are defined in (12) and (13), respectively.
In the next subsections, we provide detailed expressions for \(\mathcal {V}( \varvec{\phi };\varvec{\varphi })\), \(\mathcal {J}(\varvec{\phi };\varvec{ \varphi })\) and \(\mathcal {F}(\varvec{\phi };\varvec{\varphi })\) which exploit that the true shocks are cross-sectionally and serially independent under the null hypothesis of correct specification of the static Ica model (1) or the dynamic Svar model (2).
3.2.1 Covariance across influence functions
Consider a generic element of the matrix \(cov\{\varvec{m}[\varvec{ \varepsilon }_{t}^{*}(\varvec{\theta })],\varvec{m}[\varvec{ \varepsilon }_{t}^{*}(\varvec{\theta })]|\varvec{\varphi }\}\), say
If we exploit the cross-sectional independence of the shocks under the null hypothesis, which implies that at the true values
we obtain
3.2.2 The expected Jacobian
Straightforward application of the chain rule implies that
On this basis, the following proposition characterises the expected Jacobian matrix for any \(\varvec{h}\):
Proposition 2
Suppose that model (2) satisfies Assumption 1. Then, the expected Jacobian matrix of \( m_{\varvec{h}}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\) evaluated at the true values is given by

and

As for \(\partial m_{\varvec{h}}[\varvec{\varepsilon }_{t}^{*}(\varvec{ \theta })]/\partial \varvec{\varepsilon }^{*\prime }\), if we denote all the distinct second, third and fourth moments by

where \(\varvec{D}_{N}\), \(\varvec{T}_{N}\) and \(\varvec{Q}_{N}\) are the duplication, triplication and quadruplication matrices, respectively [see Meijer (2005) for details], the results we derive in Appendix B.1 provide an easy way to compute all those derivatives recursively.
3.2.3 The covariance with the score
Let \(\varvec{\ell }_{N}\) denote a vector of N ones and I(.) the usual indicator function. The following proposition provides the last ingredient of the adjusted covariance matrix in Proposition 1.
Proposition 3
Suppose that model (2) satisfies Assumption 1. Then, the covariance between the influence function \(m_{\varvec{h}}(\cdot )\) and the pseudo-log-likelihood scores evaluated at the (pseudo) true values is given by
where
\(\mathcal {F}_{\varvec{h}l}(\varvec{\varrho }_{\infty },\varvec{\varphi } _{0}) \) is a \(1\times N\) vector whose entries are such that for any i with \(h_{i}>0\),

and zero otherwise, \(\mathcal {F}_{\varvec{h}s}(\varvec{\varrho }_{\infty }, \varvec{\varphi }_{0})\) is a \(1\times N^{2}\) vector whose entries are such that for any i with \(h_{i}>0\) and \(i^{\prime }\) with \(h_{i^{\prime }}>0\)

and zero otherwise, and finally
with F\(_{\varvec{h}r}(\varvec{\varrho }_{\infty },\varvec{\varphi } _{0})\) another block diagonal matrix of order \(N\times q\) with typical block of size \(1\times q_{i}\),

and zero otherwise.
4 Particular cases
4.1 Testing normality
As we have mentioned before, we can use (14) to test the null hypothesis that a single structural shock is Gaussian by comparing its third and fourth sample moments with 0 and 3, respectively, which are the population values of those moments under the null of normality. Nevertheless, many authors [see, e.g. Bontemps and Meddahi (2005) and the references therein] convincingly argue that it is generally more appropriate to look at the sample averages of the third and fourth Hermite polynomials instead. In particular, one should consider \( H_{3}(\varepsilon _{it}^{*})=\varepsilon _{it}^{*3}-3\varepsilon _{it}^{*}\) and \(H_{4}(\varepsilon _{it}^{*})=\varepsilon _{it}^{*4}-6\varepsilon _{it}^{*2}+3\) rather than \(\varepsilon _{it}^{*3}\) and \(\varepsilon _{it}^{*4}\) only. The reason is that Hermite polynomials have two main advantages. First, given that
the results in Proposition 2 immediately imply that their expected Jacobians will be 0 under the null of normality, so they are immune to the sampling uncertainty resulting from using estimated shocks. Second, \(H_{3}(\varepsilon _{it}^{*})\) and \(H_{4}(\varepsilon _{it}^{*})\) are orthogonal under the Gaussian null, which means that the joint test is simply the sum of two asymptotically independent components: one for skewness and another one for kurtosis.
The properties of the estimators that we use, though, mean that the usual implementation of the Jarque and Bera (1980) test, which simply looks at the sample averages of \(\varepsilon _{it}^{*3}(\varvec{{\hat{\theta }}}_{T})\) and \(\varepsilon _{it}^{*4}(\varvec{{\hat{\theta }}}_{T})\), yields numerically the same statistics as the tests based on the Hermite polynomials despite the fact that it ignores the terms involving \( \varepsilon _{it}^{*}\) and \(\varepsilon _{it}^{*2}\). The intuition is as follows. Proposition 1 in Fiorentini and Sentana (2020) states that the PMLEs of the unconditional mean and variance of a univariate finite mixture of normals numerically coincide with the sample mean and variance (with denominator T) of the observed series. Given that log-likelihood function (4) for any given values of \(\varvec{a}\) and \(\varvec{j}\) is effectively the sum of N such univariate log-likelihoods with parameters that are variation-free, the estimated shocks will be such that
regardless of the sample size. This property also has interesting implications for the independence tests that we will consider in the next section because, in effect, each estimated shock will be standardised in the sample.
Finally, it is important to emphasise that the non-normality of a single shock does not guarantee the identification of the model parameters, in the same way as its normality does not imply they are underidentified. As we shall see in the Monte Carlo section, though, researchers can get an informative guide to the validity of Assumption 1 by looking at the normality tests for all the individual shocks.
4.2 Testing independence
At first sight, the arguments in the previous section might suggest that the sample covariances between the estimated shocks will also be 0 by construction. However, this is not generally true. The finite normal mixture PMLEs guarantee the univariate standardisation of each shock, but it does not imply their orthogonality in any given sample, unlike what would happen with a multivariate Gaussian likelihood function in which enough a priori restrictions were imposed on \(\varvec{C}\) to render the model exactly identified. Intuitively, the parameter values that maximise (4) are trying to make the estimated shocks stochastically independent, not merely orthogonal [see Herwartz (2018)].
For that reason, the first test for independence that we consider will be based on the second cross-moment condition
In other words, we are simply assessing if the sample correlation between the \(i^{th}\) and \(i^{\prime th}\) estimated shocks is significantly different from zero in the usual statistical sense.
Nevertheless, we can also go beyond linear dependence and look at moments that characterise the co-skewness across the structural shocks. These can be of two types:
and
depending on whether they involve two or three different shocks.
Finally, we can also look at the different co-kurtosis among the shocks, which may involve a pair of shocks, namely
and
three shocks
and even four shocks
Thus, we substantially expand the set of moments researchers can use to test for the independence of the components relative to Hyvärinen (2013), who only suggested looking at the co-kurtosis terms in (22). The above moment conditions also augment those considered by Lanne and Luoto (2021), who focus on (19), (22) and (23), together with \( E(\varepsilon _{it}^{*})=0\) and \(E(\varepsilon _{it}^{*2})=1\).
4.2.1 Covariance across influence functions
Next, we derive in detail the nonzero elements of the covariance matrix of the second, third and fourth moments in (16).
It is easy to see that under the null hypothesis of independence, the only nonzero elements of the covariance matrix of \(\varvec{m}^{cv}[\varvec{ \varepsilon }_{t}^{*}(\varvec{\theta })]\) are
In turn, in the case of \(\varvec{m}^{cs}[\varvec{\varepsilon }_{t}^{*}( \varvec{\theta })]\) and \(\varvec{m}^{ck}[\varvec{\varepsilon }_{t}^{*}( \varvec{\theta })]\), the nonzero elements are
and
respectively, which can be consistently estimated from \(\varvec{\varepsilon } _{t}^{*}(\varvec{{\hat{\theta }}}_{T})\) under standard regularity conditions.
Finally, the nonzero covariance terms across the different elements of \( \varvec{m}^{cv}(\varvec{\varepsilon }_{t}^{*})\), \(\varvec{m}^{cs}( \varvec{\varepsilon }_{t}^{*})\) and \(\varvec{m}^{ck}(\varvec{\varepsilon }_{t}^{*})\) are
4.2.2 The expected Jacobian
Straightforward calculations allow us to show that the expected Jacobian of the covariances across shocks in (19) will be given by

where \(\varvec{e}_{i}\) is the \(i^{th}\) canonical vector and \(\varvec{c} ^{i.} \) denotes the \(i^{th}\) row of \(\varvec{C}^{-1}\).
Analogously, for the third cross-moments in (20), we will have

while for those in (21) we get

In turn, for the fourth moments in (22), we will have

while for (23) we get

and

Similarly, the expected Jacobian of (24) involves

Finally, when we look at (25), we unsurprisingly end up with

4.2.3 The covariance with the score
As we have seen before, we need to explicitly compute the expressions in Proposition 3 to obtain (17). Fortunately, some of those expressions simplify considerably for the cross-moments we use to test independence. Intuitively, the reason is that the independence of the shocks implies that when \(\varvec{h}\) is such that \( h_{i}=1\), we will have
and
for \(i\ne i^{\prime },i^{\prime \prime }\).
As a result, (17) will be zero for the second moments \( E(\varepsilon _{it}^{*}\varepsilon _{i^{\prime }t}^{*})\), except for f\(_{\varvec{h}s(i,i^{\prime })}(\varvec{\varrho }_{\infty }, \varvec{\varphi }_{0})\), which will be 1 when \(i^{\prime }\ne i\).
In addition, if we exploit the independence between i and \(i^{\prime }\) and the fact that \(E(\varepsilon _{i^{\prime }t}^{*2})=1\), we can easily prove that the only nonzero covariance elements for the co-skewness influence functions \(E(\varepsilon _{it}^{*2}\varepsilon _{i^{\prime }t}^{*})\) will be

while all of them are zero for \(E(\varepsilon _{it}^{*}\varepsilon _{i^{\prime }t}^{*}\varepsilon _{i^{\prime \prime }t}^{*})\).
Similarly, we can also prove that for the co-kurtosis influence functions \( E(\varepsilon _{it}^{*2}\varepsilon _{i^{\prime }t}^{*2})\), the only nonzero terms are

In turn, we end up with

and

for the covariances of the co-kurtosis terms \(E(\varepsilon _{it}^{*3}\varepsilon _{i^{\prime }t}^{*})\) with the scores.
In contrast, the only nonzero covariance of the co-kurtosis influence functions \(E(\varepsilon _{it}^{*}\varepsilon _{i^{\prime }t}^{*}\varepsilon _{i^{\prime \prime }t}^{*2})\) with the scores will be f\(_{\varvec{h}s(i,i^{\prime })}(\varvec{\varrho }_{\infty },\varvec{ \varphi }_{0})=1\) when \(i^{\prime }\ne i\).
Finally, all the covariances of the scores with \(E(\varepsilon _{it}^{*}\varepsilon _{i^{\prime }t}^{*}\varepsilon _{i^{\prime \prime }t}^{*}\varepsilon _{i^{\prime \prime \prime }t}^{*})\) will be 0 too.
4.3 Combining our tests
Interestingly, we can use the expressions previously derived to prove that under the joint null hypothesis of mutually independent shocks and the normality of one of them, the two separate tests that we have discussed in Sects. 4.1 and 4.2 are asymptotically independent, so effectively the joint test would simply be the sum of those two components.
In addition, we can also prove that a test that jointly assessed the independence and normality of all the shocks would be asymptotically equivalent under the null to a multivariate Hermite-based test of multivariate normality [see Amengual et al. (2021a)] applied to the reduced form residuals once one eliminates the moment condition related to the covariance of the shocks, whose asymptotic variance when evaluated at the PMLEs would be zero under the null.
5 Monte Carlo analysis
In this section, we assess the finite sample size and power of the normality and independence tests discussed in Sects. 4.1 and 4.2 by means of several Monte Carlo simulation exercises. In addition, we provide some evidence on the effects that dependence across shocks induces on the estimators of the impact multipliers.
5.1 Design and computational details
For the sake of brevity, we focus on the bivariate case in the main text.Footnote 7 Specifically, we generate samples of size T from the following bivariate static process
with \(\tau _{1}=1\), \(\tau _{2}=-1\), \(c_{11}=1\), \(c_{12}=.5\), \(c_{21}=0\) and \( c_{22}=2\). However, our PML estimation procedure does not exploit the restriction that the loading matrix of the shocks is upper triangular. Importantly, given that we can easily prove from (4) that the estimated shocks are numerically invariant to affine transformations of the y’s, and that the same is true of the different test statistics, the results that we report below do not depend on our choice of \(\varvec{\tau }\) and \( \varvec{C}\).
We consider both \(T=250\), which is realistic in most macroeconomic applications with monthly or quarterly data, and \(T=1000\), which is representative of financial applications with daily data. The precise data generating processes (DGPs) that we consider for the shocks are described in Sect. 5.1.2.
5.1.1 Estimation details
To estimate the parameters of the model above, we assume that \( \varepsilon _{1t}^{*}\) and \(\varepsilon _{2t}^{*}\) follow two serially and cross-sectionally independent standardised discrete mixture of two normals, or \(\varepsilon _{it}^{*}\sim DMN(\delta _{i},\varkappa _{i},\lambda _{i})\) for short, so that
with
and \(\varvec{\varrho }_{i}=(\delta _{i},\varkappa _{i},\lambda _{i})^{\prime }\). Hence, we can interpret \(\varkappa _{i}\) as the ratio of the two variances and \(\delta _{i}\) as the parameter that regulates the distance between the means of the two underlying components.Footnote 8
As a consequence, the contribution of observation t to pseudo-log-likelihood function (4) will be
where \(\phi (\varepsilon ;\mu ,\sigma ^{2})\) denotes the probability density function of a Gaussian random variable with mean \(\mu \) and variance \(\sigma ^{2}\) evaluated at \(\varepsilon \). Importantly, we maximise the log-likelihood with respect to the two elements of \(\varvec{\tau }\), the four elements of \(\varvec{C}\) and the six shape parameters subject to the nonlinear constraint \(\delta _{i}^{2}<\lambda _{i}^{-1}(1-\lambda _{i})^{-1}\) , which we impose to guarantee the strict positivity of \(\sigma _{1}^{*2}(\varvec{\varrho }_{i})\). Without loss of generality, we also restrict \( \varkappa _{i}\in (0,1]\) as a way of labelling the components, which in turn ensures the strict positivity of \(\sigma _{2}^{*2}(\varvec{\varrho } _{i}) \). Finally, we impose \(\lambda _{i}\in (0,1)\) to avoid degenerate mixtures.Footnote 9
We maximise the log-likelihood subject to these three constraints on the shape parameters using a derivative-based quasi-Newton algorithm, which converges quadratically in the neighbourhood of the optimum. To exploit this property, we start the iterations by obtaining consistent initial estimators of \(\varvec{\tau }\) and \(\varvec{C}\), \(\overline{\varvec{\tau }}_{FICA}\) and \(\overline{\varvec{C}}_{FICA}\) say, using the FastICA algorithm of Gävert, Hurri, Särelä, and Hyvärinen.Footnote 10 In addition, we obtain initial values of the shape parameters of each shock by performing 20 iterationsFootnote 11 of the expectation maximisation (EM) algorithm in Dempster et al. (1977) on each of the elements of \(\overline{\varvec{\varepsilon }}_{t,FICA}^{*}=\overline{\varvec{C}}_{FICA}^{-1}\left( \varvec{y}_{t}-\varvec{\bar{\tau }} _{FICA}\right) \).
As we mentioned in Sect. 2.2, Assumption 1 only guarantees the identification of \(\varvec{C}\) up to sign changes and column permutations. Although in empirical applications a researcher would carefully choose the appropriate ordering and interpretation of the structural shocks, this leeway may have severe consequences when analysing Monte Carlo results. For that reason, we systematically choose a unique global maximum from the different observationally equivalent permutations and sign changes of the columns of the matrix \(\varvec{C}\) using the selection procedure suggested by Ilmonen and Paindaveine (2011) and adopted by Lanne et al. (2017). In addition, we impose that \(diag(\varvec{C)}\) is positive by simply changing the sign of all the elements of the relevant columns. Naturally, we apply the same changes to the shape parameters estimates and the sign of \(\delta _{i}\).
5.1.2 DGPs under the null and the alternative
The four bivariate DGPs for the standardised shocks that we consider under the null of independence are:
- dgp 1::
-
A normal distribution and a discrete mixture of two normals with kurtosis coefficient 4 and skewness coefficients equal to \( -.5 \), i.e. \(\varepsilon _{1t}^{*}\sim N(0,1)\) and \(\varepsilon _{2t}^{*}\sim DMN(-.859,.386,1/5)\).
- dgp 1d::
-
The Var(1) model
$$\begin{aligned} \left( \begin{array}{c} y_{1t} \\ y_{2t} \end{array} \right) =\left( \begin{array}{c} \tau _{1} \\ \tau _{2} \end{array} \right) +\left( \begin{array}{cc} 1/2 &{} 1/4 \\ 0 &{} 1/3 \end{array} \right) \left( \begin{array}{c} y_{1t-1} \\ y_{2t-1} \end{array} \right) +\left( \begin{array}{cc} c_{11} &{} c_{12} \\ c_{21} &{} c_{22} \end{array} \right) \left( \begin{array}{c} \varepsilon _{1t}^{*} \\ \varepsilon _{2t}^{*} \end{array} \right) \end{aligned}$$with exactly the same shocks and values of \(\varvec{\tau }\) and \(\varvec{C}\) as in dgp 1.Footnote 12
- dgp 2::
-
Independent discrete mixtures of two normals with kurtosis coefficient 4 and skewness coefficients equal to .5 and \(-.5\), respectively. In other words, \(\varepsilon _{1t}^{*}\sim DMN(-.859,.386,1/5)\) and \(\varepsilon _{2t}^{*}\sim DMN(.859,.386,1/5)\).
- dgp 3::
-
A Student t with 10 degrees of freedom (and kurtosis coefficient equal to 4), and an asymmetric t with kurtosis and skewness coefficients equal to 4 and \(-.5\), respectively, so that \(\beta =-1.354\) and \(\nu =18.718\) in the notation of Mencía and Sentana (2012).
Univariate densities of the independent shocks. Notes: dashed lines represent the standard normal distribution. a Plots a standardised discrete mixture of two normals with skewness and kurtosis coefficients of \(-.5\) and 4, respectively (with parameters \( \delta =-.859\), \(\varkappa =.386\) and \(\lambda =1/5\)); b Plots a standardised symmetric Student t with the same kurtosis (i.e. 10 degrees of freedom), while c plots a standardised asymmetric t with skewness and kurtosis as the one in (a) [i.e. with \(\beta =-1.354\) and \(\nu =18.718\), see Mencía and Sentana (2012) for details]
Densities and contours of the bivariate distributions under the alternative hypotheses. Notes: a, b plot a bivariate Student t with 6 degrees of freedom; c, d a standardised bivariate asymmetric t with \( \varvec{\beta }=-5\varvec{\ell }_{N}\) and \(\nu =16\) [see Mencía and Sentana (2012) for details], while e, f plot a standardised mixture of two bivariate normals with joint mixing Bernoulli with \(\lambda =1/5\) and scale parameters \(\varkappa _{1}=.1\) and \(\varkappa _{2}=.2\) [see Sect. 5.1.2 and Lanne and Lütkepohl (2010) for details]
The left panels of Fig. 1a–c display the density functions of these distributions over a range of \(\pm 4\) standard deviations with the standard normal as a benchmark, while the right panels zoom in on the left-tail.
In turn, under the alternative of cross-sectionally dependent shocks we simulate from the following three standardised joint distributions:
- dgp 4::
-
Bivariate Student t with 6 degrees of freedom.
- dgp 5::
-
Bivariate asymmetric t with skewness vector \( \varvec{\beta }=-5\varvec{\ell }_{2}\) and degrees of freedom parameter \( \nu =16\) [see Mencía and Sentana (2012) for details].
- dgp 6::
-
Bivariate mixture of two zero-mean normal vectors with covariance matrices
$$\begin{aligned} \varvec{\Omega }_{1}=\left( \begin{array}{cc} 1/[\lambda +\varkappa _{1}(1-\lambda )] &{} 0 \\ 0 &{} 1/[\lambda +\varkappa _{2}(1-\lambda )] \end{array} \right) , \\ \varvec{\Omega }_{2}=\left( \begin{array}{cc} \varkappa _{1}/[\lambda +\varkappa _{1}(1-\lambda )] &{} 0 \\ 0 &{} \varkappa _{2}/[\lambda +\varkappa _{2}(1-\lambda )] \end{array} \right) , \end{aligned}$$which we denote by \(DMN_{LL}(\varkappa _{1},\varkappa _{2},\lambda )\) [see Lanne and Lütkepohl (2010) for details]. Specifically, we set \(\varkappa _{1}=0.1\), \(\varkappa _{2}=0.2\) and \(\lambda =1/5\).
The left panels of Fig. 2 display the joint densities for these distributions, while their contours are presented in the right panels.
To gauge the finite sample size and power of our proposed independence tests, we generate 20, 000 samples for each of the designs under the null and 5000 for those under the alternative. Additionally, we evaluate the small sample size and power of the normality tests presented in Sect. 4.1 using the results from the simulation designs dgp 1 and 1d (null), and dgp 2 and dgp 3 (alternative).
5.1.3 Bootstrap procedures
The theoretical results in Beran (1988) imply that if the usual Gaussian asymptotic approximation provides a reliable guide to the finite sample distribution of the sample version of the moments being tested, the bootstrapped critical values should not only be valid, but also their errors should be of a lower order of magnitude under additional regularity conditions that guarantee the validity of a higher-order Edgeworth expansion.Footnote 13 For that reason, we also analyse the performance of applying the bootstrap to the testing procedures we have described in Sects. 4.1 and 4.2.
In the case of our tests for independence, for each Monte Carlo sample, we can easily generate another \(N_{boot}\) bootstrap samples of size T that impose the null with probability approaching 1 as T increases as follows.Footnote 14 First, we generate NT draws \(R_{is}\) from a discrete uniform distribution between 1 and T, which we then use to construct
where \(\tilde{\varepsilon }_{is}^{*}={\hat{\varepsilon }}_{iR_{is}}^{*}\) and \(\varvec{{\hat{\varepsilon }}}_{t}^{*}=\varvec{\varepsilon }_{t}^{*}(\varvec{{\hat{\theta }}}_{T})=\varvec{\hat{C}}_{T}^{-1}\left( \varvec{y}_{t}- \varvec{{\hat{\tau }}}_{T}\right) \) are the estimated residuals in any given sample.
As for the normality tests, whose null hypothesis is that a single shock \( \varepsilon _{it}^{*}\) is Gaussian, we adopt a partially parametric resampling scheme in which the draws of the \(i^{th}\) shock \(\tilde{ \varepsilon }_{is}^{*}\) are independently simulated from a N(0, 1) distribution, while the draws for the remaining shocks \(\tilde{\varepsilon } _{ks}^{*}\) \((k\ne i)\) are obtained nonparametrically as in the previous paragraph.
Although these bootstrap procedures are simple and fast for any given sample, they quickly become prohibitively expensive in a Monte Carlo exercise as T increases. For this reason, for the designs with \(T=1000\) we rely on the warp-speed method of Giacomini et al. (2013).
5.2 Simulation results
5.2.1 Testing normality
Table 1 reports Monte Carlo rejection rates of the normality tests proposed in Sect. 4.1 for dgp 1, 1d, 2 and 3. As can be seen, the null of normality is correctly rejected a large number of times when it does not hold, even in samples of length 250. The only possible exception is the skewness component of the Jarque-Bera test when applied to the symmetric Student t shock in dgp 3. Given that the population third moment is zero in this case, the only source of power is the fact that the sample variability of \(H_{3}\) is larger for this shock than its theoretical value under Gaussianity.
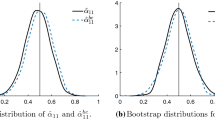
On the other hand, the first three rows of the panels dgp 1 and 1d, which are the ones with a Gaussian shock, show that the normality tests tend to be oversized at the usual nominal levels, especially for samples of length 250.Footnote 15 For that reason, we generate \(N_{Boot}=399\) bootstrap samples at each Monte Carlo replication, as described in Sect. 5.1.3. Table 2 shows that the standard bootstrap version of our tests is pretty accurate for both the third and fourth moment tests. Unlike what we observed in Table 1, though, the size-adjusted power is slightly lower for dgp 1d than for dgp 1.
However, as mentioned at the end of Sect. 4.1, researches may only get a reliable guide to the validity of Assumption 1 by looking at the normality tests for all the individual shocks, the objective being to get at least \(N-1\) rejections. To shed some light on this issue, in Table 3 we report contingency tables which fully characterise the extent to which simultaneous rejections of the individual normality tests occur. As can be seen, our proposed normality tests tend to be rather informative when used in this way.
5.2.2 Testing independence
In Tables 4 (\(T=250\)) and 5 (\(T=1000\)) we report the Monte Carlo rejection rates of the tests we have proposed in Sect. 4.2 under the null of independence. Specifically, we look at the second, third and fourth moment individual tests in \(\varvec{m} ^{cv}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\), \(\varvec{m} ^{cs}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\) and \(\varvec{m} ^{ck}[\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })]\), and also at the joint tests for the two co-skewness moments, the three co-kurtosis moments and the combined six moments, including the correlation between the shocks. The left panels of those tables report rejection rates using asymptotic critical values, while the right panels show the bootstrap-based ones for \( T=250\) and the warp-speed bootstrap-based ones for \(T=1000\).Footnote 16
We can see in Table 4 some small to moderate finite sample size distortion when \(T=250\), although in several cases they are corrected by the bootstrap. The only exceptions seem to be dgp 1 and 1d, in which some small distortions remain even with this procedure. Given that in these designs there is only one non-Gaussian shock, a plausible explanation is that the identification of \(\varvec{C}\) may be weaker, a conjecture we will revisit in the next section. For the other DGPs, the results in Table 4 clearly show that the usual bootstrap version of the tests, which is the relevant one in empirical applications, has much better size properties.
As can be seen in Table 5, finite sample sizes improve considerably for \( T=1000\). Indeed, the bootstrap versions of the tests seem unnecessary for this sample size because the empirical rejection rates based on asymptotic critical values become generally very close to the nominal ones, though the warp-speed version performs comparably well.
Next, we assess the power of the independence tests for \(T=250\) and \(T=1000\) in Tables 6 and 7, respectively. In this respect, we find that the power of our tests against dgp 4 is disappointingly low. A possible explanation is that when the true joint distribution is a symmetric Student t, the dependence between the components is mostly visible in the tails of the distribution. On the other hand, power is mostly coming from the co-skewness component (20) in the case of the joint asymmetric t. Still, the test based on the covariance of shocks (19) is also very powerful. Finally, the co-kurtosis test based on (22) is the most powerful single moment test under the Lanne and Lütkepohl (2010) alternative in dgp 6, with the joint tests that include this moment inheriting its power. Nevertheless, the test based on second moment (19) also has non-negligible power for this design.
In summary, although the rejection rates naturally depend on the type of departure from the null and the specific influence function used for testing, the joint test that considers all moments at once seems to be a winner regardless of the sample size.
5.3 Structural parameters estimates
Table 8 reports summary statistics for the Monte Carlo distribution of the PMLEs of the structural parameters. The first thing we would like to highlight is when one of the shocks is Gaussian, the sampling variability and the finite sample bias are noticeably larger than when both shocks are non-Gaussian but independent, which is in line with the conjecture we expressed in the previous section. Still, even in that case the biases are usually small and often negligible. In addition, the Monte Carlo standard deviations of the estimators in Panel B are roughly half those in Panel A, as one would expect.
The situation is completely different when the true shocks are cross-sectionally dependent. Failure of condition 2 in Assumption 1 results into significant biases, mostly in the off-diagonal terms of the impact multiplier matrix. In fact, the Monte Carlo variance of these estimators seems to increase with the sample size. In this respect, it is important to remember that the elements of the \(\varvec{C}\) matrix are no longer point identified when the joint distribution of the true shocks is either a symmetric or asymmetric Student t. This is confirmed by the fact that the bias of the estimators is lower for dgp 6, in which the rotations of the shocks are not observationally equivalent [see Lanne and Lütkepohl (2010)].
6 Conclusions and directions for further research
Given that the parametric identification of the structural shocks and their impact coefficients \(\varvec{C}\) in the Svar model (2) critically hinges on the validity of the identifying restrictions in Assumption 1, it would be desirable that empirical researchers estimating those models reported specification tests that checked those assumptions to increase the empirical credibility of their findings. For that reason, in this paper we propose simple specification tests for independent component analysis and structural vector autoregressions with non-Gaussian shocks that check the normality of a single shock and the potential cross-sectional dependence among several of them. Our tests compare the integer (product) moments of the shocks in the sample with their population counterparts. Importantly, we explicitly consider the sampling variability resulting from using shocks computed with consistent parameter estimators. We study the finite sample size of our tests in several simulation exercises and discuss some bootstrap procedures. We also show that our tests have non-negligible power against a variety of empirically plausible alternatives.
As we mentioned in introduction, there are many estimators for the parameters of the static Ica model (1) in addition to the discrete mixture of normals-based PMLEs we have considered in this paper. For example, even within the same likelihood framework, Fiorentini and Sentana (2020) discuss two other consistent estimators of the conditional mean and variance parameters of the Svar in (2):
-
1.
The two-step procedure of Gouriéroux et al. (2017), which first estimates the reduced form parameters \(\varvec{\tau }\), \(\varvec{ a}\) and \(\varvec{\sigma }_{L}=vec(\varvec{\Sigma }_{L})\) by equation-by-equation OLS, and then the \(N(N-1)/2\) free elements \(\varvec{ \omega }\) of the orthogonal rotation matrix \(\varvec{Q}\) in (3) mapping structural shocks and reduced form innovations by non-Gaussian PML.
-
2.
The two-step estimator a la Fiorentini and Sentana (2019), which replaces the inconsistent non-Gaussian PMLEs of \(\varvec{\tau }\) and \( \varvec{\psi }\) by the sample means and standard deviations of pseudo-standardised shocks computed using \(\varvec{\hat{a}}_{T}\) and \(\varvec{\hat{ \jmath }}_{T}\).
Although the specifications tests that we have proposed in this paper could also be applied to shocks computed on the basis of these alternative estimators, the asymptotic covariance matrices that take into account their sampling variability will differ from the ones we have derived in this paper. Given that some researchers may prefer to use one of those two-step estimation methods, obtaining computationally simple expressions for the adjusted covariance matrix would provide a valuable addition to our results.
In fact, the moment conditions that we consider for testing independence could form the basis of a GMM estimation procedure for the model parameters \( \varvec{\theta }\) along the lines of Lanne and Luoto (2021), although with a larger set of third and fourth cross-moments. The overidentification restrictions tests obtained as a by-product of this procedure could be used as a specification test of the assumed independence-like restrictions.
Our tests for normality tackle a single shock at a time. Although we could in principle simultaneously test the normality of two or more shocks by combining the corresponding normality tests, the implicit joint null hypothesis would violate the second identification condition in Assumption 1. The asymptotic distribution of such joint tests constitutes a very interesting topic for further research. In addition, we could formally study the limiting probability of finding \(N-1\) rejections of the univariate normality tests in those circumstances.
Another important research topic would be the limiting behaviour of the PMLEs of \(\varvec{\theta }\) when Assumption 1 does not hold, either because two or more of the shocks are Gaussian or because they are not independent.
Finally, while the integer product moment tests for independence that we have considered are very intuitive, they may have little power against alternatives in which the dependence is mostly visible in certain regions of the domain of the random shocks. With this in mind, in Amengual et al. (2021b) we study moment tests that look at the product of nonlinear transformations of the shocks, such as \(I(q_{\alpha i}\le \varepsilon _{it}\le q_{\omega i})\), where \(q_{\alpha i}\) and \(q_{\omega i}\) are the \(\alpha \) and \(\omega \) quantiles of the marginal distribution of the \(i^{th}\) shock (with \(0\le \alpha <\omega \le 1\)), or \(I(k_{li}\le \varepsilon _{it}\le k_{ui})\), where \(k_{li}<k_{ui}\) are some fixed values, or indeed \(\varepsilon _{it}I(k_{li}\le \varepsilon _{it}\le k_{ui})\). Extending this approach in such a way that it leads to a consistent test of independence constitutes another promising research avenue.
Notes
The same result applies to situations in which \(\dim (\varvec{\varepsilon } ^{*})\le \dim (\varvec{y})\) provided that \(\varvec{C}\) has full column rank.
The LQ decomposition is intimately related to the QR decomposition. Specifically, \(\varvec{Q}^{\prime }\varvec{\Sigma }_{L}^{\prime }\) provides the QR decomposition of the matrix \(\varvec{C}^{\prime }\), which is uniquely defined if we restrict the diagonal elements of \(\varvec{\Sigma } _{L}\) to be positive [see, e.g. Golub and van Loan (2013) for further details].
See section 10 of Magnus et al. (2021) for a detailed discussion of three ways of explicitly parametrising a rotation (or special orthogonal) matrix: (i) as the product of Givens matrices that depend on \(N(N-1)/2\) Tait-Bryan angles, one for each of the strict upper diagonal elements; (ii) by using the so-called Cayley transform of a skew-symmetric matrix; and (iii) by exponentiating a skew-symmetric matrix.
If the autoregressive polynomial \((\varvec{I}_{N}-\varvec{A}_{1}L-\ldots - \varvec{A}_{p}L^{p})\) had some unit roots, \(\varvec{y}_{t}\) would be a (co-) integrated process, and the estimators of the conditional mean parameters would have non-standard asymptotic distributions, as some of them would converge at the faster rate T. In contrast, the distribution of the ML estimators of the conditional variance parameters would remain standard [see, e.g. Phillips and Durlauf (1986)].
See Magnus and Sentana (2020) for some useful properties of the veco(.) and vecd(.) operators.
The rationale is as follows. If \(rank(\varvec{C}_{0})<N\), then \(rank[V( \varvec{y}_{t})]<N\), and the same will be true of the sample covariance matrix. Therefore, sampling variability plays no role in determining whether \(rank(\varvec{C}_{0})=N\) in model (1). Exactly the same argument applies to the dynamic system (2).
Nevertheless, we include simulation results for a trivariate model in Appendix C.
We can trivially extend this procedure to three or more components if we replace the normal random variable in the first branch of (27) by a k-component normal mixture with mean and variance given by \(\mu _{1}^{*}(\varvec{\varrho })\) and \(\sigma _{1}^{*2}(\varvec{\varrho } ) \), respectively, so that the resulting random variable will be a \((k+1)\) -component Gaussian mixture with zero mean and unit variance.
Specifically, we impose \(\varkappa _{i}\in [\underline{\varkappa },1]\) with \(\underline{\varkappa }=.0001\), and \(\lambda _{i}\in [\underline{ \lambda },\overline{\lambda }]\) with \(\underline{\lambda }=2/T\) and \( \overline{\lambda }=1-2/T.\)
See Hyvärinen (1999) and https://research.ics.aalto.fi/ica/fastica/ for details on the FastICA package.
As is well known, the EM algorithm progresses very quickly in early iterations but tends to slow down significantly as it gets close to the optimum. After some experimentation, we found that 20 iterations achieve the right balance between CPU time and convergence of the parameters.
Given that Monte Carlo simulations involving a regular bootstrap are very costly in terms of CPU time, we have only compared the results of a Var(1) with those of a static model for dgp 1.
Therefore, if the true shocks had unbounded variance, the bootstrap would not work, but neither would the asymptotic approximation.
To see this, notice that under the null,
$$\begin{aligned} E\left( \prod \nolimits _{i=1}^{N}\tilde{\varepsilon }_{is}^{*j_{i}}\right) =\prod \nolimits _{i=1}^{N}E(\varepsilon _{is}^{*^{j_{i}}}), \end{aligned}$$while under the alternative,
$$\begin{aligned} E\left( \prod \nolimits _{i=1}^{N}\tilde{\varepsilon }_{is}^{*j_{i}}\right) =\frac{T-1}{T}\prod \nolimits _{i=1}^{N}E(\varepsilon _{is}^{*^{j_{i}}})+ \frac{1}{T}E\left( \prod \nolimits _{i=1}^{N}\varepsilon _{is}^{*j_{i}}\right) \end{aligned}$$where the second term in the right-hand side accounts for the probability of sampling contemporaneous residuals in a sample of size T. Clearly, the second expression converges to the first one as T goes to infinity.
Given 20,000 Monte Carlo replications, the 95% asymptotic confidence intervals for the Monte Carlo rejection probabilities under the null are (.86,1.14), (4.70,5.30) and (9.58,10.42) at the 1, 5 and 10% levels, respectively.
All our i.i.d. designs are such that the individual moment tests converge in distribution to a \(\chi _{1}^{2}\) random variable, and the joint ones to \( \chi _{2}^{2}\), \(\chi _{3}^{2}\) and \(\chi _{6}^{2}\) variables, respectively.
References
Almuzara M, Amengual D, Sentana E (2019) Normality tests for latent variables. Quant Econ 10:981–1017
Amengual D, Fiorentini G, Sentana E (2021a) Multivariate Hermite polynomials and information matrix tests. CEMFI Working Paper 2103
Amengual D, Fiorentini G, Sentana E (2021b) Specification tests for non-Gaussian structural vector autoregressions. Work in progress
Beran R (1988) Prepivoting test statistics: a bootstrap view of asymptotic refinements. J Am Stat Assoc 83:687–697
Blanchard OJ, Quah D (1989) The dynamic effects of aggregate demand and supply disturbances. Am Econ Rev 79:655–673
Boldea O, Magnus JR (2009) Maximum likelihood estimation of the multivariate normal mixture model. J Am Stat Assoc 104:1539–1549
Bontemps C, Meddahi N (2005) Testing normality: a GMM approach. J Econom 124:149–186
Comon P (1994) Independent component analysis, a new concept? Signal Process 36:287–314
Dempster A, Laird N, Rubin D (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B 39:1–38
Dolado JJ, Motyovszki G, Pappa E (2020) Monetary policy and inequality under labor market frictions and capital-skill complementarity. Am Econ J Macroecon 13:292–332
Faust J (1998) The robustness of identified Var conclusions about money. Carnegie-Rochester Conf Ser Public Policy 49:207–244
Fiorentini G, Sentana E (2019) Consistent non-Gaussian pseudo maximum likelihood estimators. J Econom 213:321–358
Fiorentini G, Sentana E (2020) Discrete mixtures of normals pseudo maximum likelihood estimators of structural vector autoregressions. CEMFI Working Paper 2023
Fiorentini G, Sentana E (2021) Specification tests for non-Gaussian maximum likelihood estimators. Quant Econ 12:683–742
Giacomini R, Politis DN, White H (2013) A warp-speed method for conducting Monte Carlo experiments involving bootstrap estimators. Economet Theor 29:567–589
Golub GH, van Loan CF (2013) Matrix computations, 4th edn. Johns Hopkins, Baltimore
Gouriéroux C, Monfort A, Renne J-P (2017) Statistical inference for independent component analysis. J Econom 196:111–126
Herwartz H (2018) Hodges-Lehmann detection of structural shocks—an analysis of macroeconomic dynamics in the euro area. Oxford Bull Econ Stat 80:736–754
Hyvärinen A (1999) Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans Neural Netw 10:626–634
Hyvärinen A (2013) Independent component analysis: recent advances. Philos Trans R Soc A 371:20110534
Ilmonen P, Paindaveine D (2011) Semiparametrically efficient inference based on signed ranks in symmetric independent component models. Ann Stat 39:2448–2476
Jarque CM, Bera AK (1980) Efficient tests for normality, heteroskedasticity, and serial independence of regression residuals. Econ Lett 6:255–259
Lanne M, Luoto J (2021) GMM estimation of non-Gaussian structural vector autoregressions. J Bus Econ Stat 39:69–81
Lanne M, Lütkepohl H (2010) Structural vector autoregressions with nonnormal residuals. J Bus Econ Stat 28:159–168
Lanne M, Meitz M, Saikkonen P (2017) Identification and estimation of non-Gaussian structural vector autoregressions. J Econom 196:288–304
Magnus JR, Neudecker H (2019) Matrix differential calculus with applications in Statistics and Econometrics, 3rd edn. Wiley, New York
Magnus JR, Sentana E (2020) Zero-diagonality as a linear structure. Econ Lett 196:109513
Magnus JR, Pijls HGJ, Sentana E (2021) The Jacobian of the exponential function. J Econ Dyn Control 127:104122
Meijer E (2005) Matrix algebra for higher order moments. Linear Algebra Appl 410:112–134
Mencía J, Sentana E (2012) Distributional tests in multivariate dynamic models with Normal and Student \(t\) innovations. Rev Econ Stat 94:133–152
Mertens K, Ravn MO (2012) The dynamic effects of personal and corporate income tax changes in the United States. Am Econ Rev 103:1212–1247
Moneta A, Pallante G (2020) Identification of structural Var models via Independent Component Analysis: a performance evaluation study. LEM Working Paper 2020/44, Scuola Superiore Sant’Anna
Newey WK (1985) Maximum likelihood specification testing and conditional moment tests. Econometrica 53:1047–70
Newey WK, McFadden DL (1994) Large sample estimation and hypothesis testing. In: Engle RF, McFadden DL (eds) Handbook of econometrics, vol IV. Elsevier, New York, pp 2111–2245
Phillips PCB, Durlauf SN (1986) Multiple time series regression with integrated processes. Rev Econ Stud 53:473–495
Sentana E, Fiorentini G (2001) Identification, estimation and testing of conditionally heteroskedastic factor models. J Econom 102:143–164
Sims CA (1980) Macroeconomics and reality. Econometrica 48:1–48
Stock JH, Watson MW (2018) Identification and estimation of dynamic causal effects in macroeconomics using external instruments. Econ J 28:917–948
Tauchen G (1985) Diagnostic testing and evaluation of maximum likelihood models. J Econom 30:415–443
Uhlig H (2005) What are the effects of monetary policy on output? Results from an agnostic identification procedure. J Monet Econ 52:381–419
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to thank Giuseppe Cavaliere and Aapo Hyvärinen, as well as participants at ESEM 21 for some useful comments and suggestions. Two anonymous referees have also provided very valuable feedback. Of course, the usual caveat applies. The first and third authors acknowledge financial support from the Spanish Ministry of Economy, Industry & Competitiveness through Grant ECO 2017-89689 and the Santander CEMFI Research Chair.
Appendices
A Proofs
1.1 Proposition 1
Under standard regularity conditions [see, e.g. Newey and McFadden (1994)], we can linearise the vector of influence functions underlying our tests around \(\varvec{\theta }_{0}\) so that
But since
we can combine both expressions to write
whence the asymptotic distribution in the proposition follows. \(\square \)
1.2 Proposition 2
Fiorentini and Sentana (2021) prove in their Appendix D that
which in our case reduces to
in view of (7) and (8). Therefore, it immediately follows that
where
Similarly,
Finally,
If we combine these expressions with the fact that
we obtain the desired results. \(\square \)
1.3 Proposition 3
Expression (17) follows directly from the definition of the scores for \(\varvec{\theta }\) and \(\varvec{\varrho }\) in (5) and (6) and the law of iterated expectations after exploiting the fact that \(m_{\varvec{h}}[\varvec{\varepsilon } _{t}^{*}(\varvec{\theta }_{0}{)]}\), \(\varvec{e}_{lt}(\varvec{\phi }_{\infty })\), \(\varvec{e}_{lt}(\varvec{\phi }_{\infty })\) and \(\varvec{e} _{rt}(\varvec{\phi }_{\infty })\) are i.i.d. processes with zero mean under our assumptions.
In turn, the more detailed expressions exploit the cross-sectional independence of the shocks. For example, consider
It is clear that row i will be zero if \(h_{i}=0\) because of the cross-sectional independence of the shocks and the fact that \(E[\partial \ln f(\varepsilon _{it}^{*};\varvec{\varrho }_{i\infty })/\partial \varepsilon _{i}^{*}|\varvec{\theta }_{0},\varvec{\upsilon }_{0}]=0\).
The same argument applies to the remaining blocks. \(\square \)
B Additional material
1.1 B.1 Some useful results
As mentioned in Sect. 3, the following lemma provides an easy way to recursively compute some of the ingredients of the independence tests:
Lemma 1
Let \([\varvec{\varepsilon }_{t}^{*}(\varvec{ \theta })]^{\otimes k}=\underbrace{\varvec{\varepsilon }_{t}^{*}(\varvec{ \theta })\otimes \varvec{\varepsilon }_{t}^{*}(\varvec{\theta })\otimes ...\otimes \varvec{\varepsilon }_{t}^{*}(\varvec{\theta })}_{k\;\text { times}}\) denote the \(k^{th}\)-order Kronecker power of the \(N\times 1\) vector \(\varvec{\varepsilon }_{t}^{*}(\varvec{\theta })\). Then, for any \(k\ge 2 \)
Proof
The result follows immediately from the product rule for differentials [see section 9.14 in Magnus and Neudecker (2019)] after exploiting the fact that \( \varvec{K}_{1N}=\varvec{K}_{N1}=\varvec{I}_{N}\) and
[see section 3.7 in Magnus and Neudecker (2019)]. \(\square \)
A trivial—but useful—consequence of Lemma 1 that we make extensively use in this paper is:
Corollary 1
The differentials of the second, third and fourth powers of the structural shocks will be
and
Proof
To save space, let \(\varvec{\varepsilon }_{t}^{*}=\varvec{\varepsilon } _{t}^{*}\varvec{(\theta })\). The differential of \(\varvec{m}^{cv}( \varvec{\varepsilon }_{t}^{*})\), d\((\varvec{\varepsilon }_{t}^{*}\otimes \varvec{\varepsilon }_{t}^{*})\), follows directly from Lemma 1.
This lemma also implies that the differential of \(\varvec{m}^{cs}(\varvec{ \varepsilon }_{t}^{*})\) will be
Expression (B1) then yields
and
because \(\varvec{K}_{1N}=\varvec{K}_{N1}=\varvec{I}_{N}\).
Finally, Lemma 1 implies that the differential of \( \varvec{m}^{ck}(\varvec{\varepsilon }_{t}^{*})\) will be
Once again, expression (B1) yields
and
as desired. \(\square \)
1.2 B.2 Univariate discrete mixtures of normals
1.2.1 B.2.1 Moments
The parameters \(\delta \), \(\varkappa \) and \(\lambda \) of the two-component Gaussian mixture we consider in Sect. 5 determine the higher-order moments of \(\varepsilon _{t}^{*}\) through the relationship
where \(s_{t}\in \{1,2\}\) is a Bernoulli random variable with \(\Pr (s_{t}=1)=\lambda \). Specifically,
Given that \(E(\varepsilon _{t}^{*}|\varvec{\varrho })=0\) and \( E(\varepsilon _{t}^{*2}|\varvec{\varrho })=1\) by construction, straightforward algebra shows that the skewness and kurtosis coefficients will be given by
and
1.2.2 B.2.2 Scores with respect to \({\varepsilon }\, \mathrm{and}\, \varrho \)
Regarding the specific elements that appear in (9) and (10), we have
where we have defined the posterior probabilities of shock i being drawn from component k at time t as \(w_{kit}=\phi [\varepsilon _{it}^{*}(\varvec{\theta });\mu _{k}^{*}(\varvec{\varrho } _{i}),\sigma _{k}^{*2}(\varvec{\varrho }_{i})]/f[\varepsilon _{it}^{*}(\varvec{\theta });\varvec{\varrho }_{i}]\) to shorten the expressions [see Boldea and Magnus (2009)].
As for the derivatives with respect to the shape parameters in (11), we have
with
and
The second derivatives of the log-density with respect to the shape parameters can be derived using the chain rule for second derivatives from the expressions in Boldea and Magnus (2009), who obtain them in terms of \( \lambda \), \(\mu _{k}^{*}(\varvec{\varrho }_{i})\) and \(\sigma _{k}^{*2}(\varvec{\varrho }_{i})\) (\(k=1,2\)). The precise expressions are available on request.
C Monte Carlo results for a trivariate static model
In this appendix, we report finite sample results for a trivariate extension of our benchmark dgp 1, which we denote by dgp 1t . Specifically, we generate samples of size T from
As for the shocks, we choose \(\varepsilon _{1t}^{*}\sim N(0,1)\), \( \varepsilon _{2t}^{*}\sim DMN(-.859,.386,1/5)\) and \(\varepsilon _{2t}^{*}\sim DMN(.859,.386,1/5)\), so that \(\varepsilon _{2t}^{*}\) and \(\varepsilon _{3t}^{*}\) follow discrete mixtures of two normals with kurtosis coefficients 4 and skewness coefficients equal to \(-.5\) and .5, respectively.
Table 9 reports Monte Carlo rejection rates of the normality tests proposed in Sect. 4.1 for samples of size \(T=250\) (top panel) and \( T=1000\) (bottom panel). The first three columns of those panels report rejection rates using asymptotic critical values, while the last three columns show the bootstrap-based ones for \(T=250\) and the warp-speed bootstrap-based ones for \(T=1000\). Once again, the normality tests tend to be oversized at the usual nominal levels, especially for samples of length 250, while the standard bootstrap version of our tests is much more reliable for both the third and fourth moment tests. More importantly, the null of normality is correctly rejected a large number of times when it does not hold, even in samples of length 250. Nevertheless, there is a moderate loss of power relative to Table 2, which may reflect the need to estimate almost twice as many parameters as in the bivariate case. In larger dimensions, one might expect a similar pattern, although in general, the main determinants of the power of our normality test will be the non-normality of the structural shock under consideration and how precisely identified it is.
Finally, in Table 10 we report the Monte Carlo rejection rates of the tests we have proposed in Sect. 4.2 under the null of independence for samples of size \(T=250\) (left panel) and \(T=1000\) (right panel). As in Table 9, the first (last) three columns of those panels report rejection rates using asymptotic (bootstrapped) critical values. As in the bivariate case (cf. Table 4), we can see some small to moderate finite sample size distortion when \(T=250\), although in almost all cases they are corrected by the bootstrap. Finite sample sizes improve considerably for samples of length 1000, as expected.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Amengual, D., Fiorentini, G. & Sentana, E. Moment tests of independent components. SERIEs 13, 429–474 (2022). https://doi.org/10.1007/s13209-021-00247-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-021-00247-3
Keywords
- Covariance
- Co-skewness
- Co-kurtosis
- Finite normal mixtures
- Normality tests
- Pseudo-maximum likelihood estimators
- Structural vector autoregressions