Abstract
This paper analyzes how differences in productivity across banks and the evolution of industry productivity over time might determine the intermediation costs and the restructuring process of the banking industry in the Great Recession. With data of Spanish banks, we find that less productive banks are more likely to exit than more productive banks, and that surviving banks acquire target banks in order to expand their branch network in local markets where they are underrepresented. Competition among banks contributes to the translation of industry productivity growth into lower interest rates of loans. Nonetheless, we find that the industry profit margin in loans increases during the period because of the modest industry productivity growth and the lower intensity of competition from branch closing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The economic slowdown and the fall in the demand for banking products since the outburst of the crisis, together with the use of new technologies in the access and production of banking services, have caused a deep restructuring in the banking sector of many countries. In the process, many banks have disappeared after closing down or being absorbed by other banks, and the size of the branches network has been substantially reduced. A key policy issue is to determine whether the restructuring of the banking industry is positive or not for social welfare and under what conditions.
This paper analyzes the social benefits of the restructuring of the banking industry from two sources, the evolution of the total factor productivity in the production of banking services, and the competitive pressure to pass through productivity growth to interest rates of loans and deposits. The restructuring of the industry contributes to social efficiency if more productive banks increase their market share and the gains in production efficiency (productivity) benefit bank customers, in the form of lower intermediation costs. For this analysis, we use data from Spanish banks during the period from 2007 to 2015. The Spanish banking sector has undergone a profound restructuring process since the beginning of the crisis: savings banks transformed into shareholder-owned banks, increase in industry concentration and closure of one-third of the bank branches all over the country.
The specification of the empirical models and the hypotheses to be tested are inspired on the theoretical predictions derived from a model of spatial competition à la Salop (1979). For a given number of bank branches in the local market, we solve for the Nash equilibrium in prices (interest rates) and market shares of banks with different productivity and, thus, different operating costs. The model predicts that more productive banks charge lower (higher) interest rates for their loans (deposits) than the less productive ones, and that interest rates of loans (deposits) decrease (increase) with the average total factor productivity, TFP, of the competing banks. Also, in the short-term equilibrium, market shares and profits of bank branches increase with their TFP. During the crisis, demand falls and high-productivity banks were in a better position to acquire low productivity and reduce capacity through restructuring and branches closing.
The paper tests three main hypotheses. First, more productive banks charge lower (higher) interest rates of loans (deposits) and industry productivity gains reduce banking intermediation costs. Second, more productive banks outlast the less productive ones after a negative demand shock, since higher productivity implies lower operating costs and higher profits. And third, acquiring banks choose the acquired partner searching for complementarity in the spatial distribution of own and acquired network of branches. We also examine whether branch closures reduce the intensity of competition in local markets through increasing spatial differentiation.
We find that less productive banks exit the industry in the restructuring process, increasing average and reducing the dispersion of industry productivity. Nonetheless, the rise in industry productivity due to the exit of less productive banks is (partially) offset by the slowdown in productivity growth from the fact that the demand for banking services decreases at a pace faster than the reduction of industry capacity. The market share of exiting banks is distributed across the surviving banks, which absorb banks with the presence in markets where they are underrepresented. Taking the number of banks and branches as given, the interest rates of loans decrease with industry productivity growth, and more productive banks set lower loan interest rates than the less productive ones. Finally, we find that equilibrium interest rates of loans decrease with the size of the local market (higher density of bank branches).
All these predictions are consistent with the theoretical results. However, the empirical results do not support the model predictions in the deposits market, possibly because of the low levels of official interest rates (close to zero) and the competitive distortions due to the zero-lower bound in the deposit interest rate. From the results, we cannot be conclusive about the effect of productivity on M&A among banks, because of the difficulty of separating size and productivity effects in the match between acquired and acquiring banks. From our theoretical setup, more productive banks have larger market share in the equilibrium, so it is productivity that determines size and not the other way around. Indeed, Moral-Benito (2018) demonstrates that this is the case in Spanish nonfinancial firms. But it cannot be ruled out that size gives banks some idiosyncratic advantage that is reflected in higher estimated productivity, for reasons different from higher production efficiency (for example, economies of scope across the portfolio of services).
This paper is related to Castro and Galán (2019) measurement and analysis of productivity gains and cost efficiency of Spanish banks in the period 2000–2015 (follow-up of Galán et al. 2015 for Colombian banks). The key difference is that Castro and Galán (2019) focus on explaining the effect of restructuring in the evolution of productivity and cost efficiency of banks, while this paper extends the views of productivity as a driver of the process of industry restructuring and intermediation costs. In this respect, the paper is related to the literature that focuses on the exit decisions of industrial plants in declining industries and that predicts that more cost-efficient firms outlast the less efficient ones in the process of exit and capacity reduction (Ghemawat and Nalebuff 1985; Fudenberg and Tirole 1986; Reynolds 1988). The results from the empirical analysis support this prediction, and they are in line with Caiazza et al. (2016) in their analysis of cross-border M&A. However, the focus in this paper is on domestic banks competing in the same market during a period of demand contraction.
Our paper is also related to the literature that focuses on bank competition during the crisis (Montes 2014; Fernández et al. 2013; Weill 2013), but competition is determined by the density of bank branches rather than by the concentration of banks. Finally, the research is related to papers that explain differences in banks’ profits as a function of differences in productivity (Caiazza et al. 2016; Almanidis 2013; Fiordelisi and Molyneux 2010; Berger and Mester 2003; Grifell-Tatje and Lovell 1999). These papers tend to use productivity measures estimated from stochastic frontier models (SFA) or with the application of data envelopment analysis (DEA), while here, productivity is a parameter of the production function of banks, estimated with the methodology proposed by Levinsohn and Petrin (2003).
The rest of the paper is structured as follows. Section 2 presents the conceptual framework underlying the empirical analysis, as well as the empirical equation for testing the posed. Section 3 details the database used in the analysis, main variables and their descriptive statistics. In Sect. 4, the main results of the empirical models are analyzed and Sect. 5 presents the main conclusions of the study.
2 Theoretical framework
Retail banking markets have been traditionally local markets where bank branches compete for customers located at relatively short distance to the branch. The framework has two parts. First, we solve for the Nash equilibrium in markets where banks compete in interest rates of loans and deposits, for given number of banks and branches in each market. Second, we model the adjustment of capacity in the form of mergers and acquisition of banks and the closing of branches after the fall in demand, taking into consideration the effect of price competition in the profits of individual banks.
2.1 Price competition
The basic model of spatial price competition with a given number of bank branches is presented in “Appendix A,” together with the Nash equilibrium solution. Retail banking markets are represented by a Salop’s (1979) circle, with banks’ customers uniformly distributed around the circumference of the circle of length L = 1. In the same circumference, there are bank branches of different productivity-operating costs symmetrically located, and customers have to pay a cost per unit of distance to access the branch for loan or deposit services (horizontal product differentiation). Banks can borrow and lend in an interbank market at a market given interest rate. From the Nash equilibrium, the empirical model of the determinants of the interest rate of loans and deposits is formulated as follows:
The subscripts i, j and t refer to bank branch, market and year, respectively. The dependent variables \( r_{ijt}^{L} \), \( r_{ijt}^{D} \) refer to the interest rates of loans and deposits of bank branch i in market j at time t. The variable \( r_{t}^{IB} \) is the interbank interest rate. The variable \( A_{t}^{IND} \) is the size-weighted banking industry average productivity in year t, common to all banks, and RAijt is a measure of the relative difference in productivity between the bank i and its market competitors. \( N_{jt} \) is the number of bank branches that operate in the market j and time t. CV is a vector of control variables.
From the theoretical results in “Appendix A,” equilibrium interest rates will increase with the interbank market \( \left( {\beta_{1}^{L} > 0; \beta_{1}^{D} > 0} \right) \). Increases in average industry productivity over time will lower interest rates of loans \( \left( {\beta_{2}^{L} < 0} \right) \) and increase interest rates of deposits \( \left( {\beta_{2}^{D} > 0} \right) \). More efficient banks will set lower (higher) interest on loans (deposits) than less efficient ones (if bank i is more productive than j, then \( {\beta_{3}^{L} < 0; \beta_{3}^{D} > 0} \)). Higher density of branches in the market implies less spatial differentiation, more structural competition and lower (higher) interest rates of loans (deposits) \( \left( {\beta_{4}^{L} < 0; \beta_{4}^{D} > 0} \right) \). With free entry and exit, the number of branches is endogenous and, in the equilibrium, higher density of demand implies higher density of branches and more structural competition.
2.2 Productivity and restructuration of the banking system
In the crisis, when the expansion of the balance sheet of banks suddenly stops and growth rates turned negative, the size of the banking industry appeared over dimensioned. The process to reduce excess of capacity involved the closing of bank branches, together with mergers and acquisitions among banks. In the Nash equilibrium (“Appendix A”), more productive banks earn higher profits than the less productive ones. When demand falls, less productive banks are the first that show losses and, thus, they are expected to exit the market first. The second issue is how the market share of the exit banks will be allocated among the surviving banks.
2.2.1 Exit of banks
The hypothesis from rational-efficient restructuring is that the likelihood that a bank exits the industry decreases with the relative productivity, i.e., the less productive banks are more likely to exit than the more productive ones (Ghemawat and Nalebuff 1985; Fudenberg and Tirole 1986; Reynolds 1988). To test this hypothesis, we formulate the empirical model:
where the dependent variable \( y_{it} \) takes the value of 1 if bank i exits the market at time t and zero otherwise. The variable RAijt is a measure of the relative productivity of the entity compared to its competitors. The empirical prediction is that the estimated coefficient of the relative productivity variable will be negative. CV is a vector of control variables that, among others, include proxies of bank size and profitability. The theoretical model predicts that more productive banks are more profitable and have a larger market share in the equilibrium. Size and profits can influence the exit decision, independently from the productivity effect. For example, more profits can be associated with higher cash flows, and large banks might have higher than proportional restructuring costs. So, for similar levels of production efficiency, more profitable and larger banks can delay the market exit.
2.2.2 Branch expansion through mergers and acquisitions
We posit an empirical model to test two complementary hypotheses on the allocation of the market share of exiting banks. First, efficient restructuring requires not only that less productive banks exit first, but also that the market share is allocated to the surviving banks that are more productive. Second, from the logic of the acquiring banks, it can be expected that they prefer target banks whose branch network is complementary to their own, that is, branch networks do not overlap. To test these predictions, we formulate the following probit model:
where yikt is a dummy variable that takes the value 1 if bank i absorbs bank k in period t, and zero otherwise. The dependent variable needs to be defined for all the possible binary combinations of banks, including the combinations i-k and k-i, though yikt only takes the value of 1 if bank i absorbs bank k, but not the other way around. RAijk is now a measure of the relative productivity of bank i with respect to bank k at time t, and Targetikt is a measure (to be explained latter) of how attractive is the market share of target bank for the potentially acquiring bank j. We expect that the likelihood that bank j merges with or acquires bank k increases when bank j is more productive than bank k, and increases with the attractiveness of the target’s market.
Implicit in the formulation of (3) is the hypothesis of symmetry, in the sense that we are assuming that a large bank has the same probability of acquiring a small bank than the other way around. But market frictions make this hypothesis unrealistic. To account for the effect of size, we include a control variable that accounts for differences in size between acquired and acquiring bank. We also include variables that identify relative differences in banks’ profitability and risk, since mergers and acquisitions might also be conditioned by the cash flows and soundness of the bank.
3 Database and variables
The database contains information on banks, commercial and savings banks that operated in Spain between 2007 and 2015. It contains balance and profit and loss account data extracted from Bankscope and completed with the annual reports published by the CECA and the AEB. The data on the number of bank branches have been obtained from the annual reports of the Banking Guide published by Maestre Edibán. The data of the macroeconomic variables have been obtained from the National Institute of Statistics and the Bank of Spain. The identification of M&A, auctioned banks and new entities has been constructed using the information published by the Bank of Spain about the restructuring process of the Spanish banking system. Table 1 presents a summary of data on the restructuring process of the Spanish banking system elaborated from the information published in the Bank of Spain’s Report on Banking Supervision (Memoria de Supervisión) between 2007 and 2014.Footnote 1 From this table, we can observe that the reduction in the number of banking groups is mainly explained by the disappearance and consolidation of the old savings banks. The number of bank branches in 2014 has been reduced by one-third from the maximum reached in 2008.
3.1 Interest rates on loans and deposits, and net service fees
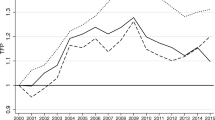
Interest rates of loans and deposits have been calculated with data from balance sheets and profit and loss accounts of each individual bank. The interest rate for loans is equal to the ratio of the item “Interest Income” (from the profit and loss account) and the item “Loans to Customers” (from the balance sheet). The interest rate for deposits has been calculated with the ratio of “Interest Expenses” (profit and loss account) and “Deposits from Customers” (balance sheet). Figure 1a shows the average of the loan and deposit interest rates and the 1-year Euribor interest rate. We observe that the Euribor interest rate has decreased during the sample period from 4.8% in 2008 to levels close to 0% in 2015. Despite that the period analyzed covers only partially the period of Quantitative Easing from the ECB (starting from March 2015), the Euribor has remained below 2% since 2009. Interest rates of loans and deposits have decreased over time in parallel to the decrease in the Euribor, as expected from the transmission of the monetary policy.
In Fig. 1b, we observe that the margin in the deposit market (difference between Euribor and interest rate of deposits) has remained at negative levels since 2008, i.e., the contribution of intermediation margin from the deposits market to the total intermediation margin of banks has been negative in practically all the period of study. However, on the loans market the average intermediation margin (interest of loans minus Euribor) shows an increasing trend reaching levels above 4 percentage points since 2012. This increase could be offsetting the decline in the deposits margin and explains the relative stability of margin of interests relative to total assets in Fig. 1b. In the same period, the net fees collected bank banks, relative to total assets, the other important source of revenues, have also increased over time (Fig. 1b).
3.2 Measurement of the productivity of banks
The measurement of productivity and efficiency in the banking sector is conditioned on different assumptions about the nature of the banking activity and the methodology followed to obtained estimates. First, there are two alternative views of the function of banks that affect the estimation of productivity. Under the intermediation view, banks act as intermediaries between depositors and borrowers and, thus, deposits are considered as inputs of the production function, together with labor and capital. Under the production approach, banks produce services attached to deposits and loans deposits and, as a result, deposits are treated as an output. Attending to the methodology, productivity and efficiency of banks can be estimated directly from the production function or indirectly from the dual cost or profit functions. Finally, productivity and cost efficiency can be estimated using parametric and nonparametric (mainly DEA) methods.
The view adopted in this paper assumes that banks produce services attached to loans and deposits (production approach). The productivity is derived from the estimation of the production function of banks using parametric methods. The approach, then, contrasts with that in Castro and Galán (2019) that use the intermediation view, with deposits as inputs, and productivity and efficiency estimated from the dual cost function (trans-log specification).
We assume that banks use labor, L, and capital, K, to produce and sell services delivered through a network of branches. The output of the bank in volume of services, Y, is assumed proportional to the sum of total loans and total deposits. The quantity of labor input of the bank is estimated by the labor costs, and the measure of the capital stock input is the volume of fixed material assets reported in the balance sheet. From the production function \( Y_{it} = A_{it} F\left( {L_{it} ,K_{it} } \right) \), the TFP of the bank is \( A_{it} = \frac{{Y_{it} }}{{F\left( {L_{it} ,K_{it} } \right)}}. \)
The estimation of \( A_{it} \) = PRODUCTIVITYit for bank i in year t is estimated as in Martín-Oliver et al. (2013) using the proposed methodology in Olley and Pakes (1996) and developed in Levinsohn and Petrin (2003), but with a different time period and definition of inputs. This methodology is based on the estimation of the parameters of the production function of banks, correcting for an endogenous bias in the estimation of the elasticity of output with respect to labor and capital due to the existence of productivity shocks that also affect the demand for labor. To correct the bias caused by productivity shocks, it is necessary to define an intermediate input τ that in our case will be the total volume of debt.Footnote 2 The results of the estimation of the production function show that the elasticity of the output with respect to the labor factor is 0.578, and with respect to the capital factor of 0.357, both coefficients were statistically significant at 1%. The null hypothesis of the existence of constant returns to scale cannot be rejected (p value of 0.47).Footnote 3
3.2.1 Productivity of banks and industry average
With the estimated values of the parameters of the production function, the TFP of bank i in year t, the (Solow) residual, is calculated, in log terms, as follows
The industry productivity, PRODUCTIV.INDUSTRYt, in year t is the average of the productivity of all banks in the time period.
From Fig. 2a, the size effect on differences in productivity among banks explains about 10% of the productivity of the industry. That is, the largest banks are the most productive and, therefore, the simple average of productivity is lower than the weighted average that reflects the productivity of the industry. Since the hypothesis of constant returns to scale in production cannot be rejected, the size effect in the productivity of banks cannot be attributed to increasing returns to scale. As the years progressed, the importance of differences in size decreases and by the end of 2015 reduces to 2.83% of the industry productivity.
Figure 2b shows the annual and cumulative growth rates of industry productivity. Comparing the levels of 2015 and 2007, we observe that productivity has a cumulative growth of 2% during the whole sample period, with an average annual growth rate around 0.37%. Overall, we observe that during the sample period, the productivity of the industry has remained relatively stable. In 2010, there was a rebound in industry productivity, which could be explained by the exit of banks with low productivity (from Table 1, there are 12 mergers in 2010 with 23 banks involved). During the two following years, the industry productivity falls again, coinciding with the years of more severe restructuring. Probably, the fall of demand for banking services was higher than the reduction in capacity in response to the contraction in demand. In the years 2013–2014, productivity grew marginally and in 2015, coinciding with the start of the Quantitative Easing, the industry productivity experienced a 5% annual growth.
Figure 2c shows the time evolution of average TFP for small, medium and large banks.Footnote 4 The figure confirms that the average productivity increases with the size of the bank, though the importance of the size effect decreases over time. There are two reasons: first, because the less productive small banks operating during the first years of the sample disappear after 2011 (merged or absorbed by others) and, second, because the differences in TFP between medium and large banks decrease over time. Therefore, the preliminary evidence is consistent with the hypothesis that most productive banks survive and that M&A generates larger and more productive institutions, reducing the heterogeneity across surviving banks.Footnote 5
3.2.2 Banks of low and of high productivity
One of the variables of the empirical model is the productivity of a bank relative to the productivity of its competitors, RAikt. We consider that the competitors of bank i are those banks with branches in the relevant market of bank i. The relevant market of bank i includes all provinces where the bank has at least five branches.Footnote 6 In the estimation of the model, banks will be classified as banks with higher and banks with lower productivity than the reference bank as follows. The variable \( Id\left( {LOW PROD_{it} } \right)_{{}} \) will take value 1 if bank i in year t has a productivity lower than the 25th percentile of the productivity distribution of banks that compete in the relevant market of bank i in year t. Similarly, the variable \( Id\left( {HIGH PROD_{it} } \right)_{{}} \) will take value 1 if bank i in year t has a productivity higher than the 75th percentile of the productivity distribution of the banks that compete in the relevant market of bank i in year t.
Figure 2d shows the distribution of the productivity of the banks during the sample period, as well as the distribution of the productivity of the banks that have a high (higher than the 75th percentile) and low (lower than the 25th percentile) productivity. We observe that productivity presents greater dispersion and wider tail in the left part of the distribution, while the productivity distribution of banks with higher productivity is more concentrated.
In the model of branch expansion through mergers and acquisitions, the explanatory variable is a measure of the direct comparison of productivity of acquiring and acquired bank. Then, we define the variable Id(PRODit> PRODkt), a binary variable that identifies the cases in which the productivity of the acquiring entity is higher than the productivity of the acquired entity.
3.3 Market sizes, target banks and target markets
In the short term, the number of bank branches in the market is taken as exogenous. Local markets with higher demand for bank services will be markets with higher density of branches (higher N in Eqs. 1A and 1B). In the empirical analysis we take the number of branches in the market as proxy for the size of the local market (provinces). Then, we define the variable MARKET SIZEit of i in year t as the average of the number of branches in provinces that are part of the relevant market of bank i.
TARGETikt is a dummy variable that takes the value 1 if bank k has branches in at least one market considered “target” of entity i. We define a province as a “target” market for bank i if the market share of i in that province is lower than the average market share of bank i in the rest of markets where it is present. In order to account for the relative importance of the number of branches held by bank k in i’s target markets, we also define the variable SUM SHARESikt as the sum of the market shares of the bank k in markets that are considered as target markets for the bank i. We expect that the attractiveness of a target bank increases with SUM SHARESikt.
Table 2 shows descriptive statistics of the previous variables. We observe that the size of the market, MARKET SIZEit, decreases over time due to the fall of the number of branches during the crisis and restructuring. TARGETikt decreases over time, possibly because the number of banks decreases, and the surviving banks are increasing the market shares in their target markets over time through the acquisition of other banks. The sum of the market shares of target banks, SUM SHARESikt, remains relatively stable over time.
Historically, the Spanish banking industry has been split between not-for-profit savings banks (the so-called cajas) and shareholder banks. The restructuring of the banking industry in the sample period has affected specially to the savings banks, since many of them have been merged or acquired and/or converted into shareholder banks (except two very small ones). The unique ownership and governance of cajas conditioned the process of merger and acquisitions. In the empirical analysis, we control for the differences in ownership and governance between savings banks and commercial banks with the variables Id(SAVINGSBANK) that takes the value of 1 if the bank is caja.
3.4 Other explanatory variables
The rest of the variables included in the models capture the heterogeneity among banks in size, return on investment, leverage and risk. Size of banks is measured by total assets in logs, ln(TOTALASSETSit). ROAit is equal to the ratio of earnings after taxes over total assets at the end of year t. CAPITAL RATIOit is the ratio between capital and reserves over total assets (leverage). The risk variables include: PROVISIONS/LOANSit, equal to the ratio of the loan loss provisions of the bank with respect to the total loan portfolio, and Zit, the Z-score of the bank, equal to the ratio between ROA + CAPITAL RATIO and the standard deviation of ROA (Goetz et al. 2016; Laeven and Levine 2009). “Appendix B” shows the list of all variables of the model and the respective definition.
Table 2 shows the descriptive statistics of the variables that capture the heterogeneity of the banking entities. The average size of banks in assets increases over time, while dispersion decreases, which is consistent with the process of concentration of the sector in a small number of large banks. The net interest income of the median bank is decreasing, consistent with Fig. 1. Z-score is a measure inversely related to the level of risk, so we find an increase in the level of risk assumed by the banks during the period of crisis that softens in the last year 2015. Similar evidence is found from the evidence from the evolution of the proxy of risk of the loan portfolio, PROVISION/LOANSit. The average ROAit of the banks has experienced a decline to negative levels during the most severe years of the crisis (where the greatest dispersion is recorded), although it has returned to the positive since 2015. The CAPITAL RATIOit has followed the same evolution, reaching its minimum during the worst years of the crisis, and increasing to 7.75% in 2015, possibly due to the efforts of the banks to improve their levels and quality of capital to comply with Basel III. All the variables used in the empirical analysis are defined in a more detailed way in “Appendix B.”
4 Results of the estimation of the empirical models
4.1 Interest rates
The results of the estimation of the model of the determinants of interest rates, Eqs. (1A) and (1B), are presented in columns I to IV of Table 3. For each interest rate, loans and deposits we present the results of two estimations, the OLS and the bank fixed effects estimation. In all cases the standard errors of the estimated coefficients are robust to heteroscedasticity and clustered at the bank level. Overall, the empirical results are consistent with the theoretical predictions in the case of interest of loans, but not consistent in the case of deposits, where the only estimated significant coefficients are those of the macroeconomic variables.
From estimation I, the coefficient of Id(LOWPROD) is positive and statistically significant at 1%, meaning that differences in productivity among banks translate into differences in loan interest rates, as predicted. On average, the interest rate on loans is 30 basis points higher in banks with low productivity, Id(LOWPROD), than in the rest of banks. However, the coefficients of Id(HIGHPROD) and Id(LOWPROD) in the case of interests of deposits are both nonstatistically significant, meaning that the predictions from the theory model are not visible in the deposits market.
Also from estimation I, the estimated coefficient of the industry productivity variable is negative and statistically significant. Increases (decreases) in industry productivity result in decreases (increases) in interest rates of loans, again consistent with the prediction from the Nash equilibrium solution. Since the cumulative growth of industry productivity during the period 2007–2015 is around 2%, this growth implies a decrease in the interest rates of loans of 4.4 basis points. In the year of 2015 with a 5% of industry productivity growth the contribution to the reduction in interest rates of loan would be of around 11 basis points.
We also observe that the estimated coefficient of the variable ln(MARKET SIZEit) is negative and significant at 1%. Therefore, higher density of bank branches in the local market implies lower interest rates of loans in the market equilibrium. This is the structural competition effect on market prices, with less spatial differentiation and more competition among bank branches in larger markets. The closing of bank branches during the sample period lowers the average value of the proxy variable for MARKET SIZE over time (Table 2). With lower density of bank branches, spatial differentiation increases and equilibrium interest rates of loans will increase (negative estimated coefficient). This can be one of the reasons why the profit margin of bank loans increases in the sample period (Fig. 1).
Finally, the interest rate of loans increases with the EURIBOR interest rate (interbank interest rate), again consistent with the prediction from the theoretical model. However, the estimated coefficient is less than the value of 1, suggesting some delays in the transmission of monetary policy.
As for the control variables of other characteristics, the negative sign of the estimated coefficient of Zit indicates that banks with a higher risk profile (low values of Z) charge higher loan interest rate. The positive sign of the variable PROVISIONS/LOANSit goes in the same direction, although the estimated coefficient is not significant. The size of the bank does not significantly affect the interest rates of loans.
The negative estimated coefficient of the variable GDP GROWTHt indicates that interest rates of loans are lower in years of economic expansion and higher in years of economic contraction (counter cyclical). INFLATIONt, does not have an effect in the interest rate of loans, additional to the effect through the sensitivity of the Euribor interest rate to the inflation of the economy.
The results of model (1B) on the interest rates of deposits are shown in estimation III of Table 3. Overall, the results differ from the theoretical predictions, particularly with respect to the productivity variables. Nonetheless, they are consistent with the predictions on effects of the macroeconomic variables. EURIBOR and INFLATION variables have a positive effect, whereas deposit interest rates are negatively related to GDP GROWTH (countercyclical interest of deposits). The positive and significant coefficient of lnASSETS indicates that larger banks pay higher interest rates on the deposits, maybe because of competition effects.
The results from the fixed effects estimation of models (1A) and (1B) appear in estimations II and IV in Table 3. Now the estimated coefficients of the bank-level variables, including the relative differences in productivity, lose statistical significance, probably because there is relatively low time variability and the coefficients in the OLS estimation captured persistence across-bank variability, now captured by the fixed effects. However, the estimated coefficients of the time-varying variables, such as industry productivity, maintain the sign and increase their statistical significance.
4.2 Fees as substitute of deposits margin
Interest rates of banks deposits have, in practice, a lower bound of zero. The possibility of negative interest rates would likely lead many people to hold cash instead of deposits. This lower bound could explain why some of the predictions from the spatial competition model are not supported by the data in the case of deposits. Under the impossibility to charge negative interest rates on deposits, the response of banks could be to increase the fees they charge for services they provide to the customers. The increasing ratio of net fees over total assets in Fig. 1b would suggest that banks responded to the decline in the deposits margin with higher services fees. We now present evidence that supports this conjecture.
Estimations V and VI in Table 3 show the results of estimating the fees per euro of total assets of banks, as a function of the relative efficiency of banks, macroeconomic variables and the deposits margin, defined as the difference between the Euribor and interest rate of deposits of the bank in the corresponding year. The estimated coefficient of MARGINit is negative and statistically significant in the OLS estimation and not significant in the fixed effects estimation. These results are in line with conjecture that banks with lower deposits margins apply higher fees for their services; in a context of high competitive pressure to maintain high levels of deposit interest rates the levels of the official interest rates are low. As for the rest of explanatory variables, the only coefficient that is statistically significant is Id(HIGHPROD) with a negative sign, implying that more productive banks charge lower prices for their services than less productivity ones.
4.3 Probability of exiting the banking market
Table 4 presents the results of the empirical model that test whether low-productivity banks are more likely to exit the market than high-productivity banks. Estimation I presents the results only including the relative variables of productivity as explanatory of the decision. We observe that the coefficient of Id(LOWPROD) is positive and statistically significant, confirming the prediction that low-productivity banks have a higher probability of not surviving than the rest of the banks. Estimation II presents the results of the model including control variables to account for other factors that might influence the probability of exit, such as risk or profitability of the banks. We observe that the coefficient of Id(LOWPROD) remains statistically significant (though at 10%) and with similar value. As for the rest of variables, we observe that cajas are more likely to exit than banks, even after controlling for variables of profits and risk. We also find that banks with low profitability and higher risk (lower Z) are more likely to exit. As for the size of the bank, larger banks are more likely to outlast competitors, since the coefficient of ln(TOTALASSETS) is negative and statistically significant at 5%. All of them are results consistent with the theoretical predictions and in alignment with the profile of the entities that experienced more problems during the crisis.
From the results in column II, we observe that the size of the bank conditions the probability of exit, controlling for differences in productivity. This suggests that, above a certain bank size, the resistance to exit dominates over any effect of differences in productivity. For robustness analysis, Table 4 also shows the results of model estimated for subsamples of small, medium and large banks. The results shown in columns III, IV and V indicate that the effect of productivity on the probability of exit remains statistically significant for the small- and medium-size banks, but not for large banks. These results suggest that size might be an obstacle to restructuring because, for large banks, differences in productivity do not affect the probability of exit.
4.4 Branch expansion through mergers and takeovers
Table 5 shows the results of estimating Eq. (3) with a logit model to analyze whether the most productive banks and those that have better withstood the crisis have taken advantage of the situation to expand their market share in “target” provinces through the acquisition of less productive banks.
From Column I, we observe that the coefficient of the variable TARGETikt is positive and statistically significant at 1%. This implies that the probability of a bank acquiring another bank increases if the acquired entity has branches operating in at least one of the markets where entity i wants to grow (lower presence in the market before the acquisition). This result is reinforced by the positive and statistically significant coefficient of the variable SUM SHARESikt, which suggests that the higher the market share of the potential acquired entity in the target market, the greater the likelihood that the entity i absorbed it. However, the coefficient of SUM SHARESikt is not statistically significant when we include the size comparison as explanatory variable. Probably, only larger banks can afford buying large networks of branches, so the size effect neutralizes the value effect.
From Column II, the positive sign of Id(PRODit> PRODkt) indicates that this strategy is more likely if the acquired banks have a productivity lower than the productivity of the acquiring banks, that is, more efficient banks are absorbing less efficient banks. However, the estimated magnitude and statistical significance of the estimated coefficient decrease when we include the differences in size in the regression. It appears that the size effect dominates, though not neutralizes, the productivity effect in the matching of merging or acquiring banks. Size and productivity are positively correlated in our sample data, and our model predicts that productivity determines size and not the other way around. But to demonstrate that the size effect hides productivity effects is out of the scope of this paper. Realistically, the asymmetry in the probability that smaller banks acquire large banks also determines why productivity differences become nonstatistically significant when controlling for the size variable.
The inclusion of profitability and risk in Column IV indicates that acquiring banks are more capitalized and more profitable than the acquired ones. At the same time, the coefficient of productivity differences becomes nonstatistically significant. Again, the model predicts that productivity drives profitability and not the other way around. But the combination of productivity and cash flows in the ROA plus the higher capitalization required to absorb a bank might explain why profitability and solvency dominate over productivity in the matching of acquiring and acquired banks.
Column V shows the results of the estimation including Id(SAVINGSBANK) among the explanatory variables. The estimated coefficient is positive and significant, indicating that savings banks are more likely to be targets of acquisitions than commercial banks.
5 Conclusions
This paper presets estimates of the evolution of total factor productivity of Spanish banks in the period 2007–2015 and examines how the differences in productivity across banks and the evolution of industry productivity over time impact on the costs of banks. We find that the industry productivity at the end of the sample period is practically the same than that at the beginning of the period. Up to 2010, productivity grows at 2.7% annually, but it decreases at annual growth rates of 5.49% and 6.34% in 2011 and 2012, respectively. Probably, the negative growth rates of productivity after 2010 can be explained by a reduction in the production capacity at a slower pace than the reduction of the demand for bank products.
We also find evidence supporting our theoretical prediction that more productive banks charge lower loan interest rates than less productive ones, and that loan interest rates are negatively correlated with the evolution of the industry productivity over time. According to the empirical results, less productive banks charge interest rates of loans 30 basis points higher than the rest of banks. Also, a growth rate in industry productivity of 1% implies an average reduction of interest rates of loans of 2.2 basis points. The predictions from the model on the effect of productivity in the interest rates of deposits are not supported by the empirical results. One plausible explanation is that banks have negative profit margins in the deposits market, since they cannot set negative interest rates on deposits in a period of zero official interest rates. However, there is evidence that banks might have compensated the negative margin in the deposits market with higher fees charged on services to consumers (payments).
We also find evidence that productivity differences across banks condition the industry restructuring process, in terms of which banks exit the industry (merged or absorbed) and in terms of the matching between acquiring and acquired banks. In particular, effects seem to dominate the restructuring process, since less productive banks are more likely to exit the industry than more productive banks, and acquiring banks are more productive than the acquired ones. The restructuring of capacity also responds to strategic interests of individual banks, in the sense that acquiring banks prefer targets with branches located in markets where they are underrepresented.
It must be said, however, that the productivity effect in the probability of exit is statistically significant only for the groups of small- and medium-size banks. We also find that differences in size, profitability and solvency between acquiring and acquired banks dominate the effect of differences in productivity to explain the matching between acquiring and target banks. Acquiring banks are larger, more profitable and better capitalized than the acquired banks. Theoretically, productivity differences drive size and profit differences among banks, but this paper has not empirically demonstrated that this is the case in our sample data. It is more accurate to say that the restructuring has increased the concentration of the Spanish banking sector in more profitable and better capitalized banks. We leave for future research a more thorough analysis of the causality of differences in productivity into differences in profitability and solvency of banks.
The evidence supporting that efficiency has driven the restructuring of the Spanish banking industry is encouraging from the public policy point of view. However, it remains to be studied whether, along a more extended period of time, the increase in the concentration of the banking sector can make loans and deposits markets less competitive, that is, productivity growth might not be sufficient to reduce the industry intermediation costs over time. So far, the results of the paper provide supporting evidence that the reduction in the density of bank branches following the fall of demand, could have had contributed to maintain or to increase the margin in the interest rates of loans during the sample period, since lower density of branches implies lower spatial differentiation and less competition.
Notes
2014 is the last year for which the Bank of Spain's Supervisory Report publishes these data.
This intermediate input fulfills the necessary assumption that the entity could increase the amount of debt to meet possible productivity shocks, for any level of capital.
Following Martín-Oliver et al. (2013), we have tried to obtain a net measure of productivity, regressing the gross productivity on variables capturing differences in business models available in Bankscope (weight of loans, weight of interbank, weight of total securities, regulatory capital and total assets) and on time dummies. Given that the coefficients of the variables were not statistically significant during this sample period, we assume that the residuals of this regression (measure of net productivity) were not different to our direct measure of productivity obtained from Eq. (4).
Classification of banks made using the whole sample data; each size class includes one-third of the observations.
The time evolution of the TFP index in Fig. 3 is not too different from the time pattern of the TFP index reported in Fig. 1 in Castro and Galán (2019), obtained with a different methodologies and with size classes of banks defined as small (25%), medium (50%) and large (25%). There are, however, some differences in cross-sectional comparisons. Castro and Galan find that small banks are more productive than medium-size banks and that the differences in average productivity between medium and large banks do not converge as much as they do in our analysis. Finally, they find evidence of scale economies in production for Spanish banks that explains part of their TFP differences across sizes of banks.
The definition of this threshold aims at identifying all the provinces where banks have a minimum level of retail activity, but excluding cases of bank branches whose existence is justified only for institutional reasons (for instance, almost all banks have one branch in Madrid).
On the upward bias in bank-level productivity estimates when IT expenditures are ignored see Koetter and Noth (2013).
References
Almanidis P (2013) Accounting for heterogeneous technologies in the banking industry: a time-varying stochastic frontier model with threshold effects. J Prod Anal 39:191–205
Berger AN, Mester LJ (2003) Explaining the dramatic changes in performance of US Banks: technological change, deregulation, and dynamic changes in competition. J Financ Intermed 12:57–95
Caiazza S, Pozzolo AF, Trovato G (2016) Bank efficiency measures, M&A decision and heterogeneity. J Prod Anal 46:25–41
Castro Ch, Galán J (2019) Drivers of productivity in the Spanish banking sector: recent evidence. J Financ Serv Res 55:115–141
Fernández AI, González F, Suárez N (2013) How do bank competition, regulation, and institutions shape the real effect of banking crises? International evidence. J Int Money Finance 33:19–40
Fiordelisi F, Molyneux P (2010) Total factor productivity and shareholder returns in banking. Omega 38:241–253
Fudenberg D, Tirole J (1986) A theory of exit in duopoly. Econometrica 54:943–960
Galán J, Veiga H, Wiper W (2015) Dynamic effects in inefficiency: evidence from the Colombian banking sector. Eur J Oper Res 240:562–571
Ghemawat P, Nalebuff B (1985) Exit. RAND J Econ 16:184–194
Goetz MR, Laeven L, Levine R (2016) Does the geographic expansion of banks reduce risk? J Financ Econ 120:346–362
Grifell-Tatjé E, Lovell CA (1999) Profits and productivity. Manag Sci 45:1177–1193
Koetter M, Noth F (2013) IT use, productivity, and market power in banking. J Financ Stab 9(4):695–704
Laeven L, Levine R (2009) Bank governance, regulation and risk taking. J Financ Econ 93:259–275
Levinsohn J, Petrin A (2003) Estimating production functions using inputs to control for unobservables. Rev Econ Stud 70:317–341
Martín-Oliver A, Ruano S, Salas-Fumás V (2013) Why high productivity growth of banks preceded the financial crisis. J Financ Intermed 22:688–712
Martín-Oliver A, Ruano S, Salas-Fumás V (2014) Productivity and welfare: an application to the Spanish banking industry. Working Paper 1426, Bank of Spain
Montes CP (2014) The effect on competition of banking sector consolidation following the financial crisis of 2008. J Bank Finance 43:124–136
Moral-Benito E (2018) Growing by learning: firm-level evidence on the size-productivity nexus. SERIEs 9:65–90
Olley GS, Pakes A (1996) The dynamics of productivity in the telecommunications equipment industry. Econometrica 64:1263–1297
Reynolds SS (1988) Plant closings and exit behaviour in declining industries. Economica 55:493–503
Salop SC (1979) Monopolistic competition with outside goods. Bell J Econ 10:141–156
Weill L (2013) Bank competition in the EU: how has it evolved? J Int Financ Mark Inst Money 26:100–112
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Production, demand and interest rates competition
In this Appendix we present the conceptual framework that supports the empirical analysis on the determinants of interest rates of loans and deposits by banks. This includes a description of the production function that is estimated for the calculation of the productivity of banks and industry average, a description of the demand functions and the Nash equilibrium solution from price competition.
1.1 Production and cost function
The production unit of banking services, giving loans and collecting deposits, is the branch. The production function for the representative bank branch i is given by:
The output of the bank branch is equal to the sum of loans (L) and deposits (D). Each branch has a fixed capacity q determined by the physical space and a variable capacity that depends on the quantities of variable inputs, the number of employees per branch (E) and the IT capital per branch (IK).Footnote 7 Parameter A represents the level of productivity of the branch. Previous research with a similar data set (Martín-Oliver et al. 2014) has found that output per bank branch does not vary with the physical capital of the bank, confirming that physical capital is a quasi-fixed input tied to the capacity of the branch; the function F() is linear homogeneous (i.e., it exhibits constant returns to scale) in labor and IT capital inputs, and there are constant returns to scale at the bank level. These results justify the output of the bank being written as the product of the output per branch times the number of bank branches, and also that the cost of physical capital per branch is fixed.
Let w and ccIT be the labor cost and the user cost of IT capital services, respectively. Since (A1) is linear homogeneous in labor and IT capital, the minimum total variable cost of producing output (L + D) in branch i is given by:
The per-unit variable production cost of bank branch i, \( c_{i} = \frac{{v_{i} (w,cc_{IT} )}}{{A_{i} }} \), increases with the input prices and decreases with the level of operating efficiency, Ai.
The current market price per unit of capacity of the branch is pK, so the investment in capacity per branch is pkqi= Ki. If ccK is the user cost of physical capital (interest rate plus depreciation), then the fixed cost period of the branch capacity is ccKKi.
1.2 Demand functions
Bank branches are located around a circle as in Salop (1979) spatial competition model. Bank customers are uniformly located in each point of the circumference of length 1. The N bank branches in the market are symmetrically located, so the distance between branches is 1/N. Markets of deposits, subindex D, and loans, subindex L, are taken to be independent (i.e., no bundling decisions). Let riL, riD be the interest rates of loans and deposits of bank i, and rL. rD be those of the representative competing bank. Except for distance to the branch, the buyers perceive banks products as perfect substitutes. Thus, they will choose one branch or another depending only on differences in the costs measured by the sum of interest rates and transportation costs. If τ is the cost per unit of distance, there is a distance xi to branch i at which the buyer located in this point is indifferent about branch i or the closer competing one:
From (A3) and taking into account that there are customers at both sides of the branch, the demand for loans per branch for bank branch i and for that of the representative competitor are:
Respectively, for deposits,
Banks face the constraint that demand for funds must be equal to supply of funds. To balance the constraint, in addition to loans and deposits banks also finance their activity with a stock of capital K and have access to financial markets where they can borrow and lend amounts M of funds at the market interest rate r:
1.3 Equilibrium interest rates, market shares for loans and deposits and profits
Taking into account (A8) and after arranging the terms, the respective profit functions per branch of bank i and of the competing representative bank can be written as:
where L() and D() functions are given by Eqs. (A4) to (A7).
Each bank chooses the interest rates of loans and deposits that maximize profits. The Nash equilibrium solutions for bank i, interest rate and demand are:
According to Eqs. (A11) and (A12), equilibrium interest rates of loans and deposits increase with the market interest rate r. Interest rates of loans (deposits) will be lower (higher) in markets with higher density of branches (N) and in markets with lower (higher) perceived differentiation (τ). Within a given geographical market, the interest rate of loans (deposits) charged by a given bank will increase (decrease) with the weighted average of the per-unit operating costs of the bank (ci) and the per-unit operating cost of its competitors (c) (weights of 2/3 and 1/3, respectively).
The weighted sum of operating costs, \( \frac{2}{3}c_{i} + \frac{1}{3}c \) (indistinctly for loans and deposits), can be written as \( \frac{2}{3}c_{i} + \frac{1}{3}c = \frac{1}{6}\left( {c_{i} - c} \right) + \bar{c} \), where \( \bar{c} = \frac{{c_{i} + c}}{2} \) is interpreted as the market average cost. Therefore, the interest rate of loans of bank i in the Nash equilibrium can be written as a function of the difference between the own operating cost and the cost of competitors and of the market average cost. In the empirical analysis of the determinants of interest rates we substitute unobserved unit operating costs by measures of productivity of banks. This substitution is justified because the per-unit operating costs are inversely related to the total factor productivity parameter A. The total effect of productivity on the interest rates is separated into the effect from market average productivity, \( A_{t}^{Mi} \) (average \( A_{j} \) for all banks j in the same market than bank i), and the effect from the productivity of bank i relative to that of its competitors in the same market (\( RA_{ijt} ). \) Since operating costs are inversely rated to productivity, increasing average market productivity would result in lower (higher) interest rates of loans (deposits), and interest rates of loans (deposits) of more productive banks are expected to be lower (higher) than interest rates of the less productive ones.
Higher density of bank branches in the market reduces the volume of loans and deposits per branch in the market. In equilibrium, bank branches with higher productivity (lower operating unit costs) have a higher market share in loans and deposits than banks with lower productivity (from the inverse relationship between unit operating costs and productivity). Substituting the equilibrium values of prices and quantities from (A11) and (A12) in (A9), the maximized volume of profit for branch bank branch i is equal to:
Profits per branch are the sum of profits in the loans and in the deposits markets. More efficient banks earn higher profits per branch than less efficient ones (if Ai> A, then ci< c and Π*i > Π*). The higher profits come from two sources, higher profit margin and larger market share. Profit per branch is higher if the bank operates in markets with higher buyers’ perceived differentiation, higher τ, and/or in markets with lower density of branches, lower N.
Appendix B: Definition of variables
Variables | Definition |
|---|---|
Dependent variables | |
Loan interest rateit | Interest rate for loans of bank i at year t, calculated as the ratio of the item “Interests’ Income” and the item “ Loans to Customers” obtained from balance sheet items and profit and loss accounts published by each entity |
Deposit interest rateit | Interest rate for deposits of entity i at year t, calculated as the ratio of “Interests Expenses” and “Deposits from Customers” obtained from balance sheet items and profit and loss accounts published by each entity. With this variable, we also construct MARGIN_DEPit, which is the difference between the 12-month Euribor interest rate and the average rate of deposits offered by the entity i at year t |
Net Feesit | Net commissions of entity i at year t, calculated as the ratio of “net fees and commissions” and “total assets” obtained from balance sheet items and profit and loss accounts published by each entity |
Pr(Entity i exits in t) | Dummy variable that takes the value of one if entity i leaves the market in t (i.e., entity i is not present in the sample from t + 1 onwards) and zero otherwise |
Pr(Entity i absorbing entity k at t) | Dummy variable that takes the value of one if entity i absorbs entity k at time t, and zero otherwise |
Independent variables | |
Productivity | |
Id(HIGH PROD)it | Dummy variable that takes the value of one if bank i in year t has a productivity higher than the 75th percentile of the productivity distribution of the banks that compete in the relevant market of bank i in year t, where the relevant market is defined as all those provinces where bank i has at least five branches |
Id(LOW PROD)it | Dummy variable that takes the value of one if bank i in year t has a productivity lower than the 25th percentile of the productivity distribution of banks that compete in the relevant market of bank i in year t, where the relevant market is defined as all those provinces where bank i has at least five branches |
ln(PRODUCTIVITY)it | Logarithm of absolute value of the productivity estimate for bank i in year t, which is recovered from the estimation of banking production function (5) following Martín-Oliver et al. (2013) |
ln(PRODUCTIV. INDUSTRY)t | Logarithm of absolute value of productivity of the industry in year t, calculated as the average of estimated productivity for all banks as explained above |
Id(PRODit> PRODkt) | Dummy variable that takes the value of one if the productivity of the acquiring entity i in year t is higher than the productivity of the acquired entity k in year t, and zero otherwise |
Market size and target markets | |
ln(MARKET SIZE)it | Size of the markets in which entity i operates in year t, approximated by the average number of branches operating in the provinces in which the bank i has at least 5 branches, in logs |
TARGETikt | Identifies bank k as a potential target of bank i. It is a dummy that takes value of one if bank k has branches in year t in at least one market considered “target” of bank i. A market is considered a “target” for bank i if the market share of bank i in that market is lower than the average value of i’s market shares in the rest of the markets |
SUM SHARESikt | Sum of the market shares (in terms of number of branches) of bank k in year t of all the markets that are considered as target markets for bank i |
Id(SAVINGS BANKit) | Dummy variable that takes the value of one if entity i is a savings bank (i.e., caja) and zero otherwise |
Control variables | |
ln(TOTAL ASSETS)it | Book value of the bank i’s assets at the end of the year t, in logs |
ROAit | Ratio of after-tax profit and the assets of bank i in year t |
CAPITAL RATIOit | Ratio of own funds over assets of entity i in year t, winsorized at 1% |
Zit | Z-score of the entity i in year t, winsorized at 1%, calculated as the sum of the ROA and the CAPITAL RATIO of the entity divided by the standard deviation of the ROA of the entity |
PROVISIONS/LOANSit | Ratio of the insolvency provision of entity i in year t to the total loan portfolio |
Id(VARit> VARkt) | Dummy variable that takes the value of one if the variable “VAR” of the acquiring entity i in year t is higher than the value of “VAR” of the acquired entity k in year t, and zero otherwise |
Macrovariables | |
INFLATIONt | Inflation rate in year t |
EURIBORt | Average 12-month Euribor in year t |
GDP GROWTHt | GDP growth rate in year t |
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Llorens, V., Martín-Oliver, A. & Salas-Fumas, V. Productivity, competition and bank restructuring process. SERIEs 11, 313–340 (2020). https://doi.org/10.1007/s13209-020-00214-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-020-00214-4