Abstract
This paper analyzes how changes in the firing-costs gap between permanent and temporary workers affect firms’ TFP in a dual labour market. We argue that, under plausible conditions, firms’ temp-to-perm conversion rates go down when this gap increases. Temporary workers respond to lower conversion rates by exerting less effort, while firms react by providing less paid-for training. Both channels lead to a decline in TFP. We test these implications in a large panel of Spanish manufacturing firms from 1991 to 2005, looking at the effects of three labour market reforms which entailed substantial changes in the firing-costs gap. Our empirical findings provide some support for the above-mentioned mechanism.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Different conclusions emerge from the available literature on how Employment Protection Legislation (EPL) affects total factor productivity (TFP) growth. On the one hand, there is the view that more stringent EPL reduces TFP. For example, Hopenhayn and Rogerson (1993) and Autor et al. (2007) argue that the distortion and the lower reallocation flows induced by stringent EPL lead firms to use resources less efficiently. Likewise, Saint-Paul (2002) shows that stricter EPL induces firms to adopt mature technologies to improve existing products rather than to experiment with riskier primary innovations. Wasmer (2006), in turn, emphasizes that, by inducing substitution of specific for general skills, stringent EPL hinders worker relocation across industries in the presence of sectorial shocks. Finally, Ichino and Riphahn (2005) claim that layoff protection may reduce workers’ effort (a component of TFP) by inducing higher absenteeism. On the other hand, there is an alternative strand of the literature which argues in favour of favourable effects of stringent EPL on TFP. For instance, since EPL raises reservation wages, Lagos (2006) argues that firms become more selective and only realize more productive matches, while MacLeod and Navakachara (2007) and Belot et al. (2007) claim that EPL induces firms and workers to invest more in match-specific training, therefore improving TFP growth.
It should be noticed, however, that the setup considered in most this literature is one where all workers get hired under the same (open-ended) labour contracts, so that a single EPLregime is assumed to operate in the labour market. Yet, this assumption leaves out the case of dual EPL regimes which have been prevalent in several southern European countries, where there are substantial differences between the dismissal regulations pertaining to workers under permanent (open-ended) and temporary (fixed-term) contracts. As a result, the issue of how a dual EPL regime affects TFP has received much less attention and remains an open issue (see Sect. 2 below).
Our goal here is to help fill this gap in two different ways. First, by providing some novel theoretical underpinnings of how labour market dualism could affect technical efficiency through two specific components of TFP, namely, workers’ effort and occupational training. Second, by empirically testing the predictions of our model using longitudinal firm-level data for Spain, which has been often considered as an epitome of dual EPL in southern Europe.
Dualism is the Spanish labour market dates back to the mid-eighties. To fight high unemployment, a radical “two-tier” labour reform was passed in 1984 allowing firms to use very flexible fixed-term contracts (entailing low or no severance pay) not only for seasonal/replacement jobs but also for regular activities. Yet, previous stringent EPL rules for open-ended contracts (entailing high redundancy pay) remained effectively unchanged (see, e.g., Dolado et al. 2002 and Bentolila et al. 2008). The share of temporary workers in dependent employment shot from 15% at the time of the reform to 35.4% during the mid-1990s. Since then, temporary contracts have represented more than 90% of all new contracts signed each year. Subsequently, following several EPL reforms at the margin, a plateau of 30% was reached. More recently, despite a massive destruction of temporary jobs during the Great Recession, and a more radical EPL reform approved in 2012 to fight dualism, the rate of temporary work has only dropped to 25%, which still remains one of the highest rates among OECD countries.
On top of labour market dualism, another salient feature of the Spanish economy is the large slowdown in labour productivity experienced during the decade preceding the global financial crisis, when both employment and hours worked soared. This fall in productivity growth was not due to lower capital accumulation per worker in the aftermath of rapid employment growth, but rather to a drastic reduction in TFP growth, from 1.5% in 1980–1994 to −0.5% in 1995–2005. Although part of this productivity drop was due to the strong dependence of the Spanish economy on several low value-added industries (like residential construction, tourism and personal services), there is ample evidence documenting that TFP also performed very poorly in tradable sectors, including manufacturing (see e.g., Escribá and Murgui 2009, and Garcia-Santana et al. 2015). This negative outcome at a time where the use of IT technologies was very intense worldwide contrasts sharply not only with TFP growth in the US, which accelerated since the 1990s, but also with the rest of the EU-15, where the productivity slowdown was less acute than in Spain.Footnote 1 As Jimeno and Santos (2014) have argued in their narrative of the crisis in the Spanish economy, the increasing bias in its sectorial composition towards labour-intensive and low- productive industries has been due to two intertwined channels: (i) a labour market regulation which favoured the intensive use of temporary contracts, and (ii) a banking system capable of feeding the huge increase in credit demand by consumers and firms through recourse to external funding and lax facilities for the use of real assets a loan collateral in a context of very low real interest rates.
In view of these considerations, our focus here is on issues related to channel (i) above. In particular, we analyze how exogenous variations in the large differential between the firing costs of permanent and temporary workers (dubbed the firing-costs or EPL gap hereafter) impinges on TFP growth through changes in the relative job performance and on-the-job training of these two types of workers. The specific mechanism we highlight here is one where regulatory changes in the EPL gap influence firms’ decisions to upgrade contracts from temporary to permanent status (in short, temp-to-perm conversion rate). These decisions, in turn, affect both workers’ incentives to exert effort and the amount of paid-for training that firms invest on their employees. To the extent that effort and training are relevant unobserved components of TFP, this channel may have played a relevant role in linking changes in dual EPL and firms’ productivity.
To make this argument transparent, we propose a stylized model of how employers’ and workers’ decisions interact in a prototypical dual labour market, akin to the Spanish one. Our setup is one where firms find optimal to open jobs under fixed-term contracts which last for one period and cannot be renewed with the same worker in sequence.Footnote 2 At their termination, the employer faces the decision to dismiss the worker (paying a small severance compensation for contract termination) or to upgrade her temporary contract into a permanent one (subject to much higher severance pay). Temporary workers supply effort by trading off its disutility against a combination of a higher wage and promotion prospects. Firms bargain wages with these workers and design contracts (in terms of conversion rates and paid-for-training provision) to elicit that level of non-contractible effort that maximizes their expected profits, subject to participation and incentive compatibility constraints.
Insofar as severance pay cannot be fully neutralized in the wage bargaining (see Lazear 1990), our main theoretical prediction is that, unless permanent workers respond to a high EPL gap by exerting much more effort (thus making their jobs much more attractive for firms and temporary workers), a rise in the EPL gap is likely to reduce firms’ temp-to-perm conversion rates. The basic insight is as follows: absent a large increase in effort by permanent workers, a higher EPL gap reduces the profitability of permanent jobs, decreasing firms’ conversion rates and their provision of paid-for-training for temporary workers since their job tenures are short. As a result, the latter opt for lower effort which, ceteris paribus, hinders firm productivity. Conversely, reductions of the EPL gap would lead to opposite results.
To corroborate this intuition, we use longitudinal firm-level data from the Survey on Business Strategies (Encuesta sobre Estrategias Empresariales, ESEE) which offers detailed annual information on a representative sample of Spanish manufacturing firms over the period 1991–2005. Although ESEE lacks information on workers’ effort and paid-for training, a unique feature of this dataset is that it provides all the key variables required to compute TFP and temp-to-perm conversion rates for each firm level in each year of the sample. This allows us not only to use TFP as a composite embedding unobserved worker’s effort and training, but also to have a precise measure of the other key variable in the mechanism explored here. Further, ESEE includes information on other relevant variables which could affect TFP, such as R&D expenditure and the proportions of public and foreign capital. Since it reasonable to assume that these variables affect TFP in a more sluggish way than effort and training, they are used as predetermined covariates in the empirical exercise, isolating in this way the relationship between conversion rates and the two specific components of TFP we focus on here.
Using TFP as a composite of the two outcome variables of interest raises the issue of how to disentangle the responses of temporary and permanent workers’ performance to changes in the EPL gap. Our identifying strategy relies upon testing the above-mentioned mechanism separately for firms with very high and very low rates of temporary work. We expect the decisions concerning temporary workers to be much more prevalent in the first group of firms. Our main finding is that the response of permanent workers to changes in the EPL gap has been rather minor in comparison to the response of temporary workers. This could be due to two specific features of the two-tier EPL reforms in Spain that we analyze in the empirical section. The first one is that none of these reforms changed the EPL rights of permanent workers in a retroactive fashion (i.e., legal changes applied exclusively to new workers) while those affecting the EPL of temporary workers had immediate effects on them (see Dolado et al. 2002). The second one is that the share of newly hired permanent workers after the reforms was fairly small (less than 5% per year) and evolved very slowly over time. Fragmentary evidence supporting this finding is also provided using data from the European Community Household Panel (ECHP) which, unlike ESEE allows us to examine differences in training practices between permanent and temporary workers.
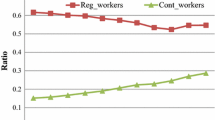
Some suggestive motivation for our empirical approach is provided in Fig. 1 where the (employment weighted) annual averages of the temp-to-perm conversion rates (left axis) and TFP growth rates (right axis) are jointly displayed for our sample of manufacturing firms.Footnote 3 As can be inspected, both variables exhibit strikingly similar patterns over the sample period, including a common declining trend from the late 1990s to the mid-2000s.
In view of this preliminary evidence, we evaluate the impact of changes in the firing-cost gap on firms’ TFP using three dual EPL reforms that took place during the sample period. Since these were nationwide reforms, variation of their effects across firms is obtained by assuming that those firms (or industries) with a higher share of temporary workers prior to the implementation of the reforms were more strongly affected than other firms with lower shares of temporary work. Indeed, we show that, in those instances when the EPL gap went down (up), conversion rates and TFP move up (down) together much more closely in firms with high shares of temporary workers than in those firms with lower shares. Hence, we take this empirical finding as supportive of our main prediction.
However, on its own, this direct mechanism cannot explain the collapse in TFP growth and in conversion rates from the late 1990s to the mid-2000s. This is so since the only reform raising the firing-costs gap during this period took place in 2002, i.e. in the middle of that period. We present some additional empirical evidence indicating that the declining patterns in both variables could be related to the expansion of ancillary industries (with high rates of temporary work) to the real estate sector, where a bubble started to grow at the turn of the century. Insofar this specialization pattern into low-TFP industries responds to the possibility of using flexible fixed-term contracts in an otherwise rigid labour market, we conjecture that this channel may have provided an indirect detrimental effect of dualism on productivity growth.
Using Hsieh and Klenow’s 2009 well-known methodology, Garcia-Santana et al. (2015) have recently argued that the poor productivity performance of the Spanish economy between 1995 and 2007 was due to a pervasive misallocation of resources across all sectors. This was especially relevant in those industries more prone to cronyism (e.g., construction and real estate), where the role of connections with public officials is key for business success. Admittedly, our approach abstracts from this channel and instead focuses on the impact of changes in dual EPL on average TFP growth through the mechanism described before. Incorporating their effects on the allocation of resources across firms remains an open issue to be more deeply analyzed in future research.
The rest of the paper is organized as follows. Section 2 offers a brief overview of the related literature. Section 3 lays out a model of the relevant decisions taken by workers and firms in a dual labour market, and draws relevant predictions for the subsequent empirical analysis. Section 4 describes the EESE dataset and provides descriptive statistics on the main variables in our mechanism. Section 5 presents empirical evidence about the impact of three dual EPL reforms on firms’ TFP, via its effects on conversion rates, as well as some scant evidence based on a different dataset about its effect on training . Finally, Sect. 6 concludes. An Appendix with three parts contains some algebraic derivations and more detailed definitions of the variables.
2 Related literature
Our paper relates to a small literature dealing with the impact of dual EPL on labour market outcomes, which has mainly focused on its effects on unemployment and labour turnover.Footnote 4
There is a strand of the literature analyzing the effects of changes in a (single) EPL regime on (labour) productivity, but from a different angle than ours. For example, Autor et al. (2007) and Bassanini et al. (2009) provide empirical evidence showing that strict EPL has a depressing impact on productivity in the US and the EU. It does so because it reduces the level of risk that firms are ready to endure in experimenting with new technologies. In a similar vein, Cingano et al. (2010) use an Italian EPL reform in 1990, where firing costs in small firms were increased, to analyze the effects of changes in EPL on a variety of labour market outcomes, including firms’ TFP. Yet, none of these studies considers a dual EPL system affecting workers, as we do here. They focus instead on assessing the impact of overall EPL changes on productivity by testing for significant differences in the outcomes of a treatment group (e.g., smaller firms in Italy or US states adopting wrongful discharge protections) and a control group (e.g., larger firms in Italy or US states not adopting those rules).
Our focus here also differs from a smaller strand of this literature which does consider dual EPL in relation to productivity. For example, Boeri and Garibaldi (2007) analyze the Italian two-tier labour market and find evidence of a negative relationship between the share of temporary work and labour productivity growth. They interpret this result in terms of a transitory increase in labour demand induced by the higher flexibility of temporary jobs (i.e., the so-called “honeymoon” effect of this type of reforms) which leads firms to increasingly hire less productive workers through these flexible contracts. Likewise, Sánchez and Toharia (2000) estimate the reduced form of a standard efficiency-wage model using the same Spanish database we use here, albeit for a much shorter period (1991–1994), and also find a negative relationship between temporary work and labour productivity. Similar but more updated results have been reported by Alonso-Borrego (2010) using the Firms’ Balance Sheets of the Bank of Spain. More recently, using variation across sectors and over time, Cappellari et al. (2012) have evaluated the effects on a variety of outcomes of an Italian reform in 2001 which relieved employers from justifying the use of temporary workers in the employment contract. Yet, despite sharing a similar empirical approach to ours, none of these papers explore the specific mechanism linking changes in the EPL gap to conversion rates and TFP growth that we stress here.
Regarding those specific studies which analyze the effect of dual EPL on training incidence, especially in Spain, Alba-Ramirez (1994) and Rica et al. (2008) document that firms invest less in temporary workers, due to their high turnover rate. Yet, they do not look at how this training gap changes with the firing-costs gap. Recently Garda (2012), using a large dataset of the Spanish Social Security, analyzes wage losses of permanent and temporary workers due to displacement during massive layoffs in Spain. Her findings suggest that the former suffer larger and more persistent wage losses than the latter, a result which is interpreted as firm specific human capital being more important for workers under permanent contracts than for those under fixed-term contracts.
Finally, as regards the effect of dual EPL on effort, the closest paper in spirit to ours is Engellandt and Riphahn (2005), who find evidence that Swiss temporary workers undertake more unpaid overtime work than permanent workers. Yet, as will be discussed further below, this seemingly opposite results to ours could be rationalized within our analytical framework. The insight is that, being the EPL gap and the share of temporary workers in Switzerland (these authors report 3.4% on average during 1996–2001) much lower than in Spain, Swiss firms often use temporary contracts as a screening device, rather than as a (“dead end”) cost-reduction device. As a result, Swiss temporary workers enjoy much larger conversion rates (about 26% per year) than in Spain and hence get incentivized to exert higher effort.
3 A simple model of decisions in a dual labour market
Before moving to the details of the model, it is important to clarify that, in our setup, firms do not use temporary contracts (TC, henceforth) as a pure screening device (indeed, workers are assumed to be ex-ante equally skilled).Footnote 5 This is not that restrictive since the probation period for workers under TCs in Spain is much shorter (typically 1 or 2 months) than the standard duration of these contracts (2 or 3 years), which are kept alive until their termination (see Cahuc et al. 2012). Firms use TCs to hire workers because they yield a larger initial surplus than permanent contracts (PC, hereafter) due to their much less stringent EPL. The key feature of the TC considered here is that it has a fixed-term duration and that it cannot be renewed using the same worker. Hence, upon expiration of a TC, the firm faces the decision of either non renewal or conversion into a PC.
Our characterization of TC builds upon ideas reminiscent of promotion tournaments in setups where effort is not contractible. In addition to wages, firms have another instrument available to improve temporary workers’ performance when their incentives are not aligned. This instrument is the fraction of temporary workers that employers upgrade from a set of eligible candidates (i.e., the temp-to-perm conversion rate), subject to workers’ incentive and participation constraints. In particular, the (endogenously determined) upgrading probability is modeled as the product of two probabilities: p(e, \(e_{a})R\). The first term, p(e, \(e_{a})\), is the hazard rate at which a temporary worker becomes eligible for promotion, which depends on her effort (e) relative to the average effort exerted by co-workers (\(e_{a}\)). The second term, \(R\in [0,\) 1], is the conversion rate set by the employer among the set of eligible candidates holding TC.
Moreover, the tournament we consider here differs from a pure rank tournament, where individuals get ranked and the top one gets a predetermined prize (see Lazear and Rosen 1981). The main difference is that this prize cannot be guaranteed in our setup because the employer may abstain from promoting any temporary worker, and instead continue using TC in sequence. In other words, even if the worker exerts maximal effort, her TC might not be upgraded because the much more stringent EPL for PC may prevent any promotion. Hence, the conventional result in rank tournaments that a lower value of R (to be interpreted here as a larger prize) induces greater effort among all workers does not necessarily hold here.Footnote 6
For convenience, effort is assumed to be bounded and normalized such that \( e\in [0,1]\). Temporary (subscript T) and permanent (subscript P) workers’ effort are denoted as \(e_{T}\) and \(e_{P},\) respectively. Denoting the first (second) partial derivatives of \(p(\cdot ,\cdot )\) with respect to (w.r.t., hereafter) \(e_{T}\) and \(e_{a}\) by \(p_{1}\) and \(p_{2}\) (\(p_{11}\) and \(p_{22}\)), respectively, the hazard rate is assumed to satisfy the following properties: (i) \(p_{1}(e_{T},e_{a})>0\) and \(p_{2}(e_{T},e_{a})<0\), (ii) \( p_{11}(e_{T},e_{a})<0\) and \(p_{22}(e_{T},e_{a})>0,\) (iii) \(p(e_{a},e_{a})<1\) for \(e_{a}<1\), (iv) \(p(0,e_{a})=0,\) and (v) \(p(1,1)=1\). Thus, \(p(\cdot ,\cdot )\) is increasing and concave on \(e_{T}\), and decreasing and convex on \(e_{a}.\) In a symmetric equilibrium with \(e_{T}=e_{a}\), which is the one considered in the sequel, the hazard rate is less than unity if \(e_{T}<1,\) whereas it equals unity if \(e_{T}=1\). For illustrative purposes, we will consider below the specific functional form \(p(e_{T},e_{a})=e_{T}^{\lambda }e_{a}^{-\kappa },\) with \(\lambda ,\kappa \in (0,1)\) and \(\lambda >\kappa \), that satisfies all the previous properties.Footnote 7
Workers under TC negotiate a wage schedule with the firm, \(w_{T}(e_{T})\), which depends on their level of effort, \(e_{T}\). Their instantaneous utility is of the form \(U=w_{T}(e_{T})-\frac{\phi }{2}e_{T}^{2}\), where \(\phi >0\) captures an increasing and convex cost of exerting effort. The difference between PC and TC is not only that the former are open-ended contracts but also that they are subject to a much more stringent EPL. To simplify the analysis, we assume that PC entail a firing cost \(F>0\) while TC contracts entail none. This allows us to interpret F directly as the firing-costs gap (\(=F-0\)), which should not to be confused with the overall level of EPL since temporary workers enjoy none. Workers under a PC receive a wage, \(w_{P}(e_{P})\), and exert a level of effort, \( e_{P}\). In contrast to \(e_{T}\), \(e_{P}\) happens to be contractible and is determined by Nash bargaining jointly with the wage.Footnote 8 Furthermore, unlike temporary jobs which are kept alive until their termination date, permanent jobs are subject to an exogenous destruction rate, denoted as \(\delta \).
Finally, the remaining notation to be used in the sequel is as follows. Let \( V^{i}\) and \(\Pi ^{i},\) for \(i=\{T,P\},\) be the asset values of a worker with contract i and of a firm with job i, respectively. Also \({\overline{V}} ^{u} \) and \({\overline{H}}\) denote the asset values for the outside options of workers being unemployed and of firms opening a vacancy (always consisting of a temporary job), respectively. To highlight in a tractable way the incentives’ channel explored here, we simplify the analysis by taking both of these asset values to be exogenously given. Thus, our approach is a partial equilibrium one where we focus on the short-term effects of changes in F on the endogenous variables in the model (effort, conversion rates, wages, and training). Rents to be shared arise in this setup because we consider those cases where the asset values of workers being employed and firms opening vacancies exceed the given values of their outside options.
To explain concisely the mechanism stressed here, we start by laying out a simplified version of the model which focuses exclusively on workers’ effort decisions. Training decisions by employers will be incorporated later.
3.1 Temporary jobs
3.1.1 First-order conditions
Temporary workers decide how much effort to exert, \(e_{T}\), taking as given both the wage schedule, \(w_{T}(e_{T}),\) and the firm’s choice of the conversion rate, R. These workers maximize their discounted utility, given by,
For an interior solution, the first-order condition (f.o.c.) to this problem is given by,
where \(w_{T}^{\prime }(e_{T})\) denotes the first derivative of \(w_{T}(e_{T})\) . For given values of R, the RHS of (3.2) captures the marginal cost to the worker of exerting additional effort, while the two terms in the LHS represent the worker’s marginal benefits. These involve a wage rise and a higher upgrading probability. Notice that, since \(\beta p_{1}(e_{T},e_{a})R[V^{P}-{\overline{V}}^{u}]>0\), (3.2) implies that the wage rise is lower than the marginal disutility of effort (\(w_{T}^{\prime }(e_{T})<\phi e_{T}\)) because the employer can also use the conversion rate to incentivize temporary worker’s effort. Thus, Eq. (3.2) defines the locus of the optimal level of effort chosen by the worker, taking as given the conversion rate selected by the employer. Once \(w_{T}(e_{T})\) is defined below, it will be shown that the fact that \(w_{T}^{\prime }(e_{T})<\phi e_{T} \), together with the concavity of \(p(e_{T},e_{a})\) on \(e_{T}\), ensures the second-order condition (s.o.c.) for the maximization of \(V^{T}\) w.r.t. \( e_{T} \).
Next, given that effort by temporary workers is assumed not to be contractible, the firm chooses \(e_{T}\) and R subject to the worker’s participation and incentive constraints, denoted in short as PAC and INC, respectively. Since INC is given by (3.2), the firm chooses the point in this locus that maximizes the value of a filled job. Then, the firm’s optimization problem becomes,
where \(f(e_{T})\) is the amount of goods produced by the worker, such that \( f^{\prime }(e_{T})>0,\) \(f^{\prime \prime }(e_{T})<0\). For simplicity, this production function is taken to be Cobb-Douglas (CD): \(f(e_{T})=e_{T}^{ \alpha },\) with \(0<\alpha <1\). Under the assumed hazard function, replacing (3.5) into (3.3) and restricting attention to interior solutions leads to the following f.o.c.,Footnote 9
where \(D=\) \((\Pi ^{P}-{\overline{H}})/(V^{P}-{\overline{V}}^{u})\) is the ratio in equilibrium of the (net) asset values of firms and workers in permanent jobs which, as will be shown below, depends on the firing-costs gap, F. Hence, the optimal values of \(e_{T}\) and R can be obtained recursively: (i) first, equation (3.6) can be solved for \(e_{T},\) once the value of D is plugged in, and (ii) next, R is determined from (3.5).
The wage schedule. The firm and the worker in a temporary job negotiate the wage schedule through Nash bargaining. With \(\gamma _{T}\in (0,1)\) denoting the worker’s bargaining power, the wage paid to a temporary worker exerting effort \(e_{T}\) becomes,
3.1.2 Second-order conditions
The next step is to check the s.o.c. for an interior maximum in the worker’s and employer’s optimization problems. To do so, we use (3.7) to rewrite INC and the f.o.c. in (3.6) as follows,
As regards the worker’s optimization problem, both terms in the LHS of (3.8) are decreasing in \(e_{T}.\) Thus the objective function in (3.1) is strictly concave on \(e_{T}\) ensuring the s.o.c. for an interior solution.
However, this may not be the case in the employer’s optimization problem in (3.3). In effect, it is easy to check that the first term in the LHS of (3.9) is decreasing while the second term is increasing in \(e_{T}.\) Hence, the first part of the objective function in (3.3) is concave while the second one is convex. As a result, the s.o.c. cannot be ensured. In Appendix A we derive a condition (labeled as concavity condition or CC in short) which ensures the strict concavity of \(\Pi ^{T}\) and the existence of interior solutions for \(e_{T}\) and R in (3.3).
Concavity condition (CC). The optimization problem (3.3)–(3.5) has interior maxima in \(e_{T}\) and R when the following condition holds,
Remark 1
For given values of D and \(\alpha \), notice that CC requires sufficiently low values of the temporary workers’ bargaining power, \(\gamma _{T},\) and/or high values of \(\lambda \), that is, the elasticity of \(p(\cdot ,\cdot )\) w.r.t. \(e_{T}\).Footnote 10 The insight for these parameter bounds comes from the opposite signs of the two terms that arise from differentiating the f.o.c. (3.9) w.r.t. \(e_{T}\), namely, \((1-\gamma _{T})[f^{\prime \prime }(e_{T})-\phi ]+\gamma _{T}(D/\lambda )\left[ 2\phi -\alpha f^{\prime \prime }(e_{T})\right] \). The overall sign of this expression is ambiguous because \( [f^{\prime \prime }(e_{T})-\phi ]\) is negative while \(\left[ 2\phi -\alpha f^{\prime \prime }(e_{T})\right] \) is positive. The role of CC is to increase (reduce) the weight of the first (second) term ensuring that the overall sign of the sum of the two terms becomes negative, as required by the s.o.c.
3.1.3 The relationship between effort and conversion rate
Having replaced (3.7) into (3.2), differentiation of INC yields,
from where it is straightforward to check that \(de_{T}/dR>0.\) In particular, using the chosen functional forms for \(p(e_{T},e_{a})\) and \(f(e_{T}),\) in a symmetric equilibrium with \(e_{T}=e_{a}\), we have that,
Thus, for a given value of F, our assumptions imply that firms’ temp-to-perm conversion rates and temporary workers’ effort are unambiguously positively related.
3.2 Permanent jobs
As mentioned earlier, workers under PC are entitled to firing costs \(F>0\) if dismissed. Given the higher job stability of these workers, we assume that their level of effort, \(e_{P},\) is contractible (see below). Moreover, to capture the fact that these are “better” jobs than temporary jobs, we assume that workers under PC produce an amount of output given by \(z(F)f(e_{P}),\) where \(z(F)>1\) is a technology parameter representing higher productivity in these jobs.Footnote 11 The assumption that z depends on F is a convenient one to model changes in permanent workers’ effort when F changes. It captures the two views discussed in the Introduction about the effects of overall EPL strictness on technical efficiency. On the one hand, if the stringency of dismissal laws induces firms to choose better technologies (due to the higher stability of their workers), then \(z^{\prime }(F)>0\). On the other hand, if firms were to choose less advanced technologies (due to the lower mobility of workers), then \(z^{\prime }(F)<0\) . Under these assumptions, the corresponding asset values to firms and workers under PC become, respectively,
where \(\delta \in (0,1)\) is an (exogenously given) job destruction rate.
The level of effort and the wage associated to a PC are determined by Nash bargaining, with \(\gamma _{P}\in (0,1)\) denoting permanent workers’ bargaining power, which may differ from \(\gamma _{T}\). Thus, both variables are chosen to maximize the Nash maximand \([V^{P}-({\overline{V}} ^{u}+F)]^{\gamma _{P}}\) \([\Pi ^{P}-({\overline{H}}-F)]^{1-\gamma _{P}}\). This implies that the optimal level of effort satisfies,
and that the sharing rule is,
so that, from (3.12)–(3.15), the wage schedule becomes,
Differentiating (3.14) w.r.t. F, and taking into account that \(f^{\prime \prime }(e_{T})<0,\) it follows that,
Hence, since z(F) and \(e_{P}\) are complements in production, a rise in F increases the effort exerted by workers under PC if firms improve their technology (\(z^{\prime }(F)>0\)), while it decreases their effort otherwise (\( z^{\prime }(F)<0\)).
Finally, using (3.15) leads to the following asset values,Footnote 12
From these two expressions and (3.14), we get that \(\frac{d(\Pi ^{P}- {\overline{H}})}{dF}=\frac{(1-\gamma _{P})[z^{\prime }(F)f(e_{P})]}{1-\beta (1-\delta )}-1\) and \(\frac{d(V^{P}-{\overline{V}}^{u})}{dF}=\frac{\gamma _{P}[z^{\prime }(F)f(e_{P})]}{1-\beta (1-\delta )}+1\). This illustrates how an increase in F affects the previous asset values through two channels. The first one is the direct effect of a rise in F on z(F), which increases (decreases) both asset values when \(z^{\prime }(F)>0\) (\(z^{\prime }(F)\le 0\)). Secondly, there are two opposite effects (\(-1\) and \(+1\)) which are just the outcome of a hold-up problem whereby the worker, once employed under a PC, cannot credibly refrain from exploiting an enhanced bargaining position. Hence, severance pay reduces the employer’s threat point \(( {\overline{H}}-F)\), whilst it increases the worker’ s threat point \((\overline{ V}^{U}+F)\). As a result, the ratio of asset values, \(D(\equiv \frac{\Pi ^{P}- {\overline{H}}}{V^{P}-{\overline{V}}^{U}})\), required to pin down the optimal value of \(e_{T}\) from Eq. (3.6), declines with F when \(z^{\prime }(F)\le 0\), while their relationship remains ambiguous when \(z^{\prime }(F)>0\). These key properties will be used in the next section to analyze the impact of changes in F on \(e_{T}\) and R.
3.3 The effect of a change in the firing-costs gap on effort and conversion rate
To analyze how a change in F affects firms’ and workers’ decisions in temporary jobs, it is convenient to start by examining the response of \( e_{T} \) to this change. To simplify the derivations, let us denote the first and the second term (excluding D) in the LHS of (3.9) by \(h_{1}(e_{T})\) and \(h_{2}(e_{T})\), respectively. Then, totally differentiating the f.o.c. \( h_{1}(e_{T})+h_{2}(e_{T})D=0\) w.r.t. F yields,
It was shown earlier that \(h_{1}(e_{T})<0\) in equilibrium. Moreover, under CC, \([h_{1}^{\prime }(e_{T})+h_{2}^{\prime }(e_{T})D]<0\) since this term is just the s.o.c. for an interior maximum in (3.3). Hence, for \(z^{\prime }(F)\le 0\) it holds that \(de_{T}/dF<0\), whereas for \(z^{\prime }(F)>0\) the sign \(de_{T}/dF\) turns out to be ambiguous.
Next, to find how R responds to a change in F, let us totally differentiate (3.8) w.r.t. F, yielding,
Given the properties of \(p(\cdot ,\cdot ),[V^{P}-{\overline{V}}^{U}]\) and \( f(\cdot ),\) we have that \(dR/dF<0\) if \(z^{\prime }(F)\le 0\), since \( de_{T}/dF<0\). Thus, under CC, an increase in F translates into both lower effort and conversion rate. However, when \(z^{\prime }(F)>0\), such a change in F has ambiguous effects on both variables. The following proposition summarizes this discussion.
Proposition 1
Under the concavity condition (CC) in (3.10), an exogenous increase in the firing-cost gap F between permanent and temporary workers leads to: (i) a reduction in both the optimal temp-to-perm conversion rate chosen by firms and the optimal level of effort exerted by temporary workers if permanent workers respond to a change in the gap by exerting less or equal effort (\( z^{\prime }(F)\le 0\)), and (ii) ambiguous effects on both variables if permanent workers exert higher effort (\(z^{\prime }(F)>0\)).
Remark 2
The insight for the above results is as follows. As F increases, the conversion rate decreases when \(z^{\prime }(F)\le 0\) because the value to the firm of having a worker with a PC is unambiguously lower. A fall in the conversion rate decreases worker’s effort because it reduces its payoff in terms of the option value of being upgraded. However, there is a counteracting effect since a higher gap increases the value of a PC to the worker. This increases the payoff from effort and therefore tends to increase it. Under CC, the first effect dominates the second effect. However, when \(z^{\prime }(F)>0\), the value to the firm of a permanent job could go up or down as a result of a rise in F, making ambiguous the responses of both variables.
Example 1
In order to illustrate the effects of an increase in the firing-costs gap (F) on the conversion rate (R) and temporary workers’ effort (\(e_{T}\)), we present numerical results for a simple economy with \( z^{\prime }(F)=0\) and the following parameter values (which satisfy the restrictions required for interior solutions and for the profitability of permanent jobs): \(A=1.2,\alpha =0.4,\phi =1,\lambda =0.6,\kappa =0.3,\beta =0.96,\delta =0.1,(1-\beta ){\overline{V}}^{u}=0.3,{\overline{H}}=0,\) \(\gamma _{P}=0.7,\gamma _{T}=0.3,\) \(z(F)=1.4\) and \(e_{P}=0.76\).
Solutions for the endogenous variables using two different values of F (=0.55 and 0.66) are provided in Table 1.
As can be observed, an increase in F from 0.55 to 0.60 reduces \(e_{T}\) from 0.70 to 0.67, as well as R which declines from \(8.64\%\) to \(6.80\%\). Note that the value of a temporary job to the firm (\(\Pi ^{T}\)) is higher than the value of a permanent job (\(\Pi ^{P}\)), thus rationalizing why all new jobs are created under TC.
3.4 Adding paid-for-training to the model
We next extend the previous analysis to incorporate firms’ decisions on the amount of paid–for-training provided to temporary workers. Our simplifying assumption here is that this training provides specific human capital which only increases workers’ productivity with one period lag, that is, when they become permanent workers. Otherwise, the worker loses the received firm-specific training. Firms choose the amount of training, denoted by \( \tau \), facing a cost, \(C(\tau ),\) which is assumed to be linear, i.e., \( C(\tau )=c\tau \), with \(c>0\). Thus, while output in a temporary job, \( f(e_{T}),\) remains the same as in the model ignoring training, output in a permanent job becomes now \(g(\tau )z(F)f(e_{P}),\) with \(g^{\prime }>0\) and \( g^{\prime \prime }<0.\)
Therefore, in this case, the value of a permanent job to the firm, denoted as \(\Pi ^{P}\)(\(\tau )\) is given by,
Using the same Nash sharing rule as in (3.14), we get ,
The analysis proceeds as in the previous section, noticing that the new wage schedule for workers under TC now depends on both \(e_{T}\) and \(\tau \). Consequently, temporary workers’ utility maximization problem remains the same as in the model without training, while the firm’s profit maximization problem becomes now,
where \(w_{T,1}(e,\tau )\) denotes the first derivative of \(w_{T}(e,\tau )\) (shown below) w.r.t. e. The f.o.c. of the optimization problems of firms a workers under TC become,
where \(D(\tau )=[\Pi ^{P}(\tau )-H]/[V^{T}(\tau )-V^{u}],\) \(D^{\prime }(\tau )\) is its first derivative, and \(w_{T,11}(e_{T},\tau )\) is the second derivative of \(w_{T}(e_{T},\tau )\) w.r.t. e. Notice that (3.28) and (3.29) determine the optimal values of \(e_{T}\) and \(\tau \), while INC in (3.27) determines R.
Wage schedules The wages paid to a temporary worker exerting effort \(e_{T}\) and receiving paid-for- training, \(\tau \), and to a permanent worker exerting effort \(e_{P}\) become now, respectively,
Since (3.28) has the same form as (3.9), interior maxima exist under CC (i.e., for sufficiently low values of \(\gamma _{T}\) and high values of \( \lambda \)). With the same notation as in (3.20), we can use (3.30)–(3.31) to rewrite (3.28) as \(h_{1}(e_{T})+h_{2}(e_{T})D(\tau )=0\), where \( h_{1}^{\prime }(e_{T})+h_{2}^{\prime }(e_{T})D(\tau )<0\), \(h_{1}(e_{T})<0\) and \(D^{\prime }(\tau )>0.\) Then, differentiation of this expression w.r.t. \( e_{T}\) and \(\tau \) (for a given value of F) yields,
This signifies that, in equilibrium, effort and training behave as complements. Next, using the same reasoning as in Proposition 1, it is easy to check that when \(z^{\prime }(F)\le 0\), CC leads not only to a fall of \(e_{T}\) and R when F goes up but also to a fall in \(\tau \). However, when \(z^{\prime }(F)>0\), the response of the three variables to a rise in F is ambiguous. These results can be summarized as follows.
Proposition 2
When firms are allowed to choose the amount of paid-for-training provided to temporary workers, under the condition in (3.10), an exogenous increase in the firing-cost gap F between permanent and temporary workers leads to (i) lower training, effort and temp-to-perm conversion rate if permanent workers react to the change in the gap by exerting less or equal effort (\( z^{\prime }(F)\le 0\)), and (ii) ambiguous effects on these three variables if permanent workers exert higher effort (\(z^{\prime }(F)>0\)).
Example 2
The results above can be illustrated by simulating the effects of an increase in the firing-costs gap on the endogenous variables for an economy with the same parameters as in Example 1, but where now firms are allowed to provide training (\(\tau \)) to temporary workers. It is assumed that \(g(\tau )=C\tau ^{\theta }\), with \( C=1.5\) and \(\theta =0.6\), while \(c=0.04\) in the training cost function. Results are presented in Table 2
As can be observed, a rise in F from 0.55 to 0.60 reduces \(e_{T}\) from 0.7717 to 0.7438, R from \(12.53\%\) to \(10.59\%\) and \(\tau \) from 0.6887 to 0.6427. Note that the fact that \(\Pi ^{P}>\Pi ^{T}\) does not mean that the firm will choose to create new jobs under PC, as \(\Pi ^{T}\) is now the value of a job filled with a worker who has not received training yet, while \(\Pi ^{P}\) is the value of a job filled with a worker who has already been trained.
3.5 From the model to the data
Lacking any direct proxy for workers’ effort and paid-for training in our panel dataset, our indirect strategy is to embed these variables into firms’ TFP, which can then be estimated from the available data on their output and inputs. In particular, it is assumed that each firm has the following constant-returns-to-scale (CRS) Cobb-Douglas (CD) production function,
where Y is final output; A (\(\cdot \) ,\(\cdot )\) is a composite index of TFP which depends on two sets of variables: (i) our variables of interest, effort (\(e_{T}\), \(e_{P}\)) and training (\(\tau \)), collected in vector \( {\mathbf {e}}\), which are assumed to have a contemporaneous impact effect on TFP, and (ii) other determinants of technology choice (such as R&D expenditure, educational characteristics of the workforce, etc.), collected in vector \({\mathbf {z}}\), which are taken as predetermined since, by involving investment decisions on human and IT capital subject to adjustment costs, they are likely to exhibit delayed responses to changes in the dual EPL gap (F); \(L_{P}\) and \(L_{T}\) are total hours of work by each type of workers, while X denotes additional production inputs (i.e., capital and raw materials). In line with the theoretical model, it is assumed that the labour inputs \(L_{T}\) and \(L_{P}\) are substitutes, with different relative productivity captured by parameter \(\vartheta \). Denoting with small letters the logs. of capital ones, (logged) TFP, a, can be computed from the estimation of the parameters of the production function using firm-level data. An important issue to recall is that our estimate of a is constructed such that it does not depend on the composition of inputs in the production function.
Since we are interested in isolating the impact of changes in F on a, via its effect on R and then on \({\mathbf {e}}\), we use an instrumental variables (IV) approach, where a is regressed on R and the predetermined variables in \({\mathbf {z}}\), using F as an IV for R. As stressed before, the underlying mechanism is that exogenous changes in F have an impact effect on R which then translates quickly into changes in a, via \( {\mathbf {e}}\), without affecting \({\mathbf {z}}\) contemporaneously.
From these considerations, our benchmark empirical model of firms’ TFP can be simply expressed as \(a=a(e(R),{\mathbf {z}})\), or \(a=a(R,{\mathbf {z}})\) in short notation, to which a disturbance term capturing unobserved components of TFP should be appended (see Sect. 4.2 for more details). Since \( e_{P} \), \(e_{T}\) and R are endogenously determined and depend on F, our strategy relies on analyzing the impact of three major labour market reforms in Spain (in 1994, 1997 and 2002) which involved relevant regulatory changes in the EPL gap during the available sample period. Given that these were nationwide reforms, our implicit identification strategy to achieve variation at the firm level is as follows. All else equal, an exogenous change in F is likely to affect R differently in each firm, depending on their share of temporary workers (\(tw=L_{T}/(L_{P}+L_{T})\)) the year before the reforms took place, i.e., \(tw_{-1}\). Although, our theoretical model in Sects. 3.1 and 3.2 is one of the a “single vacancy-single worker” type, in reality it seems reasonable to assume that TFP in firms with a high share of TC will exhibit a stronger response to changes in R (induced by nationwide variations in F) than in firms with a low share of TC. The best way to capture this channel is to include an interaction term of R and \( tw_{-1}\) (i.e., \(R*tw_{-1})\) as an additional covariate in the previous model, so that our preferred empirical specification becomes,
Accordingly, the impact effect of changes in R (driven by changes in F) on a differs according to the lagged share \(tw_{-1}\). Notice that, since our estimation approach implies that, once we control for \(\mathbf {z,}\) a does not depend on the composition of labour inputs, \(tw_{-1}\) also becomes a predetermined variable.Footnote 13
4 Data
Our microdata at the firm level come from the Survey on Business Strategies (Encuesta sobre Estrategias Empresariales, ESEE). This is an annual survey on a representative sample of Spanish firms in 18 manufacturing sectors which has the advantage of providing the key variables required to compute TFP and temp-to-perm conversion rates (see below). The available sample period is 1991–2005. Firms were chosen in the base year according to a sampling scheme applied to each industry in the manufacturing sector where weights depend on their size category. While all manufacturing firms with more than 200 employees are surveyed and their participation rate in the survey reaches approximately 70%, smaller firms with 10–200 employees are surveyed according to a random sampling scheme with a participation rate close to 5%.
Another important feature of ESSE is that the initial sampling properties have been maintained throughout all subsequent years. Newly created and exiting firms have been recorded in each year with the same sampling criteria as in the base year. As a result of this entry and exit process, the data set is an unbalanced panel comprising 3,759 firms and 22,292 firm-year observations.
Finally, it is worth noticing that ESEE provides firm-level price indexes to deflate the different components of TFP. This is an important advantage over traditional TFP measures where nominal variables are deflated with industry- level price indexes, which have been criticized because changes in estimated TFP may reflect market power at the industry level rather than genuine differences in efficiency at the firm level (see Syverson 2011). In this sense, our productivity measure is close to the “physical productivity” defined in Foster et al. (2008).
4.1 Temporary work
Table 3 presents the average share of temporary workers, tw, by firm’s size and age. With regard to size, small firms are defined as those with less than 50 employees, while medium-sized and large firms are those with more than 50 but less than 200 employees, and more than 200 employees, respectively. Regarding age, young firms are defined as those which have been operating during less than 5 years since they were opened, while mature firms are those which have been operating for a longer period.
As can be observed, tw exhibits large variability across these categories. In general, small and medium-sized young firms exhibit larger shares of TC perhaps because newer firms are bound to make a more widespread use of flexible TC for precautionary reasons given that they often face a higher probability of failure.
Next, we proceed to describe the computation of both firms’ TFP and conversion rates.
4.2 Measuring TFP
To construct a measure of TFP at the firm level, we use Levinsohn and Petrin’ s (2003, henceforth LP) modification of Olley and Pakes (1996) well-known estimation approach for the parameters of production functions using inputs to control for unobservables.
Rather than simply using cost shares to compute conventional Solow residuals, the reason for adopting LP’s (2003) approach is that, while we allow for deviations of the one-to-one rate of substitution among workers, the payrolls reported by ESEE do not distinguish between wages paid by type of contract (PC and TC). Thus, we estimate \(a_{it}\) for firm i in period t as the residual in,
where y is logged final output; m and k are respectively logged materials and capital (weighted by its logged annual average capacity utilization rate reported by each firm). CRS imply that \(\alpha _{L}=1-\alpha _{m}-\alpha _{k}\).
To estimate the parameters in the production function, we assume that \( a_{it} \) is the sum of two unobserved components,
where \(\omega _{it}\) represents a firm-specific component which is known to the firm, and \(\upsilon _{it}\) is an idiosyncratic component unknown to the firm, but with no impact on firm’s decisions. The endogeneity problem in estimating the production function by OLS arises from the correlation of \( \omega _{it}\) with the input choices. Olley and Pakes (1996) consider k as a quasi-fixed input while the other inputs are more freely adjustable. As a result, their approach relies upon the assumption that investment, i, installed in period t only becomes productive at \(t+1\), so that \( i_{it}=i(\omega _{it},k_{it})\) can be inverted to yield \(\omega _{it}=\omega _{t}(i_{it},k_{it})\), assuming increasing monotonicity of \(i_{it\text { }}\) in \(\omega _{it}\). By contrast, instead of using the investment demand function, LP (2003) advocate to invert the materials’ demand function \( m_{it}=m(\omega _{it},k_{it})\) to obtain \(\omega _{it}=\omega _{t}(m_{it},k_{it})\), also under monotonicity plus some additional assumptions.Footnote 14 The justification for this alternative choice is that, while most firms (99.3% in our sample) report positive expenditure on materials every year, a much lower proportion (about 52%) undertake investment every year. Truncating about half of the sample would imply a severe efficiency loss, and hence our choice of LP’ s (2003) approach. Appendix B provides further details of this estimation approach.
In Table 4 we report the estimates of the parameters in each of the 18 industries considered in ESEE, where CRS is imposed in all instances since the null hypothesis that the sum of the input elasticities equals unity cannot be rejected at conventional significance levels. The similarity of the number of firms in each industry (N) and those which buy materials every year in the sample (\(N_{a}\)) illustrates the advantages of using LP’s (2003) approach. Overall, the coefficients on labour, capital and materials are in line with those available in the literature using data on Spanish firms (see, e.g., Aguirregabiría and Alonso-Borrego 2014, and González and Miles 2012). As expected, the estimate of parameter \(\vartheta \) is always above unity.
4.3 Conversion rates
Our dataset provides direct information on the types of contracts used by firms in each year of the sample, from which conversion rates at the firm level can be retrieved. In effect, we have data on the number of permanent and temporary workers in firm i at period t (\(L_{P,it}\) and \(L_{T,it}\), respectively), as well as on the number of PC which have been signed in each year by workers who previously held TC in the firm and by those directly hired under PC. The former are denoted as \(L_{TP,it\text { }}\) where the subscript “TP” signifies conversion from “T” to “P” . Using this information, we compute annual conversion rates as \(R_{it}=L_{TP,it}\) \( /L_{T,it-1}.\) On average, it yields an estimate of R equal to 0.118, namely, about \(12\%\) of temporary workers get PC contracts when their TC expire. Interestingly, this value is quite close to the conversion rates reported in other available studies in Spain on this topic which use information from aggregate labour surveys and whose estimates range between 10% and 15% (see Alba-Ramirez 1994; Amuedo-Dorantes 2000, 2001, and Güell and Petrongolo 2007).
Figure 2 displays the histogram of term-to-perm conversion rates in our sample. About 85% of firms exhibit conversion rates between 0% and 20%, and only 3% of firms exhibit rates above 50%. Industries like “Vehicles and motors” , “Textiles and apparels” and “Paper and printing products” are the ones with higher conversion rates whilst other industries, like “Food and tobacco” , exhibit very low rates. In sum, this evidence shows that, in general, Spanish manufacturing firms have been rather reluctant to offer contract conversions, most plausibly due to the high EPL gap between permanent and temporary workers.
Finally, though not reported for the sake of brevity, we also find that the fraction of the annual inflows of new hires under a PC (denoted as \( L_{NP,it})\) in the existing workforce, \(L_{NP,it}/L_{it-1},\) is always rather low, with an annual average 3.5%. Since these are the only permanent workers who would be affected on impact by the EPL reforms, these small percentages provide some support to our conjecture that changes in F mainly affect TFP on impact through temporary worker’s reactions.
5 Empirical strategy
Following the discussion above, to estimate the impact effect of changes in the EPL gap on firms’ TFP, via its effect on conversion rates, we regress our measure of TFP based on LP’s (2003) estimation approach (denoted hereafter as \({\widetilde{a}}\)), on R and \(R*tw_{-1\text {, }}\)plus the set of additional predetermined controls, \(\mathbf {z,}\) in the following dynamic panel data model at the firm-year level,
where \(\eta _{i}\) and \(\xi _{t}\) are firm fixed and time effects, respectively, while \(\eta _{I}t\) is the interaction of industry fixed effects (there are 18 industries) with a linear trend, to capture differences in the trending patterns of TFP across industries, and \(v_{it}\) is an i.i.d. error term. Our coefficients of interest are \(\beta \) and \(\psi \) which are expected to be positive, because a higher conversion rate (driven a reduction in F) leads to higher effort/ training, and the more so in firms with a higher share of temporary workers in the previous period. As mentioned earlier, vector \({\mathbf {z}}\) contains a set of controls which are predetermined. Those variables in \({\mathbf {z}}\) which are likely to capture slow changes in technology adoption are introduced with one lag (i.e., R&D expenditure, the proportion of employees with a college degree, and the proportions of foreign capital and public capital), while the remaining components of \({\mathbf {z}}\) (e.g., size, age and its square, a dummy variable for incorporated companies, two indicators on whether the firm perceives it operates in an expansive or recessive market, firm’ s entry, exit, merger and scission dummies) are not lagged.Footnote 15 Lastly, since TFP levels are highly persistent, a lagged the dependent variable is also included in the regression.Footnote 16 Detailed definitions of all these variables are provided in Appendix C.
Table 5 contains descriptive statistics of the variables used in (5.1). As can be observed, there is a large and persistent slowdown in firms’ TFP growth since the late 1990s, leading to an even negative growth rate in 2005. This path is somewhat similar to the one discussed in the Introduction for the overall market economy, although much less dramatic than in other sectors - like construction, distribution, personal and social services- where TFP growth became negative since the mid-1990s (see Escribá and Murgui 2009). It is also noteworthy that the average share of temporary workers in our sample is about 23%. This is around 10 pp. lower than the aggregate share for the whole Spanish economy because seasonal activities associated to the manufacturing industry are much less prevalent than in the services and construction sectors.
5.1 Three EPL reforms
Following the major EPL reform in 1984, there have been three important reforms during our available sample period 1991–2005. As stressed earlier, a key feature of these reforms is that changes in EPL regarding permanent workers only applied to newcomers. Thus, the EPL rights of employees under PC before the implementation of the reforms remained unaltered. On the contrary, changes in EPL affecting TC applied immediately to all temporary workers.
The first of these reforms took place in may 1994 (Law 10/94) when the conditions for “fair” dismissals of workers under PC were relaxed, while those concerning the use of TC became more restrictive. Regarding the former, fair dismissals—involving redundancy pay of 20 days’ wages per year of seniority (days) with a maximum of 12 months against 45 days with a maximum of 42 months of wages for “unfair” dismissals—that could only be used for economic reasons, also qualified for organizational and technological reasons. As for the latter, the most popular TC, i.e., the so-called contrato de fomento (with a maximum duration of 3 years) was abolished, except for some disadvantaged groups of workers. Overall, we interpret this reform as lowering the EPL gap, F, through a less stringent EPL for PC and a more stringent EPL for TC.
The next reform was implemented in may 1997 (Law Decrees 8 and 9/97) reducing the above-mentioned mandatory redundancy pay in case of “unfair” dismissals to 33 days with a maximum of 24 months of wages for most new hires, with the exception of prime-age workers (aged 30-44 years old) whose unemployment spells were below one year. In parallel, a new severance payment of 8 days, instead of no firing cost, was introduced for temporary workers whose contracts were not renewed and significant rebates of social security contributions were also approved for conversions or direct hires under the new PC (see Dolado et al. 2002).Footnote 17 Thus, as before, we interpret this reform as one where F declined.
Finally, the main feature of the reform in December 2002 (Law 45/02) was the abolition of the firm’s obligation to pay interim wages when dismissed workers appealed to labour courts, as long as the firm acknowledged the dismissal to be unfair and deposited the highest severance pay (45 days) in court two days before the dismissal. Although, in principle, is arguable whether this reform meant a reduction in F, there is evidence that, in order to avoid lengthy court procedures, most employers ended up paying much higher firing costs than the statutory ones under “fair” dismissals (Bentolila et al. 2012). Thus, in contrast to the two previous reforms, we interpret this reform as one where F increased.
5.1.1 Reform-based instruments
In line with the previous discussion, we use each of these reforms separately as a source of exogenous changes in the EPL gap. The use of the LP ’s (2003) approach when estimating TFP ensures that changes in F would subsequently affect R without a direct impact on \({\widetilde{a}}\), i.e., fulfilling the required exclusion properties for a valid IV. We construct three step dummy variables, denoted as FS (\(S=1,2,3\)), which take the value 1 from the year after the implementation of the reforms (1995, 1998, and 2003, respectively) until the year of implementation of the next reform (F3 goes until 2005, the end of our sample), and 0 otherwise.
Regarding the covariates \(R_{it}\) and \(R_{it}*tw_{i,t-1}\) in Eq. (5.1), they are instrumented using the FS dummies directly as well as their interactions with lagged temporary work shares, on top of other conventional IVs (appropriate lags of the levels and first differences of dependent variable and other predetermined controls) in dynamic panel data estimation. As for the rates of temporary work used in the interacted IVs, we have chosen the one-period lags of the average values of these rates in each of the 72 cells of firms which result from combining industry (18), size (2) and age (2) categories. This aggregate share is labeled as \( tw_{c,t-1}\) and its interactions with the FS dummies are denoted respectively as \(FS_{c,t-1}\), (\(S=1,2,3\)) where the subscript c stands for cell.Footnote 18 Hence, these IVs have variation both across cells and over time, as opposed to the nationwide FS dummies. Also, since we are also controlling for firm’s size, our thought experiment relies on obtaining variation from the comparison of the effects of the reforms on firms with similar size but rather different shares of temporary workers.
5.2 Estimation method
Since the dependent variable in (5.1), \({\widetilde{a}}_{it},\) could be highly persistent, our fixed-effects estimation method relies on Blundell and Bond (1998) System-GMM approach (Sys-GMM hereafter). This involves the estimation of a system of two simultaneous equations, one in levels (with lagged first differences of the regressors as instruments) and the other in first differences (with lagged levels as instruments). As IVs, we use the three EPL reform dummies and their interactions with grouped shares of temporary work, besides the remaining variables in (5.1) appropriately lagged (\(t-2\), and earlier, in the first-differenced equations and first differences dated at \(t-1\) in the levels equations).
As shown in columns [1] and [2] of Table 6, the choice of the three FS dummies and the \(FS_{c,t-1}\) interaction terms as our key IVs for \(R_{it}\) and \(R_{it}*tw_{i,t-1}\)is seemingly validated by the relatively high partial \(R^{2}\)’s (0.35 and 0.37) obtained in the first-stage OLS regressions of these two variables on the two instruments and the remaining IVs in (5.1). In particular, we find that the estimated coefficients on FS and \(FS_{c,t-1}\) turn out to be strongly significant. Moreover, while the estimates on the first two FS dummies in the regression for \(R_{it}\) are positive (in line with our interpretation of the 1994 and 1997 reforms as ones where F declined), the third one exhibits a smaller negative sign (indicating that F increased as a result of the 2002 reform).
These results are supported by the evidence shown in the scatter plots displayed in Fig. 3, where conversion rates the year before and after each of the three reforms are depicted, together with the 45 degree line, for each of the 72 cells defined above. Conversion rates increase after the first two reforms, and decline after the last one.Footnote 19 Finally, as a robustness check on our identification strategy, we also provide a similar scatter plot in Fig. 4 for a placebo reform taking place in 1999, namely, a year when there was no change in EPL regulations. As can be inspected, the observations are neither above the 45 degree line (as in the first two reforms) nor below it (as in the last reform).Footnote 20
5.3 Empirical results
Table 7 reports results for the regression model in (5.1). First, as a benchmark for the Sys-GMM estimates, column [1] reports Within-group estimates. Secondly, column [2] presents the Sys-GMM results using the weighting matrix discussed in Blundell and Bond (1998). To test for the validity of the overall overidentifying restrictions we use a Sargan test statistic based on the minimized value of the GMM criterion for the Sys-GMM estimator. Moreover, since the moment condition used in the first-differenced restrictions are a subset of those used by Sys-GMM, we also report a Difference (Dif) Sargan test based on the difference between the two standard Sargan tests (one for Sys-GMM and another for GMM in first differences) as a more specific check for the validity of these extra moment conditions. We report the p-values of obtained for these tests, which have chi-squared asymptotic distributions. Finally, p-values of m1 and m2 tests for first-order and second-order serial correlation in the first-differenced residuals, asymptotically distributed as N(0, 1), are also reported at the bottom of Table 7. As can be observed, neither the Sargan test nor the Dif-Sargan test reject the overall and extra overidentifying restrictions at the 10% level, pointing out that the mean-stationarity assumption required for consistency of the Sys-GMM approach is not rejected.Footnote 21 In addition, the rejection outcome of the m1 test and the non-rejection of the m2 test jointly indicate that the the (level) disturbance term in (5.1) is not serially correlated, so that the chosen lag lengths for IVs are seemingly correct.
The main findings in Table 7 estimates are as follows. First, the within-group estimated coefficients on the conversion rate and its interaction with the lagged share of temporary work are larger than the corresponding Sys-GMM estimates. This result indicates that the within-group estimates of the coefficients of interest are likely to be upward biased since they are also capturing the reverse causality going from higher TFP to higher conversion rates. Second, as expected, persistence is lower under Sys-GMM. Third, the estimated SYS-GMM coefficients on \(R_{it}\) and \( R_{it}*tw_{i,t-1}\) in column [2] are positive and statistically significant: 0.062 (t-ratio: 2.24) and 0.064 (t-ratio: 2.48), respectively. This is in line with our theoretical prediction on the relationship between TFP and conversion rates. For example, according to these estimates, a rise of 10 pp. in the conversion rate leads TFP to increase by 0.65 pp. in TFP in firms where the share of temporary workers is 5%, while the rise in TFP reaches 0.81 pp. in firms where that share reaches 30%.
Recall that the previous interpretation of the results exclusively in terms of the responses of temporary workers to changes in the EPL gap only holds under on the assumption that permanent workers hardly change their effort/training following such changes in F. As argued earlier, this assumption seems plausible due to the non-retroactive nature of the EPL reforms for this type of workers. Yet, it could be argued that this might not be the case if a currently employed worker under a PC is sufficiently forward looking to anticipate that, in case of being dismissed, the new regulation will apply when starting a new employment spell. This might affect both their effort/training and the total surplus of ongoing permanent matches. Hence, the variation in TFP which was previously attributed to changes in the behaviour of temporary workers could also be due to changes in the behaviour of permanent workers. To assess how relevant is this possibility, we run similar Sys-GMM regressions as in column [2] of Table 7 using this time three different subsamples of firms defined by the terciles of the distribution of their (average) share of temporary work (tw). The first subsample corresponds to the top tercile (firm with \(tw>\) 38.6%), the second subsample to the middle decile (14.3.%\(<tw<\)38.6%) and third subsample to the bottom decile (\(tw<\)14.3%). If our mechanism based on temporary workers’ reactions is relevant, we should expect the estimates of the impact of F on \({\widetilde{a}},\) via R, to be declining across these subsamples. This is so since temporary work in the first subsample of firms is relatively more abundant (i.e., they exhibit a higher share of TC) than in the second subsample, and the same argument applies to a comparison of the second and third subsamples. Conversely, if permanent workers were to respond to changes in F in an opposite way to temporary workers, we should observe stable or increasing estimates across the three subsamples since, for example, firms in the third subsample have a higher share of PC than in the second subsample, and so on.
Table 8 presents the results of this exercise. Overall, we can observe a declining pattern in the coefficients on \(R_{it}\) and \(R_{it}\times tw_{c,-1}\) across the three subsamples. Yet, the main finding is that they are fairly similar to those reported in Table 7. We interpret this last result as supporting our interpretation that, at least on impact, most of the reaction of TFP to changes in dual EPL stems from the response of temporary workers.
To gauge how important is the estimated effect of R on TFP, let us take at face value the previous point estimate of 0.077 in column [2] (\(=\!0.062+0.064\times 0.23\), evaluating the temporary work share in \(R_{it}\times tw_{i,t-1}\) at is average value of 23%). Then, we compute the fraction of the slowdown in TFP growth during 1992–2005 (from 1.52% in 1992 to −0.17% in 2005, that is a decrease of 1.67 pp.) which is due, ceteris paribus, to the fall in the conversion rate (from 12.2% in 1992 to 10.3 in 2005, that is, a decrease of 1.9 pp.). Once the dynamic effects of the AR(1) in (5.1) are accounted for, the observed decline in conversion rates explains 0.21 pp. of the 1.67 pp. reduction in TFP growth, namely about 13 percent. Admittedly, this is not a very large effect, since we keep constant all the remaining determinants of TFP, but it is relevant given that temporary workers represent less than one-fourth of all employees in our dataset.
Finally, a pending important issue to address is the explanation of the simultaneous decline in TFP and conversion rates between the late 1990s and the mid-2000s (see Fig. 1 above). Since the only reform during that period which induced a one and for all increase in F was the 2002 one and there are no other reforms increasing F until 2005, our mechanism is not able to explain the decline in TFP growth over that period. Our conjecture is that this reduction has to do with the surge of a housing bubble in Spain and its indirect effect on those manufacturing industries providing inputs to the real estate sector.
To check this interpretation, we report in Table 9 the estimated coefficients on the interaction term \(\eta _{I}t\) for the 18 industries considered in EESE, together with the change in TFP growth in those sectors between 2000–2005 and 1995–2000, and their share of temporary workers in 1998 (at the onset of the real estate boom). As can be observed, the estimated slopes are negative and significant in most of the industries which experienced a decline in TFP growth and had initially higher rates of temporary work. Interestingly, most of these industries- e.g., Basic Metals and Fabricated Products, Plastic and Rubber Products, Textiles and Apparel, etc.- are ancillary to the construction sector. This sector experienced a boom since the early 2000s as a result of the large reduction in real interest rates which Spain enjoyed after joining the euro area. As argued by Bentolila et al. (2012), investors in Spain partly bet rationally for low-value added industries rather than high value-added ones (like ITs) because the rigid PC would have been inadequate to specialize in more innovative industries which require higher labor flexibility to accommodate the higher degree of uncertainty typically associated with producing high value-added goods (Saint-Paul 1997).Footnote 22 Thus, they specialized in sectors where flexible TCs could be amply used. Although more research is due on this issue, this last piece of evidence seemingly points out that dual EPL may not only have had detrimental effects on firms’ TFP but also affected firms’ specialization patterns, leading to misallocation of resources, as recently stressed by Garcia-Santana et al. (2015).
5.3.1 Some evidence on training for permanent workers
Finally, we provide some further evidence as regards our interpretation of the results in Table 7 in terms of temporary workers’ responses to changes in the EPL gap. Lacking direct measures of workers’ effort, we focus exclusively on available information about differences in training incidence by type of worker in the Spanish manufacturing sector, which can be drawn from the eight available annual waves (1994–2001) of the European Community Household Panel (ECHP).Footnote 23
On the basis of the training question “Have you at any time since January (in the previous year) been in training, including part-time or short courses?”, we define training incidence to take the value 1 if the employee received any such training, and 0 otherwise. Our sample contains 2,187 workers, out of which 1,743 hold PC and 444 TC, with an average incidence of training of 14.2% and a share of temporary work of 20.3%, fairly similar to the one in our firm-level dataset. We estimate a static random-effects (RE) probit model for the observed binary dependent variable conditional on a wide set of covariates regarding individuals’ and their firms’ characteristics measured at the wave prior to the year where the training information was elicited.
Our main interest lies in examining how differences in training incidence between permanent and temporary workers (reference category) have changed after the implementation of the 1997 EPL reform, which is the only one included in the available sample period. To do so, besides including an indicator variable for holding a PC among the set of controls, we add an interaction between this indicator and a step dummy variable taking the value 1 from 1999 to 2001.Footnote 24 In line with the notation used earlier, we label this step dummy as F2.
Table 10 (column [1]) reports reduced-form marginal effects of holding a PC contract and its interaction with F2 on worker’s training incidence.Footnote 25 As expected, we find that permanent workers enjoy a higher training probability than temporary workers (i.e., a positive marginal effect of PC in first row) and that this gap went down significantly after the implementation of the 1997 reform (i.e., a negative marginal effect of the interaction term the second row). Since this reform reduced the strictness of EPL for (new) permanent workers and introduced a compensation for TC termination, the drop in the training-incidence gap could be due to a lower provision of training for permanent workers and/or to a higher provision of training for temporary workers. To dig deeper into this issue, we run separate probit models for the subsamples of permanent and temporary workers, and examine the marginal effect of the F2 indicator. As reported in columns [2] and [3] of Table 10, we find that this marginal effect is small and statistically insignificant for permanent workers, while it is positive and statistically significant (at the 10% level) for temporary workers. Thus, this admittedly partial evidence seems to validate our previous interpretation of the 1997 reform as one where the EPL gap went down, leading to higher training incidence among temporary workers and no significant change among permanent workers.
6 Conclusions
Since the early 1990s, Spain has been one the European countries with the highest proportion of temporary work, doubling the average share in the EU-15. In parallel, it has undergone a drastic productivity slowdown since the mid-1990s. In this paper we analyze one of the mechanisms that could explain both stylized features, as well as provide some empirical evidence about its relevance using an unbalanced panel of Spanish manufacturing firms from 1991 to 2005. We build a simple model of a dual labour market, with a large firing-costs gap between permanent and temporary workers. The latter choose their level of effort in order to maximize expected utility while firms choose their temp-to-perm conversion rates and paid-for-training for these workers in order to maximize profits. The main implication is that, under plausible conditions, changes in dual EPL lead to changes in conversion rates which in turn affect the level of effort exerted by temporary workers and the amount of training they receive from firms. Since workers’ effort and training can be thought of as components of TFP, this mechanism provides a channel through which dual EPL could affect TFP.
Our empirical findings imply that, all else equal, up to 13% of the slowdown of TFP growth in Spanish manufacturing firms could be due to how temporary workers reacted to the reduction in conversion rates over our sample period. Since these workers represent about 23% of employees this contribution is relevant. In addition, dual EPL also seems to have had an effect on specialization patterns since the late 1990s. In particular, it seems to have had negative spillover effects upon TFP in several industries which were ancillary to the construction sector.
One shortcoming of our empirical approach is the lack of direct information on workers’ effort and firms’ paid-for training, both embedded in our measure of TFP. Yet, even in the absence of direct information on these variables, the results reported in this paper shed some light on how excessively dual EPL in two-tier labour markets may have detrimental effects on firms’ productivity.
Notes
According to EU KLEMS, a harmonized dataset for multifactor productivity in EU countries, labour productivity and TFP growth in EU-15 fell from 2.7% in 1970–1994 to 1.3% in 1995–2005, whereas the corresponding figures for Spain are 0.7 and 0.3%, respectively (see Escribá and Murgui 2009).
As documented in Sect. 4, we ignore direct hirings of workers under permanent contracts because they have represented less than 5% of all annual hirings during the sample period.
For an analysis of this alternative mechanism, see Michelacci and Pijoan-Mas (2012).
The key result in Lazear and Rosen (1981) is that effort depends on the spread between the top prize and the other lower prizes. As can be seen in their first-order condition given in Eq. (6), where the expected spread is equated to marginal cost of exerting effort, reductions in this spread unambiguously lead to lower effort since the cost of effort is assumed to be an increasing and convex function of effort.
Similar qualitative results are obtained for other functional forms, like e.g., \(p(e_{T},e_{a})=\frac{1-\exp (-\lambda e_{T})}{1-\exp (-\lambda )}/ \frac{1-\exp (-\kappa e_{a})}{1-\exp (-\kappa )}\), with \(e_{T}\) \(\in \) [0, 1] , \(\lambda ,\kappa \in (0,1)\) and \(\lambda >\kappa .\)
As mentioned earlier, one way of modelling variable effort by workers under permanent contracts could be by introducing the possibility of shirking in these jobs, as in Güell (2003) and Ichino and Riphahn (2005). We ignore this issue here because, as discussed later on, changes in EPL did not affect on impact a large majority of these workers.
It is assumed that the bargained wage schedule below ensures that PAC in (3.4) holds.
There is abundant evidence that the bargaining power of temporary workers in Spain is quite low since, due to legal obstacles, their union affiliation rates are much lower than that of permanent workers (see., e.g., Dolado et al. 2010).
To ensure that permanent jobs have positive net value we also impose that F is subject to the following (implicit) upper bound condition, \(F\le \frac{ (1-\gamma _{P})[z(F)f(e_{P})-0.5\phi e_{P}-(1-\beta ){\overline{V}}^{U}]}{ 1-\beta (1-\delta )}.\)
As explained in Sect. 5 below, to instrument R we use dummy variables for the three major EPL reforms and their inteactions with lagged temporary work shares at a more aggregate level, which result from combining firms in different industry, size and age categories.
For example, input prices are assumed to be common across firms.
The dummy variables take value 1 in all those periods in which the firm appears in our sample.
Notice that the model in (5.1) can be reparameterized as an error correction model with TFP growth, \(\Delta {\widetilde{a}}_{it}\) as the dependent variable, so that the coefficient on the the lagged dependent variable \( {\widetilde{a}}_{it-1}\) becomes \((\rho -1)<0\). In this fashion we can rationalize the unconditional correlations between TFP growth and conversion rates shown in Fig. 1, but this time as partial correlations.
The rebates ranged from 40 to 60% during the first two years of the new contracts used to hire workers in some targeted groups (youth, long-term unemployed, and women under-represented in some industries).
In principle, the share of temporary work at the firm level, \(tw_{i,t-1}\), could also have been used in the interaction terms since, in line with LP s (2003) estimation approach of \({\widetilde{a}}_{it}\), it is also be a predetermined variable. However, since there could be some doubts about the absence of a direct effect of \(tw_{i,t-1}\) in a given year on a firm’ s TFP in future years, we prefer to use more aggregate shares at the cell level.
A relevant issue is whether some aspects of the reforms were anticipated by firms. If so, their hiring decisions could have been affected before the reforms were implemented. However, the finding that the jumps in conversion rates are rather sizeable after each of the three reforms point outs that that the anticipation effects were not so important.
Though not reported in Table 6, the corresponding interaction tem for this placebo reform is highly insignificant in the firt-stage regressions.
Although not reported in Table 7, in column (2) we also added \(tw_{i,t}\) as an additional covariate in \({\mathbf {z}}\) to check if the share of temporary work directly affects firms’ TFP, beyond its indirect effect through conversion rates. Besides the other IVs, the FS dummies and the cell-level interaction terms provide the two IVs required to instrument R and \( tw_{i,t}\) in the first stage. The resulting estimated coefficient on the latter in the second stage was \(-0.005\) (t-ratio\(=0.83\)), confirming that this share on its own is not relevant to explain firms’ TFP.
See Beaudry et al. (2010) for a somewhat related analysis of the adoption of IT in US cities.
To avoid confounding work-related training with formal vocational training education, our selected subsample of the ECHP includes individuals aged between 25 and 54 who work at least 15 h per week in the manufacturing sector and who are observed in at least two consecutive waves.
Recall that training incidence reported in the 1999 ECHP wave refers to training received in 1998, which corresponds to the year after the implementation of the EPL reform considered here.
Notice that year dummies are also included and that the estimated \(\rho \) in Table 6 is the share of the variance explained by unobserved heterogeneity.
References
Aguirregabiría V, Alonso-Borrego C (2014) Labor contracts and flexibility: evidence from a labor market reform in Spain. Econ Inq 52:930–957
Alba-Ramirez A (1994) Formal training, temporary contracts, productivity and wages in Spain. Oxf Bull Econ Stat 56(2):151–170
Alonso-Borrego C (2010) Firm behaviour, market deregulation and productivity in Spain. Banco de España, Documento de Trabajo 1035
Amuedo-Dorantes C (2000) Work transitions into and out of involuntary temporary employment in a segmented market: evidence from Spain. Ind Labor Relat Rev 53:309–325
Amuedo-Dorantes C (2001) From “temp-to-perm”: promoting permanent employment in Spain. Int J Manpow 22(7):625–647
Autor D, Kerr W, Kugler A (2007) Do employment protection reduce productivity? Evidence from US states. Econ J 117:F189–F217
Bassanini A, Nunziata L, Venn D (2009) Job protection legislation and productivity growth in OECD Countries. Econ Policy 24:349–402
Beaudry P, Doms M, Lewis E (2010) Endogenous sill-bias in technology adoption: city level evidence from the IT revolution. J Polit Econ 118:988–1036
Belot M, Boone J, van Ours J (2007) Welfare effects of employment protection. Economica 74:381–396
Bentolila S, Dolado J, Jimeno JF (2008) “Two-tier Employment Protection Reforms: The Spanish Experience” CES-Ifo-DICE. Journal for International Comparisons 6:49–56
Bentolila S, Cahuc P, Dolado J, Le Barbanchon T (2012) Two-tier labour markets in a deep recession: France vs. Spain. Econ J 122:155–187
Blanchard O, Landier A (2002) The perverse effects of partial labor market reform: fixed duration contracts in France. Econ J 112:214–244
Blundell R, Bond S (1998) Initial conditions and moment restrictions in dynamic panel data models. J Econ 87:115–143
Boeri T, Garibaldi P (2007) Two-tier reforms of employment protection: a honeymoon effect? Econ J 117:357–385
Cahuc P, Postel-Vinay F (2002) Temporary jobs, employment protection and labor market performance. Labour Econ 9:63–91
Cahuc P, Cheron A, Mahlebert F (2012) Explaining the spread of temporary jobs and its impact on labor turnover. CREST (mimeo)
Cappellari L, Dell’ Aringa C, Leonardi M (2012) Temporary employment, job flows and productivity. A tale of two reforms. Econ J 122:188–215
Cingano F, Leonardi M, Messina J, Pica G (2010) Employment protection legislation, productivity and investment. Evidence from Italy. Econ Policy 25:117–163
De la Rica S, Dolado J, Llorens V (2008) Ceilings or floors? Gender wage gaps by education in Spain. J Popul Econ 21:751–776
Dolado J, Garcia-Serrano C, Jimeno JF (2002) Drawing lessons from the boom of temporary jobs in Spain. Econ J 112(721):270–295
Dolado J, Fergueroso F, Jansen M (2010) El Conflicto entre la Demanda de Flexibilidad Laboral y la Resistencia a la Reforma del Mercado de Trabajo en España. Papeles de Economía Española 124:84–96
Engellandt A, Riphahn RT (2005) Temporary contracts and employee effort. Labour Econ 12:281–299
Escribá J, Murgui MJ (2009) Regional aspects of the productivity slowdown: an analysis of spanish sectorial data from 1980 to 2003, SGPC WP. 2009-03
Foster L, Haltiwanger J, Syverson C (2008) Reallocation, firm turnover, and efficiency: selection on productivity or profitability? Am Econ Rev 98:394–425
Garcia-Santana M, Moral-Benito E, Pijoan-Mas J, Ramos R (2015) Growing like Spain: 1995–2007, CEMFI (mimeo)
Garda P (2012) Wage losses after displacement in Spain: the role of specific human capital, Universitat Pompeu Fabra (mimeo)
González X, Miles D (2012) Labor market rigidities and economic efficiency: evidence from Spain. Labour Econ 20(6):833–845
Güell M (2003) Fixed-term contracts and unemployment: an efficiency wage analysis, CREA Working Paper 18, Universitat Pompeu Fabra
Güell M, Petrongolo B (2007) How binding are legal limits? Transitions from temporary to permanent work in Spain. Labour Econ 14:153–183
Hopenhayn H, Rogerson R (1993) Job turnover and policy evaluation. A general equilibrium analysis. J Polit Econ 101:915–938
Hsieh C, Klenow P (2009) Misallocation and manufacturing TFP in China and India. Q J Econ 124:1403–1448
Ichino A, Riphahn R (2005) The effect of employment protection on worker effort: a comparison of absenteeism during and after probation. J Eur Econ Assoc 3(1):120–143
Jimeno JF, Santos T (2014) The crisis of the Spanish economy. SERIEs 5:125–141
Jimeno JF, Toharia L (1993) The effects of fixed-term employment on wages: theory and evidence from Spain. Investigaciones Económicas 17:475–494
Lazear E (1990) Job security provisions and employment. Quaterly J Econ 105:699–726
Lazear E, Rosen S (1981) Rank-order tournaments as optimal contracts. J Polit Econ 89:841–864
Levinsohn J, Petrin A (2003) Estimating production functions using inputs as controls for unobservables. Rev Econ Stud 70:317–342
Lagos R (2006) A model of TFP. Review Econ Stud 73:983–1007
MacLeod WB, Navakachara V (2007) Can wrongful discharge law enhance employment? Econ J 117:218–278
Michelacci C, Pijoan-Mas J (2012) Intertemporal labor supply with search frictions. Rev Econ Stud 79:899–931
Olley GS, Pakes A (1996) The dynamic of productivity in the telecommunications equipment industry. Econometrica 64:1263–1297
Saint-Paul G (1997) Is labour rigidity harming Europe’s competitiveness? The effect of job protection on the pattern of trade and welfare. Eur Econ Rev 41:499–506
Sanchez R, Toharia L (2000) Temporary workers and productivity: the case of Spain. Appl Econ 32:583–591
Syverson C (2011) What determines productivity? J Econ Lit 49:326–365
Acknowledgements
We acknowledge helpful comments from César Alonso-Borrego, Manuel Arellano, Manuel F. Bagües, Raquel Carrasco, Jesus Carro, Thomas Le Barbanchon, Josep Pijoan-Mas, Nawid Saissi, and especially from the Editor (Nezih Guner) and an anonymous referee. This is a substantially revised version of an earlier paper circulated under the title “Do temporary contracts affect TFP? Evidence from Spanish manufacturing firms” by Dolado and Stucchi. Financial support from Banco de España (Research Excellence Grant) is gratefully acknowledged. The usual disclaimer applies. The views expressed in this paper are those of the authors and do not necessarily correspond to those of the Inter-American Development Bank, its Board of Executive Directors or the countries they represent.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of the concavity condition
Differentiation of (3.9) w.r.t. \(e_{T}\) yields
where the first tem in its LHS is negative and the second term is positive, so that the overall sign is ambiguous. To look for conditions under which it is negative (i.e. the s.o.c. is satisfied for an interior solution), let us multiply the previous expression by \(e_{T}\) and subtract from it the f.o.c. (3.9). Since the subtrahend is zero, the sign of this algebraic operation just coincides with the sign of \(\frac{\partial ^{2}\Pi ^{T}}{\partial e_{T}^{2}}\). In particular, under the CD specification for \(f(e_{T})\), this operation yields,
Since \(\alpha <1,\) \(\frac{\partial ^{2}\Pi ^{T}}{\partial e_{T}^{2}}\) becomes negative whenever the bracketted term is positive, that is,
which is the condition given in (3.10).
Appendix B: Levinsohn and Petrin’ s (2003) approach
In what follows we briefly review the details of LP’s (2003) procedure to estimate the (logged) production function,
where \(\phi _{t}(m_{it},k_{it})=\alpha _{0}+\alpha _{k}k_{it}+\alpha _{m}m_{it}+\omega _{t}(m_{it},k_{it}).\) This equation is estimated by NLS in the first stage, using a third-order polynomial in \(m_{it}\) and \(k_{it}\) with constant slopes over time. The estimates \({\widehat{\alpha }}_{L}\) and \( {\widehat{\vartheta }}\) will consistently identify the labour elasticity \( \alpha \) and the substitution parameter \(\vartheta \). Next, following Olley and Pakes (1996), it is assumed that \(\omega _{it}\) follows a first-order Markov process, leading to \(\omega _{it}=g(\omega _{it-1})\). Although \( g(\cdot )\) has been specifically chosen to be a fourth-order polynomial in our empirical implementation, we will consider a simple AR(1) process \( \omega _{it}=\rho \omega _{it-1}+\varepsilon _{it}\), where \(\varepsilon _{it} \) is i.i.d., to briefly illustrate the second stage of the procedure yielding the remaining input elasticities. By defining \({\widetilde{y}} _{it}=y_{it}-{\widehat{\alpha }}_{L}(\ln L_{T,it}+{\widehat{\vartheta }}\ln L_{P,it})\) and taking into account that \(\omega _{it-1}=\omega _{t-1}(m_{it-1},k_{it-1}),\) it holds that,
This is the equation estimated by NLS in the second stage, using the predicted values for \({\widetilde{y}}_{it}\) and \(\phi _{t-1}(m_{it-1},k_{it-1}) \) obtained from the first-stage estimation. As LP (2003) have shown, this second stage yields consistent estimates of \(\alpha _{k}\) and \(\alpha _{m}\). Notice that, since the predicted values have been used for \({\widetilde{y}}_{it}\) and \(\phi _{t-1}(.,.)\), the standard errors of the estimated coefficients in the second stage should be corrected by bootstrap. We implement this procedure separately for each of the 18 manufacturing industries available in our dataset.
Appendix C: Data and definition of variables
1.1 Sample selection rules
We follow five rules for dropping firms or observations, namely, we exclude those firms that: (i) change from one industry to another because their TFP in different moments of time is not comparable; (ii) report observations with negative value added or negative intermediate consumption or with ratios of labour cost to sales or material cost to sales larger than unity; (iii) report an incomplete exercise in a year different than the one in which it leaves the market; and finally (iv) do not report all the information required to compute TFP or only providesthat information for a single year.
1.2 Variable definitions
-
Output Value of the produced goods and services computed as sales plus the variation of inventories deflated by the firm’s price index of output.
-
Permanent workers Workers hired under an indefinite contract until December 31st of each year.
-
Temporary workers Workers hired under a fixed-term contract until December 31st. of each year.
-
Conversions from temporary to permanent contracts Number of workers promoted to an indefinite contract who had a temporary contract at the same firm before December 31st. of the previous year.
-
Total effective worked hours Computed as the number of workers times the average hours per worker. The average hours per worker is computed as the normal hours plus average overtime minus average working time lost at the workplace.
-
Materials Value of intermediate consumption deflated by the firm’s price index of materials.
-
Capital Capital at current replacement values is computed recursively from an initial estimate and the data on current investments in equipment goods (but not buildings or financial assets) applying the recursive formula, \(K_{it}=(1-d)\frac{P_{It}}{P_{I,t-1}}K_{i,t-1}+I_{i,t}\), where d is an industry-specific rate of depreciation and \(P_{It}\) a price index of investment in equipment goods. Real capital is obtained by deflating capital at current replacement values with the price index of investment in equipment goods.
-
Investment Value of current investment in equipment goods.
-
Wages Firm’s hourly wage rate (total labour cost divided by effective total hours of work) deflated by the firm’s price index of output.
-
Capital usage cost Weighted sum of long term interest rate with banks and other long term debt plus the industry-specific depreciation rate minus the investment inflation rate.
-
Index of human capital Proportion of workers with an engineering or other college degrees.
-
Age The age of the firm is the difference between the current year and the year of birth declared by the firm.
-
Size There categories. Firms with more than 200 employees (large firms) and firms with less than 200 but more that 50 employees (medium size firms) and firms with less than 50 employees (small firms).
-
Industry Firms are classified in 18 industries. See Table 4.
-
R & D investment Value of current investment in R& D.
-
Expansive/Recessive Market Dummy variables that take value 1 when the firm reports that its market is in expansion/recession and 0 otherwise.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dolado, J.J., Ortigueira, S. & Stucchi, R. Does dual employment protection affect TFP? Evidence from Spanish manufacturing firms. SERIEs 7, 421–459 (2016). https://doi.org/10.1007/s13209-016-0150-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-016-0150-9