Abstract
Our starting place is the first order seasonal autoregressive model. Its series are shown to have canonical model-based decompositions whose finite-sample estimates, filters, and error covariances have simple revealing formulas from basic linear regression. We obtain analogous formulas for seasonal random walks, extending some of the results of Maravall and Pierce (J Time Series Anal, 8:177–293, 1987). The seasonal decomposition filters of the biannual seasonal random walk have formulas that explicitly reveal which deterministic functions they annihilate and which they reproduce, directly illustrating very general results of Bell (J Off Stat, 28:441–461, 2012; Center for Statistical Research and Methodology, Research Report Series, Statistics #2015-03, U.S. Census Bureau, Washington, D.C. https://www.census.gov/srd/papers/pdf/RRS2015-03, 2015). Other formulas express phenomena heretofore lacking such concrete expression, such as the much discussed negative autocorrelation at the first seasonal lag quite often observed in differenced seasonally adjusted series. An innovation that is also applied to airline model seasonal decompositions is the effective use of signs of lag one and first-seasonal-lag autocorrelations (after differencing) to indicate, in a formal way, where smoothness is increased by seasonal adjustment and where its effect is opposite.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Overview
Much of this document radiates from the stationary first order seasonal autoregressive model or SAR(1),
with uncorrelated (white noise or w.n.) \(a_{t}\), whose variance \(Ea_{t}^{2}\) is denoted \(\sigma _{a}^{2}\). The autocovariances of \(Z_{t}\) are
See Chapter 9 of Box and Jenkins (1976) for example. Hence the autocorrelations are
We only consider \(0<\Phi <1\) in order to have positive correlation at the seasonal lags \(q,2q,\ldots \;\). For large enough \(\Phi \), (3) shows that \(Z_{t}\) has the fundamental characteristics of a strongly seasonal time series, namely a strong tendency for year-to-year movements in the same direction, with magnitudes (relative to the underlying level, e.g. its mean zero) that change gradually more often than not. For the monthly case \(q=12\), Fig. 1 shows that when \(\Phi =0.95\), then even after 12 years the correlation is greater than 0.5. By contrast, when \( \Phi =0.70\), after 5 years the correlation is negligible. Graphs of such a \(Z_{t}\) (not shown) do not clearly indicate seasonality.
The nonzero monthly \(\left( q=12\right) \) SAR(1) autocorrelations for seasonal lags 12, 24,..., 144 and two values of \(\Phi \). For \(\Phi =0.95\), the autocorrelations are still greater than 0.5 at a lag of twelve years, indicative of well defined and similar seasonal movements for a number of years, as Fig. 3 confirms. For \(\Phi =0.70\), they are negligible after 5 years, indicating substantially weaker, perhaps negligible “seasonality”
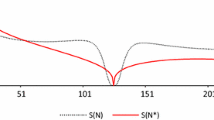
Figure 3 in Sect. 3.2 shows a simulated \(\Phi =0.95\) monthly SAR(1) series \(Z_{t}\) of length 144 displaying quite seasonal features. It also shows the residual series \(\hat{N}_{t}=Z_{t}-\hat{ S}_{t}\) resulting from removal of the estimate \(\hat{S}_{t}\) of the unobserved signal component \(S_{t}\) of a signal plus noise decomposition,
with uncorrelated components, \(ES_{t}N_{t-j}=0,-\infty <j<\infty \). The signal \(S_{t}\) is specified to have the smallest variance \(\gamma _{0}^{S}<\gamma _{0}\) compatible with having the same nonzero-lag autocovariances as \(Z_{t},\gamma _{j}^{S}=\gamma _{j},j\ne 0\). This is equivalent to specifying \(N_{t}\) as white noise with the largest variance possible for a w.n. component in an uncorrelated decomposition (4) of \(Z_{t}\). This variance, \(\gamma _{0}-\gamma _{0}^{S}\), is the minimum value of the spectral density (s.d.) of \(Z_{t}\). It has a simple formula in the SAR(1) case, as does the s.d., see (10) and (11) in Sect. 3.2.
The graph of \(\hat{N}_{t}\) in Fig. 3 appears less smooth than \( Z_{t}\), and this will be established in a formal way in Sect. 13.2. The signal estimate \(\hat{S}_{t}\) is graphed by calendar month in Fig. 4. The \(\hat{S}_{t}\) visibly smooth each of the 12 annual calendar month series of \(Z_{t}\), a property connected to the fact that the lag 12k, \(k\ge 1\), autocorrelations of \(\hat{S}_{t}\) are larger than those of \(Z_{t}\), see Sect. 13.
For any stationary \(Z_{t}\) with known autocovariances \(\gamma _{j}\), typically from an ARMA model for \(Z_{t}\), the first step toward obtaining linear estimates of an uncorrelated component decomposition (4) is the determination or specification of an appropriate autocovariance decomposition, \(\gamma _{j}=\gamma _{j}^{S}+\gamma _{j}^{N},j=0,1,\ldots \) . The SAR(1) estimated decomposition is detailed in Sect. 3.2.
For a vector of observations \(Z=\left( Z_{1},\ldots ,Z_{n}\right) ^{\prime }\) , the autocovariances at lags 0 to \(n-1\) furnish a corresponding \(n\times n \) autocovariance matrix decomposition,
This decomposition enables simplified linear regression formulas (reviewed in Sect. 4) to yield a decomposition \(Z=\hat{S}+\hat{N}\), with minimum mean square error (MMSE) linear estimates (or estimators), \( \hat{S}=\beta _{S}Z\) and \(\hat{N}=\beta _{N}Z\), of the unobserved components. Such estimates are also called minimum variance estimates. Another standard formula provides the variance matrix of the estimation errors. Everything is illustrated for the two-component SAR(1) decomposition.
Our most extensive analyses are for the simplest seasonal ARIMA model, the seasonal random walk or SRW, obtained by setting \(\Phi =1\) in (1),
The MMSE two-component decomposition filter formulas for such nonstationary \( Z_{t}\) can be obtained simply by setting \(\Phi =1\) in the stationary SAR(1) formulas. This follows from results of Bell (1984) which expand to difference-stationary series the Wiener-Kolmogorov (W-K) filter formulas presented in Sect. 6. The original W-K formulas provide MMSE component estimates from bi-infinite stationary data \( Z_{t},-\infty <t<\infty \) and immediately reproduce the SAR(1) formulas of Sect. 5.1 for the intermediate times between the first and last years, \(q+1\le t\le n-q\).
In Sect. 7, after formally defining the pseudo-spectral density (pseudo-s.d.) of an ARIMA model, we illustrate the kinds of non-stationary W-K calculations that are done with pseudo-s.d.’s in TRAMO-SEATS (Gómez and Maravall 1996), hereafter T-S, and in its implementations in TSW (Caporello and Maravall 2004), X-13ARIMA-SEATS (U.S. Census Bureau 2015), hereafter X-13A-S, and JDemetra+ (Seasonal Adjustment Centre of Competence 2015), hereafter JD+. We derive the simple formulas of all of the filters associated with the three-component seasonal, trend, and irregular decomposition of the \(q=2\) SRW. We proceed a little more directly than the tutorial article Maravall and Pierce (1987), which develops fundamental properties of this model’s decomposition estimates with somewhat different goals. In Sect. 7.2, we obtain the forecast and backcast results which are required to derive the asymmetric filters for initial and final years of a finite sample as well as the error variances of their estimates. These illustrate in a simple way the fundamental role of Bell’s Assumption A. In Sect. 10, we provide an extended and corrected version of Maravall and Pierce’s Table 1 giving variances and autocorrelations of the stationary transforms of the estimates.
For the Box-Jenkins airline model, Sect. 12 provides graphs of the MMSE filters determined by small, medium and large values of the seasonal moving average parameter \(\Theta \). Graphs also display the quite different visual smoothing effects of filters from such \(\Theta \) on the monthly International Airline Passenger totals series for which the model is named.
This is a prelude to Sect. 13, which has the most experimental material. In a formal way based on autocorrelations of the component estimates of the different types of models considered (fully differenced in the nonstationary case), it shows where smoothness is enhanced, and where an opposite result occurs, among the seasonal decomposition components. Same-calendar-month subseries are the main setting and are considered separately from the monthly series. Complete results are presented, first for the two-component SAR(1) decomposition, next for the \( q=2\) SRW’s three-component decomposition. Thereafter, smoothness results are presented for airline model series over an illustrative set of coefficient pairs.
There are many formulas. In most cases, more useful for readers than their derivations or details will be to study how the formulas are used.
2 Some conventions and terminology
A generic primary time series \(X_{t}\), stationary or not, will be assumed to have \(q\ge 2\) observations per year, with the j-th observation for the k -th year having the time index \(t=j+\left( k-1\right) q,1\le j\le q\). For simplicity, the series of j-th values from all available years of is called the \(\,\,j\) -th calendar month subseries of \(X_{t}\) even when \(q\ne 12\). When \(q=12\), these are the series of January values, the series of February values, etc., 12 series in all. Some seasonal adjustment properties, especially those of seasonal component estimates, are best revealed by the calendar month subseries. When \(X_{t}\) is stationary (mean \(EX_{t}=0\) assumed), the lag k autocorrelation of a calendar month subseries is the lag kq, or k-th seasonal autocorrelation, of \(X_{t}\). Because some formulas simplify when q / 2 is an integer, we only consider even q. In our examples \(q=2\) or 12. (In practice, \(q=3,4,6\) also occur.) Some basic features of canonical ARIMA-model-based seasonal adjustment (AMBSA for short) will be related to smoothing of the calendar month subseries or detrended versions thereof, see Sect. 11. The definition of canonical is given in Sect. 3.2.
Features of SEATS referred to are also features of the implementations of SEATS in X-13A-S and JD+.
3 The general stationary setting
Seasonal adjustment is an important example of a time series signal extraction procedure. In the simplest setting, the observed series \(Z_{t}\) is treated as the sum (4) of two not directly observable components, the “signal” \(S_{t}\) of interest and an obscuring component, the “noise” \(N_{t}\). In the case of stationary \(Z_{t}\) with known autocovariances, \(\gamma _{j},\) \(j=0,\pm 1,\ldots \), typically from an ARMA model, estimates of both components can be obtained from an autocovariance decomposition
when \(\gamma _{j}^{S}\) and \(\gamma _{j}^{N}\) have properties suitable for \( S_{t}\) and \(N_{t}\). Effectively, the additive decomposition (7) implies uncorrelatedness of the signal and noise,
see Findley (2012), which we always assume. As a consequence, for a given finite sample \(Z_{t},1\le t\le n\), simplified linear regression formulas (21) summarized in Sect. 4 provide a decomposition \(Z_{t}=\hat{S}_{t}+\hat{N}_{t},1\le t\le n\) with MMSE estimates.
3.1 Autocovariance and spectral density decompositions
The information in an autocovariance sequence \(\gamma _{j},j=0,\pm 1,\ldots \) can be reexpressed, often both compactly and revealingly, by its spectral density function (s.d.),
The second and third formulas arise from \(\gamma _{-j}=\gamma _{j}\) and \( \cos 2\pi j\lambda = {\frac{1}{2}} \big ( e^{i2\pi j\lambda }+e^{-i2\pi j\lambda }\big ) \). White noise is characterized by having a constant s.d. equal to its variance. In the AMBSA paradigm of Hillmer and Tiao (1982) implemented in SEATS, spectral densities play an essential role in specifying the canonical components, as will be demonstrated shortly.
An s.d. is nonnegative, \(g\left( \lambda \right) \ge 0\) always, see (50) for the ARMA formula. It is an even function, \(g\left( -\lambda \right) =g\left( \lambda \right) \), so it is graphed only for \(0\le \lambda \le 1/2\). See the SAR(1) example in Fig. 2. It is integrable and for any j the autocovariance \(\gamma _{j}\) can be recovered from \(g\left( \lambda \right) \) as
The \(q=12\) SAR(1) spectral densities for \(\Phi =0.70\) (darker line) and \(\Phi =0.95\) with \(\sigma _{a}^{2}=\left( 1-\Phi ^{2}\right) \), which results in \(\gamma _{0}=1\). So the area under each graph is 1/2 (in the units of the graph). The peaks are at the trend frequency \(\lambda =0\) and at each seasonal frequency, \(\lambda =k/12\) cycles per year, \(1\le k\le 6\), always with amplitude \(\sigma _{a}^{2}\left( 1-\Phi \right) ^{-2}=\sigma _{a}^{2}\left( 1+\Phi \right) \left( 1-\Phi \right) ^{-1}\). The peaks for \(\Phi =0.70\) are broader and much lower. The minimum value \(\sigma _{a}^{2}\left( 1+\Phi \right) ^{-2}\) occurs midway between each pair of peaks
An autocovariance decomposition (7) is equivalent to the s.d. decomposition
with \(g_{S}\left( \lambda \right) =\gamma _{0}^{S}+2\sum _{j=1}^{\infty }\gamma _{j}^{S}\cos 2\pi j\lambda \) and \(g_{N}\left( \lambda \right) =\gamma _{0}^{N}+2\sum _{j=1}^{\infty }\gamma _{j}^{N}\cos 2\pi j\lambda \), a key fact.
3.2 The SAR(1) canonical signal + white noise decomposition
Conceptually attractive and unique decompositions result from the following restriction, introduced by Tiao and Hillmer (1978). An s.d. decomposition with two or more component s.d.’s is called canonical if at most one of the components, usually a constant (white noise) s.d., has a non-zero minimum. A nonconstant s.d. (or pseudo-s.d. as defined in Sect. 7) is called canonical if its minimum value is zero. The two-component SAR(1) case provides the simplest seasonal example.
By calculation from (2) or from the general ARMA formula (50) below, for a series \(Z_{t}\) with model (1), the s.d. \(g\left( \lambda \right) =\sigma _{a}^{2}\left( 1-\Phi ^{2}\right) ^{-1}\sum _{j=-\infty }^{\infty }\Phi ^{\left| j\right| }e^{i2\pi jq\lambda }\) has the formula
For \(q=12\), Fig. 2 shows an overlay plot of \(g\left( \lambda \right) \) for the cases \(\Phi =0.70\) and 0.95, each with \(\sigma _{a}^{2}=\left( 1-\Phi ^{2}\right) \), which results in \(\gamma _{0}=1\) for both SAR(1) processes, showing their prominent peaks at the seasonal frequencies \(\lambda =k/12,1\le k\le 6\) cycles per year.
A canonical two-component s.d. decomposition of (10) is achieved by separating \(g\left( \lambda \right) \) from its minimum value,
which occurs at frequencies in \(-1/2\le \lambda \le 1/2\) where \(e^{i2\pi q\lambda }=\cos 2\pi q\lambda =-1\), such as \(\lambda =\pm \left( 2q\right) ^{-1}\).
The resulting decomposition
prescribes a matrix decomposition (5) for any sample size \( n\ge 1\): With \(\Sigma _{ZZ}\) \(=\left( 1-\Phi ^{2}\right) ^{-1}\sigma _{a}^{2}\left[ \Phi ^{\left| j-k\right| }\right] _{j,k=1,\ldots ,n}\) and I the identity matrix of order n,
where \(\Sigma _{SS}\) and \(\Sigma _{NN}\) have the formulas indicated. Substitution into the regression formulas (21) yields estimated signal factors \(\hat{S}_{t}\) and noise factors \(\hat{N}_{t}\) that are exemplified in Figs. 3 and 4 for the simulated SAR(1) \(Z_{1},\ldots ,Z_{144}\) shown.
The function \(g_{S}\left( \lambda \right) =g\left( \lambda \right) -\sigma _{a}^{2}\left( 1+\Phi \right) ^{-2}\), being nonnegative, even and integrable, is the s.d. of a stationary process \(S_{t}\), a SARMA(1,1)\(_{q}\) as a more informative formula (19) will reveal. Since \(g_{S}\left( \lambda \right) \) differs from \(g\left( \lambda \right) \) by a constant, it too has a peak at \(\lambda =0\). This is the trend frequency, the lower limit of the long-term cycle frequencies. This peak is identical in shape, and therefore contributes as much to the integral of \(g_{S}\left( \lambda \right) \) over \(\left[ 0,1/2\right] \), as one-half of each seasonal peak at \( \lambda =k/12,1\le k\le 6\) and the same as the seasonal peak at \(\lambda =1/2.\) Hence \(S_{t}\) has a trend component that is not negligible compared to its seasonal component. So \(S_{t}\) is not the seasonal component of \(Z_{t}\). The decomposition we will obtain from (13) can be regarded as a smooth-nonsmooth decomposition, see Sect. 13. (SEATS and its implementations calculate an algebraically more complex canonical seasonal, trend, and irregular decomposition for an SAR(1) model to estimate its seasonal and nonseasonal components, see Findley et al. 2015 for the derivation.)
A length 144 simulated monthly \( \Phi =0.95\) SAR(1) series and its estimated noise component \(\hat{N}_{t}\) (darker line) from (21). The series \(Z_{t}\) shows the consistent prominent variations by calendar month seen with quite seasonal time series. The oscillations of \(\hat{N}_{t}~\)are considerably smaller yet \( \hat{N}_{t}\) can be considered somewhat less smooth than \(Z_{t}\) also after the difference of scale is taken into account, see Sect. 13.2
The 12 calendar month subseries of Fig. 3 overlaid with their estimated signal component \(\hat{S}_{t}\) values (darker line) from Sect. 5. For each month, the horizontal line shows the calendar month average of the \(\hat{S}_{t}\). The \(\hat{S}_{t}\) closely follow all but the most rapid movements of the series, but with fewer changes of direction over the 12 years. Autocorrelation properties help to explain why they evolve somewhat more smoothly than the \(Z_{t}\) subseries. Their slightly reduced standard deviation explains why they have slightly reduced extremes, see Sect. 13.3
Further insight into the properties of \(S_{t}\) come from a formula for \( g_{S}\left( \lambda \right) \) that displays the autocovariances of \(S_{t}\) explicitly:
Thus
Key features of \(S_{t}\) with s.d. \(g_{S}\left( \lambda \right) \) are that \( \gamma _{0}^{S}<\gamma _{0}\) and \(\gamma _{j}^{S}=\gamma _{j},j\ne 0\). Hence \(S_{t}\) has autocorrelations \(\gamma _{kq}^{S}/\gamma _{0}^{S}\) proportionately greater than those of \(Z_{t}\) at all seasonal lags,
This \(S_{t}\) has the smallest variance compatible with these properties. Because the s.d. of \(N_{t}\) is constant,
\(N_{t}\) is specified as white noise with autocovariances and autocovariance matrix
The s.d.’s \(g_{S}\left( \lambda \right) \) and \(g_{N}\left( \lambda \right) \) from (12) prescribe a signal+noise decomposition of \(g\left( \lambda \right) \). Because \(g_{S}\left( \lambda \right) \) has minimum value zero, \(S_{t}\) is said to be white noise free. \(N_{t}\) has the largest variance possible for a white noise component. This white noise free plus white noise decomposition has filter formulas for the MMSE linear estimates of \(S_{t}\) and \(N_{t}\) that are especially simple and revealing, as will be seen in Sect. 5.1.
Figure 3 shows the graph of a series \(Z_{t}\) of length 144 simulated from (1) with \(q=12\) and \(\Phi =0.95\), along with its noise component estimate \(\hat{N}_{t}\) from Sect. 5. (All SAR(1) simulations use \(\sigma _{a}^{2}=\left( 1-\Phi ^{2}\right) \)). The earliest values are assigned the date January, 2002. Now we derive a compact formula for \(g_{S}\left( \lambda \right) \) to show a type of calculation that is regularly needed for nonconstant canonical spectral densities. It will be used to identify the component’s ARMA model.
It follows from (50) below that \(S_{t}\) has a noninvertible SARMA(1,1)\(_{q}\) model \(\left( 1-\Phi B^{q}\right) S_{t}=\left( 1+B^{q}\right) b_{t}\) whose white noise \(b_{t}\) has variance \(\sigma _{b}^{2}=\Phi \left( 1+\Phi \right) ^{-2}\sigma _{a}^{2}\).
4 Regression formulas for two-component decompositions
Given a column vector of data \(Z=\left( Z_{1},\ldots ,Z_{n}\right) ^{\prime } \), where \(^{\prime }\) denotes transpose, let \(S=\left( S_{1},\ldots ,S_{n}\right) ^{\prime }\) and \(N=\left( N_{1},\ldots ,N_{n}\right) ^{\prime } \) denote the unobserved uncorrelated components of a decomposition \(Z=S+N\) . From a specified decomposition of the covariance matrix \(\Sigma _{ZZ}=EZZ^{\prime }\),
standard linear regression formulas provide MMSE linear estimates \(\hat{S}\) of S and \(\hat{N}\) of N.
4.1 The estimated decomposition
Because \(\Sigma _{SN}=0\), with 0 denoting the zero matrix of order n, we have \(\Sigma _{SZ}=ESZ^{\prime }=\Sigma _{SS}\). Similarly \(\Sigma _{NZ}=\Sigma _{NN}\). Thus the usual regression coefficient formulas \(\beta _{S}=\Sigma _{SZ}\Sigma _{ZZ}^{-1}\) (with \(\Sigma _{SZ}=ESZ^{\prime }\)) and \( \beta _{N}=\Sigma _{NZ}\Sigma _{ZZ}^{-1}\) simplify. We have
It is also easy to directly verify that the coefficient formulas result in (22), the fundamental linear MMSE property, i.e., the uncorrelatedness of the errors with the data regressor Z, see Wikipedia 2013.
The final formula in (21) shows that the estimates yield a decomposition,
For \(1\le t\le n\), the t-th row of \(\beta _{S}\) provides the filter coefficients for the estimate \(\hat{S}_{t}\) and correspondingly with \( \beta _{N}\) for \(\hat{N}_{t}\), as will be illustrated in Sect. 5.
In summary, regression based on (20) provides an observable decomposition of Z in terms of MMSE linear estimates. Such a decomposition, with \(N_{t}\) specified as white noise, exists for any stationary \(Z_{t}\) whose s.d. has a positive minimum.
4.2 Variance and error variance matrix formulas
We have \(S+N=Z=\hat{S}+\hat{N}\), so if we define \(\epsilon =S-\hat{S}\), then
Thus both estimates have the same error covariance matrix,
(assuming no specification or estimation error in the model for \(Z_{t}\)). There are the usual variance decompositions,
the first following from the decomposition \(S=\hat{S}+\left( S-\hat{S} \right) \), whose components are uncorrelated by (22), and analogously for the second. In some regression literature \(\Sigma _{SS}\) is called the total variance of \(S,\Sigma _{\hat{S}\hat{S}}\) the variance of S explained by Z, and \(\Sigma _{\epsilon \epsilon }\) is the residual variance. Similarly for N with the same residual variance, from (26), which shows that
where, from (21),
Being ARMA autocovariance matrices, \(\Sigma _{ZZ},\Sigma _{SS}\) and \( \Sigma _{NN}\) are invertible. It follows that all matrices in (28) and (29) are positive definite. In particular, for each \(t,\hat{ S}_{t}\) and \(\hat{N}_{t}\) are positively correlated \(E\hat{S}_{t}\hat{N}_{t}>0\) (a property that is not generally true of differenced estimates in the ARIMA case as we will show). From (27), the estimates are less variable than their components, precisely due to estimation error.
Seasonal economic indicator series \(Z_{t}\) are generally modeled with nonstationary models, e.g., ARIMA models rather than ARMA models. Then AMBSA uses pseudo-spectral density decompositions, discussed in Sect. 7. For finite-sample estimates in the ARIMA case, McElroy (2008) provides matrix formulas for \(\hat{S},\hat{N}\) and \(\Sigma _{\epsilon \epsilon }\) which involve matrices implementing differencings and autocovariance matrices of the differenced S and N. We will be able to easily convert the SAR(1) formulas developed next to obtain the same finite-sample results as McElroy’s formulas for the two-component decomposition of the ARIMA SRW model (6).
5 SAR(1) Decomposition estimation formulas
For the SAR(1) model, the entries of the inverse matrix \(\Sigma _{ZZ}^{-1}\) have known, relatively simple formulas, see Wise (1955) and Zinde-Walsh (1988). For example, with \(q=2,n=7\),
For all \(q\ge 2\) and \(n\ge q\), as (30) indicates, \(\Sigma _{ZZ}^{-1}\) has a tridiagonal symmetric form, with nonzero values only on the main diagonal and the q-th diagonals above and below it. The sub- and superdiagonals have the entries \(-\Phi \sigma _{a}^{-2}\). The first and last q entries of the main diagonal are \(\sigma _{a}^{-2}\) and the rest are \( \sigma _{a}^{-2}\left( 1+\Phi ^{2}\right) \).
For \(\beta _{N}=\sigma _{N}^{2}\Sigma _{ZZ}^{-1}=\left( 1+\Phi \right) ^{-2}\sigma _{a}^{2}\Sigma _{ZZ}^{-1}\), one has, when \(q=2,n=7\),
Further, from \(\beta _{S}=I-\beta _{N}\),
5.1 The general filter formulas
For general q and \(n\ge 2q+1\), the \(\Sigma _{ZZ}^{-1}\) formula of Wise (1955) yields the filter formulas for \(\hat{N}\) and \(\hat{S}=Z-\hat{N}\) shown in (33)–(37) and (38)–(40), generalizing from the special cases (31) and (32). For the intermediate times \(q+1\le t\le n-q\), the noise component estimate \(\hat{N}_{t}\ \)is given by the symmetric filter
The filters for the initial and final years are asymmetric. For the initial year \(1\le t\le q\),
The filter for the final year \(n-q+1\le t\le n\) is the time-reverse of the initial year filter,
In comparison with (33), the value \(\left( \Phi Z_{t}\right) \) in the re-expression (35) appears as the MMSE SAR(1) backcast of the missing \(Z_{t-q}\) and, in (37), as the MMSE SAR(1) forecast of the missing \(Z_{t+q}\).
For the signal component estimates \(\hat{S}_{t}=Z_{t}-\hat{N}_{t}\), at intermediate times \(q+1\le t\le n-q\), the filter formula is again symmetric,
a downweighted \(2\times 2\) seasonal moving average, with weight \(4\Phi \left( 1+\Phi \right) ^{-2}\) tending to 1 when \(\Phi \) does.
As with \(\hat{N}_{t}\), for the initial and final years, the \(\hat{S}_{t}\) filtersFootnote 1 are asymmetric. For \(1\le t\le q,\)
and for \(n-q+1\le t\le n\), the time reverse of the initial year filter,
The role of \(\left( \Phi Z_{t}\right) \) in (39) and (40) is as in (35) and (37). Because the coefficients in (38)–(40) are positive, as are also the autocovariances of \(Z_{t}\) at lags that are multiples of q, it follows that \(\hat{S}_{t}\) and \(\hat{S}_{t\pm kq}\) are positively correlated, more strongly than \(Z_{t}\) and \(Z_{t\pm kq}\) it will be shown.
5.1.1 Filter re-expressions and filter terminology
The coefficient sets in the formulas above all apply for more than one value of t when \(n\ge 2q+2\) (Recall that \(q\ge 2\)). To reveal this better, let B denote the backshift or lag operator defined as usual: for any time series \(X_{t}\) and integer \(j\ge 0, B^{j}X_{t}=X_{t-j} \) and \(B^{-j}X_{t}=X_{t+j}\) (a forward shift if \( j\ne 0\)). Since \(B^{0}X_{t}=X_{t}\), one sets \(B^{0}=1\). A constant-coefficient sum \(\Sigma _{j}c_{j}B^{j}\) is a (linear, time-invariant) filter, a symmetric filter if the same filter results when B is replaced by \(B^{-1}\), as with the intermediate time filters (33) and (38). Their backshift operator formulas reveal factorizations like others that will be useful:
These formulas apply for all t such that \(q+1\le t\le n-q\) and to all t when the conceptually important case of bi-infinite data \(Z_{\tau },-\infty <\tau <\infty \) is considered.
The one-sided filter that produces the MMSE estimate for final time \(t=n\) is called the concurrent filter. In our finite-sample context, the concurrent \(\hat{N}_{t}\) and \(\hat{S}_{t}\) filters, \(\left( 1+\Phi \right) ^{-2}\left\{ -\Phi B^{q}+1\right\} \) and \(\Phi \left( 1+\Phi \right) ^{-2}\left\{ B^{q}+\left( \Phi +2\right) \right\} \) respectively, could be applied to all \(Z_{t}\) after the first year, \(q+1\le t\le n\), but are only MMSE in the final year.
5.2 The error covariances of the SAR(1) estimates
For the SAR(1) model, the formulas (27), (18) and (21) yield
Hence, for \(q=2\) and \(n=7\), from (18) and (32),
which reveals the general pattern. The error variances of the initial and final years are larger than the error variance \(2\sigma _{a}^{2}\left( 1+\Phi \right) ^{-4}\Phi \) at intermediate times by the amount \(\sigma _{a}^{2}\Phi ^{2}\left( 1+\Phi \right) ^{-4}\). This is the mean square errorFootnote 2 of using \(\Phi \left( 1+\Phi \right) ^{-2}\left\{ \Phi Z_{t}\right\} \) to backcast/forecast \(\Phi \left( 1+\Phi \right) ^{-2}Z_{t\pm q}\) in (34) and (37), since from (2) we have
The intermediate-time mean square error is \(\gamma _{0}^{\epsilon }=E\left( S_{t}-\hat{S}_{t}\right) ^{2}=E\left( N_{t}-\hat{N}_{t}\right) ^{2}=2\sigma _{N}^{2}\Phi \left( 1+\Phi \right) ^{-2}=2\Phi \left( 1+\Phi \right) ^{-4}\sigma _{a}^{2}\). On the scale of the variance \(\sigma _{N}^{2}\) of \( N_{t}\), this is \(\gamma _{0}^{\epsilon }/\sigma _{N}^{2}=2\Phi \left( 1+\Phi \right) ^{-2}\), which is approximately 0.4997 for \(\Phi =0.95\) and therefore quite substantial. By contrast, for \(S_{t}\) we have \(\gamma _{0}^{\epsilon }/\gamma _{0}^{S}=\left( 1-\Phi \right) \left( 1+\Phi \right) ^{-2}\) from (15). This is approximately 0.013 for \(\Phi =0.95\). The fact that the intermediate-time mean square error has the same positive value for all \(n\ge 5\) reminds us that the error does not become negligible with large n.
The two-component SAR(1) decomposition derived above has exceptional pedagogical value because of the simplicity of its filter and error variance formulas derived above. With the aid of results of Bell (1984), a rederivation of the filter formulas via the Wiener-Kolmogorov formulas, presented next, makes possible a quick transition to the nonstationary SRW model (6) and its canonical MMSE two-component decomposition filter and error autocovariance formulas, all obtained by setting \(\Phi =1\) in the SAR(1) formulas above.
6 Wiener–Kolmogorov formulas applied to SAR(1) and SRW models
Initially for the two-component case (4) with bi-infinite data, we consider a fundamental and relatively simple approach to obtaining MMSE decomposition estimates. It also applies to the ARIMA case under a productive assumption of Bell (1984) discussed and applied in Sect. 7.
6.1 Filter transfer functions and the input–output spectral density formula
Not only finite filter formulas but also general bi-infinite filter formulas \(Y_{t}=\sum _{j=-\infty }^{\infty }\beta _{j}X_{t-j}\) are usefully reexpressed as \(Y_{t}=\beta \left( B\right) X_{t}\) with filter \(\beta \left( B\right) =\sum _{j=-\infty }^{\infty }\beta _{j}B^{j}\). The s.d. of the filter output series \(Y_{t}\) is related to the input series s.d. \( g_{X}\left( \lambda \right) \) by the fundamental formula
see (4.4.3) of Brockwell and Davis (1991). The function \(\beta \left( e^{i2\pi \lambda }\right) \) is called the transfer function of the filter \(\beta \left( B\right) \) and \(\left| \beta \left( e^{i2\pi \lambda }\right) \right| ^{2}\) is its squared gain. When a filter’s transfer function \(\beta \left( e^{i2\pi \lambda }\right) \) is known, then the filter coefficients can be obtained from it, in general by integration
but in practice, for ARMA or ARIMA related transfer functions, by algebraic/numerical algorithms such as those encoded in SEATS.
For example, the transfer function of \(\hat{S}_{t}\) in (42) is
Hence from (46), the spectral density of \(\hat{S}_{t}\) is
A stationary ARMA series \(Z_{t}\) has a representation
with AR and MA polynomials \(\varphi \left( B\right) =1-\phi _{1}B-\cdots -\phi _{r}B^{r}\) and \(\vartheta \left( B\right) =1-\theta _{1}B-\cdots -\theta _{m}B^{m}\) satisfying
where \(a_{t}\) is white noise with variance denoted \(\sigma _{a}^{2}\). (\( \vartheta \) is script \(\theta ,\varphi \) is script \(\phi \).) The general ARMA s.d. formula,
follows from two applications of (46) as in Brockwell and Davis (1991, p. 123). Conversely, if (50) and (49) hold, then so does (48) for some w.n. process \(a_{t}\) with variance \(\sigma _{a}^{2}\).
This fact can be used to identify ARMA models for bi-infinite data component estimates. For example, from (47) and (50), \(\hat{S}_{t}\) has the noninvertible SARMA(1,2)\(_{q}\) model
Note from (50) that an ARMA model is noninvertible, i.e. \(\vartheta \left( e^{i2\pi \lambda }\right) =0\) for some \(\lambda \), if and only if its spectral density is zero at some \(\lambda \).
6.2 The W–K formulas
For a stationary series \(Z_{t}\) with a spectral density decomposition (9) specifying a two-uncorrelated-component decomposition \( Z_{t}=S_{t}+N_{t}\), Kolmogorov (1939) and Wiener (1949) independently derived the formulas
of the transfer functions of each component’s MMSE linear estimate
from bi-infinite data, \(Z_{\tau },-\infty <\tau <\infty \). For decompositions with more components, the same ratio form applies: each component estimate’s transfer function is the ratio of its spectral density to \(g\left( \lambda \right) \). The filters are finite only when \(Z_{t}\) has an AR model but at most one component also does. The W–K formulas are implemented in SEATS using an algorithm of Tunnicliffe Wilson, presented in Burman (1980), which yields finite-sample MMSE estimates. From a moderate number of forecasts and backcasts, the algorithm efficiently calculates the result of using backcasts and forecasts for the infinitely many missing past and future ARMA or ARIMA data. This has led to all finite-sample MMSE component estimates being confusingly called Y–K estimates in some of the literature.
The bi-infinite error processes \(\epsilon _{t}=S_{t}-\hat{S}_{t}\) and \( -\epsilon _{t}=N_{t}-\hat{N}_{t}\) are stationary with spectral density
see Whittle (1963) or Appendix A of the research report Findley et al. (2015) for derivations of (52) and (54). The formulas (52) and (54) are analogues of the matrix formulas of (21) and (29). Finite-sample mean square errors variances and covariances cannot be obtained from \(g_{\epsilon }\left( \lambda \right) \). In their place, the measures of uncertainty output by SEATS for its finite-sample estimates are measures for semi-infinite data estimates, used as approximations. JD+ obtains exact finite-sample measures from state space algorithms.
6.3 SAR(1) intermediate-time filters again and an alternate model form
As a simple W-K application, for the SAR(1), from (10) and (17), the intermediate-time \(\hat{N}_{t}\) filter has the transfer function
Substituting \(B^{j}\) for \(e^{i2\pi j\lambda }\) and \(B^{-j}\) for \(e^{-i2\pi j\lambda }\) yields (41), and (42) follows similarly using \(\beta _{S}\left( B\right) =1-\beta _{N}\left( B\right) \).
We enter new territory by substituting \(Z_{t}=\left( 1-\Phi B^{q}\right) ^{-1}a_{t}\) into (41). This yields the model formula
the forward-time form of a seasonal MA(1). This form is used by SEATS for revision variance calculations illustrated in Maravall and Pierce (1987). It will also be the form provided by the most direct derivations of seasonal random walk component models in later sections.
Remark A formula of the usual backward-time form, \(\hat{N} _{t}=\left( 1+\Phi \right) ^{-2}(c_{t}-\Phi c_{t-2})\), can be obtained for (56) with \(c_{t}=\left( 1-\Phi B^{2}\right) ^{-1}\left( 1-\Phi B^{-2}\right) a_{t}\). Complex conjugation preserves magnitude, so \( \left| 1-\Phi e^{i2\pi 2\lambda }\right| ^{-2}\left| 1-\Phi e^{-i2\pi 2\lambda }\right| ^{2}=1\) for all \(\lambda \). Thus, from (46), the spectral densities satisfy \(g_{c}\left( \lambda \right) =g_{a}\left( \lambda \right) =\sigma _{a}^{2}\) showing that \(c_{t}\) is white noise with variance \(\sigma _{a}^{2}\). The expanded formula \(c_{t}=\left( 1-\Phi B^{-2}\right) \sum _{j=0}^{\infty }\Phi ^{j}a_{t-2j}\), shows that \( c_{t}\) is a function of future and past \(a_{t}\), specifically of \( a_{t+2-2j},0\le j\,<\infty \). Analogues of these results hold for all forward-time moving average models derived below.
6.4 Going nonstationary with the seasonal random walk
The ARIMA W-K formula generalization of Bell (1984), discussed in detail in the next section, shows that setting \(\Phi =1\) in (41)–(42) yields the MMSE estimates of the two-component decomposition \( Z_{t}=\hat{S}_{t}+\hat{N}_{t}\) of the SRW model (6) with
This is the result obtained with \(\Phi =1\) in (42) and (41). From (57), the forecasting and backcasting results of Sect. 7.2 will yield that the initial year and final year estimates of \(\hat{ N}_{t}\) and \(\hat{S}_{t}\) are obtained by setting \(\Phi =1\) in (34) and (36) and in (39) and (40), respectively. Also, error variances and covariances of the estimates are obtained by setting \(\Phi =1\) in (44) and in the general matrix result described below (44).
The formulas (57) start from the directly verifiable decomposition of
given by
which also follows from setting \(\Phi =1\) in the formulas associated with the component s.d.’s of (12). The functions \(g\left( \lambda \right) \) and \(g_{S}\left( \lambda \right) \) are pseudo-spectral densities, see (61), of the model (6) and the SARIMA (1,1)\(_{q}\) model of \(\hat{s}_{t}\) obtained by setting \(\Phi =1\) in (51).
In Sect. 8, we will detail the seasonal, trend, irregular decompositions of (58) and the SRW with \(q=2\).
7 ARIMA component filters from pseudo-spectral density decompositions
For an ARIMA \(Z_{t}\) with degree \(d\ge 1\) differencing operator \(\delta \left( B\right) =1-\delta _{1}B-\cdots -\delta _{d}B^{d}\) and model
the pseudo-spectral density (pseudo-s.d.) is defined by
Its integral is infinite because of the \(\lambda \) at which \(\delta \left( e^{i2\pi \lambda }\right) =0\).
In the nonstationary signal plus nonstationary noise case of interest, \( \delta \left( B\right) =\delta _{S}\left( B\right) \delta _{N}\left( B\right) \), and \(\delta _{S}\left( e^{i2\pi \lambda }\right) \) and \(\delta _{N}\left( e^{i2\pi \lambda }\right) \) have no common zero. In the seasonal plus nonseasonal case, \(\delta _{S}\left( e^{i2\pi \lambda }\right) \) has zeroes only at seasonal frequencies \(\lambda =k/q,k=\pm 1,\ldots ,q/2\), and \(\delta _{N}\left( e^{i2\pi \lambda }\right) =0\) only for \(\lambda =0\), as with \(\delta _{S}\left( B\right) =1+B+\cdots +B^{q-1}\) and \(\delta _{N}\left( B\right) =\left( 1-B\right) ^{2}\) for \(\delta \left( B\right) =\left( 1-B\right) \left( 1-B^{q}\right) \) of the airline model. The pseudo-s.d. \(g\left( \lambda \right) \) must be decomposed into a sum of seasonal and nonseasonal pseudo-s.d.’s associated with \(\delta _{S}\left( B\right) \) and \(\delta _{N}\left( B\right) \), respectively.
Under mild assumptions described below, Bell (1984) established the MMSE optimality of the pseudo-spectral generalization of the W-K transfer function formulas for ARIMA component signal extraction. Tiao and Hillmer (1978), Burman (1980), and Hillmer and Tiao (1982) developed the canonical approach used with extensions and refinements in SEATS and its implementations. The last reference provides a number of examples of canonical seasonal, trend and irregular pseudo-s.d. decompositions
as well as examples of ARIMA models whose pseudo-s.d. does not admit such a decomposition (e.g. airline models with certain parameter values), the inadmissible case. Stationary components in addition to the irregular occur with s.d.’s for cyclical or other “transitory” components, see Gómez and Maravall (1996) and Kaiser and Maravall (2001). SEATS has options for several.
Generalizing the stationary case definition, a pseudo-s.d. decomposition is canonical if, with at most one exception, its component pseudo- s.d.’s and s.d.’s have minimum value zero, as in (59).
7.1 Bell’s assumptions
In addition to the requirements on \(\delta _{S}\left( B\right) \) and \(\delta _{N}\left( B\right) \), Bell (1984) also requires that the series \(\delta _{S}\left( B\right) S_{t}\) and \(\delta _{N}\left( B\right) N_{t}\) be uncorrelated. This can be obtained “automatically” from the implied s.d. decomposition \( g_{\delta \left( B\right) Z}\left( \lambda \right) =g_{\delta \left( B\right) S}\left( \lambda \right) +g_{\delta \left( B\right) N}\left( \lambda \right) \), see Findley (2012). From here, Bell’s Assumption A provides MMSE optimality for finite-sample component estimates from the matrix formulas of McElroy (2008), for bi-infinite data estimates from pseudo-spectral W-K formulas, and for semi-infinite data estimates like those considered in Bell and Martin (2004).
Bell’s Assumption A: For \(\delta (B)\) of degree d, the d initial values, say \(Z_{1},\ldots ,Z_{d}\), are uncorrelated with the bi-infinite ARMA series \(w_{t}=\delta \left( B\right) Z_{t},-\infty <t<\infty \), which generates the bi-infinite \(Z_{t}\) via
An assumption is necessary. Inference about the initial values is impossible because they are nonstationary and there is one observation of each. Assumption A provides both signal extraction optimality and, as we demonstrate next, a more fundamental MMSE optimality, that of ARIMA forecasts as commonly produced.
7.2 Assumption A yields MMSE forecasts and backcasts
Forecasts of ARIMA \(Z_{t}\) are traditionally obtained as in Box and Jenkins (1976, Ch. 5), namely by generating future \(Z_{t},t>d\) from initial \( Z_{1},\ldots ,Z_{d}\) and subsequent \(w_{t}=\delta \left( B\right) Z_{t}\,, t>d\,\), replacing unobserved \(w_{t}\) by their MMSE ARMA forecasts to obtain desired forecasts of \(Z_{t}\). The MMSE optimality of such forecasts follows somewhat straightforwardly from the forecasting results obtained under Assumption A in the third text paragraph on p. 652 of Bell (1984). For backcasts the reverse recursion in (63) is used.
We illustrate this procedure by deriving results we require for \(Z_{t}\) from the biannual SRW model,
which is analyzed in detail in the next section. The white noise variates \( a_{t}\) are all uncorrelated with one another and, under Assumption A, also with the initial values \(Z_{1,}Z_{2}\) of any \(n\ge 2\) observations \( Z_{1},\ldots ,Z_{n}\). For \(t>2\), repeated application of the recursion \( Z_{t}= Z_{t-2}+a_{t}\) yields all \(Z_{t},t\ge 3\) from the left hand formulas of (65) and (66) below: odd “months” \(Z_{2\left( m+k\right) -1}\) and even “months” \(Z_{2\left( m+k\right) } m\ge 1,k\ge 1\) are generated independently. The right most white noise sum in (65) shows the forecast error when \(Z_{2m-1}\) is the forecast of \( Z_{2\left( m+k\right) -1}\) from data \(Z_{1},Z_{2},\ldots ,Z_{2m-1}\) or from \( Z_{1},Z_{2},\ldots ,Z_{2m-1},Z_{2m}\). The right most white noise sum in (66) shows the error of the forecast \(Z_{2m}\) of \(Z_{2\left( m+k\right) },k\ge 1\) from \(Z_{1},Z_{2},\ldots ,Z_{2m-1},Z_{2m}\):
For any \(k\ge 1,Z_{2m-1}\) is the MMSE forecast of \(Z_{2\left( m+k\right) -1}\) because each term of the error \(\sum _{i=m+1}^{m+k}a_{2i-1}\) is uncorrelated with the data, as explained above. Similarly \(Z_{2m}\) is the MMSE forecast of \(Z_{2\left( m+k\right) },k\ge 1\), because its error \(\sum _{i=m+1}^{m+k}a_{2i-1}\) is uncorrelated with \(Z_{1},Z_{2},\ldots ,Z_{2m-1},Z_{2m}\). In both cases the mean square error is \(k\sigma _{a}^{2}\).
For backcasts the result that, for all \(k\ge 1,Z_{1}\) and \(Z_{2}\) are the MMSE optimal backcasts of \(Z_{-1-2\left( k-1\right) }\) and \(Z_{-2\left( k-1\right) }\) respectively, follows from Assumption A and the analogues of (65) and (66) yielded by the backward form \( Z_{t-2}=Z_{t}-a_{t}\) of the recursion used above.
8 The 3-component \(q=2\) SRW decomposition
For (64), paralleling what the software does with more complex models, the differencing operator \(\delta \left( B\right) =\left( 1-B^{2}\right) \) is factored into the product of the seasonal sum operator \( \delta _{s}\left( B\right) =1+B\) and the differencing operator for the trend \(\delta _{p}\left( B\right) =1-B\). The next step is a partial fraction calculation (see Wikipedia (2011)) to decompose the pseudo-s.d. \(g\left( \lambda \right) \) of \(Z_{t}\) into a sum of two ratio functions, one with \(\left| \delta _{s}\left( e^{i2\pi \lambda }\right) \right| ^{2}=\left| 1+e^{i2\pi \lambda }\right| ^{2}\) as the denominator and the other with \(\delta _{p}\left( e^{i2\pi \lambda }\right) =\left| 1-e^{i2\pi \lambda }\right| ^{2}\) as denominator. For
we seek \(\alpha _{1},\alpha _{2}\) such that for all \(\lambda \),
This requires
for all \(\lambda \), which is equivalent to \(2\left( \alpha _{1}+\alpha _{2}\right) =1,-\alpha _{1}+\alpha _{2}=0\), whose unique solution is \(\alpha _{1}=\alpha _{2}=1/4\). Thus we have an initial decomposition,
Both pseudo-s.d.’s on the right have a nonzero minimum value of 1 / 16. So the canonical 3-component pseudo-s.d. decomposition is
with \(\sigma _{a}^{-2}g_{s}\left( \lambda \right) =\frac{1}{4}\left| 1+e^{i2\pi \lambda }\right| ^{-2}-1/16,\sigma _{a}^{-2}g_{p}\left( \lambda \right) =\frac{1}{4}\left| 1-e^{i2\pi \lambda }\right| ^{-2}-1/16\), and \(\sigma _{a}^{-2}g_{u}\left( \lambda \right) =1/8\). (Note our use of lower case letters, e.g. s instead of S, for components of three-component decompositions.) It is easily verified that
Thus \(s_{t}\) and \(p_{t}\) are nonstationary, with differencing polynomials \( \delta _{s}\left( B\right) =1+B\) and \(\delta _{n}\left( B\right) =1-B\), with \(\delta _{n}\left( B\right) \) also the differencing polynomial of \( sa_{t}=p_{t}+u_{t}\). Using the W-K formulas as before, e.g. \(\beta _{s}\left( e^{i2\pi \lambda }\right) =g_{s}\left( \lambda \right) /g\left( \lambda \right) \), one obtains from (68) the decomposition’s transfer functions
For the seasonal adjustment filter, we have \(\beta _{sa}\left( e^{i2\pi \lambda }\right) =1-\beta _{s}\left( e^{i2\pi \lambda }\right) \). These provide the estimates \(\hat{s}_{t}=\beta _{s}\left( B\right) Z_{t},\;\hat{ p}_{t}=\beta _{p}\left( B\right) Z_{t},\;\hat{u}_{t}=\beta _{u}\left( B\right) Z_{t}\) and \(\widehat{sa_{t}}=\left( 1-\beta _{s}\left( B\right) \right) Z_{t}\) from bi-infinite data, and also for intermediate times \(3\le t\le n-2\) from \(n\ge 3\) observations.
8.1 The estimates’ symmetric filters and ARIMA models
For translations from squared gains \(\left| \Sigma _{j}\alpha _{j}e^{i2\pi q\lambda }\right| ^{2}\) to filters, we adopt a useful convention of Maravall and Pierce (1987) which uses replacement of \(e^{\pm i2\pi j\lambda }\) by \(B^{\pm j}\) to obtain the symmetric filter formula,
For example, \(\left| 1+B\right| ^{2}=\left( 1+B\right) \left( 1+B^{-1}\right) =B+2+B^{-1}\), so from (69), the trend filter is
To obtain the (forward-time) moving average polynomial of each estimates’ model, we use the result that if \(\beta \left( B\right) =\delta \left( B\right) \tilde{\beta }\left( B\right) \), then the substitution \(Z_{t}=\delta \left( B\right) ^{-1}a_{t}\) is allowed in \(\beta \left( B\right) Z_{t}\) and results in \(\beta \left( B\right) Z_{t}=\tilde{\beta }\left( B\right) a_{t}\), see Theorem 4.10.1 of Brockwell and Davis (1991). Applying this to \(\left( 1-B\right) \hat{p}_{t}=\frac{1}{16}\left( 1-B\right) \left( 1+B\right) ^{2}\left( 1+B^{-1}\right) _{{}}^{2}Z_{t}=\frac{1}{16}\left( 1-B^{2}\right) \left\{ \left( 1+B\right) \left( 1+B^{-1}\right) _{{}}^{2}\right\} Z_{t}\), we have
So \(\hat{p}_{t}\) has an ARIMA (0,1,3) model, noninvertible due to the factors \(\left( 1+B\right) \) and \(\left( 1+B^{-1}\right) _{{}}^{2}=B^{-2}\left( 1+B\right) ^{2}\).
Similar calculations from (69) provide the symmetric filters and ARIMA or ARMA models of the other estimates of three-component \(q=2\) SRW decomposition shown below. The factored filter formulas reveal the differencing factor(s) latent in each filter, causing each model to be noninvertible. Further consequences are described in Sect. 9. Also, we difference each estimate appropriately to obtain its model’s stationary moving average component, for calculation of autocorrelations of its stationary transform for tables in later sections. The MA order is noted after each model.
Apart from the seasonal adjustment formulas, the preceding formulas are equivalent to canonical filter and model formulas in Maravall and Pierce (1987), who in addition consider non-canonical MMSE estimates. Maravall (1994, p. 169ff) shows how the forward-time form of the MA polynomials can facilitate economic analyses.
8.2 The estimates’ asymmetric filter formulas
As in Sect. 5.1, we can use MMSE forecasts and backcasts, now from Sect. 7.2, to obtain the filters for the MMSE estimates from the initial and final years. We give final-year examples for a series of odd length \(n=2m+1\). (Their time reverses provide the initial year filters). The factored formulas reveal the differencing operator factor, often of lower degree than in the symmetric filter. Starting with the concurrent filters, the asymmetric seasonal and seasonal adjustment filters for the last year are:
Those for trend and irregular component estimates are
Without deriving the forecasts needed for MMSE concurrent estimates of the \( q=2\) SRW, Maravall and Pierce (1987) derive formulas for the mean square revisions of the concurrent trend and seasonal estimates, \(\hat{p}_{2m+1}\) and \(\hat{s}_{2m+1}\), from when \(Z_{2m+2}\) and \(Z_{2m+3}\) become available to replace the forecasts, also for non-canonical estimates.
8.3 Symmetric and concurrent SWP filter coefficient features
Consider the coefficients of the symmetric midpoint (also intermediate time) and the one-sided concurrent seasonal adjustment filters of a span of length \(2m+1\). The mid-point adjustment is given by
and the concurrent adjustment by
Figure 5 shows the similar but more elaborate coefficient patterns of the midpoint filter and the concurrent seasonal adjustment filter of the monthly random walk model \(Z_{t}=Z_{t-12}+a_{t}\). All of these filters are very localized, ignoring data more than a year way from the time point of the estimate, which gets the largest weight, always positive, contrasting with the next largest coefficients, negative for the closest same-calendar-month data. They are therefore very adaptive in a way that is appropriate for series with such erratic trend and seasonal movements.
Symmetric central and one-sided concurrent seasonal adjustment filters for a monthly (\(q=12\)) seasonal random walk series of length \(n=97\). As with the \(q=2\) formulas (76) and (77), the coefficients are largest at the estimation time t, staying positive until a year’s remove, when the final nonzero value is negative and substantial. Short filters like this smooth heavily and can result in large revisions
9 What seasonal decomposition filters annihilate or preserve
The occurrence of the trend and seasonal differencing factors of \(\delta \left( B\right) \) and \(\delta \left( B^{-1}\right) \), sometimes squared, in the filter formulas of the Sect. 8.1 reveal which fixed seasonal or trend components the filters annihilate and which their complementary filters preserve. Regarding symmetric filters, \(\beta _{s}\left( B\right) \) contains \(\delta _{s}\left( B\right) \delta _{s}\left( B^{-1}\right) =\left( 1-B\right) ^{2}\left( 1-B^{-1}\right) ^{2}=B^{-2}\left( 1-B\right) ^{4}\). Differencing lowers the degree of a polynomial by one, e.g., \(\left( 1-B\right) t^{3}= t^{3}-\left( t-1\right) ^{3}=3t^{2}-3t+1\). Hence this \(\beta _{s}\left( B\right) \) will annihilate a cubic component \(at^{3}\) and the seasonal adjustment filter \(\beta _{sa}\left( B\right) =1-\beta _{s}\left( B\right) \) will reproduce it. \( \beta _{sa}\left( B\right) \) has \(\left( 1+B\right) ^{2}\) as a factor. A \( q=2 \) stable seasonal component \(a\left( -1\right) ^{t}\) has the property that \(\left( 1+B\right) a\left( -1\right) ^{t}=a\left\{ \left( -1\right) ^{t}-\left( -1\right) ^{t-1}\right\} =0\). Hence \(\beta _{u}\left( B\right) \) and \(\beta _{sa}\left( B\right) \) annihilate such a component (and also an unrealistic linearly increasing \(at\left( -1\right) ^{t}\)) and \(\beta _{s}\left( B\right) \) preserves it. This is also true for their concurrent filters. The reader can further observe that \(\beta _{p}\left( B\right) a\left( -1\right) ^{t}=0\) and that the irregular filter \(\beta _{u}\left( B\right) =-\frac{1}{8}B^{-2}\left( 1+B\right) ^{2}\left( 1-B\right) ^{2}\) will eliminate both a linear trend and a stable seasonal component.
These are quite general results, applying to AMBSA filters, finite or infinite, symmetric or asymmetric, from any ARIMA model whose differencing operator has \(1-B^{q}=\left( 1-B\right) U\left( B\right) ,q\ge 2\), with \(U\left( B\right) =1+B+\cdots B^{q-1}\) as a factor. The tables of Bell (2012) cover more general differencing operators and also several generations of symmetric and asymmetric X-11 filters. In many cases, linear functions in t, and in exceptional cases, such as (71) and others covered in Bell (2015), even higher degree polynomials in t are eliminated by \(\beta _{s}\left( B\right) \) and preserved by \(\beta _{sa}\left( B\right) \).
10 Auto- and cross-correlations of stationary transforms of \(q=2\) SRW components
We continue the exploration of properties of estimated components, including how they differ from properties of the unobserved components, now for the ARIMA case, using the \(q=2\) SRW 3-component decomposition. We examine the most accessible properties, those of autocorrelations and cross-correlations of the minimally differenced components estimates, with numerical results in Table 1. These can be used as diagnostics. We begin with an important difference between the ARIMA case and the stationary case after setting the scene.
Consider an ARIMA \(Z_{t}\) whose pseudo-s.d. has a 3-component decomposition associated with a seasonal-nonseasonal differencing polynomial factorization \(\delta \left( B\right) =\delta _{s}\left( B\right) \delta _{n}\left( B\right) \). We reexpress the MMSE decomposition \(\delta \left( B\right) Z_{t}=\delta \left( B\right) \hat{s}_{t}+\delta \left( B\right) \hat{p}_{t}+\delta \left( B\right) \hat{u}_{t}\) (see Sect. 13.1) as
This makes clear how each estimate is being overdifferenced: \(\delta _{s}\left( B\right) \hat{s}_{t}\) , \(\delta _{n}\left( B\right) \hat{p}_{t},\delta _{n}\left( B\right) \widehat{sa}_{t}\) and \(\hat{u}_{t}\) are already stationary. In SEATS’ output, each of these correctly (minimally) differenced estimates is called the stationary transformation of its estimate, and the same term is used with unobserved unobserved components. The right hand sides of the Sect. 8.1 model formulas provide examples we will use.
The important difference from the stationary case: From (72) and (73), in contrast to \(E\hat{S}_{t}\hat{N}_{t}>0\) for stationary SAR(1) decompositions, we have \(E\big ( \big \{ \left( 1+B\right) \hat{s}_{t}\big \} \left\{ \left( 1-B\right) \widehat{sa}_{t}\right\} \big ) =0\). This result might suggest that estimates have the uncorrelatedness property, required of unobserved components from Sect. 7.1, the property that all stationary transforms with different differencing operators must be uncorrelated, requiring in particular \(E\left( \left\{ \left( 1+B\right) s_{t}\right\} \left\{ \left( 1-B\right) sa_{t-j}\right\} \right) =0\) for all j. However, \(E(\left\{ \left( 1+B\right) \hat{s}_{t}\right\} \{\left( 1-B\right) \widehat{sa}_{t-1}\}=13\sigma _{a}^{2}/16^{2}\) and \(E\left( \left\{ \left( 1+B\right) \hat{s}_{t}\right\} \left\{ \left( 1-B\right) \widehat{sa}_{t-2}\right\} \right) =-8\sigma _{a}^{2}/16^{2}\) show otherwise.
SEATS has diagnostics, illustrated in Maravall (2003) and Maravall and Pérez (2012), to detect when sample-moment correlation and cross-correlation estimates, calculated from the stationary transform series of the estimates, differ significantly from the correlations and cross-correlations expected from the MA models of the stationary transforms. SEATS does not yet provide theoretical model-based cross-correlations between the stationary transforms of \(\hat{s}_{t}\) and \(\widehat{sa}_{t}\). Its method for calculating cross-correlations is shown in the Appendix of Maravall (1994). For components other than \(sa_{t}\), Table I of Maravall and Pierce (1987) provides lag 1–3 autocorrelation results for the stationary transforms of the components and estimates of the \(q=2\) SRW model (64). It has typographical errors (no minus signs). Table 1 is a corrected table extended with autocorrelations of the stationary transforms of \(sa_{t}\) and \(\widehat{ sa}_{t}\), all calculated from the MA formulas in Sect. 8.1 and Appendix 2.
11 Reciprocal smoothing properties of seasonal and trend estimates
Consider a finite detrended series, \(Z-\hat{p}=\hat{s}+\hat{u}\) in vector notation. In the X-11 method, \(\hat{s}\) is estimated from the detrended series, see Ladiray and Quenneville (2001). With AMBSA estimates, Theorem 1 and Remark 4 of McElroy and Sutcliffe (2006) for ARIMA \(Z_{t}\) show that, in addition to being the MMSE linear estimate of s from \(Z,\hat{s}\) is also the MMSE linear function of \(Z-\hat{p}\) for estimating s. Further, reciprocally, the estimated trend \(\hat{p}\) is the MMSE linear estimate of p from the seasonally adjusted series \(Z-\hat{s}\) (a parallel to how the “final” X-11 trend is estimated). Under correct model assumptions, their paper also provides convergence results to the MMSE estimates of trend and seasonal for iterations starting with a non-MMSE estimate of trend (or seasonal).
For the canonical seasonal, trend and irregular decomposition of a series simulated from the Box-Jenkins airline model,
with \(\theta =\Theta =0.6\), Fig. 6 shows how the \(\hat{s}_{t}\) visually smooth the detrended calendar month subseries.
12 Airline model results: the role of \(\Theta \)
We continue with (79) and special cases thereof to demonstrate important aspects of AMBSA. Hillmer and Tiao (1982) show that, when \(\Theta \ge 0\), the airline model is admissible (i.e., has a pseudo-s.d. decomposition) for all \(-1\le \theta <1\). (Admissible decompositions exist for negative \(\Theta \ge -0.3\) for a \(\Theta \,\)-dependent interval of \( \theta \) values.) We display the influence of \(\Theta \ge 0\) on the effective length of the filter through the rate of decay of its largest coefficients away from the time point of estimation. In general, for the estimate at time t, the observation \(Z_{t}\) gets the largest coefficient. The coefficients of the same-calendar-month values \(Z_{t\pm 12k}\) in the observation interval \(1\le t\le n\), decrease effectively exponentially in k. The dominating effect of \(\Theta \) is most clearly observed with the concurrent seasonal adjustment filters.
Decay rate differences lead to a frequently observed feature of seasonal adjustment filters of all seasonal ARIMA models with a seasonal moving average factor: The greater the value of \(\Theta \) is, the less localized and adaptive but more stable the estimate will be. When \(\Theta \) is small, the filters are quite localized and adaptive but more likely to have large revisions when future data at next future times \(n+12,n+24\), etc. are first adjusted.
With \(\theta =0.9,\Theta =0.6\), the effective length of the filter is c. 3 years or so longer than in Fig. 7, which could reduce revisions from \(Z_{n+12k},k=\) 1, 2, 3
12.1 Seasonal filters from various \(\theta ,\Theta \) and their seasonal factors for the international airline passenger series
Figures 7, 8, 9 show the concurrent seasonal adjustment filter coefficients for \(n=97\) from airline models with \(\left( \theta ,\Theta \right) =(0.6,0.0),\left( 0.9,0.6\right) , \left( 0.9,0.9\right) \). Same-calendar-month values \(Z_{n-12k}, k=0,1,\ldots \) have the larger coefficients, with greatest positive weight for the latest month n.
When \(\theta =0.9\) and \( \Theta =0.9\), the effective length of the filter is the length of the data span (also for somewhat larger \(n>97\,\)). The filter resists domination by rapid changes of \(Z_{t}\) values. However, revisions from \(Z_{n+12}\,,Z\,_{n+24},\ldots \) need not diminish in size over time and could cumulatively be large
Two extremes. The very smooth, trend-like seasonal adjustment of the Airline Passenger series shown is obtained from division by the volatile \(\Theta =0.0\) seasonal factors of Fig. 10, whose text explains why revisions from future data are likely to be large. By contrast, the nearly stable \(\Theta =0.9\) same-calendar-month factors of Fig. 11 produce a much less smooth adjustment, with residual seasonality visible in the later years against the background of the original series
Since \(\beta _{s}\left( B\right) =1-\beta _{sa}\left( B\right) \), at non-zero lags the magnitude effect of \(\Theta \) on seasonal filter coefficients is the same. Figures 7, 8, 9 show the calendar month seasonal factor estimates for the International Airline Passenger data from the filters determined by small, intermediate and large values of \( \Theta \), always with \(\theta =0.6\). The coefficient values were specified as fixed in X-13ARIMA-SEATS and thus are not data-dependent. (For the Airline Passenger series the estimates are \(\left( \hat{\theta },\hat{\Theta } \right) =(0.4,0.6)\)). The factors from \(\Theta =0.0\) change rapidly, resulting in excessive smoothing of the seasonal adjustment, see Fig. 12, and in large revisions (not shown). For \(\Theta =0.9\) the seasonal factors are effectively fixed and not locally adaptive. They thus have small revisions (whose cumulative effect over time can be large).
13 Smoothness properties of the models’ estimates
13.1 Simplistic autocorrelation comparison criteria for smoothness and nonsmoothness
We begin our autocorrelation-based consideration of the smoothing properties of estimates. The simplistic definitions used will support a systematic analysis that provides insight regarding seasonal decompositions.
Given two stationary series \(X_{t}\) and \(Y_{t}\), we say that \(X_{t}\) is smooth if \(\rho _{1}^{X}>0\). If also \(\rho _{1}^{X}>\rho _{1}^{Y}\), then \(X_{t}\) is smoother than \(Y_{t}\). If \(\rho _{1}^{Y}<0\), the series \(Y_{t}\) is nonsmooth. A smooth series is therefore smoother than all white noise series and all nonsmooth series. If \(Y_{t}\) is nonsmooth and \(\rho _{1}^{Y}<\rho _{1}^{X}\) holds, then \(Y_{t}\) is more nonsmooth than \(X_{t}\). A nonsmooth series is thus more nonsmooth than all white noise series and all smooth series. To examine if visual impressions of smoothness or nonsmoothness align with the conclusions of these formal criteria, differences of scale must be accounted for, see Sect. 13.2 and 13.3 and associated figures for illustrations.
We make smoothness/nonsmoothness comparisons between the series \(Z_{t}\) and its intermediate-time/bi-infinite-data component estimates. This is done for the two SAR(1) component estimates in Sect. 13.2 and 13.3. In the nonstationary cases, the comparisons are made for the stationary decompositions
These represent MMSE optimal three- and two-component decompositions of \( \delta \left( B\right) Z_{t}\). For example, the MMSE property of \(\hat{s}_{t} \), that \(\hat{s}_{t}-s_{t}\) is uncorrelated with \(Z_{\tau }\) for all t and \(\tau \), immediately yields that \(\delta \left( B\right) \left( \hat{s}_{t}-s_{t}\right) \) is uncorrelated with \(\delta \left( B\right) Z_{\tau }\) for all t and \(\tau \).
When a series considered is a calendar month subseries, the autocorrelations considered are the seasonal autocorrelations in the time scale of the original \(Z_{t}\). We sometimes say that the conclusion of smoother is strengthened if the relevant autocorrelation at lag 2 (and perhaps consecutive higher lags) is also positive. This calls attention to the stronger smoothness properties of monthly trends and calendar month seasonal factors or their stationary transforms. Other intensifiers are only suggestive and will not be formally defined.
13.2 SAR(1): increased nonsmoothness of \(\hat{N}_{t}\)
By direct calculation from (33) or from its seasonal MA(1) model (56), the autocorrelations of intermediate-time \(\hat{N}_{t}\) are
Whereas calendar month series of \(Z_{t}\) are smooth because \(\rho _{q}=\Phi >0,\rho _{q}^{\hat{N}}<0\) so \(\hat{N}_{t}\) has more nonsmooth calendar month series than \(Z_{t}\). Of course, the calendar month subseries of \(\hat{N }_{t}\) are less variable than those of \(Z_{t}\) in the sense that, from (56), \(\gamma _{0}^{\hat{N}}=\left( 1+\Phi \right) ^{-4}\left( 1+\Phi ^{2}\right) \sigma _{a}^{2}=\left( 1-\Phi \right) \left( 1+\Phi ^{2}\right) \left( 1+\Phi \right) ^{-3}\gamma _{0}\) is less than \(\gamma _{0}\). Consequently, the scale of the \(\hat{N}_{t}\) is related to that of the \( Z_{t} \) through
The scale reduction factor \(\sqrt{\left( 1-\Phi \right) \left( 1+\Phi ^{2}\right) \left( 1+\Phi \right) ^{-3}}\) is approximately 0.113 for \(\Phi =0.95\). This factor quantifies the diminished scale of oscillations about the level value 0 seen for the intermediate years in Fig. 3. Figure 13 shows calendar month graphs of the nonsmooth component \(\hat{N}_{t}\) and the scale-reduced \(Z_{t}\), the latter downscaled to have \(\hat{N}_{t}\)’s standard error. \(\hat{N}_{t}\) is visibly less smooth, in alignment with the formal conclusion.
Calendar month plots of the SAR(1) intermediate-time white noise factor estimates \(\hat{N}_{t}\) (darker line) and the rescaled \(Z_{t}\), downscaled to have the same standard deviation as the \(\hat{N}_{t}\) for \(\Phi =0.95\). The horizontal lines are the calendar month averages of the rescaled \(Z_{t}\). The \(\hat{N}_{t}\) calendar month subseries are visually less smooth than the rescaled \(Z_{t}\), in alignment with result of the lag 12 autocorrelation analysis
13.3 SAR(1): greater calendar month smoothness of \(\hat{S}_{t}\)
Directly calculating the seasonal lag autocovariances of \(Z_{t-q}+2Z_{t}+Z_{t+q}\) and (3), we obtain from (38) that the variance and the nonzero autocovariances \(\gamma _{kq}^{\hat{S}}, k\ge 1\) of intermediate-time \(\hat{S}_{t}\) are
Division by \(\gamma _{0}^{\hat{S}}\) yields the intermediate-time autocorrelations (84).
Using \(\left( 3+\Phi \right) ^{-1}>1/4\) and \({\frac{1}{2}} \left( 1+\Phi \right) >\Phi \) for \(0< \Phi <1\), one readily obtains from (84), (16) and (3) that the intermediate-time calendar month autocorrelations of \(\hat{S}_{t}\) dominate those of \(Z_{t},\)
By calendar month, \(\hat{S}_{t}\) is smoother than \(Z_{t}\) in alignment with the visual impression from Fig. 4. (The scale of \(\hat{S}_{t}\) is only slightly smaller than the scale of \(Z_{t}\): From (83), we have \(\sqrt{\gamma _{0}^{\hat{S}}/\gamma _{0}} \doteq 0.981\) for \(\Phi =0.95\)).
13.4 Smoothness properties of \(q=2\) SRW component estimates
For \(q=2\) SRW smoothness results, we require autocorrelations of the fully differenced components of (80):
These formulas yield the autocorrelations of Table 2.
\(\delta \left( B\right) Z_{t}=a_{t}\) is white noise, so \(\rho _{j}^{\delta \left( B\right) Z}=0,j>0\). Thus in Table 2, \(\rho _{2}>0\) indicates a differenced estimate with smoother calendar month series than \(\delta \left( B\right) Z_{t}\), whereas \(\rho _{1}<0\) indicates a differenced estimate whose monthly series is more nonsmooth than monthly \(\delta \left( B\right) Z_{t}\), etc. Regarding the monthly series: as determined by \(\rho _{1} ,\delta \left( B\right) \widehat{sa}_{t}\) and \(\delta \left( B\right) \hat{p}_{t}\) are smoother than \(\delta \left( B\right) Z_{t}\) with strengthened smoothness. The seasonal’s \(\delta \left( B\right) \hat{s}_{t}\) is more nonsmooth than \(\delta \left( B\right) Z_{t}\). Regarding calendar month series, the seasonal adjustment’s, \(\delta \left( B\right) \widehat{sa}_{t}\) and especially the irregular’s \(\delta \left( B\right) \hat{u}_{t}\)’ s are more nonsmooth than \(\delta \left( B\right) Z_{t}\). The seasonal’s \(\delta \left( B\right) \hat{s}_{t}\) and the trend’s \(\delta \left( B\right) \hat{p}_{t}\) are smoother than \(\delta \left( B\right) Z_{t}\) , with strengthened smoothness.
13.5 Airline model component estimates: autocorrelations after full differencing
13.5.1 Empirical lag 12 autocorrelation results of McElroy (2012) for seasonal adjustments
With a set of 88 U.S. Census Bureau economic indicator series for which the airline model was selected over alternatives, McElroy (2012) found that all but one had negative lag 12 sample autocorrelation in the fully differenced seasonally adjusted series, \(\delta \left( B\right) \widehat{sa}_{t}\) in our notation. This negative autocorrelation is statistically significant at the 0.05 level for 46 of the series. From the perspective of detrended calendar month series, which seem always to be visually smoothed by seasonal factor estimates (in logs when appropriate for AMBSA), this should not a be surprising result–removal of a smooth component causes loss of smoothness, which negative autocorrelation can formally identify.
13.5.2 Correct model results for various \(\theta ,\Theta \) and component estimates
For monthly series from (79), with \(\delta \left( B\right) =\left( 1-B\right) \left( 1-B^{12}\right) \), we examine the estimates in the corresponding version of (80). The autocorrelations of \(\delta \left( B\right) Z_{t}=a_{t}-\theta a_{t-1}-\Theta a_{t-12}+\theta \Theta a_{t-13}\) of interest are
For any choices of \(-1<\theta <1\) and \(0\le \Theta <1\), SEATS outputs the coefficients of the ARIMA or ARMA models of \(\hat{s}_{t},\widehat{sa}_{t}=Z_{t}-\hat{s}_{t},\hat{p}_{t}\), and \(\hat{u}_{t}\), with innovation variances given in units of \(\sigma _{a}^{2}\) (so \(\sigma _{a}^{2}=1\)). With this information, W-K formulas can be used to obtain models for \(\delta \left( B\right) \hat{s}_{t},\delta \left( B\right) \hat{p}_{t}\) and \( \delta \left( B\right) \hat{u}_{t}\). From these models, the autocorrelations needed for smoothness analysis like those presented below can be calculated. The simplest differenced estimate’s model, that of \(\delta \left( B\right) \hat{u}_{t}\), is derived in Appendix 1 as an illustration, after that of \( \hat{u}_{t}\). We start with the calendar month series.
13.5.3 Seasonal autocorrelations and calendar month smoothness
Results are presented in the Tables 4, 5, 6, 7, 8 for comparison with the autocorrelations of \(\delta \left( B\right) Z_{t}\) in Table 3 from (86). Our formal relative smoothness criterion only involves first seasonal lag autocorrelations. Some higher lag results are presented for a broader perspective. Here is a summary of the tabled seasonal lag results. Tables 4, 5,6 show that, in contrast to \(\delta \left( B\right) Z_{t}\) from Table 3, the series \(\delta \left( B\right) \hat{s}_{t}\) from the seasonal estimates \(\hat{s}_{t}\) is positively correlated at all seasonal lags considered, 12, 24 and 36, often strongly, indicating that the calendar month subseries of \(\delta \left( B\right) \hat{s}_{t}\) will often be substantially smoother than \(\delta \left( B\right) Z_{t}\). Table 7 shows that the opposite holds for the seasonally adjusted series \(\delta \left( B\right) \widehat{sa}_{t}= \delta \left( B\right) Z_{t}-\delta \left( B\right) \hat{s}_{t}\), and Table 8’s results for \(\delta \left( B\right) \hat{u}_{t}\) are similar. Both have more negative autocorrelations at lag 12 than \(\delta \left( B\right) Z_{t}\) and positive autocorrelations at lag 24 (and negligible autocorrelations at lag 36–not shown), increasing the tendency for more changes of direction than \(\delta \left( B\right) Z_{t}\).
13.5.4 Lag 1 autocorrelation and monthly smoothness results
Familiarly, an estimated trend visually smooths a seasonally adjusted monthly series. We examined the lag 1–12 autocorrelations (not shown) of the differenced trend estimates, \(\delta \left( B\right) \hat{p}_{t}\) for the \( \Theta ,\theta \) under consideration. At lags 1–6 all are positive. At lags 7–11, some or all can have either sign. Thus \(\delta \left( B\right) \hat{p}_{t}\) will have at least a half-year of resistance to oscillation. At lag 12, all are negative. This is in strong contrast to \(\delta \left( B\right) Z_{t}\), which, among lags 1–6, has a non-zero autocorrelation only at lag one, with a negative value indicating nonsmoothness (except when \( \theta <0\)), see (86).
For the differenced irregular component \(\delta \left( B\right) \hat{u}_{t}\) , Tables 9 and 10 below show that \(\delta \left( B\right) \hat{u}_{t}\) is more nonsmooth than the nonsmooth \(\delta \left( B\right) Z_{t}\).
14 Concluding remarks
The simple seasonal models considered have provided very informative formulas for two- and three-component decompositions of seasonal time series. The factored formulas for the seasonal random walk simply display the full range of differencing operators (in biannual form) of ARIMA model-based seasonal decomposition filters identified in Bell (2012, 2015). The formulas for the estimates’ auto- and cross-correlation formulas have led to new insights and results. For example, the finding of negative sample autocorrelations at the seasonal lag of the differenced seasonally adjusted series now appears as an inevitable result of removing a seasonal component whose calendar month subseries are smooth. It is not a defect of the seasonal adjustment procedure, contrary to a view expressed in some of the literature motivating McElroy (2012).
For the irregular component, there are the common empirical findings, with airline and similar models, of negative sample autocorrelations, often at the first lag (see Table 11 in Appendix 1) and at the first seasonal lag of the estimated irregular component \(\hat{u}\) or differenced \(\hat{u}\) as in Tables 1 and 10. These can now be anticipated from the knowledge that \(\hat{u} \) can be regarded both as the detrended version of the seasonally adjusted series \(Z-\hat{s}\), and also as the deseasonalized version of the detrended series \(Z-\hat{p}\), in both cases resulting from removal of a smooth component.
The capacity to provide illuminating precise answers to many questions is a very valuable feature of ARIMA-model-based seasonal adjustment, as is its conceptual simplicity relative to nonparametric procedures, at least for adjusters with sufficient modeling background and experience. (The challenge is always to find an adequate model for the data span to be adjusted, if one exists.) Also valuable are the error variance and autocovariance measures (not accounting for sampling or model error) that AMBSA easily provides (only) for additive direct seasonal adjustments and their period-to-period changes. The latter, with log-additive/multiplicative adjustments, the most common kind, yield approximate uncertainty intervals for growth rates, quantities of special interest for real-time economic analysis.
Disclaimer Results of ongoing research are provided to inform interested parties and stimulate discussion. Any opinions expressed are those of the authors and not necessarily those of the U.S. Census Bureau or the Bank of Spain.
Notes
A more general perspective, applicable to any finite sample estimate, is that there is just one filter, a filter whose coefficients change with t. The coefficients of \(\hat{S}_{t}=c_{1}\left( t\right) Z_{t-q}+c_{2}\left( t\right) Z_{t}+c_{3}\left( t\right) Z_{t+q}\) are piecewise constant, fixed at different values in the first year, last year, and the interval between.
With more general models for \(Z_{t}\), more forecasts and backcasts are needed, and their error covariances at nonzero leads and lags occur in the more complex mean square error formulas.
References
Bell WR (1984) Signal extraction for nonstationary time series. Ann Stat 12:646–664
Bell WR (2012) Unit root properties of seasonal adjustment and related filters. J Off Stat 28:441–461 (http://www.census.gov/srd/papers/pdf/rrs2010-08)
Bell WR (2015) Unit root properties of seasonal adjustment and related filters: special cases. Center for Statistical Research and Methodology,- Research Report Series, Statistics #2015-03, Washington, D.C.: US Census Bureau, https://www.census.gov/srd/papers/pdf/RRS2015-03
Bell WR, Martin DEK (2004) Computation of asymmetric signal extraction filters and mean squared error for ARIMA signal component models. J Time Series Anal 25:603–625
Box GEP, Jenkins GM (1976) Time Series Anal Forecast Control, Revised edn. Holden-Day, San Francisco
Brockwell PJ, Davis RA (1991) Time Series Theory Methods, 2nd edn. Springer Verlag, New York
Burman JP (1980) Seasonal adjustment by signal extraction. J Royal Stat Soc 143:321–337
Caporello G, Maravall A (2004) Program TSW: revised manual. Documentos Ocasionales 0408, Bank of Spain
Census Bureau US (2015) X-13-ARIMA-SEATS Reference Manual, Version 1.1. http://www.census.gov/ts/x13as/docX13AS
Findley DF (2012) Uncorrelatedness and other correlation options for differenced seasonal decomposition components of ARIMA model decompositions. Center for Statistical Research and Methodology,- Research Report Series, Statistics #2012-06, Washington, D.C.: U.S. Census Bureau, http://www.census.gov/ts/papers/rrs2012-06
Findley DF, Lytras DP, Maravall A (2015) Illuminating model-based seasonal adjustment with the first order seasonal autoregressive and airline models. Center for Statistical Research and Methodology,- Research Report Series, Statistics #2015-02, Washington, D.C.: U.S. Census Bureau, http://www.census.gov/srd/papers/pdf/RRS2015-02
Gómez V, Maravall A (1996) Programs TRAMO and SEATS : Instructions for the User (beta version: June 1997). Banco de España, Servicio de Estudios, DT 9628. Updates and additional documentation at http://www.bde.es/webbde/es/secciones/servicio/software/econom.html
Hillmer SC, Tiao GC (1982) An ARIMA-model-based approach to seasonal adjustment. J Am Stat Assoc 77:63–70
Kaiser R, Maravall A (2001) Measuring business cycles in economic time series. Springer, New York
Kolmogorov AN (1939) Sur l’Interpolation et l’Extrapolation des Suites Stationnaires. C R Acad Sci Paris 208:2043–2045
Ladiray D, Quenneville B (2001) Seasonal adjustment with the X-11 method. Lecture Notes in Statistics Vol. 158, Springer Verlag, New York
Maravall A (1994) Use and misuse of unobserved components in economic forecasting. J Forecast 13:157–178
Maravall A (2003) A class of diagnostics in the ARIMA-model-based decomposition of a time series. In: Manna M, Peronaci R (eds) Seasonal adjustment. European Central Bank, Frankfurt am Main, pp 23–36
Maravall A, Pérez D (2012) Applying and interpreting model-based seasonal adjustment–The Euro-Area Industrial Production Series, Ch. 12. In: Bell WR, Holan SH, McElroy TS (eds) Economic time series: modeling and seasonality. CRC Press, Boca Raton
Maravall A, Pierce DA (1987) A prototypical seasonal adjustment model. J Time Series Anal 8:177–293
McElroy TS (2008) Matrix formulas for nonstationary ARIMA signal extraction. Econometric Theory, 28: 988–1009. Preprint available at http://www.census.gov/ts/papers/matform3
McElroy TS (2012) An alternative model-based seasonal adjustment that reduces residual seasonal autocorrelation. Taiwan Econ Forecast Policy 43:33–70. http://www.econ.sinica.edu.tw/academia-02.php
McElroy TS, Sutcliffe A (2006) An iterated parametric approach to nonstationary signal extraction. Comput Stat Data Anal 50:2206–2231. http://www.census.gov/ts/papers/rrs2004-05
Seasonal Adjustment Centre of Competence (2015) http://www.cros-portal.eu/content/seasonal-adjustment-centre-competence
Tiao GC, Hillmer SC (1978) Some consideration of decomposition of a time series. Biometrika 65:496–502
Whittle P (1963) Prediction and regulation. Van Nostrand, Princeton
Wiener N (1949) The extrapolation, interpolation and smoothing of stationary time series with engineering applications. Wiley, New York
Wikipedia Contributors (2011) Partial Fraction. Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/wiki/Partial_fraction. Accessed 21 Oct 2011
Wikipedia Contributors (2013) Minimum mean square error. Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/wiki/Minimum_mean_square_error. Accessed 7 Feb 2013
Wise J (1955) The autocorrelation function and the spectral density function. Biometrika 42:151–160
Zinde-Walsh V (1988) Some Exact Formulae for Autoregressive-Moving Average Processes. Econometric Theory 4:384–402 (Errata. Econometric Theory 6:293)
Acknowledgments
The SAR(1) results were presented by the first author at the March 13-14, 2014 Bank of Spain conference “Celebrating 25 Years of TRAMO-SEATS and honoring the 70th Birthday of Agustin Maravall”. The authors are indebted Brian Monsell, Tucker McElroy and Bill Bell for beneficial comments on earlier drafts. Bell’s comments and suggestions were especially extensive and influential. We are also grateful to Domingo Pérez, Brian Monsell and especially Tucker McElroy for computational support.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Derivation of the SARMA models of \(\hat{u}_{t}\) and \( \delta \left( B\right) \hat{u}_{t}\) for the airline model
The W–K estimate \(\hat{u}_{t}\) of the canonical airline model decomposition’s irregular component \(u_{t}\) has the pseudo-s.d.
with \(g_{u}\left( \lambda \right) =\sigma _{u}^{2}\). Thus, from (79 ), \(\hat{u}_{t}\) has the stationary noninvertible seasonal ARMA(1,1)(1,1)\(_{12}\) model
for white noise \(c_{t}\) with variance \(\sigma _{u}^{4}/\sigma _{a}^{2}\), leading to
Similarly, from (46), \(\hat{J}_{t}=\delta \left( B\right) \hat{u}_{t}\) , the fully differenced \(\hat{u}_{t}\) has s.d.
So its model is the noninvertible seasonal ARMA(1,2)(1,2)\(_{12}\) model \(\left( 1-\theta B\right) ( 1-\Theta B^{q}) \hat{J}_{t}=\left( 1-B\right) ^{2}\left( 1-B^{12}\right) ^{2}c_{t}\). Multiplied out, this model is
Expanded model formulas like (87) and (88) are what the algorithms for calculating autocovariances of Sect. 13.5.2 require and what SEATS outputs for Tables 1 and 10.
Appendix 2: Correlations of stationary transforms of SRW components
The component models below from (68) include an IMA(1,1) for \( sa_{t}=Z_{t}-s_{t}=p_{t}+u_{t}\),
The mutually uncorrelated white noise series \(\tilde{a}_{t},\tilde{b}_{t}\) and \(u_{t}\) have the respective variances \(\sigma _{a}^{2}/16,\sigma _{a}^{2}/16\) and \(2\sigma _{a}^{2}/16\). For Table 1, we calculate the nonzero autocovariances and autocorrelations of the MA(1) series on the right hand sides in (89),
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Findley, D.F., Lytras, D.P. & Maravall, A. Illuminating ARIMA model-based seasonal adjustment with three fundamental seasonal models. SERIEs 7, 11–52 (2016). https://doi.org/10.1007/s13209-016-0139-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-016-0139-4