Coverage of infertility treatment and fertility outcomes

Abstract

Policy interventions that increase insurance coverage for infertility treatments may affect fertility trends, and ultimately, population age structures. However, such policies have ignored the overall impact of coverage on fertility. We examine short-term and long-term effects of increased insurance coverage for infertility on the timing of first births and on women’s total fertility rates. Our main contribution is to show that infertility mandates enacted in the United States during the 80s and 90s did not increase the total fertility rates of women by the end of their reproductive lives. We also show evidence that these mandates induced women to put off motherhood.

1 Introduction

The average age at first birth in the United States has been rising steadily over the past decades, from 21.49 in 1968 to 23.72 in 1985 and 25.26 in 2004. As shown in Fig. 1, this increase has been accompanied by remarkable changes in the age distribution of first-time mothers, which has become less skewed with a substantially higher density of first-time mothers older than 25 and an extension of first-time motherhood beyond the age of 40.

Fig. 1

Distributions of maternal age at first birth in 1968 and 2004

Women, however, face a biological time constraint on bearing children because fecundity decreases with age. The introduction of and the subsequent increase in the use of assisted reproductive therapies (ARTs) have helped women in extending their reproductive lives (CDC 2007). ARTs, particularly in-vitro fertilisation (IVF), are very expensive procedures. For example, in 1992, a birth from an IVF procedure cost between 44,000 and 211,942 USD (Neumann et al. 1994). Over time, however, ART patients have faced substantially lower costs due to increased competition (Hamilton and McManus 2012), a reduced number of cycles due to better technology,¹ $^{,}$ ² and most importantly, the availability of insurance in both the United States and in Europe.³ In this paper, we analyse whether easier access to ARTs induces women to delay motherhood and whether, in the long term, it affects women’s completed fertility by the end of their reproductive lives.

The perception that ARTs increase fertility has led the European Parliament to call on member states to insure ‘the right to universal access to infertility treatment’ (Ziebe and Devroey 2008). This movement’s incarnation in the United States has sponsored several attempts at approving the ‘Family Building Act of 2009’, which would extend coverage for infertility treatments, and the enactment by several states of infertility insurance coverage laws, which are referred to as infertility treatment mandates.⁴ Considering the high cost of infertility treatments (Bitler and Schmidt 2012; Collins 2001), policy interventions that grant insurance coverage for infertility treatments may affect fertility trends and ultimately, population age structures. The mid- to long-term consequences of ARTs are central to the European debate on possible solutions to an ageing population—i.e., can ARTs be part of a package of policies intended to increase fertility rates in Europe? (Grant et al. 2006; Ziebe and Devroey 2008).⁵

The answer is complex because the short-term effect of an increase in coverage for infertility treatments may be very different from the long-term effect. In the short term, an increase in the aggregate fertility rate is expected due to an increase in fertility amongst the least fertile women (a compositional effect). Typically, these are relatively old women who delayed motherhood and would be unlikely to conceive otherwise (Buckles 2005; Schmidt 2005a, 2007). Moreover, increased access to ARTs increases the frequency of multiple births in the population (Bundorf et al. 2007). These two effects are short-term and non-strategic and may be referred to as ex-post moral hazard. In the long term, however, easier access to infertility treatments and the possibility of extending reproductive life may induce women to further delay motherhood, possibly because of overly optimistic perceptions about the effectiveness of infertility treatments (Lampi 2006; Benyamini 2003). This response by relatively young women, which may be referred to as ex-ante moral hazard, is strategic and would increase the average age at first birth for several years after the policy was implemented.⁶ Such a response would be consistent, for example, with the delay in marriage due to increased infertility coverage documented in Abramowitz (2014). Therefore, it is possible that an increase in insurance coverage for infertility treatment may have negative effects on total fertility in the mid- to long-term. This paper examines these issues in the United States, where, by 2001, more than 1 % of live births were due to IVF (CDC 2007).

Our objective in this paper is twofold. First, we analyse the impact of an increase in infertility insurance on the timing of first births. Although this question was first explored by Buckles (2005), we believe that our paper contributes in a substantial way to the few existing manuscripts that address this topic by using more adequate data and methodology. Moreover, we go a step further by looking into the long term effects of increasing infertility insurance. Second, we ask whether the increase in infertility insurance affects completed fertility, i.e., fertility by the end of a woman’s reproductive life. This study represents, to the best of our knowledge, the first to address this issue.⁷ Both objectives are analysed using data from the United States.

To assess whether infertility insurance induces a delay in motherhood, one needs to combine evidence about reduced fertility of young women with information on when women become mothers, i.e., when (if at all) they stop delaying motherhood. This precisely describes the approach we adopt in the first part of this paper; we not only offer similar evidence as Buckles (2005) on the reduced probability that relatively young women in mandated states have children, but we also demonstrate that the average age of first-time mothers continues to increase in the medium to long term after the enactments of infertility mandates.⁸ Our long-term estimate (10–16 years after the first and the last mandates were passed) ranges from 3 to 5 months. These effects are substantial insofar as they represent between 15.7 and 18.8 % of the total increase in the age of first-time mothers during the period considered for the group of six states that enacted infertility treatment mandates⁹ and between 24.8 and 34.3 % for the three states with the most generous coverage (Illinois, Massachusetts, and Rhode-Island).¹⁰

The ageing of first-time mothers may impact women’s completed fertility in the long term. Hence, our second goal is to determine whether infertility insurance indeed increases women’s completed fertility by the end of their reproductive lives, a question that has not been addressed in the existing literature. In principle, any potential negative effects on fertility induced by a delay of motherhood may eventually be offset by a higher prevalence of multiple births,¹¹ so the impact of infertility insurance on completed fertility is ultimately an empirical question. Overall, our estimates, based on data on the number of biological children from the June CPS, show no statistically significant effect of either the strong or the comprehensive mandates on completed fertility.

In sum, our paper shows that, despite being associated with higher birth rates among relatively older women and with a higher prevalence of multiple births, infertility insurance does not have a statistically significant effect on women’s fertility at the end of their reproductive lives. The reason lies, as we further show, in the fact that infertility insurance mandates also appear to delay motherhood among relatively younger women and, hence, make conception more difficult because fecundity decreases with age.

The rest of the paper is structured as follows: Sect. 2 describes the characteristics of infertility treatment mandates including where and when they were enacted; Sect. 3 describes the data sources used in this paper; Sect. 4 presents our evidence on the delay of motherhood; Sect. 5 presents an analysis of the impact of the mandates on women’s completed fertility; Sect. 6 presents conclusions; Sect. 7 contains figures and tables; and Sect. 8 is the “Appendix”.

2 Infertility treatment mandates

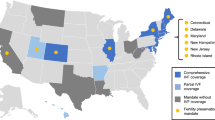
Table 1 summarises the major features of infertility insurance mandates and their timing. The classification of mandates is consistent with those presented in Buckles (2005) and Schmidt (2007). Mandates can either require mandatory coverage of infertility treatment for all plans (‘mandates to cover’) or demand that employers offer at least one plan that covers infertility treatment (‘mandates to offer’). In addition, mandates to cover are described as ‘strong’ when they cover IVF treatment and at least $35\,\%$ of the women are affected by the mandate; otherwise they are described as ‘weak’.¹² According to the American Society for Reproductive Medicine, of the six states classified as ‘mandate-to-cover-strong’, only Arkansas does not apply the mandate to all plans (HMOs are exempt). In addition, out of the six strong mandate states, three require women to be married to benefit from the insurance coverage (see Mookim et al. 2008 for more detail on mandates).

Table 1 Infertility treatment mandates classifications

Other authors, such as Hamilton and McManus (2012), Bundorf et al. (2007), and Mookim et al. (2008), classify Illinois, Massachusetts, and Rhode-Island (hereafter IL-MA-RI) as having ‘universal’, ‘comprehensive’, and the ‘most comprehensive coverage’, respectively. In this paper, the effects of infertility treatment mandates on this specific group of states are also analysed.

Concerns about policy endogeneity have been discussed in previous studies, such as Bitler and Schmidt (2012) and Hamilton and McManus (2012). The latter two studies in particular reached the conclusion that the enactment of infertility treatment mandates was largely the result of the efforts of a national infertility association (RESOLVE) and the political rather than fertility preferences of state residents. We briefly revisit this issue in our sample in Sect. 4.1.

The “Appendix” describes state-specific changes made to the original strong mandates in later periods. Because most of the revisions that occurred within the sample period (i.e., before 2001) undercut benefits, they are expected to decrease the estimated effects of the mandates.

3 Data sources

Our data comes from three main sources: (1) birth certificates from the National Vital Statistics System of the National Center for Health Statistics; (2) the March Annual Social and Economic Supplement of the Current Population Survey (March CPS) and (3) the June Marriage and Fertility Supplement of the Current Population Survey (June CPS).¹³

In Sect. 4.1, we use individual-level data from the June CPS to analyse the impact of the mandates on the probability of having a child by the age of 30/35. The period of analysis is restricted to 1979–1995 due to the unavailability of the main dependent variable beyond that period.

In Sect. 4.2, we aggregate individual-level data from birth certificates on the age of new mothers at the state and year level to analyse the impact of the mandates on the age at first birth. The birth certificates contain individual records for 50 % of the births occurring within the United States from 1968 to 1971; from 1972 to 1984, the data are based on 100 % samples of birth certificates from some states and on 50 % samples from the remaining states; as of 1985, the data cover every birth from all reporting areas.¹⁴ These data also contain information on the mother, including her age, race and state of residence as well as specific information about the timing, parity (whether the birth was a first or subsequent birth), and plurality (the number of children per delivery that is, whether it was a single, twin, triplet, or higher-order birth) of each birth. This information allows the identification of first births and, therefore, the determination of the average age of new mothers, which is the main variable of interest in Sect. 4.2. When multiple births occur, only one observation per delivery is kept in our sample to avoid oversampling multiple-birth mothers, who are more likely to be older and/or to have used ARTs.¹⁵

The birth certificate data also contain other potentially relevant socioeconomic variables, such as marital status and maternal education, but the information is not always complete or available throughout the sample period.¹⁶ Thus, for the multivariate analyses in Sect. 4.2, we combine the aggregate state and year level birth certificate information on the age of new mothers with a richer set of socioeconomic characteristics obtained from the March CPS, including race, education, marital and labour market status, wages, and health insurance coverage. Note that controlling for employment-sponsored health insurance coverage is important in this context given that uninsured individuals are not directly affected by the mandates and that most non-elderly insured individuals in the United States obtain insurance through their workplace.¹⁷

Our analysis in Sect. 4.2 could, in principle, be conducted until 2005, when state identifiers become unavailable in the natality files. However, we restrict our sample to the period before 2001 (i.e., from 1972 to 2001) so that Louisiana and New Jersey can be included as controls (these two states passed infertility insurance laws in 2001). Including Louisiana and New Jersey in the treated group would not have provided us with sufficient post-intervention years to analyse the long-term impact of these latest mandates. Moreover, because states were not uniquely identified in the CPS until 1977, the controls from the March CPS are only included from 1977 onwards. The period of analysis, unless otherwise stated, is 1972–2001, inclusively. To further enrich the set of control variables, state-year legal abortion rates by 1000 women aged 15–44 and state of residence obtained from The Guttmacher Institute are included.

Finally, in Sect. 5, we again use data from the June CPS to estimate the effects of the mandates on completed fertility using information for 1979–2000 as well as for the extended period 1979–2008 as a robustness check. Unlike the March CPS data, which is available on a yearly basis and only provides information on the presence of children in the household without discriminating between biological and non-biological children, the June questionnaire is not administered every year but contains information on the number of biological children ever born. In particular, the June CPS provides this information for the following years during our sample period: 1979–1985, 1990–1992, 1994–1995, 1998, and 2000.¹⁸ Additionally, the June CPS contains information on other potential determinants of fertility, such as age, marital status, and labour market status, which we incorporate as controls in the regressions. An important handicap of both the June and March CPS questionnaires for our purposes is that only information about the current state of residence is given and not, for example, information on the birth state of a child.

4 The effect of infertility treatment mandates on the delay of motherhood

In this section, we provide evidence that infertility insurance mandates cause a strategic delay of motherhood. We start in Sect. 4.1 by showing that relatively young women are less likely to have children after the mandates. Although this exercise is similar to Buckles’ (2005), we use more adequate data and a different empirical specification. The premise in Buckles (2005) is that insurance for infertility treatment allows women to postpone motherhood and invest in their careers.¹⁹ Buckles uses the enactments of mandates to cover infertility treatment in several states of the United States during the late 1980s and 1990s as natural experiments and reports that the mandates increased the probability that relatively old women (40–49) would have young children. We refer to this non-strategic response as a short-term compositional effect or as ex-post moral hazard.²⁰ Additionally, Buckles (2005) shows that the mandates reduced the probability that relatively young women (22–26 and 26–30) would have young children. Showing a decrease in the probability of having children while young, however, falls short of proving delay because it fails to consider what these women do when they grow older. Indeed, these women could decide to remain childless. To demonstrate delay, one needs to combine this evidence with evidence of the timing of first-time motherhood, i.e., when (if at all) women decide to become mothers and stop delaying motherhood. This is exactly what we do in Sect. 4.2. The idea is as follows: if young women postpone childbearing because of the mandates, then we should see an increase in the average age at first birth several years after the policies are implemented. We compute the average age of first-time mothers at the state-year level from birth certificate data and show that mandates not only increase the average age in the short-run—consistent with a compositional effect—but, more importantly, that the first motherhood age-gap relative to the counterfactual increases with time since enactment—consistent with a behavioural effect. The counterfactual in this exercise is constructed using the synthetic control method recently developed by Abadie et al. (2010) (henceforth ADH), which exhibits several advantages over the conventional DID estimator. The ADH methodology is explained in Sect. 4.2 in detail.

4.1 The probability of having a first child by 30 and 35 years of age

In this section, we estimate the effect of time since the enactment of a mandate on the probability of having at least one biological child by the ages of 30 and 35 using the June CPS data.

Table 2 presents the estimated marginal effects from probit estimations of the number of years of mandated coverage at age 30 on the probability of having at least one biological child by that age. In all regressions, women are, by definition, older than 30. The first four columns show the marginal effects for all strongly treated states, whereas the last four columns show the marginal effects for IL-MA-RI. Each set of four columns is further split between the effects for ‘all’ women and the effects for ‘whites’ only. Finally, the table presents the results of regressions where the control group is composed of all non-treated states (columns labelled ‘control’) and of regressions where the control group is restricted to the states belonging to the synthetic control group constructed in Sect. 4.2 with the ADH methodology (columns labelled ‘synth’; see the note to Table 2 for a complete list of states in this control group).²¹ Panel A shows the marginal effects when the independent variables of interest are year intervals since enactment by the age of 30, i.e., ‘1–5’ and ‘6–10 years’. Panel B shows the marginal effects when the independent variable of interest is instead expressed as a quadratic polynomial of years since enactment by the age of 30. In a given state and year, the number of years of mandated coverage by 30 varies by women according to age. For example, a woman from Maryland who turned 30 before 1985 had zero years of mandated coverage by 30; a woman from Maryland who turned 30 in 1990 had 5 years of mandated coverage at age 30 but would have had 10 years of mandated coverage by 30 had she turned 30 in 1995. Therefore, the coefficient on the variable ‘1–5 years of mandated coverage at age 30’ is being identified by relatively older women, while the coefficient on the variable ‘6–10 years of mandated coverage at age 30’ is being identified by the younger cohorts. Additionally, note that because states enacted their mandates in different years, the number of years of mandated coverage by a certain age is not collinear with age (e.g., a woman who experienced 5 years of mandated coverage by age 30 in Illinois would be 6 years younger than a woman from Maryland with the same duration of coverage by age 30). A large set of controls are included in all regressions, such as state fixed effects, year fixed effects, educational attainment dummy variables (viz., high school, beyond high school), working status, married status, and age dummy variables in 5-year intervals. Standard errors are clustered at the state level.

Table 2 Marginal effects of infertility insurance mandates on the probability of having at least one child by age 30

The results in Panel A of Table 2 show that having a strong or comprehensive mandate enacted by age 30 for 1–5 years is associated with a higher probability of having at least one child before age 30, and this effect is statistically significant for the strong mandates (‘whites’ sample) and for the comprehensive mandates (both for ‘all’ and for ‘whites’). As noted above, the 1–5 years effect is identified by the relatively older cohorts, who did not act strategically and who increased their fertility due to the mandates. This result, which is consistent with that of Bundorf et al. (2007), is suggestive of a moral hazard effect among relatively fertile couples.²² However, facing a strong or comprehensive mandate by the age of 30 for longer than 6 years is associated with a lower probability of having a biological child by 30. The marginal effects for ‘6–10 years’ are identified by the relatively younger cohorts, and, hence, constitute evidence of strategic delay. The magnitudes of these marginal effects are, as expected, larger for IL-MA-RI and are generally statistically significant. Moreover, the marginal effects are not small in magnitude, as they imply a reduction of 2.9–3.3 percentage points (pp) in the probability of having a child by age 30 for all women (representing a decrease of 4.2–5 % in the average probability of the treated presented at the bottom of Table 2) and between 1.1 and 2.2 pp for white women (or a decrease of 1.7–3.4 % in the average probability of the treated presented at the bottom of Table 2).

The fit obtained with the quadratic polynomial specification (Panel B) is essentially identical to the one obtained in Panel A, as can be observed from the values of the log-likelihood. The marginal effects of the mandates are now consistently negative when evaluated at 5 and 10 years after their enactment and are always statistically significant, except for the strong-mandates ‘all’-women sample. The quadratic specification also delivers more intuitive results; for example, the effect for ‘whites’ is always larger than the effect for ‘all’. The magnitudes of the marginal effects evaluated at 10 years are also quite large, especially for the strong-mandates ‘whites’ sample as well as for the comprehensive mandates.

A general concern with policy evaluation studies based on non-experimental designs is the possibility that such studies are flawed because the adoption of policies is often endogenous. This would be the case if, for example, the enactment of infertility treatment mandates was linked to low fertility or to a systematic pattern of motherhood delay. As briefly explained in Sect. 2, the endogeneity of the infertility treatment mandates is rejected by several authors (Bitler and Schmidt 2012; Hamilton and McManus 2012; Abramowitz 2014). Nonetheless, because our approach and variables are different from theirs, we assess the extent to which endogeneity might be an issue in our own data. Similar to Bitler and Schmidt (2012), we have included leads of the mandate variables in our analysis of the probability of at least one child by age 30. In particular, we have experimented with a linear measure of ‘years to enactment of mandate’ as well as with indicator variables for ‘future mandate’ together with indicator dummies for 1–3 or 1–5 years to the enactment of the mandates (these results are not displayed for the sake of brevity). None of these variables is statistically significantly different from zero.

Finally, Table 3 reports the marginal effects of the probability of having at least one child by age 35. The results displayed show that most marginal effects are not statistically significantly different from zero, indicating that delay is no longer statistically significant by the age of 35.

Table 3 Marginal effects of infertility insurance mandates on the probability of having at least one child by age 35

Our estimations, although similar, offer some advantages over those of Buckles (2005). First, our dependent variable does not suffer from two important shortcomings present in her indicator ‘own children younger than six present in the household’. Her variable, constructed from the March CPS, does not distinguish between biological and non-biological children, and its universe is restricted to children who live in the household. To construct our variable, we use data from the June CPS on biological children ever born. Second, in our case, the relevant number of years since the mandates is measured at age 30, and all women in the sample are, by definition, older than 30. Buckles (2005), uses the number of years since the mandates at the time of the interview in a sample which includes women who were children—as young as 8-year-old—at the time the mandates were enacted. Her linear specification forces the coefficients on the interaction terms between the years since the mandates and age to be close to zero and not significant because a 22-year-old woman who experiences a mandate for 14 years, for example, is hardly more affected than a 22-year-old who has only been under a mandate for 2 years. Unfortunately, our approach comes at a cost: the variable from the June CPS used to construct the dependent variable used in the regressions of Tables 2 and 3 was not recorded beyond 1995, thereby restricting the estimation of the effects of the mandates to the medium run.²³

Using the March CPS proxy ‘age of own eldest child in the household’, which was recorded until 2008, to increase the number of available periods would be unlikely to bias the results for relatively young women (whose children have not yet left the household and whose probability of adoption is smaller), but it would likely bias the results for older women whose eldest child has already left the household. Indeed, the latter could be wrongly classified as having zero children by the ages of 30/35. Moreover, older women are also more likely to have zero years of mandated coverage by 30/35 (the omitted category in the regressions of Panel A). Consequently, using the March CPS data would imply mistakenly assigning less relative fertility by age 30/35 to older women who have had less exposure to the mandates by the age of 30 or 35, causing an upward bias in the estimated effect of the number of years of coverage on the probability of having at least one child by ages 30/35. Buckles (2005) estimates of the probability of the ‘presence of small children in the household’ for older women (Table 4 of her paper) are likely to suffer from this bias.

Table 4 Means of predictors used in synthetic control group estimation for maternal age at first birth

It is important to recognise that the June and March CPS data share a shortcoming due to the lack of information on past states of residence. This limitation would be problematic if women with infertility issues were more likely to travel to mandated states to pay lower prices for infertility treatments. Abramowitz (2014) claims that this is unlikely because interstate migration during 1981–2010 was only 3 %, and mandated states in general had lower immigration than non-mandated states. Finally, some readers may wonder whether the welfare reform enacted in 1996 [the Personal Responsibility and Work Opportunity Act (PRWORA)] affects or biases our results; therefore in the “Appendix”, we explain why it does not.

4.2 Average maternal age at first birth

We begin this part of the analysis by providing some descriptive evidence that broadly characterises the patterns of fertility timing across groups of states and over time. Figure 2a–c plot the evolution of the average age of new mothers in control states versus all treated states, all strongly treated states, and IL-MA-RI (the states with ‘comprehensive coverage’), respectively. The two vertical lines in each figure indicate the years in which the first and last of the corresponding mandates were passed for all of the treated states (1977; 1991), for the strongly treated states (1985; 1991) and for IL-MA-RI (1987; 1991). Although the average age of first-time mothers was higher in treated states than in control states even before any mandate was enacted, Fig. 2b, c show that, for states with ‘strong mandates to cover’ and for IL-MA-RI, the treated-control gap became larger after the passage of the mandates. For example, in 2001, the age gap between IL-MA-RI and the control states was slightly more than 16 months, that is, nearly 4 months longer than in 1991, the year in which the latest strong mandate passed in Illinois.²⁴

Fig. 2

Average maternal age at first birth. All women

More interestingly, from the viewpoint of this paper, the observed increase in the treated-control gap is statistically significant at standard levels of testing, which suggests that the effect of the mandates is larger in the long run than in the short run.²⁵ The observed treated-control gap follows an analogous pattern, and its magnitude is similar, albeit somewhat larger, when the sample is restricted to white mothers.²⁶ It is also worth noting that the increasing trend that we have documented is not so evident when all of the thirteen treated states are considered together (Fig. 2a). The reason lies in the much more limited scope of the ‘weak mandates to cover’ and the ‘mandates to offer’, described in Sect. 2. Interestingly, visual inspection of Fig. 2 indicates that the treated-control gap may have been increasing even before the mandates were enacted, especially for IL-MA-RI. Although this evidence is merely descriptive, it highlights the importance of selecting a control group that successfully mimics the dynamics of the treated states to estimate the true impact of the mandates.

To construct a control group that maximises the similarities between women in treated and control states, we use the synthetic control method (Abadie et al. 2010)²⁷ which benefits from several advantages over the conventional DID estimator. The synthetic control group approach limits the discretion of researchers in the choice of the control units by offering a procedure for the construction of an ‘ideal’ control group denoted as the ‘synthetic’ control group. The synthetic control group uses a weighted average of the potential control units, which provides a better counterpart for the treated units than any single actual control unit or set of actual control units. The weights assigned to each control unit are chosen to minimise the differences in pre-treatment trends and other predictors between the treated unit and the synthetic control group. This estimation procedure is very transparent because it reports the estimated relative contribution, which may be zero, of each control unit to the synthetic group. It is worth noting that, although the synthetic control group approach is obviously related to the standard DID estimator, which it extends, the synthetic control group approach also has features in common with matching estimators insofar as both approaches attempt to minimise observable differences between the treatment and control units. Indeed, some of the latest developments in the literature attempt to minimise the chances of selection into treatment based on unobservables.²⁸ The synthetic control approach is a step in this direction because it relies on more general identifying assumptions than the standard DID model, allowing the effects of unobserved variables on the outcome to vary with time.

To apply the synthetic control group, the birth certificate data on the age of new mothers for the period 1972–2001 must be aggregated at the state and year levels.²⁹ This aggregation is advantageous in our case because it allows us to control for socioeconomic characteristics by merging the aggregated birth certificate data with socioeconomic variables available in the March CPS for the period 1977–2001 (also aggregated at the state and year levels).³⁰ Moreover, births from all strongly treated states are also aggregated as if they belonged to the same state with initial treatment in the year 1985, the year the first strong mandate was enacted. Similarly, we aggregated the data for the subset of comprehensive states (IL-MA-RI) with initial treatment in the year 1987 when the first mandate was enacted in Massachusetts.³¹ The synthetic control group is constructed as the convex combination of control states that are most similar to the states with strong coverage and comprehensive coverage with respect to various socioeconomic predictors as well as lagged values of the average age of first motherhood before treatment (i.e., before 1985 and 1987, respectively). More precisely, the predictors chosen include the following: (1) variables that control for the demographic and family structure of the female population, such as the percentage of new mothers older than 35 and the percentage of married women in the state; (2) variables that control for the state’s race composition, such as percentage of white and black females; (3) variables that control for the education level of the female population, such as the percentage of highly educated women; (4) variables related to the female labour market, such as the participation rate and employment rate, the average logarithm of the hourly wage, and the percentage of women covered by Employment Sponsored Insurance (ESI); (5) variables that control for differences in abortion laws or attitudes, such as the abortion rate per 1000 women by state of residency; and (6) several lags of average age at first birth.³² All of these predictors are averaged over different periods to maximise the fit of the estimation. Although the predictors are roughly the same for the four estimations (strong, strong whites only, IL-MA-RI, IL-MA-RI whites only), the composition of the synthetic control group is not exactly the same. It is always the case, however, that New Jersey is systematically the most important state in the composition of the four synthetic control groups, representing between 26 and 41 %, followed by Minnesota, whose contribution ranges between 11 and 17 % of the estimated synthetic control group.³³

Table 4 presents the pre-treatment (i.e., before 1985) sample averages of all predictors for the states with strong coverage (column 2), as well as for the synthetic control group (column 3), and for the full group of control states (column 4). As shown, prior to the passage of the first strong mandate to cover, new mothers in control states were already younger than in states where strong mandates to cover eventually passed. These mothers also earned lower wages on average and, were less educated, more likely to be married, less likely to have an abortion, less likely to participate in the labour market, less likely to be employed and less likely to have employer-provided health insurance coverage. The predictors’ pre-treatment values for the strongly treated states resemble the pre-treatment values of the synthetic control group (column 3) much more than the pre-treatment values for the full set of control states (column 4 ). Hence, the synthetic control group should be a better counterfactual for the treated groups. Tables for the white sample and for IL-MA-RI are similar but are not reported here in the interest of brevity.

Our synthetic control estimate of the impact of the infertility coverage mandates on the timing of the first child is the difference between the average age of new mothers in states with strong mandates to cover (or the subset of IL-MA-RI) and the synthetic control group at a given date. Panel A of Table 5 shows the estimates for the group of states with strong mandates to cover, whereas Panel B shows the same estimates for IL-MA-RI. The second column reports the synthetic control group estimate in 2001, that is, 16 and 10 years after the first and the last strong mandates were passed, respectively. We refer to this estimate as the long-term effect of the mandates. For the group of states with strong mandates, the long-term effect amounts to 0.266 and 0.317 years, approximately 3.2 months for all women and 3.8 months for white women, respectively. For IL-MA-RI, the effects are larger despite the shorter period since the first mandate: an increase of approximately 4.1–5.4 months in the average age at first child for all and for white new mothers, respectively. The estimated long-term effects of the mandates are considerable—between 15.7 and 18.8 % of the total increase from 1985 to 2001 for the group with strong coverage and between 24.8 and 34.3 % for IL-MA-RI. The synthetic control estimates are slightly smaller than the raw DID aggregate estimate, which amounts to approximately 0.42 years (5 months). The third column of Table 5 shows the root mean squared prediction error (rmspe), which is a measure of the difference in age at first birth between the treated and the synthetic control group during the pre-treatment period. Hence, the lower the rmspe, the better is our counterfactual. The rmspe values, displayed in column 3, are all small, demonstrating the good fit of the models.

Table 5 The long-run impact of strong infertility insurance coverage mandates on the age of new mothers

Inference in the synthetic control estimation method is often non-standard because the number of non-treated units is typically small. However, as ADH argue in both their 2010 and their 2014 papers, “by systematizing the process of estimating the counterfactual of interest, the synthetic control method enables researchers to conduct a wide array of falsification exercises” or “placebo studies” that can be used for inference. We follow this approach and apply the synthetic control method to every potential control state to create distributions of 38 placebo treatment effects and other statistics. ADH recommend using the resulting distribution of the ratio post/pre-intervention rmspe values to construct a p value for this statistic. The p value is constructed by simply calculating the proportion of the estimated placebo ratios of post/pre-intervention rmspe values that are greater than or equal to the ratio for the truly treated states. The idea is that, in the absence of a treatment effect, the ratio of the post/pre-intervention fit should be similar for treated and non-treated units. As the last column in Table 5 shows, the p values for the post/pre-intervention rmspe are all very small, implying the existence of a statistically significant treatment effect for all four samples.

Figure 3 shows the annual average age at first birth in strongly treated states and in IL-MA-RI compared with the synthetic control group counterpart for the sample period (1972–2001) for all women and for white women. The synthetic control group does a good job in tracking the pre-treatment evolution of new mothers’ ages in states with strong coverage and in IL-MA-RI, which indicates we have a good approximation to the counterfactual trend in maternal age at first birth that states with strong or comprehensive coverage would have experienced had the mandates not been enacted. It is worth noting the contrast with the evolution of all non-treated units used in Fig. 2b, c, which has failed to track the treated states’ pattern as closely as the synthetic control group has done. This result is not surprising, given the low rmspe values and the closeness in terms of predictor values between the states with strong coverage and their synthetic version shown in Table 4, for example.

Fig. 3

Average maternal age at first birth: treated vs. synthetic control groups

Fig. 4

Gap between treated and synthetic groups for age at first birth

More important than the size of the estimated long-term effect is its evolution over time, which is shown in Fig. 4. Regressions of the estimated annual effects of the 17 post-treatment periods for the strong mandate states (and the 15 post-treatment periods for IL-MA-RI) on indicators of time since the mandates (i.e., less than 5 years since the mandate, between 6 and 10 years, or more than 10 years), shown in Table 6, confirm that the impact of the mandates grew significantly over time. Figure 4 and Table 6 are crucial because they demonstrate that the long-term cumulative impact of the mandates on the timing of first births extends beyond its short-term non-strategic impact on older women with infertility problems. The increasing impact of the mandates together with the results from Sect. 4.1 constitute evidence of the delay of motherhood. We believe that the mechanism operating here is simple; suppose no supply constraints existed for infertility treatments when the mandates were enacted. If mandates had only a non-strategic effect on older women (i.e., ex-post moral hazard), the estimated effect should therefore be positive but nearly constant over time. The long-term effect may be larger than the short-term effect because, for example, women who were young when the mandates were enacted strategically delay motherhood (i.e., exert ex-ante moral hazard). An alternative explanation for the increasing effect may be that supply constraints for fertility treatments existed when the mandates were enacted but gradually disappeared due to technological improvements and/or price reductions, giving access to a larger number of users of infertility treatments. Our analysis cannot identify the exact contribution of each of these potential explanations to the increasing effect of the mandates.³⁴

Table 6 Evolution of the synthetic control gap in maternal age at first birth. OLS estimates

Table 7 The effect of infertility insurance mandates on the number of biological children

Table 8 The effect of infertility insurance mandates on the number of biological children

Table 9 The effect of infertility insurance mandates on the number of biological children

Table 10 The effect of infertility insurance mandate on the number of biological children

5 The effect of infertility treatment mandates on completed fertility

In the previous section, we presented evidence that infertility treatment mandates induced ex-ante moral hazard leading women to delay motherhood. However, would delaying motherhood necessarily result in a lower number of children per woman? There are at least two elements that may operate in opposite directions. On the one hand, by inducing delay, mandates may negatively affect the total number of pregnancies per woman; on the other hand, the higher probability of multiple births amongst patients of infertility treatments may compensate for any negative effect on the number of deliveries.³⁵ In this section, we estimate the effect of infertility insurance coverage mandates on the total number of biological children per woman.

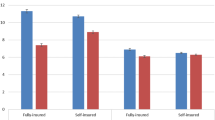
Figure 5 plots the average number of biological children over a woman’s reproductive life for two cohorts (women born between 1949–1952 and between 1954–1957) in the control, strongly treated and comprehensive states (IL-MA-RI) using data from the June CPS.³⁶ When the first strong mandate was enacted in Maryland in 1985, women in the older (younger) cohort were between 33–36 (28–31) years old. The figure shows that women in strongly treated and comprehensively treated states have, on average, a smaller number of biological children and do not catch up with women in the control group by the age of 44. In our estimations below, we account for differences in observable characteristics between treated and control states in two ways. First, we control for covariates that may affect the trends shown in Fig. 5 . Second, we restrict the control group in the estimation to states that have a positive weight in the construction of the synthetic control group of Sect. 4.2.³⁷

Fig. 5

Average number of own biological children for two cohorts in June CPS

We estimate the effects of time passed since the mandates were enacted on the total number of biological children using a zero-inflated Poisson regression for 44-year-old women, i.e., women at the end of their reproductive lives, controlling for individual characteristics.³⁸ Table 7 shows the estimated marginal effects of time since the mandates for sample years 1979–2000 (including Louisiana and New Jersey in the control group as in the previous sections). The first four columns of Table 7 show the marginal effects for all strongly treated states, whereas the last four columns show the marginal effects for IL-MA-RI. Each set of four columns is further split into two groups of results. The first group is obtained from regressions in which the control group is composed of all non-treated states (the first two columns); the second group is obtained from regressions in which the control group is restricted to states used in the construction of the synthetic control group of Sect. 4.2 (the last two columns). The table shows the results for all women and white women separately. Standard errors are clustered at the state level. Finally, the p-values of the Vuong test show that the zero-inflated Poisson model is preferred (in all cases) to the Poisson model.

The relatively large positive impact in the first five years under the mandates, although not statistically significant, plunges to negative values in the following years. None of these effects statistically differs significantly from zero, however, due to their large estimated standard errors. To improve efficiency, we replicate the estimation by extending the sample up to 2008 (see Table 8).³⁹ Consistent with the rest of the paper, when presenting results using data until 2008, we exclude Louisiana and New Jersey from the sample because these states enacted mandates in 2001. Results with the sample years until 2008 remain qualitatively the same, and none of the marginal effects of time since enactment are statistically significant.⁴⁰ $^{,}$ ⁴¹

Conceivably, the large standard errors obtained in Tables 7 and 8 may result from poor specification. We re-estimated the model using polynomials of the years since enactment instead of the time intervals ‘1–5’, ‘6–10’, and ‘more than 10’ used in Tables 7 and 8. Tables 9 and 10 show the results for the quadratic specification. The log-likelihood with the quadratic specification is slightly worse than that obtained with the time intervals, but the values are generally similar. The estimated marginal effects at 5, 10 and 15 years after the mandates are small and statistically insignificant for strongly treated states, with some statistically negative values for IL-MA-RI. Because the quadratic specification has little flexibility to accommodate the ups and downs of the marginal effects within the first few years, we re-estimate the model using a cubic specification, not shown for the sake of brevity. The cubic specification, however, produces marginal effects of the same order of magnitude, where even more terms are statistically negative for the case of IL-MA-RI. Thus far, our results do not show evidence of a positive effect of infertility treatment mandates on total fertility.

Finally, we estimated the effects of years since the mandates on total fertility conditional on being a mother, i.e., we drop the zeros from the estimation. Table 11 shows the marginal effects from a truncated Poisson regression for the sample up to 2000. Not surprisingly, we find that the marginal effects on the intensive margin are smaller in magnitude and also not statistically significantly different from zero.

Overall, the results show no statistically significant effect of either the strong or the comprehensive mandates on completed fertility.

6 Conclusions

In this paper we ask two questions about the impact of infertility treatment insurance coverage on women’s fertility. First, does an increase in the coverage of infertility treatments lead to greater delay of motherhood? Second, does the coverage of infertility treatment increase completed fertility by the end of a woman’s reproductive life? Variation in the timing of the enactment of infertility insurance mandates during the late 1980s and early 1990s across the United States is exploited to answer the two questions.

Table 11 The effect of infertility insurance coverage mandates on the number of biological children conditional on being a mother

We focus our analysis on the effect of ‘strong mandates to cover’, which were passed in six states in the United States (the treatment group): Arkansas (1987), Hawaii (1987), Illinois (1991), Maryland (1985), Massachusetts (1987), and Rhode-Island (1989), as well as on a subset of this group that enacted the most comprehensive mandates (Illinois, Massachusetts, and Rhode-Island). Our analysis uses birth certificate data from the National Vital Statistics, data from the March Annual Social and Economic Supplement of the Current Population Survey (March CPS), and data from the Marriage and Fertility Supplement of the Current Population Survey (June CPS). Our results indicate that, despite the fact that infertility insurance coverage has been shown to increase birth rates among relatively older women as well as the prevalence of multiple births, strong or comprehensive mandates have no statistically significant and positive effect on completed fertility. This is because infertility insurance mandates also appear to delay motherhood among relatively younger women and hence make conception more difficult due to the fact that fecundity decreases with age. In particular, we find evidence in favour of a behavioural response in the form of a delay of motherhood in the states that have enacted strong and comprehensive mandates both through a reduction of the probability of having a child by the age of 30 and through an increasing effect of the mandates on the average age at first birth over time. Therefore, our results suggest that the coverage of infertility treatments, which has been considered a potential policy tool to increase European fertility rates, would not contribute to a long-term increase in fertility.

Appendices

Appendix 1: Could the welfare reform explain our results?

Other potential causes may exist for the growing gap between treated and synthetic states. For example, during the post-treatment years either treated or control states may have enacted laws—e.g. welfare reform—that affected the mean age at first birth. Welfare reform is likely to have discouraged maternity at younger ages through its demanding work requirements and stringent eligibility standards for acceptance into the assistance programs and, therefore, could have increased the mean age at first birth.⁴² The welfare reform was enacted in 1996 [Personal Responsibility and Work Opportunity Act (PRWORA)] and became effective in July 1997, four years before the end of our sample. Before that, however, some states had already introduced work requirements for welfare eligibility in the 1980s and early 1990s (Mead 2004). For the interpretation of our analysis it is important to know the group (treatment, control, or not in the sample) to which these early adopters of welfare reform belong. If some of the treated states were early adopters of welfare reforms, then the present results would likely overestimate the effects of strong infertility treatment mandates on the mean age at first birth. In contrast, if early adopters constitute part of our synthetic group, then the estimated gap in mean age at first birth between treated and synthetic states would be underestimated. Reports show that early adopters [California, Colorado, Iowa, Michigan, Oregon, Wisconsin, and Utah (see Mead 2004)]—with the exception of California (which is neither a treated nor a control state)—are control states and, thus if anything, we should expect a downward bias in our estimates of the effects of the strong infertility treatment mandates on the average age at first birth.

Table 12 Revisions of infertility treatment mandates

Appendix 2: Changes in infertility treatment laws

Four out of the six strongly treated states (Arkansas, Hawaii, Maryland and Massachusetts) revised their mandates during our sample period, i.e. before 2001. Table 12 briefly describes these revisions. The revisions in Arkansas and Maryland reduce coverage and hence would tend to decrease the estimated impact of the original mandates. The 1995 revision in Massachusetts established that the IVF procedures ICSI and ZIFT should be covered. ICSI is a particularly effective IVF procedure in cases of male infertility in which a single sperm is injected directly into an egg. Because this procedure was invented in 1991, it could not have been explicitly contemplated in the original mandate, although the original Massachusetts mandate covered IVF procedures. ICSI accounts for a large percentage of the fresh non-donor eggs or embryos, according to CDC (2001). The usage of ZIFT, however, has been declining gradually and in 2001 it accounted for less than 2 % of ART procedures (CDC 2001). Finally, the Hawaiian revision in 1995 is clearly an expansion of coverage to dependent unmarried individuals. Simple DID estimates of the effect of this revision on the marriage probability of first-time mothers show either no effect or a positive effect for whites.⁴³ Hence, since there is no evidence that the Hawaiian revision decreased the marriage rate in the state, it is unlikely that it had a significant impact on the number of covered users.