Minimum coverage regulation in insurance markets

Abstract

We study the consequences of imposing a minimum coverage in an insurance market where enrollment is mandatory and agents have private information on their true risk type. If the regulation is not too stringent, the equilibrium is separating in which a single insurer monopolizes the high risks while the rest attract the low risks, all at positive profits. Hence individuals, regardless of their type, “subsidize” insurers. If the legislation is sufficiently stringent the equilibrium is pooling, all insurers just break even and low risks subsidize high risks. None of these results require resorting to non-Nash equilibrium notions.

1 Introduction

A widespread regulation in the private health insurance industry is the existence of a minimum standard, which puts a lower bound on the coverage that can be offered to agents in different services. Most states in the US consider legal mandates for health insurance in the individual and small group markets.¹ Importantly, there are large differences in both the number of mandates across states and their estimated cost. Figure 1 depicts these facts and is based on Keating (2011) and Bunce and Wieske (2008).² How stringent the legislation should be is of a great importance since US authorities have to establish the minimum standards nationwide as signed in the federal legislation.

Fig. 1

Mandates and cost heterogeneity across States in the US

As it turns out, this regulation comes at the expense of low risks. Hence it is often accompanied by mandatory enrollment laws, whereby all individuals are forced to pick one of the outstanding contracts in the market. This indeed is the case in Patient Protection and Accountable Care Act of 2010 (PPACA)³ that is in the process of implementation at the time of writing this paper.

One of the arguments for such regulation is the underprovision of coverage for a large segment of the population. This phenomenon can be caused by several reasons,⁴ but here we focus on the presence of asymmetric information between insurers and insurees, an issue that has attracted a great deal of attention for more than thirty years. Since the seminal work of Rothschild and Stiglitz (1976) (henceforth RS), it is well known that when individuals have privileged information on their own health risks, the market will respond by providing a set of contracts, one intended for low risks with low coverage and low premium, and the other contract intended for high risks with full coverage and high premium.

The fact that high risks are forced to pay a high premium is seen as unfair to many analysts and regulators. Hence, many researchers have been devoted to find ways to regulate this market in order to implement some degree of cross-subsidization. An extreme form of such cross-subsidization is present in a pooling equilibrium, where all risks obtain the same coverage at the same premium, regardless of their risk.⁵ RS also showed that no such pooling equilibrium can exist in the absence of regulation, since one of the insurers can profitably deviate by offering a contract with a slightly cheaper premium and lower coverage, which will only attract the low risks. This action is labeled as “cream skimming” (also known as “cherry picking”).

Our aim is to determine whether a minimum coverage legislation (henceforth MCL) can implement some degree of cross-subsidization among different risks. The idea is that undesirable cream skimming deviations might be ruled out through such legislation. As mentioned above, since cross-subsidization comes at the expense of low risks, such legislation is often accompanied by mandatory enrollment laws.

Using the model of RS as a benchmark, we show that the effects of MCL drastically depend on how demanding this regulation is. In a nutshell, our main result is that a weak MCL could bring an unexpected result. Namely, insurers might increase their profits while all types of individuals might be worse off. In other words, a weak MCL may result in individuals subsidizing the insurers rather than low-risks subsidizing high-risks. In contrast, a sufficiently stringent MCL can indeed restore the desired cross-subsidization from low risks to high risks while all insurers make zero profits.

We focus on single contract competition as evidence suggests that it may be difficult for a single insurer to implement a perfect screening menu by itself. We do not claim that single contract competition holds in every market, but that there is evidence for this being an accurate description in some markets. We provide empirical support for this assumption in Sect. 5.

Regarding the relevant literature, the closest paper to ours is by Neudeck and Podczeck (1996) (henceforth NP). They were the first authors to point out that a weak MCL could have perverse effects. However, our analysis and results differ from theirs in several respects. First and foremost, their results are less dramatic than ours. Namely, they focused on an equilibrium where only insurers attracting low risks make positive profits (p. 400), whereas we show existence of an equilibrium where all insurers make positive profits and all individuals are worse-off –even the high risks– as compared to the laissez faire. Second, their result is based on the use of a non-Nash equilibrium notion, namely, Grossman Equilibrium, a point that we return to below, whereas we stick to the Nash concept.⁶ Finally, their prediction on the equilibrium market structure is quite imprecise. Except from exhibiting a separating equilibrium, there is no prediction regarding how many insurers are offering each contract in the separating set. In contrast, we are able to predict a unique market structure that is fully spelled out below.⁷

The comment on NP by Encinosa (2001) also focuses on MCL. Instead of Grossman’s equilibrium notion, he takes two independent routes to restore equilibrium. The first one is to use the so-called Wilson–Miyazaki–Spence (WMS) equilibrium notion.⁸ The second one is to stick to the Nash equilibrium notion but assume that (i) insurers offer contracts in a limited amount (or “capacity”, in his terminology) and that (ii) there is a sufficiently large proportion of high risks in the population.⁹ He concludes that, under both alternatives, there is a menu equilibrium that is second best and where insurers make zero profits. We prefer to stick to the Nash equilibrium notion and not assume any capacity constraints.

Let us now present our results in detail. We make two working assumptions. First, an exogenous number of insurers strictly larger than 2 serve this market.¹⁰ Second, the proportion of low risks is below the threshold for existence in the RS model, which we refer to as the RS threshold. This ensures existence of a laissez faire equilibrium. As in RS, we have a two stage game. In the first stage, insurers offer their contracts simultaneously. In the second stage, individuals choose one of the outstanding contracts in the market. By backward induction, once the optimal choice by individuals among any possible profile of contract offers has been determined, we use the Nash equilibrium notion to find the equilibrium set of contracts. Hence, we do not restrict deviations by an insurer to be robust to further deviations by other insurers.¹¹ Also, unlike Grossman’s notion, we do not allow insurers to withdraw contracts that were previously offered.¹²

In the absence of a binding MCL, the standard separating equilibrium of RS arises. As soon as the MCL becomes binding, there exists an open set of parameter values such that there exists an equilibrium where all insurers make identical strictly positive profits. This equilibrium is still separating and coexists with the equilibrium studied by NP for any given vector of parameter values in the aforementioned open set. In both equilibria, a single insurer, which we name “the scapegoat” for reasons that will become clear below, attracts all the high risks in the population while the rest of insurers “free ride” on the scapegoat to obtain profits at least as large as the scapegoat’s. In the NP equilibrium, the high risks enjoy the same contract as under laissez faire, which in turn coincides with the one that obtains under symmetric information. In the new equilibrium that we find, the high risks enjoy the same coverage as under laissez faire but pay a higher premium. Hence the scapegoat obtains positive profits as well.

In contrast, if the MCL is sufficiently demanding, then a pooling equilibrium, where all insurers offer the same contract, is the only possible equilibrium. In this equilibrium all insurers make zero profits and the desired cross-subsidization from high to low risks is attained. Obviously, as compared to the laissez faire, low risks are worse off and high risks are better off. Notice however that the low risks are always worse-off no matter how stringent the MCL is.

The intuition for the result arising under a weak MCL is the following. The same legislation that impedes cream skimming deviations also has a severe anti-competitive effect. Suppose all free riders make positive profits. A free rider trying to undercut his free-rider rivals can only do so by decreasing his premium, due to the MCL. This breaks separation and the deviation becomes unprofitable. What is new in our analysis is the following additional intuition. Suppose that the scapegoat also enjoys positive profits. Obviously, he is not going to undercut himself. If he tries to undercut the free riders then again separation is broken and the deviation becomes unprofitable. Lastly, we need to ensure that a free rider does not want to undercut the scapegoat. Hence our result that in equilibrium, each free rider obtains no less profits than the scapegoat. This (perhaps) justifies our terminology.

To sum up, our contribution is two fold. First, we are able to sustain the equilibrium studied by NP without having to resort to non-Nash equilibrium notions. Interestingly, this allows us to be much more precise in our prediction of the market structure that will arise. Second, we show that this market structure is compatible with other equilibria where also the insurer serving the high risks makes positive profits.¹³

We have also analyzed a variation of the game described above where a large set of potential insurers, in the first stage of the game, not only choose their contract but also whether to offer a contract at all. If they do offer a contract they must bear some fixed (entry) cost.¹⁴ Hence the number of insurers becomes endogenous. Unfortunately, in such a model, Nash Equilibria in the entry stage never exist under laissez faire. Interestingly, however, introducing a MCL may allow for the existence of such equilibria. The idea is that, as mentioned above, there exists a middle range of MCL where a finite number of insurers obtain positive (variable) profits. This allows these insurers to recover the entry costs and it is possible to sustain an equilibrium that is separating with the structure described above (one scapegoat and at least two free riders).

The paper is organized as follows. In Sect. 2 we introduce the game and the equilibrium notion and we present the benchmark case of RS. In Sect. 3 we solve the game. In Sect. 4 we introduce the game where insurers choose whether to enter or not and sustain equilibria for a range of minimum coverage levels. Section 5 presents empirical evidence supporting our model. Section 6 concludes. Proof of all lemmas and propositions are relegated to the appendix.

2 The model

The model of RS is our benchmark. Suppose a population of risk averse individuals who are identical except in their probability of falling sick that is private information. The probabilities have two possible values: $p_{H}$ and $p_{L}$ with $0<p_{L}<p_{H}<1$ and the subpopulations are named high-risks and low-risks accordingly. The share of the low risk types in the population is public knowledge and denoted by $0<\lambda <1$. Consequently, the average probability $\bar{p}$ is given by $\bar{p}=(1-\lambda )p_{H}+\lambda p_{L}$.

As it is customary in the literature, we use the final wealth representation to derive our results and present figures. Let $s$ and $n$ be the final wealth if the individual is sick and healthy respectively. The expected utility function $V^{i}$ of type $i\in \{L,H\}$ is given by $V^{i}(s,n)=(1-p_{i})U(n)+p_{i}U(s)$ with $U^{\prime }(\cdot )>0$ and $U^{\prime \prime }(\cdot )<0$. The marginal rate of substitution for type $i$ is given by:

$$\begin{aligned} MRS_{i}=\frac{\frac{\partial V^{i}}{\partial n}}{\frac{\partial V^{i}}{\partial s}}=\frac{(1-p_{i})}{p_{i}}\frac{U^{\prime }(n)}{U^{\prime }(s)} \text {.} \end{aligned}$$

A contract $C$ is defined by its coverage $c$ and premium $\widetilde{P}$. The insurer is risk neutral and the expected profit given by a general contract $C$ with a risk-type $i$ individual is $(1-p_{i})\widetilde{P}+p_{i}\left( \widetilde{P}-c\right) =\widetilde{P}-p_{i}c$.

Becoming sick is represented by a loss in wealth $\ell >0$ relative to initial wealth $w>0$. Thus, the future states of the world for an uninsured individual are $n=w$ if remains healthy and $s=w-\ell$ if he becomes sick. We refer to the uninsured situation as the status quo point and is denoted by $A$.

We perform the usual change of variable to express contracts in the space of final wealth $(n,s)$.¹⁵ If an individual has purchased a contract $(\widetilde{P},c)$, his final wealths are either $s=w-\ell -\widetilde{P}+c$ or $n=w-\widetilde{P}$. Notice that these two scenarios are independent of the individual’s risk type.

Using the expressions above, an insurer offering a contract associated to $\left( n,s\right)$ to a type $i$ individual expects to obtain a profit per capita equals to:

$$\begin{aligned} \pi _{i}(n,s)=w-n-p_{i}\left( s-n+\ell \right) \text {.} \end{aligned}$$

(1)

Similarly, an insurer attracting an unbiased mix of both risk types expects to obtain:

$$\begin{aligned} \bar{\pi }(n,s)=w-n-\bar{p}\left( s-n+\ell \right) \!. \end{aligned}$$

(2)

Thus, isoprofits associated to an individual of type $i=L,H$ have slope $ds/dn=-(1-p_{i})/p_{i}$ in the $(n,s)$ space. It is easy to check that the zero isoprofit line goes through status quo point $A$. The zero isoprofits associated to each type are depicted in Fig. 2 as two straight lines.

Fig. 2

The equilibrium under symmetric information

As proven by RS, the equilibrium outcome under symmetric information is given by the contracts $H^{*}$ (for high risks) and $L^{*}$ (for low risks) in Fig. 2, where attracting a single risk-type yields zero profits and contracts are efficient, that is, both contracts offer full insurance ($n_{i}=s_{i}$ for $i=L,H$).

Of course, the high risks would be better off if they could have the contract intended for low risks. This is the basic nature of the adverse selection: some agents have the incentives to hide their type.

As also proven by RS, the only possible equilibrium under asymmetric information has two separating contracts $\left\{ H^{*},L^{RS}\right\}$ being offered in the market. Contract $H^{*}$ has high-premium-high-coverage, intended for the high risk type; while contract $L^{RS}$ has low-premium-low-coverage and is intended for the low risk type. Denote the coverage of the latter contract by $c_{L}^{RS}$.

Formally, the two separating contracts $\left\{ H^{*},L^{RS}\right\}$ are determined by four equations, namely, zero expected profits for insurers offering $L^{RS}$ and for insurers offering $H^{*}$, full insurance at $H^{*}$, and binding incentive compatibility constraint for the high-risks. Mathematically,

$$\begin{aligned}&\displaystyle \pi _{L}\left( n_{L},s_{L}\right) =0\text {;} \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \pi _{H}\left( n_{H},s_{H}\right) =0\text {;} \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle s_{H}=n_{H}\text {;} \end{aligned}$$

(5)

$$\begin{aligned}&\displaystyle V^{H}\left( n_{H},s_{H}\right) =V^{H}\left( n_{L},s_{L}\right) . \end{aligned}$$

(6)

The two contracts are depicted in Fig. 3, where $p_{L}=1/5$ and $p_{H}=4/5$, so the slopes of the corresponding zero isoprofits are $-4$ and $-1/4$ respectively.

Fig. 3

The equilibrium under asymmetric information. Notes: In Definition 1 we characterize a competitive nash equilibrium (CNE). CNE contracts are $\{H^{*}, L^{RS}\}$. The candidate $\{H^{*}, L'\}$ is not an equilibrium even if only Firm 1 offers $H^{*}$ and only 2 firms offer L’. One of the latter gains by deviating to the shaded area

One important insight of RS is that equilibrium does not exist if the proportion of low risks $\lambda$ exceeds a threshold denoted by $\lambda ^{RS}$. The threshold ensures that the indifference curve of the low-risks at $L^{RS}$ does not cross the zero isoprofit line of the fair pooling contracts, which we denote by $\pi ^{P}(\Pi =0)$, where $\Pi$ represents the total profits obtained by an insurer.

2.1 The game and the equilibrium notion

Suppose there are $N$ individuals in this market. The set of insurance providers is exogenously given and denoted by $\Phi =\{1,2,\ldots ,k,\ldots ,M\}$. The only feature that can distinguish two insurers in the eyes of a consumer is the contract it offers (no ex-ante differentiation). The game has two stages. In Stage 1, each insurer $k\in \Phi$ decides which contract, $S_{k}=\left( n_{k},s_{k}\right)$ $\in \mathfrak {R}_{+}^{2}$, to offer. All insurers take this decision simultaneously. Contract offers cannot be withdrawn later on and all individuals choosing a contract must be accepted (open enrollment). Let $\Sigma =\left\{ S_{1},S_{2},\ldots S_{\sigma }\right\}$ be the set of different outstanding contracts. The set of all possible such sets is denoted as $\mathbf {\mathfrak {I}}$. In Stage 2, all consumers observe the set $\Sigma \in \mathbf {\mathfrak {I}}$. Each individual then picks a firm. We make the following assumptions.

Assumption 1

Suppose contracts $\left\{ S_{i_{1}},S_{i_{2}}\ldots ,S_{i_{f}}\right\} \subset \Sigma$ are the best (and therefore indifferent) for individual $I$.¹⁶ Then $I$ will choose a firm offering the contract in $\left\{ S_{i_{1}},S_{i_{2}}\ldots ,S_{i_{f}}\right\}$, say $S_{i^{*}}$, with most coverage.¹⁷

Assumption 2

Suppose $M^{\prime }\le M$ firms offer contract $S_{i^{*}}$ as described in Assumption 1. Then individual $I$ will choose one of these firms randomly. Hence, each of these $M^{\prime }$ firms has a $1/M^{\prime }$ probability of attracting that individual.

Assumption 1 is also implicitly imposed by RS.¹⁸ Assumption 2 is consistent with the absence of ex-ante differentiation.¹⁹ Notice also that firms only care about the profits that a given type of individual brings-in given the contract offered. Therefore, for any given $\Sigma$, it suffices to describe which firm offers which contract and the number of individuals of each type that each firm attracts. We do so by means of a function $g_{\Sigma }:\Phi \rightarrow \Sigma \times \mathbb {N} ^{2}$. This function assigns, to each insurer $k$ in $\Phi$, one of the contracts $S_{k}$ in $\Sigma$ and two natural numbers: the number of individuals of type $L$ and the number of individuals of type $H$ that will accept insurer $k$’s contract. We now introduce our equilibrium concept.

Definition 1

Given any pre-specified set of insurers $\Phi$, we say that the pair $\left\{ \Sigma ^{*},\left\{ g_{\Sigma }\right\} _{\Sigma \in \mathbf {\mathfrak {I}}}\right\}$ constitutes a Competitive Nash Equilibrium (CNE) if

(i):

(Second stage) For every possible set $\Sigma \in \mathbf {\mathfrak {I}}$, function $g_{\Sigma }$ is consistent with individuals choosing one of their best contracts in $\Sigma$ as well as Assumptions 1 and 2.

(ii):

(First stage) Given the best response by individuals for each possible set of contracts, no insurer in $\Phi$, by unilaterally offering a contract $S^{\prime }\not \in \Sigma ^{*}$, can obtain larger profits than in $\left\{ \Sigma ^{*},g_{\Sigma ^{*}}\right\}$.

Notice that we are assuming a compulsory insurance scheme. Thus, we do not include a voluntary participation constraint in our model.

2.2 Recasting RS

We cast the results in RS using our definition. We will incorporate the minimum coverage legislation in Sect. 2.4. Due to the constant returns to scale, the equilibrium can be sustained with $M\ge 3$ number of insurers offering any of the two contracts as long as at least 2 offer contract $L^{RS}$. In our notation, the CNE is given by (i) $\Sigma ^{*}=\left\{ H^{*},L^{RS}\right\}$, (ii) any partition of $\Phi$ into two subsets $\Phi _{L}$ and $\Phi _{H}$ with the only constraints that $\left| \Phi _{L}\right| \ge 2$ and that $\left| \Phi _{H}\right| \ge 1$, and (iii) $g_{\Sigma ^{*}}\left( i\right) =\left( H^{*},0,\frac{\left( 1-\lambda \right) N}{\left| \Phi _{H}\right| }\right)$ for all $i\in \Phi _{H}$ and $g_{\Sigma ^{*}}\left( i\right) =\left( L^{RS},\frac{\lambda N}{\left| \Phi _{L}\right| },0\right)$ for all $i\in \Phi _{L}$. We say that this is an equilibrium with full specialization (Olivella and Vera-Hernandez 2010).

Lets us explain the requirement of three or more insurers ($M\ge 3$) through an example of profitable deviations with two insurers that are ruled out with three insurers and easy to generalize for $M>3$.²⁰ If there are only two insurers ($M=2$), the RS equilibrium is not robust to a deviation by the insurer offering the contract $L^{RS}$. This deviation consists in raising the premium of $L^{RS}$. Incentive compatibility (IC) is preserved (since the low risk IC constraint was slack at $L^{RS}$) and there is no rival also offering $L^{RS}$ to rule out this deviation.

We now show why an equilibrium with positive profits cannot be sustained with $M=3$. Consider for instance the pair of contracts $\left\{ H^{*}, L^{\prime }\right\}$ depicted in Fig. 3. One insurer, say insurer 1, offers contract $H^{*}$ and the rest of insurers offer contract $L^{\prime }$. Then insurer 2 (or 3) could gain through a cream-skimming deviation by offering a contract in the wedge formed by indifference curves $V^{H}\left( H^{*}\right)$ and $V^{L}\left( L^{\prime }\right)$. We emphasize this very standard argument of cream-skimming deviations because this is precisely the deviation that we could rule out in the presence of a minimum coverage regulation. This in turn allows us to sustain equilibria with positive profits. Hence, the same type of legislation has very different effects depending on how restrictive the legislation is: if it is sufficiently stringent it sustains cross-subsidization from the low to the high risk (namely a pooling equilibrium); if it is sufficiently weak it sustains cross-subsidization from all individuals to all insurers.

2.3 General isoprofit lines

To represent equilibria with positive profits, we first identify the corresponding isoprofit line associated to an arbitrary level, say $\Pi \ge 0$, of profits. Obviously, larger profits require a parallel shift downwards relative to the initial zero isoprofit line. As mentioned above, we assume individuals split equally among insurers if attracted by a contract that is offered by more than one insurer. Since isoprofits are depicted in the space of individual contracts, the shift due to raising profits from zero to $\Pi$ will also depend on both the number and mix of individuals accepting the contract. In contrast, we prove below that the slope of the isoprofits only depends on the risk mix.

To ease notation, let

$$\begin{aligned} \alpha =\Pi /N\text {,} \end{aligned}$$

where $N$ is the number of consumers. We label the isoprofit associated to contracts that yield profits $\Pi$ by $\pi ^{Jm}$, where $m$ indicates the number of insurers offering a given set of contracts in the isoprofit and $J\in \left\{ L,H,P\right\}$ indicates the risk-mix of the insurees: low risks only, high risks only, and pooling respectively.

The next lemma establishes the slope and position of strictly positive isoprofits. The position is established using, as a reference point, the contract associated to a positive premium, $\widetilde{P}>0$, but with zero coverage, $c=0$. Hence, $\left( n,s\right) =\left( w-\widetilde{P},w-\widetilde{P}-\ell \right)$. Using the same notation as above, we denote this reference point by $A^{Jm}$. For instance, if a single insurer is attracting all high risks, then the reference point is denoted by $A^{H1}$ and the isoprofit by $\pi ^{H1}$. Notice that if $\Pi$ is set to zero then it implies $\widetilde{P}=0$ and $A^{Jm}=\left( w,w-\ell \right) =A$ for all $J\in \left\{ L,H,P\right\}$ and $m\in \left\{ 1,\ldots ,M\right\}$.

Lemma 1

For any $\Pi >0$, point $A^{JM} \$ is located at a South West (45${{}^o}$) positive distance from the status quo point $A=\left( w,w-\ell \right)$. The distance between $A$ and $A^{Pm}$ is $\alpha m$; the distance between $A$ and $A^{Lm}$ is $\frac{ \alpha m}{\lambda }$; and the distance between $A$ and $A^{Hm}$ is $\frac{\alpha m}{1-\lambda }$. Isoprofit line $\pi ^{Jm}$ has slope $-\frac{1-p_{J}}{p_{J}}$ for $J=\left\{ L,H,P\right\}$ for any $m\in \left\{ 1,\ldots ,M\right\}$.

In general, contract $A^{Pm}$ is always to the North-East of both contract $A^{Hm}$ and contract $A^{Lm}$ for any $m$, because pooling the entire population ensures a larger mass of consumers to attain the same profit. Instead, the relative position of $A^{Hm}$ and $A^{Lm}$ depends on the proportion $\lambda$. To illustrate this, Fig. 4 shows the different isoprofit lines associated to some $\Pi >0$ for a number of insurers $m=\{1,2,3\}$ that are specialized in attracting low-risks. As mentioned, the slopes remain equal to $ds/dn=-(1-p_{L})/p_{L}$. The distances between each isoprofit and the status quo are $\left\{ \alpha /\lambda ,2\alpha /\lambda ,3\alpha /\lambda \right\}$. To provide the full variety of cases, Fig. 5 depicts isoprofit lines for different risk mixes and different numbers of providers for $\lambda =1/3$. Since $\lambda <1/2$, the distance between $A$ and $A^{L1}$ (here, $\frac{\alpha }{1/3}=3\alpha$) is larger than the distance between $A$ and $A^{H1}$ (here, $\frac{\alpha }{1-1/3}=\frac{3}{2} \alpha$).

Fig. 4

Isoprofit lines associated to a fixed positive profit by a contract attracting only $L$-risks, offered by $M=1, 2, \mathrm{and}\,3$ firms

Fig. 5

Isoprofit lines associated to a fixed positive profit under various mix of risk and number of firms $(\lambda =1/3)$

2.4 Minimum coverage regulation

This paper focuses on the consequences of a mandatory minimum coverage in the model, hence we provide the graphical illustration of the region that is restricted due to the regulation.

To fix ideas, suppose first that a regulation sets a fixed coverage $c^{*}$. Only the premium can vary and the feasible contracts can only be in a given 45${^\circ }$ line since changes in premium affect equally both final wealth levels. Notice that under a fully fixed coverage regulation there is no self-selection possible. If two contracts have the same coverage and different premia, only the low premium contract is chosen by the agents.

Consider now that regulation sets a minimum coverage, so that $c\ge c^{*}$. Hence any contract on or above the 45${^\circ }$ limit line is legal. Figure 6 illustrates this situation.

Fig. 6

Coverage regions for a given MCL $c^{*}$

The literature has identified minimum standard regulation with restricting insurers to guarantee a minimum wealth in case of the bad outcome for the Neudeck and Podczeck (1996), Encinosa (2001), Finkelstein (2004). We also studied this alternative regulation and our findings still hold (see Appendix C for details).

3 Solving the game

We first present the separating equilibrium, which arises when MCL is not too stringent. Afterwards we present the pooling equilibrium, which arises when MCL is stringent enough.

3.1 Sustaining a separating equilibrium

Assume a fixed number of insurers, $M\ge 3$, operate in the market. First, we prove a useful lemma, which provides necessary conditions for a separating CNE.

Lemma 2

Under a binding MCL ($c^{*}>c_{L}^{RS}$), any separating pair of contracts $(H,L)$, where $H$ is the contract aimed to attract high risks and $L$ the contract aimed to attract the low risks, is a CNE only if it satisfies the following conditions:

• (i) Contract $H$ offers full coverage.

• (ii) Contract $L$ lies in the intersection between the minimum coverage line and the high risk’s indifference curve through $H$.

• (iii) At least two insurers offer $L$, each one at total profit that we denote by $\Pi _{i}^{L}$.

• (iv) Exactly one insurer (henceforth insurer 1 without loss of generality) offers $H$ at profit that we denote $\Pi ^{H}$.

• (v) $\Pi _{i}^{L}\ge \Pi ^{H}\ge 0$.

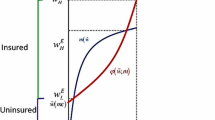
A very important consequence of this Lemma is that equilibrium candidates are parameterized by the premium offered at $H$. Since contract $H$ offers full coverage, its position in the 45${^\circ }$ line is determined by the premium. This also determines per-capita profits derived by insurer 1 at $H$, or $\pi ^{H}$, as well as its total profits $\Pi ^{H}=\left( 1-\lambda \right) N\pi ^{H}$. Hence we state that the equilibrium candidates are parameterized by $\Pi ^{H}$. Once the position of $H$ is given, we find the high-risk indifference curve going through it. This curve, together with the minimum coverage line, gives the exact position of $L$ and also the per capita profits obtained at this contract, $\pi ^{L}$. The total industry profits obtained at $L$ are $\lambda N\pi ^{L}$ which are split among the $\left( M-1\right)$ insurers offering $L$, i.e., $\Pi _{i}^{L}=\lambda N\pi ^{L}/\left( M-1\right)$. Notice that as $\Pi ^{H}$ increases (and $H$ slides down the 45${^\circ }$ line), the corresponding $L$ contract also slides down on the minimum coverage line. This implies that also $\pi ^{L}$ is increasing as $\Pi ^{H}$ increases. Hence there exists a monotonically increasing function $\phi$ that relates insurers’ profits in the following fashion: $\Pi _{i}^{L}=\frac{ \lambda N\phi \left( \Pi ^{H}\right) }{M-1}$. It is easy to see that $\phi \left( 0\right)$ takes a positive value. Indeed, if $\Pi ^{H}=0$ then contract $H$ becomes the same contract as under symmetric information, $H^{*}$. The high risk indifference curve through $H^{*}$ intersects the minimum coverage line (if MCL is binding) to the South West of the contract aimed at low risks under laissez faire, or $L^{RS}$ (the RS separating equilibrium). Since profits are zero at $L^{RS}$, profits at $L$ must be positive. Notice also that $0<\frac{\partial \Pi _{i}^{L}}{ \partial \Pi ^{H}}=\frac{\lambda N\phi ^{\prime }\left( \Pi ^{H}\right) }{M-1 }$ so that, for sufficiently small $\lambda$ and/or sufficiently large $M$, we also have $\frac{\partial \Pi _{i}^{L}}{\partial \Pi ^{H}}<1$. The facts that $\frac{\lambda N\phi \left( 0\right) }{M-1}>0$ and that $\frac{\partial \Pi _{i}^{L}}{\partial \Pi ^{H}}<1$ jointly imply that there exists a unique $\hat{\Pi }^{H}$ such that $\Pi _{i}^{L}=\frac{\lambda N\phi \left( \hat{\Pi } ^{H}\right) }{M-1}=\hat{\Pi }^{H}$, that is, a unique fixed point in the relation between the two profits. A corollary of Lemma 2 then is that the continuum of equilibrium candidates is characterized by $\Pi ^{H}$ in the closed interval $\left[ 0,\hat{\Pi }^{H}\right]$. Higher profits at $H$ cannot be sustained since condition (iv) in Lemma would be violated.

Lemma 2 only provides necessary conditions for existence of a separating equilibrium. We now construct such equilibria for a given MCL. The fact that there may exist separating candidates where profits are positive was already shown by NP, but in the equilibrium they focused on only insurers attracting low risks enjoyed such profits. We show next that in fact it is possible to support an equilibrium where $\Pi _{i}^{L}=\Pi ^{H}=\hat{\Pi }^{H}>0$.

Consider Fig. 7, where we give an example using $\lambda =1/2$, $p_{L}=1/5$ and $p_{H}=4/5$, so that $\bar{p}=\frac{1}{2}\frac{1}{5}+\frac{1 }{2}\frac{4}{5}=\frac{1}{2}$ and the slope of $\pi ^{P1}$ is $\frac{1-\bar{p} }{\bar{p}}=1$.

Fig. 7

The CNE under Minimum Coverage Legislation. Notes: The double arrows denote the continuum of pairs that are candidates for a separating equilibrium

Suppose $M=3$. Consider contracts $H^{1a}$ and $L^{2a}$, where numerical superscripts denote the number of insurers offering that contract. Insurer 1 is offering contract $H^{1a}$ (so we say $M_{H}=1$) at profits $\Pi >0$ while $M_{L}=2$ insurers offer contract $L^{2a}$. As depicted, these insurers also make profits $\Pi$. To see this, notice first that there exists a positive distance $\alpha$ from $A^{P1a}$ to $A$. This distance entails profits per capita equal to $\alpha$ for any contract in the isoprofit $\pi ^{P1}(\Pi >0)$ stemming from $A^{P1a}$ as long it is a pooling monopoly. Hence $\Pi =\alpha N$. Now, $A^{H1a}$ is at twice the distance $\alpha$. Hence profits per capita would be doubled at contracts on the isoprofit $\pi ^{H1a}$stemming from $A^{H1a}$ if all individuals in the economy were high risks and were attracted by the same insurer. However, only half of them are high risks. But they are indeed attracted by insurer 1 only, so insurer 1 makes profits $\Pi$. Finally, notice that $A^{L2a}$ lies at four times the distance $\alpha$. Profits per capita are quadrupled at $\pi ^{L2a}$ but only low risks are attracted (half of the population since $\lambda =1/2$) plus two insurers must share this low risk population. Hence insurers 2 and 3 make profits $\Pi$ as well. This is our fixed point in the relationship between $\Pi _{i\text { }}^{L}$ and $\Pi ^{H}$. Importantly, we have made an assumption on the utility function ensuring that no profitable monopolizing pooling deviations exists. Isoprofit $\pi ^{P1}(\Pi >0)$ does not intersect the low risk indifference curve through $L$ (labeled $V^{L}\left( L\right)$). Notice also that mandatory enrollment is binding for the low risk. If insurance was voluntary, the low risk could preferred to remain uninsured at the initial endowment point $A$.

Let us consider all possible deviations from this CNE candidate. Insurer 1 cannot deviate to any other contract without either loosing all of its clients (here the fact that the high-risk incentive-compatibility constraint is binding becomes crucial), or making less profits, or becoming a pooling monopoly (which we have already shown is unprofitable). Insurers 2 or 3 cannot offer a contract with a higher premium and the same coverage without loosing their clients, since more than one insurer is offering contract $L$ (in other words, the rival disciplines the deviant insurer). If any of these insurers offers a contract with more coverage or lower premia, it attracts all high risks, becoming a pooling monopoly. The only alternative deviation left is that either insurer 2 or insurer 3 undercuts insurer 1, that is, it offers full coverage with a slight lower premium. However, the most that such a deviation can yield is profits $\Pi$, and therefore is not profitable.

The equilibrium studied by NP is given by the pair of contracts $\left( H^{*},L^{2b}\right)$, where $\Pi _{i}^{L}>0$ while $\Pi ^{H}=0$. It is easy to check that it is sustained by the same market structure: insurer 1 offers $H^{*}$ while two insurers offer $L^{2b}$. However, notice that now one can have any arbitrary number of insurers offering $L^{2b}$ since it is always the case that $0=\Pi ^{H}<\Pi _{i}^{L}$ so condition (v) in the lemma is always satisfied. Note that $\Pi _{i}^{L}$ is lower than under the previous CNE, but positive and therefore higher than under laissez-faire. This is the other extreme case in the continua of CNE candidates. To ensure that no profitable pooling deviation exists we have depicted the zero isoprofit line associated to the zero profit pooling contract, which stems from point $A$. Notice that the low risk indifference curve trough $L^{2b}$ does not intersect this isoprofit.

As we did for the RS separating equilibrium (or laissez faire) we now use our definitions to express this result more formally:

Proposition 1

Suppose that $\Phi =\{1,2,3\}$. Under a sufficiently weak MCL it is possible to construct at least two CNE. One is given by $\Sigma ^{*}=\left\{ L^{2a},H^{1a}\right\}$ and $g_{\Sigma ^{*}}\left( 1\right) =\left( H^{1a},0,\left( 1-\lambda \right) N\right)$; $g_{\Sigma ^{*}}\left( 2\right) =g_{\Sigma ^{*}}\left( 3\right) =\left( L^{2a},\frac{\lambda N}{2},0\right)$; where all insurers make the same profits $\Pi >0$. The other equilibrium is given by $\Sigma ^{*}=\left\{ L^{2b},H^{*}\right\}$ and $g_{ \Sigma ^{*} }\left( 1\right) =\left( H^{*},0,\left( 1-\lambda \right) N\right)$; $g_{ \Sigma ^{*} }\left( 2\right) =g_{ \Sigma ^{*} }\left( 3\right) =\left( L^{2b},\frac{\lambda N}{2},0\right)$; where only insurers 2 and 3 make profits $0<\Pi ^{\prime }<\Pi$.²¹ $^{,}$ ²²

Also in Fig. 7 we have depicted the continuum of equilibrium candidates, that is, the pairs of contracts fulfilling the necessary conditions spelled in Lemma 2. They are stressed by two thick double pointed arrows. For each contract in the arrow at the 45${^\circ }$ line, aimed at high risks, the corresponding incentive compatible contract aimed at low risks is found in the arrow at the minimum coverage line. Notice that it is always the case that per insurer profits are larger at the $L$ contract than in the $H$ contract.

This analysis has been carried out for a specific level of minimum coverage. For lower coverage level the analysis remains intact. Also, it does for larger MCL as long as the set contracts $\left( L^{2a},H^{1a}\right)$ associated with the fixed point $\Pi _{i}^{L}\left( \Pi ^{H}\right) =\Pi ^{H}$ satisfies that no profitable pooling deviation exists. This will be the case as long as the minimum coverage is not too high. In the next section we show that for a sufficiently large MCL the unique MCL is a pooling equilibrium.

To conclude, we have shown that a weak MCL could have unintended results in this market. All insurers may obtain positive profits and all risks may be worse off as compared to the laissez faire. Whereas NP already warned that introducing a MCL did not necessarily imply a cross-subsidization from low risks to high risks (in their equilibrium high risks enjoy the same contract as under laissez faire), we point out that the outcome could be even worse: all individual types cross subsidize all insurers. This is the case in the first equilibrium of the two described in Proposition 1. Notice, moreover, that the two equilibria in Proposition 1 are Pareto-ranked for insurers: all insurers prefer the first equilibrium to the second. This stresses our caveat for the combination of minimum coverage and mandatory enrolment legislation: not only redistribution between risks fails to materialize (as we still have a separating equilibrium), but also insurers could coordinate on an equilibrium where both low and high risks are worse-off as compared to laissez-faire.

3.2 Sustaining a pooling equilibrium

Suppose that the MCL is stringent enough so that the crossing between the minimum coverage line and the high risk indifference curve at $H^{*}$, or $V^{H}\left( H^{*}\right)$, lies exactly at the zero pooling isoprofit line. This situation is depicted in Fig. 8. This level of MCL, $c^{*}=c^{P}$, is the lowest mandatory coverage possible consistent with a pooling equilibrium. Notice that the separating candidate $\left( H^{*},L\right)$ is still a CNE as long as at least two insurers offer contract $L$. But all insurers offering $L$ is also a pooling equilibrium. The reason is simple, the usual cream skimming deviations are ruled out by the MCL.

Fig. 8

The Pooling Equilibrium under Minimum Coverage Legislation. Notes: For a MCL at $c^{*} = c^{P}$ there exist two equilibria: one is given by the separating pair of contracts $\{H^{*}, L\}$, the other by pooling contract $\{L\}$. For a MCL at $c^{*} = c' > c^{P}$ , the only equilibrium is given by pooling contract $\{P\}$, since the only separating candidate $\{H^{*}, L'\}$ is not robust to a pooling deviation by Firm 1 in the interior of the segment $PL'$

As the MCL becomes even more stringent, say $c^{*}=c^{\prime }>c^{P}$, the separating candidate (the pair $(H^{*},L^{\prime })$ in Fig. 8) is no longer robust to a pooling deviation, namely a contract in the interior of the segment $PL^{\prime }$, which yields positive profits. In that case the only CNE is the pooling contract (contract $P$ in Fig. 8). In this case the redistributive aim is perfectly fulfilled: high risks are cross subsidized by the low risks and all insurers make zero profits.

4 An entry game

This section extends the model to allow for an endogenous number of insurers. In Stage 1, a large set of potential insurers simultaneously decide whether to enter or not and the contract offered if entering. If an insurer enters he pays a fixed entry cost, denoted by $F>0$ as in Smart (2000). Thus, the set of entrants $\Phi$ becomes endogenous in this game. The rest of the game proceeds as in previous game: individuals choose among the available contracts. Formally, assume that there is large set of potential entrants $\Sigma ^{P}$. Each of these potential entrants chooses an element in $\left\{ \varnothing \right\} \cup \mathfrak {R}_{+}^{2}$, where choosing $\varnothing$ represents the “do not enter” option, and $\left( n,s\right) \in \mathfrak {R}_{+}^{2}$ represents the option “enter with contract $\left( n,s\right)$”. As before, once a potential entrant has decided to enter with a given contract he cannot withdraw that contract and must accept any individual choosing it. We let $\Phi$ be the set of insurers that choose to enter and $\Sigma _{\Phi }=\left\{ S_{i}\right\} _{i\in \Phi }$ be the set of different outstanding contracts in the beginning of stage 2. All possible pairs $\left\{ \Phi ,\Sigma _{\Phi }\right\}$ are in the set $\mathfrak {I}^{E}$. Function $g_{\Sigma _{\Phi }}:\Phi \rightarrow \Sigma _{\Phi }\times \mathbb {N} ^{2}$ assigns, to each insurer $k$ in $\Phi$, one of the contracts $S_{k}$ in $\Sigma _{\Phi }$ and two natural numbers: the number of individuals of type $L$ and the number of individuals of type $H$ that will accept insurer $k$’s contract. We also impose Assumptions 1 and 2 here. We can now give our equilibrium notion.

Definition 2

In the Entry Game, the pair $\left\{ \left\{ \Phi ^{*},\Sigma _{\Phi ^{*}}^{*}\right\} ,\left\{ g_{\Sigma _{\Phi }}\right\} _{\left\{ \Phi ,\Sigma _{\Phi }\right\} \in \mathbf {\mathfrak {I}}^{E}}\right\}$ constitutes an Entry Game Competitive Nash Equilibrium (ENE) if

• (i) (Second stage) For every $\left\{ \Phi ,\Sigma _{\Phi }\right\} \in \mathfrak {I}^{E}$, function $g_{\Sigma _{\Phi }}$ is consistent with individuals choosing one of their best contracts in $\Sigma _{\Phi }$ as well as Assumptions 1 and 2.

• (ii) (First stage) (ii-1) No insurer in $\Phi ^{*}$ expects negative profits in $\left\{ \Phi ^{*},\Sigma _{\Phi ^{*}}^{*}\right\}$ given $g_{\Sigma _{\Phi ^{*}}^{*}}$; (ii-2) no insurer not in $\Phi ^{*}$ expects positive profits by offering a contract $S^{\prime }\in \mathfrak {R}_{+}^{2}$ given $g_{\Sigma ^{\prime }}$, with $\Sigma ^{\prime }=\Sigma _{\left\{ \Phi ^{*}\right\} }^{*}\cup \left\{ S^{\prime }\right\}$; and (ii-3) no insurer $k$ in $\Phi ^{*}$ expects larger profits by offering a contract $S^{\prime \prime }\in \mathfrak {R}_{+}^{2}$ given $g_{\Sigma ^{\prime \prime }}$, with $\Sigma ^{\prime \prime }=\left[ \Sigma _{\left\{ \Phi ^{*}\right\} }^{*}/\left\{ S_{k}^{*}\right\} \right] \cup \left\{ S^{\prime \prime }\right\}$, than in $\left\{ \Phi ^{*},\Sigma _{\Phi ^{*}}^{*}\right\}$ given $g_{\Sigma _{\Phi ^{*}}^{*}}$.

Unfortunately, it can be shown that no ENE exists under laissez faire . A natural way to restore existence of equilibrium would be to assume some degree of market power. However, Bates et al. (2012) found no evidence of market power in the health insurance market. In the theoretical literature some authors have explored certain degree of differentiation between firms. Olivella and Vera-Hernández (2007) and Jack (2006) study product differentiation in markets with adverse selection and competitive screening. However, all of these articles assume horizontal differentiation à la Hotelling with no entry of firms along the linear city. To the best of our knowledge there is no research exploring differentiation with entry à la Salop. Moreover, Mimra and Wambach (2014) in a recent survey of RS models never discuss entry or exit of firms. We think that studying the entry and exit of firms and the existence of ENE under laissez faire is an interesting question but beyond the focus of this paper.

Nevertheless, the MCL can overturn this non-existence result. In fact we have already seen an example. Recall that in Fig. 7 we depicted the equilibrium contract pair $\left( H^{1a},L^{2a}\right)$, where minimum coverage ensures the same (variable) profits $\Pi >0$ for all insurers, and exactly two insurers offer contract $L^{2a}$. If fixed cost is exactly equal to $\Pi$ we have an ENE. We now provide a more complete characterization of such equilibria.

For a given fixed entry cost $F$, the contract aimed at the high risk offers full coverage at a premium that ensures that the only insurer offering it, insurer 1, recovers $F$. Denote the indifference curve by $V^{H}(H^{1})$. The $M-1\ge 2$ other insurers, say insurers $2-i$ with $i=1,\ldots ,M$; attract all the low risks with a contract $L^{2-i}$ satisfying the binding high-risk incentive compatibility constraint, and coverage exactly satisfying the regulation. The actual number of insurers offering that can be sustained in equilibrium and the total profits each insurer makes, which need not be zero, depends on how strict the minimum coverage regulation is.

Figure 9 illustrates the candidate for several positions of the minimum coverage $c^{*}$. The origins of the isoprofits for insurers $2-i,i=1,\ldots ,M$ are given in the Lemma 1.

Fig. 9

The entry game

Given the contract $H^{1}$ and a minimum coverage $c^{*}$ between $c_{1}^{*}$ (included) and $c_{2}^{*}$ (excluded), one insurer finds profitable to specialize in low-risks. Denote by $x$ the intersection between the minimum coverage line and the indifference curve $V^{H}(H^{1}).$ Obviously, $x$ is in segment $L^{1}-L^{2}$ and is an incentive compatible contract intended for low-risks. Importantly, this contract yields positive profits as long as the contract is offered by a single insurer only. If more than one insurer offer $x$, the market will yield losses to all insurers specialized in low-risks.

In the initial case of $c^{*}\in [c_{1}^{*},c_{2}^{*}[$, where a single insurer specialized in low-risks, there are profitable deviations. Basically, for any given contract $x$ that yields zero profits with a single insurer, there is a deviation $x^{\prime }$ along $V^{H}(H^{1})$ that is slightly to the left in segment $L^{1}-L^{2}$ that yield positive profits. Of course, $x^{\prime }$ allows for a potential entrant to undercut and monopolize the market, ruling out the existence of separating equilibrium in this range of minimum coverage.

As minimum coverage increases, there comes a point where two insurers attracting low risks fit in the market. Following the same construction, given a contract $H^{1}$ and a minimum coverage $c^{*}\in [c_{2}^{*},c_{3}^{*}[$, denote by $y$ the intersection between the minimum coverage line and the indifference curve $V^{H}(H^{1})$. Now, the regulation generates enough profits for two insurers offering contract $y$ that falls into the segment $L^{2}-L^{3}$. The reason is that as the minimum coverage increases, the contracts intended for low-risks start making positive profits. Since now two insurers are offering contract $y$, if one of them tries to make additional profits it will either attract high risks or will lose all clients. Note that this competitive effect only exists with two or more active insurers specialized in low-risks. Therefore, the pair of contracts $(H^{1},y)$ is a separating Nash equilibrium.

As the minimum coverage keeps increasing, more insurers could fit into the market, replicating the case above with more insurers, under fixed costs and endogenous entry. However, there is high enough minimum coverage that allows for profitable pooling deviations. In this regard, notice that the parameter configuration in Fig. 9 ensures that the pair $(H^{1},L^{M})$ –$H^{1}$ is not depicted– is robust to pooling deviations (a monopolizing pooling contract must lie above the low risk indifference curve through any of the points in the $H$-risk indifference curve, which implies that they are also above the zero-isoprofit line associated to such deviation).

5 Empirical support

Although this paper is primarily a theoretical contribution, we provide empirical support for our single-contract competition assumption. We also refer to Finkelstein (2004), who find evidence consistent with the predictions of our model.

Regarding the single-contract competition assumption, for markets with available plan-level data we show that (1) insurers specialize in attracting a single risk type (even if they are offering a menu of contracts), and (2) insurers offering a single type of contract are able to survive in the long run. Several hypotheses has been explored in the literature to explain this specialization. First, large costs of bargaining with specialized networks make less attractive to serve all types inducing health providers to switch from hospitals (who serve all risk types) to specialized healthcare centers.²³ Similarly, insurers might also see profitable to specialize in one risk type since bargaining with many specialized providers decrease the profitability of serving all types of risk. Second, the large transaction and screening costs at the insurer level make it less attractive to serve all types, as pointed out by Pauly (2012) who states that “of course managed competition wanted to take risk variation out of the problem, but I strongly suspect, based on page after page in the ACA, that doing so is more trouble than it’s worth”. Third, the screening menu may entail a very asymmetric coverage among customers within the same insurance company, causing a negative perception of the provider by society (McFadden et al. 2012).

(1) Evidence on insurers specializing in a dominant plan serving a single-risk type.²⁴ The first piece of evidence can be found in Bundorf et al. (2012), who study a market where two insurers offer health plans to employees of mid-size firms. Although each insurer is offering a menu of two plans, each insurer attracts a single risk type only. Comparing the characteristics of the two dominant plans and their market shares in Table 1, one concludes that the non-integrated insurer, $N$, serves the riskier employees and the cheaper integrated insurer, $I$, serves the less risky employees, consistent with the observed price gap in fees due to the greater managed-care limitations of insurer $I$ relative to $N$.²⁵

Table 1 Plan enrollment and premia in Bundorf et al. (2012)

The second piece of evidence to support single-contract competition can be found in the prescription drug insurance market, Medicare Part D. Based on data of Decarolis (2015), we find 19 insurers offering just a single contract.²⁶ Moreover, we observe many insurers specialized in one contract type despite of offering multiple contracts. We distinguish basic and enhanced plans that attract different risk types in Medicare Part D following the regulator (CMS) who has defined the two plan types based on the official standard plan.²⁷ A clear and very relevant example of this is shown in Table 2, which reports that United Health Group-one of the largest insurer in the US- has been consistently specialized in basic plans between 2007 and 2012.

Table 2 Medicare Part D specialization of United Health Group, Inc

(2) Evidence on insurers offering a single type of contract are able to survive in the long run. Also in Medicare Part D, we find that 61 insurers specialized in basic plans and 34 insurers specialized in enhanced plans (including large insurance companies like Blue Cross and Blue Shield). This evidence suggests that the business strategy based on specialization is financially sound and that the presence of competitors offering menus has not put the specialized insurers out of the market. ²⁸

Finally, we have found regional markets where most insurers are specialized in a single contract type and non-specialized insurers represent a small market share of the enrollment. Namely, if we consider the Maine and New Hampshire region in 2010 (see Table 3 below) specialized insurers attracted about 95 % of the Medicare Part D enrollees in this region.

Table 3 Medicare Part D specialization in Maine and New Hampshire (2010)

On the empirical literature studying minimum coverage regulations, Finkelstein (2004) focuses on the effects of minimum standards in the Medigap market that took place during the late 70’s. She finds evidence of a substantial decrease in the (voluntary) enrollment, especially for the most vulnerable population. This stress the importance of the assumption on mandatory enrollment in our model.

Finkelstein also finds a change in the nature of equilibrium from separating to pooling equilibrium. Her findings are along the same lines as our model and NP.

6 Conclusions

Using the model of Rothschild and Stiglitz (1976), we have shown that a minimum coverage legislation (MCL) may have undesirable effects on the market. Namely, rather than implementing a desired cross-subsidization among individuals, it may benefit the insurers and make all individuals worse off. This will be that case if the binding MCL is sufficiently weak. For instance, in Obamacare, the minimum coverage is determined by the so called Bronze Plan. Our results imply that, in the context of our model, if this plan is not too demanding then Obamacare could have anti-competitive effects. For sufficiently stringent MCL we recover the desired result: a pooling equilibrium with zero profits becomes the unique equilibrium of the game. In doing this, we have abstained from using non-Nash equilibrium notions and we obtain a much more precise prediction on the market structure arising once the MCL is established.

It remains for further research to build a model of entry that can satisfactorily endogeneize the number of insurers. We have made a small step in this direction by proposing such a game and proving existence of a competitive-Nash equilibrium with entry for some intermediate range for the minimum coverage. Alas, the nonexistence of Nash equilibria under laissez faire impedes any normative judgements on the desirability of the legislation in the entry game proposed.

Appendices

Appendix A: Change of variable

Recall that if an individual has purchased a contract $(\widetilde{P},c)$, his potential wealth outcomes are $s=w-\ell -\widetilde{P}+c$ if sick, and $n=w-\widetilde{P}$ if healthy. Notice that these two equations are independent of type. It is easy to check that these two equations can be expressed as $\widetilde{P}=w-n$ and $c=s-n+\ell$. Denote by $p_{i}$ the risk probability of group $i\in \{H,L\}$ and by $\bar{p}=\lambda p_{L}+(1-\lambda )p_{H}$, the risk probability of the entire population.

An insurer attracting risk type $i$ with contract $\left( \widetilde{P},c\right)$ expects to obtain

$$\begin{aligned} \pi _{i}(\widetilde{P},c)=\widetilde{P}-p_{i}c\text {.} \end{aligned}$$

(7)

Using the previous expression for $c$ and $\widetilde{P}$ we can rewrite the expression for expected profits as a function of final wealth $\left( n,s\right)$ as follows:

$$\begin{aligned} \pi _{i}(n,s)=w-n-p_{i}\left( s-n+\ell \right) \text {.} \end{aligned}$$

(8)

Similarly, for an insurer attracting an unbiased mix of both risks expects to obtain

$$\begin{aligned} \overline{\pi }(\widetilde{P},c)= & {} \lambda \left( \widetilde{P}-p_{L}c\right) +\left( 1-\lambda \right) \left( \widetilde{P}-p_{H}c\right) \nonumber \\= & {} \widetilde{P}-\left( \lambda p_{L}+\left( 1-\lambda \right) p_{H}\right) c=\widetilde{P}-\bar{p}c\text {.} \end{aligned}$$

(9)

That can be expressed as function final wealth as follows:

$$\begin{aligned} \overline{\pi }(n,s)=w-n-\bar{p}\left( s-n+\ell \right) . \end{aligned}$$

Appendix B: Proofs of all Lemmata and Propositions

1.1 Proof of Lemma 1

Proof

Step 1 Change of variable given a contract $\left( \widetilde{P} ,c\right)$. Recall that $s=w-\widetilde{P}-\ell +c$ and that $n=w- \widetilde{P}$. Solving these two equations for $\widetilde{P}$ and $c$ yields

$$\begin{aligned} \widetilde{P}=w-n \end{aligned}$$

(10)

and

$$\begin{aligned} c=s-n+\ell \text {.} \end{aligned}$$

(11)

Step 2. Isoprofits associated to $\Pi >0$

Take a single insurer attracting all individuals of type $H$ with contract $\left( \widetilde{P},c\right)$. The isoprofit is given by $N\left( 1-\lambda \right) \left( \widetilde{P}-p_{H}c\right) =\Pi$. By using $\alpha =\Pi /N$, (10) and (11), we can rewrite the expression as the explicit formula

$$\begin{aligned} s=\frac{w-n\left( 1-p_{H}\right) -p_{H}\ell -\frac{\alpha }{1-\lambda }}{ p_{H}}\text {.} \end{aligned}$$

(12)

Notice that the slope is $\frac{1-p_{H}}{p_{H}}$.²⁹ As for the position of the no-coverage point, we let $c=0$, or using the change of variable, $s-n+\ell =0$, or

$$\begin{aligned} n=s+\ell \text {.} \end{aligned}$$

(13)

Substitute into (12) yields

$$\begin{aligned} s=\frac{w-\left( s+\ell \right) \left( 1-p_{H}\right) -p_{H}\ell -\frac{ \alpha }{1-\lambda }}{p_{H}}\text {,} \end{aligned}$$

(14)

or

$$\begin{aligned} s=w-\ell -\frac{\alpha }{1-\lambda }\text {.} \end{aligned}$$

Replacing into (13) yields

$$\begin{aligned} n=w-\frac{\alpha }{1-\lambda }\text {.} \end{aligned}$$

Take now a single insurer attracting all individuals of type $L$ with contract $\left( \widetilde{P},c\right)$. Then use (12) substituting $1-\lambda$ by $\lambda$ and $p_{H}$ by $p_{L}$:

$$\begin{aligned} s=\frac{w-n\left( 1-p_{L}\right) -p_{L}\ell -\frac{\alpha }{\lambda }}{p_{L}} \text {.} \end{aligned}$$

Notice that the slope is $\left( 1-p_{L}\right) /p_{L}$. As for the position of the No-coverage point: $c=0$, we get $n=w-\frac{\alpha }{\lambda }$ and $s=w-\ell -\frac{\alpha }{\lambda }$. (Notice that if $\lambda =1-\lambda =1/2$ then the no-coverage locus coincide across types. This is used in the figures.)

Take a single insurer attracting all individuals with (pooling) contract $\left( \widetilde{P},c\right)$. Using a similar argument as above, and letting $\bar{p}=\lambda p_{L}+\left( 1-\lambda \right) p_{H}$, the isoprofit line becomes

$$\begin{aligned} s=\frac{w-n\left( 1-\bar{p}\right) -\ell \bar{p}-\alpha }{\bar{p}}\text {,} \end{aligned}$$

where the slope is $\frac{1-\bar{p}}{\bar{p}}$. At zero coverage, the point is given by $n=w-\alpha$ and $s=w-\ell -\alpha .$

Finally, take an $m$-poly attracting low risks. The isoprofit becomes $\frac{N}{m}\lambda \left( \widetilde{P}-p_{L}c\right) =\Pi$. Use $\alpha =\Pi /N$, (10) and (11) to get

$$\begin{aligned} s=\frac{w-n\left( 1-p_{L}\right) -\ell p_{L}-\frac{\alpha m}{\lambda }}{p_{L} }\text {.} \end{aligned}$$

The slope is $\left( 1-p_{L}\right) /p_{L}$ and the No coverage point becomes $n=w-\frac{\alpha m}{\lambda }$, $s=w-\ell -\frac{\alpha m}{\lambda }$.

We compare the status quo point $n=w$, $s=w-\ell$ with each of these no-coverage $\Pi$ isoprofit points to obtain the proposition. $\square$

1.2 Proof of Lemma 2

Proof

We use Fig. 10 to illustrate this result.

Part (i) Take a inefficient contract like $h$ in Fig. 10. Any insurer offering $h$ can deviate to contract $h^{\prime }$ that covers more and costs more but leaves the high risks indifferent, so that IC is preserved. Contract $h^{\prime }$ yields more profits.

Part (ii) The contract aimed at low risks should not be preferred to $H$ by the high risks and also should satisfy the MCL. Therefore, it must lie on or above the minimum coverage line as well as on or above the indifference curve $V^{H}(H)$. Consider first contract $x$ in Fig. 10, which is neither in curve $V^{H}\left( H\right)$ nor in the minimum coverage line. A small deviation in the direction towards the crossing $\ L$ (as indicated by the arrow) will yield almost the same, albeit lower, profits but it will monopolize all low risks and attract no high risks. If $x$ was exactly on either $V^{H}\left( H\right)$ or the minimum coverage line but not in $L$, a small approach towards $L$ will be a profitable deviation for the same reasons.

Fig. 10

Lemma 2

Part (iii) Suppose by contradiction that a single insurer offers $L$. This insurer could raise premium while maintaining the same coverage. This would be legal and preserve separation (since the incentive compatibility constraint for the low risks is slack and the high risks’ one is reinforced) while profits would increase.

Parts (iv) and (v) If no insurer was offering $H$ then $L$ would become a pooling contract. Let us now prove that no more than one insurer can be offering and that $\Pi ^{H}\le \Pi _{i}^{L}$.

Suppose first that $\Pi ^{H}>0$. Suppose by contradiction that two insurers were offering $H$. Then one of them could gain by undercutting the other, that is, by offering a contract slightly cheaper than $H$. This would preserve separation (since the incentive compatibility constraint for the low risks is slack and the high risks’ one is reinforced) and profits would be almost doubled. Suppose by contradiction that $0\le \Pi ^{L}<\Pi ^{H}$ and at least two insurers offer $L$. Then one of these insurers gains by undercutting insurer 1, that is, by offering a contract $H^{\prime }$ that offers the same coverage as $H$ at a slightly lower premium, so that it obtains $\Pi ^{H}-\varepsilon >\Pi ^{L}$. Separation is preserved in this undercutting since the IC of the low risks is slack.

Suppose now that $\Pi ^{H}=0$ . It is obvious that $\Pi ^{L}<0=\Pi ^{H}$ cannot be part of an equilibrium (just let one of the insurers offering $L$ deviate to an arbitrarily expensive premium). Hence $\Pi ^{L}\ge \Pi ^{H}=0$. Suppose that more than one insurer offers $H$. Then one of these insurers would gain by offering instead contract $L$. This would preserve separation and yet this insurer would now make positive profits. $\square$

Appendix C: Minimum net coverage legislation

This appendix shows that the main results are robust to consider the alternative regulation that sets a fixed wealth when sick. Formally, suppose regulation sets a fixed wealth when sick, that is, $s=s^{*}$. Then we can write $s=w-\ell +c-P=s^{*}$. Since $w$ and $\ell$ are exogenous, this defines a one-to-one relationship between premium and coverage given by $c=s^{*}+P+\ell -w$. If an insurer raises $P$ by $x$ dollars, then the coverage must be raised by the same amount. Graphically, this implies the combination of two shifts: a downward South West shift that reflects the increase in premium affecting both states of nature; and an upward shift reflecting the increase in coverage that only takes place in the sick state. Since individual’s final wealth when healthy is $n=w-P$, the previous finding implies $n=w-\left( w-\ell +c-s^{*}\right) =\ell -c+s^{*}$, that is consistent with horizontal changes in the final wealth space, as depicted in Fig. 11. We refer to the horizontal locus associated to $s=s^{*}$ as “the minimum net coverage line at $s^{*}$” (MNCL).³⁰

Fig. 11

Net coverage regions for a given MNCL $s^{*}$. Notes: To preserve a given level of wealth when sick $s^{*}$ after a premium increase $\Delta P$ requires an equal increase in coverage $\Delta c$

The possibility to sustain equilibria where all insurers obtain positive profits also holds under this regulation. In short, the same line of arguments apply. Let us start by showing in Fig. 12 that the equilibrium suggested by NP, where only insurers attracting low risks make positive profits, can also be sustained as a CNE. The equilibrium set of contracts is $(H_{np},L_{np})$. Notice that a insurer offering contract $H_{np}$ attracts high risks only at zero profits. Insurers offering $L_{np}$ only attract low risks and make some positive profits per insuree. Only a single insurer can be offering $H_{np}$, however, given two insurers one of them would have a gain by offering $L_{np}$ instead. The rest of insurers offer contract $L_{np}$. There are no constraints on how many insurers are in the market to sustain this equilibrium. However, to rule out pooling deviations we require (as usual) that the proportion of low risks be small enough. This is ensured in Fig. 12.

Fig. 12

Sustaining equilibrium with positive profits under MNCL. Notes. $(H_{oo}, L_{oo})$ is an equilibrium set of contracts as long as (i) only Firm 1 offers $H_{oo}$; (ii) a number of firms $M_{L} > 2$ offer contract $L_{oo}$; (iii) ML is small enough that each firm offering $L_{oo}$ shares a fraction of total industry profits at $L_{oo}$, which is at least as large as the profits obtained by Firm 1

Let us now show that, as under the same MNCL legislation, other equilibria exist. Take the contract pair $(H_{oo},L_{oo})$ in Fig. 12. Suppose a single insurer, say insurer 1, is offering contract $H_{oo}$ and the rest of insurers offer contract $L_{oo}$. This is an CNE pair of contracts as long as the total profits at each of the insurers offering $L_{oo}$ is at least as large as the profits obtained by insurer 1. This implies that the total number of insurers in the market cannot be too large, as the per-insurer profits at $L_{oo}$ would become too small. In that case one of these insurers would deviate by undercutting insurer 1, that is, by offering a contract slightly cheaper than $H_{oo}$ instead. Notice that the restriction on the proportion of low risks is more stringent than when sustaining NP’s CNE.

Appendix D: Evidence of single contract specialization

The plan-level enrollment data of Medicare Part D is from Decarolis (2015). We focus on the enrollees who choose freely their prescription drug plan. Therefore, we excluded the poor LIS population, and we studied only the proper Part D Prescription Drug Plans (PDP), so we dropped MA plans and all the employer and other special plans (Tables 4, 5, 6).

Table 4 Insurers offering a single contract

Table 5 Insurers specialized in basic plans

Table 6 Insurers specialized in enhanced plans