1 Introduction

How should scarce resources be allocated among claimants? Such problems, in which the available quantity of a perfectly divisible good (or endowment) is not sufficient to satisfy the aggregate claim against the good, are known as claims problems. The formal analysis of these situations, which originates in a seminal paper by O’Neill (1982), proposes a number of well-behaved rules recommending a division of the resources among agents that depends both on the endowment and on the agents’ claims. The term “well-behaved” indicates that these rules may satisfy principles of fairness or other appealing properties. In this context, how can claimants commit to a distribution of resources? How can claimants agree on the properties that must be applied to solve such a problem?

Nowadays, conflicts in which two or more agents cannot decide the allocation have been resolved by a trial. In such cases, a neutral third agent (the mediator) dictates the manner by which the endowment is distributed. This is the philosophy behind mediation, as used in legal, commercial, family and public policy disputes. More precisely, the World Mediation Forum defines mediation “as a process by which a neutral third agent, called a mediator, helps agents in conflict to negotiate a mutually acceptable agreement.”

Accordingly, we analyse the figure of a mediator taking as our starting point claims problems with legitimate principles. To this respect, Giménez-Gómez and Marco-Gil (2014) synthesize earlier work to thoroughly analyse the consequences of enriching the classical model of rationing by adding an additional element, \(\mathcal {P},\) that represents the legitimate principles set. This set consists of a group of some fair axioms or properties that are commonly accepted by the agents, or that are imposed by law and tradition. Nevertheless, fairness hardly leads to a unique commitment: the same claims problem faced by two different agents may lead to the use of two different points of view (Moulin 1988; Schokkaert and Overlaet 1989; Young 1987, among others). Particularly, two natural dual points of view appear in claims problems: awards and losses. In the former case, each agent is worried about “what she receives”, while in the latter one, she cares about “what is not satisfied of her claims”.

In the current approach, mediation combines these two dual points of view with the imposition of fair principles. Specifically, a mediator proposes a way of distributing the endowment, \(F\), among those that satisfy the legitimate principles\(\mathcal {P}\) on which the society has agreed, so that the admissible rules should fulfil \(\mathcal {P}\) and propose an allocation between \(F\) and its dual rule, \(F^{d}.\)

Then, we study the consequences of establishing a warranty in awards (lower bound on awards), and the obligation of incurring minimum losses (lower bound on losses, or, equivalently, an upper bound on awards). The idea of establishing a lower bound on awards can be found in many papers on claims problems (O’Neill 1982; Herrero and Villar 2001, 2002; Moulin 2002; Moreno-Ternero and Villar 2004; Giménez-Gómez and Marco-Gil 2014; Dominguez 2013). In fact, the formal definition of a rule already includes both upper and lower bounds on awards by requiring that no agent receives more than her claim or less than zero. Actually, there are many situations where this warranties appear: bankruptcy law, inheritance, divorce, the universal basic income (Tobin et al. 1967; Noguera 2010). On the other hand, since claims problems can be faced from the point of view of the incurred losses, the notion of an upper bound on awards naturally arises.

From this reasoning, the so-called Double Recursive Process provides a manner to solve claims problems as the recursive application of both:Footnote 1

  • a lower bound, which guarantees that each agent should receive at least the smallest amount recommended by all the admissible allocations; and

  • an upper bound, which limits the awards an agent should receive by the highest amount provided by these allocations.

Our process can be summarized in the following way: Given a claims problem \((E,c),\) a mediator determines a set of legitimate principles\(\mathcal {P}\) and a criterion\(\mathcal {D}\) to choose a particular rule \(F\) that delimits the set of admissible proposals. Accordingly, the agents compute their minimal expected award (that we call F-right) among all admissible proposals; and accept this award. At the same time, they also compute their maximal expected award (that we call F-utopia); and give up any claims greater than their utopia. If there are available resources after distributing the rights, the process continues until the endowment is exhausted. We show that this process ends at the midpoint of the two dual proposals, \(F\) and \(F^{d}\). This result provides a new justification of the average of two extreme and dual ways of distributing the endowment.

The paper is organized as follows: Sect. 2 presents the preliminaries, and Sect. 3 provides our approach. Sections 4 and 5 contain our main definitions and results, respectively. Section 6 applies them to different legitimate principles sets, and Sect. 7 summarizes our final remarks. Finally, the Appendices gather the technical proofs.

2 Preliminaries

Given a set of agents \(N=\{ 1,2, \ldots ,n\} ,\)a claims problem is a pair \((E,c)\in {\mathbb {R}}_{+}\,\times {\mathbb {R}}_{+}^{n}\) such that \(\sum _{i\in N}c_{i}\ge E,\) where \(E\) is the endowment, that represents the quantity of a perfectly divisible good to be allocated to the agents, and for each \(i\in N,\)\(c_{i}\) is the claim that agent \(i\) has on the endowment \(E.\) We will denote by \(C=\sum _{i\in N}c_{i}\) the aggregate claim. \(\mathfrak {B}\) represents the set of all claims problems.

A rule (claims problems solution) is a function, \(\varphi :\mathfrak {B}\rightarrow {\mathbb {R}}_{+}^{n},\) such that for each \((E,c)\in \mathfrak {B},\) satisfies:

  1. 1.

    \(\sum _{i\in N}\varphi _{i}(E,c)=E\) (efficiency); and

  2. 2.

    \(0\le \varphi _{i}(E,c)\le c_{i}, \forall i\in N\) (non-negativity and claim-boundedness).

Following Thomson (2013), in claims problems,no claimant should be asked to pay (non-negativity), no claimant should be awarded more than his claim (claim-boundedness) and the distributions must bebalanced: the sum of the awards should be equal to the endowment (efficiency).

Each claims problem can be faced from two points of view: those of awards and losses. Thus, we have two dual positions depending on whether we are focused on awards or on the unsatisfied demand, \(L=\sum _{i\in N}c_{i}-E\). Given a rule \(\varphi ,\) its dual rule distributes “what is missing” in the same way that \(\varphi \) divides “what is available” (Aumann and Maschler 1985). Formally,

The dualof a rule \(\varphi \), denoted by \(\varphi ^{d},\) is defined by setting for each \((E,c)\in \mathfrak {B}\) and each \(i\in N, \varphi _{i}^{d}(E,c)=c_{i}-\varphi _{i}(L,c).\)

It is straightforward to check that the duality operator is well defined, since for each \((E,c)\in \mathfrak {B}, (L,c)\in \mathfrak {B}\) and if \(\varphi \) satisfies efficiency, non-negativity and claim-boundedness, so does \(\varphi ^{d}\). It is also clear that \((\varphi ^{d})^{d}=\varphi .\)

2.1 Rules

In this paper we will focus on some particular rules: the Proportional, the Constrained Equal Awards, and the Constrained Equal Losses rules.

The Proportional (P) rule recommends a division of the endowment proportionally to the claims: for each \((E,c)\in \mathfrak {B}\) and each \(i\in N,\)

$$\begin{aligned} P_{i}(E,c)=\dfrac{c_{i}}{C}E. \end{aligned}$$

The Constrained Equal Awards (CEA) rule (Maimonides, twelfth century, among others) recommends equal awards to all agents, subject to no one receiving more than her claim: for each \((E,c)\in \mathfrak {B}\) and each \(i\in N,\)

$$\begin{aligned} \textit{CEA}_{i}(E,c)\equiv \min \{c_{i},\mu \}, \end{aligned}$$

where \(\mu \) is chosen so that \(\sum _{i\in N}\min \{ c_{i},\mu \} =E.\)

The Constrained Equal Losses rule (CEL), discussed by Maimonides (Aumann and Maschler 1985), is the dual of the Constrained Equal Awards (Herrero and Villar 2001). Specifically, it chooses the awards vector at which all agents incur equal losses, subject to no one receiving a negative amount: for each \((E,c)\in \mathfrak {B}\) and each \(i\in N,\)

$$\begin{aligned} \textit{CEL}_{i}(E,c)\equiv \max \{ 0,c_{i}-\mu \}, \end{aligned}$$

where \(\mu \) is chosen so that \(\sum _{i\in N}\max \{ 0,c_{i}-\mu \} =E\).

Note that the dual of the Proportional rule is itself (this property is known as self-duality, see Sect. 2.2).

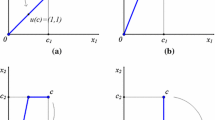
For the sake of facilitate the understanding of the mentioned rules, we provide the graphical representation (in the two agents case) of these rules, and a simple numerical example.

Example 1

Consider now the claims problem \((E,c)=(15,(8,12)).\) Table 1 shows the proposals of the different rules we have introduced.

Table 1 Proposals given by rules, \((E,c)=(15,(8,12))\)
Full size table

In Figs. 1 and 2 we show the path defined by the above mentioned rules. Then, for a given claims problem \((E,c) \in \mathfrak {B}\) with two agents, the proposed solution is obtained where this path intersects the efficient boundary \(x_1 + x_2 = E.\)

Fig. 1
figure 1

The Proportional rule

Full size image
Fig. 2
figure 2

The CEA and CEL rules

Full size image

Note that the more properties are required by a society, the fewer the number of admissible rules.

2.2 Properties

We present in this section some properties on the rules that will be useful in our discussion.

Resource monotonicity (Curiel et al. 1987; Young 1987) demands that if the endowment increases, then all individuals should get at least what they received initially. Note that, no rule violating this property has been proposed in claims problems literature. Otherwise we could have situations where an increment of the endowment would cause some disadvantages to certain agents. This property is stated as follows: for each \((E,c)\in \mathfrak {B}\) and each \( E^{\prime }\in {\mathbb {R}}_{+}\) such that \(C>E^{\prime }>E,\) then, for each \(i\in N,\)

$$\begin{aligned} \varphi _{i}(E^{\prime },c)\ge \varphi _{i}(E,c). \end{aligned}$$

Order preservation (Aumann and Maschler 1985) requires that agents with higher claims should receive, and lose, at least as much as agents with lower claims do: for each \((E,c)\in \mathfrak {B}\), and each \(i,j\in N\), such that \(c_{i}\ge c_{j}\), then

$$\begin{aligned} \varphi _{i}(E,c)\ge \varphi _{j}(E,c),\quad \text {and}\quad c_{i}- \varphi _{i}(E,c)\ge c_{j}- \varphi _{j}(E,c). \end{aligned}$$

Composition up (Moulin 2000) states that if after having distributed the endowment, this increases, then a rule recommends the same if (i) we cancel the initial distribution and apply the rule to the revised problem, or (ii) we let agents keep their initial awards, adjust their claims down by these amounts, and re-apply the rule to allocate the increment of the endowment. For each \((E,c)\in \mathfrak {B},\) each \(E^{\prime }\in {\mathbb {R}}_{+}\) such that \(C>E^{\prime }>E\), then

$$\begin{aligned} \varphi (E^{\prime },c)=\varphi (E,c)+\varphi (E^{\prime }-E,c-\varphi (E,c)). \end{aligned}$$

Self-duality (Aumann and Maschler 1985) demands that a rule recommends the same allocation for a claims problem \((E,c)\) when dividing “what is available” (awards) or “what is missing” (losses). That is, the rule coincides with its dual: for each \((E,c)\!\in \!\mathfrak {B},\)

$$\begin{aligned} \varphi (E,c)= \varphi ^{d}(E,c). \end{aligned}$$

Table 2 summarizes the properties that fulfil the solutions we work on.

Table 2 Properties and rules
Full size table

3 Mediation

Our notion of mediation is given by both a set of properties and an admissible zone that selects some of the rules that satisfy those properties. First, a group of properties are accepted by a particular society (either these properties can be assumed by the agents involved in the problem, or they can be established by law).Footnote 2 Then, among the rules fulfilling these properties, a reference rule \(F\) and its dual rule \(F^d\) delimit the set of proposals that are admissible by a particular mediator. In this sense, mediation involves:

  1. 1.

    a set of legitimate principles (properties) \(\mathcal {P}\);

  2. 2.

    a criterion\(\mathcal {D}\) that selects a reference rule\(F,\) satisfying the properties in \(\mathcal {P};\) and

  3. 3.

    an admissible zone delimited by rule \(F\) and its dual \(F^{d}.\)

In Sect. 6 we propose the Lorenz domination as the criterion to be used in order to select the reference rule \(F.\) So, we consider first a society in which the distribution of the endowment must be based on the selected reference rule, that delimits a set of admissible allocations for a specific mediator. Next, we formally present our model.

Definition 1

A claims problem with mediation is a triplet \((E,c,F),\) wherein \((E,c)\in \mathfrak {B}\), and \(F\) is a fixed rule determined from a set of principles \(\mathcal {P}\) upon which a particular society has agreed. Let \(\mathfrak {B}_{F}\) be the set of all claims problems with mediation.

Then, we identify the mediator with the rule \(F,\) that will delimit the admissible zone. Although \(F\) depends on the set \(\mathcal {P}\) of legitimate principles, and the criterion \(\mathcal {D}\) used, \(F=F(\mathcal {P}, \mathcal {D}),\) we omit this fact in the notation, unless needed. We now formally define the admissible rules for a given mediator.

Definition 2

A rule \(\varphi : \mathfrak {B}\rightarrow \mathbb {R}_{+}^{n}\) is said to be admissible for mediator \(F=F(\mathcal {P}, \mathcal {D})\) if \(\varphi \) satisfies all properties in \(\mathcal {P}\) and for all \(i \in N,\)

$$\begin{aligned} \min \{F_{i}(E,c),F^{d}_{i}(E,c)\}\le \varphi _{i}\left( E,c\right) \le \max \{F_{i}(E,c),F^{d}_{i}(E,c)\}. \end{aligned}$$

Let \(\Phi (F)\) denote the set of admissible rules for mediator \(F.\)

Example 2

(Proportional mediator) Consider a mediator such that she asks the rules to fulfill self-duality and composition-up. In this case, the only rule that satisfies these properties is the Proportional. So that, \(F =P.\) Since this solution is self-dual, \(F = F^{d},\) the only admissible rule is the Proportional one. In this case, the criterion of the mediator determines directly the solution.

Example 3

(Egalitarian mediator) Consider a mediator such that every rule is accepted and assume that the criterion to select one of the rules (see Sect. 6) determines \(F = CEA.\) Then, the admissible rules are those whose proposals for each agent \(i\) are between the values \(CEA_{i}(E,c)\) and \(CEL_{i}(E,c).\)

For instance, if \((E,c) = (15,(8,12))\), the admissible rules consist of the proposals within the set \(\lbrace (a,b) \in {\mathbb {R}}^{2}:a+b =15:5.5 \le a \le 7.5 \rbrace \), see Fig. 2. In this case the distribution of the endowment is undetermined and a process is needed to obtain a solution for the claims problem.

4 The double recursive process

Given the set of admissible rules for mediator \(F,\)\(\Phi (F),\) we can obtain a minimal and a maximal level of awards that each agent should receive on the basis of the ordinary meaning of a guarantee. The maximal level on awards implies a limit on the losses the agent incurs. In this sense, we can associate to every claims problem with mediation two bounds on the awards each agent should receive:

  • the \(F\)-rights value, which is a lower bound on awards that provides each agent the smallest amount recommended to her by all admissible rules (see Giménez-Gómez and Marco-Gil 2014); and

  • the \(F\)-utopia value, which is an upper bound that limits the awards that each agent can receive to the highest amount recommended to her by all admissible rules.

Definition 3

Given \((E,c,F)\in \mathfrak {B}_{F}\), the F-rights value, \(r\), is for each \(i\in N\),

$$\begin{aligned} r_{i}(E,c,F) = \underset{\varphi \in \Phi (F)}{\min }\{ \varphi _{i}(E,c)\}. \end{aligned}$$

Definition 4

Given \((E,c,F)\in \mathfrak {B}_{F}\), the F-utopia value, \(u\), is for each \(i\in N,\)

$$\begin{aligned} u_{i}(E,c,F)=\underset{\varphi \in \Phi (F)}{\max }\{ \varphi _{i}(E,c)\}. \end{aligned}$$

Remark 1

Given a particular claims problem \((E,c)\) the admissible rule that provides the F-rights (F-utopia) for agent \(i,\) could be different from the admissible rule that provides the F-rights (F-utopia) for agent \(j\ne i\).

The F-rights can be understood as the part of the claims that are not disputed (an idea that has been already used in claims problems (see, for instance, Aumann and Maschler 1985)), so that it should be ensured to each agent. Furthermore, assigning to each agent her F-rights (as we have defined it) is compatible with the existing endowment \(E,\) that is \(\sum _{i \in N} r_i \le E\). Moreover, all the admissible rules recommend to each agent at least this amount. As, in general, the sum of the agents’ F-rights does not exhaust the endowment, a recursive process arises in a natural way in order to obtain an efficient allocation: we can allocate her F-rights to any agent, and then proceed again in the new problem defined by the remaining estate (\(E\) minus the allocated amounts), and the claims resulting from subtracting to the initial ones the amount which has already been granted \((c_i - r_i).\) As we will see (Example 5) this process may end up at one of the extremes of the admissible zone, defined by the reference rule \(F\) and its dual.

By applying the idea of guaranteeing a minimum amount on losses rather than awards, we propose truncate the claims by the maximum amount that each agent can expect to receive, the F-utopia. The idea of truncate the claims is not new and, in fact, it is also commonly assumed that the part of the claims that are not feasible should not to be considered in the problem (see, for instance, Aumann and Maschler 1985).

Therefore, we define an iterative process, that we call the Double Recursive Process in which, at any step, each agent receives her F-rights and, at the same time, her claim is truncated by her F-utopia.

Definition 5

The Double Recursive Process, \(DRP\), associates for each \((E,c,F)\in \mathfrak {B}_{F}\) and each \(i\in N,\)

$$\begin{aligned} DRP_{i} (E,c)=\underset{m=1}{\overset{\infty }{\sum }}r_{i}(E^{m},c^{m},F), \end{aligned}$$

where for each step \(m\in {\mathbb {N}}, r_{i}(E^{m},c^{m},F)\) is defined in the following way:

step \(1\), for \(m=1,\) define \((E^{1},c^{1})=(E,c)\) and compute

$$\begin{aligned} r_{i}(E^{1},c^{1},F)&= \underset{\varphi \in \Phi (F)}{\min }\{ \varphi _{i}(E^{1},c^{1})\},\\ u_{i}(E^{1},c^{1},F)&= \underset{\varphi \in \Phi (F)}{\max }\{ \varphi _{i}(E^{1},c^{1})\}. \end{aligned}$$

step \(m\), for \(m\ge 2,\) define

$$\begin{aligned} E^{m}&= E^{m-1} - \underset{i\in N}{\sum } r_{i}(E^{m-1},c^{m-1},F),\\ c_{i}^{m}&= u_{i}(E^{m-1},c^{m-1},F) - r_{i}(E^{m-1},c^{m-1},F), \end{aligned}$$

and compute

$$\begin{aligned} r_{i}(E^{m},c^{m},F)&= \underset{\varphi \in \Phi (F)}{\min }\{ \varphi _{i}(E^{m},c^{m})\},\\ u_{i}(E^{m},c^{m},F)&= \underset{\varphi \in \Phi (F)}{\max }\{\varphi _{i}(E^{m},c^{m})\}. \end{aligned}$$

As shown in Theorem 1 this process completely exhausts the endowment \(E,\) so it provides an efficient allocation. In Example 4 we show this process in a particular claims problem with mediation.

Example 4

Consider the Egalitarian mediator as in Example 3, and the claims problem \((E,c) = (15,(8,12)).\) We know that the reference rule is \(F= CEA,\) so \(F^{d}= CEL\). Then,

  • \(m=1:\) \(E^{1} = 15; \) \(c^{1} = (8,12);\)

    $$\begin{aligned} CEA(E^{1},c^1)&= (7.5,7.5); \quad CEL(E^{1},c^1)= (5.5,9.5);\\ r(E^{1},c^1,F)&= (5.5,7.5);\quad u(E^{1},c^{1},F) = (7.5,9.5). \end{aligned}$$

  • \(m=2:\) \(E^{2} = 2; \) \(c^{2} = (2,2);\)

    $$\begin{aligned} CEA(E^{2},c^2)&= (1,1)=CEL(E^{2},c^2);\\ r(E^{2},c^{2},F)&= (1,1)=u(E^{2},c^{2},F). \end{aligned}$$

  • \(m=3:\) \(E^{3} = 0; \quad c^{3} = (0,0).\)

Therefore, \(DRP(E,c)= (5.5,7.5)+(1,1)=(6.5,8.5).\)

5 Main results

Our first result proves that the Double Recursive Process ends at the midpoint of the allocations provided by \(F\) and \(F^{d}.\)

Theorem 1

For each \((E,c,F)\in \mathfrak {B}_{F}\)

$$\begin{aligned} DRP(E,c)=\frac{F(E,c)+F^{d}(E,c)}{2} \end{aligned}$$

Proof

See Appendix A. \(\square \)

The next theorem establishes that the final allocation provided by the Double Recursive Process corresponds with the average of the F-rights and the F-utopia. The proof is obtained as part of the proof of Theorem 1.

Theorem 2

For each \((E,c,F)\in \mathfrak {B}_{F}\)

$$\begin{aligned} DRP(E,c)= \frac{r(E,c,F) + u(E,c,F)}{2} \end{aligned}$$

Theorem 1 shows that the Double Recursive Process proposes the midpoint between the two rules which represent extreme and opposite ways of sharing awards among claimants. As a consequence, it can be stated that the rationing of the endowment obtained by the recursive double imposition of the F-rights and F-utopia, neither favours nor hurts any particular agent. Following Thomson and Yeh (2008),

“When two rules express opposite points of view on how to solve a bankruptcy problem, it is natural to compromise between them by averaging”.

Note that, from Theorem 1, we obtain that the Double Recursive Process satisfies efficiency, non-negativity and claim-boundedness. Furthermore, the following result shows that it also fulfils self-duality, whatever the legitimate principles set, \(\mathcal {P}\), and the reference rule, \(F\), are.

Proposition 1

For each \((E,c,F)\in \mathfrak {B}_{F}, DRP(E,c)= c-DRP(L,c)\).

Proof

See Appendix B. \(\square \)

In our context of claims problems with mediation, we understand by a process any algorithm that associates to each problem \((E,c,F)\in \mathfrak {B}_{F}\) an allocation satisfying efficiency, non-negativity and claim-boundedness. For instance, apart from our Double Recursive Process, we may define a process that in each step assigns the F-rights value, and solves the residual problem, as shown by next example.

Example 5

Consider the Egalitarian mediator as in Example 3, and the claims problem \((E,c) = (15,(8,12)).\) We know that the reference rule is \(F= CEA,\) so \(F^{d}= CEL\). Then, we define a recursive process \(M_r\) in the following way:

$$\begin{aligned} (M_r)_i = \sum _{m=1}^{\infty } r_i(E^m,c^m,F) \end{aligned}$$

where \(E^m\) is as in Definition 5, and \(c^m = c^{m-1}-r^{m-1}\) for all \(m.\) Then

  • \(m=1:\) \(E^{1} = 15; \) \(c^{1} = (8,12);\)

    $$\begin{aligned} CEA(E^{1},c^1)&= (7.5,7.5); \quad CEL(E^{1},c^1)= (5.5,9.5); \\ r^1&= r(E^{1},c^1,F) = (5.5,7.5). \end{aligned}$$

  • \(m=2:\) \(E^{2} = 2; \) \(c^{2} = (2.5,4.5);\)

    $$\begin{aligned} CEA(E^{2},c^2)&= (1,1); \quad CEL(E^{2},c^2)= (0,2); \\ r^2&= r(E^{2},c^{2},F)= (0,1) \end{aligned}$$

  • \(m=3:\) \(E^{3} = 1; \) \(c^{3} = (2.5,3.5);\)

    $$\begin{aligned} CEA(E^{3},c^3)&= (0.5,0.5); \quad CEL(E^{3},c^3)= (0,1); \\ r^3&= r(E^{3},c^{3},F)= (0,0.5) \end{aligned}$$

  • \(m=k:\)

    $$\begin{aligned} r^k=r(E^{k},c^{k},F)= (0,(1/2)^{k-2}) \end{aligned}$$

Therefore, \(M_r(E,c)= (5.5,9.5),\) that does not coincide with the allocation provided by the Double Recursive Process, \(DRP(E,c)= (6.5,8.5).\)

Now, let us consider the “extra awards” each agent receives from a process, i.e., the amount of awards each agent gets apart from what she has guaranteed, \(r_i(E,c).\) Given that the process we are looking for is self dual, we ask that the extra amount each individual receives after rights should be the same in a problem \((E,c)\) and in its dual problem \((L,c).\) We call this property dual right-egalitarian:

$$\begin{aligned} M_i(E,c) - r_{i}(E,c) = M_i(L,c) - r_i(L,c). \end{aligned}$$

Now, by combining self-duality and dual right-egalitarian, we obtain a characterization of the Double Recursive Process.

Theorem 3

If \(M\) is a process such that for each \((E,c,F)\in \mathfrak {B}_{F},\) satisfies self-duality and dual right-egalitarian, then \(M(E,c) = DRP(E,c)\).

Proof

See Appendix C. \(\square \)

Finally, note that there are some properties that are always satisfied by the result of this process independently of the legitimate principles set, \(\mathcal {P}\), and the reference rule, \(F.\) Among the properties we have introduced in Sect. 2.2, the Double Recursive Process fulfils: resource monotonicity, order preservation and self-duality. Nonetheless, other properties depend on \(\mathcal {P}\) and/or on \(F,\) as the next example shows with respect to the composition-up property.

Example 6

Consider \(F = CEA\) (the Egalitarian mediator) and the problems \((E,c) = ( 100, (80,120) )\) and \((E',c) = ( 120, (80,120)).\) Then,

$$\begin{aligned}&DRP(E,c) = (40,60), \quad DRP(E',c) = (50,70)\\&\text {and} \quad DRP( 20,(40,60) ) = (5,15). \end{aligned}$$

So composition-up is not fulfilled. Now, consider \(F=P\) (the Proportional mediator). In this case, \(DRP\) provides an allocation that always coincides with the proportional one, so it satisfies composition-up.

6 The mediator: reference rules

In Sect. 3 we have introduced the notion of mediation as a specific rule \(F,\) that fulfills a set of legitimate principles, \(\mathcal {P},\) and determines the set of admissible rules. Now, we provide some rationale about the selection of the reference rule, \(F,\) by the mediator. As we have mentioned in Sect. 1, the Lorenz criterion is a usual equity manner of comparing rules (see Thomson 2012; Bosmans and Lauwers 2011). Under some usual conditions, this criterion provides a comparison of rules so that if a rule \(\varphi \)Lorenz dominates a rule \(\psi \), this means that \(\varphi \) favours smaller claimants relative to larger ones. Under such a perspective, the Lorenz maximal rule can be considered as the more equitable one. Then, once the legitimate principles have been defined by society, the Lorenz-optimality can be the criterion the mediator uses to select the reference rule \(F.\) We call this Lorenz mediation, which involves: (1) a set of properties, \(\mathcal {P}\) (legitimate principles); and (2) an admissible zone delimited by the Lorenz maximal rule in \(\mathcal {P}, F = \mathcal {L}\), and its dual rule, \(F^d = \mathcal {L}^d\). Therefore, as a consequence of Theorem 1 we obtain that the Double Recursive Process coincides with the average of the Lorenz maximal and its dual.

Then, by varying the set of legitimate principles, the reference rule may change and so the result of the \(DRP\) process. The following example and results show this fact.Footnote 3

Example 7

Let us consider the following sets of legitimate principles, and the Lorenz-maximal in each one of them:

  • If \(\mathcal {P}_{1}=\){efficiency, claim-boundedness, non-negativity}, \(\mathcal {L} = CEA.\)

  • If \(\mathcal {P}_{2}=\){efficiency, claim-boundedness, non-negativity, composition-up, self-duality}, \(\mathcal {L}=P.\)

Proposition 2

Given a society with legitimate principles \(\mathcal {P},\) such that a Lorenz maximal \(\mathcal {L}\) exists, if \(F=\mathcal {L}\), then for each \((E,c,F)\in \mathfrak {B}_{F}\),

$$\begin{aligned} DRP(E,c)=\frac{\mathcal {L}(E,c) + \mathcal {L}^d(E,c)}{2}. \end{aligned}$$

By applying the result in Proposition 2 to the different sets of legitimate principles introduced in previous example, we obtain the following:

Corollary 1

We consider the sets of legitimate principles defined in Example 7. Then,

  1. (a)

    If \(\mathcal {P}=\mathcal {P}_{1}, \quad DRP(E,c)=\frac{CEA(E,c)+CEL(E,c)}{2}\)

  2. (b)

    If \(\mathcal {P}=\mathcal {P}_{2}, \quad DRP(E,c)=P(E,c)\)

7 Final remarks

In this paper, we have established that the application of a recursive process, in contexts where two dual reference criterion \(F\) and \(F^{d}\) appear, retrieves the midpoint between these two dual positions. This fact, apart from its own logic, allows us to anticipate the result of such negotiations. Moreover, we also find that this process concludes at the midpoint between the F-rights and the F-utopia—that is, the midpoint between the worst and the best position, among the proposals given by the admissible rules.

Two interesting questions remain open. On the one hand, what happens if instead of considering an admissible zone delimited by a reference function, \(F\), and its dual, \(F^d\), we consider that this zone can be delimited by two any reference functions, \(F\) and \(G\), satisfying \(\mathcal {P}\). In this case the admissible rules are those satisfying \(\mathcal {P}\) such that:

$$\begin{aligned} \min \{F_{i}(E,c),G_{i}(E,c)\}\le \varphi _{i}( E,c) \le \max \{F_{i}(E,c),G_{i}(E,c)\}. \end{aligned}$$

The Double Recursive Process may be adapted to this situation merely by changing \(F^d\) by \(G\) in Definition 5. We denote by \(DRP2\) this new process. Next proposition tells us that the result in Theorem 1 remains true if we consider two-agent problems. Nevertheless, we cannot generalize this result to n-agent problems, as shown in Example 8.

Proposition 3

For each two-agent claims problems \((E,c)\in \mathfrak {B}\), and given two any reference rules, \(F\) and \(G\),

$$\begin{aligned} DRP2(E,c)= \frac{F(E,c) + G(E,c)}{2} \end{aligned}$$

Proof

See Appendix D. \(\square \)

Example 8

Consider that the admissible zone is delimited by the Constrained Equal Awards, \(CEA,\) and Proportional, \(P,\) rules. Let us consider the claims problem \((E,c) = ( 100,(50,70,80)).\) Then, we obtain that

$$\begin{aligned} DRP2=\left( 28+\frac{3}{4},34+\frac{7}{12},36+\frac{2}{3}\right) , \end{aligned}$$

which does not coincide with the average of \(CEA(E,c)= (\frac{100}{3},\frac{100}{3},\frac{100}{3}),\) and \(P(E,c) = (25,35,40).\)

On the other hand, as suggested by a referee “sometimes, the lower bound \(r(E,c, F)\) may be considered as too low (or even to high), we would like to impose an adjustedF-right\(r^{\alpha }(E,c,P) = \alpha \cdot r(E,c,F).\)” So, what happens if we consider some speed in the recursive process by means of a parameter \(\alpha \)? This is an interesting question since it seems that some relationship between the end of the recursive process and some convex combination of the rules \(F\) and \(F^{d}\) should exist. Nevertheless, no general relationship is fulfilled.

Finally, in Sect. 6 we have provided a way of selecting the reference rule \(F,\) that coincides with the Lorenz maximal rule in a specific set of legitimate principles. However, there are other possibilities for comparing rules and, so that, defining such a rule (see, for instance, the Rawls criterionRawls 1971). In any case, the Double Recursive Process ends at the midpoint of any two dual reference rules, \(F\) and \(F^d.\)